High-resolution proxies for wood density variations in Terminalia superba

Abstract

Background and Aims

Density is a crucial variable in forest and wood science and is evaluated by a multitude of methods. Direct gravimetric methods are mostly destructive and time-consuming. Therefore, faster and semi- to non-destructive indirect methods have been developed.

Methods

Profiles of wood density variations with a resolution of approx. 50 µm were derived from one-dimensional resistance drillings, two-dimensional neutron scans, and three-dimensional neutron and X-ray scans. All methods were applied on Terminalia superba Engl. & Diels, an African pioneer species which sometimes exhibits a brown heart (limba noir).

Key Results

The use of X-ray tomography combined with a reference material permitted direct estimates of wood density. These X-ray-derived densities overestimated gravimetrically determined densities non-significantly and showed high correlation (linear regression, R² = 0·995). When comparing X-ray densities with the attenuation coefficients of neutron scans and the amplitude of drilling resistance, a significant linear relation was found with the neutron attenuation coefficient (R² = 0·986) yet a weak relation with drilling resistance (R² = 0·243). When density patterns are compared, all three methods are capable of revealing the same trends. Differences are mainly due to the orientation of tree rings and the different characteristics of the indirect methods.

Conclusions

High-resolution X-ray computed tomography is a promising technique for research on wood cores and will be explored further on other temperate and tropical species. Further study on limba noir is necessary to reveal the causes of density variations and to determine how resistance drillings can be further refined.

INTRODUCTION

Density is one of the most important variables in forest and wood science as it is crucial for understanding tree structures and functions, and is relevant for timber properties and energy content of the material. Many of the density variations within a tree can be ascribed to the anatomical structure of wood, such as characteristics of vessels and fibres (Roque and Filho, 2007), while wood density also serves as an indicator of wood quality due to its strong positive correlation with, for example, mechanical strength properties (Nepveu, 1976). Furthermore, reliable models of biomass and carbon content include density measurements (Chave et al., 2005).

The most common, direct method for estimating wood density consists of a gravimetric procedure in which wood samples with clearly defined dimensions are weighed and measured with a vernier calliper (Kollmann, 1951). In this study, sampling with a Pressler borer resulted in wood cores that were easy to weigh. Their volume, however, was difficult to determine due to irregular sample shapes. As such, the gravimetric assessment of wood density is a time-consuming and destructive procedure because wood cores are split into small, irregularly shaped pieces. Each subsample has to be weighed and its volume needs to be measured accurately by water displacement methods or via specialized techniques such as gas pycnometry. Moreover, gravimetry is only suitable for low-resolution assessments of wood density variations (millimetre scale).

There are also numerous indirect methods to estimate wood density. Most of these densitometric methods are based on high-resolution imaging of differences in attenuation of non-visible (short-wavelength) radiation by the objects that are studied. In the following overview, methods were ranked by the dimension of their outputs: one-, two- or three-dimensional information.

Typical one-dimensional (1-D) estimates for density are obtained from tree-ring series in which tree-ring widths are related to density variations (Alvarado et al., 2010), from resistance drillings (Rinn, 1996), the measurement of cell-wall thickness with a transmission light microscope (Decoux et al., 2004) and high-frequency densitometry, which measures relative density variations along wood surfaces using the dielectric properties of wood (Schinker et al., 2003).

Two-dimensional estimates of wood density are typically extracted from radiographies: X-ray (Bergsten et al., 2001; Moya and Filho, 2009) and gamma-ray (Macedo et al., 2002) as ionizing radiation techniques, neutron imaging (Lehmann et al., 2001; Mannes et al., 2007), colour video camera imaging (Clauson and Wilson, 1991), magnetic resonance imaging (Müller et al., 2002) and microwave polarimetry (Kästner and Niemz, 2004). However, the two last methods focus on changes in moisture content for rot detection and the detection of cavities instead of density. Other 2-D density estimates can be generated by thermograms (e.g. infrared thermography) (Wyckhuyse and Maldague, 2001) and acoustics methods (Martinis et al., 2004; Bucur, 2005). But again, these two techniques are related rather with decay diagnosis.

Density studies in three dimensions are possible with X-ray (Entacher and Petutschnigg, 2007; Freyburger et al., 2009; Skog and Oja, 2009), gamma-ray (Macedo et al., 2002) and neutron tomography (Frei et al., 2009). Acoustic reconstruction can also be scaled from two to three dimensions by taking measurements at different heights. Nevertheless, the reconstruction is based on 2-D images that are interpolated over considerable distances (intervals of 50 cm) (Bucur, 2005), gaining rather low-resolution information on the dispersal of decay.

Among the above-mentioned methods, the use of ionizing radiation probably has the longest tradition in the field of research on wood density (Polge and Nicholls, 1972; Lenz et al., 1976; Lindgren, 1991; Lehmann et al., 2001; Bucur, 2005) and the highest resolution, up to sub-micrometre level (Trtik et al., 2007; Van den Bulcke et al., 2009). Both X-ray and neutron imaging are applied in this study, but the equipment is expensive and bound to the laboratory. In particular, the number of neutron imaging beam lines is very low. Therefore, the results of these laboratory methods are compared with resistance drillings, which are obtained with a fast, low-cost, semi-destructive technique that is employable in the field. In addition, all three techniques are compared with standard gravimetrical analysis.

The studied tree species is Terminalia superba Engl. & Diels (commercial name: limba), a pioneer species, characterized by large buttresses and typically found in secondary forests and fallows (Groulez and Wood, 1985). Limba has a very large distribution area (from Sierra Leone to Angola) and is one of the major veneer timber species exported by African timber producers (Lamprecht, 1989). The species also has characteristics that reduce its popularity: the formation of a darker heart in some cases (the so-called limba noir) and heart rot in older trees. From a commercial and ecological point of view, the assessment of a tree and its characteristics before harvesting are important, especially in the tropics, in order to limit the impact on the forest. We consider limba as a model species in which precise information on density fluctuations in the trunk might be relevant to judge the presence of either unwanted heart rot or sought-after heartwood figures. During this study, density in limba trees and wood cores was estimated in order to answer to the following questions: Do microdensitometric profiles assessed by means of high-resolution computed tomography (CT) correspond with gravimetrically obtained data? Do neutron and X-ray densitometric scans produce similar microdensity patterns? Are drilling resistance measurements reliable as a quick estimate of these density variations? Can density variations be related to the presence of brown heart in limba trees?

MATERIALS AND METHODS

Study site

Eleven trees of Terminalia superba Engl. & Diels were sampled at three natural forest sites in western Ivory Coast (6–7°N, 7 – 8°W). The forest of Scio (six trees) can be classified as a primary forest while the forests of Bin Houye (three trees) and Goya (two trees) are young secondary forests, often with cacao plantations in the understorey. All three forest types are classified under the Guineo-Congolian regional centre of endemism by White (1983) as evergreen moist rain forest. Sampling sites were located between 200 and 300 m above sea level. Annual mean temperature is 25°C, with a minimum of 18 °C in January and a maximum of 33°C in February/March. Mean annual rainfall is approx. 1800 mm; during the dry season from November to February/March, monthly rainfall does not exceed 100 mm (Van Oldenborgh and Burgers, 2005). Sampling took place in January 2009, during the dry season. According to FAO (1986), soils in the study areas are classified as Ferralsols and Acrisols, i.e. typical acid soils of tropical lowlands.

Materials

From every sampled tree, one or more stem discs were collected and eight radii from pith to bark were marked at equal distances around the circumference of the discs starting from the north side and following in an anti-clockwise direction. From the 11 trees, 15 radii on 14 stem discs were selected for detailed density measurements. The selected set includes a large distribution of circumferences and ages, and is representative of trees with and without brown heart. Tree characteristics are summarized in Table 1. All discs were air-dried in the laboratory until they reached a moisture content between 12 and 15 % as measured with a wood moisture sensor.

Table 1.

Characteristics of the 15 stem discs used in this study

Tree code*	Circumference of stem disc (m)	Number of rings
B3R2	1·26	16
B5R1	1·67	17
B7·1R4	2·02	41
B7·2R7†	1·69	37
B7·3R7†	1·36	31
G2R3	1·54	24
G8R1	1·37	25
S1R5†	2·29	Unknown
S2·2R5†	2·13	>100
S2·3R1†	1·76	±100
S2·3R8†	1·76	±100
S4R6†	2·22	Unknown
S6R5†	2·04	64
S7R3†	2·04	±100
S8R1	1·80	40

* S = Scio; G = Goya; B = Bin Houye; R = radius; X.1 = stem disc taken just above the buttresses; X.2 = stem disc taken halfway up the stem; X.3 = stem disc taken just under the crown. The number after the forest site indicates the number of the sampled tree, the number after R the sampled radius.

^† Trees with limba noir (brown heart) and/or wood rot.

Drilling resistance measurements

Drilling resistance was measured on air-dried discs (1 year after exploitation) with an IML Resi B-400 resistograph. With this tool, the drilling resistance at the front end of a thin drilling needle (maximum length of 40 cm, diameter of 3 mm) is registered along a trajectory from bark to pith at a resolution of 40 µm. The resistance value is expressed as a percentage, a relative measure of power consumption when the needle penetrates the wood (Rinn, 1996).

Neutron and X-ray scanning

For neutron and X-ray imaging, 15 wood cores with a diameter of 5 mm were extracted from the stem discs with a Pressler corer (Table 1). Cores were taken a maximum of 3 cm away from the resistance drilling. The cores were fixed (but not glued) between two profiled boards to prevent warping. These cores had the same moisture content as the stem discs. No further preparation of the cores was required for neutron and X-ray scans. Extractives were not removed as the difference between bright sapwood and a brown heart was ascribed to their presence (Bauch et al., 1982) and could be the factor distinguishing white from brown coloured limba wood.

Neutron imaging

Two-dimensional radiographs of all wood cores were taken at the neutron imaging beamline NEUTRA at the spallation neutron source SINQ of the Paul Scherrer Institute. For general information on the principles of neutron scanning and details on the sampling parameters, reference is made to the work of Mannes et al. (2007). The wood cores were wrapped in aluminium foil and attached to neutron-sensitive imaging plates that function as detectors. After exposure to the neutron beam, information on the imaging plates was read out and digitized with a dedicated image-plate-reader (Fujifilm BAS-2500) at a resolution of 50 µm per pixel. The resulting images, showing grey levels of neutron beam intensities, were analysed with AIDA software. Within a rectangular frame of 1 mm width and the length of the wood core (drawn in AIDA) the attenuation coefficients (Σ; cm⁻¹) from bark to pith are calculated as follows (neglecting possible spatial variation in intensity):

(1)

where I₀ is the incident intensity of the neutron beam (grey levels outside the sample), I is the weakened intensity of the neutron beam (grey levels inside the sample) and D is the sample thickness (cm). The grey levels outside the sample were obtained by copying the same rectangular frame to the area outside the sample.

A selection of wood cores was also visualized in three dimensions with neutron tomography. Sub-samples of six wood cores, with a maximum height of 8·8 cm, were scanned tomographically with a neutron-sensitive CCD detector at a resolution of 86 µm. The data were reconstructed with the Octopus software package (Vlassenbroeck et al., 2007) and uploaded in MATLAB^® for subsequent image analysis. Straightforward segmentation of air and wood allowed us to calculate mean attenuation coefficients for each slice. The edges of the samples were excluded from analysis. Both 2-D and 3-D neutron scans were examined and compared with the results of 3-D X-ray scans.

X-ray imaging

The CT scanner used in this study was built at the Ghent University Centre for X-ray Tomography (UGCT; http://www.ugct.ugent.be). To obtain a resolution of 50 µm, all cores were scanned with a closed microfocus X-ray tube reaching a spot size of approx. 30 µm. Wood cores were mounted in a custom-made holder made of a reference material with known density (Fig. 1). This material was chosen as its atomic composition and density approach the composition and density of wood cell walls (1·56 g cm⁻³; Kollmann, 1951). By using this material and including the average grey level of air (zero density), grey values of reconstructed wood cores can be directly converted to densities.

Fig. 1.

(A) X-ray scan of the reference material and wood cores: sectioning longitudinally through the holder (2) with two wood cores of limba (3) and air (1) with indication of the travel direction of the frame used for average density calculation. (B) Cross-section through two cores, with the rectangular frame shown as an overlay on the upper core.

Calibration of grey levels into densities was done by applying the following formula:

(2)

where D_i is the absolute density value of voxel i (g cm⁻³), D_holder is the absolute density value of the reference material (1·4 g cm⁻³), G_i is the grey level of voxel i, G_air is the grey level of air and G_holder is the grey level of the reference material.

A fast and automated CT scanning protocol was developed at UGCT (unpublished) for high-throughput 3-D analysis of microdensitometry on wood cores. Helical X-ray scanning reduces the time required to perform a full 3-D scan and volume reconstruction in comparison with classical tomography. The maximum length of a single core that could be scanned in one operation was 16·3 cm. Therefore, some wood cores were split up and the parts were scanned separately. Broken wood cores were orientated correctly and recomposed with glue. Split or broken parts were stitched manually. After scanning and reconstruction, a rectangular window was placed in tangentially orientated slices (i.e. LT-slices, see Fig. 1A, B) and the average grey level within this window was calculated. In addition, the average grey levels of air and of the reference material were also calculated. The average X-ray density of the wood within the window was then transformed to an absolute density value using eqn (1). This results in a 1-D microdensitometric profile based on a 3-D X-ray scan of the wood core.

Gravimetric method

Twenty-one reference samples with a maximum length of 1·6 cm were extracted from three wood cores and their gravimetric density was determined. These reference samples were selected based on the largest possible range of densities observed in the microdensitometric profiles and with respect to their location within the wood core. The gravimetric density is defined as the air-dry weight over the air-dried volume of the reference samples.

The air-dry weight was determined with a laboratory balance (readability of 0·0001 g). The air-dried volume of the reference samples is determined with a sliding calliper as a first approximation (volume of a cylinder) and on 3-D X-ray scans of the samples with a resolution of 25 µm (cone beam). For this volume measurement, reference samples were again mounted in a holder made of the chosen reference material to determine the density profile at the same time. These small cylindrical samples were extracted from the reconstructed dataset manually and air and wood were segmented based on greyscale thresholding. The volume of each cylindrical sample was then calculated based on a binarized and mathematically filled version of the sample.

Data analysis

On the reference samples, mean density values from the X-ray scans are compared with the gravimetric results (ANOVA, SPSS 16·0). The results of this analysis also allow us to evaluate the reference material. Linear regressions between the gravimetric densities, mean X-ray-derived densities, mean neutron attenuation coefficients and mean drilling resistance values are tested in SPSS 16·0. Next, the complete profiles are interpolated with MATLAB^® to a resolution of 50 µm, i.e. to the resolution of the density profiles obtained with the X-ray scans. The correlation between the different indirect methods is analysed with TSAP-Win Scientific™ 4·64, a program for the measurement and analysis of tree-ring data. Within the module Cross date, the different profiles are shifted until they reach the best fit based on the t-value of Baillie-Pilcher (TV_BP) and the cross-correlation (% CC). In general, significant values for these two statistical parameters are fixed at 3·0 for TV_BP and 60 for % CC (Rinn, 2003). Complementary visual control is indispensable and can overrule the statistical results. For all samples, the presence and location of a brown heart is known. The density values inside and outside the border of this brown heart have been examined for trends and the location of peak densities and tree ring borders has been determined.

RESULTS

Gravimetric method versus indirect methods

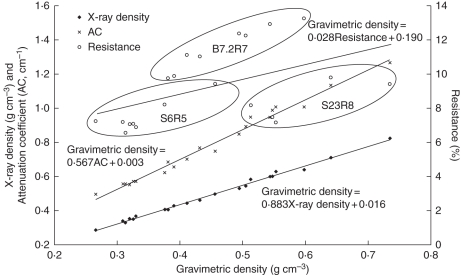
Gravimetric densities and densities resulting from the X-ray scans on 21 reference samples showed a normal distribution, were homoscedastic (P < 0·05) and did not differ significantly (P = 0·31). The linear relationship between gravimetric (X-ray volume-based) and X-ray-derived density was positive and highly significant (R² = 0·995; P < 0·01). Densities derived from X-ray scans overestimated the gravimetric density by 9 % on average, based on manually segmented volumes in X-ray images (Fig. 2), whereas this was only 6 % for volumes determined with a sliding calliper. Highly significant positive relationships (P < 0·01) were also found between the gravimetric density and the attenuation coefficients of 2-D neutron scans (R² = 0·986). Only drilling resistance was not directly related to the gravimetric density for the reference samples (R² = 0·243).

Fig. 2.

Gravimetric density and relationship with mean density of X-ray scans, mean 2-D attenuation coefficients of neutron scans and mean resistance of drillings on 21 reference samples. The relationship between gravimetric and X-ray density is linear, as is the relationship for gravimetric density and neutron attenuation, but the relationship between drilling resistance and gravimetric density is rather weak.

The mean X-ray-derived density (mean of all wood cores) was 0·55 ± 0·07 g cm⁻³, which is in agreement with the air-dry density mentioned in the wood density database of the World Agroforestry Centre (0·48–0·65 g cm⁻³; http://www.worldagroforestrycentre.org/sea/Products/AFDbases/WD/).

Attenuation coefficients based on 2-D or 3-D neutron imaging

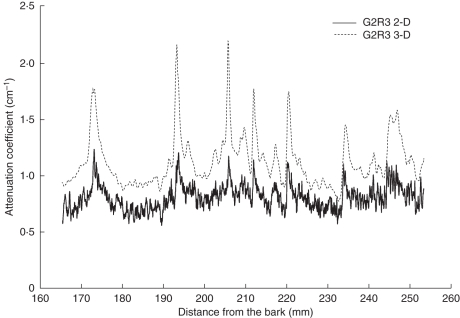
Visual control (Fig. 3) of the fits by TSAP-Win revealed similar trends inside the 2-D- and 3-D-based profiles of attenuation coefficients of all six samples, except for S2·2R5 and S2·3R8. This was also reflected by the lower cross-correlation obtained for these two samples (Table 2).

Fig. 3.

Overlay of a 3-D- and a 2-D-based profile of attenuation coefficients for sample G2R3. The solid line represents a profile based on 2-D scans; the dotted line is based on 3-D scans. The 3-D profiles show less fluctuation.

Table 2.

Cross-correlation (% CC) and t-value of Baillie–Pilcher (TV_BP) for the profiles of attenuation coefficients based on 2-D and 3-D neutron scans (both profiles have the same length, max. 8·8 cm)

Tree code	% CC	TV_BP
G2R3	78*	7·2*
S2·2R5†	44	7·2*
S2·3R8†	12	7·3*
S4R6†	88*	16·7*
S6R5†	89*	4·1*
S8R1	79*	3·0*

Significant values (P > 0·05) are marked with an asterisk.

^† Trees with limba noir (brown heart) and/or wood rot.

Mean attenuation coefficients for all six profiles based on 3-D scans were 19 % (S2·2R5) to 74 % (S2·3R8) higher than those of profiles based on 2-D scans. Profiles based on 3-D scans also showed less fluctuation.

A potential disadvantage is the shift within 2-D- and 3-D-based profiles. Figure 3 reveals coincident peaks at the start of the 3-D profile but shifts to the right (from 20 cm onward) compared with the 2-D profile.

Comparison of estimated density profiles with X-ray scans, neutron scans and drilling resistance

Although the statistical parameters used to assess similarity between X-ray densities and 2-D attenuation coefficients were not always significant (Table 3, Fig. 4), 13 of 15 samples were visually matched. Only two cores were rejected: G2R3 because of an irregular shift between peak densities and peak attenuation coefficients and G8R1 because of a diagonal crack that caused a large gap between densities and attenuation coefficients which could not be stitched manually. However, 3-D attenuation coefficients and X-ray densities all showed sufficient statistical and/or visual agreements.

Table 3.

TSAP parameters of X-ray, neutron and resistance drilling profiles

	X-ray – neutron		X-ray – resistance		Neutron – resistance
Tree code	% CC	TV_BP	% CC	TV_BP	% CC	TV_BP
B3R2	52*	3·0	32**	2·0**	2**	8·5
B5R1	73	3·2	42*	6·2	54**	11·2
B7·1R4	83	3·0	85	17·6	76	16·0
B7·2R7†	76	3·1	71	4·4	67	8·1
B7·3R7†	72	2·3*	66	7·0	60	6·0
G2R3	41**	1·7**	−3	1·4**	–6**	5·6
G8R1	47**	2·0**	18	13·1	32**	5·7
S1R5†	46*	2·1*	22*	1·6*	15*	4·1
S2·2R5†	68	4·3	48**	4·6	47*	10·5
S2·3R1†	65	4·6	62	2·9*	50*	5·2
S2·3R8†	59*	4·0	22*	7·5	29**	9·2
S4R6†	69	5·1	24*	8·1	27**	8·1
S6R5†	78	2·7*	71	9·6	65	7·3
S7R3†	76	3·6	55*	3·4	53**	9·3
S8R1	70	2·5*	63	6·0	62	7·6

% CC, cross-correlation; TV_BP, t-value of Baillie–Pilcher.

* Values too low according to TSAP measures but visually OK; ** values too low according to TSAP measures and visually not OK.

^† Trees with limba noir (brown heart) and/or wood rot.

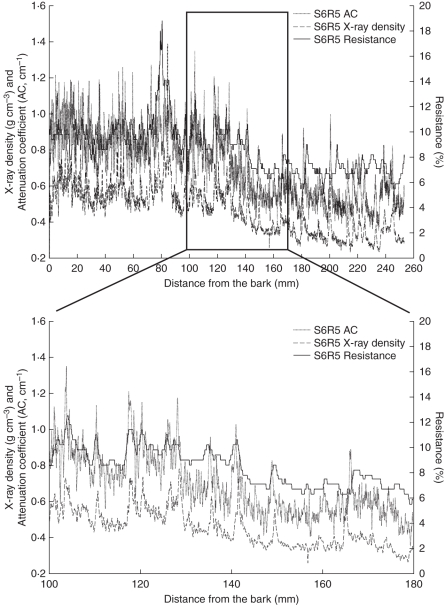
Fig. 4.

Overlay of X-ray densities, neutron attenuation coefficients and resistance drillings on a limba noir (S6R5) sample. The box is expanded to visualize details as the shift in peaks of the different methods (from 15 cm onwards, larger shifts become visible). The large peak at 8 cm indicates the boundary between white and dark limba wood.

X-ray density and resistance drilling profiles corresponded rather well, if the problem of shifts in peaks was accounted for. After visual and statistical control, only B3R2, G2R3 and G8R1 were insufficiently matching.

Although t-values were significant for all comparisons between attenuation profiles of 2-D scans and resistance drillings, only five of 15 samples were significantly cross-correlated. After visual control, half of the samples showed an acceptable agreement between resistance drillings and 2-D neutron scans. When comparing the 3-D scans of sub-samples with the corresponding section cut from the drilling resistance profile, a similar pattern was observed: all t-values were significant while only two of six samples (S6R5 and S8R1) were significantly cross-correlated (visual control revealed no other options).

DISCUSSION

Microdensitometric analysis of wood cores is a valuable method resulting in important information related to, among others, tree physiology, wood anatomy and wood technology. Three techniques were investigated in this paper and compared with classical gravimetry of smaller sub-samples with a large range of densities.

Gravimetric method versus indirect methods

The results here confirm the high correlation between X-ray density and gravimetric density (Fig. 2), yet gravimetric density is overestimated by approx. 9 %. This is possibly due to the composition of the reference material not being 100 % comparable with that of wood as reported in the literature (due to the presence of mineral compounds in wood; limba has prismatic calcium crystal inclusions) and the gravimetric density being measured on supposedly perfect cylinders whereas the X-ray-derived density is measured on the central part of the cylinder, avoiding the edges and preventing the incorporation of mixed air–wood voxels. Application of a linear correction factor, similar to that described in Mothe et al. (1998), based on gravimetrically determined densities can eliminate the difference. The need for good reference material is clearly stated in the literature. In the past, many microdensitometric studies were performed with classical radiography using film and cellulose acetate wedges for calibration (Polge and Nicholls, 1972; Koga and Zhang, 2004; Martinez-Meier et al., 2008; Moya and Filho, 2009; Nock et al., 2009). Polge and Nicholls (1972) were probably the first to focus on the non-linear relationship between the optical density of an image on film and the actual density of a specimen. A better calibration method with superior reference materials to improve the accuracy of density measurements was suggested (Lenz et al., 1976; Lindgren, 1991; Macedo et al., 2002). Bergsten et al. (2001) found that variations from different machine runs (Woodtrax scanner) were small but could possibly be avoided by using a standard sample with known density. Freyburger et al. (2009) also used a calibration and a validation set of air-dried samples covering a large range of densities, showing a strong linear relationship between wood density and Hounsfield numbers (R² > 0·99). Although density was not determined exactly, the combination of small cylindrical reference samples of the same species covering a large density range (approx. 0·3–0·8 g cm⁻³) and embedded in a reference material indicates that the protocol described in this paper is promising for research on wood cores.

The results of neutron imaging are also in accordance with the literature (Fig. 2). Neutron attenuation coefficients for spruce (Mannes et al., 2007; Keunecke et al., 2010) have proven to correlate well with X-ray wood density (R² = 0·92) yet no comparison was made with gravimetric densities. These authors conclude that neutron imaging is a good alternative to standard X-ray methods based on films and non-linear correction and calibrations with a step wedge. In a later experiment, oven-dry gravimetric density and oven-dry measured attenuation coefficients resulted in an R² of 0·99 based on four tropical species (Mannes et al., 2009). Attenuation coefficients and oven-dry density of beech and spruce were again closely related (R² = 0·97), without scattering correction, which is also the case in this paper as imaging plates were used. Better results are obtainable when using CCD detectors and scattering correction.

Resistance drillings were validated in the past with gravimetric density results and showed moderate to good correlations, depending on the species (Isik and Li, 2003; Lima et al., 2007). For dry wood, drilling resistance correlates with gross density (Rinn, 1996). The results of this study show only a low correlation between gravimetric density and drilling resistance. This could be due to the generally smaller density variations observed in tropical woods compared with those of temperate species. The graph in Fig. 2, however, shows an interesting finding: the tree cores from which the 21 reference samples were taken are lumped in three separate point clouds. Clearly, drilling resistance depends on more than only density; moisture is one of the factors that play an important role as well (Eckstein and Sass, 1994). Samples from the youngest tree (B7·2R7; no limba noir) have the highest drilling resistance values and average gravimetric density whereas the oldest tree (S23R8; few limba noir) shows the highest densities and low resistance values. Rot might have played an important role here. The tree of intermediate age (S6R5; limba noir) has a low density and low drilling resistance. As the results are not unequivocal, further research is necessary but X-ray density might be an important indicator for limba noir, albeit also age related.

Comparison of estimated density profiles with X-ray scans, neutron scans and drilling resistance

When comparing profiles acquired with the three techniques (Fig. 4 and Table 3), X-ray and neutron scans show similar patterns with rather distinct peaks. Mannes et al. (2007) found that neutron profiles for spruce appear less noisy and more clearly than the X-ray densitometric profile, but this is not very distinct here. The two types of curves differed slightly in specific parts and some of the amplitudes of the neutron gradient appear higher than those from the X-ray data, which is also the case with the profiles of limba. It is possible that, in these areas of the sample, different components are crucial for the attenuation of neutrons and X-rays, as they have different interaction probabilities, in particular for hydrogen; neutron imaging is more sensitive to hydrogen than X-ray imaging (Lehmann et al., 2001).

The resistance drilling profiles are less sensitive than the other techniques. The lag in peak drilling resistance from bark to pith is of note, especially from 170 mm onward. Several effects can cause this lag and the lesser accuracy in general. Eckstein and Sass (1994) mention the built-up phase of the needle penetrating the wood. They also observed an increasing trend in drilling resistance from bark to pith due to the properties of the technique and warn that the needle can deflect during the measurement. Chantre and Rozenberg (1997) gave weights to the profiles that were proportional to the distance from the pith. This was due to the decreasing accuracy with distance from the bark, but it is difficult to discern between a measurement error due to needle bending and a change in drilling resistance of the wood.

Density variations in limba

X-ray density and neutron attenuation coefficients increase from pith to bark in 13 of the 15 samples, which is typical of heliophilous tree species. This increase has also been reported in the literature for six tropical species from Thailand (Montes et al., 2007; Moya and Filho, 2009), whereas Nock et al. (2009) showed radial gradients that increased by approx. 70 % from pith to bark in a shade-intolerant species but decreased by approx. 13 % in a shade-tolerant species. According to Montes et al. (2007), the difference in density between the pith and bark is larger where trees grow faster. They explained this phenomenon by a shift in resources from height growth to structural reinforcement of the trunk as the trees reach the canopy. It can also be expected that wood density is significantly determined by age of the tree, climatic conditions and management regimes (Moya and Filho, 2009), yet no density trends are found in relation to age or growing speed in this study. The lower density for limba at a young age could be caused by juvenile wood, as explained by Nepveu (1976) who focused on the important influence of age on the density of Terminalia ivorensis A. Chev. in Ivory Coast and the fact that the first 15 years are characterized by juvenile wood with lower densities. Yet wood degradation might be another explanation. The strong decrease in density in trees with limba noir is striking. Bauch et al. (1982) found heavy incrustations in vessels, fibres and ray parenchyma of limba noir. However, tyloses were very infrequent in the brown heart. Extractives could also affect density, but Mannes et al. (2009) did not find any great influence of extractives; the influence of elements other than carbon, oxygen and hydrogen appeared to be insignificant during neutron imaging. They suggest that the extractive content influences the attenuation coefficient only as far as it affects density. Bergsten et al. (2001) found that the true density of pine is affected by extractives but not the density of spruce. Within the brown heart, a zone was identified as wetwood associated with bacterial activity. This wetwood (high moisture content) is considered to increase the density, attenuation coefficients and resistance values (Eckstein and Sass, 1994; Mannes et al., 2009). Nevertheless, several wood cores with limba noir showed sudden peaks followed by a rather abrupt decrease in density, attenuation coefficients and drilling resistance, for example for S1R5, S2·2R5, S2·3R1, S4R6 and S6R5. One possible explanation is the destruction of the wooden structure by bacteria and/or other wood-destroying organisms that can cause density losses (Klaassen, 2008). Eckstein and Sass (1994) observed the same phenomenon in temperate trees (beech, ash) and related this to wood rot; before the profile drops down into the decomposed area, a peak indicates compartmentalization. This peak is interpreted as a defence mechanism of the tree against fungal/bacterial attack. Future research will focus on this phenomenon, analysing microscopic slides for bacteria and fungi.

General performance comparison

Obviously, the X-ray approach is the preferable technique for obtaining high-resolution information on density with a relative high speed and easy access to the equipment. With helical X-ray scanning in combination with a reference material, it is possible to approximate the actual density of the wood material. Tomographic imaging is still time-consuming, but compared with the classical use of film and with the advantage of high-throughput scanning, the time for the almost automatic retrieval of a densitometric profile for up to eight wood cores of each maximum 16·3 cm is limited to 2·5–3 h, with total operator-time being limited to less than 30 min (depending on sample imperfections). As such, very accurate results can be obtained and the cores can be scanned at a relatively high resolution of 20 µm in three dimensions without additional sample preparation. Orientation of the samples is still of concern, although tilt is already partially overcome in the reconstruction software. Although 2-D-based neutron attenuation coefficient profiles were reconstructed from a 1-mm-wide frame, 3-D-based profiles were reconstructed from a larger circular surface for every 2-D slice. In this way, errors due to a weak alignment of the measurement frame with the plane of the tree rings are more dispersed in the resulting profiles. Mannes et al. (2007) drew profiles on the scans perpendicular to the tree rings but encountered the same problem near the pith of the samples. Polge and Nicholls (1972) found that a ring boundary inclination of 10° in a 5-mm-thick sample leads to a blurred profile. Bergsten et al. (2001) found that fibre orientation played an important role, which makes mounting of the samples very important. Both fibre and ring orientation are known to cause poor matching between measured density profiles and visually assessed wood structural variations. Methods are being developed to detect ring borders automatically and to use these for correcting errors caused by local changes in ring orientation. Advantageously, microdensity values determined with 3-D tomographic methods are not subject to the effects of variations in sample thickness (due to sample shape irregularities), which inherently cause errors when using 1-D or 2-D imaging techniques. For instance, in classical radiography of 5-mm cylindrical cores, it has been shown that the ‘depth’ of 5 mm only exists in the central pixel at every radial position along the core (Polge and Nicholls, 1972). Sample thickness variations have also to be accounted for in 2-D X-rays of thin cross-sectional strips (Mothe et al., 1998). By contrast, the grey value of a voxel measured by X-ray CT does not integrate information over a certain depth or thickness, but it represents the relative amount of matter versus void present in that unit volume. The same is valid for 3-D neutron tomography. Results indicate that the profiles show less fluctuations due to the larger area per slice that was integrated compared with the densitometric profile extracted from a window on a 2-D radiograph (Fig. 3). However, this larger reduction of noise offers only a small advantage over the X-ray CT scanning method as 3-D neutron scans are more time-expensive (approx. 5–6 h for a 360° scan of a single core of 8·8 cm) and because the latter remains problematic due to neutron beam instability and artefacts. Furthermore, neutron imaging requires the use of small samples – if not, more extensive scattering corrections are needed – and is available only at a few large-scale research facilities. Nevertheless, resolutions can still be enhanced by improved detector systems, the use of cold neutrons, etc. In essence, the two techniques are complementary for research purposes regarding their different sensitivity and the fact that differences can be captured in the contrast of some selected features (Osterloh et al., 2008). Resistance drillings reveal trends within the density patterns and as such are useful, but these profiles do not deliver quick estimates of absolute density. Further study on limba noir is necessary to reveal the causes of density variations and to see how the resistance drillings can be further refined.

High-resolution X-ray CT is a promising technique for the research on wood cores and will be explored further on other temperate and tropical species. In addition to the assessment of microdensitometric profiles, the proposed X-ray CT-scanning method also opens possibilities for quantitative analysis of wood anatomy (Van den Bulcke et al., 2009; Fonti et al., 2009), expanding the possibilities for dendroclimatology.