Abstract
We extend the Kohn–Sham potential energy expansion (VE) to include variations of the kinetic energy density and use the VE formulation with a 6-31G* basis to perform a “Jacob’s ladder” comparison of small molecule properties using density functionals classified as being either LDA, GGA, or meta-GGA. We show that the VE reproduces standard Kohn–Sham DFT results well if all integrals are performed without further approximation, and there is no substantial improvement in using meta-GGA functionals relative to GGA functionals. The advantages of using GGA versus LDA functionals becomes apparent when modeling hydrogen bonds. We furthermore examine the effect of using integral approximations to compute the zeroth-order energy and first-order matrix elements, and the results suggest that the origin of the short-range repulsive potential within self-consistent charge density-functional tight-binding methods mainly arises from the approximations made to the first-order matrix elements.
INTRODUCTION
The development of fast, accurate quantum methods are central to modeling biochemical reactions through molecular simulation. There has been considerable progress in the advancement of methods based on density-functional theory (DFT) in recent years,1 including the development of improved functionals for the exchange-correlation energy, and robust parameterizations for chemical applications. Nonetheless, the sheer size and complexity of many biocatalysis applications precludes the use of so-called ab initio DFT methods with the extensive sampling required. Consequently, for many biochemical problems, one must take recourse into the use of much faster approximate quantum models in molecular simulations.
As a result, the development of improved semiempirical and approximate DFT methods is an area of ongoing interest and activity. There have been a host of advancements in the field ranging from improved parameterization of existing models,2, 3, 4, 5 to the development of new models that more robustly capture correct chemical behavior of systems.5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 To date, there have been a number of aspects of conventional semiempirical and approximate density-functional methods that have been identified as problematic. These include the realistic modeling of electronic response properties,13, 18 proper inclusion of dispersion interactions,9, 14, 19 accurate representation of electrostatics, and inclusion of the effects of orthogonalization of molecular orbitals.20 As the field progresses, there is growing interest to develop next-generation models that overcome these problems and provide an improved description of chemical processes. A particularly promising method is the self-consistent charge density-functional tight-binding (SCC-DFTB) model.21, 22 This method is based on a second-order expansion of the Kohn–Sham potential energy in terms of the electron density (and spin density), and has recently been extended to third order.11, 12 A comparison of the first-generation SCC-DFTB method with neglect of diatomic differential overlap (NDDO)-based semiempirical methods has been made for organic compounds.23 There remains many challenges, however, with regard to which directions may be the most fruitful to pursue in developing next-generation approximate DFT methods that deliver even higher accuracy and robustness, while maintaining the tremendous computational advantages these methods have over ab initio DFT methods.24
In order to facilitate the development of such new methods, we systematically explore the effect of different approximations inherent in the SCC-DFTB method, and discuss potential new directions for methodology development. The purpose of this manuscript is fourfold: (1) we extend the Kohn–Sham potential energy expansion (VE) to include variations of the kinetic energy density, (2) we use the VE formulation to perform a “Jacob’s ladder” comparison25 of small molecule properties using density functionals classified as being either LDA, GGA, or meta-GGA, (3) we show that the VE reproduces standard Kohn–Sham DFT results well if all integrals are performed without further approximation, and (4) we explore the effect of common integral approximations to compute the zeroth-order energy, first-order matrix elements, and second-order terms.
METHODS
Expansion of the Kohn–Sham potential energy
This section expresses the Kohn–Sham potential energy as a functional of the density and kinetic energy density and derives the VE energy as a Taylor expansion of the Kohn–Sham potential energy to second order in density response and first order in kinetic energy density response. The minimization of the energy in orbital variations is described and expressions for the Fock matrix are given.
The total Kohn–Sham energy is
| (1) |
where T and V are the noninteracting kinetic energy and potential energy, respectively, and take as functional arguments the total electron density ρ(r)=ρα(r)+ρβ(r), spin density ω(r)=ρα(r)−ρβ(r), kinetic energy density τ(r)=τα(r)+τβ(r), and kinetic energy spin density θ(r)=τα(r)−τβ(r). The above representation can be alternately mapped into one that uses the individual spin-resolved electron and kinetic energy density components through the relations: ρα(r)=[ρ(r)+ω(r)]∕2, ρβ(r)=[ρ(r)−ω(r)]∕2, τα(r)=[τ(r)+θ(r)]∕2, and τβ(r)=[τ(r)−θ(r)]∕2. The spin-resolved densities can be expressed in the basis of atomic orbitals {χi}, herein assumed to be real, as
| (2) |
| (3) |
where Pσ is the spin-resolved single-particle density matrix in the atomic orbital (AO) basis.
The kinetic and potential energies are
| (4) |
| (5) |
where
| (6) |
P is the single-particle density matrix in the AO basis, v(r) is the external potential (e.g., the electrostatic potential due to the nuclei),
| (7) |
is the electron–electron Coulomb repulsion, and Exc[ρ,ω,τ,θ] is the exchange correlation energy.
We now consider the reference state defined by reference densities ρ0(r), τ0(r) and reference spin densities ω0(r)=0, θ0(r)=0, which we henceforth denote collectively by a “0” subscript outside functional derivatives. Expansion of V[ρ, ω, τ, θ] about the reference state to second-order response in ρ(r) and ω(r) and first order response in τ(r) and θ(r) produces
| (8) |
where the terms on the right hand side of the equation are the kinetic energy, zeroth-order reference potential energy, and first and second order potential energy corrections, respectively.
The zeroth-order reference potential energy is
| (9) |
The first-order potential energy is
| (10) |
where P0 is the reference single-particle density matrix which reconstructs the reference density from the AO basis. δρ(r) and δτ(r) are
| (11) |
| (12) |
and Vi,j(1,0,0,0) and Vi,j(0,0,1,0) are
| (13) |
| (14) |
The first-order functional derivatives of V [Eq. 5] are
| (15) |
| (16) |
where φ0(r) is the classical electrostatic potential of the reference electron density ρ0(r). The contributions to the first-order energy due to variations in ω(r) and θ(r) vanish with our choice of expansion reference, i.e., ω0(r)=0 and θ0(r)=0.
The second-order energy (neglecting terms involving τ and θ) is
| (17) |
where
| (18) |
| (19) |
and
| (20) |
| (21) |
Note that the mixed functional derivative δ2V∕δρ(r)δω(r′) is zero when using the reference ω0(r)=0, and we have chosen for the sake of simplicity to limit the expansion of the kinetic energy densities to first order.
The energy [Eq. 8] is minimized with respect to variations in the orbitals under orthonormality constraints using the standard self-consistent field (SCF) procedure to solve the Kohn–Sham equations, where the σ-spin Fock matrix is
| (22) |
Computational details
This section describes several models based on the method described in the previous section and provides computational details used in their evaluation and of the calculation of reference data. The description of the models consists of (1) the density functionals, (2) the basis set, (3) the choice of reference density, and (4) the integral approximations.
We consider the LDA functional SVWN5,26 the GGA functionals PBE27 and HCTH147,28 and the meta-GGA functionals τ-HCTH29 and M06L.30 Unless otherwise specifically stated, we use the SPW9227 functional to evaluate the exchange-correlation second functional derivatives in Eqs. 20, 21.
In this work, we consider the reference state to be a superposition of atomic electron and kinetic energy densities. In order to evaluate the integrals in the previous section, one must obtain atomic orbitals, a reference density matrix, and a corresponding reference density. The reference atomic electron and kinetic energy densities were obtained from numerical solution of the restricted open-shell Kohn–Sham equations using a spherical harmonic 6-31G* basis whilst enforcing spherical symmetry of the density through uniform occupation of degenerate orbitals. These atomic calculations do not involve the VE approximations; however, the resulting atomic orbitals and reference densities are used as input to the VE. The atomic calculations use the same density functional as that used in the VE.
In Tables 1, 2, 3, 4, 5, 6, 7, 8, we will refer to three variants of the VE method: “VE”, “VE0,” and “VE1.” The VE model is the base model that results from solution of the equations verbatim as written in the previous section using reference densities formed from the sum of atom-centered atomic densities. The VE0 and VE1 models involve approximations that have certain computational advantages, as described below.
Table 1.
Bond length error statistics (Å) using 114 data points.
| Functional |
Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| Errors relative to standard MP2(FULL)∕6-31G* calculations. Avg. = 1.312 Å | |||||||
| SVWN5 | Std. | 0.006 | 0.022 | 0.017 | 0.016 | −0.162 | Na2 |
| SVWN5 | VE | 0.006 | 0.022 | 0.017 | 0.016 | −0.159 | Na2 |
| PBE | Std. | 0.010 | 0.013 | 0.013 | 0.009 | −0.080 | Na2 |
| PBE | VE | 0.012 | 0.013 | 0.015 | 0.009 | −0.071 | Na2 |
| HCTH147 | Std. | 0.005 | 0.010 | 0.009 | 0.007 | 0.044 | CN |
| HCTH147 | VE | 0.006 | 0.010 | 0.010 | 0.007 | 0.046 | CN |
| τ-HCTH | Std. | 0.003 | 0.010 | 0.008 | 0.007 | 0.042 | CN |
| τ-HCTH | VE | 0.007 | 0.011 | 0.011 | 0.008 | 0.048 | Na2 |
| M06L | Std. | −0.002 | 0.010 | 0.007 | 0.008 | −0.047 | Li2 |
| M06L | VE | 0.010 | 0.021 | 0.018 | 0.014 | 0.105 | Li2 |
| Errors relative to standard PBE∕6-31G* calculations. Avg. = 1.322 Å | |||||||
| PBE | VE | 0.002 | 0.002 | 0.002 | 0.001 | 0.009 | Na2 |
| PBE | VE0 | −0.013 | 0.014 | 0.014 | 0.013 | −0.078 | C2H6 |
| PBE | VE1 | −0.473 | 0.199 | 0.473 | 0.199 | −1.339 | Na2 |
Table 2.
Angle error statistics (degrees) using 98 data points.
| Functional |
Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| Errors relative to standard MP2(FULL)∕6-31G* calculations. Avg. = 112.745° | |||||||
| SVWN5 | Std. | −0.009 | 0.863 | 0.531 | 0.681 | 3.143 | CH2 |
| SVWN5 | VE | 0.013 | 0.967 | 0.636 | 0.729 | 3.832 | CH2 |
| PBE | Std. | −0.199 | 0.642 | 0.416 | 0.528 | −2.146 | PH3 |
| PBE | VE | −0.205 | 0.821 | 0.554 | 0.640 | 2.596 | CH2 |
| HCTH147 | Std. | −0.161 | 0.624 | 0.402 | 0.503 | 2.460 | CH2 |
| HCTH147 | VE | −0.201 | 0.809 | 0.567 | 0.611 | −2.399 | NH2 |
| τ-HCTH | Std. | −0.170 | 0.639 | 0.436 | 0.497 | −1.997 | NH2 |
| τ-HCTH | VE | −0.236 | 0.764 | 0.536 | 0.593 | −2.591 | NH2 |
| M06L | Std. | −0.188 | 0.520 | 0.385 | 0.396 | −1.706 | PH3 |
| M06L | VE | −0.321 | 0.943 | 0.670 | 0.737 | −2.899 | PH3 |
| Errors relative to standard PBE∕6-31G* calculations. Avg. = 112.5° | |||||||
| PBE | VE | −0.006 | 0.340 | 0.177 | 0.290 | 2.229 | CH4S |
| PBE | VE0 | −0.629 | 1.152 | 0.858 | 0.993 | −3.940 | CH4O |
| PBE | VE1 | 0.785 | 16.155 | 10.666 | 12.159 | 78.425 | HOCl |
Table 3.
Dipole moment error statistics (atomic units) using 52 data points.
| Functional |
Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| Errors relative to standard MP2(FULL)∕6-31G* calculations. Avg. = 0.539 a.u. | |||||||
| SVWN5 | Std. | −0.032 | 0.089 | 0.048 | 0.081 | −0.425 | CN |
| SVWN5 | VE | −0.039 | 0.100 | 0.055 | 0.092 | −0.457 | CN |
| PBE | Std. | −0.042 | 0.081 | 0.048 | 0.078 | −0.421 | CN |
| PBE | VE | −0.050 | 0.094 | 0.057 | 0.090 | −0.483 | CN |
| HCTH147 | Std. | −0.039 | 0.074 | 0.044 | 0.071 | −0.394 | CN |
| HCTH147 | VE | −0.046 | 0.087 | 0.054 | 0.082 | −0.474 | CN |
| τ-HCTH | Std. | −0.044 | 0.077 | 0.049 | 0.073 | −0.368 | CN |
| τ-HCTH | VE | −0.045 | 0.083 | 0.054 | 0.077 | −0.469 | CN |
| M06L | Std. | −0.018 | 0.054 | 0.029 | 0.049 | −0.275 | CN |
| M06L | VE | −0.042 | 0.087 | 0.052 | 0.081 | −0.491 | CN |
| Errors relative to standard PBE∕6-31G* calculations. Avg. = 0.496 a.u. | |||||||
| PBE | VE | −0.007 | 0.019 | 0.012 | 0.016 | −0.076 | LiH |
| PBE | VE0 | −0.005 | 0.024 | 0.015 | 0.019 | −0.076 | LiH |
| PBE | VE1 | 0.120 | 0.571 | 0.373 | 0.449 | 1.847 | HOCl |
Table 4.
Bond lengths (Å) of Zinc-containing small molecules. Shown are the CCSD(T) results from reference 40, and the signed errors of each method with respect to the CCSD(T) reference. The Zn−X bond lengths in ZnF2 and ZnCl2 are identical by symmetry. All calculations use a B2 basis for Zn and MG3S basis for O, F, S, and Cl. Molecules with an even number of electrons are computed with singlet multiplicity; doublet multiplicity otherwise.
| Functional |
Model |
ZnF |
ZnF2 |
ZnCl |
ZnCl2 |
ZnO |
ZnS |
Zn2 |
μSE |
μUE |
| CCSD(T) | Std. | 1.775 | 1.723 | 2.151 | 2.078 | 1.711 | 2.066 | 4.104 | — | — |
| SVWN5 | Std. | −0.011 | −0.016 | −0.031 | −0.031 | −0.039 | −0.043 | −1.254 | −0.204 | 0.204 |
| SVWN5 | VE | −0.010 | −0.015 | −0.033 | −0.030 | −0.038 | −0.042 | −1.268 | −0.205 | 0.205 |
| PBEPBE | Std. | 0.031 | 0.021 | 0.017 | 0.011 | −0.005 | −0.004 | −0.912 | −0.120 | 0.143 |
| PBEPBE | VE | 0.033 | 0.021 | 0.017 | 0.010 | −0.005 | −0.004 | −0.938 | −0.124 | 0.147 |
| HCTH147 | Std. | 0.036 | 0.023 | 0.037 | 0.017 | −0.004 | −0.001 | −0.321 | −0.030 | 0.063 |
| HCTH147 | VE | 0.033 | 0.021 | 0.027 | 0.014 | −0.006 | −0.000 | −0.402 | −0.045 | 0.072 |
| τ-HCTH | Std. | 0.028 | 0.016 | 0.031 | 0.012 | −0.011 | −0.011 | −0.795 | −0.104 | 0.129 |
| τ-HCTH | VE | 0.017 | 0.009 | 0.017 | 0.006 | −0.016 | −0.010 | −0.832 | −0.116 | 0.130 |
| M06L | Std. | 0.022 | 0.012 | 0.008 | −0.002 | −0.007 | −0.023 | −0.868 | −0.122 | 0.135 |
| M06L | VE | 0.026 | 0.016 | 0.007 | −0.002 | −0.012 | −0.027 | −0.854 | −0.121 | 0.135 |
Table 5.
Bond dissociation energies (kcal∕mol) of zinc-containing small molecules. Shown are the CCSD(T) results from reference 41, and the signed errors of each method with respect to the CCSD(T) reference. The ZnF2 and ZnCl2 correspond to the reaction ZnX2→ZnX+X. Isolated atoms are computed using their ground state electronic configuration.
| Functional |
Model |
ZnF |
ZnF2 |
ZnCl |
ZnCl2 |
ZnO |
ZnS |
Zn2 |
μSE |
μUE |
| CCSD(T) | Std. | 63.90 | 116.77 | 45.88 | 99.11 | 29.14 | 27.87 | 0.43 | — | — |
| SVWN5 | Std. | 26.33 | 25.97 | 17.55 | 17.88 | 36.52 | 26.03 | 4.68 | 22.14 | 22.14 |
| SVWN5 | VE | 26.82 | 26.46 | 16.85 | 17.42 | 39.45 | 26.97 | 4.82 | 22.68 | 22.68 |
| PBEPBE | Std. | 10.63 | 5.31 | 6.99 | 2.59 | 16.72 | 11.09 | 1.28 | 7.80 | 7.80 |
| PBEPBE | VE | 15.68 | 12.59 | 8.26 | 6.31 | 25.80 | 16.99 | 1.30 | 12.42 | 12.42 |
| HCTH147 | Std. | 5.69 | 5.82 | 0.29 | 0.14 | 8.99 | 3.01 | 0.04 | 3.43 | 3.43 |
| HCTH147 | VE | 15.07 | 11.23 | 5.61 | 2.53 | 23.38 | 12.48 | −0.04 | 10.04 | 10.05 |
| τ-HCTH | Std. | 9.91 | 8.13 | 4.99 | 1.77 | 10.58 | 7.07 | 1.09 | 6.22 | 6.22 |
| τ-HCTH | VE | 19.59 | 15.97 | 8.75 | 5.41 | 28.42 | 15.90 | 1.08 | 13.59 | 13.59 |
| M06L | Std. | 3.64 | 4.03 | 6.46 | 8.40 | 4.37 | 8.77 | 1.37 | 5.29 | 5.29 |
| M06L | VE | 24.45 | 23.74 | 13.15 | 14.23 | 33.95 | 22.89 | 1.27 | 19.10 | 19.10 |
Table 6.
Water O−H bond (Å) and H−O−H angle (degrees) errors for PBE VE1 models with and without the use of reference atomic density confinement [Eq. 25]. The errors are reported as signed differences defined by error = model − reference, where the reference values result from standard PBE∕6-31G* calculations. Entries marked “frozen” indicate partial geometry optimization with the coordinate fixed at the PBE∕6-31G* value.
| Model |
O−H |
H−O−H |
| VE1 | −0.297 | 29.007 |
| VE1 | Frozen | −5.831 |
| VE1[5Rcov] | Frozen | −3.034 |
| VE1[4Rcov] | Frozen | −2.466 |
| VE1[3Rcov] | Frozen | −2.189 |
Table 7.
Error statistics (kcal∕mol) for homolytic bond dissociation energy of symmetric molecules to form identical radical species using PBE∕6-31G* reference data (six data points) corresponding to the reactions: C2H6→2CH3, C2H4→2CH2, C2H2→2CH, N2H4→2NH2, Si2H6→2SiH3, and H2O2→2OH. The computed energies are SCF energy differences without zero-point energy nor other approximate thermochemical corrections. The average reference dissociation energy is 125.378 kcal∕mol.
| Functional |
Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| PBE | VE | 9.445 | 2.607 | 9.445 | 2.607 | 14.322 | C2H4→2CH2 |
| PBE | VE0 | 26.683 | 10.337 | 26.683 | 10.337 | 42.148 | C2 H6→2CH3 |
| PBE | VE1 | 1201.001 | 222.306 | 1201.001 | 222.306 | 1612.073 | H2O2→2OH |
Table 8.
Error statistics (kcal∕mol) for relative homolytic bond dissociation energy (with respect to H2) using PBE∕6-31G* reference data (six data points) corresponding to the closed-shell reactions: C2H6+H2→2CH4, C2H4+H2→2CH4, C2H2+3H2→2CH4, N2H4+H2→2NH3, Si2H6+H2→2SiH4, H2O2+H2→2H2O. The computed energies are SCF energy differences without zero-point energy nor other approximate thermochemical corrections. The average reference dissociation energy is −50.587 kcal∕mol.
| Functional |
Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| PBE | VE | 0.076 | 0.282 | 0.221 | 0.191 | 0.636 | C2H2+3H2→2CH4 |
| PBE | VE0 | −8.408 | 15.610 | 11.708 | 13.314 | −38.400 | C2H2+3H2→2CH4 |
| PBE | VE1 | 369.505 | 445.538 | 511.706 | 270.546 | 887.490 | H2O2+H2→2H2O |
The VE0 model is like VE, but employs a two-center cluster approximation toV(0), i.e.,
| (23) |
where ρ0,a and τ0,a are the reference electron and kinetic energy atomic densities of atom a and similarly for b. Note that the VE0 model is equivalent to the VE model for any two-atom system.
The VE1 model, like VE0, employs Eq. 23 as an approximation to V(0) but further applies a two-center approximation for the reference density within the V(1,0,0,0) and V(0,0,1,0) matrix elements, i.e.,
| (24) |
where the reference state denoted by a0 is the atomic density centered on atom a, and the reference state denoted by a0+b0 is the sum of atomic densities centered on atoms a and b. The VE1 integral approximation to V(0,0,1,0) is analogous to Eq. 24; the functional derivatives are taken with respect to δτ(r) instead of δρ(r).
In the next section, we compare covalent bond lengths, angles, molecular dipole moments, and homolytic bond dissociation energies for 52 small molecules31 taken from the G2∕97 neutral small molecule test set.32 Our test set consists of 25 dimers, 11 three-atom molecules, 7 four-atom molecules, and 9 five-to-eight atom molecules, and the multiplicities of these molecules include 35 singlets, 11 doublets, and 6 triplets. We proceed by describing the calculation details for these molecules.
The VE, VE0, and VE1 models are compared against MP2(FULL) and standard DFT results (Tables 1, 2, 3) using a spherical harmonic 6-31G* basis, and each molecule was geometry optimized for every model. All geometry optimizations were performed using the GAUSSIAN 03 program33 patched with the MN-GFM34 module using tight convergence criteria. The MN-GFM module allowed us to use the M06L30 functional. The VE, VE0, and VE1 geometry optimizations were performed using numerical gradients computed via a finite difference displacement of 0.001 bohr.
The VE, VE0, and VE1 calculations compute all integrals fully numerically using atom centered quadrature grids composed of the outer product of 150 radial Gauss–Laguerre35 and 590 angular Lebedev36, 37, 38 quadrature points (88 500 points per atom). The molecular quadrature grid is partitioned using Becke’s fuzzy voronoi, including his use of Bragg–Slater radii.39 The standard LDA and GGA calculations run with GAUSSIAN 03 used the “ultrafine” pruned quadrature grid for the evaluation of the exchange-correlation; whereas the standard meta-GGA calculations were run with an unpruned grid with every atom containing 120 radial and 590 angular grid points.
The tables in this paper contain error statistics, including the mean signed and unsigned errors (μSE and μUE , respectively), the standard deviation of the signed and unsigned errors (σSE and σUE , respectively), the maximum error (Max.), the molecule which produced the maximum error, and the average reference value (Avg.). The abbreviation “Std.” refers to a standard, as opposed to a VE-based, calculation.
Tables 4, 5 compare bond lengths and bond dissociation energies for several small molecules containing Zn. The 6-31G* basis is inadequate for calculations involving Zn, therefore, the reference values are taken directly from Ref. 40, whom performed CCSD(T) calculations using a relativistic effective core potential (ECP) and the B2 basis40, 41, 42, 43 for Zn and a MG3S44 basis for the remaining elements. All other results within Tables 4, 5, which are computed as a part of this work, do not use a ECP but do use the spherical harmonic B2 and MG3S basis sets. The VE calculations in these tables were performed using the procedure described above, i.e., for the construction of the atomic orbitals and reference densities, but with the B2 and MG3S basis instead of the 6-31G* basis.
Table 6 explores the effect of reference density confinement45 on the H–O–H angle of water when using the PBE VE1 model. The atomic orbitals and reference densities for the models denoted by VE1[xRcov] have been constructed by solving the regular Kohn–Sham equations for the isolated atoms while applying a radial confinement potential that modifies the energy so that the Kohn–Sham effective Hamiltonian matrix elements contain the additional term
| (25) |
where x is some factor, which in this work is either 3, 4, or 5, and Rcov is the covalent radius46, 47, 48, 49, 50 of the atom. Solution of the Kohn–Sham equations with the confinement potential yields confined orbitals and reference densities; however, we note that, since we use the entirety of the 6-31G* basis, the total space spanned by the confined orbitals is the same as that of the unconfined orbitals. The VE1 models which employ the confined orbitals and reference densities use the confined reference in all aspects of the model except for the one-center terms appearing in Eq. 24, which instead evaluates the first-order potential arising from the unconfined atomic densities. This usage of unconfined atomic densities has been chosen to mimic SCC-DFTB’s use of free-atom eigenvalues for these matrix elements [see, e.g., Eqs. (22) and (23) in Ref. 45].
Tables 7, 8 compare adiabatic bond energies between VE, VE0, and VE1 relative to the standard PBE∕6-31G* results. These energies are differences in SCF energies, i.e., they do not contain enthalpic, entropic, nor zero-point corrections to the energy. The bond energies in Table 7 correspond to the cleavage of a homolytic bond in a symmetric molecule to form two identical radical species, and the molecules were chosen because both the molecules and radical fragments were included within the test set used to generate Tables 1, 2, 3. Table 8 differs from Table 7 by saturating the molecular fragments with hydrogens and subsequently mass balancing with hydrogen molecules so that all species have a closed shell electronic structure.
Table 9 compares dipole moments computed by standard PBE and various models based on the VE using the PBE functional. For this table, the dipole moments are computed using the geometries obtained from standard PBE. A list of the various models appearing in this paper are summarized below with their respective abbreviations:
VE: The base model that results from solution of the equations verbatim in Sec. 2A using reference densities formed from the sum of atom-centered atomic densities.
VE0: The VE0 model is like VE, but employs a two-center cluster approximation to V(0) as in Eq. 23.
VE1: The VE1 model is like the VE0 model, with the additional two-center approximation on the reference density as indicated in Eq. 24.
VEJ: The VE model excluding the exchange-correlation contribution toV(2), i.e., this is a second-order Coulomb approximation without the use of an auxiliary basis.
VE1J: The VE1 model with a second-order Coulomb approximation without the use of an auxiliary basis.
VEJ(S): The VEJ model, but the molecular dipole moments are computed from Mulliken-partitioned charges.
VE1J(S): The VE1J model, but the molecular dipole moments are computed from Mulliken-partitioned charges.
VEJ∕S: The VEJ model where the second-order Coulomb energy is computed with an auxiliary basis of Slater monopoles of Mulliken-partitioned charges. The Slater ζ-exponent was chosen such that the self-Coulomb energy of Slater function reproduces the atom’s experimental hardness. Unlike VEJ(S), VEJ∕S affects the Fock matrix and resulting SCF-converged density matrix. The dipole moments are computed from Mulliken-partitioned charges. The Slater functions are represented by a contracted Gaussian containing four primitive functions.
VE1J∕S: The VE1J model where the second-order Coulomb energy is computed with an auxiliary basis (see VEJ∕S).
VE1TB: The VE1 model where the second-order energy is zero, i.e., there is no SCF procedure.
VE1TB(S): The VE1TB model where the dipole moments are computed from Mulliken-partitioned charges.
VE1[xRcov]: The VE1 model that uses confined orbitals and reference densities, where the term in square brackets defines the magnitude of the radial confinement potential as shown in Eq. 25.
Table 9.
Dipole moment error statistics (atomic units) relative to standard PBE∕6-31G*. All calculations use the PBE functional and the standard PBE∕6-31G* optimized geometries. The statistics include 52 data points and the average reference value is 0.496 a.u.
| Model |
μSE |
σSE |
μUE |
σUE |
Max. |
|
| VE | −0.007 | 0.019 | 0.012 | 0.016 | −0.077 | LiH |
| VEJ | −0.043 | 0.079 | 0.051 | 0.074 | −0.420 | LiH |
| VEJ(S) | −0.067 | 0.363 | 0.176 | 0.324 | −1.908 | LiH |
| VEJ∕S | −0.174 | 0.413 | 0.236 | 0.381 | −1.914 | NaCl |
| VE1 | 0.078 | 0.233 | 0.179 | 0.169 | 0.565 | PH2 |
| VE1J | 0.050 | 0.262 | 0.184 | 0.193 | −0.805 | LiH |
| VE1J(S) | −0.136 | 0.468 | 0.249 | 0.419 | −2.101 | LiH |
| VE1J∕S | −0.115 | 0.352 | 0.185 | 0.321 | −1.641 | LiH |
| VE1TB | 0.355 | 0.341 | 0.358 | 0.337 | 1.088 | SiO |
| VE1TB(S) | 0.122 | 0.364 | 0.242 | 0.298 | −1.153 | LiH |
RESULTS AND DISCUSSION
Comparison between LDA, GGA, and meta-GGA functionals
It is well established that GGA functionals are more reliable, especially for predicting hydrogen bonding, than LDA functionals, and that meta-GGA functionals can offer a modest improvement over GGA functionals, particularly for transition metal systems,41, 51 when statistics over a large dataset are examined. In this section, we explore the degree to which Kohn–Sham VE models follow this trend, i.e., to answer the question: does a meta-GGA VE offer any advantage over a GGA VE?
Table 1 displays covalent bond length error statistics relative to MP2 reference data, and shows that standard DFT agrees with MP2 to within a μUE of 0.02 Å. The largest errors occur for Na2 and Li2, which also have exceptionally large bond lengths: 3.16 and 2.78 Å, respectively. The VE models yield error statistics very similar to what is seen for standard DFT; their differences in bond length μUE values are typically below 0.004 Å. The exception to this are the M06L VE results, which yield the largest bond length μUE value for any method (0.018 Å).
With respect to the bond angles, the standard DFT results show a 0.4°–0.5° μUE relative to the reference MP2 results (Table 2), and the VE models are slightly worse by an additional 0.1°–0.2°, typically, but with the M06L VE being the exception. The M06L VE μUE is 0.3° larger than the standard M06L μUE and yields the highest μUE of any method. VE’s based on GGA and meta-GGA functionals tend to yield slightly better angle error statistics than the LDA VE, but the differences are small (typically 0.1°) and there is no clear improvement of meta-GGA functionals relative to GGA functionals.
One of the largest and most common maximum errors reported in Table 2 is the H–C–H angle in 3B1 CH2. MP2 predicts this angle to be 131.6°, whereas the standard DFT results are 134.8° (SVWN5), 133.6° (PBE), 134.1° (HCTH147), 133.3° (τ-HCTH), and 130.9° (M06L). The VE angles are slightly larger than their standard DFT counterparts, typically by 0.3°–0.5°, except for the M06L VE result which is 133.7°. The CH2 angle has been experimentally measured via laser magnetic resonance and found to be 133.8°,52 and so the DFT and VE results are in better agreement with experiment than the MP2 reference.
There is almost no distinction between LDA, GGA, and meta-GGA dipole moments relative to the MP2 reference (Table 3), with all models yielding a μUE of approximately 10% of the average MP2 reference value. A large difference in dipole moment can be an indicator of a difference in geometries, and Tables 1, 2 suggested minor differences in geometries only. The largest difference in dipole moments between all methods and the MP2 results are for the 2 Σ+ CN radical; however, all DFT methods predict fairly similar dipole moments relative to each other. HF and MP2 tend to predict a CN dipole moment that is one and a half to two times larger than what DFT methods predict, and this overestimation of the dipole moment is not particularly sensitive to the size of the basis set. The dipole moment predicted by the DFT methods is in good agreement with those obtained from Stark effect measurements.53
Analysis of errors for Zn-containing compounds
We have selected some small Zn-containing compounds for further analysis (Tables 4, 5) in order to assess to what extent a meta-GGA versus a GGA-based VE affects the results for transition metal systems. These molecules were selected due to the availability of their recently reported high-level benchmark results.40, 41 We observe larger bond length errors in Zn-containing molecules (Tables 4) for all functionals other than HCTH147; however, the standard and VE calculations are in good agreement with each other, as was observed in Table 1. The errors of PBE and the meta-GGA functionals are very similar and the LDA errors are almost twice as large in comparison.
Standard HCTH147 has the smallest bond dissociation energy μUE in Table 5, and the standard meta-GGA’s μUE are 2–3 kcal∕mol larger. Unlike the bond lengths, angles, and molecular dipole moments, the bond dissociation energy error statistics show discrepancies between standard DFT and VE calculations, except for the LDA calculations; however, the Zn2→2Zn calculation shows close agreement between the standard and VE calculations. This reaction is the only calculation in Table 5 that results from singlet molecule constituents only. With this in mind and the fact that the standard and VE LDA calculations are always in close agreement suggests that the discrepancies between standard and VE calculations when computed with the GGA and meta-GGA functionals results from the LDA treatment of the V(2) energy [Eq. 17].
Effect of integral approximations
In the previous sections standard DFT and VE results were compared with respect to the class of functional used, i.e., LDA, GGA, and meta-GGA. The VE method used in the comparison performed the integrals described in the Methods section verbatim; however, the Kohn–Sham VE is typically only used as a motivational starting point to which further and more severe approximations are made in the interest of reducing computational effort21 and thus form the foundation for a semiempirical model. The VE method requires the calculation of nonadditive multicenter integrals, but a more tractable model, such as SCC-DFTB,21 approximates the multicenter integrals by a series of two-center integrals whose results can be pretabulated and stored as cubic splines, but at the detriment of requiring parameterization within the framework of the model via ad hoc corrections. This section explores the effect of integral approximations to the zeroth and first-order terms in the expansion without including additional ad hoc corrections.
Error statistics resulting from the comparison of the VE, VE0, and VE1 models relative to the standard PBE calculations are summarized at the bottom of Tables 1, 2, 3. In general, VE is a very good approximation, with μUE values of 0.002 Å (bond lengths), 0.290° (bond angles), and 0.012 a.u. (dipole moments). The VE0 model shows some breakdown resulting from the two-center cluster approximation to V(0) [Eq. 23]. More concerning, however, is the significant deterioration of the VE1 model, which utilizes the two-center approximation for the reference density when computing the first-order integrals [Eq. 24]. This approximation is a cornerstone for the practical implementation of approximate density-functional expansion methods, since it allows the first-order integrals to be precomputed and tabulated on numerical splines, and then efficiently rotated into the molecular orientation using Slater–Koster tables or spherical tensor gradient operator methods.54
The VE and standard PBE yield almost identical covalent bond lengths, whereas the VE0 yields bond lengths that are too small by 0.01 Å. The VE1 model, however, results in bond lengths that are completely artificial (i.e., too small by 0.473 Å).
The VE0 angles exhibit errors four times larger than the VE results when compared to standard PBE, and the VE1 angle errors are 50–60 times larger than those observed for VE. We observe VE1 geometry optimizations causing nonlinear molecules to become either linear (e.g., HOCl) or severely bent (e.g., H2Si), which is anecdotally why the VE1 μSE and μUE’s differ. The VE1 μUE value of 10.666° may seem surprising because SCC-DFTB angles have previously been shown23 to agree with MP2 results to within 1.5°, and it may not be obvious that a short-ranged pairwise repulsive potential would account for such a discrepancy. It has been our experience, through partial geometry optimizations in which the bond lengths are held fixed, that the errors in the angles are significantly coupled to the errors in the bond lengths. This coupling can be seen by comparing the first two rows of Table 6, and our interpretation is that the coupling occurs through the first-order energy, as opposed to the zeroth-order energy. There are other differences between the VE1 model presented in this work and the SCC-DFTB model used in Ref. 23: The VE1 model uses an all-electron 6-31G* basis and calculates a numerically accurate V(2) energy, whereas SCC-DFTB uses a minimal valence basis and employs a Slater monopole auxiliary basis. Another difference is that SCC-DFTB uses atomic reference densities that have been confined by a radial potential. We address the use of confined reference densities in Table 6, which displays the error of water’s angle for several VE1 models which employ confined atomic densities. The results support the idea that the VE1 angle errors are reduced when (1) the errors in the bond lengths are small, (2) the one-center terms in Eq. 24 are evaluated using the potential arising from the unconfined reference density, and (3) the remainder of the model is computed using confined reference densities. Thus, one should not be overly pessimistic when interpreting the VE1 results in Table 2.
The comparison of VE, VE0, and VE1 dipole moment error statistics relative to standard PBE follow similar trends. The VE model yields the smallest errors, VE0 produces slightly larger errors, and VE1 results in very large errors, and this can be explained by noting that the dipole moments are coupled to the quality of the molecular geometry, and the VE1 geometries are quite poor, whereas the VE0 geometries compare much more reasonably with VE and standard PBE.
The coupling of the properties to the quality of the geometry is also apparent in Table 7, which compares the adiabatic bond energies for a small set of reactions corresponding to the homolytic cleavage of symmetric molecules into radical fragments. Like Table 5, Table 7 displays large errors for VE because of our LDA treatment of V(2). Table 8 circumvents this approximation by saturating the radical fragments with hydrogens to yield closed shell molecules. When open-shell molecules are not involved, the VE μUE drops from 9.445 to 0.221 kcal∕mol, which is less than the chemical accuracy of PBE.
Overall, the error statistics for the VE1 model relative to the full Kohn–Sham PBE results suggest that straightforward application of the two-center approximation to the reference density will require considerable reliance on other forms of empiricism to develop highly accurate models.
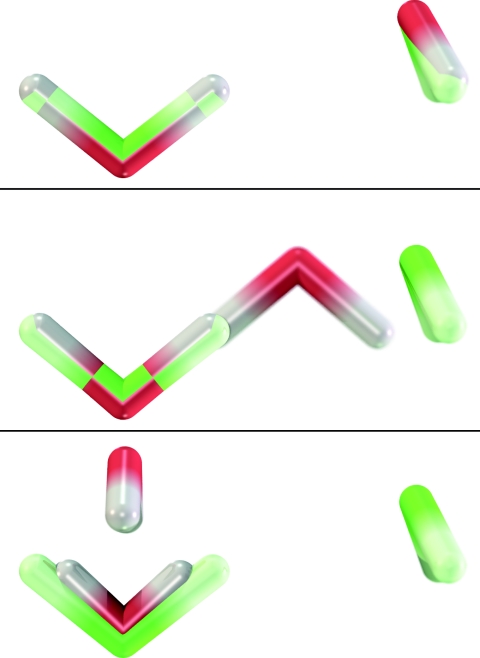
Up to this point, we have yet to discuss nonbonded interactions, therefore we address this here by comparing geometry optimized water dimer structures computed from standard PBE, VE, VE0, and VE1 in Fig. 1. The VE and standard PBE structures agree almost identically, following the good agreement observed in Tables 1, 2. We have compared VE and standard DFT using other functionals as well (not shown) and similar good agreement is found. For example, standard SVWN5∕6-31G* does not predict a hydrogen bonding structure to be a minimum, but instead produces a “parallel displaced” structure in which the planes formed by each water are parallel to each other, and yet the SVWN5 VE faithfully reproduces this erroneous dimer structure.
Figure 1.
Optimized water dimer geometries using VE (top), VE0 (middle), and VE1 (bottom) superimposed onto the standard PBE∕6-31G* geometry (green). The water dimers are bound by 8.84 (standard PBE), 8.79 (VE), 16.77 (VE0), and 477.58 (VE1) kcal∕mol.
In Tables 1, 2, we found that the pairwise integral approximation to V(0) produced only minor changes in the covalent bond lengths and angles; however, Fig. 1 suggests that this approximation can greatly affect the geometries of nonbonded complexes. The PBE VE0 water dimer structure is qualitatively similar to what we observe from standard LDA calculations. To investigate the role of many-body effects, we performed a test whereby the water dimer structure was computed from a model which we describe as being a PBE VE model whose V(0) energy is computed by a nonadditive LDA V(0) [Eq. 9] term and then having subtracted a LDA cluster approximant V(0) [Eq. 23] and added a PBE cluster approximant V(0) [Eq. 23]. In this way, the model contains one- and two-body PBE V(0) and many-body LDA V(0). This model does predict the hydrogen bonded structure as the global minimum, albeit not with the accuracy of the VE model. This result was intriguing to us because, if one were to construct an ab initio-like expansion model, it would be advantageous to perform quadrature evaluation of an LDA functional, as opposed to a GGA functional, and then supplement the calculation with one- and two-body GGA corrections which can be precomputed on numerical splines. Alas, when we construct a model described as a PBE VE whose first-order matrix elements are computed from a nonadditive LDA [Eq. 10] and which includes one- and two-body [Eq. 24] GGA corrections, the global minimum of the water dimer is similar to the LDA optimized structure.
The VE1 water dimer structure is poor and defies physical intuition. This is not entirely unexpected, because the approximation to the first-order matrix elements [Eq. 24] ignores the fact that the system is composed of atoms, except for those atoms involved in the basis function product. Therefore, as an example, the basis function product involving the hydrogens of water ignore the first-order potential arising from the oxygen. This is not to say that a semiempirical model based on these approximations cannot be constructed; even the additive molecular mechanical TIP3P water model predicts hydrogen bonding.55 These observations only imply that parameterization of such a model would be necessary and likely coupled to some basis. Furthermore, the observation that the VE1 bond lengths are substantially too small suggests the need for an ad hoc repulsive potential, i.e., the repulsive potential used in SCC-DFTB largely results from the approximation for the first-order integrals. We are not the first to attribute the presence of a repulsive potential to mask other approximations within a DFTB-based model, and we direct the reader to Refs. 56 and 57 and references therein for further discussion.
Given the importance of including an ad hoc repulsive potential to retain good geometries when integral approximations are used, let us suppose that we have modified the VE energy expressions to include an “ideal” repulsive potential that is not a functional of the electron density response and which causes the VE models to reproduce the standard PBE geometries exactly. Then, under this supposition, we can explore how different integral approximations affect the dipole moments by performing single point calculations at the standard PBE geometries. The dipole moments resulting from this scenario are shown in Table 9 for a variety of approximations. We observe that VE reproduces standard DFT well and then progressively increases in error as the following approximations are applied: Coulomb approximation (VEJ), Mulliken partitioning of the final density matrix [VEJ(S)], and inclusion of Mulliken partitioned Slater-charge electrostatics (VEJ∕S). The extent to which the errors increase suggest that using a Slater monopole auxiliary basis increases the errors much more than using a Coulomb approximation forV(2), and therefore an avenue of future development may be to incorporate a more complete auxiliary basis, such as Gaussian multipole expansions,58 for the second-order density response. If the model is based on VE1 (or VE1J), then a complete auxiliary basis can do no better than VE1 (or VE1J), which does not use an auxiliary basis. We see that VE1J∕S has a μUE very close to that of VE1J, so using a more complicated auxiliary basis may only serve to reduce the σUE and maximum error to that of VE1J. One could therefore hypothesize that a VE1J model with a more complicated auxiliary basis may result in a more costly method that does not offer great advantage over VE1J∕S.
CONCLUSION
We have explored the use of approximate density-functional models based on the Kohn–Sham potential energy expansion in both the electron and kinetic energy densities and spin densities, and investigated the effect of base density functional and various integral approximations on the accuracy of the models. It has been demonstrated that the VE to second order, with no additional approximations, reproduces very well the full Kohn–Sham results for a variety of systems. A large source of error, however, is introduced when the first-order integrals are computed using a two-center approximation for the reference densities. The Coulomb approximation for the second-order integrals does not introduce substantial error to molecular dipole moments; however, this work does not explore its effect on geometry. For the cases examined here, there seems to be no substantial advantage to using models based on meta-GGA functionals relative to GGA functionals, both of which are substantially better than LDA functionals for some properties, including hydrogen bonding. Overall, the results indicate that a potentially promising direction for further development of fast, approximate DFT models may involve consideration of atomic orbital basis functions beyond a minimal basis set, and extension of the electrostatic representation of the second-order term to include a more complete auxiliary basis; however, the benefits of doing so would only be garnered via significant recourse in empiricism or removing the other integral approximations altogether.
ACKNOWLEDGMENTS
The authors are grateful for financial support provided by the National Institutes of Health (GM084149). Computational resources from the Minnesota Supercomputing Institute for Advanced Computational Research (MSI) were utilized in this work.
REFERENCES
- Cohen A. J., Mori-Sánchez P., and Yang W., Science 321, 792 (2008). [DOI] [PubMed] [Google Scholar]
- Nam K., Cui Q., Gao J., and York D. M., J. Chem. Theory Comput. 3, 486 (2007). 10.1021/ct6002466 [DOI] [PubMed] [Google Scholar]
- Winget P. and Clark T., J. Mol. Model. 11, 439 (2005). 10.1007/s00894-005-0236-y [DOI] [PubMed] [Google Scholar]
- Kayi H. and Clark T., J. Mol. Model. 13, 965 (2007). 10.1007/s00894-007-0214-7 [DOI] [PubMed] [Google Scholar]
- Rocha G. B., Freire R. O., Simas A. M., and Stewart J. J. P., J. Comput. Chem. 27, 1101 (2006). 10.1002/jcc.20425 [DOI] [PubMed] [Google Scholar]
- Repasky M. P., Chandrasekhar J., and Jorgensen W. L., J. Comput. Chem. 23, 1601 (2002). 10.1002/jcc.10162 [DOI] [PubMed] [Google Scholar]
- Tubert-Brohman I., Guimaraes C. R. W., Repasky M. P., and Jorgensen W. L., J. Comput. Chem. 25, 138 (2004). 10.1002/jcc.10356 [DOI] [PubMed] [Google Scholar]
- Tubert-Brohman I., Guimarães C. R. W., and Jorgensen W. L., J. Chem. Theory Comput. 1, 817 (2005). 10.1021/ct0500287 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin B. and Clark T., Int. J. Quantum Chem. 106, 1208 (2006). 10.1002/qua.20856 [DOI] [Google Scholar]
- Stewart J. J. P., J. Mol. Model. 13, 1173 (2007). 10.1007/s00894-007-0233-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Y., Yu H., York D. M., Cui Q., and Elstner M., J. Phys. Chem. A 111, 10861 (2007). 10.1021/jp074167r [DOI] [PubMed] [Google Scholar]
- Elstner M., J. Phys. Chem. A 111, 5614 (2007). 10.1021/jp071338j [DOI] [PubMed] [Google Scholar]
- Giese T. J. and York D. M., J. Chem. Phys. 123, 164108 (2005). 10.1063/1.2080007 [DOI] [PubMed] [Google Scholar]
- Giese T. J. and York D. M., J. Chem. Phys. 127, 194101 (2007). 10.1063/1.2778428 [DOI] [PubMed] [Google Scholar]
- McNamara J. P. and Hillier I. H., Phys. Chem. Chem. Phys. 9, 2362 (2007). 10.1039/b701890h [DOI] [PubMed] [Google Scholar]
- Tuttle T. and Thiel W., Phys. Chem. Chem. Phys. 10, 2125 (2008). 10.1039/b718795e [DOI] [PubMed] [Google Scholar]
- Řezáč J., Fanfrlík J., Salahub D., and Hobza P., J. Chem. Theory Comput. 5, 1749 (2009). 10.1021/ct9000922 [DOI] [PubMed] [Google Scholar]
- Chang D. T., Schenter G. K., and Garrett B. C., J. Chem. Phys. 128, 164111 (2008). 10.1063/1.2905230 [DOI] [PubMed] [Google Scholar]
- Kumar A., Elstner M., and Suhai S., Int. J. Quantum Chem. 95, 44 (2003). 10.1002/qua.10715 [DOI] [Google Scholar]
- Sattelmeyer K. W., Tubert-Brohman I., and Jorgensen W. L., J. Chem. Theory Comput. 2, 413 (2006). 10.1021/ct050174c [DOI] [PubMed] [Google Scholar]
- Elstner M., Porezag D., Jungnickel G., Elsner J., Haugk M., Frauenheim T., Suhai S., and Seifert G., Phys. Rev. B 58, 7260 (1998). 10.1103/PhysRevB.58.7260 [DOI] [Google Scholar]
- Elstner M., Frauenheim T., Kaxiras E., Seifert G., and Suhai S., Phys. Status Solidi. B 217, 357 (2000). 10.1002/(SICI)1521-3951(200001)217:1357::AID-PSSB3573.0.CO;2-J [DOI] [Google Scholar]
- Sattelmeyer K. W., Tirado-Rives J., and Jorgensen W. L., J. Phys. Chem. A 110, 13551 (2006). 10.1021/jp064544k [DOI] [PubMed] [Google Scholar]
- Elstner M., Theor. Chem. Acc. 116, 316 (2006). 10.1007/s00214-005-0066-0 [DOI] [Google Scholar]
- Perdew J. P., Ruzsinszky A., Tao J., Staroverov V. N., Scuseria G. E., and Csonka G. I., J. Chem. Phys. 123, 062201 (2005). 10.1063/1.1904565 [DOI] [PubMed] [Google Scholar]
- Vosko S. H., Wilk L., and Nusair M., Can. J. Phys. 58, 1200 (1980). 10.1139/p80-159 [DOI] [Google Scholar]
- Perdew J. P. and Wang Y., Phys. Rev. B 45, 13244 (1992). 10.1103/PhysRevB.45.13244 [DOI] [PubMed] [Google Scholar]
- Hamprecht F., Cohen A., Tozer D. J., and Handy N. C., J. Chem. Phys. 109, 6264 (1998). 10.1063/1.477267 [DOI] [Google Scholar]
- Boese A. D. and Handy N. C., J. Chem. Phys. 116, 9559 (2002). 10.1063/1.1476309 [DOI] [Google Scholar]
- Zhao Y. and Truhlar D. G., J. Chem. Phys. 125, 194101 (2006). 10.1063/1.2370993 [DOI] [PubMed] [Google Scholar]
- The molecules in the test set are: BeH, C2H2, C2H4, C2H6, CH2, CH3, CH4, CH4O, CH4S, CH3Cl, CN, CS, HC, HCN, HCO, HF, HCl, LiH, NH, HO, H2O, H2O2, OCl, NO, OS, O2, CO, SiO, CO2, SO2, F2, Cl2, FCl, Li2, LiF, Na2, NaCl, N2, NH2, NH3, N2H4, HOCl, H2CO, P2, PH2, PH3, S2, H2S, SiH2, SiH3, SiH4, and Si2H6.
- Curtiss L. A., Raghavachari K., Redfern P. C., and Pople J. A., J. Chem. Phys. 106, 1063 (1997). 10.1063/1.473182 [DOI] [Google Scholar]
- Frisch M. J., Trucks G. W., Schlegel H. B.et al. , GAUSSIAN 03, revision E.01, Gaussian, Inc., Wallingford, CT, 2004.
- http://comp.chem.umn.edu/mn-gfm.
- Press W. H., Teukolsky S. A., Vetterling W. T., and Flannery W. P., Numerical Recipes in Fortran, 2nd ed. (Cambridge University, Cambridge, 1992). [Google Scholar]
- Lebedev V. I., Russ. Acad. Sci. Dokl. Math. 50, 283 (1995). [Google Scholar]
- Lebedev V. I. and Laikov D. N., Russ. Acad. Sci. Dokl. Math. 59, 477 (1999). [Google Scholar]
- Delley B., J. Comput. Chem. 17, 1152 (1996). 10.1002/(SICI)1096-987X(19960715)17:91152::AID-JCC73.0.CO;2-R [DOI] [Google Scholar]
- Becke A. D., J. Chem. Phys. 88, 2547 (1988). 10.1063/1.454033 [DOI] [Google Scholar]
- Sirkin A., Truhlar D. G., and Amin E. A., J. Chem. Theory Comput. 5, 1254 (2009). 10.1021/ct900038m [DOI] [PubMed] [Google Scholar]
- Amin E. A. and Truhlar D. G., J. Chem. Theory Comput. 4, 75 (2008). 10.1021/ct700205n [DOI] [PubMed] [Google Scholar]
- Feller D., J. Comput. Chem. 17, 1571 (1996). [Google Scholar]
- Schuchardt K. L., Didier B. T., Elsethagen T., Sun L., Gurumoorthi V., Chase J., Li J., and Windus T. L., J. Chem. Inf. Model. 47, 1045 (2007). 10.1021/ci600510j [DOI] [PubMed] [Google Scholar]
- Lynch B. J., Zhao Y., and Truhlar D. G., J. Phys. Chem. A 107, 1384 (2003). 10.1021/jp021590l [DOI] [Google Scholar]
- Frauenheim T., Seifert G., Elstner M., Hajnal Z., Jungnickel G., Porezag D., Suhai S., and Scholz R., Phys. Status Solidi B 217, 41 (2000). 10.1002/(SICI)1521-3951(200001)217:141::AID-PSSB413.0.CO;2-V [DOI] [Google Scholar]
- Sanderson R. T., Chemical Periodicity (Reinhold, New York, 1962). [Google Scholar]
- Table of Interatomic Distances and Configuration in Molecules and Ions, edited by L. E. Sutton (The Chemical Society, London, 1965), Supplement 1956–1959, Special Publication No. 18. [Google Scholar]
- Huheey J. E., Keiter E. A., and Keiter R. L., Inorganic Chemistry: Principles of Structure and Reactivity, 4th ed. (HarperCollins, New York, 1993). [Google Scholar]
- Porterfield W. W., Inorganic Chemistry: A Unified Approach (Addison-Wesley, Reading, MA, 1984). [Google Scholar]
- James A. M. and Lord M. P., Macmillan’s Chemical and Physical Data (MacMillan, London, 1992). [Google Scholar]
- Zhao Y. and Truhlar D. G., Theor. Chem. Acc. 120, 215 (2008). 10.1007/s00214-007-0310-x [DOI] [Google Scholar]
- Bunker P. R. and Jensen P., J. Chem. Phys. 79, 1224 (1983). 10.1063/1.445927 [DOI] [Google Scholar]
- Thomson R. and Dalby F. W., Can. J. Phys. 46, 2815 (1968). [Google Scholar]
- Giese T. J. and York D. M., J. Chem. Phys. 129, 016102 (2008). 10.1063/1.2945897 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79, 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Frauenheim T., Seifert G., Elstner M., Hajnal Z., Jungnickel G., Porezag D., Suhai S., and Scholz R., Phys. Status Solidi B 217, 41 (2000). 10.1002/(SICI)1521-3951(200001)217:141::AID-PSSB413.0.CO;2-V [DOI] [Google Scholar]
- Seifert G., J. Phys. Chem. A 111, 5609 (2007). 10.1021/jp069056r [DOI] [PubMed] [Google Scholar]
- Giese T. J. and York D. M., J. Chem. Phys. 128, 064104 (2008). 10.1063/1.2821745 [DOI] [PMC free article] [PubMed] [Google Scholar]