Water-Proton-Spin-Lattice-Relaxation Dispersion of Paramagnetic Protein Solutions

Abstract

The paramagnetic contributions to water proton spin-lattice relaxation rate constants in protein systems spin-labeled with nitroxide radicals were re-examined. As noted by others, the strength of the dipolar coupling between water protons and the protein-bound nitroxide radical often appears to be larger than physically reasonable when the relaxation is assumed to be controlled by 3-dimensional diffusive processes in the vicinity of the spin label. We examine the effects of the surface in biasing the diffusive exploration of the radical region and derive a relaxation model that incorporates 2-dimensional dynamics at the interfacial layer. However, we find that the local 2-dimensional dynamics changes the shape of the relaxation dispersion profile but does not necessarily reproduce the low field relaxation efficiency found by experiment. We examine the contributions of long-range dipolar couplings between the paramagnetic center and protein-bound-water molecules and find that the contributions from these several long range couplings may be competitive with translational contributions because the correlation time for global rotation of the protein is approximately 1000 times longer than that for the diffusive motion of water at the interfacial region. As a result the electron-proton dipolar coupling to rare protein-bound-water-molecule protons may be significant for protein systems that accommodate long-lived water molecules. Although the estimate of local diffusion coefficients is not seriously compromised because it derives from the Larmor frequency dependence, these several contributions confound efforts to fit relaxation data quantitatively with unique models.

Introduction

Liquid dynamics at surfaces and macromolecular interfaces may impact the efficiency of surface exploration, intermolecular recognition and macromolecular function. Nuclear spin-lattice relaxation rates of liquid spins measured as a function of magnetic field strength provide a characterization of the molecular rotational and translational dynamics. The difficulty in characterizing surface dynamics by magnetic resonance is that the population of molecules at the interface generally mixes by exchange with the total population of observed molecules in a time short compared with the relaxation times in either environment. This mixing dilutes and averages the surface dynamics of the observed molecule spins with those of the bulk; however, an approach to characterizing surface dynamics is to localize a paramagnetic center on the interface and measure the paramagnetic contribution to the total observed spin-lattice relaxation rate constant. The electron-nuclear dipolar contribution to the relaxation is generally large compared with the diamagnetic contributions and also falls rapidly with distance from the paramagnetic center. Thus, the motions of the observed diffusing molecule relative to the surface localized paramagnet may be characterized in the immediate vicinity of the paramagnetic center [1-4]. In these cases, the spectral density functions needed for the intermolecular electron-nuclear relaxation equations are generally derived from translational diffusion models [5-7]. Although the translational correlation times or diffusion constants for relative motion of water in the vicinity of the surface bound paramagnetic centers deduced from these measurements using relaxation equations derived for 3-dimensional diffusion of the interacting spins are not in significant disagreement with other measurements, the protein case does not always provide a satisfying quantitative fit for the relaxation data with physically reasonable parameters. In particular, for a protein spin-labeled with a nitroxide, the nuclear spin-lattice-relaxation data fit to a 3-dimensional diffusion model often yields a distance of closest approach that is short compared with the sum of van der Waals distances of the interacting atoms; i.e., the apparent strength of the electron-nuclear dipolar coupling is too large. Understanding the origin of this problem is important to understanding both the local translational dynamics of small diffusing solutes or solvents in interfacial regions and the use of paramagnetic additives as relaxation or contrast agents in medical imaging and other applications. This paper examines the origins of this larger than expected dipolar-coupling strength for the paramagnetic contributions to water-proton relaxation in protein solutions.

In the case that the paramagnetic center is not chemically bound to the molecule observed in the relaxation experiment, the electron-nuclear dipolar coupling between a paramagnet and the observed protons in solution is made time dependent by the relative translational motion of the diffusing molecules. If the electron-spin relaxation times are short compared with the translational correlation time, as in many metal ion systems, the dipolar coupling may fluctuate with the relaxation time of the electron spin [6]; however, if the electron-relaxation time is long compared with these correlation times, the spin state of the electron is essentially constant on the time scale for diffusion and the relative translational motion dominates the fluctuations that drive the nuclear spin relaxation [5; 7]. For nitroxide radicals, the electron-relaxation times are long and easily satisfy the criteria for analysis of relaxation dispersion profiles using diffusion models that do not include electron-spin relaxation.

The nuclear relaxation models generally used were derived assuming that the nuclear accessibility to the electron spin is uniform from all directions. However, if the paramagnetic center is located at an interface, the accessibility may be asymmetric because the macromolecule or surface excludes approach from some directions. For example, an electron spin located on a plane surface would suffer a relaxation reduction by a factor of 2 because the electron spin may be approached by the nuclear spin from only one side of the plane. Therefore, the relaxation efficiency of a spin-labeled macromolecule may be a function of how closely and how rigidly the paramagnetic center is bound to the surface because of this geometric factor [8-10].

A different issue for spin relaxation at interfaces is the character of the diffusive process itself. If the paramagnet is attached sufficiently close to the surface, the diffusion of the exploring molecule is biased by the close proximity of the excluded volume imposed by the surface, and the time dependence of the re-encounter probability between the nucleus and the paramagnet is proportional to 1/t. As a consequence, the spectral density functions characterizing this motion are logarithmic in the Larmor frequency [11]. The logarithmic magnetic field dependence of the spin-lattice relaxation rate has been observed in high surface area inorganic systems, but recent data suggest that these observations are more general and found in protein systems as well [12; 13]. X For a protein in solution, the spectral density formulation is slightly different from that of a lamellar solid structure and we explore the solution case in the present work to determine whether the change in dimensionality of diffusive exploration at the interface may account for the apparent increase in the electron-nuclear dipolar coupling strength. We will show that the main consequence of 2-dimensional diffusive exploration at the interface is to change the shape of the relaxation dispersion profile but not change the magnitude of the low-field relaxation rate very much unless the surface lifetimes are very long. We show that the discrepancy in the apparent dipolar coupling strength may be resolved by considering the effects of long-range dipolar coupling between the protein-bound paramagnet and protons of rare protein-bound-water molecules that reorient with the slow rotational motion of the protein.

Experimental

The nuclear spin-lattice-relaxation-rate constants were measured at proton Larmor frequencies between 0.01 and 30 MHz using a Stelar FFC-2000 spectrometer (Stelar, Mede, Italy) that switches rapidly from a large polarization field, typically 30 MHz, to a variable evolution field and finally to a convenient detection field to provide a relaxation dispersion profile over a wide range of field strengths at essentially a constant signal-to-noise ratio. Free induction decays were recorded after a single 90° excitation pulse (5.5 μs) applied at 15.8 MHz. Sample temperatures were regulated at 25°C using a Stelar VTC90 variable temperature controller. ¹H relaxation rate constants between 36 and 300 MHz were measured using the fringe field of a 7.05 T magnet (Magnex Scientific, Oxford, UK) operating in conjunction with a Tecmag Apollo transceiver (Tecmag, Houston, TX), an AMT power amplifier (American Microwave Technologies, Brea, CA) and a transmission line probe constructed in this laboratory [14].

BSA (Fraction V, Sigma-Aldrich) used for non-covalent spin-labeling with 5-DOXYL- stearic acid (Aldrich Chemical Co., bought as a powder) was purified by dialysis against deionized water, then lyophilized to constant weight at ambient temperature using a mechanical pump. Phosphate buffer (20 mM, pH 7) was prepared using sodium phosphate dibasic (Fisher Scientific) and phosphoric acid (Mallinckrodt). Chloroform was purchased from Sigma-Aldrich. The solution of BSA with non-covalently bound 5-DOXYL-stearic acid was prepared as described by Ge et al. (1990, #116). Bovine Serum Albumin with blocked SH-groups was prepared by combining 5 ml of 1.6 mM BSA (used without preliminary purification) in 50 mM HEPES (sodium salt, Sigma) buffer at pH 7.8 with excess of methylmethanethiol-sulfonate (Aldrich, 97%) dissolved in 600 μL of dimethylformamide (Fisher Scientific) and incubated at 30°C overnight followed by dialysis against 0.15 M sodium chloride solution, then against deionized water. The resulting sample was lyophilized to constant weight at ambient temperature. Sulfhydryl content was monitored using Ellman's reaction with native and modified BSA samples (DTNB and L-cysteine from Sigma Chemical Co.) in 0.1 M phosphate buffer at pH 8 in conjunction with freshly prepared cysteine standards for calibration and a Varian Cary 4E operating at 412 nm. This procedure confirmed the absence of SH-groups in the modified BSA and the presence of approximately 0.5 moles of SH groups per mole of unmodified commercial protein.

BSA, SH-blocked BSA, and ribonuclease A were spin-labeled with 4-maleimide –TEMPO (Aldrich Chemical Co., St. Louis, MO) using 2-fold molar excess of spin-label in 50 mM phosphate buffer at pH 8 overnight at laboratory temperature. Each protein solution was then dialyzed exhaustively to remove unbound spin-label and lyophilized to constant weight.

CW electron spin resonance measurements were conducted using a Varian E-line 102 Series X-band spectrometer equipped with a Miteq microwave preamplifier (Hauppauque, NY, USA). All spectra were collected at a nominal microwave power of 2.0 mW and 1.0 G modulation amplitude. Calibration plots were obtained using the integrated intensities of EPR absorption signals from the nitroxide spin standards prepared from 4-Hydroxy-TEMPO (Aldrich Chemical Co.). Concentrations of the standard solutions were verified by measuring their optical absorption at 429 nm (ε = 13.4 M^-1cm^-1) [15; 16] In order to improve accuracy nitroxide standards were prepared to contain up to 84% glycerol by weight so that line widths and amplitudes of the EPR signal in standards and protein-bound samples were comparable.

Results

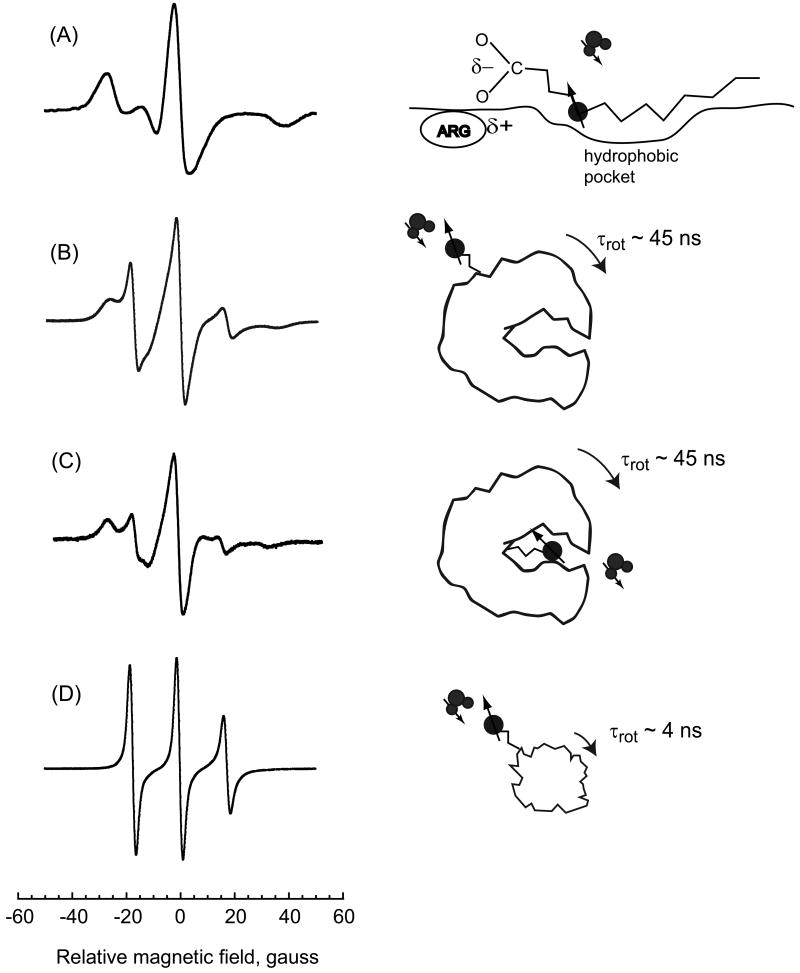
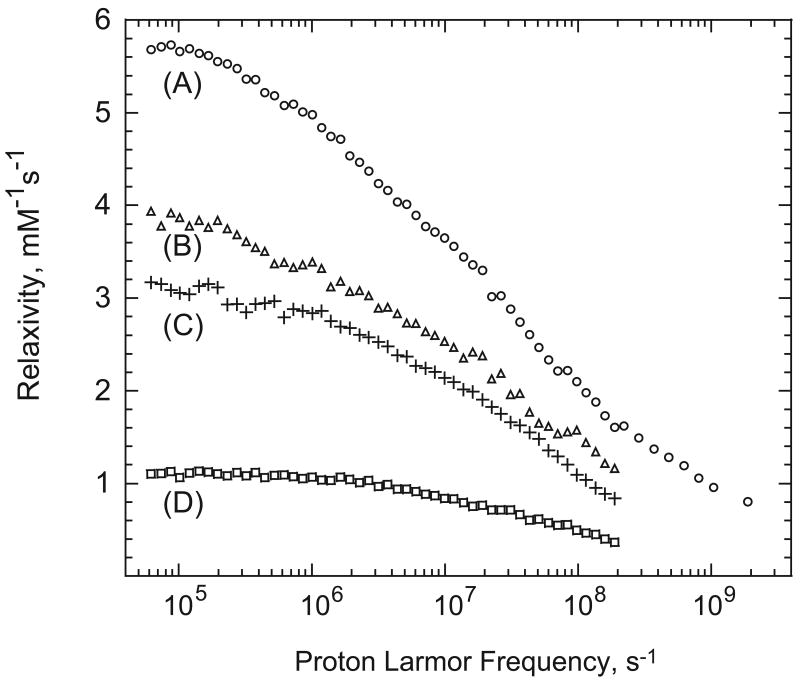
ESR spectrum for bovine serum albumin labeled with the 5-doxyl stearic acid spin label (5-DSA), which binds to the fatty acid binding sites of bovine serum albumin (BSA) is shown in Fig. 1, curve A. This spectrum reproduces well that reported by Ge and others who concluded that the ESR spectrum for the nitroxide bound in these sites showed minimal local flexibility for the spin label X [17; 18]. This spin label was used for the present study to place the spin label in the interface with minimal bound-state flexibility. The relaxation dispersion profile for this sample is shown in Fig. 2 curve A and this strong immobilization gives the highest relaxivity of the several spin-labeled proteins studied. Curves B and C of Figs. 1 and 2 summarize data taken on bovine serum albumin spin-labeled with maleimide-TEMPO BSA and BSA with blocked SH-groups spin labeled with maleimide-TEMPO which is similar to earlier work [19]. The relaxivity of these modifications is lower in part because the coupling tether is longer than that for curve A. The ESR spectrum for ribonuclease A, curve D of Fig. 1 is relatively narrow and the flexibility of the spin-label is high [20]. The water proton relaxivity shown in curve D of Fig. 2 is the lowest among the samples shown.

Figure 1.

X-band ESR spectra. A) bovine serum albumin with non-covalently bound 5-doxyl steric acid spin-label; B) bovine serum albumin spin-labeled with maleimide-TEMPO covalently bound to cysteine SH; C) bovine serum albumin spin-labeled with maleimide-TEMPO covalently bound to lysine (SH blocked); and D) ribonuclease A spin-labeled with maleimide-TEMPO at lysine.

Figure 2.

The paramagnetic contribution to the water proton spin-lattice relaxivities as a function of magnetic field strength plotted as the ¹H Larmor frequency at 298 K. A) bovine serum albumin spin-labeled with 5-doxyl stearic acid; B) bovine serum albumin with 1 equivalent of maleimide-TEMPO; C) bovine serum albumin with blocked SH and 1 equivalent of maleimide-TEMPO; D) ribonuclease A spin-labeled with maleimide-TEMPO.

The paramagnetic contribution to the water-proton-spin-lattice-relaxation-rate constant spin-labeled with 5-DSA is large for a spin ½ system. The paramagnetic contribution to the relaxation profile has a low field plateau and a dispersion that is stretched considerably compared with the Lorentzian functions characteristic of rotationally correlated first coordination sphere effects [21]. As in earlier reports [3], a fit of these data to the 3-dimensional diffusion model [6; 7] yields a distance of closest approach that is shorter than the sum of van der Waals radii for the nitrogen or oxygen atom of the nitroxide and the water-molecule-hydrogen atom. Therefore, there are additional factors or mechanisms that contribute to the observed water-proton relaxation rate constant in these solutions of spin-labeled albumin.

It was recently suggested that at the water-protein interface, the effective dimensionality for the diffusive exploration of the protein by water is reduced with the consequence that the relaxation dispersion profile becomes a linear function of the logarithm of the Larmor frequency [12]. A change in dimensionality from 3 to 2 causes an increase in the re-encounter probability between the diffusing nuclear spin and the electron spin that is fixed at the surface with a consequent change in the relaxation dispersion profile compared with the 3-dimensinoal case. We examine first the effects of diffusive dimensionality on the magnitude and magnetic field dependence of the water proton spin-lattice relaxation rate.

Relaxation Theory for 2-dimensional surface effects

Spatially confined systems force more frequent reencounters between diffusing liquid molecules and surface paramagnetic relaxation sinks. In the fast exchange limit where the exchange time between the surface and the bulk phases is shorter than the relaxation times in either environment, the overall proton relaxation rate 1/T₁ is a weighted sum of a bulk 1/T_1,bulk and a surface relaxation rate [22]. For a paramagnet immobilized on a protein, we assume that the surface relaxation rate is a superposition of the contribution 1/T_1,2D of the proton species diffusing in the proximity of the immobilized paramagnetic species and the contribution 1/T_1M of the proton species coordinated to the paramagnetic center, i.e., a first coordination sphere contribution [23],

$$\frac{1}{T_1({\omega }_I)}=\frac{1}{T_{1,\mathit{\text{bulk}}}}+\frac{N_{\mathit{\text{Surf}}}}{N}\frac{1}{T_{1,2D}({\omega }_I)}+\frac{N_M}{N}\frac{1}{T_{1M}({\omega }_I)}.$$ (1)

The bulk diamagnetic relaxation term, 1/T_1bulk, has no magnetic field dependence in the range studied here because the Larmor frequency ω_I is much smaller than the reciprocal of either the rotational or translational correlation time for all accessible magnetic fields [24]. We focus in this discussion on the outer sphere or diffusional contribution to spin-lattice relaxation. For most organic radicals like the nitroxides used here, there are no long-lived-water molecules in a first coordination sphere like those provided by metals; therefore, the electron-nuclear coupling is modulated by the relative translational motions of the two spin-bearing molecules and we drop the last term of Eq. (1). The ratio N_Surf/N=λS_pρ_liquid is the fraction of liquid molecules diffusing within a transient layer of thickness λ at the surface as shown in (Fig. A1); λ is of the order of the molecular diameters of the diffusing liquid [25], S_p is the specific surface area of the system, N the total number of molecules in the system, and ρ_liquid is the density of the proton liquid. Assuming a uniform distribution of paramagnetic sites on the surface, the surface density σ_S = (η_sρ_solidξ)= N_s / A_p, where η_S, the number of paramagnetic species per gram of protein, may be measured by electron spin resonance methods, ξ the effective surface depth, N_s is the number of spins per protein molecule, and A_p the surface area of the protein.

We consider a proton bearing liquid diffusing in the proximity of the protein-liquid interface. Although we suppose that the interface is locally flat (Fig. A1), we have shown that the frequency dependence is similar in a thin spherical layered geometry [12]. Because the magnetic moment of the paramagnetic species is large (γ_S = 658.2 γ_H), the nuclear spin-lattice relaxation is dominated by the intermolecular dipolar coupling between the electron spins, S, that is modulated by the translational diffusion of the mobile spins, I, in the interface of the slowly moving macromolecule. The interfacial nuclear spin-lattice relaxation rate constant is given formally by the general expression:

$$\frac{1}{T_{1,2D}({\omega }_I)}=\frac{2}{3}{({\gamma }_I{\gamma }_S\hslash )}^{2}S(S+1)\left[\frac{1}{3}{J}_L^{(0)}({\omega }_I-{\omega }_S)+J_L^{(1)}({\omega }_I)+2J_L^{(2)}({\omega }_I+{\omega }_S)\right]$$ (2)

where the Larmor frequencies of the electron and proton are related by ω_S=658.2ω_I when I is ¹H. The spectral densities J_L^(m)(ω) (m=0, ±1, ±2), in the Laboratory frame (L) associated with the constant magnetic field B₀ (Fig. A1) are the exponential Fourier transforms,

$$J_L^{(m)}(\omega )=\underset{-\infty }{\overset{+\infty }{\int }}{G}_L^{(m)}(\tau )e^{-i\omega \tau }d\tau ,$$ (3)

of the stationary pairwise dipolar correlation functions G_L^(m)(τ) {m∈(−2,+2)} given by:

$$G_L^{(m)}(\tau )=\langle F_L^{(-m)}(t)F_L^{(-m)}\ast (t+\tau )\rangle .$$ (4)

Equation (4) describes the persistence of the autocorrelation of the dipole-dipole interaction F_L^(m)(t) between the magnetic moments associated with the spins I and S and modulated by the translational diffusion during a short time interval τ. The notation <…> stands for the ensemble average over all the positions of the spins I at time 0 and τ for a given surface density σ_S of spins S. This ensemble average can be expressed as an integral average over the normalized diffusive propagator P(r₀, r, τ):

$$G_L^{(m)}(\tau )=\int d{\stackrel{\rightharpoonup }{r}}_{0}p({\stackrel{\rightharpoonup }{r}}_0)F_L^{(-m)}(0)\int d\stackrel{\rightharpoonup }{r}P({\stackrel{\rightharpoonup }{r}}_0,\stackrel{\rightharpoonup }{r},\tau )F_L^{(-m)}\ast (\tau )$$ (5)

where p(r₀)=σ_S/λ represents the uniform density of spin pairs I-S at equilibrium. The calculations of Eq. (5) include the following steps as summarized in Appendix A.

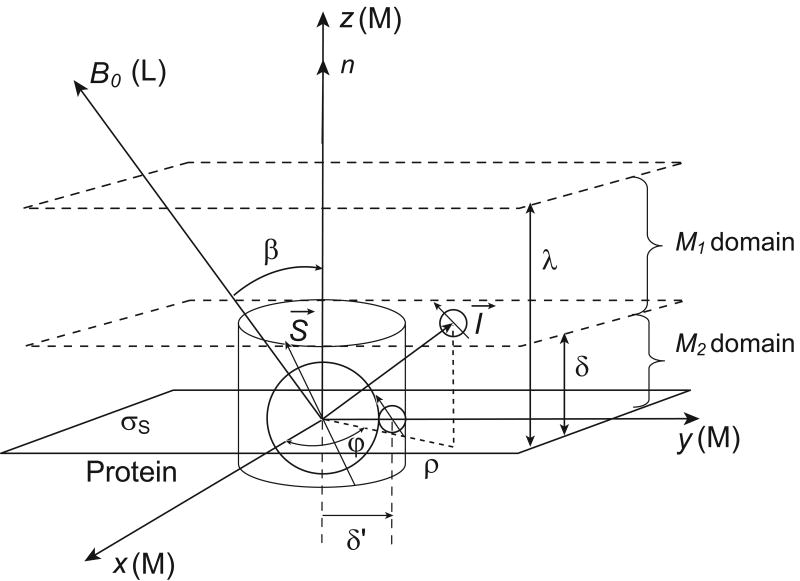
1. We use the anisotropic dynamical model shown schematically in Fig. A1 with an unbounded and isotropic diffusion perpendicular to the surface normal axis n and a bounded diffusion along such an axis. We consider an axial diffusion tensor where D_{I ∥} and D_I⊥ are the coefficients of translational diffusion of spins I in direction parallel and perpendicular to n.

2. We estimate the pair-wise dipolar correlation functions G_L^(m)(τ) for times τ much longer than the transverse diffusion correlation time τ_m = δ²/(4D_I⊥) where δ is the molecular size of the I spin-bearing molecule with a translational diffusion coefficient D_I⊥ in direction perpendicular to n.

3. We introduce the effects of the finite time of residence τ_S≫τ_m at the protein surface by an exponential cut-off in the time dependence of the pair correlations I-S.

4. We take a powder average of J_L^(m)(ω) over all the orientations of the n direction relative to the constant direction of the magnetic field B₀.

Substitution of Eq. (A10) into Eq. (2) leads, at frequencies small compared with the reciprocal of the translational correlation time, to the spin-lattice relaxation rate of the 2-dimensional diffusion of water in proximity to the protein surface:

$$\frac{1}{T_{1,2D}({\omega }_I)}=\frac{\pi }{15}\left[\frac{{\sigma }_S}{({\lambda }^2\delta {\prime }^2(1+x^2))}\right]{({\gamma }_I{\gamma }_S\hslash )}^{2}S(S+1){\tau }_m\left[3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_I^2{\tau }_m^2}\right)+7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_S^2{\tau }_m^2}\right)\right]$$ (6)

Here x = δ/δ' is a parameter introduced in Appendix A for taking into account a variable distance δ′ of minimal approach between spins I and S compared to the molecular size δ Eq. (6) has a bi-logarithmic dependence on the magnetic field strength caused by the contributions at the nuclear and electron Larmor frequencies. Eq. (6) contains two correlation times: the translational correlation time, τ_m, associated with individual translational jumps by molecules in the interface, and the residence time of the observed molecules in the interface, τ_s. τ_s limits the correlation between the I and S spins in the 2-dimensional interfacial layer.

Finally, substitution of Eq. (6) into Eq. (1) with N_Surf/N= λS_Pc_Pρ_liquid where c_P is the mass of protein per mass of liquid, and ignoring first coordination sphere contributions gives the spin-lattice relaxation rate constant for molecules mixing between the spin-labelled surface layer and the bulk,

$$\frac{1}{T_1({\omega }_I)}=\frac{1}{T_{1,\mathit{\text{bulk}}}}+\lambda S_P{c}_P{\rho }_{\mathit{\text{liquid}}}\frac{\pi }{15}\left[\frac{{\sigma }_S}{({\lambda }^2\delta {\prime }^2(1+x^2))}\right]{({\gamma }_I{\gamma }_S\hslash )}^{2}S(S+1){\tau }_m\left[\begin{array}{c}3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_I^2{\tau }_m^2}\right)\\ +7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_S^2{\tau }_m^2}\right)\end{array}\right].$$ (7)

If we use the definition of the 2D translational correlation time τ_m = δ²/(4D_I⊥) and write this equation in terms relevant to the solution where the molecular properties of the spin-labelled protein are known as shown in Appendix B,

$$\frac{1}{T_1({\omega }_I)}=\frac{1}{T_{1,\mathit{\text{bulk}}}}+\frac{\pi }{60}{({\gamma }_I{\gamma }_S\hslash )}^{2}S(S+1)\frac{N_A[S]}{1000D_{\perp }\lambda }\frac{x^2}{1+x^2}\left[\begin{array}{c}3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_I^2{\tau }_m^2}\right)\\ +7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{({\tau }_m/{\tau }_s)}^2+{\omega }_S^2{\tau }_m^2}\right)\end{array}\right]$$ (8)

where N_A is Avogadro constant and [S] is the molar spin concentration.

This model accounts for the paramagnetic relaxation associated with the interfacial layer, but not with diffusion of the observed molecules outside the interfacial layer. Therefore, we add a contribution using the 3-dimensional model with a distance of closest approach that starts at the outside of the surface layer and extends to infinity [5-7]. This long range 3-dimensional contribution adds a non-logarithmic term to the magnetic field dependence. We note that a nearly logarithmic dependence has been previously reported for spin-labeled hemoglobin which was analyzed in terms of a distribution of local sticking times [13]. While a distribution of interfacial water interactions is likely, the effects of 2-dimensinoal diffusive exploration may be at least as important.

Comparison with Experiment

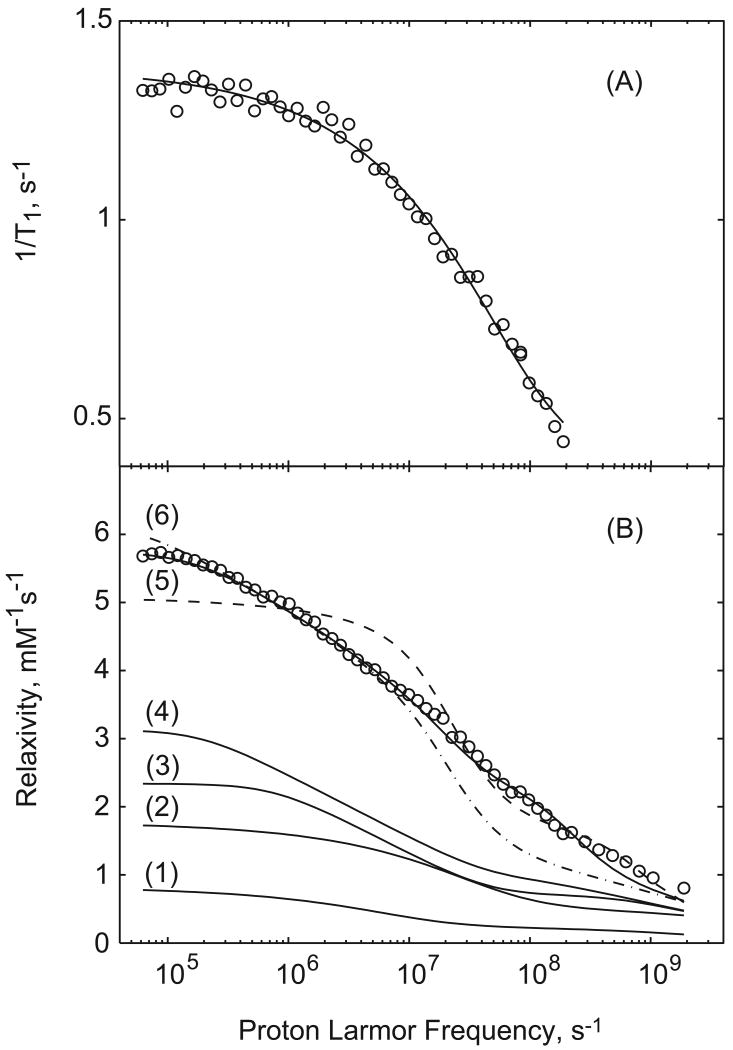
Curve 1 of Fig. 3B shows the 3-dimensional model computed for a 1 mM solution of a spin-1/2 radical with long electron relaxation time using the model of Hwang and Freed [7] with the distance of closest approach set at 5.6 Å, i.e., outside the first surface layer, and the translational diffusion constant at 6×10^-6cm²s^-1. Curve 2 of Fig. 3B shows the contribution from 3-dimensional diffusion with the distance of closest approach set at 2.6 Å and the translational diffusion constant set at 6×10^-6 cm²s^-1, i.e., no surface layer exclusion. In neither case was a geometrical factor used to compensate for the difficulty of approach from the surface side. Both curves are well below the magnitude of the observed experimental data set. Curves 3 and 4 are just 2-dimensional contributions computed from Eq. (8) with the translational jump time τ_m= 33 ps and τ_s = 2 ns and 8 ns respectively. The logarithmic dependence is apparent in the transition region of the profile, and the position and amplitude of the low-frequency plateau is determined by the surface residence time. The sum of curves 1 and 4 provides a model where the surface layer is constrained to an effective 2-dimensional motion; outside this layer, the motion is effectively 3-dimensional. Nevertheless, with this choice of the surface residence time, the low field rate constant is not very different from the 3-dimensional case alone; however, the shape in the transition region is different. The low field rate constant increases with increasing surface residence time and the logarithmic dependence extends to lower magnetic field strengths; however, there is not strong evidence for the surface residence times significantly longer than a few ns. Nevertheless, neither of the two curves provides a reasonable approximation to the data in Fig. 2, curves A-C; an additional relaxation pathway for the paramagnetic contribution is required.

Figure 3.

A) 1.2 mM Ribonuclease A spin-labeled with maleimide-TEMPO fit with the 3-dimensinoal diffusion model only using a distance of closest approach, b = 2.5 Å and a translational diffusion constant D= 9.7 × 10^-6 cm²s^-1. B) The data of Fig. 1(A) for 0.6 mM spin-labeled BSA fit in various ways: (1) just 3-dimensional diffusion with b=5.6 Å and D=6×10^-6 cm²s^-1; (2) just 3-dimensional diffusion with b = 2.6×10^-8 and D=6×10^-6 cm² s^-1; (3) just the 2-dimensionial diffusion contribution with τ_m=33 ps and τ_s=2 ns; (4) just 2-dimensional diffusion contribution with τ_m = 33 ps and τ_s = 8 ns. The solid line at the top is a sum of contributions 1 and 4 with the rotationally correlated contribution assuming a correlation time of 45 ns, S² =0.1, and a fast correlation time of 5 ns where N=38 and the unrealistic assumption that all water spins are 8 Å from the paramagnet. These parameters are not unique.

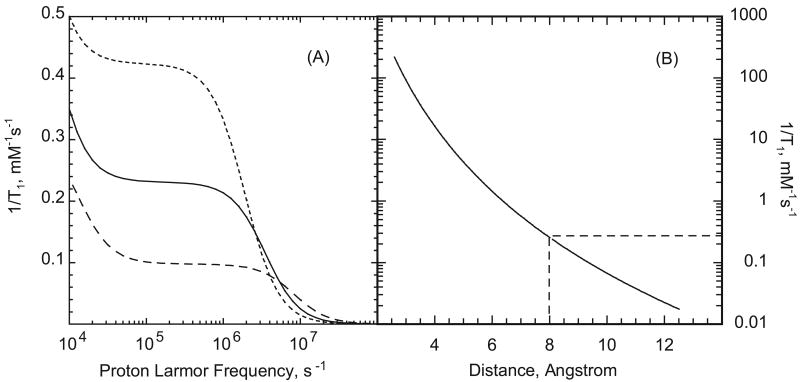
A unique feature of many proteins is that there may be long-lived water binding sites. The number of long-lived water sites is small compared to the total number of water contacts with the protein and is usually in the range 0-3 water molecules/10 kD as measured by the solution phase MRD on the diamagnetic protein [26; 27]. The actual measurement gives the product NS² where S is the generalized order parameter 0<S<1, and N is the number of bound molecules. For bovine serum albumin NS² is 25±3, [27; 28]. The characteristics of these water molecules is that they are bound to the protein for a time longer than the rotational correlation time of the protein; i.e., at least 100 ns for albumin. In the present context a critical feature of these long-lived protein-bound water molecules is that the protons may have a dipolar coupling to the electron magnetic moment. In addition, if the electron relaxation time is long as it is for organic radicals, the correlation time for this dipolar coupling is the slow global rotational correlation time of the protein. The relaxation equations for rotationally correlated electron-nuclear coupling usually referred to as the Solomon, Bloembergen, Morgan equations are widely known [21] and not reproduced here; we note that the relaxation rate constant is the sum of Lorentzian terms and the efficiency is proportional to the correlation time and inversely proportional to the sixth power of the inter-moment distance. Although the inter-moment distance for an electron coupling to a long-lived water molecule proton may exceed 10 Å, which would make the contribution small, the rotational correlation time for the protein is of order 50 ns, which is on the order of 1000 times the relative translational correlation times for the solvent in the interfacial region. Thus, even water molecules distant from the spin label may make detectable contributions to the total paramagnetic relaxation rate constant that add to the translational contribution. Figure 4(A) shows the magnetic field dependence of the rotationally correlated water proton coupling to a nitroxide bound to serum albumin normalized to 1 mM of spin-labeled protein computed assuming a correlation time of 50 ns. The low field portion of the dispersion is incomplete because very low nuclear Larmor frequencies are necessary to display the low field plateau. Taking the nuclear Larmor frequency at 100 kHz, Figure 4(B) shows the magnitude of the rotationally correlated contribution of protein-bound nitroxide as a function of intermoment distance. Although the contribution falls rapidly with distance, the long correlation times make the contributions competitive with the translational contribution. The dashed lines in Fig. 4(B) show the relaxation rate constant for a distance of 8 Å at field strength corresponding to a proton resonance frequency of 100 kHz; this calculation of 0.26 s^-1 is normalized per mM of protein bound water molecules. For a water-rich protein like albumin, this relaxation contribution depends on the distance to each bound water molecule, but there will be at least 25 potentially contributing water molecules for the BSA case. For some proteins, therefore, a rotationally correlated contribution to the water-proton-electron-relaxation rate may be quite important and adds a Lorentzian contribution to the relaxation dispersion at the rotational correlation time of the protein. This contribution may directly account for the large relaxation rates at low magnetic field as shown in Fig. 2 but not modeled satisfactorily by diffusion contributions alone.

Figure 4.

A) Paramagnetic relaxation contributions from rotationally correlated coupling between a protein-bound nitroxide and a protein-bound water molecule as a function of the proton Larmor frequency. Rotational correlation times are 20, 50, and 100 ns increasing from bottom to top, the protein concentration is set at 1.0 mM, and the inter-moment distance is set to 8 Angstroms. B) Paramagnetic relaxation contributions from rotationally correlated coupling between a protein-bound nitroxide and a protein-bound water molecule at a proton Larmor frequency of 100 kHz as a function of inter-moment distance assuming that the rotational correlation time is 50 ns and the water molecule exchange is 10⁶ s^-1.

In summary, there are possibly four different contributions to the paramagnetic relaxation rate constant for water protons in a solution of a protein spin-labeled with a long T_1e paramagnet: 1) the surface 2-dimensional diffusion contribution; 2) the 3-dimensional diffusion contribution; 3) the possible effects of a distribution of surface correlation times; and 4) the effects of electron-nuclear dipolar couplings modulated by the slow stochastic rotation of the protein. This list creates a number of difficulties for obtaining satisfactory quantitative analysis of the experimental data: 1) The several contributions to the observed relaxation profile have different shapes as a function of Larmor frequency but there are no sharp features that make fitting sums of contributions particularly reliable or unique. 2) Generally, one does not know either the number or the distances between the bound paramagnetic center and the rare bound water molecules in the protein so that one cannot compute a discrete sum of contributions in building a quantitative relaxation equation. 3) Any distribution associated with the diffusive behavior in the interface whether it is lifetimes or effective diffusion constants that vary because of the surface heterogeneity additionally confound quantitative description with parameters that may not be unique.

Recognizing these difficulties, inclusion of a rotationally correlated contribution that assumes the rotational correlation time of the protein with an adjustable scaling parameter for the amplitude improves the fit to the relaxation data in Fig. 2, but reveals additional features. An adjustable scaling parameter is necessary because we do not know the number of or the precise distances between the bound-water molecules and the nitroxide. Nevertheless, there are still significant discrepancies at the highest frequencies. This observation is expected if one considers that a long-lived-bound water molecule may experience some local motion in the binding site, which reduces the magnitude of the low-field relaxation rate in proportion to S² and adds a small high frequency dispersion [29; 30]. A similar deviation is expected if some water molecules near the paramagnet have bound-state lifetimes that are shorter than the rotational correlation time of the protein. In either case there will be a dispersion at a frequency characteristic of the local motion or lifetime. Adding an adjustable Lorentzian contribution to the relaxation equation to account for these local effects yields the fit shown in Fig. 3(B) by the solid line at the top. It is not possible to assign the high-field correlation time or times uniquely; however, the contribution is in the range of 1-10 ns for the data of Fig. 2 curve A.

In earlier studies of spin-labeled phospholipids and glass surfaces [4], the 3-dimensional model fits the data with reasonable parameters. In the glass case [4], there is not likely to be a significant population of long-lived-bound water molecules that would provide a rotationally correlated coupling. In addition, the surface binding tether used was not particularly short, so that the spin-label was not precisely at the surface making water accessibility to the spin label more uniform and 3-dimensional diffusion a more likely dominant contribution to the electron-nuclear correlation function. In the phospholipid case [1], three spin-labels were used with similar results when analyzed using the 3-dimensional model. That analysis, we note, did not include a geometrical factor which may be of order 0.5 for access to the spin label in a lipid interfacial environment, which is also a cause for the large value of the distance of closest approach. It is far less likely than in the protein case that there are long-lived-water-molecule binding sites at the lipid interface to provide long correlation times for the electron-nuclear coupling. Further, the relatively large amplitude motions of the lipid which are fast compared with the relaxation times measured cause significant averaging of the orientation and dipolar couplings.

Ribonuclease A is a small (13.7 kD) protein compared with bovine serum albumin and solution phase MRD experiments show that the coupling of the protein rotational motion to the water-spin-lattice-relaxation time is weak [31; 32]. Therefore, a rotationally correlated paramagnetic contribution from protein-bound water for spin-labeled ribonuclease A is expected to be much smaller than for the BSA case for two reasons: the protein rotational correlation time is approximately 5-10 times smaller and the number of bound water molecules is smaller by a factor of order 25 for ribonuclease A. Figures 1 and 2 show the ESR and MRD profiles for Ribonuclease A labeled with a maleimide-TEMPO spin label. The ESR spectrum is much narrower than that for spin-labeled albumin indicating that motion of the nitroxide on the tether of the protein is significant. The MRD profile is shifted to higher magnetic field strengths and fit well by the 3-dimensional diffusion model only with a distance of closest approach of 2.5 Å as shown by Fig. 3(A). Therefore, the rotationally correlated contribution to the paramagnetic relaxation is unimportant for spin-labeled ribonuclease A which is consistent with the relative absence of long-lived water binding sites on the protein. Further, this spin label is not strongly localized at the surface as shown by the ESR spectrum in Fig. 1(D) and a 2-dimensional diffusive contribution is not detected.

The paramagnetic center may relax the protein protons including labile protein protons and the relaxation effects transmitted to the water proton pool by chemical exchange of protons. As in the protein-bound-water exchange case, there will be a distribution of distances between the labile protein protons and the nitroxide such that the distant sites are unimportant. However, proton exchange from amino, amide, hydroxyl, and caboxyl sites in protein functional groups are generally much slower than water-molecule exchange but depends on pH. The relaxation rate contribution to the water depends on the mean lifetime for exchange according to the equation

$$\frac{1}{T_1}-\frac{1}{T_{1o}}=\frac{P}{T_{1b}+{\tau }_{ex}}$$

where T_1b is the relaxation time of the bound and labile proton at the protein site, and τ_ex is the mean lifetime at the site. In the case where the lifetime is large compared with the relaxation time of the bound proton, the exchange time dominates the denominator and the total contribution is small or negligible. Proton exchange rates in protein systems are generally first order in hydroxide ion concentration so that contributions from labile proton exchange may become more important at high pH values and add to the paramagnetic water-exchange-relaxation pathway in a similar way.

Conclusion

The analysis of paramagnetic contributions to nuclear spins relaxed by protein bound radicals with long electron spin-lattice relaxation times in solution may be complicated by two additional factors that may be unimportant in other cases. If the spin-label is embedded in the surface, the geometrical constraints on diffusion may reduce the dimensionality of the diffusive exploration process and change the shape of the spin-lattice relaxation profile. The importance of reduced dimensionality is greater the longer the diffusing molecule is confined to the surface. If there are long-lived small molecule binding sites on the protein, a rotationally correlated relaxation contribution may be important even if the binding site is at significant distance from the paramagnetic center because of the large magnitude of the protein rotational correlation time compared with the correlation times for relative diffusion of the spins. These complications may make detailed quantitative interpretation of paramagnetic effects on diffusing small molecules difficult and not unique. Nevertheless, the magnetic field dependence of the water proton spin-lattice relaxation rate constant in spin-labeled protein systems will still provide a reasonable assessment of the relative correlation time for translational diffusion in the interfacial region because the value of the diffusion coefficient is determined mostly by the Larmor frequency dependence rather than the magnitude of the relaxation rate constant. In the case that the paramagnetic center is a metal ion, similar contributions may be important including contributions from long-lived water molecules at some distance from the paramagnetic center. However, the effects from rotational correlation may be truncated when the electron-spin-lattice-relaxation time is short compared with the global protein rotational correlation time, which is the usual case for a protein-bound metal system. Two-dimensional effects are expected to be important for nanoparticulate systems with paramagnetic sites and for molecularly dense systems such as some biological tissues where effective surface entrapment may be caused by close macromolecular contacts.

Appendix A: Calculation of the dipolar correlation functions G_L^(m)(τ) and spectral densities $J_L^{(m)}(\omega )$ for planar geometry

We outline here the main steps of the calculations of the pairwise dipolar correlation functions G_L^(m)(τ) and spectral densities J_L^(m)(ω) for an interfacial layer following the earlier work [33]. The integral average of the dipole-dipole interaction over the propagator of diffusion is given in the laboratory frame (L) by Eq. (5). To evaluate this equation the following steps were taken:

1. The correlation functions in the laboratory fixed coordinate system (L) are related to their counterparts in the molecular axis system (M) by a series of Euler rotations:

   $$G_L^{(m)}(\tau )=\sum _{m\prime =-2}^{+2}{\left|d_{-m\prime ,m}^{(2)}(\beta )\right|}^2{G}_M^{(m\prime )}(\tau ),$$ (A1)

   where $d_{-m\prime ,m}^{(2)}(\beta )$ denotes the (-m′,m) element of the second rank Wigner rotation matrix for the transformation β [34]. The correlation functions G_M^(m)(τ) are given by an integral average over the diffusion propagator in the frame (M) that are formally similar to Eq. (5).

2. When considering translational diffusion of the I-spin molecules in the quasi two-dimensional geometry of Fig. A1, the anisotropy of the dynamics is described by an unbounded and isotropic (independent of φ) diffusion perpendicular to the normal axis n and a bounded diffusion parallel to the normal. With this model, the normalized diffusive propagator P in the molecular frame (M) is defined as a product of bounded P_∥ and unbounded P_⊥ factors,

   $$P(\rho ,z,\tau \mid {\rho }_0,z_0,0)=P_{\perp }(\rho ,\tau \mid {\rho }_0,0)P_{\mathit{\parallel }}(z,\tau \mid z_0,0).$$ (A2)

   The bounded propagator P_∥ is given by the solution of a 1-dimensional diffusion equation with no flux out of the layer. The Gaussian unbounded propagator P_⊥ is expressed by its Fourier transform in the reciprocal k space [35],

   $$\begin{array}{l}{P}_{\mathit{\parallel }}\left(z,\tau \mid z_{0}0\right)\approx \frac{1}{\lambda }\left[1+2cos(\pi z/\lambda )cos(\pi z_0/\lambda )exp(-D_{I\mathit{\parallel }}\tau /{\lambda }^2)+\dots \right]\\ P_{\perp }\left(\rho ,\tau \mid {\rho }_0,0\right)=\frac{1}{2\pi }\sum _{m=-\infty }^{+\infty }{\int }_0^{\infty }dkkexp(-k^2{D}_{I\perp }\tau )j_m(k\rho )j_m(k{\rho }_0)exp\left[\mathit{\text{im}}({\mathit{\varphi }}_0-\mathit{\varphi })\right]\end{array}$$ (A3a, b)

   Here D_I∥ and D_I⊥ are the translational diffusion coefficients of spin I in the direction parallel and perpendicular to n and the j_m(kρ) are cylindrical Bessel functions of order m.

3. We are only interested in the situations encountered at times long compared with the translational correlation time; i.e., τ → ∞ (or low frequency). In Eq. (A3a), P_∥ thus simplifies to the inverse of the “volume” (1/λ) visited with the boundary conditions of zero flux along the n direction on the two limits of the layer of size λ [35]. In Eq. (A3b), only the long wavelength transverse diffusing modes (k → 0) dominate for time τ much longer than the translational correlation time τ_m = δ²/(4D_I⊥), where δ is the mean molecular size of the I-spin bearing molecule. The diffusion propagator in the molecular axis system, P(ρ,z,τ∣ρ ₀,z₀,0)=P_⊥ (ρ,τ∣ρ₀,0)P_∥(z,τ∣z₀,0), is then substituted into the integral definition of $G_M^{(m\prime )}(\tau )$ with {m′∈ (−2,+2)}, giving at long times (τ≫τ_m),

   $$G_M^{(m\prime )}(\tau )=\frac{2\pi {\sigma }_S}{{\lambda }^2}{\int }_0^{\infty }dkkexp\left(-k^2{D}_{I\perp }\tau \right){\left|\int dz\int d\rho \rho j_m(k\rho )f_2^{(m\prime )}(\rho ,z)\right|}^2.$$ (A4)

   Here f₂^(m′⁾(ρ,z) is the dipolar interaction expressed in the cylindrical coordinates of the molecular frame (M). We have separated the integral calculations in Eq. (A4) into two domains M₁ = {δ ≤ z ≤ λ and 0 ≤ ρ< ∞}and M₂ = {0 ≤ z ≤ δ and δ′ ≤ ρ< ∞} (Fig. (A1)). The integrals simplify for times τ much longer than the diffusion correlation time τ_m. This approximation permits considering only the dominant term coming from the long wavelength two-dimensional transverse modes kδ′→ 0 when τ ≫ τ_m in the exponential part exp[−(kδ′)² x²τ/(4τ_m)] of Eq. (A4). After some calculations, one finds that the leading terms come from the two-dimensional part of $G_M^{(0)}(\tau )$ integrated only over the M₂ domain:

   $$\begin{array}{l}{G}_M^{(0)}(\tau )\approx \frac{3\pi {\sigma }_S}{2{\lambda }^2\delta {\prime }^2}\left\{\frac{1}{1+x^2}\left(\frac{{\tau }_m}{\tau }\right)-\frac{2\sqrt{\pi }}{x\sqrt{1+x^2}}{\left(\frac{{\tau }_m}{\tau }\right)}^{(3/2)}+2\frac{3+4x^2}{x^2(1+x^2)}\left(\frac{{\tau }_m}{\tau }\right)+\dots \right\}\\ G_M^{(1)}(\tau )=G_M^{(2)}(\tau )\approx \text{O}\left[{\left(\frac{{\tau }_m}{\tau }\right)}^2\right]\end{array}$$ (A5 a,b)

   At long times (τ ≫ τ_m), corresponding to the low frequency range studied, all the other terms integrated within the M₁ domain behave at long times as (τ_m/τ)² and thus will be neglected in comparison with the leading term of $G_M^{(0)}(\tau )$ integrated within the M₂ domain:

   $$G_M^{(0)}(\tau )\approx \frac{3\pi {\sigma }_S}{2{\lambda }^2\delta {\prime }^2(1+x^2)}\left(\frac{{\tau }_m}{\tau }\right)$$ (A6)

4. The dipolar correlation function G_M⁽⁰⁾(τ) must also fulfil the requirements [24] that (a) At short times, when τ→0, G_M⁽⁰⁾(τ) must tend to a finite constant C, such as $G_M^{(0)}(0)={\int }_{-\infty }^{\infty }{J}_M^{(0)}(\omega )d\omega =C$, where $J_M^{(0)}(\omega )$ is the spectral density function; (b) At long time G_M⁽⁰⁾(τ) must behave as 1/τ, characteristic of the two-dimensional translational diffusion relaxation process, and the effect of the finite residence time, τ_S, at the protein surface is included as an exponential cut-off $G_M^{(0)}(\tau )\propto (C/\tau )exp(-\tau /{\tau }_S)$; (c) The form of G_M⁽⁰⁾(τ) on the time scale 0≤τ∼τ_m≪τ_S is characterized by the correlation time for the surface diffusion events.

   These requirements lead to the following expression of the correlation function G_M⁽⁰⁾(τ) which is, as expected, always positive:

   $$G_M^{(0)}(\tau )\approx C\frac{{\tau }_m}{\tau }\left[exp\left(-\frac{\tau }{{\tau }_S}\right)-exp\left(-\frac{\tau }{{\tau }_m}\right)\right]\text{when}{\tau }_{\text{m}}\ll {\tau }_S$$ (A7)

   Straightforward calculations give C = 3πσ_S/[2λ²δ′²(l + x²)]. The spectral density function is thus given by the exponential Fourier transform of Eq. (A7):

   $$J_M^{(0)}(\omega )=\frac{3\pi {\sigma }_S}{2{\lambda }^2\delta {\prime }^2(1+x^2)}{\tau }_{m}ln\left[\frac{1+{\omega }^2{\tau }_m^2}{{({\tau }_m/{\tau }_S)}^2+{\omega }^2{\tau }_m^2}\right].$$ (A8)

5. Last, we make a powder average of J_M^(m)(ω) over all the orientations β of the (M) frame relative to the constant direction of B₀ and obtain the average spectral densities

   $$\langle J_L^{(0)}(\omega )\rangle =\langle J_L^{(1)}(\omega )\rangle =\langle J_L^{(2)}(\omega )\rangle \approx \frac{1}{5}{J}_M^{(0)}(\omega ).$$ (A9)

   Substitution of Eq. (A8) into Eq. (A9), finally gives the powder average of the spectral density in the laboratory frame (L):

   $$\langle J_L^{(m)}(\omega )\rangle =\frac{3\pi {\sigma }_S}{10{\lambda }^2\delta {\prime }^2(1+x^2)}{\tau }_{m}ln\left[\frac{1+{\omega }^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_S\right)}^2+{\omega }^2{\tau }_m^2}\right].$$ (A10)

Fig. A1.

Schematic diagram of the model. The nuclear spins I diffuse in an infinite layer of thickness λ in the dipolar field of a very small quantity of paramagnetic spins S fixed on the surface. The z-axis of the laboratory coordinate system (L) is parallel to the direction of the static magnetic field B₀ and constitutes angle β with the z-axis of the molecular axis system (M). The cylindrical polar coordinates ρ, φ and z were used to conduct calculations in the (M) frame. The smallest value of ρ and z corresponding to the distance of minimal approach of the two I- and S-spin-bearing molecules at the surface is δ′. To simplify calculations, the diffusion layer λ was subdivided into two domains: M₁ ={δ ≤ z ≤ λ and 0 ≤ ρ < ∞}and M₂ ={0 ≤ z ≤ δ and δ′≤ ρ <∞ }. In the M₂ domain spin I has diffusion motions restricted within a single layer of molecular size δ.

Appendix B. Change to solution concentrations

Beginning with Eqn. (6) with B = (γ_Iγ_Sħ)²S(S+1), and D_⊥ = δ²/4τ_m, rearrangement gives

$$\frac{1}{T_{1,2D}({\omega }_I)}=\frac{\pi }{15}\left[\frac{{\sigma }_S{\delta }^2}{{\lambda }^{2}4D_{\perp }\delta {\prime }^2(1+x^2)}\right]B\left[3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_I^2{\tau }_m^2}\right)+7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_S^2{\tau }_m^2}\right)\right]$$ (B1)

With N_s the number of electron spnis per protein molecule and A_p the surface area of the of the protein, σ_s=N_s/A_p. We write the probability that the diffusing molecule is at the surface as the mass of liquid in the surface layer per protein molecule times the number of protein molecules per unit mass of solution:

$$P_{\mathit{\text{surf}}}=(A_p\lambda \rho )(n_p/g\mathit{\text{soln}})$$ (B2)

where n_p is the number of protein molecules and the total solution mass is 1 g or 1 cm³ for water with density ρ. With [P] representing the concentration of protein in mol/L, and N_A Avogadro's constant,

$$n_p=N_A[p]/1000\rho .$$ (B3)

Substitution gives P_surf= A_pλN_A[P]/1000. Substitution then yields

$$\frac{P_{\mathit{\text{surf}}}}{T_{1,2D}}=\frac{\pi }{60}\frac{N_{S}B{x}^2}{A_p{\lambda }^2{D}_{\perp }(1+x^2)}\frac{A_p\lambda N_A[P]}{1000}\left[3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_I^2{\tau }_m^2}\right)+7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_S^2{\tau }_m^2}\right)\right]$$ (B4)

With N_S[P]=[S],

$$\frac{P_{\mathit{\text{surf}}}}{T_{1,2D}}=\frac{\pi }{60}\frac{B{x}^2}{\lambda D_{\perp }(1+x^2)}\frac{N_A[S]}{1000}\left[3ln\left(\frac{1+{\omega }_I^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_I^2{\tau }_m^2}\right)+7ln\left(\frac{1+{\omega }_S^2{\tau }_m^2}{{\left({\tau }_m/{\tau }_s\right)}^2+{\omega }_S^2{\tau }_m^2}\right)\right]$$