Abstract
In-vivo measurement of bone lead by means of K-X ray fluorescence (KXRF) is the preferred biological marker of chronic exposure to lead. Unfortunately, considerable measurement error associated with KXRF estimations can introduce bias in estimates of the effect of bone lead when this variable is included as the exposure in a regression model. Estimates of uncertainty reported by the KXRF instrument reflect the variance of the measurement error and, although they can be used to correct the measurement error bias, they are seldom used in epidemiological statistical analyses. Errors-in-variables regression (EIV) allows for correction of bias caused by measurement error in predictor variables, based on the knowledge of the reliability of such variables. The authors propose a way to obtain reliability coefficients for bone lead measurements from uncertainty data reported by the KXRF instrument and compare, by use of Monte Carlo simulations, results obtained using EIV regression models versus those obtained by the standard procedures. Results of the simulations show that Ordinary Least Square (OLS) regression models provide severely biased estimates of effect, and that EIV provides nearly unbiased estimates. Although EIV effect estimates are more imprecise, their mean squared error is much smaller than that of OLS estimates. In conclusion, EIV is a better alternative than OLS to estimate the effect of bone lead when measured by KXRF.
Keywords: Lead, KXRF, measurement error, errors-in-variables model, simulations
1. INTRODUCTION
Bone lead concentration constitutes a very useful biological marker of chronic lead exposure as it is an estimate of the intensity of the exposure throughout the most recent 5 to 19 years of a subject's life (Rabinowitz,1990); however, it is intrinsically difficult to measure. The preferred method for determination of bone lead is in-vivo K X-Ray Fluorescence (KXRF), which has been described in detail elsewhere (Burger, 1990, Chettle, 1991, Hu 1991, Gordon 1993). Briefly, the technique utilizes gamma radiation from a cadmium-109 source. Lead atoms are excited by this radiation and emit photons with X-ray wavelength, which are in turn detected by a high-purity germanium detector in a back-scatter geometry. The number of lead fluorescent photons is compared with the number of photons from the coherent scatter signal (which comes principally from calcium hydroxyapatite), resulting in μg of lead per g of bone mineral [μg/g or parts-per-million (ppm)] as the unit of measurement. This method of normalization makes the measurement relatively insensitive to variations in bone shape, size, density, histomorphometry, overlying tissue thickness, and movement (Somervaille, 1985). However, it has been suggested that the tissue thickness in subjects with a Body Mass Index>40 kg/m2 does attenuate the bone lead measurements even after normalization (McNeill, 1999).
In addition to measuring bone lead concentration, KXRF instruments derive an estimate of the measurement uncertainty (imprecision) that reflects the variance both in the X-ray signal and in the background underlying the signal. The reported uncertainty is an estimate of the standard deviation of multiple measurements of the same anatomic site. A detailed explanation of how KXRF uncertainty estimates are calculated appears in Gordon (1994) and Todd (2000). A consensus has been reached on the formulas used to calculate both the point estimate and the uncertainty in KXRF measurements (Chettle, 2003). Regardless of how the estimate of uncertainty is obtained, its existence allows for the correction of measurement error-induced bias in epidemiologic statistical analyses.
KXRF measurement uncertainty tends to increase with obesity (due to thicker overlying tissue) and lower bone density (Hu, 1991). Male gender has also been shown to be associated with increased uncertainty, as well as age and bone Pb concentrations (Chettle, 1991). Other sources of measurement uncertainty are within-individual (and even within-bone) variations in skeletal lead (Hu, 1995). Bone Pb measurement error is of the classical type; unfortunately, this means that when bone Pb is included in a regression model as a predictor variable, its estimated effect on the outcome will likely be biased towards the null hypothesis (Armstrong, 2000). Our research question was whether it is possible to correct biases in bone Pb effect estimates from regression models, induced by the uncertainty of KXRF measurements.
The literature on measurement error is vast, and numerous methods have been proposed to correct for it. Guolo (2008) provides an extensive review on the subject and comments on the fact that few software tools offer implementations of correction techniques in standard statistical packages.
Few strategies have been followed in order to obtain unbiased estimates from models where bone Pb is an independent variable. Uncertainty estimates in particular, have been seldom incorporated into statistical analysis of epidemiologic studies on this topic. As early as 1995, a review appeared which stated the importance of using uncertainty estimates to adjust for measurement error in regression models where bone lead is an independent variable (Hu, 1995). However, as of October 2009, a search on Pubmed using the words: bone lead, measurement error, and K-X-ray only yielded four original articles (Hu, 1994, 1995, 1996; Hernández-Avila, 1996). Of these, only Hu et al (1994, 1996) reported using any means to account for measurement error using uncertainty estimates, namely the Fuller procedure (Fuller, 1987). In order to adjust the effect estimates for measurement error, the Fuller procedure depends on a reliability ratio ρxx, which can be defined as the ratio of the variance of the true variable X to the variance of the observed variable Z (which is in turn the sum of the variance of X and the variance of the measurement error)
| (1) |
where var(X) is the variance of the true variable, var(Z) is the variance of the observed variable, and var(U) is the variance of the measurement error. In the case of bone Pb measurements, var(U) can of course be derived from uncertainty estimates reported by the KXRF instrument. The unbiased beta estimate is the product of the estimated β coefficient and the reliability ratio ρxx. However, the Fuller correction, as described above, only applies to bivariate regression analysis, particularly for confidence interval estimation and, as Fuller himself states (Fuller, 1987, pp 7), it does not extend to models with multiple covariates.
One strategy used in the field of econometrics is errors-in-variables (EIV) regression (Kmenta, 1997) which is useful in cases where reliability coefficients are available. EIV is quite simple to manage and is conveniently implemented in the core package of the widely used statistical software Stata (Stata, release 10.0; Stata Corporation, College Station, TX). Unlike Ordinary Least Squares regression (OLS, also known simply as “linear regression”), which requires the often unwarranted assumption that the independent variables in a model are perfectly measured, EIV recognizes the presence of noise in predictor measurement and incorporates this noise (e.g. measurement error) into the estimation process. Whenever accurate reliability coefficients are available, EIV regression is supposed to provide unbiased β point estimates and confidence intervals. In the case of bone lead, reliability coefficients can be calculated in terms of the uncertainty reported by the KXRF device (See the Appendix for an explanation of the EIV procedure and calculation of reliability coefficients).
The objective of the work presented here was to compare the bias of the estimated beta coefficients obtained by errors-in-variables regression vs. that obtained by Ordinary Least Squares (OLS) when bone lead is an independent variable. To illustrate this comparison, we will focus on the research problem of bone lead mobilization, as measured by the interaction between bone resorption and bone Pb concentrations, and its effect on plasma Pb levels, explored in Tellez-Rojo et al (2004).
2. MATERIAL AND METHODS
To compare the different estimation methods, we generated a set of data tailored as closely as possible to a real dataset. We chose to generate a dataset instead of performing the simulations directly on empirical data since this approach allows us to try different scenarios by modifying parameters such as variable distribution, correlation structure, etc. and quantify its effect on bias and its correction strategies. The generated dataset consisted of 10,000 observations, including variables A,W,H, C, and M representing age, weight, height, calf circumference, and bone resorption rate, respectively, that were drawn from a multivariate normal distribution. The chosen values of the variables’ means, variances and correlation structure were derived from empirical data previously analyzed by Tellez-Rojo et al (2004). Tables 1 and 2 show these values (more details available upon request to the authors). True bone Pb concentrations X, were generated as a function of age, weight and calf circumference. The uncertainty of the i-th measurement, was generated as a linear function of age, weight, height, calf circumference and random variability. Finally, variable y (representing plasma Pb) was generated as a function of the product of true bone Pb and bone resorption, and random variation.
Table 1.
Correlation structure assigned to variables used in the simulation study.
| Age | Weight | Height | Calf | |
|---|---|---|---|---|
| Age | 1 | |||
| Weight | 0.1797 | 1 | ||
| Height | -0.0219 | 0.4316 | 1 | |
| Calf | 0.1743 | 0.7214 | 0.2096 | 1 |
| ln(NTX) | -0.2658 | 0.0067 | -0.1655 | -0.0855 |
NTX: N-telopeptides of type I collagen in urine.
Table 2.
Means and standard deviations assigned to variables used in simulation study.
| Estimate | Mean | SD |
|---|---|---|
| Age (years) | 25.78 | 5.35 |
| Weight (kg) | 61.38 | 9.76 |
| Height (cm) | 154.38 | 5.83 |
| Calf circumference (cm) | 34.06 | 3.14 |
| NTX (nmol/mmolCreat/L) | 96.26† | 1.72‡ |
NTX: Bone resorption marker: N-telopeptides of type I collagen in urine.
Geometric mean
Geometric standard deviation
Using this dataset as a starting point (base dataset), we performed 10,000 simulations (that is 10,000 simulations of the 10,000 subject dataset). Each one of these simulations consisted of modifying the base dataset with the following three steps:
Variable Z representing observed bone Pb, was generated as a function of true bone Pb and measurement error.
The reliability coefficients of observed bone Pb and its product with bone resorption were calculated. In order to calculate the reliability coefficient for the product term, we assumed that bone Pb and bone resorption were independent.
- We fitted the model :
by means of OLS, and EIV, and stored the values of the reliability coefficients, beta estimates, standard errors and t-statistics; that is, one set of OLS and one set of EIV estimates by each one of the simulations. The description above implies that in each simulation observed bone Pb and the reliability coefficients were re-generated while the values of the rest of the variables in the base dataset remained unchanged. Variables centered around their mean were included in this model; the product variable ZM was the product of the Z and M variables after their centering. The reason for centering is explained in the Appendix.(2)
Finally, we compared the obtained estimates by means of the Mean Squared Error (MSE) which takes into account not only the bias, but also the variance of the estimator. The simulations and subsequent analyses were performed using Stata release 10.0 (Stata Corporation, College Station, TX). See the Appendix for the detailed methods of the simulation process.
3. RESULTS
After running the simulations, we observed that EIV performed better than OLS as defined by the mean squared error (Table 3). In Figure 1, it can be seen that EIV estimates of the main effect of bone Pb were nearly unbiased, although their variance was much greater than that of OLS estimates. However, in the case of EIV coefficients, the MSE was much smaller mainly due to the large bias in OLS estimates introduced by measurement error. The same occurred in the estimation of the interaction coefficient which can be seen in Figure 2. Some differences with respect to the results for the main effect are evident. Firstly, the distribution of EIV estimates deviated, albeit slightly, from normality, mainly due to it being skewed to the right (the skewness coefficient of the EIV estimates was 0.43 vs. 0.02 of the OLS estimates). This deviation was sufficient to yield a significant result in a Skewness-Kurtosis test (p<0.001). Secondly, there was some overlap in the distribution of OLS and EIV estimates which, together with the skewness of the EIV distribution, implies that some of the EIV estimates were even further from the true value of the parameter than those of OLS. However, the probability of obtaining EIV estimates even more biased than the expected value of the OLS estimates was 0.004.
Table 3.
Summary statistics, bias and square root of the mean squared error (RMSE) of Beta estimates.
| Estimate | Mean | SD | Min | Max | Bias | RMSE | |
|---|---|---|---|---|---|---|---|
| Bone Pb main effect (β=0.0537) | |||||||
| OLS | 0.00853 | 0.00099 | 0.00498 | 0.01236 | -0.04517 | 0.04518 | |
| EIV | 0.05354 | 0.00904 | 0.02613 | 0.09972 | -0.00016 | 0.00904 | |
| Pb×Resorption interaction (β=0.0005) | |||||||
| OLS | 0.00009 | 0.00002 | 0.00002 | 0.00016 | -0.00042 | 0.00042 | |
| EIV | 0.00052 | 0.00015 | 0.00005 | 0.00162 | 0.00002 | 0.00015 | |
EIV: Errors In Variables; Max: Maximum; Min: minimum; OLS: Ordinary Least Squares, RMSE: Root of the Mean Squared Error; SD: Standard Deviation
Figure 1.
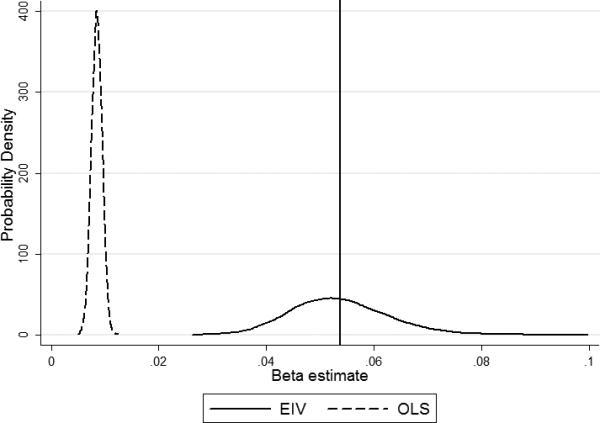
Distribution of Ordinary Least Squares (OLS) vs Errors-in-Variables (EIV) beta estimates of the main effect of bone Pb after 10,000 simulations. The vertical line represents the true value of the parameter.
Figure 2.
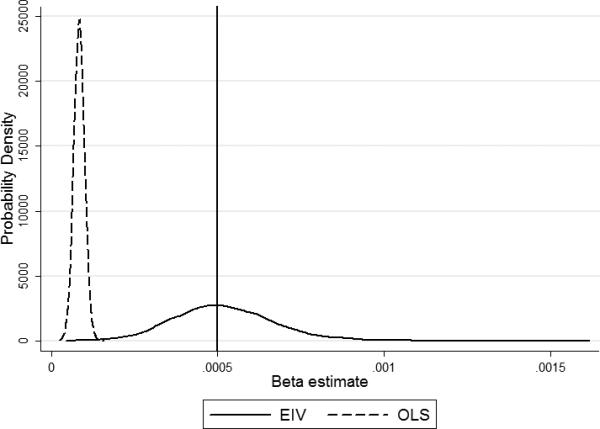
Distribution of Ordinary Least Squares (OLS) and Errors-in-Variables (EIV) beta estimates of the bone Pb×bone resorption interaction after 10,000 simulations. The vertical line represents the true value of the parameter.
As an additional analysis, we compared the statistical significance yielded by the different estimation procedures. Since p-values were, in general, very close to zero, we focused on comparing t-values instead. The mean values of t were slightly larger using OLS for both the main effect and the interaction estimates (Table 4).
Table 4.
Arithmetic means of t-values and standard errors of Beta estimates obtained after 10,000 simulations.
| Estimate | Mean t-value† | Mean standard error | |
|---|---|---|---|
| Bone Pb main effect | |||
| OLS | 7.96924 | 0.00107 | |
| EIV | 7.6821 | 0.00700 | |
| Pb×Resorption interaction | |||
| OLS | 5.47614 | 0.00002 | |
| EIV | 4.97693 | 0.00010 |
EIV: Errors In Variables; OLS: Ordinary Least Squares.
9,996 degrees of freedom
4. DISCUSSION
Results of the simulations show that EIV performs better than OLS for linear models where bone Pb, as measured by KXRF, is a predictor variable using the MSE as the judging criterion. EIV estimates yielded larger standard errors than OLS estimates, however, EIV t-values were comparable since beta coefficients were, on average, much farther from the null value than those of the OLS approach. EIV estimates had much larger variance than OLS estimates, whereas OLS estimates were highly biased but much more precise. The large variance of EIV estimates could in theory lead to undesirable situations such as large overestimations of effect in individual studies due only to random variability. So, is it worth using this method? Or, should we just use the results from OLS models knowing that they are underestimated and, thus, reporting that the “true” effect of the mismeasured variable is likely much larger?
In principle, the answer would depend on the purpose of the study. That is, whether the study's objective is for hypothesis testing or for estimation purposes. If the purpose of the study is hypothesis testing, and assuming the probability of rejecting a true null hypothesis remains the same regardless of the estimation method, then perhaps it would be preferable to use OLS. Based on the results of this work, that, in fact, appears to be the case. Our results show that t-values were slightly smaller when using EIV, indicating that the statistical power achieved is actually smaller with this approach (see Table 4). However, if the objective of the study is for the purpose of estimation, then it would be better to obtain an unbiased estimate of the effect, as it would assure us that after multiple studies we will be, in average, correct (the estimate will underestimate just as often as it overestimates). Based on these conclusions, we consider that, in the particular case of the article by Tellez-Rojo et al (2004), hypotheses tests on the interaction between bone Pb and bone resorption are valid. However, it is likely that the slope of the relationship between bone Pb and plasma Pb is actually underestimated and the confidence intervals much narrower than they should be.
The skewness of the distribution of the EIV interaction estimates may be due to the strong assumption of independence that was made regarding the interacting variables in order to obtain the reliability coefficient for the interaction term. Although we judge that, in this particular case, the deviation from normality is still not enough to invalidate our conclusions, we caution readers that this result places some restrictions in the use of EIV for interactions if the assumption of no correlation between the interacting variables is not supported by the data or prior evidence.
We have performed our simulations in a scenario based on KXRF measurements of lead in bone. However, it is important to note, that our conclusions hold regardless of the XRF method used. An estimate of uncertainty, which is also available from other XRF methods such as L-XRF or XRF with a 57-cobalt source, is all that is needed to use the EIV method. Moreover, and following this line of reasoning, EIV is likely useful for any epidemiological setting where the outcome is a continuous variable and the variance of the measurement error of explanatory variables is known. We acknowledge that the variance of the measurement error is sometimes difficult to estimate. If that is the case, we recommend reporting EIV results using different scenarios on the magnitude of the error variance in addition to the uncorrected OLS results.
5. CONCLUSION
Our results show that Errors-in-Variables regression, a statistical procedure readily available in commonly used statistical software, constitutes a better alternative than ordinary linear regression if one seeks to estimate the effect of bone Pb concentration on continuous outcomes. However, OLS remains a valid option, if the purpose of the statistical analysis is simply for “effect/ no effect” hypothesis testing. EIV can also be used, with some restrictions, in the case of interaction estimations.
Supplementary Material
6. ACKNOWLEDGEMENTS
We thank Manuel Mendoza, Víctor Borja-Aburto, Belem Trejo-Valdivia, Thomas Mroz, and Adrienne Ettinger for their valuable comments and suggestions to improve the work presented here.
FUNDING
This work was supported in part by the Environmental Protection Agency; and the National Institute of Environmental Health Sciences at the National Institutes of Health (grants EPA/NIEHS P01 ES12874, NIEHS P42 ES05947 and NIEHS R01 ES007821). These grants supported the collection of the original data on which this study was based.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Abbreviations. KXRF: K X-Ray Fluorescence; EIV. Errors-in-Variables; OLS: Ordinary Least Square; NTX: N-tellopeptides of type I collagen; mmolCreat: millimoles of Creatinine in urine. MSE: Mean Squared Error.
- Uncertainty in bone Pb measurements induces bias in linear regression estimates
- Errors-in-variables regression (EIV) corrects bias at the expense of precision
- The Mean Squared Error criterion indicates EIV is preferable to linear regression
- Ordinary regression remains a valid option for effect/no-effect hypothesis testing
- EIV is also useful for interaction estimation, under certain conditions
7. REFERENCES
- Armstrong BG. Effect of measurement error on epidemiological studies of environmental and occupational exposures. Occup. Environ. Med. 1998;55:651–656. doi: 10.1136/oem.55.10.651. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chettle DR, Scott MC, Somervaille LJ. Lead in bone: sampling and quantitation using K X-rays excited by 109Cd. Environ Health Perspect. 1991;91:49–55. doi: 10.1289/ehp.919149. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chettle DR, Arnold ML, Aro AC, Fleming DE, Kondrashov VS, McNeill FE, Moshier EL, Nie H, Rothenberg SJ, Stronach IM, Todd AC. An agreed statement on calculating lead concentration and uncertainty in XRF in vivo bone lead analysis. Appl Radiat Isot. 2003;58:603–605. doi: 10.1016/s0969-8043(03)00060-5. [DOI] [PubMed] [Google Scholar]
- Fuller WA. Measurement error models. John Wiley and Sons; New York: 1987. [Google Scholar]
- Gordon CL, Webber CE, Chettle DR. The reproducibility of 109Cd-based X-ray fluorescence measurements of bone lead. Environ. Health Perspect. 1994;102:690–694. doi: 10.1289/ehp.94102690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guolo A. Robust techniques for measurement error correction: a review. Stat Methods Med Res. 2008;17:555–580. doi: 10.1177/0962280207081318. [DOI] [PubMed] [Google Scholar]
- Hernandez-Avila M, Gonzalez-Cossio T, Palazuelos E, Romieu I, Aro A, Fishbein E, Peterson KE, Hu H. Dietary and environmental determinants of blood and bone lead levels in lactating postpartum women living in Mexico City. Environ. Health Perspect. 1996;104:1076–1082. doi: 10.1289/ehp.961041076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Aro A, Rotnitzky A. Bone lead measured by X-ray fluorescence: epidemiologic methods. Environ. Health Perspect. 1995;103:105S–110S. doi: 10.1289/ehp.95103s1105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Milder F, Burger DE. The use of K-X-ray fluorescence for measuring lead burden in epidemiological studies: high and low lead burdens, and measurement uncertainty. Environ. Health Perspect. 1991;94:107–110. doi: 10.1289/ehp.94-1567946. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hu H, Watanabe H, Payton M, Rotnitzky A. The relationship between bone lead and hemoglobin. JAMA. 1994;272:1512–1517. [PubMed] [Google Scholar]
- Hu H, Payton M, Korrick S, Sparrow D, Weiss ST, Rotnitzky A. Determinants of bone and blood lead levels among community-exposed middle-aged to elderly men. The normative aging study. Am. J. Epidemiol. 1996;144:749–759. doi: 10.1093/oxfordjournals.aje.a008999. [DOI] [PubMed] [Google Scholar]
- Kmenta J. Elements of Econometrics. 2nd ed. University of Michigan Press; Ann Arbor, MI: 1997. pp. 352–357. [Google Scholar]
- McNeill FE, Stokes L, Chettle DR, Kaye WE. Factors affecting in vivo measurement precision and accuracy of 109Cd K x-ray fluorescence measurements. Phys Med Biol. 1999;44:2263–2273. doi: 10.1088/0031-9155/44/9/313. [DOI] [PubMed] [Google Scholar]
- Rabinowitz MB. Toxicokinetics of bone lead. Environ. Health Perspect. 1990;91:33–37. doi: 10.1289/ehp.919133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Somervaille LJ, Chettle DR, Scott MC. In vivo measurement of lead in bone using X-ray fluorescence. Phys. Med. Biol. 1985;30:929–943. doi: 10.1088/0031-9155/30/9/005. [DOI] [PubMed] [Google Scholar]
- Tellez-Rojo MM, Hernandez-Avila M, Lamadrid-Figueroa H, Smith D, Hernández-Cadena L, Mercado A, Aro A, Schwartz J, Hu H. Impact of bone lead and bone resorption on plasma and whole blood lead levels during pregnancy. Am. J. Epidemiol. 2004;160:668–678. doi: 10.1093/aje/kwh271. [DOI] [PubMed] [Google Scholar]
- Todd AC. Calculating bone-lead measurement variance. Environ. Health Perspect. 2000;108:383–386. doi: 10.1289/ehp.00108383. Erratum in: Environ. Health Perspect. 2000. 108, A298.
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


