Evaluation of ¹³C isotopic tracers for metabolic flux analysis in mammalian cells

Abstract

¹³C metabolic flux analysis (MFA) is the most comprehensive means of characterizing cellular metabolic states. Uniquely labeled isotopic tracers enable more focused analyses to probe specific reactions within the network. As a result, the choice of tracer largely determines the precision with which one can estimate metabolic fluxes, especially in complex mammalian systems that require multiple substrates. Here we have experimentally determined metabolic fluxes in a tumor cell line, successfully recapitulating the hallmarks of cancer cell metabolism. Using these data, we computationally evaluated specifically labeled ¹³C glucose and glutamine tracers for their ability to precisely and accurately estimate fluxes in central carbon metabolism. These methods enabled us to to identify the optimal tracer for analyzing individual fluxes, specific pathways, and central carbon metabolism as a whole. [1,2-¹³C₂]glucose provided the most precise estimates for glycolysis, the pentose phosphate pathway, and the overall network. Tracers such as [2-¹³C]glucose and [3-¹³C]glucose also outperformed the more commonly used [1-¹³C]glucose. [U-¹³C₅]glutamine emerged as the preferred isotopic tracer for analysis of the tricarboxylic acid (TCA) cycle. These results provide valuable, quantitative information on the performance of ¹³C-labeled substrates and can aid in the design of more informative MFA experiments in mammalian cell culture.

Introduction

¹³C metabolic flux analysis (MFA) is an effective tool for characterizing the metabolic phenotype of organisms at the systems level. This technique has been described extensively in the literature and typically involves the application of a labeled substrate to a biological system, measurement of label incorporation within metabolite pools, and computational estimation of intracellular fluxes that fit the observed data (Sauer, 2006, Tang et al., 2009b). The acquisition of systemwide information on cellular metabolism enables identification of novel therapeutic targets for disease (Munger et al., 2008), provides information on substrate utilization within specific metabolic pathways (Kharroubi et al., 1992, Neese et al., 1993), and offers insight into key reactions of product synthesis (Kleijn et al., 2007, Antoniewicz et al., 2007b). Regardless of the specific application, MFA must generate precise and accurate flux data to effectively differentiate between cellular phenotypes (Tang et al., 2009a).

The choice of tracer dictates the mass isotopomer distribution (MID) of each metabolite for a given set of fluxes. The sensitivity of the MIDs, in turn, to changes in the pathway fluxes ultimately determines the confidence of flux estimates, which are as important as the flux values themselves (Antoniewicz et al., 2006). Stationary MFA is conducted when the labeled substrate is at isotopic steady state and does not utilize pool size or transient data; as such, this technique is especially reliant upon the specific tracer used. Depending on the particular bioreaction network, nonstationary MFA may be preferable and can also benefit from a informed choice of tracer (Noh and Wiechert, 2006, Noh et al., 2006). The issue of tracer choice is more complex in mammalian cell systems that utilize multiple carbon sources (e.g., glucose and glutamine) and are grown in complex media. To probe specific pathways, researchers have applied a wide array of isotopically labeled substrates, including glucose, glutamine, or atypical substrates such as propionate or succinate (Burgess et al., 2007, Yang et al., 2008, Yoo et al., 2008). For example, [1,2-¹³C₂]glucose is commonly employed for analysis of the pentose phosphate pathway (PPP) (Boros et al., 2005), whereas [3-¹³C]glucose or [3-¹⁴C]glucose provide information on pyruvate oxidation (Holleran et al., 1997, Munger et al., 2008). Many tracers effectively label metabolites in the tricarboxylic acid (TCA) cycle, but the presence of anaplerotic reactions and glutamine incorporation (through glutaminolysis or reductive carboxylation) make it difficult to identify the optimal tracer for measuring all net and exchange fluxes within the network.

Systems biology concerns itself with the acquisition, integration, and analysis of complex data sets. MFA was one of the first manifestations of systems-level analysis in complex, biological systems and is unique among systems biology tools in that it allows determination of actual enzyme function (i.e., fluxes) (Stephanopoulos and Vallino, 1991, Nielsen, 2003, Hellerstein, 2004). Unlike concentration-based methodologies, MFA requires both experimental measurement and computational models to elucidate these time-dependent parameters (Sauer, 2006). As such, experimental design to maximize meaningful information is crucial in MFA and requires model-based interpretation. Researchers have recently described methods to optimize measurement sets for flux determination (Rantanen et al., 2006, Chang et al., 2008); however, the choice of tracer is an equally important parameter. Because the tracer strongly influences flux estimation quality and can usually be chosen from a wide array of available isotopic substrates, judicious tracer selection is a major component of this experimental design process. As a result, a systematic analysis of available ¹³C-labeled tracers and associated confidence intervals (i.e., sensitivities) for each estimated flux is warranted. Optimization of tracer choice will enable researchers to more precisely measure specific fluxes in high-throughput applications that aim to screen the metabolic effects of drugs in cells (Borner et al., 2007, Sekhon et al., 2008).

Some initial investigation has occurred in this area. Sriram and colleagues have conducted a Monte Carlo-based analysis of experimental precisions (using standard deviations) when using different combinations of [U-¹³C₆]glucose, [1-¹³C]glucose, and naturally labeled glucose in a mammalian network (Sriram et al., 2008). Similar studies have been performed in microbial systems, which typically consume a single carbon source (Noh et al., 2006). However, a detailed investigation of confidence intervals generated from different, unique tracers in a two-substrate network has never been completed.

Here we have experimentally determined the flux network in a carcinoma cell line and used these data to calculate the confidence intervals for each flux when using different ¹³C-labeled glucose and glutamine tracers. An elementary metabolite unit (EMU)-based method was used to rapidly estimate flux profiles and confidence intervals from simulated measurements in stationary MFA experiments (Antoniewicz et al., 2007a, Young et al., 2008). We were able to quantitatively validate the effectiveness of specific ¹³C tracers in a cancer cell network and identify the best choice for analysis of individual reactions and pathways. A scoring algorithm was employed to determine the optimal tracer for the overall model and for subnetworks representing glycolysis, the PPP, and the tricarboxylic acid (TCA) cycle. These results may significantly improve the efficiency of MFA experiments in high-throughput applications and clinical samples where biological material is limited (Boros et al., 2003).

Materials and Methods

Cell culture and metabolite extraction

The A549 lung carcinoma cell line was obtained from ATCC and maintained in high-glucose DMEM supplemented with 4 mM glutamine, 10% FBS, and 100 U ml⁻¹ penicillin/streptomycin (Invitrogen). For labeling experiments, semi-confluent cells in a 10-cm dish were cultured in glucose-free DMEM (Sigma) with the above supplements and a 25mM 1:1 mixture of [U-¹³C₆]glucose and [1-¹³C]glucose (Cambridge Isotope Laboratories) for 6 hours to achieve isotopic steady state. Spent medium was collected and analyzed for glucose, lactate, and glutamine consumption on a YSI7100 analyzer. Cells were quenched with 1 ml ice cold methanol, an equal volume of water was added, and cells were collected with a cell scraper. Four volumes of chloroform were added, and the cells were vortexed and held on ice for 30 minutes for deproteinization. After addition of 2 ml water, samples were centrifuged at 3000 g for 20 minutes at 4°C. The aqueous phase was collected in a new tube and evaporated under airflow at room temperature.

Derivatization and GC/MS measurements

Dried polar metabolites were dissolved in 60 µl of 2% methoxyamine hydrochloride in pyridine (Pierce), sonicated for 30 minutes, and held at 37°C for 2 hours. After dissolution and reaction, 90 µl MBTSTFA + 1% TBDMCS (Pierce) was added and samples were incubated at 55°C for 60 minutes. Gas chromatography/mass spectrometry (GC/MS) analysis was performed using an Agilent 6890 GC equipped with a 30m DB-35MS capillary column connected to an Agilent 5975B MS operating under electron impact (EI) ionization at 70 eV. One µl of sample was injected in splitless mode at 270°C, using helium as the carrier gas at a flow rate of 1 ml min⁻¹. The GC oven temperature was held at 100°C for 3 min and increased to 300°C at 3.5° min⁻¹ for a total run time of approximately 60 min. The MS source and quadrupole were held at 230°C and 150°C, respectively, and the detector was operated in selected ion monitoring (SIM) mode. MIDs were obtained for each measured metabolite and incorporated with extracellular flux measurements for flux determination. The identity and values of these measured fragments and fluxes are listed in Supplementary Table 1.

Flux estimation

Intracellular fluxes were estimated for a model reaction network by minimizing the lack of fit between actual and simulated flux and GC/MS measurements. The network contained simplified versions of glycolysis, the PPP, anaplerotic reactions, the TCA cycle, and amino acid biosynthesis. (The Supplement lists specific assumptions regarding the network and metabolism that were made for the sake of the flux analysis. Also see Supplementary Table 2 for a list of all network reactions and atom transitions.) We additionally calculated 95% confidence intervals for each flux using parameter continuation (Antoniewicz et al., 2006). All flux simulation, estimation, and continuation in this study was conducted using Metran, a flux analysis tool built upon an EMU framework (Antoniewicz et al., 2007a, Yoo et al., 2008, Young et al., 2008). Some fluxes were virtually unidentifiable and approximate values were obtained from the literature (Hofmann et al., 2008, Munger et al., 2008).

Tracer evaluation

The effects of 18 ¹³C-labeled tracers (11 glucose and 7 glutamine) on flux estimation precision were evaluated (see Table 1). Tracers were chosen if they were commercially available or if they had been previously cited in literature. The effectiveness of each tracer was gauged as follows:

1. A defined set of GC/MS and flux measurements was simulated for a given tracer (see Supplementary Table 3).

2. Standard errors of 5% for external flux measurements and 0.1–1 mol% for GC/MS MIDs were introduced randomly and normally.

3. Flux values and 95% confidence intervals were determined for each reaction.

Table 1.

Glucose and glutamine tracers

Tracer	Abbreviation
[1-13C]glucose	[1]Gluc
[1,2-13C2]glucose	[1,2]Gluc
[1,6-13C2]glucose	[1,6]Gluc
[2-13C]glucose	[2]Gluc
[3-13C]glucose	[3]Gluc
[3,4-13C2]glucose	[3,4]Gluc
[4-13C]glucose	[4]Gluc
[4,5-13C2]glucose	[4,5]Gluc
[5-13C]glucose	[5]Gluc
[6-13C]glucose	[6]Gluc
[U-13C6]glucose	[U]Gluc
[1-13C]glutamine	[1]Gln
[1,2-13C2]glutamine	[1,2]Gln
[3-13C]glutamine	[3]Gln
[3,4-13C2]glutamine	[3,4]Gln
[4-13C]glutamine	[4]Gln
[5-13C]glutamine	[5]Gln
[U-13C6]glutamine	[U]Gln

The usefulness of a tracer was assumed to be directly linked to the precision with which it was able to estimate fluxes of interest; i.e., tracers producing narrower confidence intervals have greater value.

Precision scoring

To more easily compare estimate precision on a group basis, we created a precision scoring metric. Similar optimality criteria have been used previously for experimental design (Noh and Wiechert, 2006, Noh et al., 2006); however, these earlier methods have been based on the parameter covariance matrix, which assumes linearity and does not always truly capture the nonlinear, constrained systems studied in flux analysis. This precision scoring metric relies on the more robust and accurate nonlinear confidence intervals obtained via parameter continuation (Antoniewicz et al., 2006). First, a normalized range is calculated for each flux using the formula

$$r_i=\text{min}(\frac{u_i}{|v_i|},\frac{v_i}{|v_i|}+\alpha )-\text{max}\left(\frac{l_i}{|v_i|},\frac{v_i}{|v_i|}-\alpha \right)$$ (1)

where v_i, l_i, u_i, and r_i are the estimated flux, lower bound, upper bound, and normalized range for the ith flux, and α is a cut-off parameter that prevents one excessively distant bound from overly influencing the scoring. The individual ranges are next converted into scores using a negative exponential function and summed into a final overall score via the expression

$$S={\displaystyle \sum _i{w}_i\text{exp}\left(-\frac{r_i}{\beta }\right)}$$ (2)

where w_i is a weighting parameter for the ith flux, β is a range-scaling parameter, and S is the overall precision score. We empirically found that values of 1 and 3 for α and β result in a good dynamic range of scores. If each w_i can be simply zero or one (serving to either exclude or include fluxes in the overall score), each flux’s precision score will range between zero (unidentifiable) and one (perfectly identifiable). The overall score will then range between zero and the number of fluxes under consideration.

Because the upper and lower bounds of any given confidence interval are sensitive to the random error introduced into the simulated measurements, the corresponding precision scores will also vary for simulated experiments with different random errors. To account for this, we conducted six simulated experiments for every tracer of interest and generated a distribution of precision scores, allowing us to report a mean precision score and a precision score standard deviation.

Results and Discussion

Experimental flux analysis

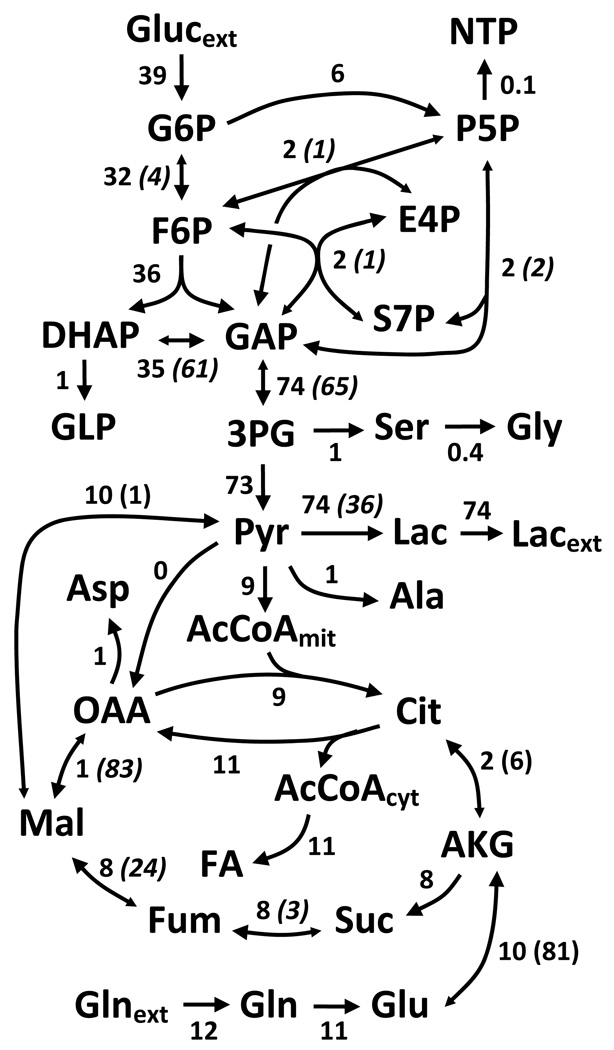
The metabolic phenotype of a cell is a key component of its overall behavior, and evidence suggests that metabolism plays an important role in maintaining the tumor phenotype (DeBerardinis et al., 2007). Metabolic analysis of cancer cells has again become an active area of research, and technological improvements have expanded our ability to investigate metabolism using stable isotopically labeled substrates. In this study we used the A549 cancer cell line as a model system for evaluating isotopic tracers in mammalian cells. This line is often used in molecular and metabolic studies of cancer and exhibits aerobic glycolysis, commonly known as the Warburg effect (Christofk et al., 2008, Hatzivassiliou et al., 2005). To obtain baseline values for our metabolic network we estimated fluxes of semi-confluent cells using an equimolar mixture of [U-¹³C₆]glucose and [1-¹³C]glucose, a combination of tracers commonly used in the literature (Noh et al., 2006, Sriram et al., 2008). The actual proportion of each tracer and naturally labeled glucose from serum was obtained from GC/MS measurements of extracellular glucose. Extracellular fluxes and MIDs of intracellular metabolites were used to estimate the flux distribution (see Supplementary Table 1 for all measurement data). The system possessed 101 redundant measurements and the expected upper bound of the 95% confidence region is 130, assuming that the minimized sum of squared residuals (SSR) followed a χ² distribution. Flux estimation resulted in a minimized SSR of 52, indicating that the fit was statistically acceptable. Estimated values and 95% confidence intervals for each independent flux are listed in Table 2. The overall metabolic network is depicted in Figure 1. Several exchange fluxes were difficult to precisely determine; in these cases, values were culled from literature.

Table 2.

Experimentally determined net (→) and exchange (↔) fluxes and 95% flux confidence intervals for the A549 carcinoma cell

Glycolysis
Reaction	Flux	Interval
Glucext → G6P	38.6	[34.7, 43.2]
G6P → F6P	32.4	[29.7, 35.1]
G6P ↔ F6P	0.0	[0.0, Inf]
F6P → DHAP + GAP	36.5	[32.6, 40.7]
DHAP → GAP	35.5	[31.6, 39.7]
DHAP ↔ GAP	0.0	[0.0, 258.7]
GAP → 3PG	74.0	[65.7, 82.8]
GAP ↔ 3PG	0.0	[0.0, Inf]
3PG → Pyr	73.1	[64.8, 81.9]
Pyr → Lac	73.6	[65.8, 83.3]
Pyr ↔ Lac	13420	[0.0, Inf]
Lac → Lac.x	73.6	[65.8, 83.3]

Pentose Phosphate Pathway
Reaction	Flux	Interval
G6P → 6PG	6.2	[5.4, 7.4]
6PG → P5P + CO2	6.2	[5.4, 7.4]
2 P5P → S7P + GAP	2.0	[1.8, 2.4]
2 P5P ↔ S7P + GAP	19290	[0.0, Inf]
S7P + GAP → F6P + E4P	2.0	[1.8, 2.4]
S7P + GAP ↔ F6P + E4P	0.0	[0.0, 0.4]
P5P + E4P → F6P + GAP	2.0	[1.8, 2.4]
P5P + E4P ↔ F6P + GAP	0.0	[0.0, 0.6]

TCA Cycle/Anaplerosis
Reaction	Flux	Interval
Pyr + CO2 → OAA	0.0	[0.0, 1.7]
Mal → Pyr + CO2	9.6	[8.5, 10.7]
Mal ↔ Pyr + CO2	1.3	[0.9, 1.6]
Pyr → AcCoAmit + CO2	8.6	[5.5, 11.0]
AcCoAmit + OAA → Cit	8.6	[5.5, 11.0]
AKG + CO2 → Cit	2.0	[0.2,3.6]
AKG + CO2 ↔ Cit	5.7	[4.6, 7.1]
AKG → Suc + CO2	8.2	[6.6, 10.7]
Suc → Fum	8.2	[6.6, 10.7]
Suc ↔ Fum	0.2	[0.0, Inf]
Fum → Mal	8.2	[6.6, 10.7]
Fum ↔ Mal	23.8	[5.2, Inf]
OAA → Mal	1.4	[0.8, 2.9]
OAA ↔ Mal	106200	[35.9, Inf]

Amino Acid Metabolism
Reaction	Flux	Interval
Glnext → Gln	11.5	[10.4, 12.6]
Gln → Glu	11.0	[9.9, 12.1]
Glu → AKG	8.2	[7.0, 9.3]
Glu ↔ AKG	81.3	[35.9, 480.3]
Pyr + Glu → Ala + AKG	0.5	[0.4, 0.6]
OAA + Glu → Asp + AKG	0.6	[0.5, 0.7]
3PG + Glu → Ser + AKG	0.9	[0.8, 1.1]
Ser → Gly + MEETHF	0.4	[0.3, 0.4]

Biomass Formation
Reaction	Flux	Interval
P5P → NTP	0.1	[0.1, 0.1]
DHAP → GLP	1.0	[0.8, 1.2]
Cit → AcCoAcyt + OAA	10.7	[5.3, 14.5]
AcCoAcyt → FA	10.7	[5.3, 14.5]
Amino acids → Biomass	3.3	[2.7, 4.0]

Figure 1.

Experimentally determined fluxes representing central carbon metabolism in tumor cells. Extracellular fluxes and MIDs were measured and incorporated into the network shown (see Supplementary Table 2). An acceptable fit was obtained with a sum of squared residuals (SSR) of 52, well under the upper bound of the 95% confidence region for a χ² distribution. Net fluxes are listed first for each reaction and exchange fluxes are within parenthesis. Units for all fluxes are nmol min⁻¹ mg protein⁻¹. Italicized numbers represent flux values that were taken from literature since they were unidentifiable for our particular experiment.

As expected, the cancer cells displayed a high glycolytic flux and excreted most of the carbon as lactate. Approximately 15% of the glucose flux was diverted to the pentose phosphate shunt. However, these estimations did not include explicit measurements of pentose phosphate intermediates; as such, exchange fluxes within this pathway were unidentifiable (Table 2). TCA cycle fluxes were relatively low and largely driven by glutamine consumption. Interestingly, we observed a net flux toward citrate for the isocitrate dehydrogenase (IDH) reaction, indicating that this cell line undergoes reductive carboxylation of α-ketoglutarate (Figure 1). Finally, we estimated a significant flux from malate to pyruvate (malic enzyme) and a negligible flux through pyruvate carboxylase (pyruvate to oxaloacetate). Malic enzyme flux, which regenerates NADPH, can be assumed to compensate for the excessive NADPH requirements of fatty acid synthesis and any lost in the reductive carboxylation pathway (Deberardinis et al., 2008). Our results successfully described the metabolic phenotype of cancer cells and serve as a benchmark for our tracer analysis below.

Tracer confidence intervals

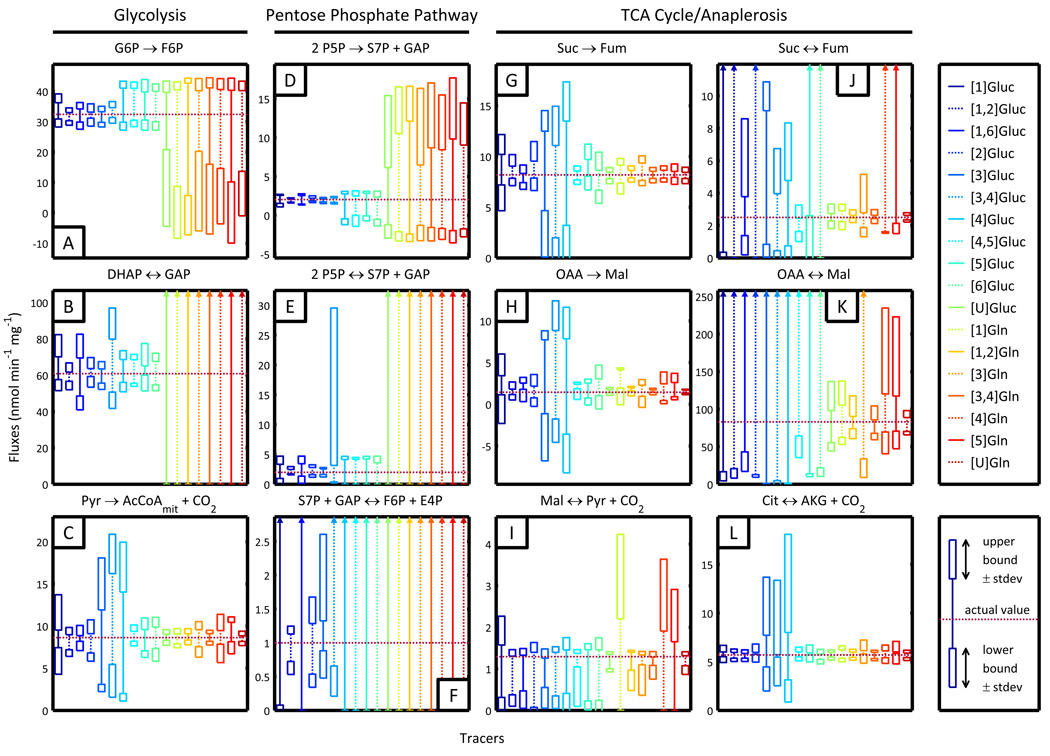
We next calculated confidence intervals for every combination of tracer and flux. Results for selected fluxes are shown in Figure 2, and the complete set of confidence intervals over all fluxes is available in Supplementary Figures 1 and 2.

Figure 2.

Simulated confidence intervals for selected fluxes when using specific isotopic tracers. Horizontal dashed lines indicate actual fluxes. Upper and lower bounds of the 95% confidence interval are illustrated for each simulated tracer. The standard error of both upper and lower bounds is represented by the boxes at the top and bottom of each interval. (A) Glucose-6-phosphate isomerase and (B) triose-phosphate isomerase fluxes demonstrate the effectiveness of glucose tracers in estimated glycolytic fluxes. (C) Pyruvate dehydrogenase flux is most precisely estimated by most glutamine tracers and some glucose tracers. (D–F) Net and exchange fluxes within the pentose phosphate pathway are best determined with glucose tracers labeled at the 1st, 2nd, or 3rd carbon, with [1,2]glucose performing best. (G,H) Net fluxes and (I–L) exchange fluxes in the TCA cycle are characterized well using [U]Gluc, [1,2]Gln, [3,4]Gln, or [U]Gln.

Because the lower glycolytic fluxes consist primarily of stoichiometrically determined net fluxes and completely unidentifiable exchange fluxes, tracers of any kind offer no benefit in flux estimation and show little variation in confidence interval precision in this region of the network. Tracers do generate results of more diverse quality in upper glycolysis (see Figures 2A and 2B for examples). Here, glutamine tracers are completely ineffective, since there is no set of reactions by which any glutamine atom can travel to this portion of the network. Uniformly labeled glucose also gives nominal precision; because there are no other carbon sources feeding into glycolysis, all metabolites here are fully labeled by this tracer at isotopic steady state regardless of the flux distribution.

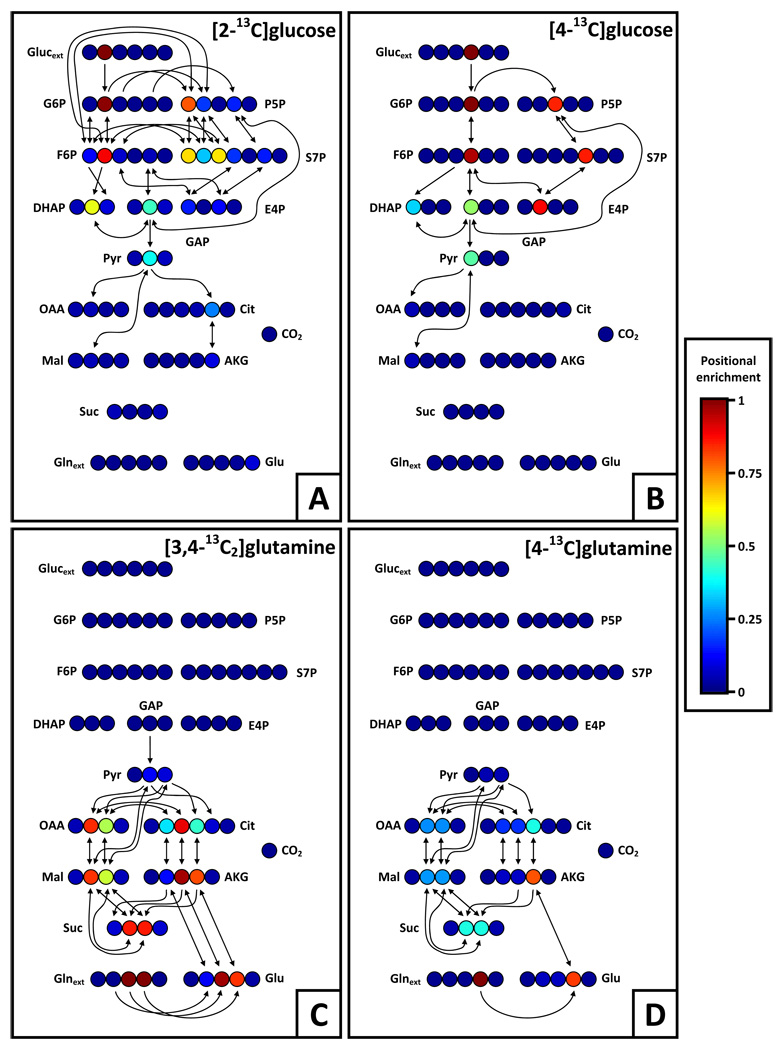
Glucose tracers labeled at some combination of the 4th, 5th, and 6th carbons give results of limited quality, primarily because these labeled atoms are trapped in a cycle. If M_i is the ith atom of metabolite M_i the atomic transitions show that glucose_i (where 4 ≤ i ≤ 6) will distribute ¹³C to only G6P_i, F6P_i, P5P_i−1, S7P_i+1, E4P_i−2, GAP_i−3, and DHAP_i−3 before permanently exiting glycolysis and the PPP (see highlighted atom transitions for [4]Gluc in Figure 3B). This uniformity means that the key GC/MS fragment behind glycolysis flux estimation (GLP) will only be labeled at a single carbon, reducing the potential measurement diversity, which in turn reduces the sensitivity to fluxes. The 1st carbon of glucose feeds into a comparable positional carbon cycle, leading to [3-¹³C]GLP and similarly decreased sensitivity. Tracers labeled at the 2nd or 3rd carbons ([1,2]Gluc, [2]Gluc, and [3]Gluc), however, capitalize on the atomic transitions of the subnetwork and distribute significant label to each carbon in GLP, producing the greatest sensitivity and most precise confidence intervals in glycolysis (see highlighted atom transitions for [2]Gluc in Figure 3A).

Figure 3.

Atom transition networks and positional fractional labeling for selected glucose and glutamine tracers. Fractional labeling is indicated by a colormap, where dark red indicates all atoms at that position are ¹³C and dark blue that all atoms are ¹²C. No natural labeling was assumed in the creation of these maps. Atom transitions are indicated for all positions where fractional ¹³C labeling exceeds 10%. (A) [2]Gluc effectively characterizes glycolytic and PPP fluxes because DHAP (and by extension GLP) is labeled in multiple positions by different combinations of fluxes, leading to greater measurement sensitivity. (B) [4]Gluc poorly identifies fluxes in glycolysis and the PPP because its sole labeled carbon is caught in a cycle and can only reach the 1st carbon of DHAP. (C and D) [3,4]Gln and [4]Gln are both able to label a majority of the carbon atoms in the TCA cycle; however, the two labeled atoms in the former lead to larger, clearer measurements and therefore more precises fluxes.

The estimation quality of the PPP closely reflects that of upper glycolysis. Instead of GLP, P5P is now the major contributing measurement. [U]Gluc and all glutamine tracers are again completely noninformative (for the same reasons as before). [4], [4,5], [5], and [6]Gluc are ineffective because label is once more restricted to a small subset of positions in the network. Because [1]Gluc loses its label to CO₂ in the oxidative PPP, P5P is predominantly unlabeled and demonstrates little sensitivity. Glucose labeled at the 2nd and 3rd positions are again the tracers that most confidently estimate fluxes. These behaviors are fairly consistent through all individual net and exchange fluxes of the PPP. Specific examples are shown in Figures 2D (transketolase net), 2E (transketolase exchange), and 2F (transaldolase exchange).

Glutamine tracers, on the other hand, generally provided better estimations of the pyruvate dehydrogenase flux, located at the junction between glycolysis and the TCA cycle (Figure 2C). Because both the 3rd and 4th carbons in glucose mostly transition to the 1st carbon of pyruvate and exit the system as CO₂ at this step, [3]Gluc, [3,4]Gluc, and [4]Gluc could not precisely resolve the PDH flux, despite their common use and effectiveness in previous experiments (Holleran et al., 1997, Munger et al., 2008). This discrepancy arises because these previous studies measured labeling in CO₂ while our analysis assumes no such measurement. Importantly, one cannot exchange measurement sets of MFA experiments and necessarily expect similar results or patterns when evaluating tracers.

While ¹³C glutamine and uniformly labeled glucose tracers offered minimal information for glycolysis and the PPP, they demonstrated considerable utility in estimating TCA cycle and anaplerotic fluxes. Net fluxes within the TCA cycle (succinate to fumarate and oxaloacetate to fumarate) were best characterized when using glutamine tracers with two or more carbons, specifically [1,2]Gln, [3,4]Gln, and [U]Gln (Figure 2G and Figure 2H). Because the glutamine flux into the TCA cycle is significantly smaller than the incoming glucose flux, multiply labeled glutamine tracers are presumably more useful because they introduce greater amounts label that are less easily diluted (see Figures 3C and 3D to compare atom transitions for [3,4]Gln and [4]Gln). The effectiveness of these tracers was further highlighted by the improved confidence intervals obtained for exchange fluxes in the TCA cycle and malic enzyme reactions (Figures 2I–2L). Exchange between succinate, fumarate, and oxaloacetate are key reactions within oxidative metabolism that also affect cofactor levels and pyruvate cycling; therefore, precise estimation of these reactions are of paramount importance for cancer research (Hatzivassiliou et al., 2005, Deberardinis et al., 2008).

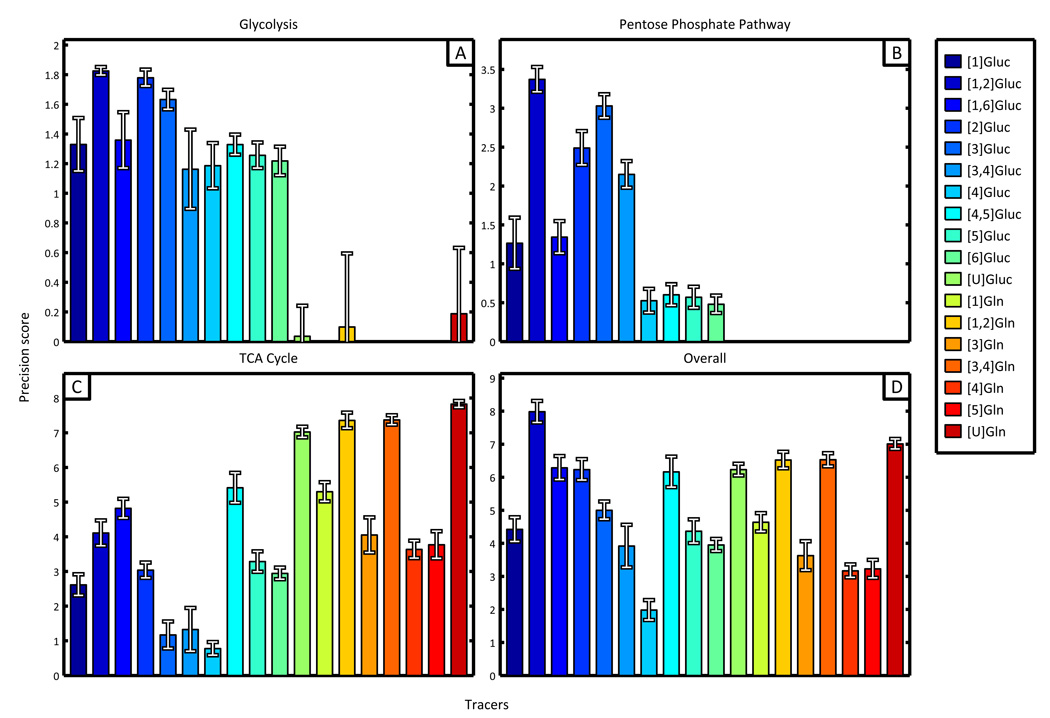
To better describe the quality of data and simulations obtained from specific tracers, we calculated precision scores for each tracer, covering both subnetworks and central carbon metabolism in its entirety. Independent fluxes included in the scoring for each subnetwork are described in Supplementary Figure 3. All glucose tracers except [U]Gluc scored well for glycolysis, with [1,2]Gluc, [2]Gluc, and [3]Gluc performing significantly better than most (Figure 4A). These three tracers provided the best scores (i.e., the most precise estimates) for the PPP as well (Figure 4B). The highest scoring glucose tracer for TCA cycle analysis was [U]Gluc (Figure 4C). Three glutamine tracers also generated similarly high scores and precise estimates within the TCA cycle subnetwork; in particular, those tracers labeled at two or more positions scored best ([1,2]Gln, [3,4]Gln, and [U]Gln). Finally, the best overall tracer for analyzing the entire cancer cell flux network was [1,2]Gluc, followed by other glucose tracers labeled at the 2nd or 3rd carbons (Figure 4D). Although these tracers did not generate the best results for the TCA cycle, their unique ability to consistently characterize fluxes throughout the entire network resulted in superior scores compared to other tracers.

Figure 4.

Results obtained from precision scoring algorithm identify the optimal tracer for analysis of subnetworks and central carbon metabolism. The precision scores resulting from simulated experiments involving only natural labeling have been subtracted from each displayed tracer score to aid in visual differentiation and comparison. (A) Glycolysis and (B) pentose phosphate subnetworks are best described by [1,2]Gluc, [2]Gluc, and [3]Gluc. (C) TCA cycle scores were highest for [U]glucose and several glutamine tracers labeled at two or more carbons. (D) The most precise tracer for analysis of the entire network was [1,2]Gluc.

Conclusion

The metabolic phenotype of tumors has reemerged as an important area of study and potential clinical target (Kroemer and Pouyssegur, 2008). Fueled by advanced computational software and technologies, researchers can now characterize cellular metabolism in unprecedented detail. To better demonstrate the utility of isotopic tracers for cancer research, we have quantitatively and comparatively described the precision of uniquely labeled ¹³C glucose and glutamine tracers for flux determination in mammalian cells. An EMU-based algorithm enabled the high-throughput flux estimations and confidence interval calculations required for this description. Table 3 summarizes the optimal tracers to use for estimating each flux, specific subnetworks, and central carbon metabolism as a whole. [1,2]Gluc provided the highest level of precision for the overall network, glycolysis, and the PPP, while [U]Gluc and multiply labeled glutamine tracers were most informative for the TCA cycle. Specific instances of their use are present in the literature (Boros et al., 2005, Munger et al., 2008, Yoo et al., 2008); however, we hope the demonstrable improvements of precision described here help to propagate the use of more effective tracer molecules in future MFA experiments.

Table 3.

Optimal tracers for net (→) and exchange (↔) fluxes for the A549 carcinoma cell

Glycolysis
Reaction	Best Tracer(s)
Glucext → G6P	[1,2] & [2]Gluc
G6P → F6P	[1,2]Gluc
G6P ↔ F6P	[3] & [3,4]Gluc
F6P → DHAP + GAP	[1,2] & [2]Gluc
DHAP → GAP	[1,2]Gluc
DHAP ↔ GAP	[1,2]Gluc
GAP → 3PG	[1,2] & [2]Gluc
GAP ↔ 3PG	none
3PG → Pyr	[1,2]Gluc
Pyr → Lac	[1,2] & [2]Gluc
Pyr ↔ Lac	none
Lac → Lac.x	[1,2] & [2]Gluc

Pentose Phosphate Pathway
Reaction	Best Tracer(s)
G6P → 6PG	[1,2]Gluc
6PG → P5P + CO2	[1,2]Gluc
2 P5P → S7P + GAP	[1,2] & [3]Gluc
2 P5P ↔ S7P + GAP	[1,2]Gluc
S7P + GAP → F6P + E4P	[1,2]& [3]Gluc
S7P + GAP ↔ F6P + E4P	[1,2]Gluc
P5P + E4P → F6P + GAP	[1,2] & [3]Gluc
P5P + E4P ↔ F6P + GAP	[1,2] & [3]Gluc

TCA Cycle/Anaplerosis
Reaction	Best Tracer(s)
Pyr + CO2 → OAA	[U]Gln
Mal → Pyr + CO2	[U] & [3,4]Gln
Mal ↔ Pyr + CO2	[U]Gln
Pyr → AcCoAmit + CO2	[U]Gln
AcCoAmit + OAA → Cit	[U]Gln
AKG + CO2 → Cit	[U], [1,2] & [3,4]Gln
AKG + CO2 ↔ Cit	[U]Gln
AKG → Suc + CO2	[U] & [3,4]Gln
Suc → Fum	[U] & [3,4]Gln
Suc ↔ Fum	[U] & [1,2]Gln
Fum → Mal	[U] & [3,4]Gln
Fum ↔ Mal	[U]Gln
OAA → Mal	[U]Gln
OAA ↔ Mal	[U]Gln

Amino Acid Metabolism
Reaction	Best Tracer(s)
Glnext → Gln	[3], [U] & [3,4]Gln
Gln → Glu	[3], [U] & [3,4]Gln
Glu → AKG	[3], [U] & [3,4]Gln
Glu ↔ AKG	[U]Gln

The tracer evaluation process and accompanying results in this study provide a general procedure for the experimental design of isotopic tracer studies. However, it should be noted that specific cell types exhibit particular flux profiles, which in turn will affect the results generated by simulated tracer studies such as those presented here. As such, our findings are network dependent and therefore most relevant to the study of tumor cells. Furthermore, the precision of our flux estimations are dependent upon the metabolites measured. As mass spectrometry and other related technologies continue to improve, researchers will obtain richer data sets to incorporate into the estimation process (Munger et al., 2008, Hofmann et al., 2008). Nevertheless, our results should be valid for most mammalian systems given the conserved nature of atom transitions in central carbon metabolism. In cells with significantly different networks and/or flux distributions (e.g., gluconeogenic hepatocytes) these specific tracer simulations may not apply (Yang et al., 2008). However, our methodology will still prove useful in optimizing experimental design, especially in complex systems where the best tracer cannot be determined a priori. Future studies requiring more rigorous simulations will aim to identify combinations of differentially labeled substrates that can further improve the precision of flux estimations. In the meantime, these results can serve as a guide for systems biologists to more effectively design experiments to study metabolism at a global level.

Nomenclature

3PG

3-phosphoglycerate

6PG

6-phosphogluconate

AcCoA

acetyl coenzyme A

AKG

α-ketoglutarate

Ala

alanine

Asp

aspartate

Cit

citrate

Cyt

cytosolic

DHAP

dihydroxyacetone phosphate

E4P

erythrose 4-phosphate

Ext

extracellular

F6P

fructose 6-phosphate

FA

fatty acids

Fum

fumarate

G6P

glucose 6-phosphate

GAP

glyceraldehyde 3-phosphate

Gln

glutamine

GLP

glycerol 3-phosphate

Glu

glutamate

Gluc

glucose

Gly

glycine

Lac

lactate

Mal

malate

Mit

mitochondrial

NTP

nucleotide tri-phosphate

OAA

oxaloacetate

P5P

pentose 5-phosphate

Pyr

pyruvate

S7P

seduheptulose 7-phosphate

Ser

serine

Suc

succinate