Kinetic analysis in human brain of [¹¹C](R)-rolipram, a positron emission tomographic radioligand to image phosphodiesterase 4: a retest study and use of an image-derived input function

Abstract

[¹¹C](R)-rolipram provides a measure of the density of phosphodiesterase 4 (PDE4) in brain, an enzyme that metabolizes cAMP. The aims of this study were to perform kinetic modeling of [¹¹C](R)-rolipram in healthy humans using an arterial input function and to replace this arterial input in humans with an image-derived input function.

Methods

Twelve humans had two injections of [¹¹C](R)-rolipram. An image-derived input function was obtained from the carotid arteries and four blood samples. The samples were used for partial volume correction and for estimating the parent concentration using HPLC analysis.

Results

An unconstrained two-compartment model and Logan analysis measured distribution volume V_T, with good identifiability but with moderately high retest variability (15%). Similar results were obtained using the image input (ratio image/arterial V_T = 1.00 ± 0.06).

Conclusions

Binding of [¹¹C](R)-rolipram to PDE4 can be quantified in human brain using kinetic modeling and an arterial input function. Image input function from carotid arteries provides an equally accurate and reproducible method to quantify PDE4.

INTRODUCTION

3', 5'-cyclic adenosine monophosphate (cAMP) is a prevalent second messenger that mediates the actions of several neurotransmitters and may play an important role in the mechanism of action of antidepressants. In vivo, cAMP is synthesized from adenosine 5'-triphosphate by adenylyl cyclase and is metabolized by cyclic nucleotide phosphodiesterases (PDEs), including PDE4, which is selective to brain cAMP (Houslay, 2001). Animal studies suggest that the cAMP cascade is a mechanism of action common to several antidepressant drug treatments and to electroconvulsive therapy (Duman et al., 1997). All these effective treatments upregulate components in the cAMP cascade: cAMP-dependent protein kinase, cAMP response element binding protein, and PDE4 (D'Sa and Duman, 2002). Human studies also suggest that upregulation of the cAMP cascade is a mechanism of antidepressant action. The PDE4 inhibitor, rolipram, which acutely increases the intracellular concentration of cAMP, has antidepressant activity in patients with depression (D'Sa and Duman, 2002). Although rolipram showed promising efficacy in these initial trials, studies were discontinued because of side effects, especially nausea and vomiting.

The radiolabeled active enantiomer of rolipram, [¹¹C](R)-rolipram, has been used with positron emission tomography (PET) to image and to quantify PDE4 in brain (DaSilva et al., 2002; Matthews et al., 2003). However, a rigorous test-retest quantitative study on a large number of subjects has not been reported yet.

One disadvantage of rigorous quantitative studies is that they typically require measurement of radioligand in arterial plasma so as to calculate delivery of radioligand to brain. Insertion of an arterial catheter is sometimes painful and often discourages subjects from participating in PET studies. To avoid arterial catheterization, several methods have been proposed to estimate the concentration of total radioactivity in whole blood from PET images of the internal carotid artery (Chen et al., 1998; Naganawa et al., 2005a; Su et al., 2005; Zanotti-Fregonara et al., 2009b). These methods of “image-derived input function” have typically been tested with [¹⁸F]fluorodeoxyglucose, which has minimal metabolism in human blood. There have been only a few studies that dealt with brain imaging tracers like [¹¹C](R)-rolipram, which are characterized by the presence of variable amounts of radiometabolites and the measurement of metabolite-corrected arterial input function is required for the quantification. Those studies did not address the problem of metabolite correction (Mourik et al., 2008; Naganawa et al., 2005b).

The two aims of this study were 1) to quantify uptake of [¹¹C](R)-rolipram in human brain using the “gold standard” method of a metabolite-corrected arterial input function in a substantial number (twelve) of subjects, and 2) to explore the possibility of replacing this gold standard with an image-derived input function. All subjects were scanned twice so as to measure test-retest reproducibility.

MATERIALS AND METHODS

Radioligand preparation

[¹¹C](R)-rolipram was synthesized as previously described (Fujita et al., 2005) and according to our Investigational New Drug Application #73,149, submitted to the US Food and Drug Administration. A copy of our application is available at: http://pdsp.med.unc.edu/snidd/nidpulldownPC.php. The radioligand was obtained in high radiochemical purity (> 99%).

Image acquisition and processing

Twelve healthy subjects (2 females and 10 males) participated and were 28 ± 11 years of age and had body weight of 74 ± 12 kg. All subjects were free of current medical and psychiatric illness, based on history, physical examination, electrocardiogram, urinalysis including drug screening, and blood tests (complete blood count, serum chemistries, thyroid function test, and antibody screening for syphilis, HIV, and hepatitis B). Subjects returned to repeat urinalysis and blood tests about 24 h after the PET scan. The protocol was validated by the Ethical Committee of the NIH and the subjects signed a written informed consent.

PET scans

PET images were acquired using the High Resolution Research Tomograph (HRRT; Siemens/CPS, Knoxville, TN, USA) for 120 min. The PET camera has spatial resolution of 2.5 mm measured as the reconstructed full-width at half maximum. We performed two [¹¹C](R)-rolipram scans in 12 subjects for a total of 24 scans. Six subjects had two scans on the same day (morning and afternoon), and six had scans on separate days with an interval of 45 ± 43 days. For the 12 test scans, the injected activity was 421 ± 144 MBq and the specific activity at time of injection was 152 ± 86 GBq/µmol, which corresponded to 4.0 ± 3.0 nmol (49.9 ± 34.1 pmol/kg). These figures in the 12 retest scans were: injected activity: 420 ± 121 MBq; specific activity: 125 ± 56 GBq/µmol, which corresponded to 4.3 ± 2.7 nmol (58.8 ± 37.8 pmol/kg). One of the twelve subjects was scanned for only 90 min instead of 120 min. Head motion was corrected by monitoring its position during the scan with the Polaris Vicra Optical Tracking System (NDI, Waterloo, Ontario, Canada) (Bloomfield et al., 2003). The dynamic scan consisted of 33 frames (6 frames of 30 seconds each, then 3 × 60 s, 2 × 120 s and 22 × 300 s). All PET images were corrected for attenuation and scatter (Carson et al., 2004). PET data were reconstructed on a 256×256 matrix with a pixel size of 1.22×1.22×1.23 mm³ using the Motion-compensation OSEM List-mode Algorithm for Resolution-recovery (MOLAR) (Carson et al., 2004).

Because one of the 12 subjects had unusually poor reproducibility in the initial set of two scans, we scanned him for an additional set of two scans - i.e., four scans in total. The unusually poor reproducibility was caused by low brain activity in the first scan. The activity was ~2 SD below the mean of all other subjects. The first set of test retest scans was not included in the analysis.

Magnetic resonance imaging

To identify brain regions, magnetic resonance images (MRIs) were obtained using a 1.5-T GE Signa device. Three sets of axial images were acquired parallel to the anterior-commissure-posterior commissure line with Spoiled Gradient Recalled (SPGR) sequence of TR/TE/flip angle =12.4 ms/5.3 ms/20°, voxel size = 0.94×0.94×1.2 mm, and matrix=256×256. These three MRI sets were realigned, averaged, and then coregistered to the PET images (see below).

Measurement of [¹¹C](R)-rolipram in plasma

Blood samples (1 mL each) were drawn from the radial artery at 15 s intervals until 150 s, followed by 3 mL samples at 3, 4, 6, 8, 10, 15, 20, 30, 40, and 50 min, and 4.5 mL at 60, 75, 90, and 120 min. The plasma time-activity curve was corrected for the fraction of unchanged radioligand (Fujita et al., 2005; Zoghbi et al., 2006). The plasma free fraction (f_P) of [¹¹C](R)-rolipram was determined by ultrafiltration (Sawada et al., 1990) for each of the two scans in all 12 subjects. Radioactivity in whole blood was used to correct radioactivity in brain for that in the vascular compartment (~ 5% of tissue volume).

Image analysis

Preset regions of interest were positioned on the PET images with the following methods. The average MR image from three acquisitions of each subject (see above) was coregistered using SPM5 to the average PET image created from all frames. Both MR and all PET images were spatially normalized to a standard anatomic orientation (Montreal Neurological Institute space) based on transformation parameters from the MR images. Preset regions were positioned on the spatially normalized MR images to overlie thalamus (12.6 cm³), caudate (5.6 cm³), putamen (6.5 cm³), cerebellum (51.2 cm³), frontal (27.2 cm³), parietal (26.6 cm³), lateral temporal (25.0 cm³), occipital (31.2 cm³), anterior cingulate (7.5 cm³), and medial temporal (14.3 cm³) cortices.

Measurement of [¹¹C](R)-rolipram binding using arterial input function

Using the concentration of radioactivity in brain and the concentration of [¹¹C](R)-rolipram in plasma, we calculated [¹¹C](R)-rolipram binding with one- and two-tissue compartmental models and with Logan analysis. Three binding parameters were calculated: 1) total distribution volume (V_T), which equals the ratio at equilibrium of total radioactivity in brain to the total plasma concentration (i.e., free plus protein bound) of [¹¹C](R)-rolipram, 2) total distribution volume corrected for plasma free fraction (V_T/f_P) and 3) binding potential (BP_ND), which equals the ratio at equilibrium of the concentration of specific binding to nondisplaceable uptake, which itself equals free and nonspecifically bound radioligand. In theory, correction for f_P (V_T/f_P) should more accurately reflect binding than that without correction (V_T), because only free ligand enters the brain. However, the inclusion of f_P may introduce additional noise associated with its measurement.

The PET brain data were analyzed with both one- and two-tissue compartment models. The two-compartmental analysis was performed in two ways: 1) without constraining the rate constants and 2) fixing the ratio K₁/k₂ to the value obtained in the whole brain excluding the areas of mostly white matter. The purpose of the constraint was to estimate parameters with greater identifiability.

The serial concentrations of radioligand in plasma, referred to as the "input function," was analyzed as linear interpolation of the concentrations of [¹¹C](R)-rolipram before the peak and a tri-exponential fit of concentrations after the peak. The concentration of [¹¹C](R)-rolipram separated from radiometabolites was used as the sole input function, because our prior study showed that only a small percentage (~3% at 30 min) of radioactivity in rat brain derived from radiometabolites (Fujita et al., 2005). Rate constants in standard one- and two-tissue compartment models were estimated with weighted least squares and the Marquardt optimizer. The brain radioactivity due to whole blood was estimated as a variable during kinetic modeling. Brain data of each frame were weighted using the inverse square of the normalized standard deviation of the image data. The standard deviation was assumed to be proportional to the inverse square root of noise equivalent counts. Brain radioactivity was corrected for its vascular component estimated by compartmental fitting. Finally, the delay between arrival of [¹¹C](R)-rolipram in radial or femoral artery and brain was estimated by compartmental fitting of data from the whole brain but excluding areas of mostly white matter. Blood and brain time activity curves are expressed in SUV units.

To determine the minimal scanning time necessary to obtain stable values of distribution volume, we analyzed the PET data from each subject after removing variable durations of the terminal portion of the scan – namely, by analyzing data from 0 – 30 min to 0 – 120 min, with 10 min increments.

Image and kinetic analyses were performed using PMOD 2.85 (pixel-wise modeling software; PMOD Technologies Ltd., Zurich, Switzerland) (Burger et al., 1998).

Measurement of [¹¹C](R)-rolipram binding using image-derived input function

Using the 12 sets of test-retest images previously acquired for kinetic modeling, we sought to validate the measurement of [¹¹C](R)-rolipram binding in brain using an image input function plus limited blood data. This method has two steps: 1) estimating the concentration of radioactivity in whole blood from the PET images, and 2) calculating metabolite-corrected image input. The concentration of radioactivity in whole blood was estimated from the internal carotid artery and from surrounding regions following the method of Chen and colleagues (Chen et al., 1998). This method was chosen because it provided very reliable results in a previous comparative analysis between eight different image input methods (Zanotti-Fregonara et al., 2009a). Carotid and surrounding regions were manually drawn on the summed PET frames of the first two min and then copied to all the frames of the 90 min session. The right and left carotid regions were round-shaped and the two surrounding regions were shaped like a comma, as proposed in the original paper (Chen et al., 1998) (Fig.1). One advantage of this method is that it is very insensitive to the size of the manual-drawn regions of interest (Chen et al., 1998).

Figure 1.

Example of manually defined carotid and background regions of interest identified in the early summed PET frames.

The carotid signal measured from the images was represented as a linear combination of the radioactivity from the blood and spill-in from the surrounding tissue.

$${\mathrm{C}}_{\text{carotid}}(\mathrm{t})=\text{RC}*{\mathrm{C}}_{\text{wb}}(\mathrm{t})+\text{SP}*{\mathrm{C}}_{\text{surround}}(\mathrm{t})$$ (1)

where C_carotid is the concentration of radio activity obtained from the carotid region in the PET image; C_wb is the concentration of radio activity in whole blood directly sampled from the radial catheter; RC is the recovery coefficient necessary to correct the carotid PET measurement for partial volume effect; C_surround is the radio activity in the surrounding tissues; and SP is the percentage spill -in from surrounding tissues to the carotidregion. RC and SP were estimated with linear least square fitting of C_carotid, C_wb, and C_surround in equation (1), with C_wb directly measured at 6, 20, 60 and 90 min. The concentration of [¹¹C](R)-rolipram was also measured in these four blood samples (6, 20, 60 and 90 min). The concentrations of [¹¹C](R)-rolipram for the entire duration of the scan were estimated by fitting a monoexponential function to the [¹¹C](R)-rolipram /whole blood ratios at the four time points.

Logan-derived V_T values by the metabolite-corrected image inputs were compared to those calculated with the arterial input, measured at all 23 time points of arterial blood sampling. We selected the Logan analysis because it is less sensitive than compartmental modelling to accurate identification of the initial portion of the input curve. The initial portion of whole blood activity curve has rapid changes of the concentrations of radioactivity and is usually difficult to estimate correctly from images. In this situation, the individual rate constants and resulting V_T values are sometimes poorly estimated. In contrast, Logan analysis relies on the area under the curve of the input function and is less sensitive than compartmental modelling to the initial shape of the input function.

Statistical analysis

Goodness-of-fit by nonlinear least squares analysis was evaluated using the Akaike Information Criterion (AIC) (Akaike, 1974) and Model Selection Criterion (MSC). MSC is a modification of the AIC, was proposed by Micromath Scientific Software (Salt Lake City, Utah, USA), and is implemented in their program, "Scientist." The equation can be found elsewhere (Fujita et al., 1999). The most appropriate model is that with the smallest AIC and the largest MSC score. Although AIC scores are affected by the unit or the concentration of the brain activity, MSC normalizes the score by weighting the sum of squares using average observed data or fitted data for each datum in the numerator or denominator, respectively. Goodness-of-fit by the compartment models was compared with F statistics (Hawkins et al., 1986). A value of P < 0.05 was considered significant for F statistics.

The identifiability of kinetic variables was calculated as standard error obtained from the diagonal of the covariance matrix (Carson, 1986) and expressed as a percentage of the rate constant. Standard error (%) of V_T and BP_ND was calculated from the covariance matrix using the generalized form of error propagation equation (Bevington and Robinson, 2003), where correlations among parameters were taken into account. Greater values of identifiability (%) indicate poorer identifiability.

Retest variability (expressed as the absolute difference between the two scans divided by the mean of the two scans) and intraclass correlation coefficient (ICC) were calculated for both V_T values and plasma areas under the curve (AUC).

Group data are expressed as mean ± SD.

RESULTS

Pharmacological effects

Injection of [¹¹C](R)-rolipram caused no pharmacological effects based on vital signs, ECG, and laboratory testing.

Brain images

The peak uptake occurred at ~10 min and was 2 – 2.5 SUV, followed by a gradual wash-out. Brain activity decreased to 50% of the peak by 90 – 100 min. Consistent with distribution of [³H]rolipram binding in postmortem human brain (Perez-Torres et al., 2000), the in vivo distribution of radioactivity was widespread and fairly uniform in gray matter of cerebral cortices, cerebellum, basal ganglia, and diencephalon.

Plasma analysis

The concentration of [¹¹C](R)-rolipram peaked at ~90 s and then declined slowly, following a curve that was well fit as a tri-exponential function. The peak concentration was ~26 SUV and decreased to 50% of the peak at 2 min, to 20% at 10 min, and to 10% at 30 min (Fig. 2A). Tri-exponential fitting converged in all scans with 4.4% average error of fitting. The fraction of unchanged [¹¹C] (R)-rolipram in total plasma activity was 51.9 ± 15.0% at 75 min (Fig. 2B). Radiometabolites in plasma were less lipophilic than [¹¹C](R)-rolipram. The mean value of f_P was 6.4 ± 0.9%.

Figure 2.

Concentration of [¹¹C](R)-rolipram (●) and total radioactivity (○) in plasma (A) and percentage of unchanged [¹¹C](R)-rolipram in total plasma radioactivity (parent plus radiometabolites) (B). Symbols show mean ± SD from 24 scans in 12 subjects.

Kinetic analysis

Kinetic analysis of brain and plasma data had five major results. First, brain time-activity curves were better fit with an unconstrained and constrained two- than a one-tissue compartment model. Second, the two compartment model with a constraint of K₁/k₂ did not show a clear advantage over the unconstrained two-compartment model to measure binding of [¹¹C](R)-rolipram. Third, despite additional measurement errors for plasma free fraction, V_T/f_P showed retest variability similar to that of V_T. Fourth, 90 min data were adequate to measure V_T. Fifth, Logan analysis and the two-tissue compartment model provided very similar values of V_T.

For the first result, unconstrained two-compartmental fitting converged in all regions and in all scans, but the constrained model did not converge in two of the 240 data sets. F-test showed that the two-tissue compartment models were clearly superior to the one-tissue compartment model in all of 240 fittings in a total of 24 scans (Fig. 3). In addition, the two-tissue compartment models showed lower mean AIC and higher mean MSC scores than the one-compartment model. The unconstrained two-compartment model identified V_T with average standard error across brain regions of 4.7%.

Figure 3.

The concentrations of radioactivity in lateral temporal cortex from a typical healthy subject were fitted with a one- and an unconstrained two-tissue compartment model. The two-tissue compartment model () more closely followed the measured values than did the one-compartment model ().The values of V_T were 0.668 mL/cm³ from the one-tissue compartment model and 0.756 mL/cm³ from the two-tissue compartment model. Weighting using Noise Equivalent Counts is influenced by radioactive decay, and that explains the slight deviation of the two-tissue compartment model to the measured data at late time-points. Brain data for this region were also quantified with the Logan method using either the arterial input function or the image input function. The values of V_T (derived from the slope of the lines) were similar for both inputs: 0.781 mL/cm³ for arterial and 0.783 mL/cm³ for image.

For the second results, the constrained two-compartment model did not show a clear advantage over the unconstrained two-compartment model to measure binding of [¹¹C](R)-rolipram. The constrained two-compartment model provided a similar goodness-of-fit as the unconstrained model with AIC and MSC scores (60 and 4.4 respectively for the unconstrained model and 65 and 4.3 for the constrained model). One advantage of constrained fitting is improved identifiability of parameters. Therefore, we investigated whether fixing K₁/k₂ improved identifiability of two measures of [¹¹C](R)-rolipram binding, V_T and BP_ND and found that the constraint did not improve identifiability (standard error) of V_T but tended to improve that of BP_ND. Unconstrained and constrained two-compartmental fitting equally well identified V_T with average identifiability across brain regions of 4.7% and 5.1%, respectively. On the other hand, another measure of radioligand binding, BP_ND, was not well identified without constraint. The unconstrained model gave average identifiability of 16.2% across brain regions. By fixing K₁/k₂, standard errors of BP_ND tended to improve to 8.6%. However, BP_ND values showed larger variability than V_T values (see below). Therefore, the constraint of K₁/k₂ was not useful to measure [¹¹C](R)-rolipram binding more precisely.

For the third result, precision of V_T/f_P was evaluated based on retest variability. V_T/f_P corrects V_T using the plasma free fraction measured in each subject. V_T by the unconstrained model of 120 min of data showed an average variability of 18.5%. V_T/f_P showed a similar retest variability of 15.4%. BP_ND showed larger retest variability (29.6%).

For the fourth result, to determine the minimal scan time required to obtain stable values of V_T/f_P in human by the unconstrained two-compartment model, we increasingly truncated the brain data of the 23 scans which had a length of 120 min to only the initial 30 min. In all regions, V_T/f_P determined using the data of the initial 90 min was relatively well identified (standard errors ranging 2.1 – 12.2%) and showed small biases (<4%) from that determined from the entire 120 min (Fig 4). Standard errors exceeded 10% in only putamen (11.9%) and cerebellum (12.2%).

Figure 4.

V_T/f_P was calculated for caudate using an unconstrained two-tissue compartment model. Scans were analyzed using brain data from time 0 to the specified time on x-axis. V_T/f_P was expressed as a percentage of terminal value – i.e., V_T/f_P calculated from the entire 120-min data set. Error bars are identifiability (standard errors %) of V_T/f_P. Imaging for the initial 80 min provided V_T/f_P within 10% (dashed lines) of that obtained with the full length data and also provided good identifiability of < 12%. Note that V_T and V_T/f_P have the identical dependency on the length of data.

Finally, the Logan-derived V_T values, calculated using a 90 min scan, were very similar to those obtained with two-tissue compartment model, with a difference of <10% (Table 1).

Table 1.

Distribution volume calculated from compartmental rate constants are similar to the distribution volume calculated with Logan plot in 12 healthy subjects.

	Compartmental rate constants *				Compartmental distribution volume *	Logan distribution volume *
Region	K1 (mL • cm−3 • min−1)	k2 (min−1)	k3 (min−1)	k4 (min−1)	VT (mL • cm−3)	VT (mL • cm−3)
Frontal Cortex	0.058 ± 0.013 (3.1 %)	0.18 ± 0.04 (6.9%)	0.049 ± 0.024 (12%)	0.041 ± 0.017 (10.2%)	0.73 ± 0.18 (2.8%)	0.70 ± 0.13
Temporal Cortex	0.058 ± 0.011 (3.5%)	0.17 ± 0.03 (7.3%)	0.038 ± 0.017 (16.1%)	0.037 ± 0.015 (14.1%)	0.72 ± 0.16 (3.4%)	0.69 ± 0.12
Medial Temporal Cortex	0.030 ± 0.001 (5.1%)	0.15 ± 0.03 (11.8%)	0.045 ± 0.022 (23.9%)	0.041 ± 0.018 (20.1%)	0.60 ± 0.22 (6.5%)	0.55 ± 0.11
Parietal Cortex	0.056 ± 0.011 (3.1 %)	0.18 ± 0.03 (6.4%)	0.044 ± 0.021 (12.0%)	0.039 ± 0.015 (9.2%)	0.67 ± 0.12 (2.2%)	0.66 ± 0.11
Occipital Cortex	0.066 ± 0.020 (7.1%)	0.24 ± 0.04 (13.6%)	0.048 ± 0.034 (23.1%)	0.041 ± 0.017 (19.5%)	0.59 ± 0.14 (5.4%)	0.58 ± 0.11
Anterior Cingulum	0.052 ± 0.014 (7.0%)	0.19 ± 0.04 (14.7%)	0.054 ± 0.033 (25.6%)	0.043 ± 0.021 (21.5%)	0.64 ± 0.19 (6.5%)	0.61 ± 0.13
Caudate	0.055 ± 0.011 (7.5%)	0.18 ± 0.04 (17.6%)	0.056 ± 0.036 (36.6%)	0.052 ± 0.029 (26.1%)	0.68 ± 0.25 (7.4%)	0.62 ± 0.12
Putamen	0.067 ± 0.013 (5.7%)	0.19 ± 0.03 (13.0%)	0.046 ± 0.028 (31.5%)	0.055 ± 0.026 (20.9%)	0.69 ± 0.15 (3.8%)	0.67 ± 0.12
Thalamus	0.055 ± 0.011 (4.8%)	0.16 ± 0.03 (13.0%)	0.051 ± 0.036 (31.8%)	0.065 ± 0.036 (21.8%)	0.66 ± 0.19 (5.1 %)	0.63 ± 0.13
Cerebellum	0.060 ± 0.012 (2.8%)	0.20 ± 0.03 (5.8%)	0.039 ± 0.025 (16.6%)	0.061 ± 0.037 (13.5%)	0.52 ± 0.13 (3.1 %)	0.52 ± 0.11

Values are mean ± SD from twelve human subjects each having two scans.

For each brain region, standard errors are listed in parentheses and are expressed as % of the variable itself.

^*Compartmental rate constants and distribution volumes are calculated from 90 min of brain and plasma data.

Image-derived input function

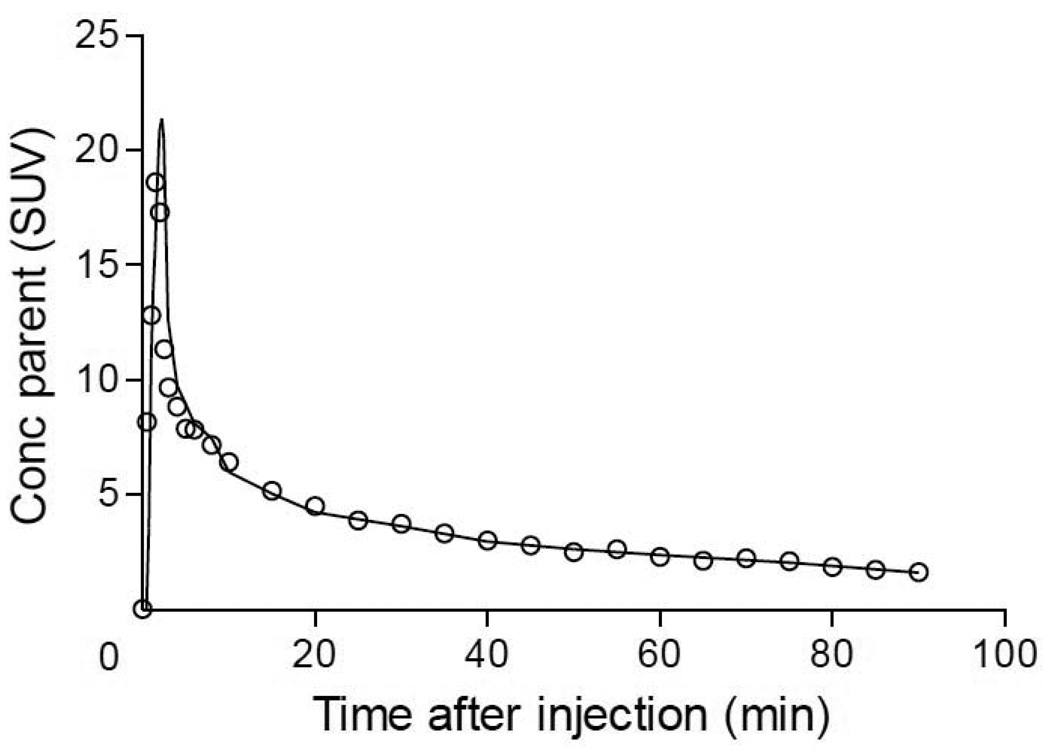
We compared image and arterial inputs relative to their time-activity curves and to their effect on measurement of distribution volume. With regard to the time-activity in whole blood, the shape of the image-derived curves closely matched that of the arterial input, especially at later times (Fig. 5). The peak heights (at ~1 min) sometimes varied between methods, with the image input underestimating the peak in 9 of 12 subjects. We further evaluated the time-activity curves by comparing AUC (the area integrated over the entire scan duration) from image and arterial inputs. The AUCs were similar for both methods, especially for the latter portions of the curves. For the first 90 s, the ratio of the AUC of image input compared to that of arterial input was 0.84 ± 0.23 (mean ± SD in 12 scans). The tails of the curves were better estimated, so that the ratio of AUCs from 90 s to 90 min was 1.05 ± 0.05. For the entire 90 min, the ratio of AUCs from image to that from arterial inputs was 1.03 ± 0.04.

Figure 5.

[¹¹C](R)-rolipram parent concentration over time obtained from the image input function () and from the arterial input function (○) of a representative healthy subject. The parent fraction has been estimated by fitting a monoexponential function through the parent/whole blood ratio measured in the four blood samples used to calculate the image-derived input function.

With regard to the accuracy of image input on measurement of distribution volume, the values of Logan V_T values were almost identical for the two methods. The ratio of the image to arterial V_T was 1.00 ± 0.06, measured in 12 scans. In addition, the image input had no significant effect on the reproducibility of quantification, since retest variability for V_T was 15.2 ± 12.7% for the arterial input and 14.1 ± 10.9% for the image input. These two methods also showed similar inter-subject variability among 12 subjects: 19.4% for arterial and 20.9% for image input. ICC values were slightly higher for image input (0.60) than for arterial input (0.47), but this difference was not significant by F-test. For the plasma data, the retest variability of AUC and the values of ICC were similar for the two inputs.

DISCUSSION

In this study we evaluated the ability of PET to quantify [¹¹C](R)-rolipram binding in human brain using arterial blood samples as the gold standard method. We also examined whether an input function derived from PET images of the internal carotid artery could substitute for the arterial input function. The major findings of this study were:

1. By using arterial blood sampling, unconstrained two-tissue compartmental modeling and the Logan plot provided well identified values of distribution volume, which reflected binding of [¹¹C](R)-rolipram to PDE4. Total distribution volume corrected for plasma protein binding (V_T/f_P) was about 9.3 mL/cm³ and these values showed moderately high retest variability (15%).

2. For the Logan plot to calculate distribution volume, we found that full arterial blood samples could be replaced with a less invasive input function derived from PET images of the internal carotid artery. The ratio of V_T by arterial- and image-inputs was 1.00 ± 0.06. Further, the retest variability of Logan-V_T determined from arterial input (15.2%) was the same as that using the image input (14.1%).

Duration of scan

We found that 90 min of brain and plasma data are adequate to measure distribution volume with small bias and good identifiability. This length is consistent with an early peak and fast washout from brain (Fig. 3A). Scanning for an additional 30 min (i.e., for a total of 120 min) provided stable values for V_T, suggesting that radiometabolites do not substantially accumulate in human brain. In summary, the in vivo kinetics of [¹¹C](R)-rolipram are well matched to the half-life of its radionuclide (20 min) to reliably measure binding to PDE4 in human brain with minimal contamination by radiometabolites.

Image-derived input function

To avoid insertion of an arterial catheter, several investigators have explored the possibility of using an input function derived from images of the internal carotid artery, which is typically within the field of view for brain studies (Chen et al., 1998; Naganawa et al., 2005a; Su et al., 2005; Zanotti-Fregonara et al., 2009b). However, the small diameter of this artery (~ 5 mm) introduces errors of partial volume and spill-in from surrounding structures. Compared to [¹⁸F]FDG, which generates minimal radiometabolites in plasma, the current study with [¹¹C](R)- rolipram had the additional challenge of correcting the image input for the percentage of parent radioligand.

Despite these errors and challenges, the image input for [¹¹C](R)-rolipram replicated the arterial input with high fidelity. Although the peaks of the plasma curves from the two methods were not reproduced as well as the tails, the total AUC from 0 to 90 min was almost identical for the two methods, with a ratio of arterial to image input of 1.03 ± 0.04. In addition, the two methods generated equivalent values of distribution volume, with a ratio of arterial to image input for V_T of 1.00 ± 0.06. This fidelity is likely explained by two favorable characteristics of [¹¹C](R)-rolipram. First, the concentration of total radioactivity in blood can be accurately measured by the image input because the internal carotid has high radioactivity and the surrounding region has relatively little. Thus, the artery can be easily visualized, and spill-in from surrounding tissue is relatively small, even at the end of the scan. Second, we can accurately calculate the percentage of radioactivity in whole blood that is due to parent radioligand because it is relatively high (parent/whole blood ratio is ~ 80% at 90 min) and because the parent/whole-blood ratio over time is well fit by a monoexponential function.

The method to obtain image input used four arterial samples. Blood sampling cannot be completely eliminated for two reasons. First, because of the small diameter of the internal carotid artery, direct blood samples are required to correct for the effect of partial volume errors (Zanotti-Fregonara et al., 2009a). Second, the ratios of [¹¹C](R)-rolipram to whole blood activity must be estimated to obtain metabolite-corrected input function. By using only four blood samples to measure total radioactivity in whole blood and the percentage of parent radioligand, the image-derived input function gave values of V_T almost identical to those from the arterial input function. With the aim of eliminating the need to catheterize an artery, we are currently determining whether these four arterial blood samples could be replaced by venous samples without introducing a too great further source of error.

Retest and intersubject variability of [¹¹C](R)-rolipram measurements

Quantification of [¹¹C](R)-rolipram binding as V_T had relatively high retest variability, measured with both arterial and image inputs (15.2% and 14.1%, respectively, using a Logan analysis) . Such high retest variability could be caused by measurement errors or by physiological changes in the target itself (i.e., PDE4). To localize potential measurement errors, we examined the retest and intersubject variability of the two variables that are used to calculate V_T – namely, brain radioactivity measured with PET and the concentration of parent radioligand in plasma. We performed a similar analysis for retest data of a radioligand, [¹¹C]MePPEP, to measure cannabinoid CB₁ receptors in brain (Terry et al., 2010). In that case, intersubject variability of both V_T and plasma AUC were poor (>50%), and the retest variability of plasma AUC was also poor (>50%). Since both the intersubject and retest variability of brain uptake was good (<16%), we concluded that plasma measurements were likely the largest source of variability in calculating V_T of [¹¹C]MePPEP. For the current retest study using [¹¹C](R)-rolipram, the retest and intersubject variabilities of all three parameters (brain activity, plasma measurements, and compartmental V_T) were similar (~18 – 25%; Table 2). We conclude that measurements errors in both brain and plasma contribute to the retest variability of V_T and that neither of the two has a markedly disproportionate contribution.

Table 2.

Retest and intersubject variability of brain uptake, arterial input function, distribution volume, and plasma free fraction

Variability	Brain Uptake (AUC0–90)	Arterial Input (AUC0–90)	Distribution Volume (VT)	Plasma Free Fraction (fP)
Retest	12.9%	10.2%	18.8%	12.8%
Intersubject (COV)	18.5%	24.8%	25.0%	12.3%

Retest variability is the difference between test and retest studies expressed as a percentage of the mean of test and retest. Intersubject variability is the coefficient of variation (COV) in 12 subjects and is expressed as a percentage.

Brain uptake and arterial input were calculated with the trapezoidal rule for data from 0 to 90 min. Distribution volume (V_T) was calculated using compartmental modeling of 90 min of data from both brain and plasma.

In addition to measurement errors, the target itself (PDE4) could have changed between the two scans – for example, the density of the enzyme or its affinity for the radioligand. In fact, the enzyme activity of PDE4 is regulated in a feedback manner such that high concentrations of cAMP activate PKA, which phosphorylates PDE4 and thereby increases enzymatic activity, which then decreases the concentration of cAMP (Houslay, 2001). Furthermore, phosphorylation of PDE4 and increased enzymatic activity are paralleled by about 8-fold higher sensitivity to inhibition by rolipram (Hoffmann et al., 1998). We recently confirmed in vivo the relationship between phosphorylation of PDE4 and increased affinity for [¹¹C](R)-rolipram in rat brain (Itoh et al., 2010). Unilateral injection of drugs that would either increase or decrease phosphorylation of PDE4 had the expected unilateral effect on uptake of [¹¹C](R)-rolipram but not of its less active enantiomer [¹¹C](S)-rolipram.

To explore whether PDE4 itself could have changed between scans, we examined the effect of the length of time between scans and diurnal variation. We thought that longer time between scans would be more likely allow changes in PDE4, either enzyme density or affinity for the radioligand. In fact, the retest variability of V_T measured on different days (18.5% in 6 subjects having a mean interval of 38 ± 42 days) was 50% greater than that measured on the same day (12.0% in 6 subjects). Although this difference was not significant (p = 0.327 by t-test) in these small samples of six subjects each, the trend suggests that PDE4 enzymatic activity can vary over time in human subjects.

In the six subjects who had the test scan in the morning and the retest scan in the afternoon, the results showed an insignificant trend towards higher V_T values for the scans acquired in the afternoon (0.638 vs. 0.557 mL/cm³; p = 0.59 using a t-test for correlated samples).

In summary, we are uncertain of the causes of the relatively high retest variability of brain distribution volume of [¹¹C](R)-rolipram, but both measurement errors as well as physiological changes in the target itself (PDE4) are potential causes.

CONCLUSIONS

Binding of [¹¹C](R)-rolipram to PDE4 in brain can be quantified in healthy human subjects with ~90 min of imaging combined with serial concentrations of [¹¹C](R)-rolipram in arterial plasma. An input function derived from PET images of the internal carotid artery can substitute for multiple arterial blood sampling without reducing the overall accuracy and reproducibility of [¹¹C](R)-rolipram quantification. The favorable imaging characteristics of [¹¹C](R)-rolipram suggest it will be a useful research tool to study the second messenger cAMP cascade, which is a largely unexplored area in molecular imaging of the brain.

Highlights

• Binding of [¹¹C](R)-rolipram to phosphodiesterase 4 can be reliably quantified in human brain using a two-tissue compartment model and a Logan plot.

• [¹¹C](R)-rolipram binding has a moderate test-retest variability of about 15%

• An image-derived input function method, using the PET blood pool of carotid arteries, gives almost identical distribution volumes to those obtained with invasive arterial blood sampling.

• This image input method allows not only the estimation of the whole-blood time activity curve, like all the methods described in the literature up to now, but also the estimation of the parent concentration in plasma.