A mechanistic study of electron transfer from the distal termini of electrode-bound, single-stranded DNAs

Abstract

Electrode-bound, redox-reporter-modified oligonucleotides play roles in the functioning of a number of electrochemical biosensors, and thus the question of electron transfer through or from such molecules has proven of significant interest. In response, we have experimentally characterized the rate with which electrons are transferred between a methylene blue on the distal end of a short, single-stranded polythymine DNAs to a monolayer-coated gold electrode to which the other end of the DNA is site-specifically attached. We find that this rate scales with oligonucleotide length to the −1.16±0.09 power. This weak, approximately inverse length dependence differs dramatically from the much stronger dependencies observed for the rates of end-to-end collisions in single-stranded DNA and through-oligonucleotide electron hopping. It instead coincides with the expected length dependence of a reaction-limited process in which the overall rate is proportional to the equilibrium probability that the end of the oligonucleotide chain approaches the surface. Studies of the ionic strength and viscosity dependencies of electron transfer further support this “chain-flexibility” mechanism, and studies of the electron transfer rate of methylene blue attached to the hexanethiol monolayer suggest that heterogeneous electron transfer through the monolayer is rate limiting. Thus, under the circumstances we have employed, the flexibility (i.e., the equilibrium statistical properties) of the oligonucleotide chain defines the rate with which an attached redox reporter transfers electrons to an underlying electrode, an observation that may be of utility in the design of new biosensor architectures.

Introduction

Recent years have seen the development of a number of reagentless, electrochemical sensors based on the redox-reporter-modified, electrode-bound oligonucleotides. Examples reported to date include sensors for the detection of specific oligonucleotides^1–4, proteins^5–7, small molecules and ions^{8, 9}, and protein-small molecule interactions¹⁰. Sensors in this class are rapid, specific and, often, selective enough to deploy directly in complex clinical and environmental samples such as whole blood¹¹, soil extracts, and foodstuffs^{9, 12, 13} and have thus garnered significant attention^14–18.

Two distinct mechanisms have been put forth to explain how binding is coupled to signaling in members of this broad class of sensors. In the first, Barton and others report that signaling arises due to binding-induced changes in through-DNA charge transport upon hybridization² or protein binding⁵ [see also refs.^{19, 20}]. For other sensors in this class, we and others have argued that binding-induced changes in the flexibility of the oligonucleotide probe alters the ability of the attached redox reporter to approach the electrode and thus modulates the rate of electron transfer directly from the reporter to the electrode^21–26. Anne and Demaille have shown, for example, that electron transfer from a ferrocene on the distal terminus of a 20-base pair double-stranded construct is well-described by a simple model in which transfer is limited by the rate with which the flexible surface attachment site bends, allowing the terminal redox reporter to strike the surface of the electrode.^{25, 26}.

In order to further explore the relationship between chain flexibility and the rate of electron transfer from a terminal redox reporter we report here the chain-length, N, (i.e., the number of nucleotide monomers), persistence-length and solution-viscosity dependencies of electron transfer from a redox reporter attached to the distal end of various single-stranded, electrode-bound DNA constructs. Specifically, we have measured the apparent electron transfer rates (the rate with which the electrode and the redox reporter exchange electrons and reach equilibrium) from a methylene blue moiety covalently attached to the 5′ terminus of single-stranded polythymine constructs ranging from 3 to 70 bases in length when attached by their 3′ terminus to a gold electrode via a self-assembled, hexanethiol monolayer (Fig. 1). We selected polythymine as our test-case because of this sequence’s intrinsic flexibility^27–29, and because thymine’s high redox potential³⁰ (relative to guanine³¹) precludes through-DNA hopping mechanisms. Likewise we selected methylene blue as our redox reporter because its relatively sluggish electron transfer kinetics renders it possible for us to measure apparent electron transfer rates over a wide range of chain lengths, persistence lengths and solution viscosities.

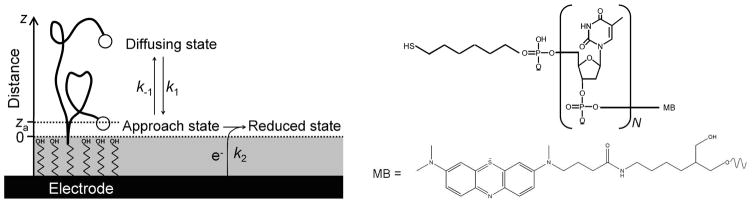
Figure 1.

We have measured the rate with which a redox reporter on the distal terminus of single-stranded DNAs exchanges electrons with a gold surface to which the opposite terminus of the DNA is attached. (Left) we find that this rate is orders of magnitude slower than end-to-end collision rate of single-stranded DNA²⁷, suggesting that the dynamics with which the distal terminus approaches the surface do not define the apparent electron transfer rate. Instead electron transfer appears to be well described by a reaction-limited, “chain-flexibility” mechanism in which the equilibrium probability of forming a reactive, “approach state” (K = k₁/k₋₁) and the rate with which that state then exchanges electrons with the electrode (k₂) define the overall, apparent electron transfer rate observed experimentally. (Right) The structure of the polythymine constructs employed in this study. The redox reporter (methylene blue, MB) is attached on the 3′ terminal of a polythymine oligonucleotide (N = 0 to 70) modified on its other terminus with hexane thiol.

Results

Assuming that through-DNA electron transfer is not limiting, the apparent rate of electron transfer from a distal redox reporter will be limited either by the rate of heterogeneous electron transfer through the self-assembled monolayer (k₂ in Fig. 1 left) or by the rate with which the attached methylene blue diffuses to the surface of the monolayer via reconfigurations driven by internal rotations within the polymer backbone²⁶ (k₁ in Fig. 1 left). In order to ascertain which of these two processes is rate-limiting we have measured apparent electron transfer rates using the method of Creager and Wooster³² [see Fig. 2 left for the typical analysis, Fig. S1 for typical raw data, and the supplemental information for both a detailed description of and further support for our implementation of this method]. This approach uses the AC-frequency dependence of the faradaic currents arising from the redox reporter to determine the rate with which the electrode and the redox reporter exchange electrons and re-equilibrate after an infinitesimal perturbation away from equilibrium (we measure the faradaic current at the top of the ACV peak, which is within error of the formal redox potential of methylene blue -Fig. S2). We refer to this rate as the apparent electron transfer rate to denote that, a priori, we have no knowledge as to whether it reflects the rate with which motions within the DNA chain allow the methylene blue to approach the electrode or instead reflects the rate of heterogeneous electron transfer across the monolayer (that is, the “standard” electron transfer rate in the nomenclature of Creager, who employed strongly adsorbed redox moieties and thus did not consider other potential rate-limiting effects³²).

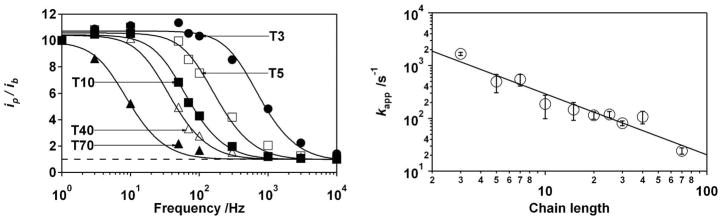
Figure 2.

(Left) The normalized ratio of peak to background current (i_p/i_b) as a function of AC frequency provides a measure the apparent electron transfer rate of methylene blue when attached to the distal terminus of varying length (T3, T5, T10, T40 and T70 represent 3-, 5-, 10-, 40- and 70-thymine constructs respectively), single-stranded polyhtymines³². Measurements were taken at room temperature (25°C) in 10 mM phosphate, pH 7, 1 M ionic strength (controlled using NaCl). (Right) The apparent electron transfer rate exhibits a power-law dependence on chain length, N (number of monomers) with an exponent of −1.16±0.09. The error bars indicated here and in the following figures reflect 95% confidence intervals derived from multiple, independent measurements.

The apparent electron transfer rates observed for specific constructs via the method of Creager and Wooster (Fig. 2, right) are many orders of magnitude slower than the reconfiguration rates of single-stranded DNAs in solution, suggesting that the dynamics of the DNA polymer itself are not rate limiting. Specifically, the reconfiguration rates of single-stranded oligonucleotides, which can be crudely estimated as D/R_g², where R_g is the molecule’s radius of gyration and D its diffusion coefficient³³, range from 10⁹ s⁻¹ to ~10⁵ s⁻¹ for the polymer lengths employed here. Similarly, the apparent electron transfer rate associated with, for example, our 15-thymine construct is, at 1.5±0.5 × 10² s⁻¹ (Fig. 2, right; all reported confidences reflect 95% confidence intervals), four orders of magnitude slower than end-to-end collision rate of the equivalent single-stranded construct in solution²⁷. Studies of the chain length dependence of the apparent electron transfer rate also argue that chain dynamics are not rate limiting: while the observed length-dependence of the end-to-end collision rate in solution obeys a power law with an exponent, ν, of −3.49±0.13 [ref.²⁷], and the end-to-surface chain dynamics are predicted to scale with an exponent in the range ν = −(1.8–2.2) [ref.^{23, 34}], the exponent we observe is just −1.16±0.09 (Fig. 2, right).

The “chain flexibility” model

While inconsistent with a process limited by the dynamics with which the end of the polythymine chain approaches the surface of the monolayer, the slow rate and weak chain-length dependence of electron transfer to the distal end of polythymine chains are consistent with a reaction-controlled mechanism in which electron transfer through the monolayer (heterogeneous electron transfer) is rate limiting. In this mechanism the apparent electron transfer rate is proportional to the heterogeneous electron transfer rate and equilibrium probability that the distal terminus of the oligonucleotide has approached the surface of the monolayer to allow such transfer to take place. To see this, we consider the following scheme:

in which the diffusing state reflects the rapid intramolecular dynamics of the single-stranded oligonucleotide²⁷, the approach state occurs when the end of the chain has approached the monolayer surface closely enough to affect the rate-limiting step, and the reduced state occurs when the electron has been transferred from the electrode to the oxidized methylene blue. [Note: our observations were performed within error of the formal redox potential of methylene blue, where electron transfer is reversible (see Supporting Information) and, thus, the apparent electron transfer rate corresponds to an equilibrium relaxation rate that is the sum of the oxidation and reduction rates. For convenience, however, we have employed the term “reduced state” to describe the state that participates in electron transfer.] If the heterogeneous electron transfer step (between the electrode and a methylene blue in contact with the monolayer), k₂, is rate limiting (k₋₁≫k₂), the apparent rate of electron transfer (k_app) will be given by:

$$k_{\mathit{app}}\approx k_1/k_{-1}·k_2=K·k_2,$$ (Eq. 1)

where K = k₁/k₋₁ is the equilibrium constant for the formation of the approach state. The physical interpretation of Eq. 1 is that the reaction-controlled, overall rate is proportional to both the equilibrium probability that the chain end is poised to perform the rate-limiting step and the rate of that rate-limiting step. Using more traditional electrochemical nomenclature, this is analogous to a CE type reaction in which electron transfer reaction is preceded by a chemical reaction (here this is formation of the approach complex) that generates the redox-active species. Since the rate-limiting rate k₂ is independent of chain length, the length dependence of the overall rate arises solely as a consequence of the length dependence of the equilibrium probability (K). To relate the equilibrium constant K to the properties of the DNA chain, we note that the chain flexibility can be quantified in terms of its persistence length l_p [ref.³⁵], the length scale over which the polymer retains its bending rigidity. If the contour length of the polymer, L, is longer than its persistence length then typical chain conformations look like random walks in three-dimensional space, with a step size comparable to l_p. In this limit, the probability of finding the chain end at a distance (z) from the surface can be approximated by [ref.³⁶]:

$$p(z)=3z/2l_{p}L·exp\left(-3z^2/4l_{p}L\right).$$ (Eq. 2)

We then have:

$$K=\underset{0}{\overset{z_a}{\int }}p(z)dz/\underset{z_a}{\overset{\infty }{\int }}p(z)dz=exp\left(3z_a^2/4l_{p}L\right)-1\approx 3z_a^2/4l_{p}L=3z_a^2/4l_p\sigma N,$$ (Eq. 3)

where N is the number of monomers, and thus σ = L/N is the contour length per monomer, and z_a is the distance corresponding to the approach state (Fig. 1 left). Thus, as observed experimentally, the reaction-controlled rate should vary inversely with polymer length.

The approximately inverse relationship between apparent electron transfer rate and polymer length is more general than the simple reaction scheme (Scheme 1) used above to derive it. Specifically, one can consider a more general situation where the efficiency of electron transfer depends on the distance from the surface: k_ET(z) = k₀κ(z/a). Here k₀ is the electron transfer rate observed at monolayer surface, κ(z/a) is a dimensionless function describing the distance dependence of this rate and a is a characteristic length scale over which electron transfer is appreciable. We note, however, that since our model is inherently coarse-grained in that it does not include an explicit microscopic description of the redox reporter and its linkage to the DNA, the distance z cannot be simply interpreted as the distance over which the electron tunnels. The reaction-controlled, apparent electron transfer rate is then given by [see, e.g., ref.³⁷]

Scheme 1.

$$k_{\mathit{app}}=\underset{0}{\overset{\infty }{\int }}\mathit{dzp}(z)k_{ET}(z)$$ (Eq. 4)

At length scales longer than the dimensions of the monomer, the probability distribution p(z) is described by the general scaling formula (see chapter 13 in ref.38):

$$p(z)=f(z/Z)/Z,Z={\langle z^2\rangle }^{1/2}={\left[\underset{0}{\overset{\infty }{\int }}{\mathit{dzz}}^{2}p(z)\right]}^{1/2},$$ (Eq. 5)

where the function f(x) depends on polymer statistics. Equation 2 is an example of the more general Eq. 5. Substituting Eq. 5 into Eq. 4 one finds:

$$k_{\mathit{app}}=(k_{0}a/Z)\underset{0}{\overset{\infty }{\int }}d\xi f(a\xi /Z)\kappa (\xi )$$ (Eq. 6)

Since the length scale of electron transfer is shorter than typical polymer dimensions (i.e., a/Z ≪ 1), the function f(aξ/Z) in Eq. 6 can be replaced by its asymptotic behavior at aξ/Z ≪ 1. If this behavior can be approximated as a power law, f(x) ∝ x^δ [cf. ref.38] then Eq. 6 gives the following expression for the apparent electron transfer rate

$$k_{\mathit{app}}=C{(a/Z)}^{1+\delta },$$ (Eq. 7)

where C is a numerical constant of order 1. Therefore, the scaling of the rate does not depend on the precise form of the distance dependence of k_ET(z) but does generally depend on equilibrium polymer statistics. For example, for Gaussian chains δ=1 and Z = (4N σ l_p/3)^1/2 (cf. Eq. 2). This results in the 1/Z² ∝ (N σ l_p)⁻¹ dependence predicted above in Eq. 3. In the opposite extreme where the polymer’s persistence length is longer than its contour length (such as for short lengths of double-stranded DNA), the molecule behaves as a rigid rod of length Nσ. Perhaps surprisingly, one then finds (see Supporting Information) δ = 0 and Z = Nσ/π, resulting in the same inverse scaling of the rate with chain length for both double and single-stranded DNA. Unfortunately, however, the apparent electron transfer rate from methylene-blue-modified double-stranded DNA is too slow to analyze via our electrochemical approach (data not shown), precluding so far our attempts to test this prediction experimentally.

The 1/N length dependence calculated for Gaussian chains also holds for more realistic models of single-stranded DNA, albeit with a slight adjustment that pushes the calculated exponent closer to the experimentally observed value. Specifically, we have estimated δ numerically (see Supporting Information) for long, excluded volume chains and find that in this case it also remains very close to 1. And since Z scales according to Flory’s power law, Z ∝ N^ν with ν ≈ 3/5, the resulting scaling of the overall rate is k_app ∝ N^−(1+δ)ν ≈ N ^−1.2, which is within error of the experimentally observed relationship (Fig. 2, right). Finally, using a coarse grained DNA model that takes electrostatic interactions into account, we find a similar, if somewhat weaker length dependence, k_app ∝N^{−(0.81–0.92)} (see Supporting Information). The deviations from the experimental scaling observed for this arguably more adequate model may arise due to the inadequacy of representing the polythymine chain as a string of individual beads, particularly for those (shortest) distances z from the surface at which electron transfer is most rapid. Of note, however, the same DNA model successfully predicts the much stronger length dependence (~N^−3.5) observed for the diffusion-controlled end-to-end collision rate²⁷, suggesting that it is a reasonably accurate description of DNA dynamics.

Further validation of the chain flexibility model

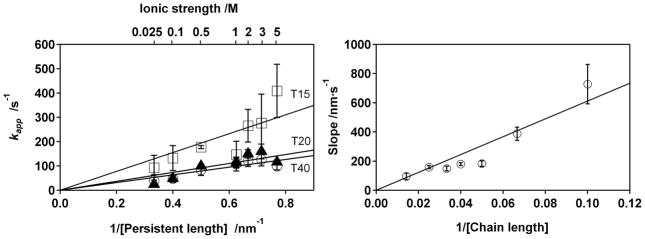
Studies of the ionic strength dependence of the apparent transfer rate also support the proposed reaction-limited, “chain flexibility” model. Specifically, ionic strength modulates the chain’s persistence length³⁹ and thus the equilibrium probability that the end of the chain will approach the surface of the monolayer closely enough to exchange electrons. For Gaussian chains, our theory (Eqs. 3 and 7) gives

$$k_{\mathit{app}}\propto {({Nl}_p)}^{-1}$$ (Eq. 8)

The reaction-limited chain-flexibility model thus predicts that the apparent electron transfer rate will be inversely proportional to the persistence length of the polymer with a proportionality constant that, in turn, is inversely proportional to the polymer’s length in monomers, N. Experimentally we find that both relationships hold: for fixed length polythymines the apparent electron transfer rate is proportional to the inverse of the estimated persistence length (Fig. 3, left), with proportionality constants that, in turn, are inversely proportional to N, the number of monomers in the chain (Fig. 3, right; R² = 0.91). Nevertheless, Eq. 8 is an approximation, as it assumes Gaussian polymer statistics. Moreover, given the short length scale of electron transfer, the precise behavior of the probability p(z) for finding the redox probe close to the surface may not be correctly captured by simple scaling laws predicted by bead-and-spring polymer models that ignore molecular details. Given that our model sidesteps these potential complications, the observed degree of correlation between experiment and theory appears promising.

Figure 3.

The apparent electron transfer rate depends quite strongly on persistence length, which supports the proposed reaction-limited mechanism. (Left) The observed dependence of the apparent electron transfer rate on persistence length [modulated by controlling the ionic strength; see ref.39] is, as predicted (Eq. 8), proportional to the inverse of the persistence length, and (Right) the slope of the rate versus inverse persistence length relationship is inversely correlated (R = 0.95) with chain length (the number of thymine bases).

Additional support for the proposed mechanism is provided by the observations that, unlike solution-phase chain dynamics²⁷, the apparent electron transfer rate is only a weak function of solvent viscosity. Specifically, where as the end-to-end collision rate of a 26-base polythymine construct in solution falls three-fold when the viscosity is raised four-fold²⁷, the apparent electron transfer rate of our 25-base polythymine construct falls by only two-fold in 46% w/w glucose, a solution that raises the viscosity eight-fold (Fig. 4). We must note, however, that, while the apparent electron transfer rate varies far less strongly with added glucose than does the end-to-end collision rate, it does vary. This contrasts with the apparent electron transfer rate of a methylene blue attached to the monolayer via a 13-atom, phosphodiester-linked alkane chain, for which the apparent electron transfer rate is effectively independent of solvent viscosity (falling by an inconsequential 1.08 ± 0.07-fold in 46% glucose; Fig. S3). This discrepancy may indicate that, although the equilibrium flexibility model captures most of the relevant physics, chain dynamics also contributes to the rate-limiting process. Alternatively, however, the observed effect of glucose may be due to its ability to reduce the equilibrium flexibility of the polythymine chain due to increases in base stacking (via glucose-induced strengthening of the hydrophobic effect⁴⁰) and/or increasing electrostatic repulsion along the DNA backbone²⁷ (via glucose-induced reduction of the dielectric constant). If either effect increases the persistence length of single-stranded DNA, the small glucose-induced reductions in rate we observe would occur even in the absence of any chain dynamics contribution to the rate-limiting mechanism.

Figure 4.

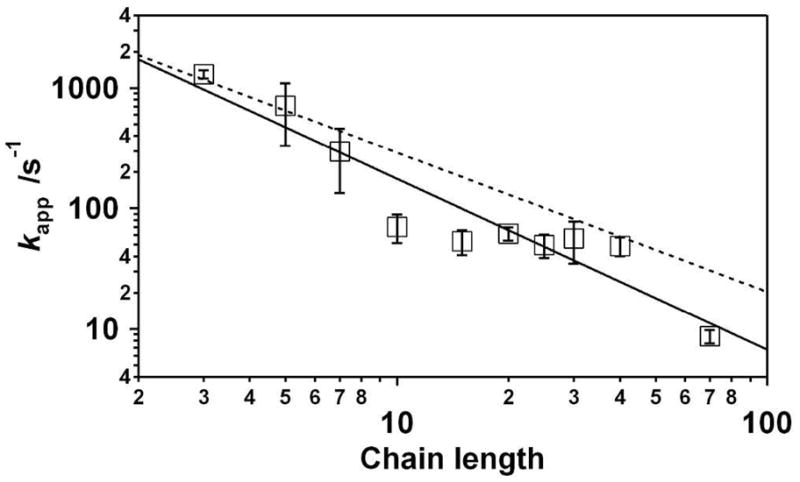
The apparent electron transfer rate depends only weakly on solvent viscosity. Despite the eight-fold increase in viscosity associated with such solutions, the apparent electron transfer rates observed in 46% glucose (w/w) differ by less than a factor of three (for even the longest, most glucose-sensitive construct) from those observed in the absence of glucose (dotted line). This weak viscosity dependence and its still weaker dependence on chain length contrasts significantly with the much stronger (and much more strongly length dependent) viscosity dependence of the end-to-end collision rate observed in solution³².

Finally, the apparent electron transfer rate of our shortest construct, 1670 ± 110 s⁻¹ (Fig. 2, right), is within a factor of two of the ~1,000 s⁻¹ rate observed for methylene blue attached directly to the hexanethiol monolayer via a 13-atom, phosphodiester-linked alkane chain (see Fig. 1, right, and Fig. S3). At first glance this discrepancy appears troubling: the proposed flexibility model predicts that such a “zero-thymine” construct should exhibit a higher apparent electron transfer rate than even this three-thymine construct. This result, however, may instead reflect important differences in the chemical environments of the methylene blue redox reporter in these two experiments: methylene blue interacts with base pairs (which are lacking on the zero-thymine construct) and with monolayers⁴¹ (which is closer for the zero-thymine construct), thus changing its reorganization energy and electron transfer kinetics. Given these potentially important differences between the “zero thymine” construct thymine-containing constructs we believe the factor-of-two similarity in the apparent electron transfer rates associated with our shortest construct and with the “zero thymine” construct further supports the argument that through-monolayer electron transfer is rate limiting.

Crowding effects

The above-described correlation between theory, simulation and experiment holds despite the fact that both the theory and the simulations we have employed ignore potentially complicating interactions between adjacent chains on the electrode surface^{21, 42}. Indeed, despite the fact that we employ a large excess of co-deposited 6-hydroxyhexanethiol as a diluent to increase inter-chain spacing and suppress any interactions between neighboring oligonucleotides (the density of our oligonucleotides are several fold below saturating packing densities: for example, our 30-thymine construct is, at ~9.3 × 10¹² molecules/cm², about four-fold below saturating coverage for such an oligonucleotide⁴³ –see Fig. S4), the mean spacing between adjacent oligonucleotides is less than the length of most of our constructs (coverage determined using previously established electrochemical methods^43–45; see materials and methods). Nevertheless, the strong correlation between theory and experiment suggests that any crowding effects are experimentally negligible. Consistent with this argument, we do not observe any statistically significant dependence of the apparent electron transfer rate on probe packing density. For example, we do not observe significant change in apparent electron transfer rate over a five-fold range of packing densities for our 30-thymine construct (Fig. S4). We note, however, that this result contrasts with our previous observation in which the sensor signal (i.e., the change in electron transfer efficiency upon hybridization) depends strongly on probe density²¹. The difference presumably reflects crowding effects occurring associated with the double-stranded state, which is far more rigid, and thus, presumably, more sensitive to steric clashes than the flexible, single-stranded oligonucleotides employed here.

Discussion

We have measured the rate with which a redox probe on the distal-end of a surface-attached, single-stranded DNA exchanges electrons with its attachment surface and found that this is well approximated as a reaction-limited process in which the apparent electron transfer rate depends on the equilibrium statistics of the oligonucleotide chain rather than its dynamics (Fig. 1). This occurs because the heterogeneous electron transfer rate from a gold electrode to methylene blue through a 6-hydroxy hexanethiol monolayer is orders of magnitude slower than the reconfiguration dynamics of single-stranded DNA, leading to a mechanism in which the apparent electron transfer rate is defined by the probability of forming an approach state, which is in pseudoequilibrium, and the rate of electron transfer to this state, which is rate-limiting. In support of this “chain-flexibility” mechanism, the apparent electron transfer rate scales with polythymine length to the −1.16±0.09 power (Fig. 2, right), which is close to the −1 exponent expected for the equilibrium probability that the distal end of a Gaussian chain will approach the surface to which the other end is attached, and within error of the −1.2 exponent estimated numerically for excluded volume chains. The chain flexibility model likewise correctly predicts that the apparent electron transfer rates of fixed length polythymines varies inversely with persistence length (Fig. 3, left), with proportionality constants that are, in turn, inversely proportional to chain length (Fig. 3, right). Finally, the apparent electron transfer rate varies only weakly upon the addition of 46% glucose (Fig. 4), which contrasts sharply with the diffusion controlled regime typically encountered in the studies of end-to-end collisions in DNA and other polymers, for which the rate is inversely proportional to viscosity³⁷ with a proportionality constant that, in turn, depends strongly on chain length⁴⁶.

The chain-flexibility model differs significantly from several previously described models of electron transfer from (or through) similarly modified, electrode-bound oligonucleotides. For example, Barton and co-workers have investigated the apparent electron transfer rate from daunomycin-modified, double-stranded DNAs and report that it is essentially length-independent, an observation that they interpret in terms of a rapid, through-DNA electron transfer mechanism in which charge transfer is limited by tunneling through the attaching monolayer⁴⁷. Given that single-stranded DNAs, such as those we have employed here, are not thought to support efficient through-DNA electron transfer ^{2, 5, 19, 20}, the discrepancy between Barton’s work and the work reported here may simply arise due to the different DNA conformations employed. Alternatively, however, Barton’s group explored only a single, short double-stranded DNA (with the redox reporter placed either 2 or 11 base pairs from the electrode) and thus, at the reported level of experimental precision⁴⁷, the weak, ~1/N length dependence predicted here (even for double-stranded DNA; see results) would not be detectable. Waldeck and co-workers have similarly investigated electron transfer from short, ferrocene-modified, single- and double-stranded peptide nucleic acids but find, in contrast, strong, biphasic length dependencies⁴⁸. Based on this observation they propose a two-phase mechanism in which strongly length-dependent, superexchange-mediated tunneling (k_app ∝ N⁻¹⁴) occurs for shorter chains (N = 3–6 bases) and somewhat less length-dependent “charge hopping” (k_app ∝ N⁻³) occurs for longer chains (N = 7–15 bases). Reconciliation of these conflicting models may likewise lie in the observation that, while these studies were conducted with the modified oligonucleotides under closely packed, polymer brush conditions^{47, 48}, our work and that by Anne and Demaille²⁶ on double-stranded, ferrocene-modified DNA was conducted in a more “dilute” regime in which the mean separation between adjacent strands is several nanometers (Fig. S5) and thus interactions between them are reduced. Under these conditions, direct electron transfer mediated by the flexibility of our single-stranded constructs may be more rapid than through-chain electron tunneling or hopping, allowing direct transfer to dominate. In support of this argument, Waldeck and co-workers observe much more rapid electron transfer at lower (non-closely-packed) oligonucleotide densities⁴⁹.

The existence of a mechanism by which electron transfer is modulated via changes in the equilibrium flexibility of a DNA probe suggests the possibility of designing sensors in which even subtle, binding-induced changes in probe flexibility produce large changes in apparent electron transfer rates. Indeed, The observation that effectively any protein-DNA interaction⁶, including even indirect binding events mediated by small molecules pendant to a rigid DNA scaffold^{7, 10}, produce readily quantifiable changes in electron transfer efficiency has already opened the door to a number of new electrochemical biosensor architectures⁵⁰.

Materials and Methods

As our surface we employed gold electrodes purchased from BAS (Indiana, USA). All DNA constructs were purchased from Biosearch Inc. (California, USA), which synthesized them modified with hexanethiol and methylene blue via 3′ and 5′ terminal phosphodiester-linkers, respectively (Fig. 1, right). All reagents were used the highest grade available. All confidence intervals reflect 95% confidence levels calculated from multiple independent, replicate experiments except for specifically noted cases.

Preparation of the modified gold electrode

The polycrystalline gold disk rod-electrodes (1.6 mm diameter) were prepared as previously described⁴. In brief, the protocol is as follows. The electrode was first cleaned via polishing with diamond dust, sonication in ethanol, polishing with alumina, sonication in water and, finally, electrochemical cleaning. Following this, the DNA constructs were immobilized on the surface of gold electrodes via chemisorbtion of the hexanethiol attached to the 3′ terminal of the DNA. We incubated the freshly prepared gold surface for over night in the solution of 10 mM phosphate, 1 M sodium chloride and the hexanethiol-modified poly-thymine (0.2 to 1 μM), which had been treated in 1 mM tris(2-carboxyethyl)phosphine for 1 hour beforehand to reduce the protecting group (hexanethiol) to yield a free thiol. We subsequently immersed the gold electrode with 1 mM 6-mercaptohexanol in deionized water for 2 hours before thoroughly rinsing it with deionized water.

Determination of the surface coverage

We determined the density of surface-bound DNAs by following a previously established method^43–45. Briefly, we employed ruthenium(III) hexaammine as the counter ion for the DNA-on-gold in a low ionic strength electrolyte (10 mM Tris buffer at pH 7.4) and estimated the accumulated amount of this cation on the negatively charged DNA using the difference in the chronocoulometric intercepts observed in the presence and absence of the ruthenium compound in the electrolyte. From this we calculate the amount of DNA assuming a stoichiometric ratio of ruthenium to phosphates in the DNA construct. The surface area of the electrode is separately estimated from the gold oxide reduction peak obtained in 0.05M H₂SO₄ prior to modification with the polythymine constructs. And while, as reported previously⁴³, the estimated surface coverage varies slightly with chain length (Fig. S5), the surface coverage of all constructs employed were significantly less than the 6 × 10¹³ to 9 × 10¹³ molecules/cm² theoretically estimated to represent maximum coverage for single-stranded DNA [see the discussion in ref. 43].

Measurement of Electron Transfer rate

We have employed the method of Creager and Wooster³² to measure apparent electron transfer rates using AC voltammetry (see Supporting Information for detailed description). Briefly this was done as follows. Assuming a Randles circuit to represent the electrochemical reaction (Fig. S6), we estimated the charge transfer resistance (R_CT) and adsorption pseudo-capacitance (C_ads) from the fitting of frequency dependence of i_p/i_b (Fig. 2, left, and see also supporting information and the chapter 10 in ref.51). Assuming the charge transfer coefficient as 0.5 and Langumuir isotherm, we estimated the apparent electron transfer rate using k_app=1/(2R_CTC_ads) [refs.^{32, 51}]. These measurements were carried out on a CHI 630B (CHI instrument potentiostat, TX, USA). AC voltammograms were recorded from 0 to −0.4 V with an amplitude of 25 mV in a standard three electrodes cell with an oligonucleotide-modified working electrode, a platinum counter electrode and a Ag/AgCl (3M sodium chloride) reference electrode. All measurements were taken at room temperature (25°C) in 10 mM phosphate, pH 7 and 1 M ionic strength (adjusted by adding NaCl), save for the experiments presented in figure 3, in which the ionic strength was varied (again by controlling the concentration of NaCl: http://www.bioinformatics.org/JaMBW/5/4/index.html)⁵². For the viscosity dependence measurements we employed 46% glucose in our standard 1M ionic strength buffer. In order to more precisely estimate the characteristic parameters of the redox probe (series resistance and pseudocapacity) [ref.³², and see also ref.53] under these conditions we separately estimated the solution resistance and double layer capacitance of both solutions using gold electrodes modified with 6-mercaptohexanol lacking methylene blue by employing chronoamperometry on CHI 730C Electrochemical Workstation (data not shown). See Supporting Information of these parameters and the validity of the estimation of apparent electron transfer rate.

Estimation of the rate of heterogeneous electron transfer though a six carbon monolayer

We have measured the heterogeneous electron transfer rate of a methylene blue covalently attached to a six carbon monolayer without an intervening thymine via two approaches: chemisorbtion of a methylene blue conjugated to a hexanethiol and the conjugation of methylene blue to a pre-existing, amino hexane monolayer using NHS activated methylene blue. The frequency dependence of the AC voltammetry of a monolayer formed using methylene blue conjugated to hexanethiol, however, exhibits non-ideal electron transfer (Fig. S3) that presumably reflects inhomogeneities in the methylene blue’s chemical environment. Nevertheless, if we use these data to crudely estimate the heterogeneous electron transfer rate we find that it is ~1000 s⁻¹. The heterogeneous electron transfer rate observed with gold electrodes that have been co-absorbed with hydroxy hexanethiol and amino hexanethiol overnight (in a 9:1 ratio) followed by treatment with an NHS-activated methylene blue (emp Biotech GmbH, Berlin, Germany) produces a crudely estimated, heterogeneous electron transfer rate of 840 ± 270 s⁻¹ (Fig. S3).