Micromechanics of Alveolar Edema

Abstract

The decrease of lung compliance in pulmonary edema underlies ventilator-induced lung injury. However, the cause of the decrease in compliance is unknown. We tested the hypothesis that in pulmonary edema, the mechanical effects of liquid-filled alveoli increase tissue stress in adjacent air-filled alveoli. By micropuncture of isolated, perfused rat lungs, we established a single-alveolus model of pulmonary edema that we imaged using confocal microscopy. In this model, we viewed a liquid-filled alveolus together with its air-filled neighbor at different transpulmonary pressures, both before and after liquid-filling. Instilling liquid in an alveolus caused alveolar shrinkage. As a result, the interalveolar septum was stretched, causing the neighboring air-filled alveolus to bulge. Thus, the air-filled alveolus was overexpanded by virtue of its adjacency to a liquid-filled alveolus. Confocal microscopy at different depths of the liquid-filled alveolus revealed a meniscus. Lung inflation to near-total lung capacity (TLC) demonstrated decreased compliance of the air-filled but not liquid-filled alveolus. However, at near TLC, the air-filled alveolus was larger than it was in the pre-edematous control tissue. In pulmonary edema, liquid-filled alveoli induce mechanical stress on air-filled alveoli, reducing the compliance of air-filled alveoli, and hence overall lung compliance. Because of increased mechanical stress, air-filled alveoli may be susceptible to overdistension injury during mechanical ventilation of the edematous lung.

CLINICAL RELEVANCE.

The high mortality associated with acute lung injury is attributed to the injurious effects of mechanical ventilation on alveoli. However, the micromechanical basis of these injuries is unknown. In a single-alveolus model of pulmonary edema, unexpected micromechanical effects ensue when air-filled and liquid-filled alveoli are juxtaposed. The liquid-filled alveolus shrinks, imposing mechanical stress on its air-filled neighbor. The mechanical stress reduces compliance of the air-filled alveolus, making it a target for overexpansion injury. Interalveolar micromechanics may determine spatiotemporal injuries to lungs during mechanical ventilation.

Pulmonary edema occurs in a stepwise manner such that in its initial stages, liquid-filled and air-filled alveoli lie juxtaposed to one another. This liquid-filling pattern is thought to result from the all-or-none mechanism (1), according to which the curved air–liquid interface in the alveolus establishes a transinterfacial force balance, governed according to the equation of Laplace. In this equation (P_alv − P_liq) = 2T/R, where P_alv and P_liq are pressures in the alveolar air and liquid, respectively, T is the air–liquid interfacial surface tension, and R is the interfacial radius. The alveolar entry of edema liquid at constant P_alv is thought to increase T, thereby reducing P_liq and further promoting liquid entry from the interstitium. This process continues until the interfacial curvature, and thus the pressure difference across the interface, is abolished. Importantly, these force considerations may be sufficiently localized that a single alveolus fills with fluid, while its immediate neighbor remains air-filled.

Although the all-or-none mechanism provides an explanation of how single alveoli become liquid-filled during the initiating phase of pulmonary edema, there is little understanding of how the juxtaposition of air-filled and liquid-filled alveoli affects lung mechanics. The critical questions involve whether meniscus formation occurs in the liquid-filled alveolus (1, 2), and whether a meniscus modifies mechanical interactions between liquid-filled and air-filled alveoli. Because alveolar mechanics can be addressed through real-time optical sectioning microscopy (OSM) (3), we tested the extent of alveolar meniscus formation in a model of edema in which a single alveolus was liquid-filled, while surrounding alveoli remained air-filled. This model, which simulates the juxtaposition of air-filled and liquid-filled alveoli in pulmonary edema (1), revealed unexpected aspects of alveolar mechanics that may be important in understanding the lung mechanics of early edema.

MATERIALS AND METHODS

Reagents

We used 5% human albumin (ZLB Behring, King of Prussia, PA) or 4% dextran (Sigma Aldrich, St. Louis, MO) in Ringer's solution. Fluorophores included the cell membrane–permeable cytosolic dye calcein red–orange acetoxymethyl (AM) ester (13 μM in dextran solution) and the membrane-impermeable 2′,7′-bis-(2-carboxyethyl)-5-(and-6)-carboxyfluorescein (BCECF, 32 μM in albumin solution; Invitrogen, Carlsbad, CA). All solutions were isosmotic with plasma.

Animals

Animals were treated in accordance with a protocol approved by the Institutional Animal Care and Use Committee of St. Luke's Roosevelt Institute for Health Sciences (New York, NY). We anesthetized adult, male Sprague–Dawley rats (n = 17, 300–600 g) with 5% isoflurane, followed by 80 mg/kg ketamine and 8 mg/kg xylazine. Then we produced the isolated, perfused lung preparation, as described previously (3). Perfusion pressures were 10 and 3 cm H₂O in the pulmonary artery and left atrium, respectively.

Experimental Protocol

We imaged lungs by confocal microscopy, using morphologic landmarks to identify the same alveolus at different lung volumes (3). To view the margin of air-filled alveoli, we loaded the alveolar epithelium with calcein red–orange AM (3). To establish edema in a single alveolus, we microinfused alveoli with albumin solution containing the cell-impermeable dye BCECF until the liquid remained in one alveolus. At least 75% of the perimeter of the liquid-filled alveolus lay adjacent to air-filled alveoli. Alveoli were imaged with a ×40 water immersion objective (numerical aperture 0.80, Zeiss, Oberkochen, Germany) at alveolar air pressures (P_alv) of 15 and 5 cm H₂O, corresponding to near total lung capacity (TLC) and functional residual capacity (FRC), respectively. We avoided higher P_alv to avoid overexpansion injury. All images were obtained within 15 minutes of changing P_alv. We determined alveolar dimensions and meniscus radii using commercial image analysis software (3).

Calculation of Alveolar Compliance

Using the relationship volume ∼ area^3/2 (4), we calculated the percent change in alveolar compliance, ΔC(%), as

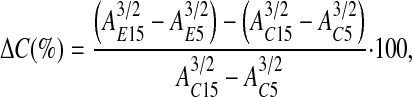(1)

where A is alveolar cross-sectional area, subscripts C and E refer to the control and edema conditions, respectively, and subscripts 5 and 15 refer to a P_alv of 5 and 15 cm H₂O, respectively.

Statistics

For paired comparisons, we used the Student t test at a significance level of P < 0.05. For multiple comparisons, we used the Wilcoxon signed rank test (SPSS, Inc., Chicago, IL), at a significance level of P < 0.02, to reduce the likelihood of Type I errors. Data are expressed as mean ± SEM.

RESULTS

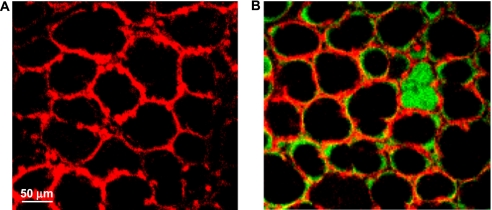
As in our previous study (3), calcein-loaded, air-filled alveoli were well-demarcated by the alveolar wall fluorescence in images obtained by OSM (Figure 1A). After liquid-filling with albumin solution, as shown in Figure 1B, the liquid-filled alveolus was identified by green luminal fluorescence, whereas the surrounding air-filled alveolar lumens remained nonfluorescent.

Figure 1.

Low-power images of alveolar field. (A) Air-filled lung with calcein red–orange loaded into alveolar epithelial cells. Epithelium fluoresces red; alveolar liquid lining layer and air appear black. (B) Single alveolar edema model. Calcein red–orange labels the alveolar epithelium. Albumin solution labeled with green fluorescent 2′,7′-bis-(2-carboxyethyl)-5-(and-6)-carboxyfluorescein (BCECF) fills a single alveolus. All other alveoli are air-filled, with BCECF labeling the liquid lining layer. Images were obtained with a ×10 air objective.

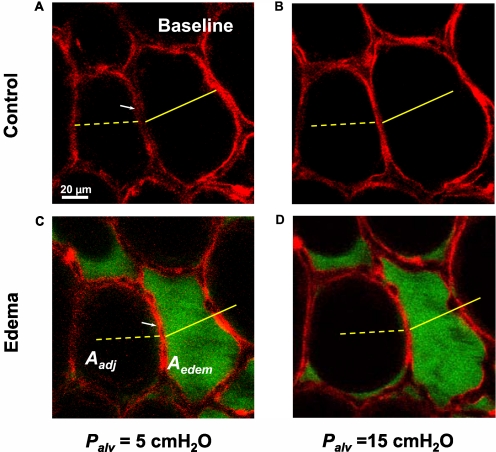
To determine alveolar dimensions, we imaged each alveolus in 2-μm-thick optical sections at high power (Figure 2A). Using the line-measuring cursor of the image analysis software, we traced the alveolar margin and determined the alveolar perimeter length (3). From the number of pixels enclosed by the traced line, we determined the alveolar cross-sectional area. In the air-filled lung, we imaged a pair of adjoining alveoli at P_alv of 5 and 15 cm H₂O, respectively (Figures 2A and 2B). Scale bars across the alveolar diameters in Figure 2A and superimposed on Figure 2B demonstrate, as expected, that lung inflation expanded both alveoli.

Figure 2.

Single alveolar edema model. Optical sections (2 μm thick) of two alveoli at a depth of 20 μm below the pleural surface. Alveolar epithelium is labeled with calcein red–orange at transpulmonary pressures (P_alv) of 5 (A, C), and 15 (B, D) cm H₂O. Alveoli are air-filled (Control) or liquid-filled with albumin solution (Edema), as indicated. White arrows indicate septum separating the two alveoli. Yellow scale marks indicate alveolar diameters at P_alv of 5 cm H₂O in control condition. A_edem, cross-sectional area of right alveolus that becomes liquid-filled. A_adj, cross-sectional area of adjacent left alveolus that remains air-filled.

The dimensional changes in an alveolus after liquid-filling are also shown in Figure 2. Before liquid-filling at a baseline P_alv of 5 cm H₂O, the septum between the alveoli lacked curvature (Figure 2A, white arrow). Filling the right alveolus with liquid, at constant P_alv, induced a marked septal curvature (Figure 2C, white arrow), such that the air-filled alveolus bulged into its liquid-filled neighbor. As a result, the cross-sectional area of the liquid-filled right alveolus (A_edem) decreased, as indicated by overlay of the solid yellow scale mark from Figure 2A. Concomitantly, the cross-sectional area of the adjacent air-filled alveolus (A_adj) increased. Thus, liquid-filling caused a septal translation that decreased the cross-sectional area of the edematous alveolus and increased the area of the air-filled alveolus, whereas the total area of the alveolar pair remained unchanged.

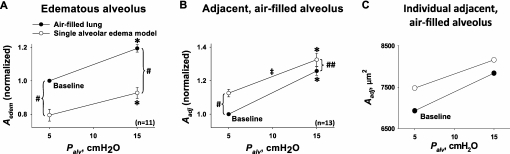
To determine alveolar mechanics, we performed a linear regression of alveolar area against P_alv. Figure 3 summarizes the P_alv-induced area responses in a pair of juxtaposed alveoli. When both alveoli were air-filled, the elevation of P_alv increased their diameters by similar extents (Figure 3, solid circles), indicating that expansion was similar in both in the air-filled state. However, liquid-filling one alveolus of the pair revealed two unexpected effects.

Figure 3.

Pressure-induced alveolar expansion. Cross-sectional area data for alveolar air pressures (P_alv) of 5 and 15 cm H₂O. Lines connecting data points at different P_alv are inflation curves, with slopes indicating degree of pressure-induced alveolar expansion. Solid circles, before induction of single-alveolar edema model. Open circles, after induction of edema model. (A) Data for cross-sectional area (A_edem) of the alveolus that became liquid-filled. All four data points were obtained in the same alveoli (n = 11, from nine different lungs). (B) Data for cross-sectional area (A_adj) of the alveolus adjacent to the one that became liquid-filled. All four data points were obtained in the same alveoli (n = 13, from eight different lungs). (C) A_adj data for a representative individual alveolus. Combining all data in the air-filled lung before liquid-filling an alveolus: inflation increased alveolar cross-sectional area A from 7.0 ± 0.6 × 10³ μm² by 23% ± 2%, and alveolar perimeter length L from 3.2 ± 0.1 × 10² μm by 8% ± 1% (P < 0.01, n = 24). *Area greater at P_alv of 15 than 5 cm H₂O (P < 0.01), for either control air-filled state or edema model. ^#Area different in edema model than air-filled state, at constant P_alv (P < 0.01). ^##Area different in edema model than in air-filled state, at constant P_alv (P < 0.02). ^‡Slope less in edema model than in air-filled state (P < 0.01), indicating decreased compliance.

First, despite the decrease in alveolar area in the liquid-filled alveolus, the slope of the area–P_alv relationship was unchanged (Figure 3A), indicating that alveolar expansion remained unchanged after liquid-filling. Thus, liquid-filling modified the alveolar size but not the expansion mechanics.

Second, in the adjacent air-filled alveolus, area increased but the slope of the area–P_alv relationship decreased (Figure 3B). The effects on the adjacent air-filled alveolus are evident through a comparison of the area–P_alv relationships before (Figure 3B, solid circles) and after (Figure 3B, open circles) its neighbor was liquid-filled. After liquid-filling, the regression line for the air-filled alveolus shifted upward, whereas its slope decreased. At a P_alv of 15 cm H₂O, A_adj was significantly greater after liquid-filling than before, i.e., after liquid-filling, inflation overdistended the adjacent air-filled alveolus.

In the example shown for one air-filled alveolus in Figure 3C, inflation from 5 to 15 cm H₂O increased the alveolar area from 6.9 × 10³ μm² to 7.8 × 10³ μm² at baseline, but from 7.5 × 10³ μm² to 8.2 × 10³ μm² after the neighboring alveolus was liquid-filled. Thus, liquid-filling decreased the slope of the area–P_alv relationship for the air-filled alveolus from its baseline value of 91 μm²/cm H₂O by 25%. Calculated according to Equation 1 (see Materials and Methods), the corresponding decrease in alveolar compliance was 23%. This result for a single alveolus is representative for the group as a whole, in which alveolar compliance decreased 24% ± 5% (P < 0.01).

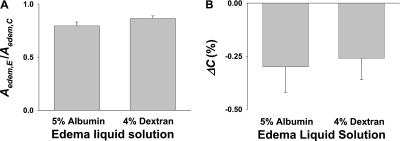
To determine the effect of protein concentration on alveolar mechanics, we repeated the alveolar filling experiments, using dextran solution instead of albumin as the edema liquid. The absence of albumin had no effect on the induced decrease in alveolar cross-sectional area (Figure 4A) or the liquid-filling–induced change in alveolar compliance (Figure 4B).

Figure 4.

Effect of albumin on alveolar mechanics. (A) Effect on liquid-filling induced decrease in alveolar cross-sectional area. Data comprise ratios of area values in edematous state after liquid-filling (A_edem,E) to those in control state before liquid-filling (A_edem,C). (B) Liquid-filling induced changes in compliance (ΔC(%)) of alveolus that became edematous. Albumin solution: n = 11 alveoli from nine lungs. Dextran solution: n = 9 alveoli from eight lungs.

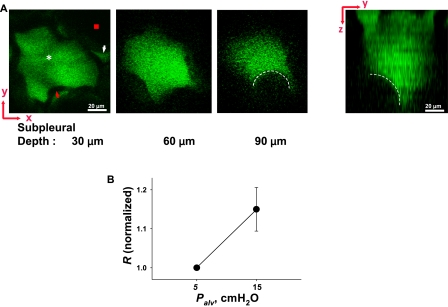
We considered that in the liquid-filled alveolus, meniscus formation might account for the inhibition of compliance increase. Accordingly, we imaged through the depth of the liquid-filled alveolus in 2-μm-thick optical sections. At a subpleural depth of ∼ 80–100 μm (n = 9 alveoli), the presence of a curved air–liquid interface was evident, as depicted in the images of the x–y plane and the integrated y–z plane (Figure 5A). Increasing the P_alv from 5 to 15 cm H₂O increased the meniscus radius by 14% ± 3% (Figure 5B). These findings indicate that a meniscus was present in the liquid-filled alveolus lying adjacent to an air-filled alveolus, and that the meniscus curvature was P_alv-responsive.

Figure 5.

Meniscus observed in edematous alveolus. (A) Left, 2-μm-thick optical sections (x–y plane) of an edematous alveolus at indicated depths below the pleural surface, at P_alv of 15 cm H₂O. Edema liquid (white asterisk) and liquid lining layer of neighboring alveolus (white arrowhead) are fluorescent. Alveolar wall (red arrowhead) and air-filled lumen of neighboring alveolus (red square) appear black. Starting at ∼ 85 μm below the pleural surface, a black crescent (dashed white line) bulges into the edema liquid. Right, y–z plane reconstructed from multiple sections. Dashed white line indicates meniscus. (B) Inflation increases meniscus radius (R) (P < 0.05). Data are paired, and normalized by baseline value of 32 ± 2 μm (n = 9).

DISCUSSION

In a historic experiment, von Neergaard showed that lung compliance increases markedly when the lung is completely filled with saline (5). This finding gave rise to the classic understanding that alveolar air–liquid interfacial tension restricts lung expansion. Although the loss of air–liquid interface accounted for the increased compliance in von Neergaard's experiment, in pulmonary edema, although edematous alveoli are liquid-filled and presumably lack the air–liquid interface, lung compliance decreases (1, 6). This decrease in compliance is counterintuitive, because the loss of alveolar air–liquid interface should increase global compliance.

The best explanation for this contrary response draws on the surfactant-inhibiting ability of plasma proteins (7). According to this theory, plasma proteins that gain alveolar entry in pulmonary edema insert into the air–liquid interface, thereby blocking surfactant action. However, this explanation presents two problems. First, the supportive evidence is indirect, because it is derived largely from in vitro surface-tension data (7).

Second, the classic theory of alveolar liquid-filling, as based on the equation of Laplace (see introductory paragraph), predicts that alveoli fill to completion in an all-or-none manner to abolish both the curvature of the air–liquid interface and the alveolus-collapsing effect of the interfacial tension. In this scenario, the role of plasma proteins as tension-enhancing agents may be redundant. Consistent with this notion, we show that liquid-filling the alveolus produced the same result, whether or not the liquid contained albumin (Figure 4). Thus, the effect of protein was not important.

Importantly, the pattern of alveolar liquid-filling in pulmonary edema is likely to differ markedly from the saline-filling in von Neergaard's experiment. Clearly, a major difference exists: whereas all alveoli are liquid-filled in the saline-filled lung, in pulmonary edema, liquid-filled and air-filled alveoli are interspersed. This raises a possibility that was not considered previously, that the juxtaposition of liquid-filled and air-filled alveoli may induce unexpected effects on alveolar mechanics that in sum could affect global lung mechanics. A consideration of these issues requires the assessment of the mechanical properties of single alveoli under conditions that satisfy the juxtaposition of air-filled and liquid-filled states.

Here, to the best of our knowledge, we established these conditions for the first time by the combined application of confocal microscopy, which allows precise geometric determinations of the alveolar wall (3), and the micropuncture technique that allows access to individual alveoli. Thus, to model partially edematous conditions, we successfully established juxtaposed pairs of air-filled and liquid-filled alveoli that were amenable to geometric quantifications. Accordingly, we quantified alveolar area at a fixed landmark at different inflation pressures, to determine alveolar compliance both before and after liquid-filling.

Our findings indicate that although alveolar mechanics were more or less identical in the air-filled state for each member of the alveolar pair, filling one alveolus with liquid resulted in unexpected effects in each. We expected alveolar size to increase after the loss of air–liquid interfacial tension effects, given the findings of von Neergaard (5) and of Wilson and colleagues (8) that high pressure causes nonlinear increases of compliance in edematous lungs. However, the opposite result occurred, i.e., the size of the liquid-filled alveolus decreased. Further, the liquid-filled alveolus retained its ability to expand to the same extent in response to an increase in inflation pressure as in its previous air-filled state, indicating that liquid-filling did not alter its compliance. The explanation for our unexpected findings became evident when we took optical slices of the alveolus along the vertical axis by means of confocal microscopy. This procedure revealed the presence of a meniscus at the mouth of the liquid-filled alveolus, indicating that in the presence of an air-filled neighbor, the liquid-filled alveolus retained curvature of the air–liquid interface.

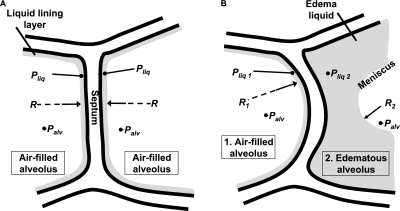
This meniscus formation, we believe, has an important bearing on the combined mechanics of the system. When both alveoli are air-filled, the alveolar pressures on either side of the separating septum are identical (Figure 6A). Hence, forces are in balance across the septum. But when one alveolus becomes liquid-filled, the meniscus decreases the radius of the curvature of the air–liquid interface of the liquid-filled alveolus below that of the air-filled alveolus (Figure 6B). Hence, according to the Laplace relationship, the pressure drop across the air–liquid interface is greater in the liquid-filled than the air-filled alveolus. Consequently, the liquid phase pressure is lower in the liquid-filled than the air-filled alveolus. This difference in trans-septal pressures is likely to cause deformation of the intervening septum. Our findings confirmed this predicted septal deformation, which was evident as a septal bulge that increased the size of the air-filled alveolus and decreased the size of the liquid-filled alveolus.

Figure 6.

Model of trans-septal forces. (A) Model of septum between two alveoli in normal, air-filled lung. In each alveolus, airway pressure is indicated as P_alv. A thin liquid layer with liquid pressure (P_liq) lines each alveolus. With all forces balanced across the septum, the septum is planar. Radius (R) of air–liquid interface in each alveolus is thus infinite. (B) Model of septum between an air-filled alveolus (1) and an edematous alveolus (2). In each alveolus, airway pressure is indicated as P_alv. Because of the presence of a meniscus, however, R₂ in the edematous alveolus is less than R₁ in the air-filled alveolus. According to the Laplace relationship, a greater pressure drop across the air–liquid interface occurs in the edematous than in the air-filled alveolus. Thus, liquid phase pressure in the edematous alveolus (P_liq2) is lower than P_liq1 in the air-filled alveolus. The difference in liquid phase pressures acting across the septum displaces the septum toward the edematous alveolus. Thus, liquid-filling diminishes the edematous alveolus, and expands the adjacent air-filled alveolus.

Our interpretations assume that surface tensions were equal in the juxtaposed air-filled and liquid-filled alveoli. Although we did not determine surface tension, the air–liquid interface is continuous between alveoli, and we expect that endogenous surfactant present in the isolated, perfused lung preparation (9) would rapidly spread to equilibrium surface concentration. At FRC, surface tension is ∼ 0.5 dyn/cm (10). This low surface tension corresponds to a high surface pressure, which promotes surfactant spreading. Further, because surface tension does not differ between different sized alveoli (10), we do not expect surface tension to differ between alveoli with different interfacial radii, R. Thus, we expect that the difference in radius between alveoli dominated any difference in surface tension.

Our findings indicate that when one alveolus of a pair of juxtaposed alveoli is liquid-filled, the compliance of the air-filled alveolus decreases by ∼ 24%. Lung compliance was reported to decrease to a similar extent during the onset of pulmonary edema, when increases in extravascular lung water are moderate (11). Notably, the air-filled alveolus in our model bordered a single edematous alveolus, and was pre-expanded by deformation of the single intervening septum. In pulmonary edema, an air-filled alveolus may be juxtaposed with multiple edematous alveoli and be pre-expanded on multiple sides. Hence, our model may underestimate the severity of overexpansion injury in aerated alveoli. In addition, expansion of the air-filled alveolus at FRC may have increased tissue stiffness (12). Thus, a mechanical stress–induced reduction of compliance in air-filled alveoli may account for the global decrease of lung compliance.

Our findings in single alveoli must be interpreted with caution when translated to the whole lung. The modest decrease in compliance we report here is probably not applicable to the stage of severe edema when alveolar filling is extensive (13, 14). Because surface tension is proposed to affect alveolar area even while total lung volume remains unchanged (15, 16), our interpretations of lung volume based on quantifications of alveolar area may be in error. However, other considerations potentially support our interpretation. Because alveolar septae are expected to transmit transpulmonary pressure uniformly to all alveoli (17), mechanical properties of subpleural and internal alveoli are likely to be similar. The surface area–volume relationship is the same for subpleural and deeper alveoli (18), such that dimensional changes in the single subpleural alveolus could account for changes in global lung volume (3). Our present findings in single alveoli provide a novel understanding of alveolar mechanics that, to our knowledge, cannot be realized through other approaches.

The concern that liquid microinjections overfill the alveolus may be ruled out, because excess injected liquid spills into adjacent alveoli and flows away (19). Absorptive or secretory processes and osmotic effects are potential complicating factors. However, liquid absorption does not occur in the alveolus (20). Alveolar secretion, although present, is insufficient to modify alveolar liquid volume in the ∼ 15-minute period of our experiments (20). Osmotic effects may be ruled out, because concentrations of small and large solutes were similar to plasma, and thus no concentration gradients were present across the alveolar wall. The immediate alveolar shrinkage after liquid-filling and the subsequent retention of stable alveolar dimensions indicate that the shape changes were specifically attributable to micromechanical effects of meniscus formation rather than to nonspecific methodologic factors.

The different micromechanics of juxtaposed liquid-filled and air-filled alveoli may have some bearing on overexpansion injuries during ventilation of the edematous lung (21, 22). Although a decrease of compliance in the edematous lung results from the loss of acinar air volume, the interdependence effect between adjacent air-filled and liquid-filled alveoli, as shown in our data, could comprise an additional factor. As indicated by computed tomography (CT), mechanical ventilation causes patchy hyperinflation in the aerated part of the edematous lung (23). This CT pattern may be explained by our present findings, to the extent that the aerated part of the lung contains edematous alveoli lying next to aerated alveoli. The edematous alveoli may not be detectable by CT, but their presence may sufficiently pre-extend adjoining air-filled alveoli, predisposing them to expansion stress.

In conclusion, we show that liquid-filling one alveolus at FRC pre-expanded the adjacent air-filled alveolus. Subsequent inflation to near TLC then overdistended the air-filled alveolus. Even in the absence of pre-expansion at FRC, we previously showed a marked heterogeneity of wall stiffness in the individual alveolus (3). Thus, in certain respects, the alveolar wall may be predisposed to overdistension injury. We suggest that pre-expansion may potentiate alveolar injury. High tidal volume ventilation of the edematous lung is likely to impose excessive stresses on the pre-expanded, heterogeneously structured, air-filled alveolus. Further study is required to determine the factors that contribute to tissue stiffness at different alveolar locations, thereby setting up the spatial profile of overexpansion injury in the alveolus.