Pharmacodynamic Modeling of In Vitro Activity of Marbofloxacin against Escherichia coli Strains

Abstract

A mathematical pharmacodynamic model was developed to describe the bactericidal activity of marbofloxacin against Escherichia coli strains with reduced susceptibility levels (determined using MICs) under optimal and intestinal growth conditions. Model parameters were estimated using nonlinear least-square curve-fitting procedures for each E. coli strain. Parameters related to bactericidal activity were subsequently analyzed using a maximum-effect (E_max) model adapted to account for a direct and a delayed effect. While net growth rates did not vary significantly with strain susceptibility, culture medium had a major effect. The bactericidal activity of marbofloxacin was closely associated with the concentration and the duration of exposure of the bacteria to the antimicrobial agent. The value of the concentration inducing a half-maximum effect (C₅₀) was highly correlated with MIC values (R² = 0.87 and R² = 0.94 under intestinal and optimal conditions, respectively). Our model reproduced the time-kill kinetics with good accuracy (R² of >0.90) and helped explain observed regrowth.

Developed in the 1980s, fluoroquinolones are synthetic antimicrobial agents that have high bactericidal potency against a wide range of Gram-positive and Gram-negative organisms (1, 24). Three different, but related, mechanisms of action of fluoroquinolones have been identified and are referred to as mechanisms A, B, and C (3, 7, 8, 25). Mechanism A is shared by all quinolones and is based on the inhibition of DNA replication through interaction with two different enzymes, DNA gyrase and topoisomerase IV; this mechanism requires actively dividing bacteria and protein and RNA synthesis to be effective. Conversely, the second mechanism of action (B) is active against nondividing bacteria and does not require protein and RNA synthesis; this has been demonstrated through experiments with chloramphenicol and rifampin, which block protein and RNA synthesis, respectively. The third mechanism (C) is also effective against nondividing cells but requires protein and RNA synthesis; however, to the best of our knowledge, this mechanism of action has not been fully described (25). This multidimensional bactericidal activity could explain the high efficiency of fluoroquinolones compared to other antimicrobials.

MIC is the most commonly used pharmacodynamic (PD) parameter to determine susceptibility levels of bacterial strains exposed to a specific antimicrobial agent; it is defined as the lowest concentration of antibiotic that prevents visible growth of the bacterial population in an in vitro system (15, 17, 23). However, this parameter is measured at only one endpoint, after exposure of the bacterial population to a constant antimicrobial concentration for 16 to 20 h, and does not reflect the time-killing process. Alternative, time-kill curve studies better describe the dynamic behavior of antibacterial activity (17, 23). These curves are analyzed using pharmacodynamic mathematical models, usually based on the assumption that the relationship between antibacterial activity and antibiotic concentration has a sigmoid shape described by Hill's equation, also called a maximum-effect (E_max) model (14, 16, 21). PD parameter estimates, such as the concentration leading to a half-maximum effect (C₅₀) and Hill's coefficient (also called coefficient of sigmoidicity), are obtained by either simultaneous (10, 26, 27) or concentration-specific (9) curve fitting using nonlinear least-squares minimization procedures that compare model outputs with effective bacterial counts.

Pellet et al. (19) investigated the bactericidal activity of marbofloxacin, an antimicrobial of the fluoroquinolone group, against Escherichia coli strains with different quinolone susceptibility levels. Time-kill kinetics were studied under optimal (Mueller-Hinton broth [MHB]), intestinal growth (autoclaved fecal content [AFC]), and no-growth (saline suspension) conditions. The authors concluded that marbofloxacin has a biphasic effect combining mechanisms A and B and that medium characteristics (MHB or AFC) influenced antibacterial activity. The aim of the present study was to develop a pharmacodynamic model to analyze time-kill data for reduced-susceptibility (0.5 μg/ml ≤ MIC ≤ 2 μg/ml; called intermediate) and very-reduced-susceptibility (MIC of >8 μg/ml; called resistant) E. coli strains exposed to marbofloxacin under optimal versus intestinal growth conditions (19).

MATERIALS AND METHODS

Time-kill data.

Time-kill studies have previously been described in detail (19). Briefly, the pharmacodynamic activity of marbofloxacin was evaluated in 18 E. coli strains under optimal growth conditions in with Mueller-Hinton broth and under intestinal growth conditions using autoclaved fecal content obtained from feces collected per rectum from five pigs which had received no antibiotic treatment. These strains were classified as susceptible, intermediate, and resistant according to their MICs. MIC determination was performed using the microdilution broth method according to NCCLS M7-A5 and M31-A52 procedures (18). A reference strain (E. coli ATCC 25922) was included to ensure the validity of results (19). Time-kill curves were determined using a microdilution test with a final broth volume of 1 ml containing a 100-μl aliquot of antibiotic added to 900 μl of the bacterial suspension in propylene tubes. All tubes were incubated at 37°C in an aerobic or anaerobic environment (N₂/H₂/CO₂, 85:10:5). Sampling for colony count was performed at 0, 1, 2, 3, 4, 6, 8, and 24 h for MHB conditions and at 0, 2, 4, 8 and 24 h for AFC conditions. For all tested strains, the log₁₀ viable CFU count (CFU/ml) was plotted against time for different concentrations of marbofloxacin ranging from 0 to 512 times the MIC of selected strains.

Model description.

The pharmacodynamic model was adapted from Li et al. (10, 11) according to time-kill curve profiles and is defined by the following ordinary differential equation:

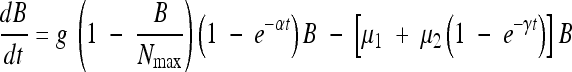(1)

where dB/dt represents the variation in the E. coli count as a function of time. In this model, the first term on the right-hand side of equation 1 corresponds to the growth phase of bacterial population in the absence of antibiotics. This was modeled using a logistic function with a growth rate constant, g, and a maximum capacity of the medium, N_max, due to limitation of nutrients and space that are inherent in in vitro systems (10, 16). As described in several studies using time-kill curve analysis (10, 11, 26), an exponential correction factor (1 − e^−αt) was added to this logistic function, representing a delay in the onset of E. coli growth, which has been clearly observed during time-kill experiments (19). The second term represents the mortality induced by antibiotic exposure, which, in contrast to the model of Li et al. (10), was modeled according to two different mechanisms: the first one, expressed through the parameter μ₁, represents a direct effect of antibiotic concentration on the bacterial population; the other one, expressed by the relation μ₂(1 − e^−γt), represents a delayed effect.

Parameter estimation and analysis.

For each bacterial strain, growth parameters (g, N_max, and α) were estimated from the data obtained in the absence of antibiotics using a nonlinear least-squares minimization procedure (lsqnonlin in Matlab; MathWorks, Inc.). Net growth rates during the exponential growing phase were derived from these estimates and compared with data from the literature. The effects of medium and strain susceptibilities on E. coli growth were explored using an analysis of variance (aov function in the R program [20]). Growth parameters (g, N_max, and α) were then incorporated into equation 1 to estimate the parameters representing the effect of the antibiotic concentrations (μ₁, μ₂, and γ) on the bacterial population. Results were compared to time-kill data using coefficients of determination (R²).

The killing rate was estimated for each concentration using the following time-dependent relationship: M(C_i, t) = μ_1i + μ_2i[1− exp(−γ_it)], where M(C_i, t) represents the killing rate obtained with concentration C_i at time t. μ_1i, μ_2i, and γ_i were estimated from time-kill data obtained at a specific concentration C_i. This equation was fitted to an E_max model that accounts for direct and delayed antibacterial effects; in this way, the killing rate could be summarized using the classical parameters used in pharmacodynamic studies (Hill's coefficient, n, and concentration leading to half-maximum effect, C₅₀) (4, 12, 13, 21). The E_max model was defined by the following relationship:

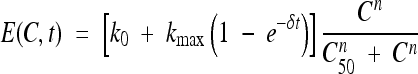(2)

where the first term, [k₀ + k_max (1 − e^−δt)], reflects the maximum effect of antibiotic concentrations (increasing with time according to an exponential correction factor) and the second term, 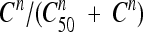, depicts the sigmoid shape related to antibiotic concentrations using a classical Hill equation. Parameters are summarized in Table 1.

TABLE 1.

Definition of model parameters and related units

Name	Definition	Unit
g	Growth rate constant	h−1
Nmax	Maximum capacity of the medium	CFU/ml
α, γ, δ	Exponential correction constant	h−1
μ1	Direct killing rate constant	h−1
μ2	Delayed killing rate	h−1
k0	Direct killing rate constant (Emax model)	h−1
kmax	Maximum time-related increase in killing rate (Emax model)	h−1
C50	Concentration leading to half-maximum effect (Emax model)	μg/ml
n	Steepness of the curve (Emax model)

RESULTS

Growth phase analysis.

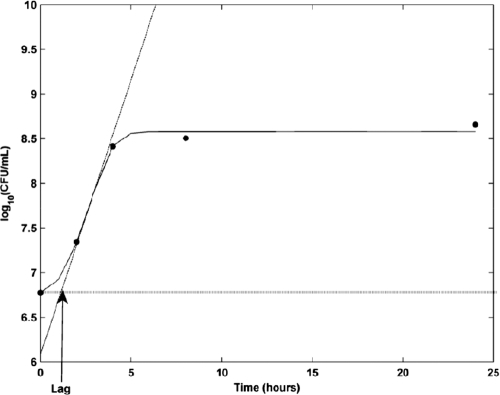
Twelve E. coli strains with different susceptibilities to marbofloxacin (intermediate-resistant and resistant) were analyzed in the time-kill experiments. In the absence of antibiotic and after a short initial adaptation phase, all strains exhibited optimal development during the first 3 h, reaching a steady state around 5 h under both MHB and AFC growth conditions. The parameters g, N_max, and α were estimated for each E. coli strain using data from time-kill kinetics in the absence of antibiotic. The estimated growth parameters were compared to data provided from different studies of E. coli growth (22, 27) by estimating the net growth rate (r) during the exponential growth phase. To do so, the slope at the exponential phase, b, was defined as the coefficient of a linear regression—with a high coefficient of determination (R² of >0.99)—on the linear portion of the growth curve on a semi-log plot (5). The net growth rate r was thus defined by the relationship r = b (ln₁₀), where ln is the natural logarithm. The lag phase duration was estimated for each strain using the conventional definition: the duration of the lag phase was calculated as “the interpolation of the tangent at the inflection point of the growth curve, back to the inoculation level” (28) (Fig. 1).

FIG. 1.

Lag time is defined as where the tangent to the curve at the inflection point intersects with the starting bacterial count (28).

Net growth rates ranged from 0.80 to 1.64 h⁻¹ and are consistent with data from the literature. No significant differences were revealed between growth rates with respect to strain susceptibilities (Table 2), but net growth rates were significantly lower under AFC (1.04 h⁻¹; 95% confidence interval, 0.95 to 1.13) than under MHB conditions (1.44 h⁻¹; 1.37 to 1.53). Moreover, the lag time duration was significantly lower under AFC conditions, showing a faster adaptation of the bacterial population in the fecal environment (1.19 h [95% confidence interval, 1.11 to 1.26] and 1.31 h [1.22 to 1.40] under AFC and MHB conditions, respectively).

TABLE 2.

Mean net growth rates and lag durations of E. coli strains with respect to their level of susceptibility and culture conditions^a

Strain susceptibility (n)b	Mean net growth rate (r)		Lag duration (h)
	MHB	AFC	MHB	AFC
Intermediate-resistant (8)	1.47 (1.34, 1.62)	0.97 (0.82, 1.12)*	1.31 (1.11, 1.51)	1.15 (1.06, 1.24)*
Resistant (8)	1.41 (1.29, 1.55)	1.11 (1.07, 1.22)*	1.31 (1.21, 1.41)	1.22 (1.08, 1.37)*
All (16)	1.44 (1.37, 1.53)	1.04 (0.95, 1.13)*	1.31 (1.22, 1.40)	1.19 (1.11, 1.26)*

^aValues in parentheses represent 95% confidence intervals. MHB, optimal growth conditions; AFC, intestinal growth conditions. Statistical comparison was performed using analysis of variance with a significance level at 0.05. For each parameter, asterisks indicate significant differences according to culture medium. No differences were observed between intermediate-resistant and resistant strains.

^bn, number of strains.

Time-kill studies.

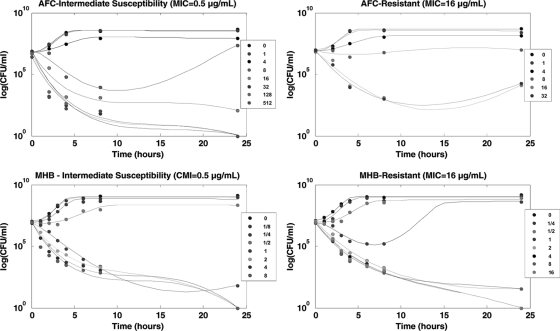
Figure 2 shows the bacterial counts of four E. coli strains (two strains with intermediate resistance and two resistant strains under MHB and AFC conditions) and the curves predicted by our model on a semi-log plot.

FIG. 2.

Bacterial counts of E. coli exposed to marbofloxacin and the time-kill curves predicted by the model for strains of intermediate susceptibility (MIC of 0.5 μg/ml) and for resistant strains (MIC of 16 μg/ml) under AFC and MHB conditions. Concentrations are given in terms of the MIC of the corresponding strain.

Under optimal growth conditions (MHB), the killing rate increased with antibiotic concentration. The time-kill kinetic profiles showed an initial rapid decrease of viable counts, followed by a slower decrease between 8 and 24 h of exposure to the antibiotic. Moreover, some strains exhibited late regrowth with concentrations close to the MIC value. Under fecal conditions (AFC), time-kill curves had similar profiles to those under MHB conditions but nevertheless showed some differences. The main difference concerned the effective concentrations, which were clearly higher than the ones observed under MHB conditions (8- to 32-fold higher than the MIC). The second difference primarily involved the resistant strains, for which no concentration produced a decrease greater than 3 log₁₀ CFU/ml against five and two strains after 4 and 24 h of exposure, respectively. Regrowth was also observed, even for concentrations producing a decrease greater than 3 log₁₀ CFU/ml after an 8-h exposure. Our pharmacodynamic model showed a close fit with the observed kinetics for each E. coli strain under both MHB and AFC environments, with coefficients of determination higher than 0.90 when values predicted by the model were compared to actual bacterial counts.

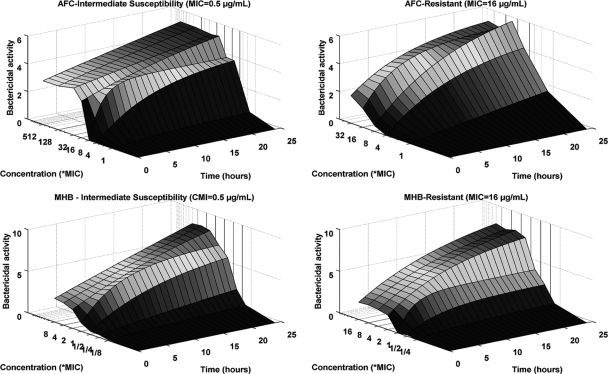
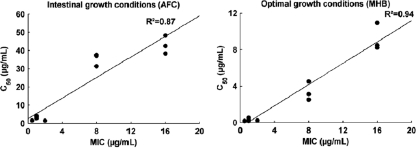
The estimated killing rates are represented in Fig. 3. Killing-rate profiles exhibited three-dimensional sigmoid shapes and were modeled using an E_max model taking the direct and indirect killing mechanisms into account (equation 2; R² = 0.88). Bactericidal activity of marbofloxacin was more efficient in MHB than in the AFC environment, with mean killing rates, after a 24-h exposure, equal to 8.14 (standard deviation [SD], 0.59) and 5.25 (SD, 0.80), respectively. Estimated values of C₅₀ were highly correlated with MIC values (Fig. 4), where C₅₀ increased with the MIC. C₅₀ estimates under MHB conditions were found 5- to 10-fold less than C₅₀ estimates under AFC conditions, showing the strong influence of the medium on antibiotic activity. Moreover, the coefficient of sigmoidicity, n, revealed a sharp increase in antibacterial effect for concentrations close to C₅₀ under MHB conditions, with a mean estimate of Hill's coefficient of 2.44 compared to 1.90 under AFC conditions.

FIG. 3.

Relationship between killing rates, marbofloxacin concentration, and time for E. coli strains of intermediate susceptibility (MIC of 0.5 μg/ml) and for resistant strains (MIC of 16 μg/ml) under AFC and MHB conditions.

FIG. 4.

Relationship between C₅₀ and MIC under AFC and MHB conditions.

DISCUSSION

Here, a pharmacodynamic model was developed to study the bactericidal effect of marbofloxacin, an antimicrobial of the fluoroquinolone group, on E. coli strains under two environmental conditions (MHB and AFC). Although three mechanisms of action have been identified in the literature, the exact activity of fluoroquinolones on bacterial population remains, to the best of our knowledge, poorly described (3). Such a mathematical approach should not be considered evidence of the existence of specific mechanisms of action but provides new insights on time-killing processes.

In the present study, we concentrated on the activity of marbofloxacin against E. coli strains with intermediate resistance and on resistant strains using a time-kill curve analysis. Pellet et al. (19) included susceptible strains in their investigation. These strains were purposely excluded from the present study because susceptible strains show complex reactions when exposed to antibacterial agents such as marbofloxacin. Susceptible populations can appear as a heterogeneous population with different susceptibility levels, and resistant subpopulations can emerge (2, 6). Hence, the development of a pharmacodynamic model representing the impact of marbofloxacin on a susceptible E. coli population would require accounting for population dynamics within different subpopulations according to their susceptibility levels. In this study, strains with intermediate resistance and resistant strains were tested, with the underlying hypothesis that these strains are stable in terms of their levels of susceptibility under selective pressure.

Growth parameters were estimated using the observed behavior of selected strains in the absence of antibiotics. Classical parameters (net growth rates and lag times) were derived from these estimates and were concordant with data from the literature (5, 27). No differences were observed in the growth of E. coli populations with respect to their susceptibility levels, but the culture media were found to have an influence on growth rates, lag times, and medium-related capacities. Bacteria under AFC conditions, which are close to natural intestinal conditions, adapted faster (i.e., showed reduced lag times), but their growth rates were lower than in the MHB environment (optimal growth conditions). The estimated growth parameters were used as baselines to analyze the antimicrobial effect of marbofloxacin against E. coli populations, assuming that the antibiotic does not directly inhibit the growth of the bacterial population.

Time-kill curves were analyzed independently for each tested concentration of antibiotic (9). This approach accurately represented the observed behavior including regrowth. In contrast with the model developed by Yano et al. (27) to study the effect of different beta-lactams on E. coli, in the present study the concentration of marbofloxacin was constant throughout the time-kill studies. Thus, in that study, regrowth could not be explained by a decrease in marbofloxacin concentration over time producing a decrease in antibacterial activity. Regrowth phenomena could be explained by the antagonistic relationship between population growth and antibiotic effects, both represented with an exponential correction factor delaying their onsets. As a result, different behaviors were highlighted over time: (i) the killing rate remained lower than the growth rate throughout the duration of observation, leading to an overall behavior similar to that in the absence of antibiotics; (ii) the killing rate overlapped the growth rate, leading to more complex behavior, including regrowth and/or plateau phases; (iii) the killing rate remained higher than the growth rate throughout the duration of observation, leading to a constant decrease in bacterial population over time.

E_max models are commonly used to represent a concentration-related drug effect (14, 15). The particularity of this model lies in the sigmoid shape which depends on three parameters: k_max, the maximum effect produced by the antimicrobial agent, the Hill coefficient (n), also called coefficient of sigmoidicity, and C₅₀, the concentration inducing half the maximum antimicrobial effect. In the present study, killing rates were concentration and time dependent and exhibited a three-dimensional sigmoid shape. An E_max model was developed to analyze the trends in killing rate with concentration and time, thereby providing estimates of Hill coefficients and C₅₀ parameters for each E. coli strain. C₅₀ parameters were highly correlated with MIC values, showing a strong relationship between this point estimate parameter and the dynamic activity of marbofloxacin. However, this approach provides only an approximation of the actual evolution of killing rates with time and concentration by smoothing the previously obtained three-dimensional sigmoid shape. Killing rates estimated using the classical E_max model monotonously increased with increasing concentrations. Hence, the E_max model should be taken as a crude representation of actual antibacterial activity, giving interesting quantitative results on the concentration-related time-kill dynamics.

The aim of the present study was to use a modeling approach to analyze the bactericidal effect of marbofloxacin against intermediate-resistant and resistant E. coli strains. Antibacterial agents are commonly classified as concentration dependent (bactericidal activity increases with increasing concentrations) or time dependent (bactericidal activity remains stable with increasing concentrations above a threshold value). Marbofloxacin is an antimicrobial of the fluoroquinolone group, commonly recognized as concentration-dependent antibiotics; however, although bactericidal activity was closely linked to concentration levels, duration of exposure was found to play a major role in killing rates. Our model predicted with good accuracy the observed time-kill dynamics of intermediate-resistant and resistant E. coli strains. Further investigations are necessary to depict the effect of this antibacterial agent on susceptible E. coli strains to account for population dynamics within different subpopulations with respect to their to susceptibility levels.