Effects of Water Placement on Predictions of Binding Affinities for p38α MAP Kinase Inhibitors

Abstract

Monte Carlo free energy perturbation (MC/FEP) calculations have been applied to compute the relative binding affinities of 17 congeneric pyridazo-pyrimidinone inhibitors of the protein p38α MAP kinase. Overall correlation with experiment was found to be modest when the complexes were hydrated using a traditional procedure with a stored solvent box. Significant improvements in accuracy were obtained when the MC/FEP calculations were repeated using initial solvent distributions optimized by the water placement algorithm JAWS. The results underscore the importance of accurate placement of water molecules in a ligand binding site for the reliable prediction of relative free energies of binding.

Introduction

The accurate computation of free energies of binding of ligands is an important goal for computational chemistry that has the potential to improve the efficiency of drug discovery.^1,2 Numerous computational methodologies exist, but among these, free energy simulations are particularly attractive because they provide a formally rigorous way to compute free energies of binding. Nevertheless, progress is hindered by the limitations of classical force fields, difficulties in adequate sampling of protein and ligand flexibility with Monte Carlo (MC) or molecular dynamics methods (MD), and challenges in accurately taking into account changes in hydration.^3–7

This report focuses on the impact of the initial placement of water molecules in a protein binding site on computed binding affinities of ligands. There is significant evidence in the literature that the computed free energies of binding can be strongly affected by the number and positions of water molecules present in a protein binding site.^8–11 For instance, information about the locations and thermodynamic properties of water molecules has been shown to substantially improve the scoring of protein-ligand interactions.¹² However, depending on the nature of the system under study, impossibly lengthy MC or MD simulations may be required before an equilibrium distribution of water molecules in the protein-ligand binding site is obtained. To efficiently address this issue, the water placement algorithm JAWS was recently developed.¹³ The procedure has been shown to accurately detect hydration sites in protein-ligand complexes, and has been used in conjunction with Monte Carlo free energy perturbation (MC/FEP) simulations to rationalize changes in free energies of binding for analogs that expel ordered water molecules from a protein binding site.⁶ The preceding study, however, was concerned with a small number of protein-ligand complexes, where clear crystallographic evidence supporting a change in hydration between different analogs was available. Further investigation is desirable, especially in the context of lead optimization, were a large number of structurally-related compounds may be considered, and for which subtle changes in hydration could affect the outcome of the fee energy calculations. For this purpose, a series of 17 inhibitors of the protein p38α MAP kinase, previously reported by Pearlman and Charifson,¹⁴ was chosen for detailed analyses (Figure 1). It is an attractive dataset since it reflects a classic problem in medicinal chemistry, optimal choice of substituents on a benzene ring. Furthermore, the series spans 2–3 orders of magnitude in activity, it involves typical small changes in substituents for a lead optimization exercise,² and it has been used as a benchmark to test alternative computational approaches for activity predictions.^14,15

Figure 1.

Left: investigated inhibitors and measured activities for inhibition of kinase activity with IC₅₀ values in M (ref. ¹⁴). Right: computed image of ligand 5 bound in the “R1, R2” pose to p38α MAP kinase. As 180 degrees flips of the thiophenyl group are not observed in the simulations, the R1 and R2 positions are considered distinct from the R4 and R5 positions. In the “R1, R2” pose, ligands 14 and 15 are able to hydrogen bond to nearby Asp168, drawn in thicker sticks. For clarity, some protein residues and all protein hydrogen atoms have been omitted. Compound 18, which was not in the experimental study, has been added as a convenient intermediate for the MC/FEP calculations. Image prepared using the software VMD.¹⁶

Methods

Protein Setup

An X-ray crystal structure of p38α MAP kinase in complex with a pyridopyrimidinone inhibitor (PDB ID: 1OUY),¹⁷ which is very similar to 17, provided the structural starting point. The ligand from the crystal structure was replaced with the parent ligand 1, which was constructed with the program BOSS,¹⁸ and protein and ligand Z-matrixes were prepared using the programs chop and pepz.¹⁸ Protein residues with any atom within 17.5 Å of a ligand atom were retained. The degrees of freedom of the side chains of protein residues with any atom within 12.5 Å of a ligand atom were sampled during the MC simulations. Backbone degrees of freedom and side chain bond lengths were kept frozen following a short conjugate-gradient relaxation. The net charge of the systems was set to zero by neutralizing protein residues distant from the ligand. The protonation states of histidine side chains were assigned with the assistance of the software PROPKA 2.0.¹⁹ The OPLS-AA force field was used for the protein.²⁰

Ligand Setup

Initial structures were generated using the molecule growing program BOMB.²¹ The unsubstituted inhibitor 1 provided the core to grow the desired analogs. For consistency, the inhibitors were numbered as originally reported,¹⁴ with the addition of the 1,3-difluoro compound as 17. As the aromatic ring to which the substituents are attached is capable of rotating relative to the rest of the molecule, it is possible for the ligand to bind in two alternative binding modes, related by a 180° flip around the thioether bond (Figure 1). As these rotamers are not expected to interconvert during the MC simulations, structures were generated for both binding modes. For the MC simulations, the ligands were treated as fully flexible and their energetics were represented with the OPLS/CM1A force field.²² The CM1A atomic charges were scaled by 1.14.²³

Solvent Setup

For the ligands alone in water, a 25 Å water cap was used containing ca. 2000 TIP4P water molecules. Each protein-ligand complex was solvated by ca. 1250 TIP4P water molecules in a ca. 25 Å radius water cap. A half-harmonic potential with a force constant of 1.5 kcal/mol/Ų was applied to water molecules at distances greater than 25 Å from the center of the system to prevent evaporation. The initial solvent distribution was derived from a stored solvent box using the default procedure with the MCPRO 2.1 program.¹⁸ Specifically, a protein or ligand atom near the center of the binding site is taken as the origin of the system and a cube containing 27 images of an equilibrated (298 K, 1 atm) cube of 512 TIP4P water molecules is centered on it. Each of the 13,824 water molecule is considered, and it is deleted, if its oxygen atom is found to be within 2.5 Å of any non-hydrogen atom of a solute, or if it is outside the system boundary defined by the cap radius. Though this straightforward procedure is typical of MC and MD programs, the number of retained water molecules and their initial coordinates depend on the choice of center atom. In principal, any associated artifacts should be removed if the MC or MD sampling is complete. However, it is easy to imagine that, for example, water molecules could be absent from or trapped in solute pockets and not be able to diffuse in or out of the pocket in the course of a simulation.

Alternatively, the initial water placement for the protein-ligand complexes was determined using the JAWS algorithm. The details of JAWS are described elsewhere.¹³ Briefly, a 3-D cubic grid with 1 Å spacing is positioned to envelop the binding site. The grid region is defined by overlapping spheres of 4 Å radius, centered on user-selected ligand atoms in the binding site. MC simulations are then performed to first find potential hydration sites and then to determine their occupancies. The putative hydration sites are detected by allowing “θ” water molecules to sample the grid volume while simultaneously scaling their intermolecular interactions between “on” or “off”. The full system that is simulated consists of the protein, ligand, θ-water molecules, and regular water molecules. After the most probable sites are identified, a new MC simulation is run with θ water molecules constrained near the sites and with θ sampling. The absolute binding affinity of a water molecule at a given site is estimated from the ratio of probabilities that the water molecule is “on” or “off”. The locations of hydration sites were determined using 5 million (5 M) MC configurations with sampling of just the water molecules, followed by 10 M configurations that sampled the water, protein, and ligand degrees of freedom. Then, the second phase covered 50 M configurations to estimate the occupancy of the sites.

Free Energy Calculations

Relative binding free energies for the ligands were computed from the standard thermodynamic cycle evaluating the free energy change in solution and in complex with the protein.^1–3 The free energy changes were computed with the MCPRO 2.1 program,¹⁸ using Metropolis MC simulations to sample configurations of the system,²⁴ the single-topology technique for the structural perturbations,²⁵ and 11 windows of simple overlap sampling to compute the free energy change between the initial and final ligand structures.^26,27 For the ligands alone in water, each FEP window consisted of 10 M configurations of equilibration and 20 M configurations of averaging. For the protein-ligand complexes using the default water setup, the equilibration period was 12.5 M configurations for the first window and 10 M for the subsequent 10 windows. The windows were run serially; the initial configuration for windows 2–11 was based on the last configuration of the previous window and was well equilibrated. The simulations where the initial solvent coordinates came from the JAWS calculations were run at a later date using a higher-throughput protocol, whereby the 11 windows for each FEP calculation were run in parallel on 11 processors. In this case, equilibration for each window entailed 5 M configurations of water-only sampling, followed by 10 M configurations of full equilibration. For both protocols, the averaging period for each window was 10 M configurations. The averaging for the JAWS-based calculations was then extended to 20 M configurations for further checking of convergence. In all cases, evaluation of the potential energy employed 9-Å residue-based cutoffs and the MC simulations were run at 298 K. The JAWS procedure takes about the same amount of computer time as running 2–3 FEP windows, so it adds ca. 25% to the overall computational effort.

A set of perturbations was devised to compute free energies of binding for all analogs relative to ligand 1. In order to minimize the steric and electrostatic changes in each perturbation, consistent with past FEP studies, larger analogues were perturbed in multiple steps, e.g. OH → F → H or Cl → F → H.^11,28 Full details of all perturbations are provided in the Supporting Information. To account for the two possible "R1, R2" or "R4, R5" poses for the unsymmetrical ligands 4–17, the relative free energies of binding of each pose were combined to produce an overall free energy of binding ΔΔG using eq 1, where R is the ideal gas constant, T is 298 K, and ΔΔG_R1,R2 and ΔΔG_R4,R5 are the relative free energies

$$\mathrm{\Delta }\mathrm{\Delta }G=-\mathit{\text{RT}}\text{ln}[\text{exp}(-\mathrm{\Delta }\mathrm{\Delta }{G}_{R1,R2}/\mathit{\text{RT}})+\text{exp}(-\mathrm{\Delta }\mathrm{\Delta }{G}_{R4,R5}/\mathit{\text{RT}})]+\mathit{\text{RT}}\text{ln}2$$ (1)

of binding of the two poses. The second term in eq 1 penalizes the computed free energies of binding of the unsymmetrical ligands 4–17 by RT ln 2 because they are relative to the symmetrical ligand 1. Thus, when the relative free energies of binding of the two poses differ by greater than ca. 2 kcal/mol, the free energy of binding is essentially that of the more favorable pose plus RT ln 2. Alternatively, if the relative free energies of binding of the two poses are the same, the RT ln 2 penalty is removed.

Though in this study the JAWS calculations were only applied to the initial state, the FEP calculations were run from the larger to smaller ligand to minimize the possibility of trapping water molecules by growing in the opposite manner. Another use for JAWS-like protocols would be to evaluate the preferred hydration pattern for the initial and final states of a proposed free-energy calculation. If significant differences were detected that would likely not be overcome by normal sampling, then alternative perturbation pathways could be considered.

Analysis

The agreement between predicted and measured free energies of binding was assessed by computing root-mean square deviations (RMSDs), mean unsigned errors (MUEs), and predictive indices (PIs). The latter has been proposed by Pearlman and Charifson to measure the quality of a rank-ordering by potency of a series of ligands, and is computed according to eq 2,¹⁴ where E(i) and P(i) are

$$\begin{array}{cc}\mathit{\text{PI}}\hfill & =\frac{{\displaystyle \sum _{j>i}{\displaystyle \sum _i{w}_{\mathit{\text{ij}}}{C}_{\mathit{\text{ij}}}}}}{{\displaystyle \sum _{j>i}{\displaystyle \sum _i{w}_{\mathit{\text{ij}}}}}}\hfill \\ w_j\hfill & =|E(j)-E(i)|\hfill \\ C_{\mathit{\text{ij}}}\hfill & \begin{array}{ccc}=-1\hfill & \text{ if }\hfill & \frac{E(j)-E(i)}{P(j)-P(i)}<0\hfill \end{array}\hfill \\ \hfill & \begin{array}{ccc}=+1\hfill & \text{ if }\hfill & \frac{E(j)-E(i)}{P(j)-P(i)}>0\hfill \end{array}\hfill \\ \hfill & \begin{array}{ccc}=0\hfill & \text{ if }\hfill & P(j)-P(i)=0\hfill \end{array}\hfill \end{array}$$ (2)

the experimental and predicted binding free energies of compound i. The PI index ranges from −1 to +1, depending on how well the predicted ranking matches the experimental ordering. A value of +1 indicates perfect predictions, a value of −1 indicates predictions that are perfectly anti-correlated, and a value of 0 arises from random results. In essence, the method considers each pair of compounds i and j in turn. Large differences in binding free energies have a large weight w_ij which provides a large positive contribution to the final PI, if the rank-ordering of the pair is correct. Conversely, if i and j have a small difference in measured binding affinity, an incorrect prediction of the most potent binder has a minor impact on the final PI.

Results and Discussion

Approximate free energies of binding for the inhibitors were obtained from the experimental pIC₅₀ values.¹⁴ While the relationship between K_i and ΔΔG is linear, the correlation between IC₅₀ and K_i is not exact, thus pIC₅₀ and ΔΔG cannot be expected to be perfectly linearly related.

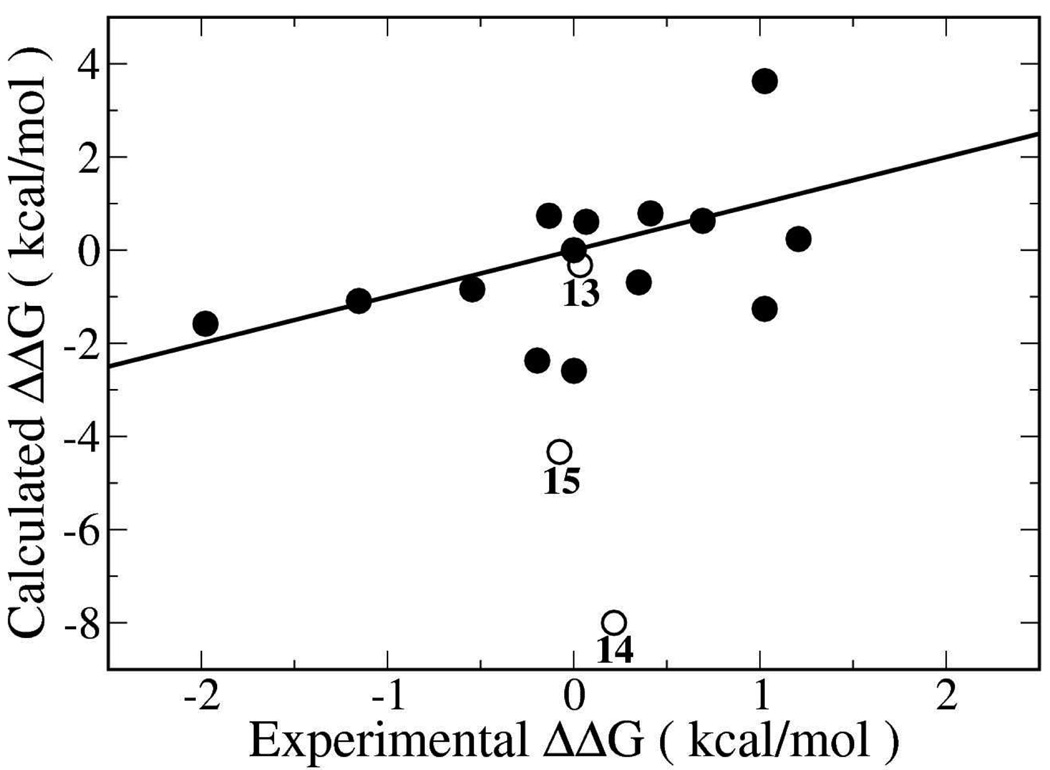
The MC/FEP results using the default hydration protocol are compared with the experimental data in Figure 2. The overall RMSD is 2.65 kcal/mol, while the MUE is 1.69 kcal/mol and the PI is 0.41, representing modest predictive power.¹⁴ Four of the ligands (8, 9, 10, and 17) were found to bind most favorably in the “R4, R5” mode while the rest bound in the “R1, R2” mode. The most significant outliers from these calculations were the 2-hydroxyl and 2-amino-substituted ligands 14 and 15, which are capable of hydrogen bonding to the carboxylate group of Asp168. No obvious features stand out for the errors for the remaining ligands. Inspection of snapshots from the calculations, however, revealed substantial inconsistencies between different ligands in the number and positioning of water molecules within the binding site.

Figure 2.

Calculated vs. experimental relative free energies of binding for the p38 inhibitors using the conventional protocol with the stored water box. Free energy differences (kcal/mol) are relative to inhibitor 1. Open circles indicate the computed relative free energy of binding for ligands 13, 14 and 15, which are discussed in the main text.

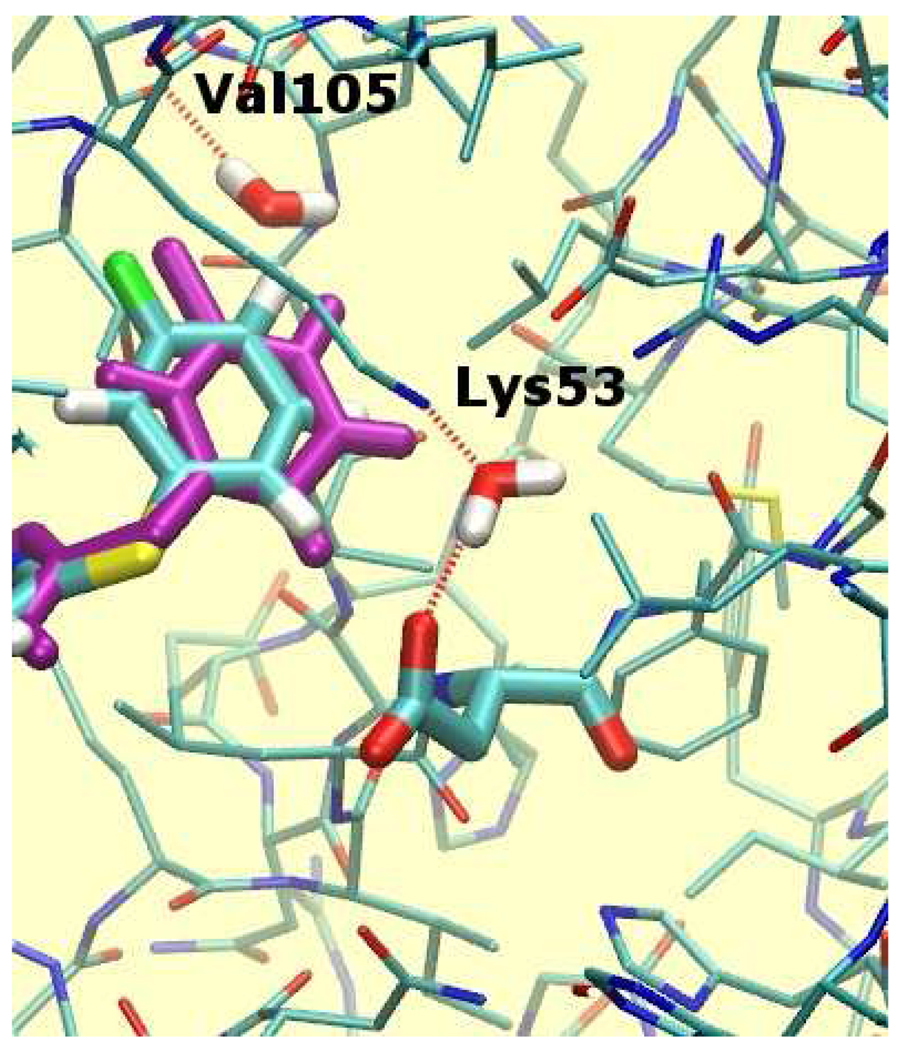
For instance, as illustrated in Figure 3, two water molecules were placed in the phenyl substituent pocket for the meta-fluoro analog 7, but they were absent for the meta-chloro analog 10. One water molecule is in a fairly hydrophobic environment and can donate only a single hydrogen bond to the backbone carbonyl of Val105. Thus, though there is sufficient space to insert a water molecule in this region of the binding site when 7 is bound, it is unclear whether this would be thermodynamically favorable. The other water molecule is involved in a strong hydrogen bonding interactions with Lys53 and Asp168 and it is doubtful that it should be absent when 10 is bound.

Figure 3.

Hydration sites in the vicinity of the p38 inhibitor 7 (colored sticks) obtained using the default hydration protocol. These hydration sites are not observed for inhibitor 10 (purple sticks). Ligand and Asp168 atoms are drawn in thicker sticks. Other water molecules, selected protein residues and all protein hydrogen atoms have been omitted for clarity. Hydrogen bonding interactions between protein atoms and water molecules are depicted by dotted red lines.

Clarification of the water distributions in the binding site was sought using the water placement algorithm JAWS for each ligand. These calculations revealed the presence of several hydration sites within the binding pocket that were inconsistently found when the stored solvent box was used. To test if consistency in solvent distribution alone was sufficient to improve accuracy, the MC/FEP calculations were repeated starting with the solvent distribution computed using the JAWS protocol for the complex of 1 for all complexes. This resulted in only marginal improvement over the original results, with an RMSD of 2.52 kcal/mol, a MUE of 1.95 kcal/mol, and a PI of 0.55 (see Supporting Information). While using the same initial solvent distribution eliminated errors resulting from varying numbers of water molecules, occasional large errors were introduced in instances where the water distribution derived for the smallest analog 1 was used for simulations of much larger analogs, for example, the 3,4-dimethyl one 6. In these cases, some water molecules were observed to be trapped in high-energy configurations between the protein and ligand. The extensive sampling of ligand, protein and solvent degrees of freedom required to resolve such steric problems is not systematically achieved with the standard MC simulation protocol.

To eliminate this source of error, the MC/FEP calculations were repeated with the JAWS-derived water distributions for each starting ligand state. This resulted in much improved accuracy with the errors roughly halved. For 10 M configurations of averaging, the RMSD for all ligands is reduced to 1.35 kcal/mol, the MUE to 0.95 kcal/mol, and the PI improved to 0.62 (Figure 4). These results changed little upon extension of the averaging period to 20 M configurations; the RMSD, MUE and PI became 1.44, 0.92, and 0.61 (Supporting Information). Only ligand 17 was found to prefer binding in the “R4, R5” pose, which is observed in the 3FC1 crystal structure.¹⁵ However, the relative free energies of binding for ligand 5 in both poses were the same within 0.2 kcal/mol; thus, it does not have a preference. The “R1, R2” pose is calculated to be significantly more favorable for the remaining unsymmetrical ligands.

Figure 4.

Calculated vs. experimental relative free energies of binding for the p38 inhibitors using the JAWS protocol to determine initial water coordinates. Details are the same as in Figure 2. To aid in comparison with Figure 2, axis scales and data symbols are the same.

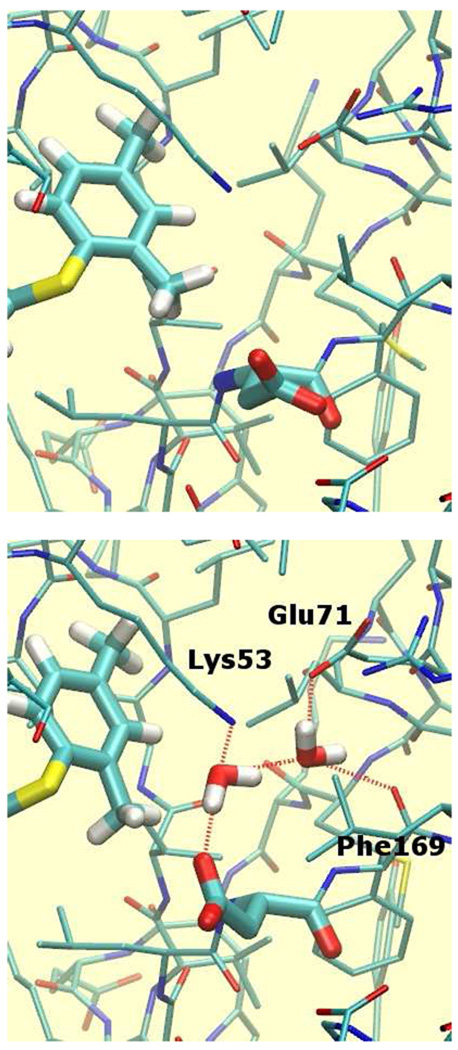
Detailed analysis of the output of the MC/FEP simulations was undertaken to elucidate the improvements in binding affinity predictions using the JAWS-derived water distributions. Analysis of the hydrogen-bonding ligands 14 and 15, which were previously predicted to bind overly favorably, revealed that the JAWS calculations located two additional hydration sites in the vicinity of Asp168, as illustrated in Figure 5 (bottom) for the hydroxyl analog 14. These hydration sites are located in a cavity partially shielded from bulk solvent and were not populated using the default solvation protocol (Figure 5, top). The first water molecule receives two hydrogen bonds from the ligand’s hydroxyl group and Lys53, and donates two hydrogen bonds to the other water molecule and Asp168. The second water molecule also donates two hydrogen bonds to Glu71 and the backbone carbonyl of Phe169. The occupancy of the additional hydration sites can be expected to affect the outcome of the FEP calculations. In the MC/FEP simulations equilibrated following the default solvent-box protocol, the hydroxyl group of 14 is donating a hydrogen bond to Asp168 (Figure 5, top). In the MC/FEP simulations equilibrated after the JAWS setup, the carboxylate group of Asp168 ends up rotated away from its initial position to accommodate better the additional water molecules. The interaction between the hydroxyl group and Asp168 is no longer direct, but it is water-mediated. Consequently, addition of the meta hydroxyl or amino group onto the phenyl ring is less favorable, in agreement with the experimental activity measurements. Specifically, the relative binding affinity of 14 was computed in two steps, 14→18 and 18→1. Compared with the original simulations, the relative free energy of binding of 14→18 is 3.3 kcal/mol less favorable for 14, and the relative free energy of binding of 18→1 is 3.5 kcal/mol less favorable for 18 with the JAWS setup. Overall the error in the computed free energy of binding for 14 is reduced from 8.2 to 1.4 kcal/mol. Similarly, the relative binding affinity of 15 was computed in two steps, 15→2 and 2→1. Compared with the original simulations, the relative free energy of binding of 15→2 is 5.5 kcal/mol less favorable for 15 and the relative free energy of binding of 2→1 is 1.1 kcal/mol more favorable for 1. Overall the error in the computed free energies of binding for 15 is reduced from 4.2 to 0.2 kcal/mol.

Figure 5.

Representative snapshots from MC/FEP simulations for inhibitor 14. Top: The solvent distribution that originated from the default procedure. Bottom: The solvent distribution obtained after equilibration using JAWS. Ligand and Asp168 atoms are drawn in thicker sticks. Hydrogen bonding interactions between the ligand hydroxyl group or buried water molecules are depicted by dotted red lines. Solvent exposed water molecules solvating Asp168 are shown in green sticks. Other water molecules, selected protein residues and all protein hydrogen atoms have been omitted for clarity.

The most significant remaining error is for the 2,4-dimethyl compound 13, whose relative binding affinity is too unfavorable by 4.2 kcal/mol with the JAWS simulation protocol, whereas the initial simulations yielded an error of only 0.4 kcal/mol. The relative binding free energy of 13 was computed in two steps, 13→3 and 3→1. The small error for 13 using the traditional solvent-box protocol is fortuitous because it represents a cancellation of errors for the two steps, +1.9 and −2.3 kcal/mol, respectively. With the JAWS protocol, the corresponding errors are +5.0 and −0.8 kcal/mol, so the problem was predominantly in the 13→3 step. One possibility is that the starting water distribution for 13 was not appropriate for or did not evolve properly for 3. As pointed out previously, substantial errors can be expected if a perturbation induces changes in hydration in the binding site, unless the computed relative free energies of binding are corrected by computing the absolute free energy of binding of the displaced water molecules.⁶ However, this situation does not seem to occur in the present case since the JAWS-computed hydration patterns for the starting and ending states, 13 and 3, are identical.

The problem with the 13→3 perturbation appears to be more complex and associated with the conformation of the Asp168 side chain. From the free energy changes for the individual FEP windows, it is apparent that the ca. 3 kcal/mol difference in free energy changes between the two simulations arises at the beginning of the perturbation, when the 2-methyl group of 13 starts to be shrunk into a hydrogen atom (see Supporting Information). Visualization of snapshots saved during the simulations with the traditional hydration protocol reveals that the carboxylate group of Asp168, which was initially pointed towards the ligand, rotates away from the 2-methyl group (Figure 6, top). This did not occur in the JAWS equilibrated simulations, presumably because rotation of the carboxylate group would break the hydrogen bond with one of the two nearby water molecules placed using JAWS (Figure 6, bottom). The MC/FEP calculations were repeated using the same JAWS-derived solvent distribution, but with Asp168 rotated to adopt the conformation observed with the solvent-box protocol. The computed change in free energy of binding for 13→3 became −2.0±0.2 kcal/mol, which is intermediate between the results obtained with the solvent box and JAWS protocols. In turn, this reduces the error for 13→1 to 2.5 kcal/mol. Thus, the conformations of Asp168, which is part of the flexible DFG motif, are likely not adequately sampled in the present MC/FEP simulations. This highlights complexities associated with the fact that hydration of the system and the conformation of the ligand and protein are all coupled. The hydration may be setup properly for one conformation, but it is possible that the system relaxes away from this conformation to one that would prefer a different population of water molecules that can not be achieved with computationally reasonable sampling periods.

Figure 6.

Representative snapshots from MC/FEP simulations of inhibitor 13 bound to p38α MAP kinase. Top: The configuration near Asp168 that arose in the simulation starting from the default hydration procedure. Bottom: The configuration near Asp168 after equilibration using JAWS. Ligand and Asp168 atoms are drawn in thicker sticks.

Finally, it is worth reflecting on the degree of agreement that can actually be achieved between the computations and experiment, given the uncertainties in the measured activity data. As noted previously, the conversion of ΔIC₅₀s into ΔΔGs of binding is approximate, but another source of error is the variability of the IC₅₀ measurements themselves. Although uncertainties were not reported for the experimental data used here,^14,15 study of a large corporate database found a median standard deviation for activity measurements of approximately 0.3 log unit.²⁹ This corresponds to a factor of 2 in IC₅₀ or ±0.41 kcal/mol. Our own experiences with repeated measurements for compounds used as standards in multiple biological assays are similar.^2,21,28 Drawing samples from a Gaussian distribution centered around the reported IC₅₀s for each ligand according to this standard deviation, the predictive index (eq 2) can be computed between two independent simulated activity measurements for the entire dataset. Following a procedure similar to the one reported by Brown et al.,²⁹ the sensitivity of the PI to uncertainties in the measured IC₅₀s is derived by repeating the calculation 1 million times. Assuming the above-mentioned errors, the median achievable PI is 0.76 for this dataset. Though the distribution of PI values is not Gaussian (see Supporting Information), approximately 67% of PI measurements would fall within the range 0.67–0.84. The median achievable PI for this dataset is thus below unity because the error bars on the measured IC₅₀s are large enough to qualitatively change the rankings of some of the ligands. Given these considerations, the improvement of the PI from 0.41 to 0.62 upon using a JAWS-optimized water distribution for the MC/FEP simulations is reinforced as being significant. The PI of 0.62 is also greater than the PI achieved for this dataset by various scoring function and MM-PBSA approaches that were previously tested.^14,15 The only higher PI, an impressive 0.85, was achieved using thermodynamic integration and molecular dynamics with the Amber program.¹⁴

Conclusion

The results presented here illustrate that the initial placement of water molecules can significantly affect the outcome of computations of protein-ligand binding affinities. Details such as this need to be considered to allow current computational methods to evolve to the accuracy required for routine, reliable guidance of lead-optimization programs in drug discovery and of molecular design in general. It was found that optimization of the distribution of water molecules in the protein-ligand binding site using the water placement algorithm JAWS substantially improved the quality of subsequent MC/FEP results for a dataset of 17 inhibitors of p38α MAP kinase. Use of the JAWS-derived water distributions reduced the RMSD for relative free energies of binding from 2.65 to 1.35 kcal/mol, and improved the predictive index (eq 2) from 0.41 to 0.62. Though further optimization of JAWS and other water-placement procedures is possible,^12,13 additional issues affecting the outcome of free-energy calculations also continue to warrant concerted attention.^1–3 Force-field and sampling problems remain, and it is sometimes necessary to consider more complex perturbation cycles where binding-site water molecules must be forced to disappear.^6,8–10 As pointed out here in the context of Figure 6, the complexity of sampling issues can be great as it simultaneously involves all components of the modeled systems. Initial choices for the placement of water molecules, every dihedral angle in the ligand and the protein, and protonation state of each ionizable residue can all have ramifications that are not removed by standard sampling procedures. Nevertheless, the present results have demonstrated that significant gains in accuracy can be realized by more thorough consideration of initial water placement in calculations of the free energetics of protein-ligand binding.