Inexact Local Alignment Search over Suffix Arrays

Abstract

We describe an algorithm for finding approximate seeds for DNA homology searches. In contrast to previous algorithms that use exact or spaced seeds, our approximate seeds may contain insertions and deletions. We present a generalized heuristic for finding such seeds efficiently and prove that the heuristic does not affect sensitivity. We show how to adapt this algorithm to work over the memory efficient suffix array with provably minimal overhead in running time.

We demonstrate the effectiveness of our algorithm on two tasks: whole genome alignment of bacteria and alignment of the DNA sequences of 177 genes that are orthologous in human and mouse. We show our algorithm achieves better sensitivity and uses less memory than other commonly used local alignment tools.

I. Introduction

Finding local matches between two long sequences is a fundamental problem in computational biology. For example one might want to find similar regions in the genome sequence of two organisms. Due to differences in the genome sequence of different organisms or to sequencing error we have to look for approximate matches. Many algorithms and tools have been created that address this need, yet finding local alignments still remains one of the most computationally intensive steps in biological sequence analysis.

We define the local alignment search problem as follows: Given two strings S₁ and S₂ of lengths n₁ and n₂, a minimum match length l and a maximum distance k, find all pairs of substrings of S₁ and S₂ of length l that are within distance k. We assume all strings are from a finite alphabet Σ of size σ. A few popular distance metrics are Hamming distance, unit-cost edit distance (Levenshtein distance) and general edit distance based on a substitution cost matrix.

A string matching problem is called offline if we are allowed to pre-process the text and make an index data structure, and online if we are not allowed to pre-process the text. The exact alignment problems can be solved optimally (meaning the running time is bounded by a linear function of the size of input strings) using eg. the KMP algorithm for the online and suffix trees for the offline case. In this paper we will focus on the offline problem.

The online local alignment problem can be solved in O(n₁ · n₂ · l) time by using each length l substring of S₂ as a pattern and using a variation of well known Smith-Waterman [14]. This running time, however, is impractical for the size of the data-sets commonly encountered in practice.

In practice the most common solution to the inexact local alignment problem is to find seeds and try to extend them to longer local alignments [2], [4], [6]. A seed is a short substring of one sequence that matches closely to a substring of the other sequence. Seed and extend algorithms are fast because they avoid trying to align every region of the two sequences and only focus on the regions that are likely to align well. Two most common type of seeds used are exact seeds and spaced seeds. Exact seeds need to match perfectly, whereas spaced seeds allow mismatches at some positions. Neither allow insertions and deletions within the seed. In this work we look at more general inexact seeds that are based on the same notion of similarity as in Smith-Waterman [14]. We describe an algorithm for finding these inexact seed, and show that an implementation of this algorithm has good performance in practice. Since our algorithm is based on dynamic programming it can use a general substitution cost matrix for distance computation.

Seed finding algorithms are evaluated by their sensitivity and specificity. Sensitivity corresponds to fraction of true local alignments that are found by the seeds. Specificity corresponds to fraction of reported seeds that can be extended to true local alignments.

In the case of exact seeds, their sensitivity and specificity depends on only parameter: seed length. Spaced seeds provide an additional parameter - weight - the number of characters within the seed that must match within the aligned strings. For the same weight spaced seeds achieve better sensitivity than exact seeds without sacrificing specificity. Computing sensitivity of a spaced seed is, however, NP-hard [10]. Most spaced seed tools use a pre-computed seed or set of seeds, making it difficult to tune their parameters at run-time in order to achieve the best trade-off between sensitivity and specificity for a given alignment task.

We will prove that our seed finding algorithm is perfectly sensitive i.e. if a good enough local alignment is present it will be detected by our seeds. Furthermore since we allow inexact seeds, by using longer seeds we can achieve better specificity too. With our algorithm the user can pick any seed length and similarity at running time without the need to re-compute the index.

Most of the tools used in practice today are based on one of two index data structures for large strings; inverted k-mer index and the family of indexes related to suffix trees (suffix arrays and Burrows-Wheeler index.) BLAST [2] uses an inverted index of exact seeds. MUMmer [5] is a whole genome alignment tool that uses suffix trees. Bowtie [9] uses a Burrows-Wheeler index of the human or other genome and can align short reads with few differences to the reference. Our algorithm uses a suffix array index.

II. Suffix Array Search Algorithm

Our algorithm systematically tries to compute dynamic programming score (similar to Needleman-Wunsch [13]) for aligning every pair of substrings of S₁ and S₂. We assume the “cost” of aligning two characters is zero if they are identical and is some positive number otherwise. What makes this algorithm fast is that it gives up as soon as it notices that the alignment cost (i.e. distance or score) is getting “too high”.

A. Recursive Search of Suffix Trie

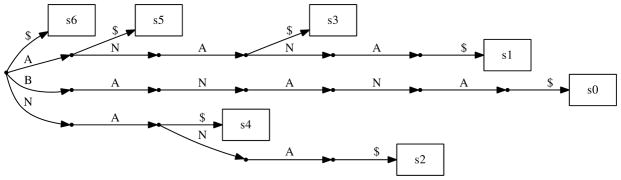
It is easier to explain our algorithm using the Suffix Trie data structure. A suffix trie is a rooted tree data structure that stores every suffix of a string. Unfortunately this representation requires up to Θ(n₂) space in general which makes it impractical for long sequences. In the next section we will adapt this algorithm to use suffix array which require only linear space. Let us assume we have built a suffix trie for each of S₁ and S₂. A representation of an example suffix trie is shown in Figure 1. Each node of the suffix trie corresponds to a substring of the original string that is spelled out by the labels of the edges on the unique path from root to that node. An exact search algorithm starts at the root and follows down the edges labeled with the same character in both trees. In other words, if the search function is called on some internal node u from the first trie and v from the second trie, then for each letter of the alphabet if both u and v have a child labeled with that letter the search function is called recursively on the corresponding child nodes. After traversing l edges down from the root (reaching depth l) the leaves under the internal node of each tree represent suffixes from each sequence that share the first l characters exactly. Thus, we find exact “alignments” of length l.

Fig. 1.

Sample Suffix Trie for String ‘BANANA’

In the case of approximate search however we may have to follow edges labeled with characters that are different in the two suffix tries. Therefore we have to call the search function recursively for every pair of children of u and v. Without limiting the number of mismatches allowed this recursive search (which is called for every pair of children) will try to align every substring of length l from S₁ to every substring of S₂. A simple solution is to stop following down branches from a pair of internal nodes as soon as the distance between the two strings corresponding to those nodes is already greater than some threshold (also when we reach depth l of course). i.e. as soon as the alignment cost becomes “too high” we simply return from recursion and will not call search function for the children of current nodes. We calculate distance by updating a dynamic programming table on the fly as illustrated in Figure 3. We only need to update one row and one column of the dynamic programming table for each edge traversal. If the distance is smaller than the threshold we recursively call the search function for every pair of children of the two current internal nodes. When we reach depth l we report all pairs of leaves under the two nodes. The cost threshold can either be a constant or for example a function of the length of the alignment so far.

Fig. 3.

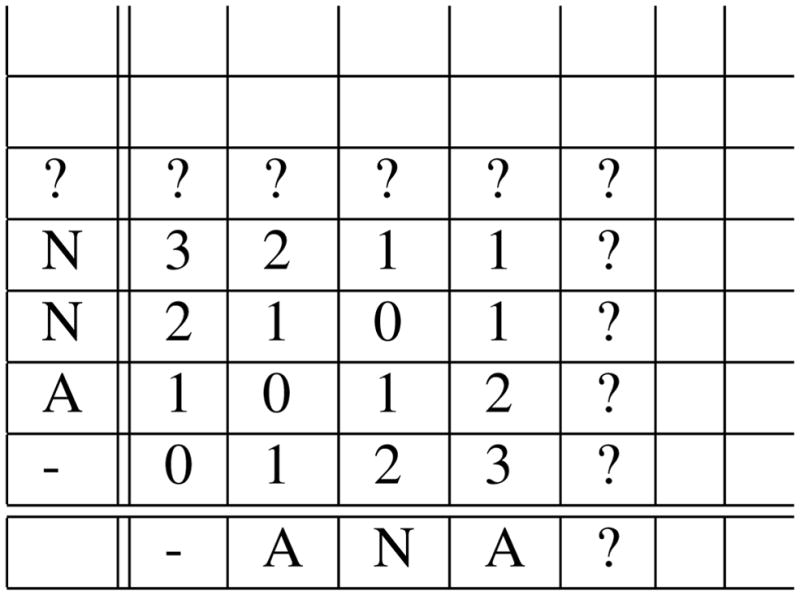
Sample dynamic programming table when the algorithm is at depth 3. Only cells marked by ? need be computed when the algorithm follows down an edge to two children of current nodes (i.e. depth 4).

A naive choice is to use a constant threshold equal to k, i.e. to stop when the distance between strings corresponding to the two current nodes is greater than k. This strategy is slow in practice however, because for most practical sequences the top levels of the suffix trie are nearly full (each node has nearly σ children), whereas deep nodes (depth ≥ log_σ n) of the trie have about one child on average. The constant threshold strategy will spend lots of time traversing top levels of the trie allowing many errors in the first few characters of the alignment. In fact for example, in the unit-cost edit distance model, it aligns every substring of length k of the first sequence to every substring of length k of the other sequence. The main intuition is that we can look for shorter seeds with the desirable property that they do not have many differences in the beginning. This causes the algorithm to backtrack more easily on the first few levels of the tree and significantly improves the running time.

We show in Lemma 1 that if L₁ and L₂ (e.g. substrings of S₁ and S₂, respectively) of length l match with distance ≤ k then there exists a seed E₁ of length e (1 ≤ e < l) in L₁ that matches a substring E₂ in L₂ in such a way that the cost of edits necessary to match any prefix of E₁ to some prefix of E₂ is never more than $\frac{k}{l-e}$ times the length of the prefix. This is a generalization of exact seeds. This lemma proves that our seed heuristic does not affect the sensitivity of the algorithm at all.

After finding the seeds one should verify that they can be extended to alignments of length l. (It is also possible to use these seed directly in a chaining algorithm if we desire a global alignment). This can be done in a post-processing step. But we assume for sufficiently long seeds (e ≥ log_σ n) the number of seed hits are small enough that the running time will be dominated by the seed search phase. Of course this is not true for highly repetitive sequences.

Lemma 1

If L₁ of length l matches L₂ with cost ≤ k, then for any seed length e, 1 ≤ e < l there exists a seed E₁ a substring of L₁ of length e and E₂ a substring of L₂ such that for every prefix of E₁ of length j, E₁ [1..j] matches some prefix of E₂ with $\le \left(j·\frac{k}{l-e}\right)$ distance.

Proof

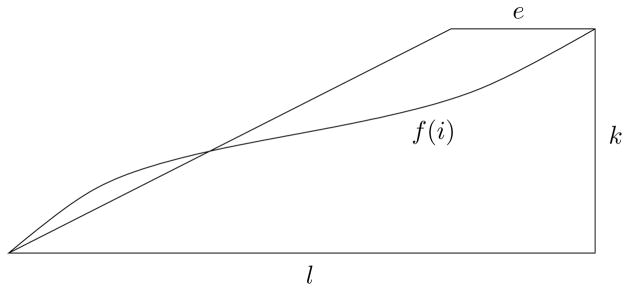
Given an alignment of L₁ to L₂ with distance ≤ k let f (i) be a the edit distance of L₁ [1..i] from the prefix of L₂ to which it is aligned. See Figure 4. It is easy to see that f is a non-decreasing function, and by definition f (l) ≤ k and f (0) = 0.

Fig. 4.

For an alignment of L₁ to L₂ with ≤ k distance, define f(i) as the edit distance of L₁[1..i] from the prefix of L₂ to which it is aligned.

We need to show that there exists an i ∈ {0, …, l − e} such that for all j = 1 … e, $f(i+j)-f(i)\le \left(j·\frac{k}{l-e}\right)$.

As a way of contradiction assume for all i = 0 … (l − e), there exists j ∈ {1 … e} such that $f(i+j)-f(i)>\left(j·\frac{k}{l-e}\right)$ or equivalently $f(i+j)>f(i)+\left(j·\frac{k}{l-e}\right)$.

In particular for i₁ = 0 there exists j₁ such that $f(0+j_1)>f(0)+\left(j_1·\frac{k}{l-e}\right)$, and for i₂ = (0 + j₁) there exists j₂ such that $f((0+j_1)+j_2)>f(0+j_1)+\left(j_2·\frac{k}{l-e}\right)>\left(f(0)+\left(j_1·\frac{k}{l-e}\right)\right)+\left(j_2·\frac{k}{l-e}\right)$, and so on up to some z such that l − e < 0 + j₁ + j₂ + … + j_z ≤ l. We have:

$$\begin{array}{l}f(l)\ge f(0+j_1+j_2+\dots +j_z)\\ >f(0)+\left(j_1·\frac{k}{l-e}\right)+\dots +\left(j_z·\frac{k}{l-e}\right)\\ =0+(j_1+j_2+\dots +j_z)·\left(\frac{k}{l-e}\right)\\ \ge (l-e)·\left(\frac{k}{l-e}\right)=k\end{array}$$

Which implies f (l) > k which is a contradiction.

B. Adapting the Algorithm to Suffix Arrays

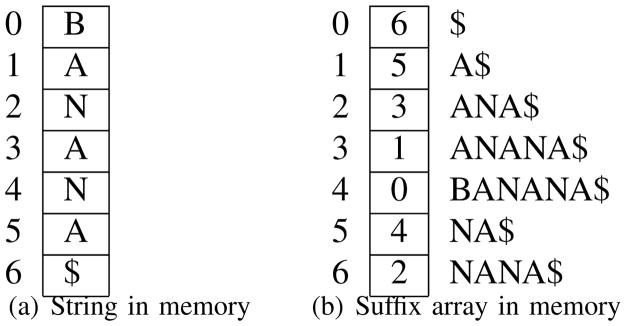
A suffix array [12] is the list of indexes all suffixes of a string in lexicographically sorted order, as illustrated in Figure 2(b). A suffix array can be built in linear time ¹ and occupies n log₂ n bits. Even though theoretically asymptotic memory requirements of suffix arrays and suffix trees is the same, in practice highly optimized implementations of suffix trees require over 10 bytes of memory per input character [8] whereas a basic suffix array implementation requires just 4+1 bytes per character². Space requirements of suffix arrays can be further reduced to O(n) bits using compressed suffix arrays. Finally it has been shown that by storing some auxiliary tables, Enhanced Suffix Arrays [1] can be used to simulate any type of traversal of suffix trees in the same time complexity.

Fig. 2.

Suffix array index requires 5 · n bytes of memory

Our algorithm over suffix arrays is inspired by the simplest exact search algorithm on a suffix array which is in essence a binary search. The main property of the suffix array that our algorithm takes advantage of is that if some prefix of the suffix pointed to by ith element of suffix array is equal to that of the suffix pointed to by j the element of suffix array, then for every k ∈ [i … j], every suffix pointed to by the kth element of suffix array shares the same prefix. This property easily follows from the fact that the suffixes are lexicographically sorted. The recursive algorithm described over suffix tries can be adapted to work on suffix arrays with at most a log₂ n factor increase in running time as will be shown in Lemma 2. The main algorithm is as follows: We maintain two windows of the two suffix arrays and the depth (length of the prefix) that we have aligned so far, If the characters at this depth from both sides of the current window match (for each window of the two suffix arrays), there is only one character to follow down in this window so we update the dynamic programming table and call search for depth+1, otherwise we simply divide the window (for which the characters from both sides at current depth do not match) in two equal windows and recursively find the matches on both halves. The window size will always remain greater than or equal to one.

The main search function

void

 sasearch (

int

 l1, 

int

 r1,
 

int

 l2, 

int

 r2, 

int

 depth);

recursively finds all approximate matches between two windows of the two suffix arrays ([l₁ … r₁] in the first suffix array and [l₂ … r₂] in the second) assuming the first “depth-1” characters in each window are the same. And the distance between the shared prefix of suffixes in first window and shared prefix of suffixes in the second window is stored in a global dynamic programming table like Figure 3.

Lemma 2

The number of calls to the recursive suffix array search function is at most log₂ n times the number of suffix trie nodes visited by recursive search algorithm, where n is the length of string.

Proof

let p be the number of nodes visited by the suffix trie recursive search algorithm. The key point is to note that each internal node of the suffix trie corresponds to a window [i_l … i_r] on the suffix array. So the p nodes of the suffix trie that contain every path from themselves to the root can only “cut” the suffix array in at most p positions. We need to bound the number of times to recursively cut the suffix array of length n in half that is needed to realize a partitioning of the suffix array in p given positions. (Note that we are free to e.g. continue cutting one half and leave the other half alone). Let us denote the number of cuts made by our recursive suffix array halving algorithm by g (n, p).

g(n, p) is bounded by the following recurrence (where p_r and p_l are two non-negative integers such that p_l + p_r ∈ {p, p − 1})

$$g(n,p)\le \{\begin{array}{ll}0,\hfill & n=1\text{or}p=0\hfill \\ g(\frac{n}{2},p_l)+g(\frac{n}{2},p_r)+1,\hfill & \text{otherwise}\hfill \end{array}$$

We will prove by induction that g(n, p) ≤ p log₂ n. Base case is trivial. For the induction step we have

$$\begin{array}{l}g(n,p)=g\left(\frac{n}{2},p_l\right)+g\left(\frac{n}{2},p_r\right)+1\\ \le p_l{log}_2\frac{n}{2}+p_r{log}_2\frac{n}{2}+1\\ =(p_1+p_r){log}_2\frac{n}{2}+1\le p{log}_2\frac{n}{2}+1\\ =p{log}_{2}n-p+1\\ \le p{log}_{2}n\end{array}$$

III. Experimental Results

To examine the practical applicability of this algorithm we have implemented this algorithm in C++. A key advantage of this algorithm is that it is very easy to implement. For example the “sasearch()” function mentioned is implemented in 50 lines of code and the whole seed searching program is less than 200 lines³. This is an experimental implementation of our algorithm and is not optimized for running time. All tests were run on a single core of a 64-bit Linux PC.

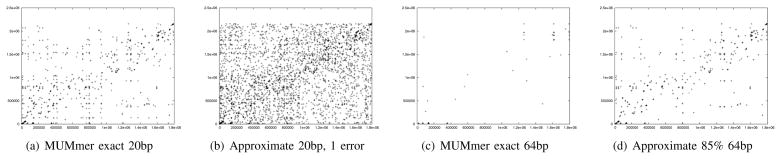
Figure 5 shows the dot plot results of running the algorithm on the full sequence of genomes of two bacterial organisms: Streptococcus pneumoniae and Streptococcus thermophilus, in comparison to the exact algorithm of MUMmer [5]. By default MUMmer finds exact matches of length 20 or longer between the two genomes, as can be seen in Figure 5(a). For comparison we have included approximate matches of length 20 with one error Figure 5(b). Note that the number of false positives increases significantly if we allow just one error in a 20 base pair match. To decrease the number of false positives one can of course increase the length of the match, an exact match of 64 bases is shown in Figure 5(c). It is clear that we have decreased sensitivity considerably by increasing the length of the match. Finally our algorithm which looks for approximate (85%) matches of length 64 bases is shown in Figure 5(d). It can be seen that our algorithm has simultaneously better sensitivity and better specificity than all variations above. Running time and memory usage for this test are shown in Figure 6.

Fig. 5.

Comparison with MUMmer exact seeds. Each + is a seed match at the corresponding coordinates in the genomes of Streptococcus pneumoniae (vertical, 2.5Mbp) and Streptococcus thermophilus (horizontal 1.8Mbp)

Fig. 6.

Comparison of resources used for two bacterial genomes.

To evaluate the quality of our seeds in a biological sense, we use the ROSETTA’s test set [3] (also used to validate LAGAN [4]), which contains 117 orthologous annotated genes with complete intron sequences from human and mouse. These sequences are of interest because they contain conserved coding regions from relatively distant genomes. Such regions are approximately similar overall but may not contain long exact seeds because of silent mutations among other differences. We simply concatenated the orthologous genes in the same order to make a long sequence of total length 602Kbp for human and 578Kbp for mouse. We compare our algorithm labeled SASearch (with different parameters) with MUMmer [6] and nucleotide-BLAST [2] exact seeds and PatternHunter [11] spaced seed as well as the improved spaced seeds suggested in [7]. Default MUMmer and BLAST seeds are exact matches of lengths 20 and 11 respectively. PatternHunter’s spaced seed is 111*1**1*1**11*111. Ilie et. al. suggest multiple spaced seeds and produce a set of 16 spaced seeds of weight (number of 1s in the seed) 11 as well as single spaced seed of weight up to 18. The single seed of weight 18 that we picked for comparison is 11111*1*11**111*11*11111.

The seeds found by each algorithm are evaluated using two criteria: exon-sensitivity and gene-specificity, which loosely capture the biological sensitivity and specificity of a set of seeds. Exon-sensitivity is the fraction of 465 human exons that will contain at least one seed. Gene-specificity is the fraction of seeds that connect only pairs of orthologous genes. (We calculate specificity at the gene level because we do not have a one-to-one correspondace between exons.) The results are shown in Table I.

TABLE I.

Comparison of different seed finding algorithms on DNA sequence of human and mouse genes. Columns are: ESn: Exon Sensitivity( $\frac{Ex}{465}$), GSp: Gene Specificity ( $\frac{OG}{OG+\mathit{NOG}}$), OG: Number of seeds that connect only true Orthologous Genes (true hits at gene level), NOG: Number of seeds that hit Non-Orthologous Genes (false hits at the gene level), Ex: Number of human exons (of 465) that contain at least one hit.

	ESn %	GSp %	OG	NOG	Ex (465)
PatternHunter spaced seed	99	14	35921	229914	462
BLAST 11bp exact seed	99	9	47918	487846	463
16 spaced seeds weight 11	100	6	165623	2689721	465
MUMmer 20bp exact	51	21	1285	4814	241
Spaced seed of weight 18	78	46	11324	13407	364
SASearch 60bp 85%	64	93	20902	1513	302
SASearch 40bp 80%	92	74	44079	15463	428
SASearch 30bp 70%	99	19	107386	459194	463

We observe that BLAST, PatternHunter and weight 11 spaced seeds are all very sensitive (for this data) but also have a very large number of false positives. Essentially they are so short (or low weight) that they hit at lots of positions by chance. Our inexact seeds of length 30 and with 70% similarity achieve the same sensitivity with a better specificity, because with our longer seed length random hits are less likely.

MUMmer exact seeds of length 20 and the single spaced seed of weight 18 (length 24) seem a better choice for these data. However they both miss a large fraction of exons. Our inexact seeds of length 40 with 80% similarity simultaneously achieve better sensitivity and specificity that both MUMmer seeds and single spaced seeds. This is due to the fact that our inexact seeds are longer and less similar and also allow for insertions and deletions in the seeds.

IV. Conclusion

For local alignment search there are many different tradeoffs: between specificity and sensitivity, sensitivity and running time, running time and memory, etc. Here we proposed an algorithm for constructing inexact alignment seeds and we show that our algorithm can have better sensitivity (than exact seeds based tools) and lower memory usage (than suffix trees based tools) for the cost of longer running time. The suffix array index we use can be build once and stored on external memory and reused while allowing for full flexibility in the choice of alignment parameters. We have, thus, shown that full flexibility in the choice of alignment seeds can be achieved without a significant penalty in terms of running time. The use of a substitution cost matrix makes our algorithm applicable to seeding protein alignments or for other “nonstandard” alignment tasks such as detecting cross hybridization of probes.