High-pressure EPR reveals conformational equilibria and volumetric properties of spin-labeled proteins

Abstract

Identifying equilibrium conformational exchange and characterizing conformational substates is essential for elucidating mechanisms of function in proteins. Site-directed spin labeling has previously been employed to detect conformational changes triggered by some event, but verifying conformational exchange at equilibrium is more challenging. Conformational exchange (microsecond–millisecond) is slow on the EPR time scale, and this proves to be an advantage in directly revealing the presence of multiple substates as distinguishable components in the EPR spectrum, allowing the direct determination of equilibrium constants and free energy differences. However, rotameric exchange of the spin label side chain can also give rise to multiple components in the EPR spectrum. Using spin-labeled mutants of T4 lysozyme, it is shown that high-pressure EPR can be used to: (i) demonstrate equilibrium between spectrally resolved states, (ii) aid in distinguishing conformational from rotameric exchange as the origin of the resolved states, and (iii) determine the relative partial molar volume (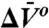) and isothermal compressibility (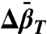) of conformational substates in two-component equilibria from the pressure dependence of the equilibrium constant. These volumetric properties provide insight into the structure of the substates. Finally, the pressure dependence of internal side-chain motion is interpreted in terms of volume fluctuations on the nanosecond time scale, the magnitude of which may reflect local backbone flexibility.

Proteins undergo structural fluctuations that span a wide range of time scales. Among these motions are fast backbone fluctuations on the picosecond–nanosecond time scale and slower conformational fluctuations on the microsecond and longer time scale (1–3). Molecular flexibility on these time scales plays a central role in protein function (4). For example, in recognition-binding sequences, dynamic disorder on the nanosecond–microsecond time scale may increase the rate of protein–protein interactions via a “fly casting” mechanism (5). An emerging disorder-to-order paradigm for interaction (6) can also give rise to promiscuity in binding that increases the size of the “interactome.”

Regulation of protein function is often linked to a conformational switch triggered by an interaction with a chemical or physical signal. One mechanistic interpretation of this event is provided by a “preequilibrium” model, which posits that all possible conformations of a protein exist at equilibrium with populations proportional to their relative energies (7). The exchange (“hopping”) event between different conformers is characterized by lifetimes in the microsecond–millisecond range (1, 2, 8). In this model, a conformational switch is viewed as a shift in the relative populations of existing conformational states rather than the creation of a new state.

To evaluate the above models and elucidate molecular mechanisms of protein function, it is essential to have experimental means for identifying dynamically disordered sequences and for characterizing conformational equilibria on a broad range of time scales. Solution NMR spectroscopy is well-established for this purpose (9, 10), but it is challenged for many systems of current interest, including intrinsic membrane proteins in their native lipid environment, and nonequilibrium systems that evolve in time. For such cases, site-directed spin labeling (SDSL) offers a promising experimental strategy (11–14).

In the usual implementation, SDSL employs the nitroxide side chain designated R1 (Fig. 1A). The EPR spectra of R1 in a protein directly reflect nitroxide motion on the picosecond–nanosecond time scale, which overlaps the time domain of fast backbone fluctuations. Hence, R1 is a direct observer of such motions and has been used to map sequence-specific backbone motion in soluble (15) and membrane-bound proteins (14, 16).

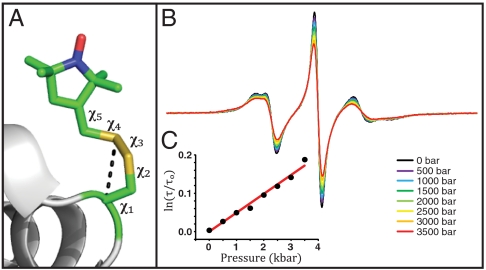
Fig. 1.

T4L 82R1. (A) Model of the R1 side chain in 82R1 based on the crystal structure [Protein Data Bank (PDB) ID code 1ZYT]. The bond numbering is indicated, and the dotted line identifies a noncovalent interaction (S_δ·HC_α) common to solvent-exposed R1 residues. This interaction constrains the internal motion of the side chain largely to torsional oscillations about the two terminal dihedral angles χ₄ and χ₅ (the χ₄/χ₅ model) (24, 26). (B) Pressure dependence of the EPR spectra normalized to the same number of spins. (C) The nitroxide τ determined from fits to the spectra is plotted as indicated vs. pressure (dots); the solid line is a fit to Eq. 3.

An important consequence of the EPR time scale is that although fast backbone motions are directly reflected in the EPR spectra, conformational exchange on the microsecond–millisecond and longer time scales is too slow to produce relaxation effects that are reflected in the lineshape; at X-band, exchange between species with lifetimes > 100 ns is in the slow exchange limit. Instead, the presence of two conformations in equilibrium will, for particular locations of R1, give rise to two components in the EPR spectrum, each corresponding to one of the conformations (17, 18) and of intensity proportional to the population, permitting the direct determination of the equilibrium constant. However, two-component EPR spectra can also arise from equilibrium between two rotameric states of R1 that place the nitroxide in distinct environments (19, 20). In this report, high-pressure SDSL-EPR is introduced as a means for distinguishing conformational and rotameric exchange as the origin of two-component EPR spectra and for providing quantitative volumetric information on conformational substates in equilibrium.

For equilibrium between two states of a system, the pressure-dependent equilibrium constant K(P) relative to that at atmospheric pressure (1 bar) is given to second order in pressure by

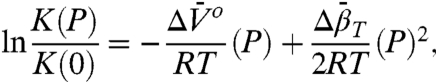[1]

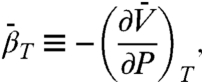[2]

where P is the gauge pressure; K(P) and K(0) are the equilibrium constants at pressures P and P = 0, respectively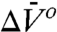; and and 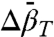are the differences in partial molar volume and partial molar isothermal compressibility of the two states, respectively, at the reference pressure and temperature (P = 1 bar and T = 294 K). According to Eq. 1, application of pressure will produce a reversible shift in the relative populations of states, and this provides an important test for true equilibrium between states detected in an EPR spectrum.

In pioneering NMR studies of high-pressure effects on proteins, Akasaka has demonstrated that the application of pressure can indeed shift the relative populations of conformational substates in equilibrium. His findings were summarized in an empirical “volume theorem,” which states that “volume parallels conformational order” (21). This is of practical interest, because low-lying excited states, which are spectroscopically “invisible” because of their low populations, have reduced conformational order compared to the ground state (22). According to the theorem, excited states have lower molar volumes, and Eq. 1 predicts that the application of pressure will populate such states, which may be intimately involved in function. Thus, pressure provides a simple and elegant means to populate excited states for study by spectroscopic techniques.

The above considerations provide a motivation for use of high pressure in SDSL. In this initial study, the effect of pressure, as viewed by an R1 spin label, is investigated using T4 lysozyme (T4L) and destabilized mutants thereof as simple model systems. The results reveal three classes of behavior reported by R1 due to a pressure change: (i) site-dependent changes in the internal dynamics of R1 that can be described by an activation volume, (ii) shifts in rotameric equilibria of R1 for which ln K(P) is linear in pressure, and (iii) shifts in protein conformational equilibria where ln K(P) is nonlinear in pressure. For the latter two, the behavior is described by Eq. 1. Hence,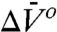 and 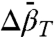can be determined from experimental values of K(P). The linear pressure dependence of rotameric equilibria indicates that 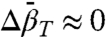, suggesting a simple means for distinguishing rotameric equilibria of R1 from conformational exchange, where in general .

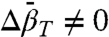Results

The sections below illustrate the three classes of pressure-dependent behavior identified. In all cases, the effect of pressure is completely and quantitatively reversible. Dynamic parameters for the nitroxide as a function of pressure (namely, the order parameter S and effective correlation time τ for anisotropic motion) are obtained from fits of the spectra to a microscopic order macroscopic disorder (MOMD) model (Methods). In the case of two-component EPR spectra, corresponding to two states of the spin label, the populations and apparent equilibrium constant K(P) are also determined from the MOMD fits. In each case, the fits are provided in SI Text.

Pressure Modulates the Motion of R1 at Solvent-Exposed Sites.

The internal motion and EPR spectra of R1 in proteins are reasonably well understood through complementary studies from crystallography (19, 20, 23, 24), mutagenesis (19, 20, 23), and spectral analysis (25, 26). One outcome of these studies has been a model for the structure and internal motion of the R1 side chain at sites where the nitroxide does not interact with neighboring residues. In this “χ₄/χ₅” model, the motion is constrained and anisotropic because of backbone interactions (Fig. 1A), giving rise to an EPR spectrum that can be characterized by an order parameter S and effective correlation time τ, the latter of which is typically 1–3 ns (26).

To investigate the effect of pressure on the internal motion of R1, sites in T4L were selected where R1 has a known crystal structure and an EPR spectrum consistent with the simple model of Fig. 1A; 82R1 serves as an example (Fig. 1). The crystal structure reveals the typical sulfur/backbone interaction with no evidence of nitroxide interactions with neighboring residues, and the crystallographic B factors of the backbone are low (23). The EPR spectrum at atmospheric pressure (Fig. 1B, black trace) can be fit with a model of anisotropic motion with S = 0.36, τ = 1.5 ns, similar to the extensively characterized internal motion of 72R1 (26). We tentatively assume that the motion of 82R1 represents predominantly internal R1 motion.

The pressure-dependent EPR spectra of 82R1 (Fig. 1B) are well fit by a model with fixed S and τ increasing with pressure. Apparently, the increase in τ with pressure does not simply reflect viscosity increases of the bulk solvent; at 20 °C, the relative viscosity of water actually decreases slightly with pressure at low pressure (P ≤ 1 kbar) and increases by approximately 15% at 4 kbar (27). In addition, replacing water by D₂O (viscosity 25% greater than water) (SI Text) or increasing the viscosity by a factor of 3 with sucrose has no effect on R1 internal motion (18).

According to activated state theories, the pressure dependence of τ is given by

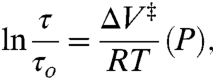[3]

where τ and τ_o are the rotational correlation times at gauge pressures P and P = 0, respectively, and ΔV^‡ is a volume of activation that corresponds to an increase in volume of a solvent cage necessary to permit the rotation of the nitroxide (28, 29). A plot of ln[τ/τ_o] versus pressure is linear (Fig. 1C), and the slope gives a value of 1.2 ± 0.5 mL/mol for ΔV^‡ at 294 K.

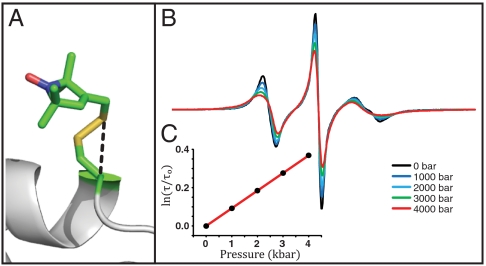
Another site of known crystal structure where the EPR spectrum reflects simple anisotropic motion is 80R1 (Fig. 2A) (24). Simulation of the EPR spectrum for 80R1 gives S = 0.17, τ = 1.0 ns at atmospheric pressure. The pressure-dependent EPR spectra (Fig. 2B) can be fit with a constant S and variable τ, as is the case for 82R1. A plot of ln[τ/τ_o] versus pressure is again linear, and the slope corresponds to ΔV^‡ = 2.3 ± 0.4 mL/mol at 294 K (Fig. 2C). Interpretation of the activation volumes for these sites will be considered in Discussion.

Fig. 2.

T4L 80R1. (A) Model of the R1 side chain in 80R1 based on the crystal structure (24). (B) Pressure dependence of the EPR spectra normalized to the same number of spins. (C) The nitroxide τ determined from fits to the spectra is plotted as indicated vs. pressure.

ln K(P) Is Linear in Pressure for the Equilibrium Between R1 Rotamers in 44R1.

The EPR spectra of R1 residues on the solvent-exposed surface of a rigid protein often have two components reflecting a relatively mobile (m) and immobile state (i) due to coexistence of two rotamers of R1; one such site is 44R1 in the B helix of T4L. The crystal structure and modeling suggest that equilibrium between two rotamers about χ₄ gives rise to the two spectral components, where the i state arises from an interaction of the nitroxide ring with glutamate residue E45 in the helix (Fig. 3A) (19). This conclusion was supported by a dramatic reduction in the amplitude of the i component in the spectrum of the 44R1/E45A mutant, which consist largely of the m component (19).

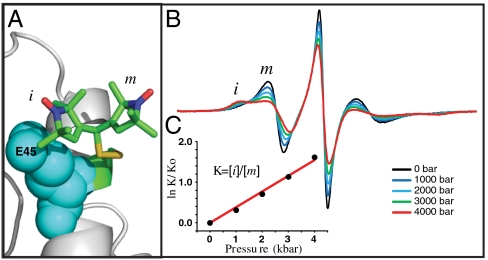
Fig. 3.

T4L 44R1. (A) Model of the R1 side chain in 44R1 based on the crystal structure (PDB ID code 2Q9E). The presence of the two rotamers is inferred from mutagenesis data (see text). (B) Pressure dependence of the EPR spectra normalized to the same number of spins. (C) The equilibrium constant determined from fits to the spectra is plotted as indicated vs. pressure (dots); the solid line is a fit to Eq. 1.

The dependence of the EPR spectra of 44R1 on pressure is striking (Fig. 3B). Fits of the spectra to a two-state model of R1 show that the changes can be accounted for by a shift in the relative populations of two states. From the populations obtained from the fits, the apparent equilibrium constant, K(P) = [i]/[m] was determined. The mutant 44R1/E45A was also studied to obtain a set of spectra corresponding to the pressure dependence of a nearly pure m state, which could then be subtracted from the spectra of 44R1 at the same pressure to provide the relative populations and K(P) without invoking spectral simulations. The results of this strategy are in reasonable agreement with K(P) determined by simulations (SI Text).

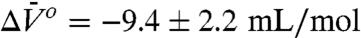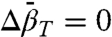A plot of the experimental values of ln[K(P)/K(0)] versus P is shown in Fig. 3C along with a fit to Eq. 1 that gives and . Apparently, pressure favors the interaction with the neighboring glutamate residue because of a smaller molar volume of the complex.

The correlation times of the individual m and i states also depend on pressure, as expected from the results of 80R1 and 82R1 presented above. The plot of ln[τ/τ_o] versus pressure for the exposed m state is linear (SI Text) and gives ΔV^‡ = 1.7 ± 0.4 mL/mol. Similar analysis for the immobilized state is not given because the motion of this state has significant contributions from protein rotary diffusion.

ln K(P) Is Nonlinear in Pressure for Conformational Equilibria in Destabilized Mutants of T4L.

T4L is exploited as a model system in development of SDSL technology because of the extensive data base of WT and mutant crystal structures, including many bearing the R1 side chain (19, 20, 23, 24), as well as solution NMR (30–32) and hydrogen exchange data (33–35). The enzyme consists of two independently folding subdomains (N and C). Based on hydrogen exchange, crystallographic B factors and NMR data, the individual domains in the WT protein each have only a single conformation with significant population, although a hinge-bending motion relates the relative position of the two subdomains (36).

In destabilized mutants of T4L, the subdomains can adopt additional conformations, and such mutants have provided valuable models for exploring conformational equilibria (31, 32). This approach was adopted here to explore the pressure response of conformational equilibria as detected by SDSL. For this purpose, T4L was specifically destabilized by introducing R1 at a partially buried site (118R1) in combination with urea and at a completely buried (46R1) site in a short helix.

118R1.

The crystal structure of 118R1 shows the R1 side chain to be partially buried in the hydrophobic interior of the four-helix bundle that constitutes the core of the C domain (20). The helix bundle has a near-native fold, but a short helix F (1.5 turn) that connects two helices of the bundle is unfolded (Fig. 4A). As anticipated from the partially buried location of R1, the EPR spectrum of the mutant reflects immobilization of the nitroxide (Fig. 4B, black trace). Application of pressure to 4 kbar produces small spectral changes (Fig. 4B) attributable in part to an increase in viscosity under pressure that slows protein rotary diffusion (SI Text). It should be noted that changes in protein rotary diffusion will contribute to the effective nitroxide correlation time for strongly immobilized states of R1 like 118R1, but not for more mobile states like 80R1 and 82R1 or the mobile component of 44R1 considered above (18).

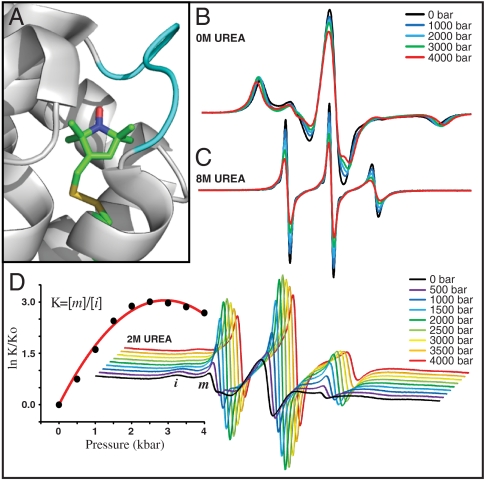
Fig. 4.

T4L 118R1. (A) Model of the R1 side chain in 118R1 based on the crystal structure (PDB ID code 2NTH); an unfolded short helix F is indicated in cyan. (B) The pressure dependence of the EPR spectra in buffer (20 mM MES, pH 6.8). (C) Pressure-dependent EPR spectra in 8 M urea in buffer. (D Right) Pressure dependence of EPR spectra in 2 M urea in buffer. (D Left) The equilibrium constant determined from fits to the spectra is plotted as indicated vs. pressure. In all cases, the EPR spectra are normalized to the same number of spins.

The equilibrium urea denaturation curve for 118R1 determined with CD follows a two-state model N(native)⇌U(unfolded) with a midpoint at 3.6 M urea; denaturation is complete at [urea] > 5 M (SI Text). The mutant is destabilized by approximately 1.5 kcal/mol relative to the WT*. The EPR spectrum of the U state in 8 M urea at atmospheric pressure is characteristic of a polypeptide disordered on the nanosecond time scale (Fig. 4C, black trace). Application of pressure increases the nitroxide correlation time and the center line width (Fig. 4C); a plot of ln[τ/τ_o] versus pressure is linear with ΔV^‡ = 4.2 ± 0.5 mL/mol (SI Text), nearly four times larger than that for simple internal motion of R1 determined for 82R1 (Fig. 1C). Increases in viscosity of the urea solution do not contribute significantly to increases in correlation time with increasing pressure. At most, the urea concentration increases by approximately 14% at 4 kbar because of solvent compression, causing an increase in relative viscosity of only approximately 8% (37), and this is too small to produce the observed effects.

In 2 M urea at atmospheric pressure, the N⇌U equilibrium is observed in the EPR spectrum, as evidenced by the presence of a highly mobile component (m) that amounts to approximately 4% of the population (Fig. 4D, black trace). This provides a very simple example of a conformational equilibrium. The pressure dependence of the EPR spectra is shown in Fig. 4D Right. A plot of ln[K(P)/K(0)], where K(P) = [m]/[i], is strongly nonlinear in pressure (Fig. 4D Left). A fit of the data to Eq. 1 gives 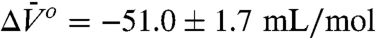and .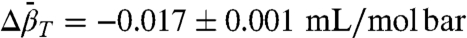

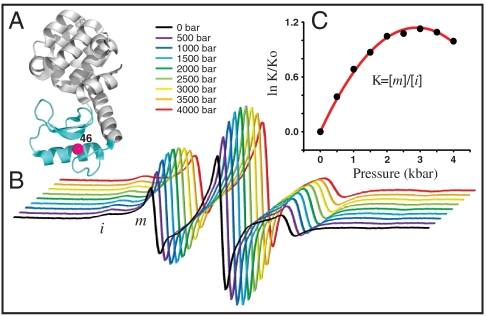
46R1.

Residue L46 is located at buried site in the B helix of the N domain (Fig. 5A), and R1 would be expected to be immobilized in the native fold, with a spectrum similar to that of 118R1. However, at atmospheric pressure the EPR spectrum of 46R1 (Fig. 5B, black trace) (19) reveals a sharp mobile component (m) in addition to the expected strongly immobilized state (i). It has been previously shown that the m and i states in 46R1 originate from two conformations of the protein as opposed to two rotamers of R1 (17). Given the narrow spectral lines, the m state undoubtedly arises from a conformer that is, at least, locally unfolded in equilibrium with a native-like state.

Fig. 5.

T4L46R1. (A) Ribbon diagram of T4L (PDB ID code 3LZM) showing the location of residue L46. (B) The pressure dependence of the EPR spectra normalized to the same number of spins. (C) The equilibrium constant determined from fits to the spectra is plotted as indicated vs. pressure (dots); the solid line is a fit to Eq. 1.

The pressure dependencies of the EPR spectra and K(P) = [m]/[i] for 46R1 are shown in Fig. 5 B and C. As for 118R1, the plot of ln[K(P)/K(0)] versus pressure is strikingly nonlinear; a fit of the data to Eq. 1 gives 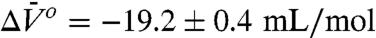and 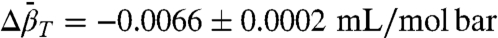. The much smaller 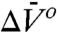compared to that of 118R1 suggests that the equilibrium observed is not that for the N⇌U equilibrium, but rather an N⇌I equilibrium, where I is an intermediate with incomplete unfolding. It is known that the stability of the N subdomain is lower than that for the C subdomain (38) and that intermediate folding states (I) exist for T4L in which the N and C terminal subdomains are unfolded and folded, respectively (30, 33, 38, 39). The broad transition region of the CD-detected urea denaturation curve of 46R1 also suggests a partially unfolded intermediate state (SI Text). A model consistent with the data for the equilibrium in 46R1 is N⇌I, where I has a folded and unfolded C and N domain, respectively. However, the conclusions of this communication do not depend on this model.

Discussion

Variable Pressure SDSL as a Potential Tool for Investigating Local Backbone and Side Chain Dynamics.

For noninteracting states of R1 on the protein surface, the pressure dependence of the nitroxide τ provides a volume of activation for rotational diffusion defined by 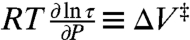. For convenience, ΔV^‡ is interpreted in terms of the transition state theory as the increase in volume of the surrounding solvent cage in the transition state necessary for a rotational diffusive step; this is appropriate for completely solvent-exposed, noninteracting nitroxides. The volume of activation scales with the size of the kinetic unit (28, 29), and ΔV^‡ estimated from EPR data on R1 should provide at least qualitative information on the size of the kinetic unit moving on the nanosecond time scale. For example, the larger ΔV^‡ for 80R1 relative to 82R1 could be due to contributions of backbone motions in the former, which resides in a loop. The largest ΔV^‡ (4.2 mL/mol) was observed for 118R1 in the urea denatured state of T4L. This is consistent with a larger volume of the kinetic unit, which includes a segment of the polypeptide chain. Note that if two independent modes (i.e., R1 motions and backbone fluctuations) with substantially different values of ΔV^‡ contribute to the motion, the ln[τ/τ_o] plot may show curvature.

Distinguishing Rotameric and Conformational Equilibria as the Origin of Two-Component EPR Spectra.

EPR spectra of R1 in proteins are more often than not two-component at the level of resolution of X-band EPR. One important use of high pressure is to demonstrate equilibrium between the states represented by the components via reversible shifts in the populations. For states in equilibrium, the origin of the spectral components can be traced to slow exchange between two rotamers of R1 or between two conformational substates of the protein (17, 18). In either case, the apparent equilibrium constant K(P) is pressure dependent and adheres in general to Eq. 1. Site 44R1 provides an example where two spectral components apparently arise from equilibrium between two rotamers, one in which the nitroxide is immobilized by an interaction with a neighboring residue in the helix (Fig. 3B); in the absence of this interaction, the two rotamers would not be distinguished in the EPR spectrum. One would expect that the compressibility would differ little between the two states, and this is indeed the case, as shown by the linear dependence of ln[K(P)/K(0)] on pressure (Fig. 3C). The 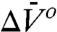of -9.4 mL/mol is on the same order as that for formation of an internal complex in flexible flavinyltryptophan peptides (40), and pressure-driven interaction of surface side chains has been previously observed in NMR (41).

Site 44R1 provides the simplest example of this behavior as the interaction driven by pressure is between the spin label and a residue on the same helix. A more complex behavior could result if the spin label interacts through tertiary contact between different secondary elements where one of them can rearrange under pressure (i.e., has a high compressibility). Such cases will be examined in future work. Nevertheless, linearity of ln[K(P)/K(0)] versus pressure provides one criterion to distinguish rotameric from conformational equilibria and complements other strategies recently developed for this purpose (17, 18).

Manipulating Populations of Protein Conformational Substates and Measuring Compressibility Differences.

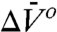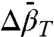In general, conformational equilibria are characterized by nonzero values of and , and the populations can be manipulated by pressure. The data of Figs. 4 and 5 clearly reveal this to be the case for the simple examples of N⇌U (118R1 in 2 M urea) and N⇌I equilibria (46R1). At low pressures, the equilibria are reversibly shifted to the more disordered state, in accordance with the volume theorem (21). The 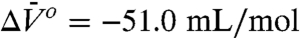for 118R1 falls within the range of negative values found for N → U transitions for proteins of similar size (42); the smaller value of -19.2 mL/mol for the N⇌I equilibrium is consistent with the smaller size of the unfolding unit (the small N terminal domain vs. the entire protein).

At higher pressures, the striking convex curvature of the ln[K(P)/K(0)] plots (Figs. 4D and 5C) reveals a negative 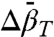in each case; the extrema occur at 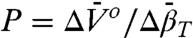, approximately 2.9 kbar for 46R1 and approximately 3 kbar for 118R1. The magnitude and sign of 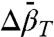for partial and complete unfolding of proteins is still a matter of debate, even for proteins of similar size, and likely depends on individual cases (42). Nevertheless, the negative signs of 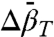found for the N⇌U and N⇌I equilibria are in agreement with those predicted for 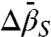(adiabatic compressibility) (43), which is similar to 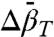near room temperature (44).

Analysis of pressure-dependent fluorescence data on protein equilibria generally assumes that 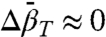(42); hence, reported values are sparse. However, it has been found that detecting nonzero values of 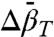may be problematic with fluorescence data, and analysis under the assumption of 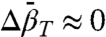may substantially influence determined values of 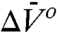(45). With SDSL data, determination of even small values of 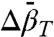, such as those measured here, are straightforward.

Summary and Future Applications.

For R1 at solvent-exposed sites, the activation volume may reflect contributions from backbone motion on the nanosecond time scale. If future studies support this proposal, variable pressure SDSL-EPR will complement lineshape analysis to identify local backbone flexibility (14, 15). Because motion about different bonds in the side chain may have different activation volumes, pressure may also provide a strategy to investigate details of R1 internal motion.

The time scale of the EPR experiment allows direct determination of pressure-dependent equilibrium constants K(P) for both R1 rotamer and protein conformational equilibria. The pressure dependence of K(P) can distinguish rotamer from conformational exchange in favorable cases; ambiguities that arise may be resolved with osmotic perturbation (18) and saturation recovery (17) methods recently introduced for SDSL. Together, these methods offer an experimental strategy to map sites of conformational exchange in proteins with SDSL.

Analysis of K(P) data for two-state equilibria provides experimental values of 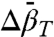that correspond to local changes in conformation. This is of particular interest for exchange between globular states where 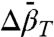is proportional to the difference in mean-square volume fluctuations according to 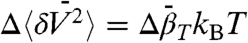, where k_B is the Boltzmann constant (46). Thus, variable pressure SDSL-EPR can provide sequence-specific data on local volume fluctuations in conformational substates.

The ability of pressure to shift populations of conformational substates according to the volume theorem leads to two interesting applications. First, pressure can be used to increase the population of “excited” (22) or “invisible” (31) substates to levels amenable to study using traditional SDSL methods. Second, a pressure-jump experiment monitored by EPR can measure exchange events with characteristic times longer than about 100 μs, limited by the field modulation frequency used in commercial EPR spectrometers. Currently, exchange measurements with EPR lie in the range of nanoseconds to about 70 μs (17), so pressure jump would extend the accessible time domain from nanoseconds to milliseconds and beyond.

Methods

Cloning, Expression, Purification and Spin Labeling of T4L mutants.

Single cysteine mutations were engineered into a pseudo wild-type T4L background (WT*) in which the two native Cys residues are replaced (C54T/C97A) (47, 48). Mutations were engineered into chosen sites, expressed, and purified as previously described (26, 49). Spin labeling of single cysteine mutants was performed in spin-labeling buffer (50 mM MOPS, 25 mM NaCl at pH 6.8) as previously described (49). After spin labeling, samples were transferred to 20 mM MES buffer (pH 6.8), chosen because it has little pH dependence in the pressure range employed here (50). Desired sample concentrations were obtained using Microcon filter concentrators (Millipore) with a 10 kDa cutoff. Final protein concentrations measured by absorption at 280 nm (ε = 23,327 L mol^-1 cm^-1) and were typically in the range of 250 to 700 μM.

Hydrostatic Pressure Generation

A high-pressure cell was adapted for EPR from the NMR cell design of Yonker and coworkers (51). Sample cells were constructed from lengths of polytetrafluoroethylene-coated fused silica capillary (100-μm i.d. × 360-μm o.d.) obtained commercially (Polymicro Technology). Details are shown in SI Text.

Pressure was generated with either a hand-operated syringe pump (High-Pressure Equipment Model 37-5.75-60) rated at 60 kpsi (4.14 kbar) or with an automated intensifier (Pressure BioSciences Model HUB440) rated at 55 kpsi (3.79 kbar). Water or 20 mM MES buffer were used as a pressure transmitting fluid. Pressures were measured using a transducer from Precise Sensors, Inc., connected in-line with the pump and the sample cell.

EPR Spectroscopy, Spectral Simulations, and Estimation of K.

EPR spectroscopy was carried out at X-band on a BrukerEleXsys 580 fitted with the High Sensitivity cavity. All spectra were recorded at room temperature (294 K) with an incident microwave power of 7 mW. Data at atmospheric pressure was taken before and after the application of pressure to demonstrate reversibility.

Experimental spectra were fit to an MOMD model using a Labview™ interface (available upon request, caltenba@ucla.edu) of the program NLSL developed by Freed and coworkers (52, 53). Strategies employed for simulation of spectra for R1 in proteins have been extensively discussed (26, 52, 54) and are reviewed in SI Text along with parameters and overlays of spectral simulations obtained for this work.

It has been previously reported that acceptable MOMD fits (χ² < 10^-5) are typically acquired with an uncertainty in the order parameter S and correlation time τ of approximately ± 6 and ± 15%, respectively (26). These values were used to estimate the error in the derived equilibrium constant K(P) for MOMD fits of two-component EPR spectra and hence the error in the reported partial molar volume and isothermal compressibility changes. In order to ensure that motion between the two domains of T4L was not the source for the observed pressure response, spin-labeled mutants were also engineered into a cross-linked (21C/142C) derivative of T4L that locks the domains in the closed configuration (47). Comparison of the spectra of the spin-labeled mutant 44R1 in both the WT* and cross-linked background were similar at all pressures (SI Text).

Samples for high pressure contained either sucrose or Ficoll-70 at final concentrations of 30% wt/vol or 25% wt/vol, respectively, to reduce the effect of protein rotational diffusion on the EPR spectra. These concentrations have been previously determined to give the same microscopic viscosity with respect to T4L rotational diffusion (18). Under pressure, the viscosity increase for Ficoll and sucrose solutions due to solvent compression (approximately 12% volume decrease) is identical and as expected (SI Text). This effect works as an advantage in further removing overall rotary diffusion effects from the EPR spectra.