Abstract
Carbon dioxide may react with free or metal-bound hydroxide to afford products containing bicarbonate or carbonate, often captured as ligands bridging two or three metal sites. We report the kinetics and probable mechanism of an extremely rapid fixation reaction mediated by a planar nickel complex [NiII(NNN)(OH)]1- containing a tridentate 2,6-pyridinedicarboxamidate pincer ligand and a terminal hydroxide ligand. The minimal generalized reaction is M-OH + CO2 → M-OCO2H; with variant M, previous rate constants are ≲103 M-1 s-1 in aqueous solution. For the present bimolecular reaction, the (extrapolated) rate constant is 9.5 × 105 M-1 s-1 in N,N′-dimethylformamide at 298 K, a value within the range of kcat/KM≈105–108 M-1 s-1 for carbonic anhydrase, the most efficient catalyst of CO2 fixation reactions. The enthalpy profile of the fixation reaction was calculated by density functional theory. The initial event is the formation of a weak precursor complex between the Ni-OH group and CO2, followed by insertion of a CO2 oxygen atom into the Ni-OH bond to generate a four center Ni(η2-OCO2H) transition state similar to that at the zinc site in carbonic anhydrase. Thereafter, the Ni-OH bond detaches to afford the Ni(η1-OCO2H) fragment, after which the molecule passes through a second, lower energy transition state as the bicarbonate ligand rearranges to a conformation very similar to that in the crystalline product. Theoretical values of metric parameters and activation enthalpy are in good agreement with experimental values [ΔH‡ = 3.2(5) kcal/mol].
Keywords: nickel hydroxide, carbon dioxide–bicarbonate conversion, reaction mechanism
Recent research in this laboratory has been directed toward the attainment of synthetic analogues of the NiFe3S4 active site of the enzyme carbon monoxide dehydrogenase (1, 2), which catalyzes the interconversion reaction CO2 + 2H+ + 2e-⇌CO + H2O. In the course of this work, we have prepared binuclear NiII/FeII bridged species with the intention of simulating the Ni…Fe component of the enzyme site that is the locus of substrate binding, activation, and product release (3). The nickel site in the binuclear species has been prepared separately in the form of the planar hydroxide complex 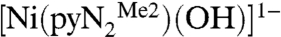 containing a N,N′-2,6-dimethylphenyl-2,6-pyridinedicarboxamidate dianion. Whereas bridging hydroxide ligation is common, terminal binding is not and in general is stabilized in divalent metal complexes by hydrogen bonding or by steric shielding, as is the case here. As reported recently (3), exposure of a solution of
containing a N,N′-2,6-dimethylphenyl-2,6-pyridinedicarboxamidate dianion. Whereas bridging hydroxide ligation is common, terminal binding is not and in general is stabilized in divalent metal complexes by hydrogen bonding or by steric shielding, as is the case here. As reported recently (3), exposure of a solution of 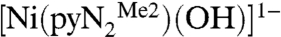 to the atmosphere results in an instantaneous color change from red to red–orange. This results in the fixation of CO2 as the bicarbonate complex
to the atmosphere results in an instantaneous color change from red to red–orange. This results in the fixation of CO2 as the bicarbonate complex 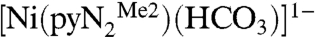 accompanied by the spectral changes in Fig. 1.
accompanied by the spectral changes in Fig. 1.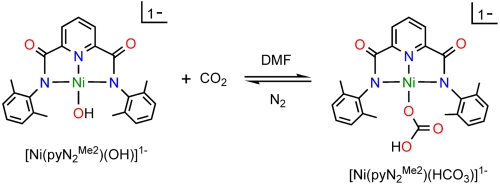
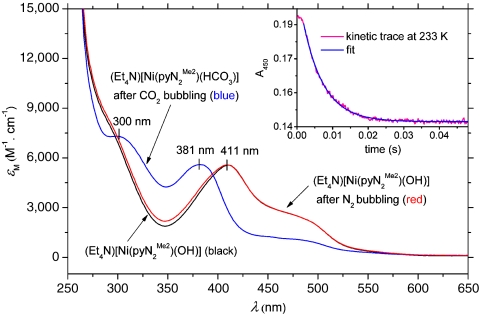
Fig. 1.
Absorption spectra in DMF: black trace—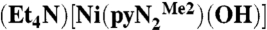 ; blue trace—after bubbling CO2 through the solution for 2 min; red trace—after vigorous bubbling of N2 through the solution of
; blue trace—after bubbling CO2 through the solution for 2 min; red trace—after vigorous bubbling of N2 through the solution of 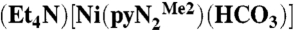 (blue trace) for 20 min. (Inset) Kinetics trace acquired at 450 nm and 233 K overlaid with a single exponential fit to A = A∞ + ΔA exp(-kobst), where A∞ is the absorbance after complete reaction, ΔA = A0 - A∞, A0 is the initial absorbance, and kobs is the observed rate constant. Reactant concentrations:
(blue trace) for 20 min. (Inset) Kinetics trace acquired at 450 nm and 233 K overlaid with a single exponential fit to A = A∞ + ΔA exp(-kobst), where A∞ is the absorbance after complete reaction, ΔA = A0 - A∞, A0 is the initial absorbance, and kobs is the observed rate constant. Reactant concentrations: 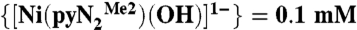 , [CO2] = 1 mM.
, [CO2] = 1 mM.
Several features of the CO2 fixation reaction 1 are noteworthy. The reactant is a terminal hydroxide species affording a unidentate bicarbonate (η1-OCO2H) product. Far more common is the reaction of bridged 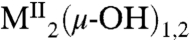 precursors to afford binuclear or occasional trinuclear products bridged by carbonate utilizing two or three oxygen atoms (4–9). A second feature is the apparently fast reaction rate, given that CO2 comprises only 0.039 vol % of the atmosphere. Although fixation of atmospheric CO2 by metal hydroxide species has been previously observed (4, 5, 7, 10), including with NiII (7, 11–13), no quantitation of reaction rates and analysis of reaction mechanism are available. The fixation of carbon dioxide, whereby this greenhouse gas is rendered in chemically combined forms, is of current environmental and biological interest. Fixation leads to utilization of the compound as a renewable carbon resource in the formation of useful organic compounds, ideally in catalytically efficient systems (14, 15). Atmospheric capture of CO2 allows its sequestration by various methods including conversion to metal carbonates (16). In biology, the ubiquitous Zn(II) enzyme carbonic anhydrase catalyzes the reversible hydration reaction
precursors to afford binuclear or occasional trinuclear products bridged by carbonate utilizing two or three oxygen atoms (4–9). A second feature is the apparently fast reaction rate, given that CO2 comprises only 0.039 vol % of the atmosphere. Although fixation of atmospheric CO2 by metal hydroxide species has been previously observed (4, 5, 7, 10), including with NiII (7, 11–13), no quantitation of reaction rates and analysis of reaction mechanism are available. The fixation of carbon dioxide, whereby this greenhouse gas is rendered in chemically combined forms, is of current environmental and biological interest. Fixation leads to utilization of the compound as a renewable carbon resource in the formation of useful organic compounds, ideally in catalytically efficient systems (14, 15). Atmospheric capture of CO2 allows its sequestration by various methods including conversion to metal carbonates (16). In biology, the ubiquitous Zn(II) enzyme carbonic anhydrase catalyzes the reversible hydration reaction 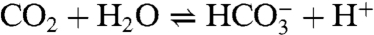 , which among other functions leads to the removal of CO2 from tissues in the mammalian respiratory process. Given the foregoing factors, we have determined the kinetics of reaction 1 and examined its mechanism with the aid of theoretical calculations.
, which among other functions leads to the removal of CO2 from tissues in the mammalian respiratory process. Given the foregoing factors, we have determined the kinetics of reaction 1 and examined its mechanism with the aid of theoretical calculations.
Results and Discussion
Kinetics of CO2 Fixation.
The kinetics of reaction 1 were determined in dimethylformamide (DMF) solutions by stopped-flow spectrophotometry at 218–243 K. As seen in Fig. 1, the absorption spectrum of 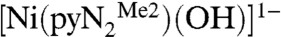 contains a peak at 411 nm and a shoulder near 490 nm, whereas the product
contains a peak at 411 nm and a shoulder near 490 nm, whereas the product 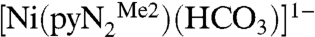 presents maxima at 300 and 381 nm. The reaction was followed by absorbance changes at 450 nm under conditions of variable and constant CO2 concentrations (≥10-fold excess of CO2 with respect to Ni). In treating the low-temperature absorbance data, no evidence of a preequilibrium was found. A typical single exponential fit of the data (233 K) in the presence of a 10-fold excess of CO2 is included as an inset, from which the pseudo-first-order rate constant kobs can be evaluated. The influence of water on the reaction rate was investigated under the conditions of Table 1. The possibility that CO2 is hydrated by small amounts of water in DMF by the reaction
presents maxima at 300 and 381 nm. The reaction was followed by absorbance changes at 450 nm under conditions of variable and constant CO2 concentrations (≥10-fold excess of CO2 with respect to Ni). In treating the low-temperature absorbance data, no evidence of a preequilibrium was found. A typical single exponential fit of the data (233 K) in the presence of a 10-fold excess of CO2 is included as an inset, from which the pseudo-first-order rate constant kobs can be evaluated. The influence of water on the reaction rate was investigated under the conditions of Table 1. The possibility that CO2 is hydrated by small amounts of water in DMF by the reaction 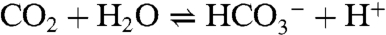 and that bicarbonate reacts with
and that bicarbonate reacts with 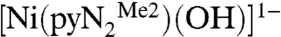 to form a carbonate complex and water appears remote. This situation has been encountered in CuII/CO2 systems in acetonitrile, resulting in formation of a dinuclear carbonato complex (8). There is no significant effect on kobs up to a mol ratio H2O/NiII ≈ 1600∶1. Further, the reaction product isolated is definitely a monoanionic bicarbonate complex (3). We conclude that our kinetics results are unaffected by the presence of small amounts of water.
to form a carbonate complex and water appears remote. This situation has been encountered in CuII/CO2 systems in acetonitrile, resulting in formation of a dinuclear carbonato complex (8). There is no significant effect on kobs up to a mol ratio H2O/NiII ≈ 1600∶1. Further, the reaction product isolated is definitely a monoanionic bicarbonate complex (3). We conclude that our kinetics results are unaffected by the presence of small amounts of water.
Table 1.
Observed rate constants as a function of water content in DMF
| Water, equiv vs NiII | kobs, s-1 |
| 0 | 88.2 |
| 800 | 82.4 |
| 1600 | 72.6 |
| 3200 | 49.7 |
Kinetics traces at 450 nm and 218 K were fitted to the single exponential A = A∞ + ΔA exp(-kt) defined in Fig. 1. Concentration of reactants: 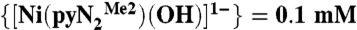 , [CO2] = 1.0 mM. Each kobs is the average of eight runs.
, [CO2] = 1.0 mM. Each kobs is the average of eight runs.
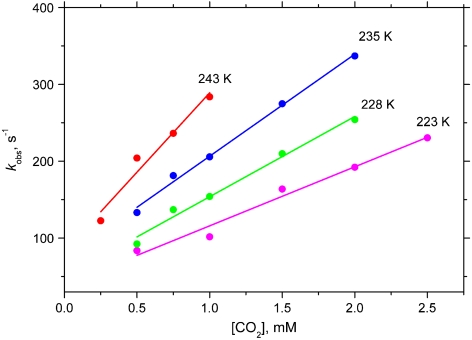
Values of kobs vary linearly with CO2 concentration at constant NiII concentration, as shown for four temperatures in Fig. 2, establishing that the reaction is first-order in CO2 concentration. The reaction is first-order in NiII as follows from the exponential shapes of the kinetics traces in the presence of excess CO2. Also, values of kobs determined from the kinetic traces do not depend on NiII concentration. Consequently, for reaction 1, 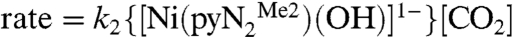 . A full set of kobs and k2 data is available (SI Text). Second-order rate constants at 228 K and 298 K are given in Table 2 together with activation parameters obtained from the Eyring equation plotted in Fig. 3. The data plotted are from the experiment with constant [CO2] = 1 mM. The negative activation entropies are consistent with an associative transition state.
. A full set of kobs and k2 data is available (SI Text). Second-order rate constants at 228 K and 298 K are given in Table 2 together with activation parameters obtained from the Eyring equation plotted in Fig. 3. The data plotted are from the experiment with constant [CO2] = 1 mM. The negative activation entropies are consistent with an associative transition state.
Fig. 2.
Plots of the observed rate constants (kobs) in DMF as a function of CO2 concentration at 223–243 K and 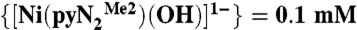 .
.
Table 2.
Kinetics parameters for carbon dioxide fixation with 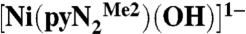 in DMF solutions
in DMF solutions
Fig. 3.
Eyring plot for the reaction of 0.1 mM 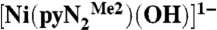 with 1 mM CO2 in DMF. The data were analyzed with the equation k2 = [(kBT)/h] exp(-ΔG‡/RT) with ΔG‡ = ΔH‡ - TΔS‡. Activation parameters are given in Table 2.
with 1 mM CO2 in DMF. The data were analyzed with the equation k2 = [(kBT)/h] exp(-ΔG‡/RT) with ΔG‡ = ΔH‡ - TΔS‡. Activation parameters are given in Table 2.
Table 3 contains a summary of second-order rate constants for CO2 fixation at ambient temperature, which may be compared with the extrapolated value of k2 = 9.5 × 105 M-1 s-1 at 298 K for reaction 1. These data were obtained in aqueous solution in a pH range sufficient to deprotonate coordinated water and thus refer to the minimal reaction M-OH + CO2 → M-OCO2H. The synthetic reactants [LnM-OH]z+ are primarily octahedral complexes of CoIII and five-coordinate [Zn(cyclen)(OH)]1+, perhaps the most successful kinetics mimic of the carbonic anhydrase site (17). Of the multitude of kinetics information available for carbonic anhydrase, data for the human enzymes I, II, and III are selected because of the availability of kcat and KM data. It is evident that the rate constant for reaction 1 enters the domain of carbonic anhydrase kinetics and is ≳102 faster than any metal-mediated synthetic system executing the same reaction. Although a more exact comparison cannot be made because of differences in solvent, this reaction is by any standard an extremely rapid CO2 fixation. Like most other fixation reactions that have been adequately described, reaction 1 is reversible. Purging a solution of preisolated 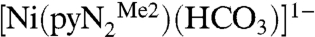 with dinitrogen results in quantitative recovery of
with dinitrogen results in quantitative recovery of 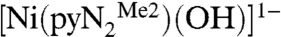 (Fig. 1).
(Fig. 1).
Table 3.
Comparative rate constants for the reaction of CO2 and M-OH groups
| Reactant |
k2 or kcat/KM, M-1 s-1* |
Ref. |
| [LnMIII-OH]z+ | 41–590 | (18†–20) |
| [Zn(cyclen)(OH)]1+ | 3.3 × 103 | (17) |
| OH- | 7.9 × 103 | (21) |
| Human carbonic anhydrase‡ | 1.1 × 105 to 1.6 × 108 | (17) |
*Aqueous solution, pH ∼ 7–9 (where specified).
†See additional data and references cited therein.
‡kcat/KM.
Reaction Mechanism.
The mechanism of reaction 1 was investigated by density functional theory (DFT) calculations. For comparison and calibration, different combinations of functionals (BP86, B3LYP) and basis sets [6-31G(d), DGDZVP] were employed on the full 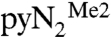 systems as well as on simpler N-H and N-Me complexes. Calculations were conducted in the gas phase, where the monoanionic complexes were found to be stable to electron autodetachment (negative highest occupied molecular orbital and positive vertical ionization energies), and also with use of a polarizable continuum solvent model to simulate the experimental DMF solvent medium. In general, the various approaches all gave the same qualitative description of the reaction pathway; attention is focused on the
systems as well as on simpler N-H and N-Me complexes. Calculations were conducted in the gas phase, where the monoanionic complexes were found to be stable to electron autodetachment (negative highest occupied molecular orbital and positive vertical ionization energies), and also with use of a polarizable continuum solvent model to simulate the experimental DMF solvent medium. In general, the various approaches all gave the same qualitative description of the reaction pathway; attention is focused on the 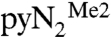 complexes. The BP86/6-31G(d) enthalpic reaction profile and stationary point geometries are provided in Fig. 4, and a schematic reaction sequence of the reactive fragments showing relative orientations and bond distances is given in Scheme 1. Calculated enthalpies with different computational models are listed in Table 4.
complexes. The BP86/6-31G(d) enthalpic reaction profile and stationary point geometries are provided in Fig. 4, and a schematic reaction sequence of the reactive fragments showing relative orientations and bond distances is given in Scheme 1. Calculated enthalpies with different computational models are listed in Table 4.
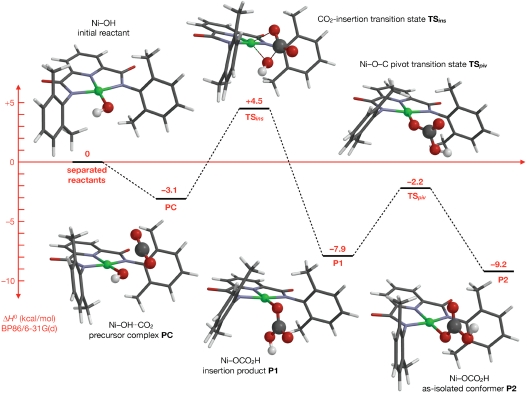
Fig. 4.
BP86/6-31G(d) reaction profile and stationary point structures for CO2 fixation by 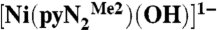 . Energy values (kcal/mol) are standard enthalpies of reaction or activation.
. Energy values (kcal/mol) are standard enthalpies of reaction or activation.
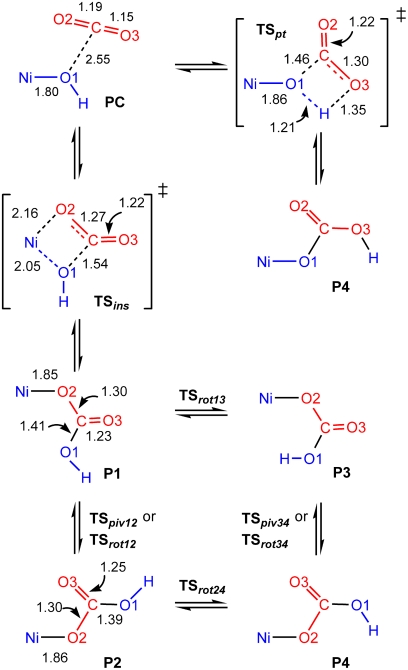
Scheme 1.
Summary of the events in Fig. 4 with computed bond lengths (Å) from BP86/6-31G(d) optimizations for species along the reaction profile of Fig. 4. Note that TSpt and P4 are not involved in the reaction scheme (see text).
Table 4.
Computed standard enthalpies (kcal/mol) and entropies (in parentheses, cal mol-1 K-1) for stationary points on reaction 1 pathway*
| Method/basis set | PC | TSins | TSpt | P1† | TSpiv12 | TSrot12 | P2† | TSrot13 | P3 | TSrot24 | P4† | TSpiv34 | TSrot34 |
| B3LYP/6-31G(d) | −5.1 | 0.6‡ | 17.7 | −12.9 | −7.3 | −4.6 | −14.6 | −4.7 | −9.1 | −6.5 | −14.9 | −5.7 | −6.7 |
| (−24) | (−34) | (−30) | (−31) | (−37) | (−39) | (−32) | (−35) | (−32) | (−32) | (−33) | (−35) | (−38) | |
| (DMF solvation) | −1.7 | 0.2‡ | 17.8 | −13.5 | −7.5‡ | −5.1‡ | −14.6 | −5.6 | −11.4 | −6.2 | −14.3 | −6.9‡ | −7.9‡ |
| (−24) | (−34) | (−32) | (−34) | (−37) | (−39) | (−34) | (−35) | (−34) | (−35) | (−33) | (−34) | (−38) | |
| B3LYP/DGDZVP | −4.4 | 2.6‡ | 18.2 | −11.9 | −6.5 | −3.6† | −13.1 | −4.0 | −8.3 | −5.4 | −13.4 | −4.9 | −5.9 |
| (−26) | (−35) | (−29) | (−36) | (−38) | (−37) | (−34) | (−37) | (−32) | (−34) | (−33) | (−36) | (−39) | |
| (DMF solvation) | 0.1 | 1.9‡ | 18.7 | −11.9 | −6.7 | −3.6 | −12.3 | −4.4 | −10.3 | −4.6 | −12.3 | −6.4 | −6.5 |
| (−25) | (−34) | (−35) | (−33) | (−36) | (−41) | (−36) | (−38) | (−35) | (−37) | (−37) | (−36) | (−42) | |
| BP86/6-31G(d) | −3.1 | 4.5 | 18.4 | −7.9 | −2.2 | 1.3 | −9.2 | −0.3 | −6.0 | −1.4 | −9.6 | −1.1 | −1.6 |
| (−26) | (−36) | (−34) | (−34) | (−38) | (−40) | (−35) | (−35) | (−34) | (−34) | (−35) | (−38) | (−41) | |
| (DMF solvation) | −0.2 | 4.6 | 18.7 | −8.8 | −2.2 | 0.7 | −9.6 | −1.2 | −7.9 | −1.5 | −9.4 | −1.7 | −2.3 |
| (−27) | (−35) | (−38) | (−36) | (−37) | (−41) | (−35) | (−37) | (−33) | (−35) | (−34) | (−35) | (−41) | |
| BP86/DGDZVP | −2.5 | 5.3 | 17.4 | −8.2 | −2.7 | 0.8 | −9.0 | −1.1 | −6.7† | −1.8 | −9.3 | −1.7 | −2.2 |
| (−24) | (−37) | (−31) | (−36) | (−37) | (−38) | (−35) | (−36) | (−34) | (−33) | (−33) | (−38) | (−39) | |
| (DMF solvation) | 1.0 | 5.1 | 17.7 | −8.7 | −3.0 | 0.5 | −8.9 | −1.7 | −8.4† | −1.4 | −9.0 | −2.9 | −2.9 |
| (−25) | (−35) | (−35) | (−36) | (−39) | (−41) | (−38) | (−39) | (−36) | (−39) | (−38) | (−38) | (−42) |
*Structures are C1 symmetric unless otherwise indicated.
†Cs symmetric.
‡Unrestricted singlet calculation due to wave function instability.
The computed reaction begins with formation of a weakly associated precursor complex (PC) from the reactants at infinite separation. The CO2 molecule approaches along the approximate mirror plane perpendicular to the NiN3 plane between the faces of the C6H3Me2 (DMP) substituents. With the exception of transition states involving nickel–bicarbonate rotation, all subsequent CO2-derived fragments lie on this plane. The closest contact between reactants in the PC occurs between the hydroxyl oxygen O1 and the CO2 carbon atom at a distance shorter than the van der Waals separation (2.5–3.0 Å, depending on the method and basis set) (22). The interaction is limited, however, as the CO2 molecule deviates little from linearity (170–177°). Although PC formation is enthalpically favorable, the loss in entropy probably renders the complex slightly higher in free energy than the separated reactants at the experimental temperatures; this, plus the limitations of DFT treatments of weak interactions, limits the experimental significance of the precursor complex.
From PC, the reaction proceeds through a four-centered transition state (TSins) that inserts an O-C fragment into the Ni-OH bond. Conceptually, this transition state represents a nucleophilic attack of metal-bound hydroxide (O1H) at electrophilic carbon atom, with concurrent formation of a new Ni-O interaction from one of the CO2 oxygen atoms (O2). This transition state closely resembles that accepted for CO2 fixation by carbonic anhydrase (23, 24), albeit with a different metal, d-electron count, and stereochemistry. For BP86 calculations, the wave function at the transition state is stable as a spin-restricted singlet. In contrast, stability tests on B3LYP calculations reveal lower energy, unrestricted solutions. The energy differences between the geometry-optimized unrestricted and restricted wave functions are minor (< 1.5 kcal/mol), however, and the corresponding structures deviate by < 0.08 Å in Ni-ligand distances. An alternative reaction pathway was also characterized, involving a transition state (TSpt) with simultaneous proton transfer and O1-C bond formation. This route does not involve direct Ni-CO2 interaction, and O1 remains bound to the Ni center from reactant to product. The calculated activation enthalpy for TSpt, however, is at least 12 kcal/mol higher than that of TSins across all calculations, and this pathway therefore appears irrelevant to the mechanism of reaction 1.
The immediate product from TSins is the nickel–bicarbonate complex P1, with the bicarbonate ligand adopting an antiperiplanar orientation of the Ni─O2─C═O3 dihedral and a synperiplanar O3═C─O1─H dihedral. This product geometry can rearrange to the more stable synperiplanar Ni─O2─C═O3 conformation P2 by pivoting about the O2 linkage through transition state TSpiv12; this trajectory is equivalent to simultaneous rotations about both the Ni─O2 and O2─C bonds. Direct rotation by 180° about the O2─C bond offers a simpler, alternative reorientation pathway; our calculations indicate that this route is less favorable energetically by > 2.4 kcal/mol (TSrot12). Further rotations about the Ni─O1 bond in P1 and P2 through transition states TSrot13 and TSrot24 lead to antiperiplanar O3═C─O1─H conformers P3 and P4, respectively. These can be interconverted directly by O2 pivot or O2─C rotation pathways analogous to those linking P1 and P2 with the barrier to rotation (TSrot34) lower than the pivot barrier (TSpiv34) in this case. Of the bicarbonate orientations, the most stable are the nearly equienergetic P2 and P4 conformers. P2 corresponds to the crystallographic product structure (3), although this structure also possesses additional interactions due to hydrogen-bonded dimerization via the bicarbonate ligand. This hydrogen bonding, which is not possible for the antiperiplanar O3═C─O1─H orientation of P4, probably determines the P2 geometry in the crystal structure, and similar interactions, either via self-association or, more likely, with the DMF solvent, may also favor P2 in solution.
The computational results agree well with available experimental findings. Structurally, the calculated geometries of 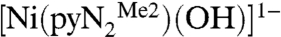 and the P2 conformer can be tested against crystallographic determinations (3) (SI Text). The Ni-ligand distances are within the expected accuracies in all DFT approaches investigated, and there is little basis to favor any particular computational model in our comparison set. The ligand conformations are predicted correctly, with the hydroxide hydrogen atom lying in the Ni coordination plane and the DMP substituents canted toward each other on one side of the coordination plane. Ignoring the hydroxide proton, the coordination unit and N-substituents assumes approximate Cs symmetry. A different conformer with the same in-plane hydroxide orientation, but with DMP groups canted in a parallel manner (approximate C2 symmetry), was also identified computationally at essentially the same energy. Because the CO2 insertion occurs via the Cs orientation, this geometry was used for the reactant reference energy in all thermochemical comparisons. For P2, distances within the bicarbonate ligand deviate significantly from the experimental data, due presumably to hydrogen bonding in the solid state structure.
and the P2 conformer can be tested against crystallographic determinations (3) (SI Text). The Ni-ligand distances are within the expected accuracies in all DFT approaches investigated, and there is little basis to favor any particular computational model in our comparison set. The ligand conformations are predicted correctly, with the hydroxide hydrogen atom lying in the Ni coordination plane and the DMP substituents canted toward each other on one side of the coordination plane. Ignoring the hydroxide proton, the coordination unit and N-substituents assumes approximate Cs symmetry. A different conformer with the same in-plane hydroxide orientation, but with DMP groups canted in a parallel manner (approximate C2 symmetry), was also identified computationally at essentially the same energy. Because the CO2 insertion occurs via the Cs orientation, this geometry was used for the reactant reference energy in all thermochemical comparisons. For P2, distances within the bicarbonate ligand deviate significantly from the experimental data, due presumably to hydrogen bonding in the solid state structure.
Energetically, the calculated activation enthalpies agree well with and bracket the values obtained from reaction kinetics (Tables 2 and 4), with the BP86 and B3LYP results higher and lower, respectively, than experiment. The magnitudes of the entropies are unreliable, being consistently higher than experiment by ca. 14–17 cal/mol K; at the computed entropies, the overall thermochemistry of reaction 1 at 298.15 K from infinite separation to the bicarbonate product is incorrectly predicted to be either endergonic (BP86) or so weakly exergonic (≤ -5 kcal/mol, B3LYP) that a substantial dissociative equilibrium arises. The erroneous entropies can be attributed to the inaccurate computational description of low-frequency vibrational modes (25). If the experimental activation entropy (-20 cal/mol K, giving TΔS = +6 kcal/mol at 298.15 K) is applied, consistently exergonic reactions are obtained. With this assumption and using the largest computed free energies of reaction [B3LYP/6-31G(d)], a solution of P2 at 1-mM initial concentration contains a low but nonneglible concentration (ca. 0.01–0.02 mM) of the hydroxide complex at equilibrium. This concentration was obtained using speciation equilibria involving 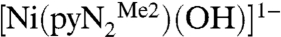 , CO2, and products P1–P4; the formation of PC is probably endergonic and was therefore excluded in the calculation. The result is consistent with the observed reversal of reaction 1 by dinitrogen sparging (Fig. 1).
, CO2, and products P1–P4; the formation of PC is probably endergonic and was therefore excluded in the calculation. The result is consistent with the observed reversal of reaction 1 by dinitrogen sparging (Fig. 1).
From the computational results, we make the following observations: (i) the planar NiII geometry provides an unhindered, out-of-plane approach for the small CO2 reactant; (ii) the insertion process involves the simultaneous formation of new C⋯O1 and Ni⋯O2 interactions that compensate for the reduction of bonding character from the initial unperturbed Ni─O1 and C═O2 moieties; and (iii) aside from the local geometry changes associated with substrate insertion, the nickel complex is otherwise unchanged over the course of the reaction. The confluence of these factors likely accounts for the exceedingly low activation for CO2 insertion. Finally, we note that our computational models do not address hydrogen bonding, and, given the low energies involved in this system, these interactions may be contributors to the overall solution thermochemistry.
Materials and Methods
Kinetics Measurement.
Commercial DMF was dried over 3-Å molecular sieves for 3 d, redistilled in vacuo from CaH2 at 55 °C, and degassed by purging with dinitrogen gas before use in the glove box. Solutions of 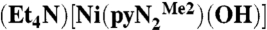 (3) were prepared in a glove box filled with argon immediately before a kinetics run and manipulated with a Hamilton gastight syringe equipped with a three-way valve. The solubility of CO2 in DMF has been reported as 0.18 M (26) and 0.20 M (27, 28); the latter value was used. Saturated solutions were prepared by bubbling CO2 through argon-saturated DMF in a syringe at 298 K for 20 min. Solutions with lower CO2 concentrations were prepared by multiple dilutions of a 0.20-M solution with argon-saturated DMF using graduated gastight syringes equipped with three-way valves; liquid phase occupied the entire available volume in the closed system and was never exposed to the atmosphere and/or the gas/vapor phase. Kinetics measurements were performed on a Hi-Tech Scientific SF-43 multimixing anaerobic cryogenic stopped-flow instrument (mixing time 4 ms) using a visible lamp. Because the reactions are very fast, data were collected in a single wavelength mode. All measurements were performed at 450 nm (the visible lamp afforded noisy spectra of
(3) were prepared in a glove box filled with argon immediately before a kinetics run and manipulated with a Hamilton gastight syringe equipped with a three-way valve. The solubility of CO2 in DMF has been reported as 0.18 M (26) and 0.20 M (27, 28); the latter value was used. Saturated solutions were prepared by bubbling CO2 through argon-saturated DMF in a syringe at 298 K for 20 min. Solutions with lower CO2 concentrations were prepared by multiple dilutions of a 0.20-M solution with argon-saturated DMF using graduated gastight syringes equipped with three-way valves; liquid phase occupied the entire available volume in the closed system and was never exposed to the atmosphere and/or the gas/vapor phase. Kinetics measurements were performed on a Hi-Tech Scientific SF-43 multimixing anaerobic cryogenic stopped-flow instrument (mixing time 4 ms) using a visible lamp. Because the reactions are very fast, data were collected in a single wavelength mode. All measurements were performed at 450 nm (the visible lamp afforded noisy spectra of 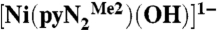 at λmax = 411 nm). Solutions of the NiII complex and CO2 in DMF were separately cooled at low temperature (218–243 K) and mixed in a 1∶1 volume ratio. The mixing cell temperature was maintained at ± 0.1 K. Concentrations of all reagents are reported for the onset of the reaction (after mixing). CO2 (0.25–2.5 mM) was always in excess with respect to
at λmax = 411 nm). Solutions of the NiII complex and CO2 in DMF were separately cooled at low temperature (218–243 K) and mixed in a 1∶1 volume ratio. The mixing cell temperature was maintained at ± 0.1 K. Concentrations of all reagents are reported for the onset of the reaction (after mixing). CO2 (0.25–2.5 mM) was always in excess with respect to 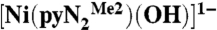 (0.1 mM). Data analysis was performed with Rapid Kinetics software (Hi-Tech Scientific) and confirmed by IgorPro program for kinetics traces at 450 nm using a single exponential fit. Each reported rate constant is an average of at least five runs with standard deviations within ± 2%.
(0.1 mM). Data analysis was performed with Rapid Kinetics software (Hi-Tech Scientific) and confirmed by IgorPro program for kinetics traces at 450 nm using a single exponential fit. Each reported rate constant is an average of at least five runs with standard deviations within ± 2%.
Computational Methods.
Density functional calculations were performed using the Gaussian 09 (G09) software package (29). B3LYP (30–32) and BP86 (30, 33) functionals were employed in combination with split valence double-zeta, singly polarized 6-31G(d) (34, 35) and DGDZVP (36, 37) basis sets. Stationary points (minima or transition states) were verified by frequency calculations, and reaction paths from transition states were identified by tracking intrinsic reaction coordinates (38, 39). Solvation effects were investigated via the polarizable continuum model using the integral equation formalism (40), which is the default self-consistent reaction field method in G09. Initial geometry optimizations were conducted on restricted singlet states, and all converged wave functions were tested for stability (41, 42); unstable wave functions were reoptimized to stable unrestricted wave functions that were then subjected to further geometry optimization and wave function stability analyses. Default convergence criteria and parameters were used throughout.
Supplementary Material
Acknowledgments.
This research was supported at Harvard University by the National Institutes of Health (GM-28856), at Tufts University by the National Science Foundation (Chemistry Grant 0750140 and Chemistry Research, Instrumentation, and Facilities Grant 0639138), and at the University of Waterloo by the Natural Sciences and Engineering Research Council, Canada Foundation for Innovation, Ontario Research Fund, and the Shared Hierarchical Academic Research Computer Network.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1017430108/-/DCSupplemental.
References
- 1.Jeoung J-H, Dobbek H. Carbon dioxide activation at the Ni,Fe-cluster of anaerobic carbon monoxide dehydrogenase. Science. 2007;318:1461–1464. doi: 10.1126/science.1148481. [DOI] [PubMed] [Google Scholar]
- 2.Kung Y, Doukov TI, Seravalli J, Ragsdale SW, Drennan CL. Crystallographic snapshots of cyanide- and water-bound C-clusters from bifunctional carbon monoxide dehydrogenase/acetyl-CoA synthase. Biochemistry. 2009;48:7432–7440. doi: 10.1021/bi900574h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Huang D, Holm RH. Reactions of the terminal NiII-OH group in substitution and electrophilic reactions with carbon dioxide and other substrates: structural definition of binding modes in an intramolecular NiII…FeII bridged site. J Am Chem Soc. 2010;132:4693–4701. doi: 10.1021/ja1003125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Kitajima N, Fujisawa K, Koda T, Hikichi S, Moro-oka Y. Fixation of atmospheric CO2 by a copper(II) Complex. Chem Commun. 1990:1357–1358. [Google Scholar]
- 5.Murthy NN, Karlin KD. A dinuclear zinc hydroxide complex which traps atmospheric carbon dioxide: formation of a tri-zinc complex with a triply bridging carbonate group. Chem Commun. 1993:1236–1238. [Google Scholar]
- 6.Looney A, Han R, McNeill K, Parkin G. Tris(pyrazolyl)hydroboratozinc hydroxide complexes as functional models for carbonic anhydrase: on the nature of the bicarbonate intermediate. J Am Chem Soc. 1993;115:4690–4697. [Google Scholar]
- 7.Kitajima N, Hikuchi S, Tanaka M, Moro-oka Y. Fixation of atmospheric CO2 by a series of hydroxo complexes of divalent metal ions and the implication for the catalytic role of metal ion in carbonic anhydrase Synthesis, characterization, and molecular structure of [LM(OH)]n (n = 1 or 2) and LM(μ-CO3)ML (M(II) = Mn, Fe, Co, Ni, Cu, Zn; L = HB(3,5-i Pr 2pz)3) J Am Chem Soc. 1993;115:5496–5508. [Google Scholar]
- 8.Company A, et al. Structural and kinetic study of reversible CO2 fixation by dicopper macrocyclic complexes. From intramolecular binding to self-assembly of molecular boxes. Inorg Chem. 2007;46:9098–9110. doi: 10.1021/ic700692t. [DOI] [PubMed] [Google Scholar]
- 9.Bergquist C, Fillebeen T, Morlok MM, Parkin G. Protonation and reactivity towards carbon dioxide of the mononuclear tetrahedral zinc and cobalt hydroxide complexes, [TpBut,Me]ZnOH and [TpBut,Me]CoOH: Comparison of the reactivity of the metal hydroxide function in synthetic analogues of carbonic anhydrase. J Am Chem Soc. 2003;125:6189–6199. doi: 10.1021/ja034711j. [DOI] [PubMed] [Google Scholar]
- 10.Bazzicalupi C, et al. CO2 fixation by novel copper(II) and zinc(II) macrocyclic complexes. A solution and solid state study. Inorg Chem. 1996;35:5540–5548. doi: 10.1021/ic9603262. [DOI] [PubMed] [Google Scholar]
-
11.Ito M, Takita Y. Atmospheric CO2 fixation by dinuclear Ni(II) complex, [TPANi(II)(μ-OH)2TPA](ClO4)2 (
 ) Chem Lett. 1996:929–930. [Google Scholar]
) Chem Lett. 1996:929–930. [Google Scholar] - 12.Kersting B. Carbon dioxide fixation by binuclear complexes with hydrophobic binding pockets. Angew Chem Int Edit. 2001;40:3987–3990. doi: 10.1002/1521-3773(20011105)40:21<3987::AID-ANIE3987>3.0.CO;2-L. [DOI] [PubMed] [Google Scholar]
- 13.Wikstron JP, et al. Carbonate formation within a nickel dimer: Synthesis of coordinatively unsaturated bis(μ-hydroxo) dinickel complex and its reactivity toward carbon monoxide. Dalton Trans. 2010;39:2504–2514. doi: 10.1039/b916832j. [DOI] [PubMed] [Google Scholar]
- 14.Sakahura T, Choi J-C, Yasuda H. Transformation of carbon dioxide. Chem Rev. 2007;107:2365–2387. doi: 10.1021/cr068357u. [DOI] [PubMed] [Google Scholar]
- 15.He L-N, Wang J-Q, Wang J-L. Carbon dioxide chemistry: Examples and challenges in chemical utilization of carbon dioxide. Pure Appl Chem. 2009;81:2069–2080. [Google Scholar]
- 16.Lackner KS. A guide to CO2 sequestration. Science. 2003;300:1677–1678. doi: 10.1126/science.1079033. [DOI] [PubMed] [Google Scholar]
- 17.Zhang X, van Eldik R. A functional model for carbonic anhydrase: Thermodynamic and kinetic study of a tetraazacyclodecane complex of zinc(II) Inorg Chem. 1995;34:5606–5614. [Google Scholar]
- 18.Palmer DA, van Eldik R. The chemistry of metal carbonate and carbon dioxide complexes. Chem Rev. 1983;83:651–731. [Google Scholar]
- 19.Acharya AN, Dash AC. Kinetics of the reversible uptake of carbon dioxide and sulphur dioxide by the cis-(Hydroxo)(imidazole)bis(ethylenediamine)-cobalt(III) ions in aqueous medium. A comparative study. Proc Indian Acad Sci (Chem Sci) 1993;105:225–233. [Google Scholar]
- 20.Jacewicz D, Chylewska A, Daakbrowska A, Chmurzynski L. Stopped-flow spectrophotometric study on the reaction between carbon dioxide and [Co(NH3)4(H2O)2]3+ ion in aqueous solution. Z Anorg Allg Chem. 2007;633:1493–1499. [Google Scholar]
-
21.Zhang X, van Eldik R, Koike T, Kimura E. Kinetics and mechanism of the hydration of CO2 and dehydration of
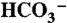 catalyzed by a Zn(II) complex of 1,5,9-triazacyclododecane as a model for carbonic anhydrase. Inorg Chem. 1993;32:5749–5755. [Google Scholar]
catalyzed by a Zn(II) complex of 1,5,9-triazacyclododecane as a model for carbonic anhydrase. Inorg Chem. 1993;32:5749–5755. [Google Scholar] - 22.Rowland RS, Taylor R. Intermolecular nonbonded contact distances in organic crystal structures: Comparison with distances expected from van der Waals radii. J Phys Chem. 1996;100:7384–7391. [Google Scholar]
- 23.Lindskog S, Liljas A. Carbonic anhydrase and the role of orientation in catalysis. Curr Opin Struct Biol. 1993;3:915–920. [Google Scholar]
- 24.Christianson DW, Fierke CA. Carbonic anhydrase: Evolution of the zinc binding site by nature and by design. Acc Chem Res. 1996;29:331–339. [Google Scholar]
- 25.Cramer CJ. Essentials of Computational Chemistry. Chichester, UK: Wiley; 2004. [Google Scholar]
-
26.Pocker Y, Bjorkquist DW. Comparative studies of bovine carbonic anhydrase in H2O and D2O. Stopped flow studies of the kinetics of interconversion of CO2 and
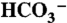 . Biochemistry. 1977;16:5698–5707. doi: 10.1021/bi00645a008. [DOI] [PubMed] [Google Scholar]
. Biochemistry. 1977;16:5698–5707. doi: 10.1021/bi00645a008. [DOI] [PubMed] [Google Scholar] - 27.Gennaro A, Isse AA, Vianello E. Solubility and electrochemical determination of CO2 in some dipolar aprotic solvents. J Electroanal Chem. 1990;289:203–215. [Google Scholar]
- 28.Tezuka M, Iwasaki M. Voltammetric study on CO2 reduction electrocatalyzed by cobalt tetraphenylporphine in DMF solution. Chem Lett. 1993:427–430. [Google Scholar]
- 29.Frisch MJ, et al. Wallingford, CT: Gaussian Inc; 2009. Gaussian 09, Revision A.02. [Google Scholar]
- 30.Becke AD. Density-functional exhange-energy approximation with correct asymptotic behavior. Phys Rev A. 1988;38:3098–3100. doi: 10.1103/physreva.38.3098. [DOI] [PubMed] [Google Scholar]
- 31.Lee C, Yang W, Parr RG. Development of the colle-salvetti correlation-energy formula into a functional of the electron density. Phys Rev B. 1988;37:785–789. doi: 10.1103/physrevb.37.785. [DOI] [PubMed] [Google Scholar]
- 32.Miehlich B, Savin A, Stoll H, Preuss H. Results obtained with the correlation-energy density functionals of Becke and Lee, Young and Parr. Chem Phys Lett. 1989;157:200–206. [Google Scholar]
- 33.Perdew JP. Density-functional approximation for the correlation energy of the inhomogeneous electron gas. Phys Rev B. 1986;33:8822–8824. doi: 10.1103/physrevb.33.8822. [DOI] [PubMed] [Google Scholar]
- 34.Rassolov VA, Pople JA, Ratner MA, Windus TL. 6-31G* basis set for atoms K through Zn. J Chem Phys. 1998;109:1223–1229. [Google Scholar]
- 35.Rassolov VA, Ratner MA, Pople JA, Redfern JA, Curtiss LA. Basos set for third-row atoms. J Comput Chem. 2001;22:976–984. [Google Scholar]
- 36.Godbout N, Salahub DR, Andzelm J, Wimmer E. Optimatization of Gaussian-type basis sets for local spin density functional calculations. Part I. Boron through neon, optimization technique and validation. Can J Chem. 1992;70:560–571. [Google Scholar]
- 37.Sosa C, et al. A local density functional study of the structure and vibrational frequencies of molecular transition metal compounds. J Phys Chem. 1992;96:6630–6636. [Google Scholar]
- 38.Hratchian HP, Schlegel HB. Accurate reaction paths using a Hessian-based predictor-corrector integrator. J Chem Phys. 2004;120:9918–9924. doi: 10.1063/1.1724823. [DOI] [PubMed] [Google Scholar]
- 39.Hratchian HP, Schlegel HB. Using Hessian updating to increase the efficiency of a Hessian-based predictor-corrector reaction pathway following method. J Chem Theory Comput. 2005;1:61–69. doi: 10.1021/ct0499783. [DOI] [PubMed] [Google Scholar]
- 40.Tomasi J, Mennucci B, Cammi R. Quantum mechanical continuum solvation models. Chem Rev. 2005;105:2999–3093. doi: 10.1021/cr9904009. [DOI] [PubMed] [Google Scholar]
- 41.Seeger R, Pople JA. Self-consistent molecular orbital methods. XVIII. Constraints and stability in Hartree-Fock theory. J Chem Phys. 1977;66:3045–3050. [Google Scholar]
- 42.Bauernschmitt R, Ahlrichs R. Stability analysis for solutions of the closed shell Kohn-Sham equation. J Chem Phys. 1996;104:9047–9052. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.