Violation of the Leggett–Garg inequality with weak measurements of photons

Abstract

By weakly measuring the polarization of a photon between two strong polarization measurements, we experimentally investigate the correlation between the appearance of anomalous values in quantum weak measurements and the violation of realism and nonintrusiveness of measurements. A quantitative formulation of the latter concept is expressed in terms of a Leggett–Garg inequality for the outcomes of subsequent measurements of an individual quantum system. We experimentally violate the Leggett–Garg inequality for several measurement strengths. Furthermore, we experimentally demonstrate that there is a one-to-one correlation between achieving strange weak values and violating the Leggett–Garg inequality.

There has been much debate in quantum physics over the question of whether measurable quantities have definite values prior to their measurement. Key ideas addressing this question include the Bell inequality, which considers correlations between measurements on components of a composite system that are space-like separated (1, 2) and contextuality tests, which examine whether identical experiments produce results in different “classically equivalent” contexts (3, 4). A conceptually elegant extension to these ideas is the Leggett–Garg inequality (LGI) (5), which is an inequality constructed from the correlation functions of a series of three consecutive measurements on a single system. Leggett and Garg derive limits based on the joint assumptions of (i) macroscopic realism: An observable for a system will have a definite value at all times; and (ii) noninvasive measurement: It is possible to determine this value with arbitrarily small disturbance on the subsequent evolution of the system. The limits on the value of the inequality derived from these assumptions differ from the predictions of quantum mechanics. Thus the LGI tests the limits of measurement and macroscopic realism.

Here we present an experimental test of a generalized LGI using weak measurements (6–9) of the polarization of single photons and measure violations by up to 14 standard deviations. Additionally, we experimentally demonstrate a one-to-one relation (10, 11) between LGI violations and strange weak-valued measurements (6–8), which also arise from the inability to assign values to physical quantities between an earlier and a later measurement.

Testing the LGI requires monitoring the system without projecting it into a specific state. For a quantum system a quantum nondemolition (QND) experiment (12–14) would be one way to do this. But QND measurements are not the only way to perform a noninvasive measurement. A generalization of the QND measurement is the so-called weak measurement (6). A weak measurement is one for which it is possible to adjust the strength of the measurement and, in principle, to reduce the back action on the system to an arbitrarily small amount. In other words, a weak measurement is one for which the level of “invasivness” can be controlled.

Shortly after Leggett and Garg introduced their inequality, Aharanov et al. (7) suggested that observing the result of a weak measurement conditioned on a specific result of a separate projective measurement leads to unusual results. One unusual property, dubbed strange weak values, is that the value assigned in this way may lie outside the eigenspectrum of the observable being measured (7). Because such strange weak values have been observed (15–19), the idea that the measured value lies outside the operator’s eigenspectrum raises questions about macroscopic realistic descriptions of the system’s state and of the measurement process (20, 21). In this sense, strange weak values explore the same concepts (or raise the same problems) as the LGI. A formal connection between a generalized LGI and weak values has been recently proposed by Williams and Jordan (10, 11). Specifically, they propose that the LGI is violated if and only if the experiment yields a strange weak value.

We want to be clear about what we mean by the term macroscopic realism and how it applies to systems of an arbitrary size. We use the same definition of macroscopic realism as Leggett and Garg: A system is described by a probability distribution for definite values of observables prior to measurement (5). The origin of the term macroscopic realism relates to the fact that one expects an ensemble of very large systems to be described by a classical distribution of definite values. However, this expectation in no way constrains the description to this class of objects. The term macroscopic realism, therefore, is not fundamentally about the size of the investigated system (which can be any size, in accordance with the generality of the Leggett–Garg treatment) but rather about the assignment of definite values to measurable quantities, either definitely (e.g., speed of a tennis ball) or probabalistically (e.g., speeds of particles in an ideal gas). This has been pointed out previously in a theoretical description connecting Leggett–Garg inequalities for Rydberg atoms (22) to hidden variables. The previous discussion holds true for the generalization proposed in ref. 8, where the probability distribution is also parametrized by a hidden-variable.

Recently, Jordan and coworkers (8, 10, 11) proposed a correlation function that generalizes the original Leggett–Garg correlation function to include nonprojective weak measurements. With this generalization, the ability to test the LGI at differing measurement strengths becomes possible, allowing for an experimental investigation of the measurement process. The generalized Leggett–Garg correlation function (8, 10, 11) is

[1]

where is a set of three consecutive weak measurements on the photon polarization. We use letters to denote the sequence of measurements in order to distinguish the ordering of the measurements from the physical quantities we measured, the Stokes’ parameters, which are denoted with numerical subscripts according to conventional notation. For a two-level system with the properties of both macroscopic realism and noninvasive detection, B must satisfy -3 ≤ B ≤ 1, which is the LGI. On the other hand, quantum measurements produce values of B satisfying (8): -3 ≤ B ≤ 1.5. Thus, there is a violation of the LGI if 1 < B ≤ 1.5. Although the original formulation of the generalized LGI, Eq. 1, is in terms of three consecutive weak measurements, the detailed analysis presented in refs. 8, 10, and 11 shows that, according to quantum mechanics, the violation of the LGI does not depend on the measurement strength of eithe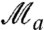r or 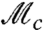. Thus, we can relax the requirement that all three measurements are weak and perform strong projective measurements f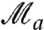or or 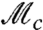thereby simplifying the experiment.

We feel it necessary to point out that the LGI as we have tested it differs from sequential contextuality tests (23). Contextuality tests using sequential measurements require the measured observables be compatible. The LGI has no such requirement; it requires noninvasive measurement of incompatible observables. Therefore some of the criticisms levelled at contextuality tests (see, e.g., ref. 24 and references therein) do not apply to the LGI. It may be that there is a deeper connection between contextuality and noninvasive measurement, but we leave that for future work.

A conceptual scheme of the experimental setup is shown in Fig. 1. We input a “signal” photon in the state 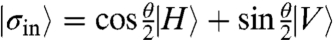where |H〉 and |V〉 represent horizontal and vertical polarization states. We consider |σ_in〉 as the state prepared by the first measurement 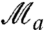; in this way, we can deterministically assign the value 1 to . The weak measurement, , measures the 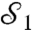Stokes’ parameter of the signal photon (14), corresponding to the degree of polarization in the horizontal-vertical basis. The final measurement, 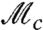, is the Stokes’ parameter 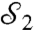of the signal photon that quantifies the degree of polarization in the diagonal-antidiagonal basis 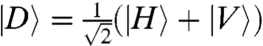, 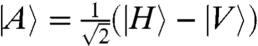. Thus, in our case we can rewrite Eq. 1 as (10, 11)

[2]

Note that 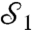is a weak measurement in the sense of Jordan et al. (8), and 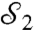is a projective measurement.

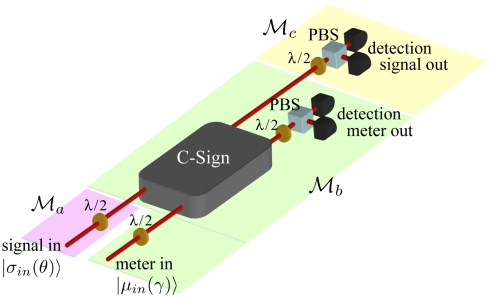
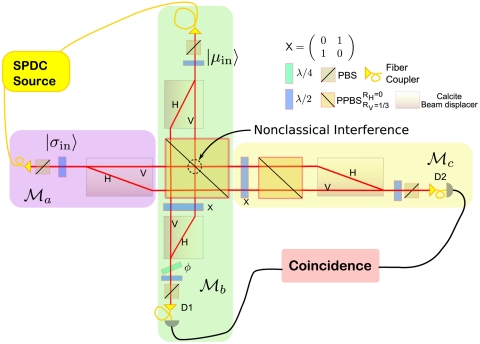
Fig. 1.

Conceptual representation of the experiment. A “signal” photon is prepared with an arbitrary linearly polarized state using a half waveplate (λ/2), 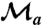. A weak measurement of the polarization is then made (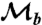) by interacting the signal photon with a “meter” photon via a C-Sign gate, which operates via a measurement-induced nonlinearity (14, 25–29). Conditional on detecting a single photon in each of the two output modes (a coincidence measurement) the gate ideally performs the operation 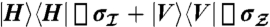on the two-qubit polarization Hilbert space , where 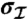(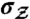) is the 1-qubit identity (Pauli 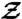) operator and |H〉 = |0〉, |V〉 = |1〉. See the main text for a full description of 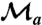, , 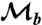and 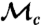and Materials and Methods for more experimental details.

The weak measurement is implemented using a nondeterministic linear optical controlled-sign gate (25–29). The polarization of the signal qubit |σ_in〉 in the gate’s control mode becomes entangled with that of a second, “meter,” photon in the target mode. A subsequent projective measurement of the meter photon realizes the weak measurement of the signal. 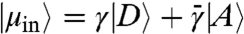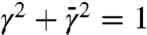The strength of the measurement can be set by changing the meter input state (with , and 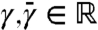without loss of generality). The strength of the measurement is quantified by the knowledge (14), K = 2γ² - 1. When K = 1 (γ = 1), full information is extracted about the polarization of the signal photon, while when K = 0 (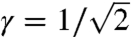), the photon is left completely undisturbed and unmeasured. Between those two extremes, the photon polarization undergoes partial disturbance, and one can extract the average value of 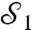as (14):

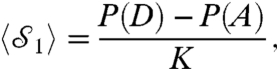[3]

where P(D) and P(A) are the probabilities of measuring the values D and A, respectively, for the meter photon. The weak character is reflected in the fact that an increasing number of copies are necessary to estimate 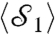to a given precision as K decreases. The weak value (6, 7) is calculated by postselecting on a measurement of that results in the value D for the signal photon. In our implementation, we considered the weak value:

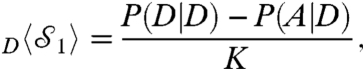[4]

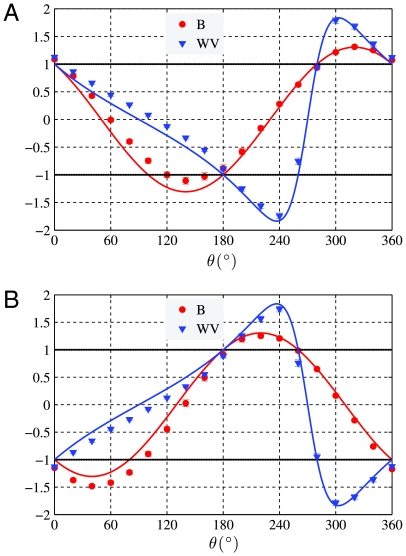
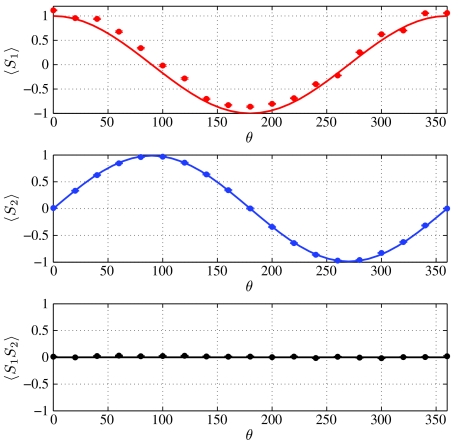
where P(A|D) is the probability of measuring the value A for the meter photon, conditioned on the postselection of the signal photon registering a value of D and similarly for P(D|D). We expect strange weak values (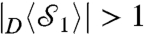) to emerge when |σ_in〉 approaches the antidiagonal state |A〉. We refer to weak values as the postselected results of any weak measurement. Notice that these coincide with the original formulation of Aharonov et al. in the limit K → 0 (7). Even for finite strengths, strange weak values may appear (13, 30). Fig. 2A shows the measured values for the generalized LG correlation function, B, defined in Eq. 2 and the weak values, WV, for the choice K = 0.5445 ± 0.0083 as θ is varied in the range [0,2π]. The maximum value we observe is B_max = 1.312 ± 0.022, which is 14 standard deviations above the classical limit of B = 1. The results show that there is a clear correlation between the violation of the LGI and the appearance of strange positive weak values. There are discrepancies between the theoretical curves and the data points for values of θ where we do not expect to see a violation of the LGI. We discuss these in more detail in Materials and Methods. We also see strange negative weak values corresponding to values of B that do not violate the LGI of Eq. 2. This does not contradict the prediction of Williams and Jordan (10, 11) because they predict that there are strange weak values when a generalized LGI is violated. There are four distinct generalized LGIs corresponding to different assignments of the ± 1 eigenvalues for the operators in Eq. 2. It is also possible to define four different weak values, by eigenvalue reassignment and varying the final postselection state of the signal. See Materials and Methods for more details.

Fig. 2.

Variation of the weak value, WV (▾), and the Leggett–Garg parameter B (•) for a range of input states |σ_in〉 parametrized by θ. Postselection is on the diagonal state |D〉, and the measurement strength is K = 0.5445 ± 0.0083. Error bars show the standard deviation and arise from poissonian counting statistics. (A) B parameter using 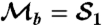. (B) B parameter 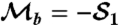. Solid lines are the theoretical predictions from Eqs. 4 and 2. The horizontal lines at ± 1 indicate the limits of the eigenspectrum of 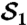. B_max = 1.312 ± 0.022.

The condition—which applies across the whole parameter range—is that whenever a strange weak value is obtained one of these four LGIs will also be violated. As shown in Fig. 2B, if we assign our eigenvalues such that 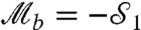rather than 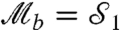as in Fig. 2A, a violation of the LGI, B > 1, corresponds to the strange weak values, in the range where previously there was no violation.

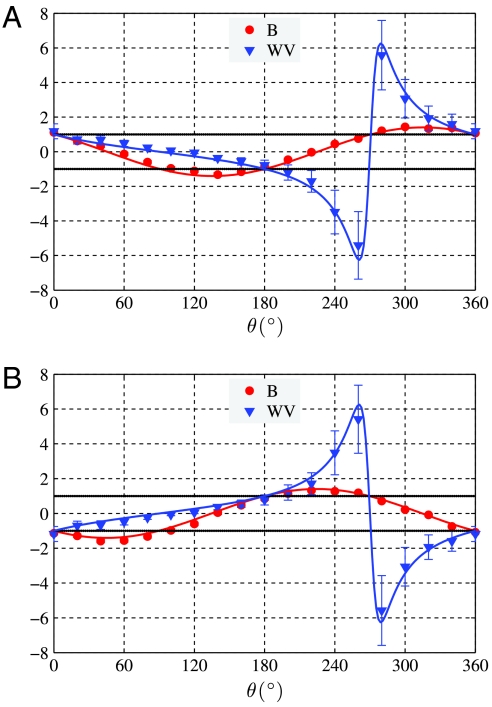
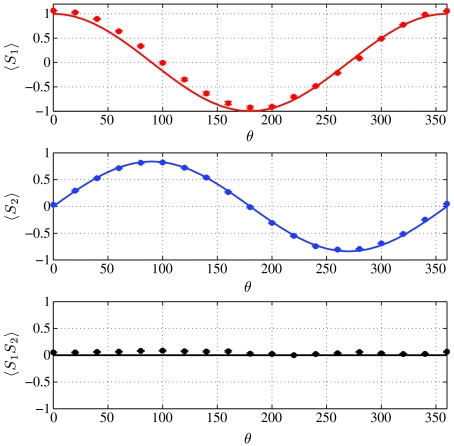
To understand the effect of the measurement strength on violation of the LGI, we decreased the knowledge to K = 0.1598 ± 0.0091, Fig. 3. This corresponds to a weaker measurement of the signal photon polarization. We now observe a maximum value B_max = 1.436 ± 0.053 (eight standard deviations), confirming that the peak violation of the LGI increases as the measurement strength decreases (8). Finally note that the range of θ values for which a violation of the LGI occurs becomes larger as the measurement becomes weaker. But even with moderate knowledge (K = 0.1598 ± 0.0091) we can violate the LGI for nearly every state (see Fig. 4). Physically, the dependence of the LGI violation on measurement strength can be understood as follows. A full strength measurement prepares the photon in an eigenstate of the measured observable regardless the initial preparation—this prevents the observation of any correlations between 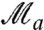and 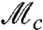. As the measurement gets weaker, the disturbance to the correlations decreases, allowing observation of an LGI violation (31).

Fig. 3.

As for Fig. 2, except now K = 0.1598 ± 0.0091. Error bars are larger than in Fig. 2 because of poorer statistics due to reduced postselection probability. (A) B parameter formed with 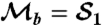. (B) B parameter from 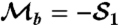. Solid lines are the theoretical predictions from Eqs. 4 and 2. B_max = 1.436 ± 0.053.

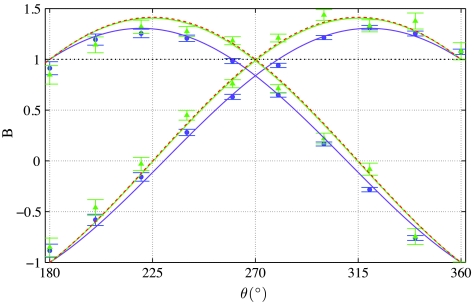
Fig. 4.

Comparison of the Leggett–Garg parameter (B) for a range of input states |σ_in〉, for the measurement strengths of Fig. 2, K = 0.5445 ± 0.0083 (•), and Fig. 3 K = 0.1598 ± 0.0091 (▴). As before, error bars show the standard deviation and arise from poissonian counting statistics. The range of violation of the LGI is larger when the measurement is less intrusive. The red dashed line is the theoretical result for a zero strength measurement, where the LGI would be violated for all states between |H〉 and |V〉. Note that even with a moderate strength of K = 0.1598 ± 0.0091, we cover most of this range.

Determination of the LGI parameter can be regarded as a more robust approach than strange weak values for investigating the effects of varying the intermediate measurement strength. This is because it involves all the measured photons, while the measurement of strange weak values only uses a subset of the measured photons (those that satisfy the postselection criterion). That is, regardless of their utility in precision measurements (18, 19), anomalous weak values are always open to the criticism of not measuring the complete system. The same criticism cannot be levelled against violating the Leggett–Grag inequalities. The connection between the LGI and strange weak values nicely illustrates that weak values provide information about the physics of the system and are more than a “mere parlor trick.”

It is tempting to conclude that the strange weak values and LGI violation arise because it is not possible to consider the signal photon as a separate system—instead, we must consider the joint signal/meter system. However, as the measurement strength decreases, the less interaction the meter has with the signal and the more the signal photon can be considered a separate system. Yet we observe that as the measurement strength gets weaker, the LGI violation becomes larger. In fact, maximal violation of the LGI occurs in the limit of a separable signal and meter state. In practice, this is unmeasurable because K = 0, and we would be unable to measure .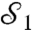

Our results suggest that macroscopic realism is intimately related to measurement. As our measurement becomes weaker—i.e., less invasive—the LGI becomes more violated not less. Thus, macroscopic realism becomes the only condition left to violate. Yet there is little difference between our result with a finite knowledge (K = 0.1598 ± 0.0091) and the theoretical limit of zero knowledge. In fact, we see a significant violation with a knowledge of 0.5445. So with a better than 50/50 shot of knowing 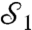, we get a violation of the LGI.

Bounded weak values also require noninvasive measurement to be observed. (10). Yet the weak values become less bounded as the measurement gets weaker. This leaves open questions about weak values as markers for a violation of local realism.

More significantly, both the LGI violation and strange weak values disappear when the measurement is strong enough. Presumably the system did not become macroscopically real as the measurement became stronger; the measurement forced a definite value on the system. These results put into the spotlight questions that are as old as quantum theory. Is measurement the only necessary condition for reality? Is macroscopic realism a superfluous condition? To answer this last question we need to devise an experimentally meaningful test of macroscopic realism that is independent of conditions on measurement strength.

Materials and Methods

Generalized Leggett-Garg Inequalities and Corresponding Weak Value Measurements.

Here we give more details on the different LGIs and weak value expressions that can be defined in our experiment. The two measurement operators in Eq. 2 of the main text have eigenvalues of ± 1, corresponding to two possible outcomes. Experimentally, two detectors are required for each measurement: one at the transmission output port of a polarizing beamsplitter and the other at the reflection output port. We must choose how to assign clicks at each detector to the eigenvalues. There are two choices for each measurement, yielding four possible configurations in total and subsequently four distinct LGIs:

[5]

[6]

[7]

[8]

A violation of the assumptions of Leggett and Garg occurs if any of the above expressions exceeds 1. This is shown in (10). Briefly, if we write 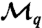, with q = a,b,c as

where ϵ is “noise” from the experiment. The assumptions of macroscopic realism and noninvasive measurement imply

and

Therefore

giving the limits of 〈B〉.

We can also define four weak values for the signal photon, given the two choices of eigenvalue assignment and two choices of the postselected signal state:

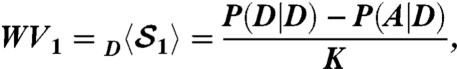[9]

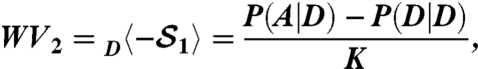[10]

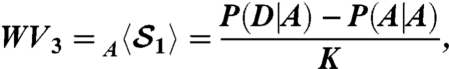[11]

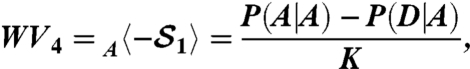[12]

where P(A|D) is the probability of measuring the value A for the meter photon, conditioned on the postselection of the signal photon in state D and similarly for P(D|D). Thus we have a weak value for each LG inequality. The condition that holds for all input signal states (parameterized by θ) is that whenever a weak value is observed one of the LGIs is violated and vice versa. Showing all eight of the above relations would produce plots that would be very difficult to read. The interested reader can see the missing relations by imagining Figs. 2 and 3 horizontally reflected about a line through 180°. We also note that these LGIs and weak values would produce the mirror image (horizontally again) of Fig. 4 of the main text with the horizontal range changed from [180°, 360°] to [0°, 180°]. Finally we note that future experiments and investigation could consider more general measurements with more than two outcomes.

Experimental Details.

Here we give a simple description of our apparatus, illustrated in Fig. 7. Single photons are produced in pairs by spontaneous parametric down conversion (SPDC) in a bismuth borate (BiBO) nonlinear crystal. The pump beam is obtained by frequency doubling a 100-fs pulsed Ti∶Sa laser lasing at 820 nm, with a repetition rate 82 MHz and bandwidth 8nm. We used a pump power of approximately 50 mW in order to reduce double pair emission to a negligible level. Single modes are selected by narrowband interference filters (IF) and fiber launchers (FL), coupling them to single mode fibers. The rate of pair production is approximately 50 s^-1 at the output of the gate.

Fig. 7.

Schematic of experimental setup. See Experimental Details for a complete description of the experiment. The calcite beam displacers are in the setup for other experiments. They are not integral to the current experiment and are included here for completeness. The ϕ waveplate is used to adjust the relative phase between the beam displacer interferometers and is an artifact of having the beam displacers.

Their original H polarization state is recovered by means of polarization controllers in the optical fibers between the SPDC source and the free-space output couplers and then prepared by means of a glan-taylor polarizing beamsplitter (PBS) and half-wave plate (λ/2). This state preparation coincides with the first measurement , which therefore assumes the value +1 deterministically.

The photons then arrive on our C-Sign gate. This is based on a single partially polarizing beam splitter (PPBS), whose transmittivities for the horizontal, H, and vertical, V, polarizations are ideally η_H = 1 and (25–27). Due to quantum interference, the event |H〉_s|H〉_m acquires a π phase shift, while the others are left unaltered—here s and m label the signal and the meter. Polarization-dependent loss induced by the gate can be either compensated directly in the state preparation (as we did for the meter arm) or by adding extra loss (the second PPBS in the signal arm). The gate is nondeterministic, but its correct functioning is heralded by a coincidence count between two distinct output arms.

The basic principle for the nondestructive measurement 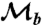derives from the action of the gate in the rotated basis 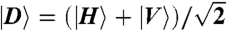and 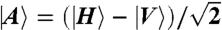. If |V〉_s|D〉_m are injected, they emerge in the same state at the output. Conversely, when |H〉_s|D〉_m is injected, there occurs the phase shift flipping the polarization of the meter from |D〉_m to |A〉_m. Therefore, one can assess the polarization of the signal by a measurement on the meter arm distinguishing between the two rotated polarizations: A measurement of |D〉_m flags the state |H〉_s, the same for the orthogonal complement. This is easily obtained by means of a half-wave plate and a glan-taylor polarizing beam splitter (PBS). Notice that the injection of |H〉_m in the meter leads no information about the state of the signal, because this remains unaffected in any case.

An intermediate situation occurs if the polarization 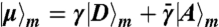is used. This is unaltered upon injection of |V〉 and rotated to 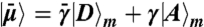in the other case. Nevertheless 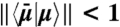, in the general case, and the two events can not be perfectly distinguished. We notice that a measure in the {|D〉_m,|A〉_m} basis is the optimal discrimination strategy (32). Consequently, only partial information can be retrieved about the state of the signal. The measurement is then nondestructive and its strength can be tuned at will by properly setting the polarization |μ〉_m. Because the signal photon is not destroyed, it can be subsequently measured in the standard way by means of a half-wave plate and PBS, so to perform the final step 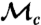. We note that the measurement results are independent of the detection efficiencies. The operation of the gate is such that we make all three measurements on the same system when we have a coincidence event.

Error Analysis.

Here we examine the systematic error in the experiment. As was noted in the main text there are values of θ for which the experimental results diverge from the theoretical results by more than the standard deviation. This error is due to imperfect mode-matching at the PPBS. We checked the outcomes of the measurement results for each of the measurements independently, as shown in Figs. 5 and 6. We can compare the measured results with the expected results for that measurement, which is known theoretically, which helps us to identify that the error is in 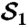but only for certain values of θ. This is consistent with our experimental observations that suggest that mode matching is the biggest error factor in the experiment. The mode matching is input-dependent because of a steering effect from rotating the input waveplate. In this case, the mode matching is optimized for the regime of interest, 180 ≤ θ ≤ 360° as demonstrated by the fact that the 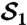measurement gives the correct result, to within statistical error, in that range. Therefore, we claim violation for the LGIs involving B₁ and B₂, while systematic error might play a role for B₃ and B₄. We also note that 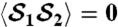over the range 180 ≤ θ ≤ 360° indicating that 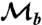is indeed a quantum nondemolition measurement over this range.

Fig. 5.

The three correlation functions that comprise the generalized Leggett–Garg correlation function for a range of input states |σ_in〉 parametrized by θ. The measurement strength is K = 0.5445 ± 0.0083. Error bars show the standard deviation and arise from poissonian counting statistics.

Fig. 6.

The three correlation functions that comprise the generalized Leggett–Garg correlation function for a range of input states |σ_in〉 parametrized by θ. The measurement strength is K = 0.1598 ± 0.0091. Error bars show the standard deviation and arise from poissonian counting statistics.