Abstract
Gibbs sampler has been used exclusively for compatible conditionals that converge to a unique invariant joint distribution. However, conditional models are not always compatible. In this paper, a Gibbs sampling-based approach — Gibbs ensemble —is proposed to search for a joint distribution that deviates least from a prescribed set of conditional distributions. The algorithm can be easily scalable such that it can handle large data sets of high dimensionality. Using simulated data, we show that the proposed approach provides joint distributions that are less discrepant from the incompatible conditionals than those obtained by other methods discussed in the literature. The ensemble approach is also applied to a data set regarding geno-polymorphism and response to chemotherapy in patients with metastatic colorectal
Keywords: Gibbs sampler, Conditionally specified distribution, Linear programming, Ensemble method, Odds ratio
1. Introduction
Since Besag (1974), the majority of the modeling for spatial observations has taken the conditional approach. For a finite system of random variables (X1, · · ·, XJ), the conditional likelihood is defined as
| (1) |
where θ is the model parameter. The product of all such conditional likelihoods, ΠLi(θ), called the pseudolikelihood, is used to replace the conventional likelihood in inference. Interestingly, maximum pseudolikelihood has developed into a franchise of its own, even though it was originally proposed as an expedient objective function for spatial data (Besag, 1974). The alteration of the likelihood function is partially motivated by the fact that conventional likelihood often contains an intractable partition function, whereas Li(θ) can be modeled in a rather simple form such as a regression or a classifier. The main disadvantage of maximum pseudolikelihood estimator is that it can be biased and is an inefficient estimator — with a reported efficiencies (ratios of variances) ranging from 100% for models with weak dependence to 10% for models with strong dependence (Besag, 1977; Jensen and Künsch, 1994; Jensen and Møller, 1991). A good approximation of the conventional likelihood derived from Li(θ), 1 ≤ j ≤ J can improve the efficiency and reduce the bias.
Similar formulations of likelihood occur in network models. Conditional models are individually created and fitted to the observed data with the objective of computing predictive probabilities. Heckerman et al. (2000) call the collection of such conditional models a dependence network and propose using a (random scan) Gibbs sampler to learn a joint distribution p̂(x1, · · ·, xJ; θ) from Li(θ), 1 ≤ j ≤ J. An important motivation of the dependency networks is to address the possible high dimensionality of data and to reduce the inference problem associated with univariate conditional distributions.
For several discrete variables, a statistical model may be formulated either as a joint model or via a system of conditional models such as (1). In general, when a joint distribution is to be recovered from a collection of conditional distributions the joint is said to be conditionally specified or conditionally modeled. Moreover, the conditional models are said to be compatible when there exists a joint distribution capable of generating all of the conditional distributions. Nevertheless conditional models are not always compatible when conditional models are non-saturated; usually no mutual consistency criteria are incorporated in the models for the individual conditional distributions. In fact, unlike joint models, mutually consistent conditional models are rather difficult to articulate. A “remedy” for incompatibility is to search for a joint distribution that deviates least from — however defined — the prescribed set of conditional distributions. One of the hurdles of conditional modeling is to calculate a reasonable joint from conflicting conditional distributions.
Arnold and Gokhale (1998) and Arnold et al. (2002) are among the first making efforts to find the most nearly compatible (or the minimally incompatible) joint distributions given a family of conditionals. Arnold and Gokhale (1998) considered Kullback-Leibler divergence and the L2-distance as the measures of incompatibility, while Arnold et al. (2002) used absolute deviations as the criterion. Understandably, constrained optimization algorithms using different objective functions are involved. Under such circumstances, two issues need to be considered. First, the constrained optimization becomes more difficult as the number of conditional models or the number of variables (the dimension of the problem) increases. Arnold et al. (2002, p. 251) expressed their concern in the statement that “In practice, the number of equations, constraints and variables will limit consideration to cases in which the coordinated random variables have very few values.” For example, in a joint distribution of 4 variables, each with 3 categories, a constrained optimization formulation (linear programming) would involve 162 variables, 648 inequalities, and one equality. Second, the performance measures that had been documented are rather limited and may not be generally applicable to all problems. Some divergence measures can further complicate the algorithm in searching for an optimal solution. For example, Arnold and Gokhale (1998, p. 386) noted that switching divergence away from Kullback-Leibler divergence “clearly leads to a much less tractable objective function.”
The goal of this paper is to propose an algorithm — the Gibbs ensemble (GE) —that overcomes both difficulties. The algorithm has two important properties: (a) ability to scale up to handle large data sets of high dimensionality, and (b) ability to accommodate different performance measures. The algorithm first uses Gibbs sampler to formulate a collection of joint distributions, which is termed an ensemble (Bühlmann, 2004). Then a weighted average of all the distributions in the ensemble is taken as a solution. The combination weights are inversely proportional to the divergences of the members in the ensemble. Using the ubiquitous Gibbs sampler as the base procedure is highly suitable for this application because the procedure is robust, scalable, and relatively easy to program. To illustrate the ensemble approach, consider the following example.
Example 1.1 Arnold, Castillo, and Sarabia (2002, Example 10) considered
Here  and
and  respectively correspond to L1(x1|x2) and L2(x2|x1). The odds ratios of
respectively correspond to L1(x1|x2) and L2(x2|x1). The odds ratios of  and
and  are 2/3 and 9/2, respectively, and they are not compatible. Arnold et al. (2002) obtained the following optimal joint distribution via linear programming (LP):
are 2/3 and 9/2, respectively, and they are not compatible. Arnold et al. (2002) obtained the following optimal joint distribution via linear programming (LP):
Table 1 compares selected divergences of the different joint distributions obtained through several different methods: linear programming (LP), π̂LP, random scan Gibbs, π̂HC, equal-weight Gibbs ensemble, π̃EQ, and differentially weighted Gibbs ensembles, π̃L, π̃I, π̃X, and π̃F. The definitions of these divergences are given in Section 2. Relative to π̂LP, the differentially weighted Gibbs ensemble reduces the L2 and F 2 divergences by 20% and 11%, respectively. The random scan Gibbs sampler and the equally weighted Gibbs ensemble are more or less on par with π̂LP.
Table 1.
Divergence of the joint distributions computed via different algorithms for Example 1.1
| Errors | π̂LP | π̂HC | π̃EQ | π̃L | π̃I | π̃X | π̃F |
|---|---|---|---|---|---|---|---|
| L2 | 0.0910 | 0.0939 | 0.0926 | 0.0700 | 0.0711 | 0.0771 | 0.0721 |
| I2 | 0.1134 | 0.1165 | 0.1148 | 0.0972 | 0.0963 | 0.1005 | 0.0968 |
| X2 | 0.2094 | 0.2140 | 0.2119 | 0.2137 | 0.2018 | 0.1977 | 0.1996 |
| F2 | 0.2201 | 0.2257 | 0.2229 | 0.1964 | 0.1928 | 0.1981 | 0.1930 |
The remainder of this paper is organized as follows. The idea of generating an ensemble from incompatible Gibbs sampler is discussed in Section 2. In Section 3, we present numerical comparisons of several methods using both examples in the literature and simulation data. In Section 4, the algorithm is applied to a data set regarding geno-polymorphism and response to treatment in patients with metastatic colorectal cancer. A brief conclusion is provided in Section 5.
2. Gibbs Ensemble
Consider a system of J discrete random variables {x1, · · ·, xJ} whose conditional model is specified by 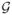 = {
= {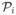 = παi|ᾱi, 1 ≤ i ≤ m}, with αi ∩ ᾱi = ∅ and αi ∪ ᾱi =
= παi|ᾱi, 1 ≤ i ≤ m}, with αi ∩ ᾱi = ∅ and αi ∪ ᾱi = 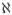 = {x1, · · ·, xJ}. Here,
= {x1, · · ·, xJ}. Here, 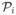 , is called a full conditional because all J variables are involved. Hence Li(θ) = πi|ī, 1 ≤ i ≤ J is a special case. In practice, both Besag (1974) and Heckerman et al. (2000) used the conditional model πα|β, β ⊂ ᾱ, but this change does not affect the Gibbs samplers as long as
.
, is called a full conditional because all J variables are involved. Hence Li(θ) = πi|ī, 1 ≤ i ≤ J is a special case. In practice, both Besag (1974) and Heckerman et al. (2000) used the conditional model πα|β, β ⊂ ᾱ, but this change does not affect the Gibbs samplers as long as
.
Let Sm be the symmetric group of all possible permutations of (1, · · ·, m) and |Sm| = m!. For every (k1, · · ·, km) ∈ Sm, arrange the given conditional distributions of 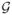 in the following sequence:
in the following sequence:
and generate simulations using Gibbs sampler in the above order. Every (k1, · · ·, km) ∈ Sm represents a scan pattern. Often, this is called a deterministic scan (Liu, 1996) or fixed scan, in contrast to scanning 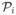 in a random order with prescribed probabilities, which is called a random scan in Levine and Casella (2006).
in a random order with prescribed probabilities, which is called a random scan in Levine and Casella (2006).
Let 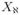 = (x1, · · ·, xJ) and Xαi = (xj, j ∈ αi). When i = kj, we replace subscript αkj with kj and subscript ᾱkj with k̄j to avoid triple subscripts. Begin with a randomly selected
. Conditioned on
, draw an
from
= (x1, · · ·, xJ) and Xαi = (xj, j ∈ αi). When i = kj, we replace subscript αkj with kj and subscript ᾱkj with k̄j to avoid triple subscripts. Begin with a randomly selected
. Conditioned on
, draw an
from 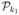 and update
to
. Next, conditioned on
, draw
from
and update
to
. Next, conditioned on
, draw
from 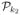 and form
. Successive sampling steps from
and form
. Successive sampling steps from 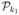 to
to 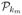 are called a cycle, and after one cycle every
of
will be updated at least once, due to ∪αi =
are called a cycle, and after one cycle every
of
will be updated at least once, due to ∪αi = 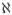 . Let
be the result at the end of the first cycle. After w burn-in cycles,
is harvested at the end of the next cycle as the first qualified simulation, and the process is repeated l times. Let the empirical distribution of {
, 1 ≤ h ≤ l} be π̂(k1, · · ·, km), where the superscript indicates the scan pattern. Every π̂(k1, · · ·, km) is called a Gibbs distribution (Geman and Geman, 1984; Israel, 2005). The collection of m! such Gibbs distributions, {π̂(k1, · · ·, km), (k1, · · ·, km) ∈ Sm}, assuming that they all converge, is named Gibbs ensemble after its base procedure. To compute the error, convert each π̂(k1, · · ·, km) to {
, 1 ≤ i ≤ m}, and measure the separation of
from the corresponding
. Let
be the result at the end of the first cycle. After w burn-in cycles,
is harvested at the end of the next cycle as the first qualified simulation, and the process is repeated l times. Let the empirical distribution of {
, 1 ≤ h ≤ l} be π̂(k1, · · ·, km), where the superscript indicates the scan pattern. Every π̂(k1, · · ·, km) is called a Gibbs distribution (Geman and Geman, 1984; Israel, 2005). The collection of m! such Gibbs distributions, {π̂(k1, · · ·, km), (k1, · · ·, km) ∈ Sm}, assuming that they all converge, is named Gibbs ensemble after its base procedure. To compute the error, convert each π̂(k1, · · ·, km) to {
, 1 ≤ i ≤ m}, and measure the separation of
from the corresponding 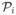 via a divergence measure. The sum of m divergences is the error of π̂(k1, · · ·, km). In theory, the error is zero if and only if
via a divergence measure. The sum of m divergences is the error of π̂(k1, · · ·, km). In theory, the error is zero if and only if 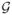 is compatible; but in simulation, such errors will not be exactly zero due to Monte Carlo variation.
is compatible; but in simulation, such errors will not be exactly zero due to Monte Carlo variation.
There are several commonly used divergences for measuring the closeness between two distributions π̂ and p (e.g., Bishop et al., 1975, p. 348–9). The divergences adopted in this study are: L2 := Σ(π̂i − pi)2 (Euclidean); (Freeman-Turkey); X2 := Σ(π̂i − pi)2/π̂i (Pearson’s chi-square); N2 := Σ(π̂i − pi)2/pi (Neyman’s chi-square); I2:= Σπ̂i log(π̂i/pi) (Information); and G2:= Σpi log(pi/π̂i) (Kullback-Leibler). To calculate the divergence between two distributions that are represented by multidimensional matrices, each matrix is cast into a row vector, and the formula listed above is applied.
Let D represent one of the divergence measures, and
measure the D-error between π̂(k1, · · ·, km) and 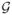 . The sum of D-errors over the entire ensemble is
. Also, let
be the weight assigned to π̂(k1, · · ·, km). The differentially weighted Gibbs ensemble is
. The sum of D-errors over the entire ensemble is
. Also, let
be the weight assigned to π̂(k1, · · ·, km). The differentially weighted Gibbs ensemble is
| (2) |
which is shortened to Gibbs solution. For example, Gibbs solution π̃L is weighted by the L2-divergence. In addition, we use π̃EQ and π̂HC, respectively, for the equally weighted Gibbs solution (ε(k1, · · ·, km) = 1/m!) and the random scan Gibbs distribution (Heckerman et al., 2000). Figure 1 illustrates the process for obtaining the Gibbs solution.
Figure 1.
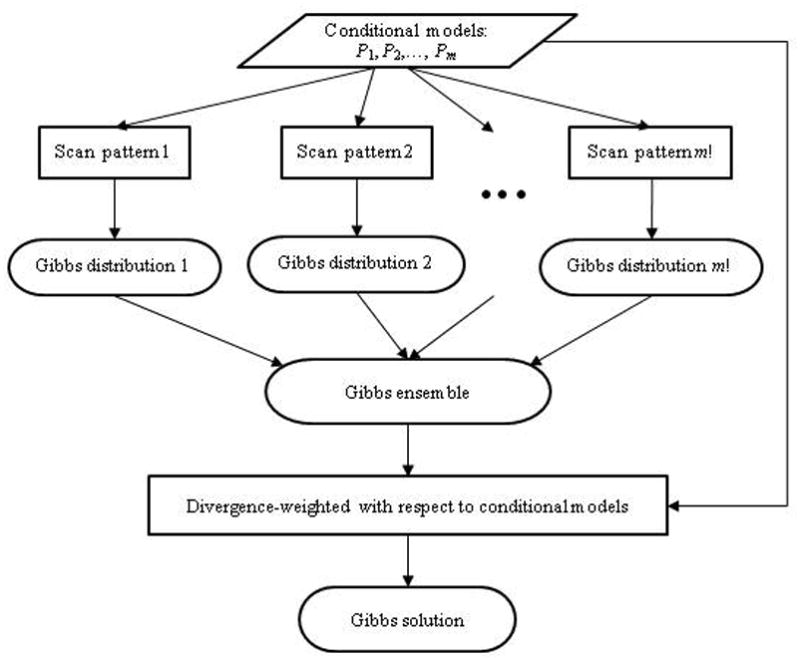
Flow diagram for Gibbs ensemble
For J = 2, let  and
and  correspond to the conditional distributions (x1|x2) and (x2|x1), respectively. The Gibbs ensemble has two distributions: π̂(1,2) is the empirical distribution of {
, 1 ≤ h ≤ l} sampled in the following manner:
correspond to the conditional distributions (x1|x2) and (x2|x1), respectively. The Gibbs ensemble has two distributions: π̂(1,2) is the empirical distribution of {
, 1 ≤ h ≤ l} sampled in the following manner:
and π̂(2,1) is derived from {
, 1 ≤ h ≤ l}, which are sampled from  →
→  → · · ·
→ · · ·  →
→  → · · ·. The Gibbs solution is
.
→ · · ·. The Gibbs solution is
.
For J = 3 and  = {πi|{ī}}, there are six Gibbs distributions. Let
= {πi|{ī}}, there are six Gibbs distributions. Let  ,
,  , and
, and  respectively denote (x1|x2, x3), (x2|x1, x3), and (x3|x1, x2). For permutation (1, 3, 2), the sampling scheme runs as follows:
respectively denote (x1|x2, x3), (x2|x1, x3), and (x3|x1, x2). For permutation (1, 3, 2), the sampling scheme runs as follows:
Then, π̂(1,3,2) is the empirical distribution of { , 1 ≤ h ≤ l}, and the three-dimensional Gibbs solution is the following weighted average of six Gibbs distributions:
3. Numerical Comparisons and Simulations
We use both numerical examples and simulated data to compare the performances of LP and GE. First, we consider a 3 × 4, two-dimensional, conditional models and its incompatible variations. Using divergence measures as criteria, we compare GE and LP for this example. The second example compares the errors of GE and of LP on a 3 × 3 × 3 conditional model and its incompatible variations. Finally, we report results from a simulation study. One hundred pairs { ,
,  } of 3×4 two-dimensional conditional distributions are randomly generated. The reported means and standard deviations of the divergences are based on 100 replications of Monte Carlo simulations, each of sample size 100, 000. The programs for simulation and analysis are developed in Matlab and can be download from the link (provided upon publication).
} of 3×4 two-dimensional conditional distributions are randomly generated. The reported means and standard deviations of the divergences are based on 100 replications of Monte Carlo simulations, each of sample size 100, 000. The programs for simulation and analysis are developed in Matlab and can be download from the link (provided upon publication).
3.1 A Two-Dimensional Example
This example is taken from Ip and Wang (2009). The conditional distributions  (c, d) and
(c, d) and  (a, b) are defined as follows:
(a, b) are defined as follows:
When a = b = c = d = 0,  and
and  are compatible. The perturbation parameters a, b, c, and d are used to locate and control the degree of incompatibility. We study the following cases:
are compatible. The perturbation parameters a, b, c, and d are used to locate and control the degree of incompatibility. We study the following cases:
-
Case (i)
a = −1/12, b = c = d = 0;
-
Case (ii)
c = −1/7, d = 1/7, a = b = 0;
-
Case (iii)
c = −1/7, d = 1/7, a = −1/12, b = 0; and
-
Case (iv)
c = −1/7, d = 1/7, a = −1/12, b = 1/12.
Case (i) and Case (ii) represent incompatibility arising from deviations in  (x2|x1 = 1) and deviations in
(x2|x1 = 1) and deviations in  (x1|x2 = 3, 4), respectively. Case (iii) represents the situation when Case (i) and Case (ii) occur simultaneously. Case (iv) represents the situation in which
(x1|x2 = 3, 4), respectively. Case (iii) represents the situation when Case (i) and Case (ii) occur simultaneously. Case (iv) represents the situation in which  of Case (iii) deviates further from compatibility. Our purpose is to access the performance of GE as
of Case (iii) deviates further from compatibility. Our purpose is to access the performance of GE as  , and
, and  increasingly depart from compatibility.
increasingly depart from compatibility.
We follow the LP method described in Arnold et al. (2002) to compute the joint probability pij with minimum εij such that |pij − aijp.j| ≤ εij, |pij − bijpi.| ≤ εij and Σi,j pij = 1. Here,  = (aij),
= (aij),  = (bij), pi. = Σj pij, and p.j = Σi pij. Because the LP formulation contains many unknowns to be solved, the restrictions εij = ε are imposed. After such restrictions, there are 48 inequalities, 1 equality, and 13 unknowns.
= (bij), pi. = Σj pij, and p.j = Σi pij. Because the LP formulation contains many unknowns to be solved, the restrictions εij = ε are imposed. After such restrictions, there are 48 inequalities, 1 equality, and 13 unknowns.
We first consider the compatible case, which has a unique solution, to validate our programs. We found that the joint distribution of LP optimization, denoted as π̂LP, indeed had zero divergence, as expected. Table 2 shows the more interesting results regarding the accuracy of Gibbs sampler, which is subject to simulation variations. Gibbs samplers, both fixed scan and random scan, were run with 5, 000 burn-in cycles, and retain the subsequent 100, 000 pairs of (x1, x2). The resulting joint distributions are denoted as π̂(1,2) and π̂(1/2,1/2), respectively, whereas π̃F is the GE solution of (2), with D being the Freeman-Tukey divergence. To assess the Monte Carlo errors, the same Gibbs samplers are repeated 100 times so that the means and standard deviations of the divergences can be computed. From Table 2 we observe that the π̃F has considerably smaller mean divergences than both π̂(1,2) and π̂(1/2,1/2). For example, the mean in L2 is reduced by more than 50% from 1.81E-4 to 7.44E-5. All divergence measures are computed with respect to the unique joint distribution. It is also observed that while the fixed scan and random scan have similar accuracies, GE solutions reduce all of the divergences by more than one half.
Table 2.
Performance of Gibbs ensemble for the compatible case of Example 3.1
| Mean Divergence (Standard Deviation) |
||||||
|---|---|---|---|---|---|---|
| L2 | I2 | G2 | X2 | N2 | F2 | |
| π̃F | 7.44E-5 | 1.38E-4 | 1.38E-4 | 2.75E-4 | 2.75E-4 | 2.75E-4 |
| Gibbs Ensemble | (3.38E-5) | (6.01E-5) | (6.01E-5) | (1.20E-4) | (1.20E-4) | (1.20E-4) |
| π̂(1/2,1/2) | 1.57E-4 | 2.92E-4 | 2.92E-4 | 5.85E-4 | 5.84E-4 | 5.85E-4 |
| Random Scan | (6.43E-5) | (1.21E-4) | (1.21E-4) | (2.41E-4) | (2.41E-4) | (2.41E-4) |
| π̂(1,2) | 1.81E-4 | 3.30E-4 | 3.31E-4 | 6.61E-4 | 6.61E-4 | 6.61E-4 |
| Fixed Scan | (8.74E-5) | (1.51E-4) | (1.51E-4) | (3.03E-4) | (3.02E-4) | (3.03E-4) |
For the incompatible Case (i) to Case (iv), Table 3 lists the divergences of two fixed scans and the GE solution weighted by L2, G2, and F2, respectively. In general, GE solutions achieve significant reductions of divergence, while the performance of LP is slightly worse than π̂(2,1). For Case (i), the F -divergence of π̃F is 40.8% of that of π̂(2,1); the L2-divergence of π̃L is only 33.5% of that of π̂(2,1). For Case (iv), π̃F and π̃L reduce the F2 and L2 of π̂(2,1) by 31.6% and 39.8%, respectively, while the reductions of F2 and L2 of π̂(1,2) are 60.1% (by π̃F) and 39.8% (π̃L), respectively. Moreover, the F2 of π̂LP is 148.1% of that of π̃F, and the L2 of π̂LP is 152.2% of that of π̃L. Later, we will show that such reductions are generally observed in randomly generated, two-dimensional — and incompatible — conditional models.
Table 3.
Mean divergences for the incompatible cases of Example 3.1 based on 100 Monte Carlo replications
| L2 | G2 | F2 | I2 | ||
|---|---|---|---|---|---|
| Case (i) | π̂(1,2) | 0.0224 | 0.0510 | 0.0971 | 0.0466 |
| π̂(2,1) | 0.0114 | 0.0332 | 0.0680 | 0.0351 | |
| π̃L | 0.0075 | 0.0201 | 0.0409 | 0.0208 | |
| π̃G | 0.0076 | 0.0197 | 0.0397 | 0.0201 | |
| π̃F | 0.0077 | 0.0196 | 0.0396 | 0.0200 | |
| π̂LP | 0.0117 | 0.0280 | 0.0557 | 0.0277 | |
| Case (ii) | π̂(1,2) | 0.0819 | 0.1237 | 0.2386 | 0.1163 |
| π̂(2,1) | 0.0697 | 0.1116 | 0.2304 | 0.1203 | |
| π̃L | 0.0376 | 0.0586 | 0.1190 | 0.0606 | |
| π̃G | 0.0377 | 0.0584 | 0.1185 | 0.0603 | |
| π̃F | 0.0378 | 0.0584 | 0.1182 | 0.0600 | |
| π̂LP | 0.0706 | 0.1093 | 0.2191 | 0.1101 | |
| Case (iii) | π̂(1,2) | 0.1038 | 0.1743 | 0.3349 | 0.1623 |
| π̂(2,1) | 0.0808 | 0.1446 | 0.2987 | 0.1559 | |
| π̃L | 0.0454 | 0.0787 | 0.1599 | 0.0815 | |
| π̃G | 0.0455 | 0.0785 | 0.1592 | 0.0810 | |
| π̃F | 0.0456 | 0.0784 | 0.1587 | 0.0806 | |
| π̂LP | 0.0788 | 0.1356 | 0.2741 | 0.1391 | |
| Case (iv) | π̂(1,2) | 0.3297 | 0.5376 | 1.0004 | 0.4776 |
| π̂(2,1) | 0.1529 | 0.3210 | 0.6637 | 0.3517 | |
| π̃L | 0.1046 | 0.1998 | 0.4140 | 0.2168 | |
| π̃G | 0.1062 | 0.1948 | 0.4018 | 0.2090 | |
| π̃F | 0.1078 | 0.1942 | 0.3995 | 0.2072 | |
| π̂LP | 0.1592 | 0.3124 | 0.6163 | 0.3068 | |
3.2 A Three-Dimensional Example
The three conditional distributions,  ,
,  , and
, and  , are listed in Table 4. We summarize the comparison of the compatible case plus cases (i) and (iv) in Table 5. Besides listing the L2 and F2, the percentages of reduction relative to π̂(1,2,3) are used to demonstrate the performance of GE. The compatible case allows us to examine the Monte Carlo simulation variations and to explore ways to reduce such variations. For the six supposedly identical Gibbs distributions, their L2 ranges from 1.466E-3 to 1.551E-3. Here, π̃EW denotes the equally weighted average of three Gibbs distributions: π̂(1,2,3), π̂(2,3,1), and π̂(3,1,2). From Table 5, π̃EW reduces the L2 and F2 of π̂(1,2,3) by 65.6% and 64.5%, respectively, and π̂EQ, which uses all six Gibbs distributions, further reduces L2 and F2 of π̃EW by an additional 51.4%. The best GE, π̃F, reduces the L2 and F2 of π̂EQ by another 7%. In summary, combining six Gibbs distributions is better than combining only three, and the use of different kinds of weights seems to play a relatively minor role. Case (i) to Case (iv) represent gradual departure from compatibility. The reductions of L2 for π̃F over π̂(1,2,3) are around 38% to 52% for Case (i) and Case (iv), respectively. In all four cases, the divergence of π̂LP is considerable larger than that of π̂(1,2,3) (except L2 in Case (iv)).
, are listed in Table 4. We summarize the comparison of the compatible case plus cases (i) and (iv) in Table 5. Besides listing the L2 and F2, the percentages of reduction relative to π̂(1,2,3) are used to demonstrate the performance of GE. The compatible case allows us to examine the Monte Carlo simulation variations and to explore ways to reduce such variations. For the six supposedly identical Gibbs distributions, their L2 ranges from 1.466E-3 to 1.551E-3. Here, π̃EW denotes the equally weighted average of three Gibbs distributions: π̂(1,2,3), π̂(2,3,1), and π̂(3,1,2). From Table 5, π̃EW reduces the L2 and F2 of π̂(1,2,3) by 65.6% and 64.5%, respectively, and π̂EQ, which uses all six Gibbs distributions, further reduces L2 and F2 of π̃EW by an additional 51.4%. The best GE, π̃F, reduces the L2 and F2 of π̂EQ by another 7%. In summary, combining six Gibbs distributions is better than combining only three, and the use of different kinds of weights seems to play a relatively minor role. Case (i) to Case (iv) represent gradual departure from compatibility. The reductions of L2 for π̃F over π̂(1,2,3) are around 38% to 52% for Case (i) and Case (iv), respectively. In all four cases, the divergence of π̂LP is considerable larger than that of π̂(1,2,3) (except L2 in Case (iv)).
Table 4.
Three conditional distributions of Example 3.2
| (·, ·, 1) |
|
|
|
|||
| (·, ·, 2) |
|
|
|
|||
| (·, ·, 3) |
|
|
|
|||
When a = b = c = d = e = f = g = 0, the three conditional distributions are compatible. There are four cases:
(i) a = −3/15, e = 1/13, d = −3/16 and b = c = f = g = 0
(ii) a = −3/15, e = 1/13, d = −3/16, b = −2/13 and c = f = g = 0
(iii) a = −3/15, e = 1/13, d = −3/16, b = −2/13, c = −2/12 and f = g = 0
(iv) a = −3/15, e = 1/13, d = −3/16, b = −2/13, c = −2/12, f = 7/30 and g = 4/15.
Table 5.
Mean of divergences reduction vs. π̂(1,2,3) of Example 3.2
| L2 | Percentage of Reduction | F2 | Percentage of Reduction | ||
|---|---|---|---|---|---|
| Compatible | π̂(1,2,3) | 1.47E-3 | – | 4.98E-3 | – |
| π̃EW | 5.04E-4 | 65.63% | 1.77E-3 | 64.49% | |
| π̃EQ | 2.45E-4 | 83.30% | 8.59E-4 | 82.74% | |
| π̃L | 2.25E-4 | 84.63% | 8.06E-4 | 89.82% | |
| π̃F | 2.28E-4 | 84.47% | 7.97E-4 | 83.99% | |
| Case (i) | π̂ (1,2,3) | 0.1846 | – | 0.6943 | – |
| π̃EW | 0.1195 | 35.26% | 0.4394 | 36.71% | |
| π̃EQ | 0.1128 | 38.89% | 0.4214 | 39.31% | |
| π̃L | 0.1148 | 37.82% | 0.4411 | 36.47% | |
| π̃F | 0.1145 | 38.01% | 0.4287 | 36.82% | |
| π̂LP | 0.3143 | −70.24% | 1.1127 | −60.27% | |
| Case (iv) | π̂(1,2,3) | 0.9191 | – | 2.9883 | – |
| π̃EW | 0.4719 | 48.65% | 1.6807 | 43.76% | |
| π̃EQ | 0.4366 | 52.50% | 1.5959 | 46.59% | |
| π̃L | 0.4369 | 52.46% | 1.5968 | 46.56% | |
| π̃F | 0.4392 | 52.21% | 1.6034 | 46.34% | |
| π̃LP | 0.8791 | 4.36% | 3.1423 | −5.15% | |
3.3 Simulation Experiments
In both Examples 3.1 (four cases) and 3.2 (another four cases), we further conducted 100 replications of Gibbs sampler. We try to address the question: Is it possible that LP outperforms GE in some of the replications? We found that for all eight different conditional models, GE outperformed LP in every replication. This implies that even the worst-case GE — due to Monte Carlo variation — still has smaller divergences than LP. Furthermore, in Example 11 of Arnold et al. (2002) (details not reported here), for a 3 × 4 models with two structural zeros, we also observed that out of 100 replications, GE, without exception, had smaller divergence than LP.
To confirm that the superiority of GE over LP and Gibbs distributions is not just an artifact of the examples we selected, we randomly generate pairs of 3 × 4 matrices with positive integers between 1 and 100 as entries. Then we normalize one matrix so that its column entries sum to 1, and we use it as  . The other matrix is similarly normalized (in rows) into
. The other matrix is similarly normalized (in rows) into  . For every randomly generated pair, LP, fixed scan Gibbs distribution and GE solution with different weights are computed. The mean and standard deviation of the percentages of reduction of the LP and GE solutions with respect to π̂(1,2) and π̂(2,1) are summarized in Table 6. In the course of the simulation, we noticed that the LP approach sometimes produced unreasonable joint distributions when there were multiple optimal solutions. Because the randomly generated conditional models do not contain any zero entry, their joint distribution is not expected to contain a zero entry. However, LP produces 11 joints (out of 100) with some zero entries, and one of the joints has an entire column of zeros. Those with any zero entry are excluded from comparison.
. For every randomly generated pair, LP, fixed scan Gibbs distribution and GE solution with different weights are computed. The mean and standard deviation of the percentages of reduction of the LP and GE solutions with respect to π̂(1,2) and π̂(2,1) are summarized in Table 6. In the course of the simulation, we noticed that the LP approach sometimes produced unreasonable joint distributions when there were multiple optimal solutions. Because the randomly generated conditional models do not contain any zero entry, their joint distribution is not expected to contain a zero entry. However, LP produces 11 joints (out of 100) with some zero entries, and one of the joints has an entire column of zeros. Those with any zero entry are excluded from comparison.
Table 6.
Mean and standard deviation of the percentage of reduction relative to π̂(1,2) and π̂(2,1) based on 100 randomly generated 3 × 4 conditional models
| L2 | F2 | G2 | ||||
|---|---|---|---|---|---|---|
| π̂(1,2) | π̂(2,1) | π̂(1,2) | π̂(2,1) | π̂(1,2) | π̂(2,1) | |
| π̃L | 63.89% (7.10) | 36.19% (7.02) | 55.74% (4.44) | 40.30% (5.26) | 59.19% (6.70) | 47.15% (8.02) |
| π̃F | 34.52% (8.28) | 63.12% (6.68) | 40.98% (4.66) | 56.18% (4.75) | 48.31% (7.48) | 60.00% (6.81) |
| π̃G | 62.40% (6.94) | 33.26% (8.75) | 55.16% (4.96) | 39.58% (5.30) | 59.53% (6.98) | 47.72% (7.53) |
| π̂LP* | 38.08% (23.12) | −15.12% (52.87) | 27.12% (27.83) | −0.10% (42.11) | 26.86% (40.55) | 4.62% (54.99) |
Based on 89 randomly generated conditional models.
The results in Table 6 indicate that the GE approach outperforms the LP approach and that the GE solutions enjoy substantial divergence reduction with respect to both π̂(1,2) and π̂(2,1). For example, the average percentages of reductions in L2 are 63.9% and 36.2% relative to the fixed scan π̂(1,2) and π̂(2,1), respectively, while the same averages for LP are 38.1% and −15.1%, respectively. Figure 2 shows the two boxplots of percentages of reductions in L2 of π̃L and π̂LP relative to π̂(1,2) (left panel), and to π̂(2,1) (right panel). The other distributions are similar and not shown because of space limitation. These simulation results give us confidence that the weighted average of ensembles can produce a joint distribution that fits the conditional models significantly better than LP and the Gibbs sampler. When we compare the coefficients of variation using values in Table 6, we find that the percentages of reduction for the LP approach is far less predictable than those of GE, whose coefficients of variation range from 8.0% to 26.3%.
Figure 2.
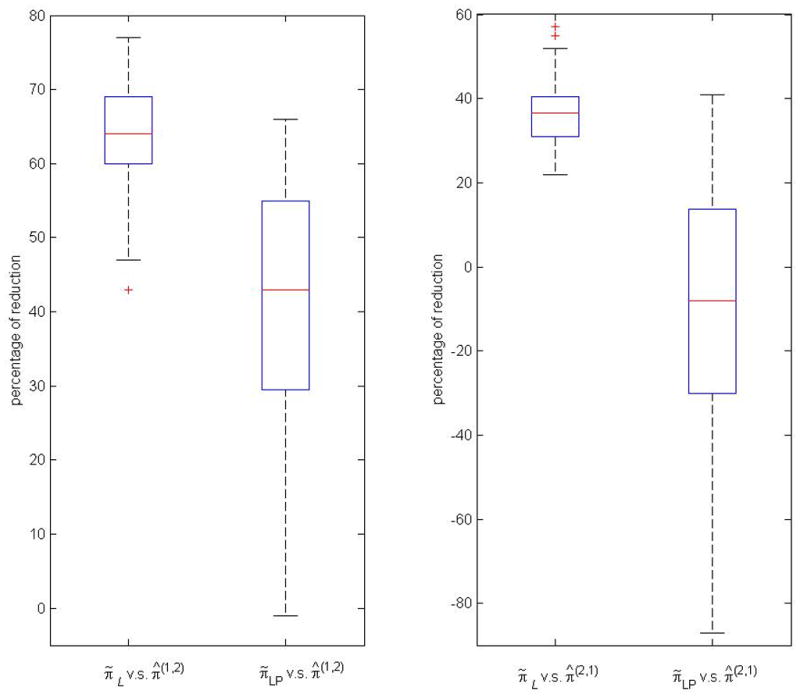
Box plots for the percentages of reductions in L2 of π̃L and π̂LP relative to π̂(1,2) (left panel), and to π̂(2,1) (right panel)
The outliers of π̂LP relative to π̂(1,2) (3 models with percentages of reductions less than −1) and to π̂(2,1) (3 models with percentages of reductions less than −87) are not shown in figure.
4. A Real Example
Table 7 is taken from Toffoli et al. (2006), which constitutes one of the largest prospective studies conducted to date to investigate the relationship between polymorphism in the gene region UGT1A1*28 and response to irinotecan for metastatic colorectal cancer patients. Toffoli et al. (2006) observed a significant increased risk of developing severe hematologic toxicity among patients carrying the TA7 allele. The hypothesis is that genetic testing for UGT1A1*28 polymorphism may have utility as a predictor of response to irinotecan. In Table 7, the row variable X1 represents polymorphism in gene region UGT1A*28 with three genotypes, TA6/TA6, TA6/TA7, and TA7/TA7. These genotypes are known to be associated with the response to treatment of a combination of irinotecan flourourail and leucovorin, which is represented by the column variable X2. The four categories of X2 are complete response, partial response, stable disease, and progressive disease, respectively coded as 1–4.
Table 7.
Cross-tabulation by UGT1A1*28 polymorphism and response to treatment (Toffoli et al., 2006)
| Polymorphism (X1) | Response to chemotherapy treatment (X2) |
Total | |||
|---|---|---|---|---|---|
| Complete response | Partial response | Stable disease | Progressive disease | ||
| TA6/TA6 | 10 | 34 | 29 | 36 | 109 |
| TA6/TA7 | 5 | 40 | 32 | 31 | 108 |
| TA7/TA7 | 3 | 11 | 5 | 2 | 21 |
Clinicians commonly use two conditional models for such data: the diagnostic model  (x1|x2) and the treatment model
(x1|x2) and the treatment model  (x2|x1). Of practical interest are the following sets of parameters: the diagnostic odds dij = P(x1 = i|x2 = j)/P(x1 = i|x2 = j + 1), 1 ≤ i ≤ 3, 1 ≤ j ≤ 3, and the response odds tij = P (x2 = j|x1 = i)/P (x2 = j|x1 = i + 1), 1 ≤ i ≤ 2, 1 ≤ j ≤ 4. We consider the following conditional models for
(x2|x1). Of practical interest are the following sets of parameters: the diagnostic odds dij = P(x1 = i|x2 = j)/P(x1 = i|x2 = j + 1), 1 ≤ i ≤ 3, 1 ≤ j ≤ 3, and the response odds tij = P (x2 = j|x1 = i)/P (x2 = j|x1 = i + 1), 1 ≤ i ≤ 2, 1 ≤ j ≤ 4. We consider the following conditional models for  and
and  in terms of dij and tij:
in terms of dij and tij:
-
Model A
dij/dij+1 = δ and tij/ti+1,j = ξ for all permissible i, j;
-
Model B
dij/dij+1 = δi and tij/ti+1,j = ξj for all permissible i, j; and
-
Model C
Logistic regression for both
 and
and  .
.
Using maximum-likelihood methods, we estimated the conditional distributions for all three models. Specifically, in Model C,  (x1|x2) was estimated by applying multinomial logistic regression of x1 on x2, and
(x1|x2) was estimated by applying multinomial logistic regression of x1 on x2, and  (x2|x1) was estimated by applying ordinal logistic regression of x2 on x1. Model A produces compatible
(x2|x1) was estimated by applying ordinal logistic regression of x2 on x1. Model A produces compatible  and
and  , while Models B and C do not. Ip and Wang (2009) show that when the odds ratios across the conditional distributions are identical, as in the case of Model A, then there exists a unique joint distribution. Table 8 shows the three pairs of respective conditional distributions under Models A, B, and C. For every conditional pairs, we compute the joint distributions of LP (π̂LP), fixed scan (π̂(1,2), and π̂(2,1)), and GE solutions via different weights (π̃L, π̃F, and π̃G). Table 9 compares the means and standard deviations of G2 divergence between the observed joint distribution (Table 7) and the estimated joint distributions out of 100 Monte Carlo replications.
, while Models B and C do not. Ip and Wang (2009) show that when the odds ratios across the conditional distributions are identical, as in the case of Model A, then there exists a unique joint distribution. Table 8 shows the three pairs of respective conditional distributions under Models A, B, and C. For every conditional pairs, we compute the joint distributions of LP (π̂LP), fixed scan (π̂(1,2), and π̂(2,1)), and GE solutions via different weights (π̃L, π̃F, and π̃G). Table 9 compares the means and standard deviations of G2 divergence between the observed joint distribution (Table 7) and the estimated joint distributions out of 100 Monte Carlo replications.
Table 8.
Conditional models for genetic data
| Model | Conditional Distributions | |||
|---|---|---|---|---|
 (x1|x2) (x1|x2) |
 (x2|x1) (x2|x1) |
|||
| A |
|
|
||
| B |
|
|
||
| C |
|
|
||
Table 9.
Mean and standard deviation of G2 divergence across 100 replications for the conditional models of genetic data
| G2 divergence | |||
|---|---|---|---|
| Model A | Model B | Model C | |
| π̂(1,2) | 1.367E-2 (4.626E-4) | 1.021E-2 (4.449E-4) | 6.733E-3 (3.671E-4) |
| π̂L | 1.367E-2 (3.175E-4) | 5.037E-3 (2.253E-4) | 5.892E-3 (2.107E-4) |
| π̃F | 1.367E-2 (3.290E-4) | 5.144E-3 (2.190E-4) | 5.566E-3 (1.997E-4) |
| π̃G | 1.367E-2 (3.291E-4) | 5.067E-3 (2.221E-4) | 5.416E-3 (2.020E-4) |
| π̂LP | 1.369E-2 | 7.899E-3 | 1.213E-2 |
Because Model A is compatible, both LP and Gibbs sampler converge to the same joint distribution, and GE offers no advantage over π̂LP and π̂(1,2), as expected. For incompatible Model B, every GE-based joint distributions outperforms both LP and fixed scan solutions. The coefficients of variation in G2 for π̃L, π̃F, and π̃G were all below 7%, suggesting that the divergences of GE-based distributions are consistent over Monte Carlo replications.
For Model C (Table 9), GE also outperforms LP and fixed scan. Several observations can be made. First, the standard deviations of the replications are slightly smaller than the standard deviations under Model B. The coefficients of variation for both Model B and Model C are less than 5%, again suggesting that GE are quite robust to Monte Carlo variations. Second, the divergences of LP in Model C are 20% to 70% larger than those in Model B across different divergence measures. Note that the observed values of the conditional distribution for P (x1|x2 = 2) are (0.400, 0.4706, 0.1294), which is close to the estimated values for the corresponding cell (0.3877, 0.5008, 0.1115) under Model C.
If only π̂LP were computed and we had adopted the G2 divergence of π̂LP as the sole criterion for selecting model, then Model B would hands-down win over Model C. However, we have computed GE solution and according to their G2 divergence, the advantage of Model B over Model C is only marginal (Table 9). This shows that goodness-of-fit indices can be quite different when using LP and GE.
The G2-statistic for Model A, B and C are respectively 6.5069, 2.4119 and 2.5780; whereas the Akaike’s information criterion (AIC) value are respectively 10.5069, 12.4119 and 12.5780. The G2-statistic is the G2-divergence multiplied by twice the sample size, here 2 × 238. Model A has the smallest value of AIC, which suggests that model A is more efficient (adjusted for model complexity) than models B and C. Using Model A as the basis, the diagnostic odds (dij) and response odds (tij) matrices calculated from its joint distribution are as follows:
Matrix (dij) is partitioned horizontally by genotype along the line of locus TA7; the values of dij in the row of TA6/TA6 are all less than 1, while the rows corresponding to TA6/TA7 and TA7/TA7 are all larger than 1. Moreover, matrix (tij) is partitioned vertically between patients who respond positively to irinotecan versus those who do not benefit from the treatment. That is, the response odds are less than 1 for x2 = 1 and 2 and larger than 1 for x2 = 3 (no response) and x2 = 4 (worsening response).
An interesting thought from examining the goodness-of-fit indices is the possibility of using the Gibbs solution to replace the pseudolikelihood in inference. Under Model C of Table 8, the G2-statistic for  (x1|x2) is 4.03 (p-value = 0.2578) and the G2-statistic for
(x1|x2) is 4.03 (p-value = 0.2578) and the G2-statistic for  (x2|x1) is 6.31 (p-value = 0.0426). Therefore, the combined G2-statistic for pseudolikelihood
(x2|x1) is 6.31 (p-value = 0.0426). Therefore, the combined G2-statistic for pseudolikelihood  (x1|x2)
(x1|x2) (x2|x1) is (4.03 + 6.31)/2 = 5.17, where the averaging is to compensate for using the observed table twice. The G2-statistic of π̃G under Model C is 2.578 (p-value = 0.7647), which is less than half of 5.17. Hence, the estimated joint distribution π̃G is a closer representation of the observed table than the pseudolikelihood. The pros and cons of these two approaches deserve further study.
(x2|x1) is (4.03 + 6.31)/2 = 5.17, where the averaging is to compensate for using the observed table twice. The G2-statistic of π̃G under Model C is 2.578 (p-value = 0.7647), which is less than half of 5.17. Hence, the estimated joint distribution π̃G is a closer representation of the observed table than the pseudolikelihood. The pros and cons of these two approaches deserve further study.
5. Discussions
For high-dimensional data, a reduced model may be formulated in at least two ways: as an undirected graphical model in which all variables are considered jointly or as a system of univariate conditional models, which can be depicted as a cyclic, directed graph (Heckerman et al., 2000). In the second approach, as observed by Dobra et al. (2004), the conditionally specified models almost surely do not cohere to a proper joint distribution. It is therefore important to study and compare the joint distributions obtained through different methods of estimation. In this paper, we compare the Gibbs distribution, LP, and GE when conditional models are not compatible.
Our results have been primarily based on empirical studies. Liu (1996) provided several observations about the behavior of Gibbs distributions that are consistent with our empirical work. As long as the transition matrix corresponding to (1) is irreducible and aperiodic, the Gibbs sampler has a recurrent joint distribution. For two-dimensional conditional models that are not compatible, the two fixed scanned Gibbs (recurrent) distributions π̂(1,2) and π̂(2,1) are known to be the two extreme points in the space of all the Gibbs distributions. The usual random scan Gibbs distribution has two characteristics: (a) any of its odds ratios will be sandwiched between the corresponding odds ratios of π̂(1,2) and π̂(2,1), and (b) its one-dimensional marginal distributions are identical to those of π̂(1,2). Briefly, the space of all the Gibbs distributions consists of joints having the same marginals and having odds ratios that are confined to ranges determined by π̂(1,2) and π̂(2,1).
In this paper, we use divergences to compute the proper weights for combining the extreme Gibbs distributions. Thus, the GE solutions represent mixtures of the Gibbs distributions. For three variables with 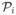 (xi|xj, j ≠ i), the space of all Gibbs distributions is more complicated: (a) only the invariant interactions (Ip and Wang, 2009), not all of the odds ratios, can reoccur in the Gibbs distributions; (b) there are four different two-dimensional marginal distributions; and (c) there are three different one-dimensional marginal distributions shared by 3! = 6 distinct fixed scan Gibbs distributions. Every GE solution is a mixture of π̂(i,j,k) and (i, j, k) ∈ S3, and its combination weights can be computed via the selected divergence.
(xi|xj, j ≠ i), the space of all Gibbs distributions is more complicated: (a) only the invariant interactions (Ip and Wang, 2009), not all of the odds ratios, can reoccur in the Gibbs distributions; (b) there are four different two-dimensional marginal distributions; and (c) there are three different one-dimensional marginal distributions shared by 3! = 6 distinct fixed scan Gibbs distributions. Every GE solution is a mixture of π̂(i,j,k) and (i, j, k) ∈ S3, and its combination weights can be computed via the selected divergence.
Two observations can be made about the mixture distributions. First, the number of odds ratios are (K1 − 1)(K2 − 1) and (K1 − 1)(K2 − 1)(K3 − 1)+ Σ(Ki − 1)(Kj − 1) for (X1, X2) and (X1, X2, X3), respectively, where Xi assumes Ki values. The optimization problem becomes more challenging because the number of parameters grows quickly with the number of variables. GE reduces the optimizations to one-dimensional problems instead of searching for optimal odds ratios in every range. Second, the marginal distributions of GE are confined to those that can be generated by the Gibbs samplers. It is possible that some perturbations of the marginal distributions could reduce the divergence. However, we observe that in the two-dimensional case the marginals of LP are always close to the marginals of GE. For the example in Section 4, the three π̃’s under Model A, Model B, and Model C produce nearly identical X1-marginal and X2-marginal distributions. Thus, we conjecture that the marginals of Gibbs distributions are not far from optimal.
The GE offers a computationally feasible approach in obtaining optimal or nearly optimal solutions for conditionally specified models. Unlike methods based on LP, the GE approach described here can be generalized to high-dimensional problems in straightforward ways. The computational burden is also more manageable than with LP. Furthermore, we provide evidence that the performance of GE is at least comparable, if not better, than LP. Finally, we show that Gibbs distributions can be improved upon by using ensembles. By varying scan patterns to generate ensembles of Gibbs distributions, we believe that the power of GE can be further expanded. Instead of using pre-determined probabilities to perform random scan, one may be able to further refine the search in the space of a Gibbs distribution for a better solution for nearly compatible and incompatible conditional models.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Contributor Information
Shyh-Huei Chen, Email: chensh@yuntech.edu.tw, Department of Industrial Management, National Yunlin University of Science and Technology, Douliu, Yunlin 640, Taiwan.
Edward H. Ip, Email: eip@wfubmc.edu, Department of Biostatistical Sciences, Wake Forest University School of Medicine, Winston-Salem, North Carolina 27157, U.S.A
Yuchung J. Wang, Email: yuwang@crab.rutgers.edu, Department of Mathematical Sciences, Rutgers University, Camden, New Jersey 08102, U.S.A
References
- Arnold BC, Castillo E, Sarabia JM. Exact and near compatibility of discrete conditional distributions. Computational Statistics and Data Analysis. 2002;16:231–252. [Google Scholar]
- Arnold BC, Gokhale DV. Distributions most nearly compatible with given families of conditional distributions. Test. 1998;7:377–390. [Google Scholar]
- Besag JE. Spatial interaction and the statistical analysis of lattice systems (with discussion) Journal Royal Statistical Society B. 1974;36:192–236. [Google Scholar]
- Besag JE. Efficiency of pseudo-likelihood estimators for simple Gaussian fields. Biometrika. 1977;64:616–618. [Google Scholar]
- Bühlmann P. Bagging, boosting and ensemble methods. In: Gentle J, Härdle W, Mori Y, editors. Handbook of Computational Statistics: Concepts and Methods. Springer-Verlag; Berlin, Heidelberg: 2004. pp. 877–907. [Google Scholar]
- Dobra A, Hans C, Jones B, Nevins J, Yao G, West M. Sparse graphical models for exploring gene expression data. Journal of Multivariate Analysis. 2004;90:196–212. [Google Scholar]
- Geman S, Geman D. Stochastic relaxation, Gibbs distributions, and the Bayesian restoration of images. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1984;6:721–741. doi: 10.1109/tpami.1984.4767596. [DOI] [PubMed] [Google Scholar]
- Heckerman D, Chickering DM, Meek C, Rounthwaite R, Kadie C. Dependence networks for inference, collaborative filtering and data visualization. Journal of Machine Learning and Research. 2000;1:49–57. [Google Scholar]
- Ip EH, Wang YJ. Canonical representation of conditionally specified multivariate discrete distributions. Journal of Multivariate Analysis. 2009;100:1282–1290. [Google Scholar]
- Israel RB. Gibbs distributions ii. In: Kotz S, Read C, Balakrishnan N, Vidakovic B, editors. Encyclopedia of Statistical Sciences. 2. Vol. 4. John Wiley & Sons, Inc; New York: 2005. pp. 2838–2843. [Google Scholar]
- Jensen JL, Künsch HR. On asymptotic normality of pseudo likelihood estimates for pairwise onteraction processes. Annals of the Institute of Statistical Mathematics. 1994;46:475–486. [Google Scholar]
- Jensen JL, Møller J. Pseudolikelihood for exponential family models of spatial point processes. Annals of Applied Probability. 1991;1:455–461. [Google Scholar]
- Levine R, Casella G. Optimizing random scan Gibbs samplers. Journal of Multivariate Analysis. 2006;97:2071–2100. [Google Scholar]
- Liu JS. Discussions on statistical theory and monte carlo algorithms (with discussions) Test. 1996;5:305–310. [Google Scholar]
- Toffoli E, Cecchin E, Corona G, Russo A, Buonadonna A, D’Andrea M, Pasetto L, Pessa S, Errante D, De Pangher V, Giusto M, Medici M, Gaion F, Sandri P, Galligioni E, Bonura S, Boccalon M, Biason P, Frustaci S. The role of UGT1A1*28 polymorphism in the pharmacodynamics and pharmacokinetics of irinotecan in patients with metastatic colorectal cancer. Journal of Clinical Oncolog. 2006;24:3061–3068. doi: 10.1200/JCO.2005.05.5400. [DOI] [PubMed] [Google Scholar]


