Bending and Puncturing the Influenza Lipid Envelope

Abstract

Lysosomes, enveloped viruses, as well as synaptic and secretory vesicles are all examples of natural nanocontainers (diameter ≈ 100 nm) which specifically rely on their lipid bilayer to protect and exchange their contents with the cell. We have applied methods primarily based on atomic force microscopy and finite element modeling that allow precise investigation of the mechanical properties of the influenza virus lipid envelope. The mechanical properties of small, spherical vesicles made from PR8 influenza lipids were probed by an atomic force microscopy tip applying forces up to 0.2 nN, which led to an elastic deformation up to 20%, on average. The liposome deformation was modeled using finite element methods to extract the lipid bilayer elastic properties. We found that influenza liposomes were softer than what would be expected for a gel phase bilayer and highly deformable: Consistent with previous suggestion that influenza lipids do not undergo a major phase transition, we observe that the stiffness of influenza liposomes increases gradually and weakly (within one order of magnitude) with temperature. Surprisingly, influenza liposomes were, in most cases, able to withstand wall-to-wall deformation, and forces >1 nN were generally required to puncture the influenza envelope, which is similar to viral protein shells. Hence, the choice of a highly flexible lipid envelope may provide as efficient a protection for a viral genome as a stiff protein shell.

Introduction

Small unilamellar vesicles (SUVs) are, by definition, liposomes with a size that goes up to 100 nm. Those highly curved, closed lipid bilayers are naturally encountered in many contexts, as they constitute the frame for organelles such as lysosomes, endosomes, exosomes, and endocytosis and exocytosis vesicles, as well as the lipid envelope for viruses, e.g., influenza, Herpes, or HIV. Most of the aforementioned species act as physiological or pathological containers, which are able to exchange molecules within a single cell or with the extracellular space by merging with the plasma membrane.

Before fusion, lipid bilayers must act as a barrier against the external environment. Whereas one could imagine mimicking nature in fabricating liposome-based containers for drug delivery, it turns out that plain liposomes are not resistant enough and often require stabilization schemes to increase their lifetime in the human body (1). In particular, SUVs are known for being less stable than giant unilamellar vesicles (GUVs) and planar bilayers (2), and are therefore expected to be relatively inefficient in pharmaceutical applications. For this reason, the choice of a lipid bilayer as a component of the genome-protecting envelope of viruses such as influenza is striking: Influenza, a 100-nm-diameter enveloped virus, was shown to be able to persist for days in rather harsh conditions (3), but unexpectedly (4), its lipid membrane is thought to be rather fluid and soft over a large range of temperatures (5). It therefore has to be determined whether the lipid envelope of the influenza virus is on its own an effective barrier, or if it requires the participation of a viral protein capsid to fulfill its protective role.

Studying the stability of highly curved vesicles and related organelles/viruses is of great interest for both fundamental and applied purposes, as this may lead to a better understanding of biological phenomena such as the assembly and stability of enveloped viruses, as well as to new solutions to stabilize liposomes as drug carriers. Unfortunately, only limited quantitative information on the mechanical properties of small liposomes exists so far (6), contrary to GUVs, which have been studied for 30 years (7).

We set out to investigate the mechanical properties of the influenza lipid envelope using a precise, atomic force microscopy (AFM)-based force spectroscopy method that relied on tight selection of particles with respect to their morphology, and finite-element methods (FEM), to extract the bending rigidity, area compressibility, and Young's modulus out of our data. Extruded SUVs made from PR8 influenza virus lipids were found to be rather stiff compared to dimyristoyl-phosphatidylcholine (DMPC) and DMPC/cholesterol liposomes, but remained flexible and reversibly deformable at rather high indentations, and no major transition in stiffness or elastic behavior was observed upon temperature decrease: This suggests that the influenza virus envelope is rather fluid and, instead of going through a major phase transition, progressively disorders from 10 to 40°C, consistent with previous findings (5).

Application of ∼1 nN point forces led to the puncture of the bilayer of influenza SUVs, which generally occurred after a full collapse of the vesicle, and was often reversible. Surprisingly the average force required to puncture an influenza SUV was in a similar range to the rupture limit of viral protein capsids (8,9). We therefore show that a relatively stiff, yet fluid lipid bilayer as a protective envelope may be as good as a strategy utilizing protein shells with high stiffness.

Materials and Methods

Lipids

DMPC (1,2-dimyristoyl-sn-glycero-3-phosphocholine) and cholesterol used in this work were purchased from Avanti Polar Lipids (Alabaster, AL). Influenza lipids were extracted from A/PR8 influenza virions that were purified from hen eggs following the procedure described by Korte et al. (10). A phosphate-buffered saline suspension of influenza viruses was treated with chloroform/methanol: Lipids were extracted following Bligh and Dyer (11). The proteins were separated from the lipids with methanol/chloroform (2:1) phase-separation. The total amount of phospholipids recovered after extraction was determined following Böttcher et al. (12). The lipid composition for egg-purified PR8 influenza viruses was determined via thin-layer chromatography (in molar %): sphingomyelin (22.1), phosphatidylserine (22.2), phosphatidylethanolamine (33.3), and phosphatidylcholine (15.1). The ratio of cholesterol over total lipids was 0.43 as determined by an enzymatic assay (13).

Liposome preparations

All SUVs were prepared by a classic extrusion method (14). To make unilamellar liposomes, lipid powder was dissolved in chloroform to ≈5 mg/mL in a glass test tube. The solvent was dried under nitrogen and then further dried for 2 h in vacuum. Dried lipids were resuspended at a 1 mM final concentration (DMPC into deionized filtered water, influenza lipids in 5 mM HEPES, 150 mM sodium chloride, pH 7.4). After vortexing and sonicating the suspension (1 min each), the liposomes were frozen and thawed in a hot water bath.

After five freeze-thaw cycles, liposomes were extruded 31 times through two layers of 100-nm or 200-nm filters (Whatman, Kent, UK). This procedure is known to yield >90% unilamellar vesicles (15). Cholesterol-DMPC liposomes were made by dissolving DMPC and cholesterol in chloroform at an equimolar ratio. The size of the vesicles in extruded preparations was verified by dynamic light scattering, vesicle concentration ≤0.05 mM). Dynamic light scattering samples were diluted below 0.1 mM in 1 mL of water and measured after 10 min equilibration on an ALV/CGS3 (Langen, Germany). Influenza lipids were kept under nitrogen at all times. Except for influenza liposomes, which were kept in buffer, all liposomes were prepared in water.

Surface chemistry

All glass substrates were first thoroughly cleaned by KOH etching, and subsequently coated with a positively-charged silane, DETA (3-[2-(2-aminoethylamino) ethylamino] propyltrimethoxysilane). Approximately 10 g of KOH were first dissolved in 20 mL water and supplemented with 200 mL ethanol. Microscope coverslips placed in a Teflon holder were immersed in the KOH-filled container. The container was sonified in a bath sonicator for 5 min; subsequently both the container and rack were rinsed and sonicated three times in filtered and deionized water, each time 5 min. For the silanization step, the coverslips were sonicated again for 5 min in a container filled with fresh water, to which 200 μL of DETA (Sigma Aldrich, St. Louis, MO) and 30 μL of acetic acid were added. Next, the coverslips were sonicated for 5 min in clean water, three times. Finally, the Teflon rack was placed in an oven until the coverslips were completely dry (20 min at 100°C).

AFM and cantilevers

AFM experiments were carried out with a MFP-3D (Asylum Research, Santa Barbara, CA). Liposomes were diluted 250 times in water or buffer and 100 μL of this dilution was deposited on a DETA surface. The cantilevers (model No. BL-RC150VB, spring constant k_cl = 0.0309 ± 0.005 nN/nm average ± SE, n = 86, tip radius ≈ 30 nm; Olympus Optical, Tokyo, Japan) were purchased from Atomic Force (Mannheim, Germany). For each sample, the cantilever spring constant was determined from the power spectral density of thermally driven cantilever fluctuations (16). Before each measurement, the cantilever was kept under the ultraviolet lamp for 15 min, and then prewetted with 20 μL buffer. If not specified, the experiments were carried out at 26°C.

Imaging and force mapping

The images of liposomes were acquired using tapping mode (oscillating the cantilever at ≈6 kHz with a 3-nm amplitude) in liquid, and the estimated forces applied on the vesicles were <0.1 nN. To determine the stiffness of the liposomes, force maps were obtained by collecting force-versus-distance curves (FZ curves, sampled at 2 kHz) on an array of 24 × 24 points covering an area of ∼300 × 300 nm square encompassing the particle. Each FZ curve gives the relation between the Z-piezo extension (height) and the bending of the cantilever (force). To avoid damaging or displacing the liposomes the applied forces were limited to 0.3 nN during force mapping. Approximately 50–70 liposomes were probed for each species (DMPC, DMPC-cholesterol (1:1), influenza liposomes).

Liposome stiffness analysis

Only approximately spherical liposomes were considered for further analysis. For each imaged liposome, the height was used to calculate the expected dilation effect of imaging with a parabolic tip (see Eq. 2). If the width of the imaged liposome deviated by <30% from this expected width, it was considered acceptable.

Routines written in LabVIEW (National Instruments, Austin, TX) were devised to perform the following operations on force maps:

• 1.Create a height image by defining for each pixel the Z-piezo position at which the liposome gets touched (i.e., when the cantilever starts to bend).
• 2.Fit a plane to the background height points and subtract this from the height image.
• 3.Average the FZ curves obtained on the background glass surface and perform a linear fit to obtain the slope, which allowed for an in situ calibration.
• 4.Find the center of the particle by averaging the X-Y position of the eight highest pixels.
• 5.Average the FZ-curves obtained on the liposomes. The particle image was divided into concentric circular regions and average FZ curves were calculated for each region. (After comparing the different regions, only curves obtained within 20 nm from the center were used; see also Fig. 2.) On average, four curves were selected and averaged per particle.
• 6.Obtain the stiffness for each region on the liposome (k_ms) by performing a linear fit between 0.1 and 0.2 nN on the average FZ curves. This stiffness is the combined stiffness of the cantilever (k_cl) and the sample placed in series.
• 7.Extract the liposome stiffness (k_l) using

$$k_l={\left(k_{ms}^{-1}-k_{cl}^{-1}\right)}^{-1}.$$ (1)

Figure 2.

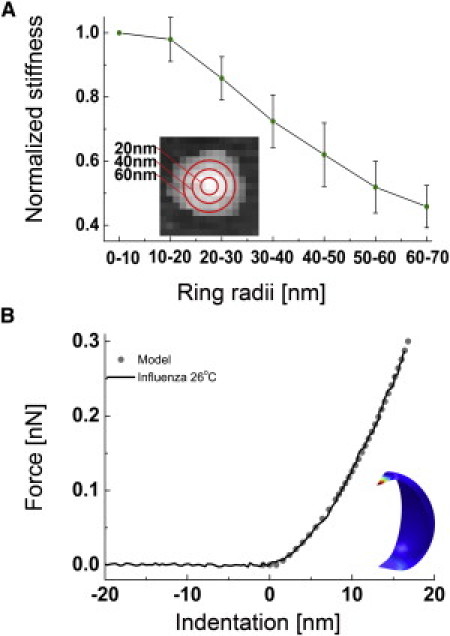
Dependency of the influenza liposome stiffness on the probed region. (A) The liposome was divided in concentric areas for which the average stiffness was measured (e.g., the pixels enclosed by the circles of 30-and 40-nm radius). The plot shows the normalized stiffness for 15 liposomes, the stiffness decreases when the liposome is probed further away from its center. (B) Averaged force versus indentation curve of a 71-nm-high influenza liposome, obtained by averaging four curves obtained within 20 nm from the center. The stiffness was obtained by performing a linear fit between 0.1 and 0.2 nN. (Shaded dots) Response calculated with FEM (d = 70 nm, E = 30 MPa). (Inset) Deformation of the thin-shell model by a hyperbolic tip and a flat surface.

Finite element modeling

To compute the relation among the diameter of a liposome, its spring constant, and the membrane elasticity, we modeled the indentation of a spherical shell with the atomic force microscope tip by finite element methods (COMSOL Multiphysics 3.5, Comsol, Stockholm, Sweden). The sphere was set to be resting on a rigid flat surface. The radial-symmetric atomic force microscope tip with a hyperbolic cross-section profile f (x) was used to indent the vesicle,

$$f\left(x\right)=\frac{1}{\tan \theta }\left(\sqrt{x^2+\frac{t_r^2}{{\tan }^2\theta }}-\frac{t_r}{\tan \theta }\right),$$ (2)

where x is the distance to the symmetry axis. The tip radius t_r was set to 20 nm, and the open angle θ (with respect to the symmetry axis) to 30°. The contacts between the shell and the tip and the supporting surface during indentation were implemented with a contact-penalty stiffness method according to the manufacturer's manual. The model was simplified to a quarter sphere by making use of the symmetry planes, and meshed with >2000 thin shell elements. A parametric, nonlinear solver was used to simulate the stepwise lowering of the tip onto the sphere.

The elastic properties of the thin shell elements used in the model are described by its Young's modulus E and the shell thickness t. However, the elastic properties of lipid bilayers are generally expressed by the bending rigidity, K_b, and the area compressibility modulus, K_a. Both parameters are a combination of E and t,

$$K_b=\frac{E\times t^3}{\alpha \left(1-v^2\right)},K_a=\frac{E\times t}{1-v^2},$$ (3)

where v (Poisson ratio) was set to 0.5, and α was set to 24, as this best describes the bending of lipid bilayers (17). The ratio K_b/K_a has been found to be almost constant with values between 3 and 5 × 10⁻¹⁹ m² (18), which allows combining the expressions in Eq. 3 to calculate the shell thickness:

$$\raisebox{1ex}{$K_b$}\!\left/ \!\raisebox{-1ex}{$K_a$}\right.=\frac{t^2}{24}.$$ (4)

Choosing K_b/K_a = 4 × 10⁻¹⁹ m² gives t = 3.1 × 10⁻⁹ m. Such a reduced thickness (with respect to the real thickness of lipid bilayers) can be understood as the effective thickness of the lipid bilayers. The two leaflets are replaced by a thinner single sheet to maintain the same bending rigidity. Indentation curves for models with diameters from 30 nm to 120 nm were calculated, varying the Young's modulus between 8 and 75 MPa in steps of 1 MPa. The stiffness of the theoretical FZ curves was obtained by a linear fit between 0.1 and 0.2 nN. For the given boundary conditions and input parameters (d, t, and E), the relations among the liposome stiffness, its height d, and the Young's modulus empirically followed within 4%:

$$k_l\approx \raisebox{1ex}{$47\times {10}^5\times E^{0.53}\times t^2$}\!\left/ \!\raisebox{-1ex}{$d^{0.66}$}\right..$$ (5)

To compare the stiffness of liposomes with different lipid compositions or temperatures, a stiffness-versus-height graph was plotted for each species, which was fitted to Eq. 5 by minimizing the residual error for all vesicles. The average stiffness k₁₀₀, the stiffness of a 100-nm high liposome, was determined using the fitting constant E. The standard error for the determination of k₁₀₀ was the square root of the average squared residual from the data fitting to Eq. 5, divided by the square root of the number of measurements (n). K_b and K_a were then calculated using the expressions in Eq. 3.

Water compression in the vesicles is inexistent on the time- and length-scale of the experiment, due to the relative high rate of water transport across the membrane. A 100-nm-diameter liposome has a surface area of 31 × 10³ nm² and the permeability of its lipid bilayer is ∼1 × 10⁴ nm/s, assuming a fluid state (19): Hence 3 × 10⁸ nm³ water diffuses through the lipid bilayer in a second, which exceeds the volume of the liposome (5 × 10⁵ nm³) by almost three orders of magnitude.

In the case of influenza liposomes that were prepared in 150 mM salt buffer, the effect of the osmotic pressure building up with indentation is also negligible. For a 100-nm-diameter liposome, the osmotic pressure calculated from our model is 3 kPa at a 15-nm indentation, at 0.2 nN. The local pressure applied by the atomic force microscope tip is much higher (∼3 MPa) under similar conditions.

Influenza membrane puncturing

Force maps recorded at nN forces most often resulted in displaced or irreversibly damaged liposomes and could therefore not be used to analyze the response of liposomes in such high force range. Hence DETA-bound influenza liposomes were subjected to single point pushes on top of them, performed at forces going up to 2 nN and at a loading rate of 1 μm/s: After tapping mode imaging, liposomes were generally subjected to four consecutive pushes at 2 nN, then imaged again to verify that the pushes were performed in the center of the liposome. If the particle was not removed after the pushing cycles, another cycle was performed. Nine FZ curves were performed on average per particle, corresponding to 2–3 cycles of imaging/pushing. Puncturing was defined as a negative change in the FZ slope which amplitude exceeded twice the standard deviation of the noncontact part of the FZ curve.

Results

In our study, we investigated the mechanical properties of the influenza lipid envelope being devoid of viral proteins. For this purpose, we prepared mimics of the influenza lipid envelope that consisted of SUVs made from lipids purified from influenza virus (A/PR8 strain). SUVs obtained by extrusion are comparable in size with influenza virions, and therefore allow performing a direct characterization of the virus lipid properties in a physiologically and geometrically relevant context.

The method used to probe the elasticity of single influenza liposomes (among others) is summarized in Fig. 1. First, a liposome was imaged once in tapping mode (Fig. 1 A) before acquiring a force map (Fig. 1 B). Horizontal cross sections of the particles show that their height and width are similar for both scans. The apparent width is exaggerated because of the tip-dilation effect. The maximum height, however, is not affected by the tip shape. Vesicles that appeared collapsed, elongated, or with an apparently aberrant (i.e., nonspherical) aspect ratio were excluded from further analysis (see Materials and Methods).

Figure 1.

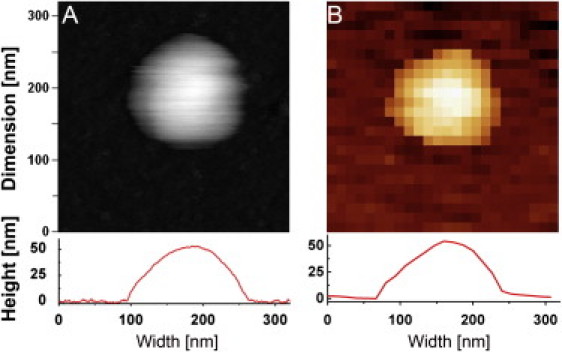
AFM imaging and stiffness measurements on small unilamellar vesicles. (A) A tapping mode height image of a liposome in buffer (320 × 320 nm scan size, 256 × 256 pixels). (Inset below) Cross-section height profile of the liposome. (B) A reconstructed height image from a force map of the same liposome (320 × 320 nm scan size, 24 × 24 pixels). Each pixel contains one FZ curve from which the height and stiffness at that point can be measured. (Inset below) Cross-sectional height profile from the force map shows the same height as in tapping mode.

The stiffness of the influenza liposomes was obtained from the slope of the FZ curves obtained on top of the liposomes (Eq. 1). Because the contact area between the tip and the liposome increases during the indentation, the load becomes more distributed and the measured stiffness (slope of the curve) is not constant during indentation. To quantify the influence of these variable boundary conditions and relate the measured stiffness to the area compressibility K_a and bending rigidity K_b of the membrane, we modeled the experiment using finite element modeling (FEM). A spherical shell model resting on a flat surface was indented by a hyperbolic atomic force microscope tip (Fig. 2 B, inset). The thickness of the shell was set to 3.1 nm and the Young's modulus adjusted to match the experimental values (see Materials and Methods). Fig. S5 in the Supporting Material shows how the calculated stiffness varies with different boundary conditions. We defined our standard stiffness as the slope of a linear fit of the force-versus-indentation curves between 0.1 and 0.2 nN. At this maximum force of 0.2 nN, the average deformation was <20% of the liposome diameter (see Fig. S2 and Table S1 in the Supporting Material).

To optimize the accuracy of the stiffness determination, FZ curves performed on top of the vesicle were averaged. However, when a vesicle is probed close to its edge, it is expected to deform more easily (due to the lack of support by the surface) than when it is probed in its center. To demonstrate the dependence of the stiffness on the distance to the vesicle center, 15 individual liposomes with diameters of 70 ± 10 nm were analyzed: The stiffness was calculated by averaging the FZ curves enclosed in concentric circles with increasing radii, centered on top of the vesicle (Fig. 2 A). As expected, the average stiffness decreased significantly as the probed perimeter was moved toward the edge of the particle. Therefore, only FZ curves from pixels within a maximum 20 nm from the liposome center were selected for averaging and stiffness analysis. The averaged FZ curves were converted into force-versus-indentation curves (Fig. 2 B and Eq. 1).

After extrusion, the size of influenza liposomes was distributed between 40 and 150 nm. The stiffness of liposomes is expected to vary as function of their size. Fig. 3 A, in which the stiffness versus height was plotted for 68 individual influenza liposomes, shows a clear negative correlation, and an average stiffness for a 100-nm-diameter particle k₁₀₀ of 0.02 ± 0.003 nN/nm. For a hollow, thin-walled spherical vesicle made out of a homogenous material and subjected to two opposing point loads, the diameter d scales with the reciprocal of the stiffness k (d ∝ 1/k) (20). In our experiments, however, there are two reasons why this scaling may be violated:

• 1.The vesicles are indented with an atomic force microscope tip and supported by a planar surface, giving rise to nonlinear boundary conditions.
• 2.The vesicles are composed of a lipid bilayer, in which the leaflets can slide on each other, and in which the lipids can diffuse in the plane of the layer.

Figure 3.

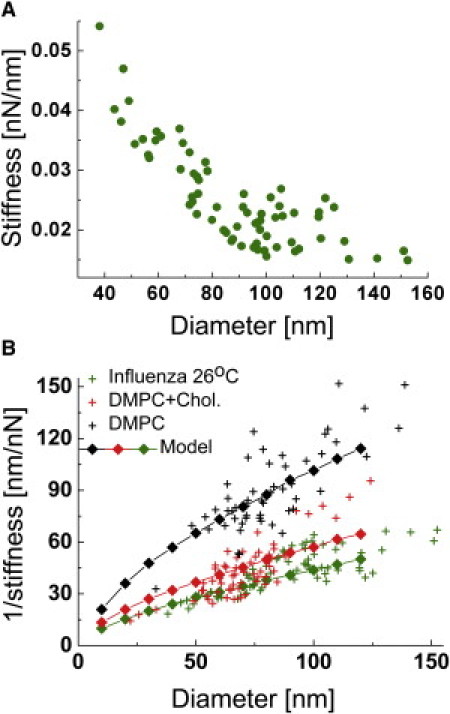
Stiffness of influenza and DMPC liposomes. (A) Stiffness versus diameter plot of influenza liposomes. The stiffness of liposomes increased with decreasing liposome diameter. (B) 1/stiffness versus diameter plot of influenza liposomes compared with DMPC and DMPC/cholesterol 1:1 (mol/mol) liposomes. (Green crosses) Reciprocal of the data presented in Fig. 3A. (Black crosses) DMPC liposomes. (Red crosses) DMPC/cholesterol (1:1, mol/mol) liposomes. Each scatter plot was overlaid with a finite element model of the liposome indentation by AFM. After fitting the stiffness distributions with Eq. 5, the average stiffness for a 100-nm-diameter vesicle was calculated. From the ratio of the average stiffness values, we found that the DMPC/cholesterol liposomes were on average 100% stiffer, and influenza liposomes 110% stiffer than DMPC liposomes.

Nevertheless, plotting the reciprocal values of the stiffness versus height (Fig. 3 B, green crosses) shows that the diameter of the particles scales almost exactly with 1/k, suggesting that SUVs do not have an unexpected mechanical behavior.

The FEM calculation was repeated for liposome diameters from 10 to 120 nm, and the modeled stiffness was matched to the experimental data (Eq. 5).The green diamonds in Fig. 3 B show that the model describes well the height dependency of the liposome stiffness, but the relation between 1/k and d is not exactly linear. For small liposomes, the atomic force microscope tip is relatively large compared to the vesicle such that it effectively is squeezed between two plates, rather than being indented with a sharp tip, as is the case for larger vesicles. This effect of the relative tip size compared to the liposome size shows in the simulation as a shallow kink in the curve at ∼40 nm (Fig. 3 B).

The actual data in Fig. 3 B shows a rather opposing trend; the model underestimates 1/k for the larger particles, which may relate to an increased effect of the fluidity for larger liposomes, reducing their stiffness. Our model assumes continuum mechanics, and therefore does not account for the fluidity of the lipids in the leaflets (which in principle can be implemented in custom-written packages (21)). The mobility of lipids is particularly important when the membrane is to undergo large changes in shape and curvature. In our experiments, such changes are most pronounced for larger liposomes. The radius of the atomic force microscope tip is relatively small for these liposomes, such that the induced change in curvature will be large.

To validate the values for K_a and K_b that were derived from the model, AFM experiments were performed with liposomes made out from lipids with known mechanical properties. Measurements on DMPC and DMPC/cholesterol 1:1 (mol/mol) liposomes are shown in Fig. 3 B: The calculated values for K_a and K_b (Table 1) are in very good agreement with those previously obtained by micropipette suction (K_b at ∼10 kT, ≈ 0.4 × 10⁻¹⁹ J for DMPC in fluid phase and 30 kT for DMPC/cholesterol 2:1) (1). Influenza lipids were much stiffer than DMPC liposomes and even stiffer than DMPC/cholesterol (1:1) liposomes, although the latter species have a comparable fraction of cholesterol. This relates to the composition of the influenza lipids, which has longer and saturated acyl chains. Despite their higher stiffness, influenza lipids were found to have a K_a and K_b reflecting a rather fluid phase at 26°C. In particular, the bending rigidity K_b was ∼20 kT—which is far lower than the value that was previously determined for DMPC GUVs in gel state (22).

Table 1.

Mechanical parameters of different liposomes

Liposome	k100 (nN/nm)	E (MPa)	Ka (N/m)	Kb (J)
Influenza, 13°C (n = 53)	0.027 ± 0.0011	68	0.28	1.13 × 10−19
Influenza, 26°C (n = 68)	0.021 ± 0.0007	45	0.19	0.75 × 10−19
Influenza, 37°C (n = 60)	0.019 ± 0.0006	37	0.15	0.61 × 10−19
DMPC, 25°C (n = 55)	0.010 ± 0.0003	11	0.05	0.18 × 10−19
DMPC+cholesterol 1:1 (mol) at 25°C (n = 60)	0.020 ± 0.0008	40	0.17	0.66 × 10−19
DPPC, gel phase (23)	n.d.	115	n.d.	∼1 × 10−18

n.d., not determined.

During their lifecycle, influenza virions are subjected to a range of temperatures that can alter the stiffness of their envelope and potentially their survival rate. We have measured the stiffness of influenza liposomes at 13 ± 2°C, 26 ± 2°C, and 37 ± 1°C (Fig. 4). The average stiffness values (Table 1) decreased with increasing temperature. Influenza liposomes were always flexible (reversibly deformed; see Fig. S1) when pushed with <0.3 nN forces and the change of stiffness was less than twofold between 13 and 37°C, suggesting that influenza liposomes do not undergo a large transition to a rigid gel or solid phase at lower temperature.

Figure 4.

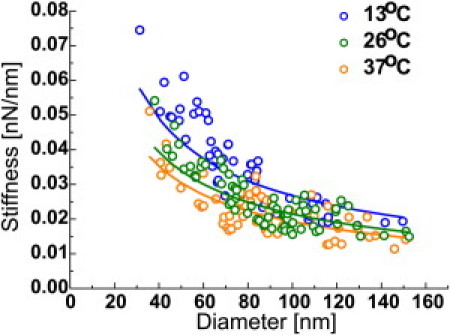
Temperature influence on the stiffness of influenza liposomes. Influenza liposomes at 13 ± 2°C (blue dots), 26 ± 2°C (green dots), and 37 ± 1°C (orange dots). After fitting the stiffness distributions for each case with Eq. 5 (solid line), the average stiffness for a 100-nm-diameter vesicle was calculated. Influenza liposomes at 13°C and 26°C were on average, respectively, 40% and 10% stiffer, than at 37°C.

Such behavior agrees with the findings of Polozov et al. (5), who had determined that the ordered fraction in influenza lipids gradually decreases as function of temperature, for the X-31 strain. The authors also suggested that influenza lipids are not in a gel or solid state between 25 and 37°C. The bending rigidity of gel phase lipids is in the 100–1000 kT range (i.e., K_b ≈ 10⁻¹⁸ J) (22,23), which is much higher than the values we found. This argues in favor of the absence of a major phase transition for those lipids, in the case of the PR8 strain, and goes against previous assumption that influenza virions select solid phase lipids (4).

Although liposomes made out of viral lipids are stiffer than DMPC ones and approach the stiffness of the influenza virus itself (≈0.04 nN/nm at 27°C) (24), they are still an order-of-magnitude softer than viruses protected by a protein shell (≈0.3 nN/nm) (25). To investigate how well the lipid envelope itself is capable of protecting its contents, we determined the force required for the tip to puncture the lipid bilayer. For that specific purpose, single indentation experiments were performed by applying ≈2 nN pushes on top of influenza liposomes.

Sudden slope changes (often negative ones) were frequently (but not systematically) observed in the vertical part of the FZ curves (Fig. 5 A): We attributed those slope changes to puncture the bilayer; 53% of those puncturing events occurred when the tip was <10 nm away from the surface, which approximately corresponds to the height of two lipid bilayers (Fig. 5 A, inset). In addition, the added length of puncture events was on average 9.3 nm (not shown), which again matches very well the expected height of two superimposed lipid membranes. In almost every case, the slope of FZ curves after the last puncture was equal to that of an FZ curve performed on glass. Therefore, puncture mostly occurred only after the tip forced the upper wall of the liposome in contact with the lower wall. The remaining 47% of the puncturing events that occurred >10 nm away from the surface could be explained by:

• 1.A membrane expansion exceeding the stretching limit of lipid bilayers (∼2% (1)) upon indentation. Our model showed that at 50% indentation, the lipid bilayer of a 70-nm liposome stretches by 2%.
• 2.Encapsulated vesicles, which would be fully collapsed at a 20 nm distance from the surface.
• 3.Small lateral displacements of the particle during the push, leading to false events.

Puncturing events only occurred at forces higher than 0.4 nN (Fig. 5 B) and the average force at which they were observed did not vary with increasing number of pushes. The average force required to generate jumps in FZ curves was 0.88 nN, taking all events into account: As mentioned above, some of those events may not be directly related to the tip penetration through the influenza envelope. When only the last puncture before contact of the tip with the substrate was considered, the average force leading to membrane puncture increased to 1.1 nN. This value is very similar to the rupture limit of some protein capsids (25).

Figure 5.

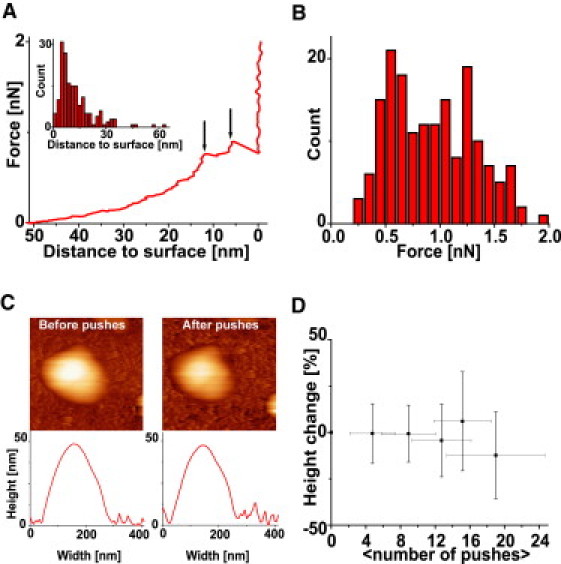
Influenza liposome puncture at high forces. (A) Jumps in the indentation curves occur at high forces: Those are indicated by the black arrows (and identified by a change of sign of the slope). (Inset) Histogram of the distance to the surface for each puncture event (172 events on 19 particles). Most of the events occur at high indentation, e.g., when the tip is only separated from surface by the two apposed bilayers of the liposome. (B) The average puncturing force is 0.88 nN (172 events, 19 particles). More than 95% puncture events occurred above 0.4 nN. (C) Pushing at high forces led to only minor morphology and height changes. Images and height profile show a liposome before (left) and after (right) four pushes at 2 nN force. (D) Multiple successive pushes at forces between 0.4 and 2 nN did not lead to a change in height (shown is the average of 12 experiments). On the abscissa, the average number of pushes between each height measurement is indicated. The puncture experiments were performed at 28 ± 2°C.

Surprisingly, imaging and sizing of liposomes after multiple pushings and punctures showed that the liposome morphology did not change (Fig. 5, C and D). Such a self-healing behavior has been also observed to occur on a minute timescale for microtubules (26). Healing of a lipid bilayer may occur as fast as the indenter is raised, due to the liquid nature of the lipid leaflets. Inspection of the retrace showed other events with a sign opposite to the rupture event (not shown), which could be interpreted as the healing of the pierced bilayer upon retraction of the tip. Due to its softness and fluidity the influenza virus envelope could be elastically deformed wall-to-wall and healed from any puncturing in a subsecond timescale. Similar properties have only been reported for the CCMV capsid so far (27). In addition, we have shown here that the influenza lipid bilayer on its own constitutes a protective shell that resists rupture equally as well as a more rigid protein capsid.

Discussion

Assessing the mechanical properties of liposomes made of virus lipids, we found that the highly curved lipid bilayer of the virus envelope is a fluid membrane of high stability, even in the absence of virus proteins. The properties of the influenza lipid envelope (soft but hard to puncture) are provided by its lipid composition: Whereas long, saturated phospholipids may be responsible for the high stiffness of influenza liposomes as compared to DMPC liposomes (28,29), a high cholesterol molar ratio is certainly the reason why those are not found to be in gel phase. Those remarkable observations suggest that the bilayer by itself is sufficient to ensure the stability of the virus and to protect the viral genome under various environmental conditions.

One important prerequisite to unraveling the mechanical properties of the influenza lipid envelope was to assess AFM as a tool for quantitative studies of lipid bilayers, and to derive the obtained stiffness values so as to gain physically and biologically relevant information. AFM indentation experiments have been used to measure the stiffness of lipid-based biocontainers such as synaptic and endocytosis vesicles (30,31). Studies that are more recent were performed at higher imaging and indentation forces which led to severely deformed and nonspherical liposomes (32,33). In those studies, moreover, the Hertz model was applied, which led to a severe underestimation of the Young's modulus as the liposomes were assumed to be massive rather than hollow spheres.

In our hands, obtaining consistent stiffness-versus-diameter plots required measuring forces below 0.3 nN and discarding SUVs that showed an aberrant aspect ratio. Occasionally liposomes were found to be nonspherical, elongated, disk-shaped, or flattened. Nonspherical liposomes can originate from the liposome extrusion process (34), excessive interaction with the surface, or forces applied during imaging. The height measured from force maps acquired with forces between 0.1 and 0.3 nN or from tapping mode images of the same particles showed no systematic differences.

In addition, because the studied vesicles were close to spherical and easily displaced by scanning, one can infer that they were only weakly adsorbed on the DETA surfaces. The stiffness of the investigated liposomes was determined by linear fitting of force-versus-indentation curves between 0.1 and 0.2 nN. In this force range, the deformation is expected to be elastic, as force curves are fully reversible (see Fig. S1). In addition, hysteresis in FZ curves was only observed at an average force of 1.1 nN, indicating that no damage was done on the bilayer below that force. Still, one may argue that the resulting deformation of ≈20% at 0.2 nN is large for such small, highly curved SUVs, because protein-based shells of similar dimensions show nonelastic responses from 15% deformations on (8,26). To see whether SUVs show consistent elastic behavior in the 0–0.2 nN range, we repeated our analysis in the 0.025–0.075 nN range and compared this to the results obtained between 0.1 and 0.2 nN: As a result, we obtained an identical qualitative response when comparing the influenza liposomes at different temperatures (Fig. S3), and after applying the FEM model, the Young's moduli agreed within 15% (Table S2).

To convert the measured stiffness values into parameters that are commonly used to describe membrane mechanics, K_a and K_b, we have created a FEM model that included the increasing contact areas among the planar surface, the liposome, and the indenting atomic force microscope tip (Fig. S5). Validation of AFM and our model as tools for the study of the lipid bilayers was gained from the quantitative determination of the effect of cholesterol on the stiffness of DMPC membranes. DMPC was chosen due to the abundance of data described in the literature on the mechanical properties of this lipid (1). The known properties of DMPC in fluid phase were accurately reproduced with our model. When cholesterol was incorporated into DMPC liposomes (1:1 mol/mol), the observed effect on stiffness was a threefold increase in the elastic modulus, which is exactly what was observed in micropipette suction experiments (35).

Another reason for studying a high cholesterol/lipid ratio comes from the fact that, due to its budding site, the virus itself has a comparable amount of sterols in its envelope (see Materials and Methods). In addition, these methods could become a relatively simple tool to characterize the K_a/K_b of lipid bilayers of unknown or complex lipid composition. The lipids have to be extruded into liposomes, meaning that the natural in/out asymmetry encountered in cellular systems will not be recovered. However, because we expect the mechanical properties of lipids to be dominated by their hydrocarbon chains, this pitfall should be a minor one. In addition, mechanical properties of natural small lipid assemblies, including other enveloped viruses, can be studied. Because the measurements are performed in liquid, conditions (pH) can be changed during the experiment, which would allow, for example, studying the relation between stiffness and rupture limits of a vesicle, and fusion with its target membrane.

The stiffness of influenza liposomes was somewhat higher than that of the DMPC/cholesterol vesicles implicating that the lipid phase of the virus envelope is of high stability. This raises the question of the phase state of virus bilayer. Indeed, the phase state of influenza lipids was controversial, because the lipid composition of the envelope was thought to be forming a solid phase (4), although more recent reports suggests a mostly liquid phase over a wide range of temperatures (5,36).

For the temperatures tested here (13–37°C), the envelope stiffness was only mildly affected by temperature, showing no drastic transition. Instead, our measurements clearly indicate a fluid state, despite a rich composition in saturated lipids. Should the influenza virus bilayer be in gel state, its stiffness might have been very high (K_b ≈ 10⁻¹⁸ J), and reversible deformation might have proven impossible (22): Previous AFM measurements on gel phase SUVs confirm that in the context of highly curved liposomes, E and K_b remain in the range measured with larger vesicles (23). Therefore, despite their saturated lipid composition, influenza lipid bilayers are rather soft and flexible, which may be a consequence of the high cholesterol concentration preventing the formation of a gel phase. The maintenance of a liquid state over a wide range of temperatures may be of particular interest, as it may facilitate the virus with self-repairing properties, as we have shown for the isolated lipid envelope.

The average stiffness k₁₀₀ = 0.021 ± 0.0007 nN/nm is only moderately less than what we found for the shell of X-31 influenza virions (including the M1 protein matrix) (≈0.04 nN/nm (24)). This confirms the hypothesis that the M1 matrix protein plays a limited role in the stability of the influenza virus (24,37). Other enveloped viruses (HIV, MLV, Herpes) that have been tested with AFM show stiffnesses at ∼0.3 nN/nm, all dominated by their internal protein capsids (38–40).

This study constitutes a small step forward in understanding the complex architecture of the influenza virus. With our results, we provide evidence that the lipid bilayer of the influenza envelope alone might be sufficient to protect the viral genome. The role played by cholesterol into making a stable bilayer fluid (hence flexible) rationalizes budding of influenza virus from cholesterol-enriched domains of the host cell plasma membrane. Although it is much softer than other viruses tested so far, it can sustain deformations up to almost 100% of its diameter. This agrees with observations on giant unilamellar lipid vesicles that can also sustain extreme changes in shape, as shown by micropipette aspiration and optical trapping experiments (41,42). When the SUV envelope does rupture, it does so at a force at ∼1 nN, which brings it into the same range as that obtained for protein capsids (8,9).

The efficiency of a biological shell in protecting its contents against chemical attacks may be best described by its fracture limits rather than its stiffness alone. Moreover, the rapid healing properties of lipid bilayers, conferred by the instability of water-exposed bilayer pores (43), may make the protection against the external environment particularly efficient. However, the relative softness of lipid bilayers might, on the other hand, represent a weak protective strategy against mechanical attacks. That said, the considerable void volume of influenza virions may allow the viral genome to remain unaffected whereas virions are deformed within the elastic limits known for protein shells. In addition, one wonders if the M1 matrix protein, which role is not yet clearly established (44,45), is required to increase the stiffness of influenza virions with the purpose of making them more resistant to mechanical stress.

From our results, we could infer that the major function of M1 is different from providing a stable shell to the influenza virus. Indeed, M1 is more likely the key organizer of virus assembly that recruits locally the different viral components, excludes components of the host cell, and drives the bending of the membrane, eventually leading to influenza virus budding.