Accounting for Protein-Solvent Contacts Facilitates Design of Nonaggregating Lattice Proteins

Abstract

The folding specificity of proteins can be simulated using simplified structural models and knowledge-based pair-potentials. However, when the same models are used to simulate systems that contain many proteins, large aggregates tend to form. In other words, these models cannot account for the fact that folded, globular proteins are soluble. Here we show that knowledge-based pair-potentials, which include explicitly calculated energy terms between the solvent and each amino acid, enable the simulation of proteins that are much less aggregation-prone in the folded state. Our analysis clarifies why including a solvent term improves the foldability. The aggregation for potentials without water is due to the unrealistically attractive interactions between polar residues, causing artificial clustering. When a water-based potential is used instead, polar residues prefer to interact with water; this leads to designed protein surfaces rich in polar residues and well-defined hydrophobic cores, as observed in real protein structures. We developed a simple knowledge-based method to calculate interactions between the solvent and amino acids. The method provides a starting point for modeling the folding and aggregation of soluble proteins. Analysis of our simple model suggests that inclusion of these solvent terms may also improve off-lattice potentials for protein simulation, design, and structure prediction.

Introduction

Most functional globular proteins have evolved such that they fold into a water-soluble native state. However, lacking the timescale of natural evolution, the de novo design of water-soluble globular proteins is a daunting task. In fact, even the design of proteins that fold quickly and uniquely into a specified native conformation is quite challenging. For this reason, much of the numerical work on protein folding has focused on the folding behavior of isolated proteins (1–4).

Similarly, the numerical study of the aggregation behavior of multiple proteins is very expensive if all-atom models are used; therefore such studies typically use a simplified representation of the proteins or focus on the aggregation of small peptides (5–9).

Simulations that aim to elucidate the competition between folding and aggregation are necessarily even more expensive than the simulations of folding or aggregation mentioned above. For this reason, it is attractive to study this problem with as simple a model as possible. If one aims to study the generic behavior of a multiprotein solution, then it becomes attractive to consider simple lattice models (1–4,10). Of course, such lattice models are not sufficiently detailed to reproduce the behavior of any specific protein. However, in what follows we will focus on the competition between protein aggregation and folding. This is a generic problem and hence lattice models can be used to gain insight into the factors that favor one process or the other. The protein lattice model that we consider has the advantage that it correctly reproduces the heterogeneity of the nonbonded interaction between the 20 distinct amino-acid residues in a protein using a statistical pair-potential, i.e., a pair interaction whose strength is related (via a multicomponent quasichemical approximation) to the frequency of contacts in (known) native protein structures.

The protein lattice model has successfully been used to simulate protein folding and has also been used to design novel proteins that will fold into a unique, preselected compact structure (e.g., see (4)). Upon heating the native state of such lattice proteins, a sharp transition takes place from the folded to the unfolded state, accompanied by a pronounced peak in the heat capacity. Thus, the simple model reproduces a feature of real proteins, which fold into a highly specific structure and show a peak in the heat capacity when unfolding. Folding of a model protein into a specific structure has also been achieved in off-lattice studies (11,12) typically using the same statistical pair-potentials as mentioned above.

Evolutionary pressure generally ensures that proteins do not aggregate in their natural biochemical environment, as aggregates may compromise the biological function of the proteins or may even be cytotoxic. The immunity against aggregation of real globular proteins is not properly reproduced by most lattice-models for protein solutions. Even if the model proteins fold well in isolation, assemblies of many such proteins often exhibit aggregate-formation close to the folding temperature (Fig. 1 F, low temperature aggregation). Much of the earlier work on lattice proteins and similar coarse-grained models therefore focuses on small peptides that lack a well-defined hydrophobic core in the folded state (5,6,9,13,14).

Figure 1.

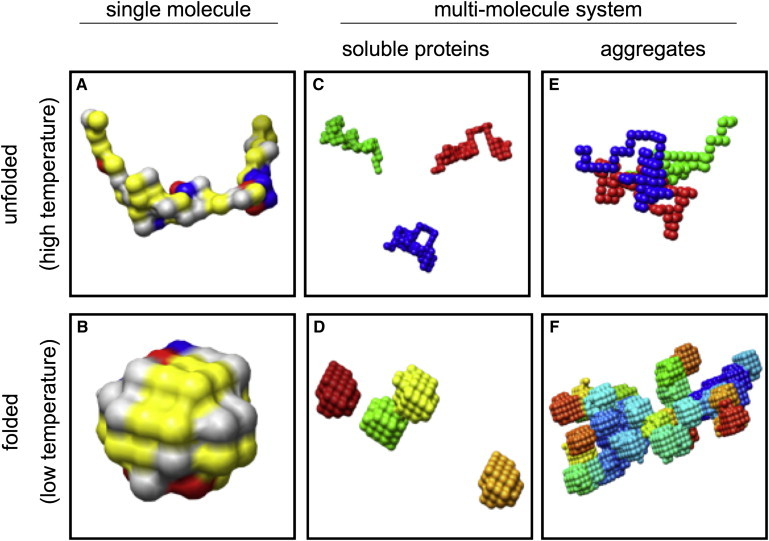
Schematic representation of aggregation behavior of lattice proteins. This figure illustrates a common problem with existing lattice protein models. Simulated as single molecules, proteins unfold at high temperatures (A), and fold into specific structures at low temperatures (B). In a multimolecule system, several scenarios for folding, unfolding, and aggregation are possible (C–F). As in nature, we would expect folded globular proteins to be soluble at low temperatures (D). However, existing models show a tendency to form large aggregates of folded proteins (F), due to (unphysically) strong attractions between hydrophilic residues. (See Fig. 4 for keys to the colors of panels A and B. In panels D–F, each protein chain has a different color.)

The unphysical aggregation behavior of many lattice proteins means that such models are of little use for studying the behavior of solutions that contain many folded soluble proteins. In particular, the existing models are ill suited for studying how subtle changes can cause initially soluble proteins to form amyloid fibers that are implicated in neurodegenerative diseases (15). Nor can the current models be used to study the assembly of large, functional complexes that play a role in the biology of multicomponent systems (e.g., see (16)).

One might therefore be tempted to give up on the use of lattice models for such complex systems, but that is not an attractive option, since multiprotein systems are computationally very challenging and, at least at present, coarse-grained models are indispensable.

In our article, we show that the unphysically strong tendency of lattice proteins to aggregate is not inherent in the use of lattice models as such, but is an effect of the pair-potentials that can be remedied by including explicitly calculated solvent interactions for the amino acids. When we do this, we find that the resulting model allows us to design proteins that remain soluble at their folding temperatures and even below—thus enabling coarse-grained simulations of multiprotein solutions.

Cubic lattice model

One of the most widely used three-dimensional coarse-grained protein models represents the protein as a chain on a simple cubic lattice (2–4). Our work also starts from such a protein model where the peptide chain is modeled with one residue per cubic lattice site (17). Nonbonded residues can only interact when they reside on neighboring lattice sites. The internal energy of a protein configuration is given by

$$E=\frac{1}{2}\sum _i^N\sum _j^N{\epsilon }_{a\left(i\right),a\left(j\right)}{C}_{ij}+\sum _i^N{\epsilon }_{w,a\left(i\right)}{C}_{wi},$$ (1)

where a(i) denotes the amino acid at residue i and w indicates the solvent. The contact matrix is C_ij = 1, when nonbonded residues i and j are located on neighboring lattice sites. If i and j are not neighbors, then C_ij = 0. The pair-potential ε_x,y gives the pairwise interactions between the amino acids x and y.

Due to the coarse-grained nature of the lattice, one typically designs a sequence for a given lattice structure, rather than using a naturally occurring protein structure-sequence combination. Once the matrix ε_x,y has been specified (see below), we can design model proteins that will fold preferentially into a unique structure that is chosen beforehand. The design procedures make use of a Monte Carlo scheme that minimizes the energy of the amino-acid sequence in the target structure while keeping the amino-acid composition diverse—this diversity is needed to ensure the uniqueness of the native state (see Methods for further details).

Pair-potentials

As stated above, the residues of lattice proteins usually interact via pairwise-additive, short-ranged interactions. In what follows, we shall focus on pair interactions that are knowledge-based in the sense that they are constructed to reflect the amino acid proximity in real protein structures (3). Despite the different geometry, lattice models and real protein structures have a similar coordination number: residues on the lattice have four contact partners, and residues in protein structures have, on average, four contacts at typical C-β interaction distances (6–7 Å) (see the Supporting Material).

In knowledge-based pair-potentials, the interaction (free) energies ɛ_i,j between amino-acid residues may, in their simplest form, be calculated as (18,19)

$${\epsilon }_{i,j}=-kT\ln \left(\frac{c_{i,j}}{{\omega }_{i,j}}\right)\text{.}$$ (2)

Here c_i,j is the number of contacts between amino-acid types i and j, and ω_i,j is the expected number of contacts between amino-acid types i and j in a set of experimentally determined protein structures.

There exist numerous additions and refinements to this basic scheme for determining the potential (20–25). A correction may be made for the solvation free energy of amino acids in water (e.g., (23,24)), the chain connectivity of the amino acids may partially be corrected for (19) and there are several ways to set a reference free energy (e.g., (21)). In particular, Leonhard et al. (25) fit two parameters to rescale the MJ matrix (23), to enable a simultaneous simulation of two protein chains folding into their native state without aggregating.

Here we will use a basic version of this scheme, where ω_i,j is based on the total number of residues of the amino-acid type and the residue coordination number. However, we will calculate the solvent term explicitly from the protein structures, making it possible to understand the effect of the solvent terms.

Methods

Potential including a pairwise solvent term

We calculate interaction free energies between amino acids from proximate residues in a representative set of Protein Data Bank (PDB) structures (26) according to Eq. 2. The expected number of contacts, ω_i,j, is based on the total number of observed amino acids n_i and the coordination number q_i:

$${\omega }_{i,j}=\frac{n_i{q}_i{n}_j{q}_j}{{\sum }_k{q}_k{n}_k}\text{.}$$ (3)

To obtain ω_i,j for all pairwise interactions between the amino acids, and between the amino acids and water, we need to calculate c_i,j, n_i, and q_i. We will not calculate water-water interaction or, more precisely, we define ω_w,w ≡ 0.

For any residue the solvent accessible-surface area (S_r) can be calculated. We use the DSSP program (27) to calculate the surface accessible area per residue. The maximum accessible surface area for an amino acid, S_a(r), indicates the surface area when the side chain is fully exposed to the solvent.

To indicate the degree of surface accessibility for a residue within a structured protein, the two quantities can be compared as

$${\alpha }_r=\frac{S_r}{\max \left\{S_{a\left(r\right)}\right\}},$$ (4)

where a(r) is the amino acid of residue r.

To translate the continuous potential to a discrete lattice potential, we use a fixed coordination number for amino acids in the PDB and set q_i = q = 4, as in the lattice model.

We approximate the number of water contacts, by comparing the observed number of contacts for a residue, n_a(r), to the expected number of contacts for a fully buried residue (q = 4).

We calculate the number of missing neighbors based on the relative surface accessibility α_r, so that qα corresponds to the number of solvent contacts.

To calculate c_i,j, we use the following procedure, while excluding all neighbors and second neighbors in the chain:

• 1.Pick a residue r and update n_a(r).
• 2.Calculate α_r.
• 3.Take the q(1−α_r) closest neighbors, and update the residue contacts counts c_a(r),a(nb).
• 4.Add solvent contacts for qα residues, and update the water-residue contacts count, c_a(r),w, and the total number of observed waters, n_w.

Here the subscript r indicates the residue, nb the neighboring residue, and w a contact with the solvent. Note that n_w is not meant as an estimate of the true number of water molecules around the protein. Instead, it indicates how much of the solvent-accessible surface could be substituted by residues, analogous to the empty sites in the lattice model.

To calculate the pair-potential, we use C-β distances in protein x-ray structures from PDB-select (25,26) (http://bioinfo.tg.fh-giessen.de/pdbselect/). (The resulting pair potential can be found in the Supporting Material.)

Comparing potentials

Potentials

Table 1 lists the four different potentials compared in this study. The Betancourt potential (24) has no explicit water term (C_wi = 0), but corrects for the solvent implicitly by rescaling the MJ matrix. We have disregarded all other existing pair-potentials, since they tend to have even stronger attractions between polar residues; it is this (unphysically) strong attraction that leads to aggregation of folded proteins, as shown later in our results. The potential we suggest in this work (P1) includes a water term calculated explicitly from protein structures, using the method described above, employing Eqs. 2 and 3. As a reference we calculated two potentials using the same method, with different weights for the water term (P0 and P2) to test how sensitive our results are to the strength of the protein-solvent interaction. The P0 potential has no water term, and should therefore be comparable to the Betancourt potential; the P2 potential has the water-amino acid interaction added twice.

Table 1.

List of pair-potentials

Symbol	Cwi	Method
Be	0	Betancourt and Thirumalai (24)
P0	0	Methods Section
P1	1	Methods Section
P2	2	Methods Section

The solvent weight, C_wi in Eq. 1, is added to the potential when a residue i is in contact with at least one empty lattice site. P1 is the potential used in this work.

Designing structures and sequences

We set out to create an unbiased, systematic, and reproducible procedure to design lattice structures and sequences to test the different potentials. This means we did not want to design either a structure, or sequence by hand, but to use automated procedures instead. Firstly, a compact structure was obtained for proteins of length 50, 60, 70, and 80 by simulating a purely hydrophobic sequence, and choosing the most compact structure from the ensemble. For the four different structures a sequence was designed for each of the four different potentials as listed in Table 1. The design procedure we used ensures the sequence heterogeneity remains high, while the potential energy is minimized as in Coluzza et al. (4). For each of the 16 sequence-structure combinations we tested if only the desired structure would form upon folding; we used the first sequence obtained from the design procedure that would fold back into the same structure. Designed sequences that failed this test were discarded; only four sequences required more than one design attempt.

Testing for aggregation

Each of the sequences was subsequently simulated to determine the aggregation behavior at a low concentration of free chains with on average 3 × 10⁻⁶ molecules per lattice site—note that in practice no molecule will fit on a single lattice site. Firstly, aggregates were collected; then the melting temperature for different sizes of aggregates was determined by simulating the preformed aggregates at different temperatures and a fixed concentration. The results are shown in Table 2.

Table 2.

Melting temperatures relative to folding temperatures

Potential	Length	Tf	Tm	Tm/Tf
Be	50	0.3	0.2	0.66
Be	60	0.34	0.19	0.55
Be	70	0.3	0.27	0.89
Be	80	0.25	0.25	1.02
〈Be〉	—	0.3	0.23	0.76
P0	50	0.18	0.15	0.86
P0	60	0.2	0.13	0.63
P0	70	0.24	0.21	0.87
P0	80	0.19	0.19	1.0
〈P0〉	—	0.2	0.17	0.84
P1	50	0.41	0.12	0.29
P1	60	0.39	0.09	0.22
P1	70	0.4	0.12	0.31
P1	80	0.36	0.08	0.22
〈P1〉	—	0.39	0.1	0.26
P2	50	0.4	0.08	0.2
P2	60	0.46	0.1	0.22
P2	70	0.4	0.08	0.2
P2	80	0.51	0.08	0.16
〈P2〉	—	0.44	0.09	0.19

The structure and sequences of the designed proteins are given in the Supporting Material. Average T_m/T_f values over the four structures designed with the same potential are indicated in bold.

Simulation and sampling

Monte Carlo simulation

To simulate the properties of the (multi) protein system, we used standard Monte Carlo simulations where trial moves are accepted according to the Metropolis rule,

$$P_{acc}=\min \left\{1,\exp \left(\frac{-\text{Δ}E}{k_{B}T}\right)\right\},$$ (5)

where T is the simulation temperature, k_B is the Boltzmann constant, and ΔE is the difference in energy between the new and old configuration of the system. Trial moves are either internal moves, changing the configuration of a chain (end move, corner flip, crank shaft and point rotation), or rigid body moves, changing the position of the chain relative to other objects (rotation, translation); see Coluzza et al. (4) for more details. At each iteration, a local trial move (end move, corner flip, or crank shaft) is performed, and in addition a global trial move (point rotation or translation) may be performed with the probability P_global = 1. The volume of the simulation box (80 × 80 × 80 lattice points) was kept constant, while using periodic boundary conditions.

Parallel tempering, or temperature replica exchange, was used to speed up both equilibration and the sampling of uncorrelated configurations. Multiple simulations at different temperatures were run in parallel, while trying to swap temperatures every 50,000 moves with 10,000 trial temperature swaps in each simulation. A trial swap between the temperatures of two replicas was accepted with a probability (28–30) of

$$P_{acc}=\min \left\{1,\exp \left(\frac{-\text{Δ}E·\text{Δ}\left(1/T\right)}{k_B}\right)\right\}\text{.}$$ (6)

Water interactions

In protein structures side chains tend to point toward the solvent (typically hydrophilic amino acids) or toward the protein interior (typically hydrophobic amino acids). On the lattice, residues have no direction, which leads to very strong solvent interactions on the corner positions of protein structures. To prevent unphysically strong water-solvent interactions at the corner points of protein structures, we define an interaction between a residue and water (C_w,j = 1, in Eq. 2) when the residue touches at least one empty lattice site (solvent).

Folding temperature

A peptide is defined to be in a folded state if

$$X_f=\{\begin{array}{c}1\text{if}{C}_n>0.8·\max \left\{C_n\right\}\\ 0\text{otherwise}\end{array},$$ (7)

where C_n is the number of native contacts, i.e., those contacts that are also present in the folded target structure. We define the folding temperature T_f as the temperature at which 〈X_f〉 = ≥ 0.5.

Melting temperature

To characterize the temperature range in which aggregation is relevant, we define a melting temperature T_m. For a designed protein T_m, we used the following definition: at low temperature we prepared aggregates of 50 proteins. We then determined T_m as the lowest temperature at which the aggregate will shrink in size (given the concentration). This definition is, of course, somewhat arbitrary. However, it does account for the fact that aggregation proceeds via nucleation and growth. Our criterion identifies the temperature below which clusters of 50 proteins will grow spontaneously.

Grand canonical simulation

A grand canonical Monte Carlo simulation was performed to investigate the aggregation behavior of the model proteins at a constant (low) osmotic pressure.

Trial insertions and deletions of free chains were performed with a probability of P_insert = P_delete = 0.005 per move.

Free chains are defined as chains that make no contacts with other chains in the simulation box. Trial insertion of new chains (with an identical sequence) were accepted with

$$P_{acc}=\min \left\{1,\frac{V}{N+1}\exp \left(\mu \beta \right)\right\},$$ (8)

and deleted with

$$P_{acc}=\min \left\{1,\frac{N}{V}\exp \left(-\mu \beta \right)\right\},$$ (9)

where

$$\beta =\frac{1}{k_{B}T},$$

N is the number of free chains in the simulation box before the move, V is the volume of the box, and μ the chemical potential. The volume was kept constant at 80 × 80 × 80 lattice points and exp(μβ) was kept constant at 3 × 10⁻⁶ chains per lattice site. A single peptide chain was simulated in a separate box at the same temperature, to generate new configurations for insertion into the main simulation box. Insertions were only accepted when no contacts were made between any of the existing chains. Deletions were performed only over the free chains in the box. We used periodic boundary conditions in combination with the grand canonical simulation. Note that this simulation technique also helps to overcome slow diffusion through the simulation box.

Because the proteins were simulated at very low density, it is likely that the simulation box becomes empty. Instead of simulating an empty simulation box explicitly, we calculate the number of time steps between deletion and reinsertion at each attempted deletion of the last chain in the box as in Abeln and Frenkel (31).

Results

Simulations without water term

As a first step, we investigated the foldability and solubility of coarse-grained model proteins designed with the Betancourt (Be) potential (24). Based on Monte Carlo simulations of these designed proteins, we defined the folding temperature, T_f as the temperature at which a given protein folded into its designed structure in 50% of the equilibrium conformations sampled. The foldability of a protein was deemed to be good when a sharp folding transition was observed around T_f, accompanied by a sharp peak in the heat capacity. The majority (>80%) of the model proteins designed with Be-potential have a good ability to fold if we use the design procedure of Coluzza et al. (4).

The solubility of the proteins was then tested by simulating the proteins at various temperatures around T_f at low concentrations (3 × 10⁻⁶ free molecules per lattice point) in the grand canonical ensemble. Fig. 2 shows a typical example of a model protein designed with the Be-potential: this model protein starts to aggregate around the folding temperature. In fact, the majority (>95%) of proteins designed with the Be-potential aggregated during MC simulations at temperatures around T_f. This may not be surprising as the design procedure does not bias against aggregation, whereas in nature there will be a strong evolutionary pressure against aggregation.

Figure 2.

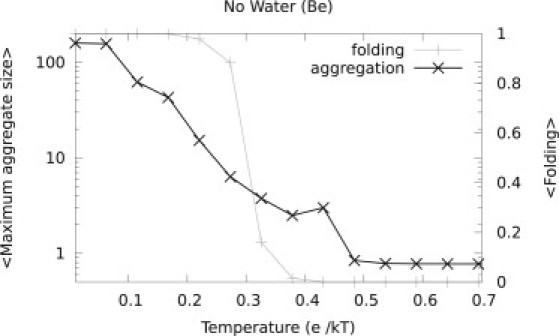
Folding and aggregation using a lattice model that does not account for water contacts. A typical example of the folding (gray curve) and aggregation (blue curve) of a protein designed with the method of Betancourt and Thirumalai (24). The structure used was 70 residues long and designed with the Be potential (see the Supporting Material for structure and sequence).

To understand the cause of the aggregation, the formed aggregates were considered in more detail. Two features that are not compatible with naturally occurring proteins were found:

• 1.The designed proteins contained large hydrophobic patches on their surface.
• 2.Polar residues often clustered together.

The Be-potential, and most other knowledge-based amino-acid pair-potentials, assign negative interaction energies to polar-polar interactions, resulting in clustering of polar groups during the simulation. In real proteins polar residues also cluster together—and this explains the apparent attraction in the knowledge-based potentials.

However, in real proteins this clustering occurs typically at the surface of the proteins, while clustering of buried polar residues is rare (32). The reason for the surface clustering is generally not that polar residues attract each other, but that they tend to be more strongly attracted to water than to other polar residues. The pairwise interaction terms between the solvent and polar amino acids indeed show a stronger attraction than polar-polar terms when calculated explicitly from protein structures (see P1 potential in the Supporting Material). In a lattice simulation the solvent terms can be incorporated cheaply by considering interactions of amino-acid residues with empty (i.e., solvent) lattice sites.

Simulations with water term

Fig. 3 shows a typical protein designed and simulated with a pair-potential that includes explicitly calculated water interactions. As before, it is easy to design proteins that fold uniquely into a predesigned native state. However, importantly, around the folding temperature the protein remains soluble, thus mimicking the biologically relevant situation where most proteins are soluble in their folded state. If we lower the temperature well below the folding temperature, we find that even these water-soluble proteins eventually aggregate.

Figure 3.

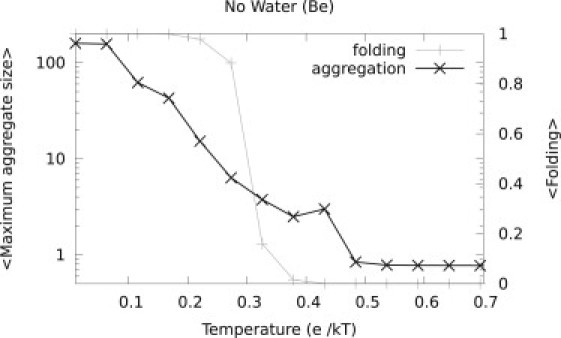
Folding and aggregation using a lattice model that does account for water contacts. A typical example of the folding (gray curve) and aggregation (black curve) of a protein designed using the potential with a pairwise water term. The structure used was 70 residues long and designed with the P1 potential (see the Supporting Material for structure and sequence).

Interestingly, Fig. 3 also shows a small peak in the aggregation curve at temperatures just above T_f. This peak is due to a phenomenon where the unfolded form of the proteins starts to aggregate due to exposed hydrophobic patches (see also Fig. 1 E). Such high-temperature aggregation has also been observed for some real proteins (33).

To get a more systematic view of the foldability and solubility properties of the potentials, we used an unbiased procedure to design structure-sequence combinations (see Methods). For four structures of different lengths, four different sequences were designed using the potentials listed in Table 1. The melting temperature T_m characterizes the temperature range in which aggregation is relevant. We defined T_m as the lowest temperature at which the aggregate shrinks in size, given a preformed cluster. Note that different potentials, and different designs, may give rise to different folding temperatures T_f, hence the melting temperatures need to be considered relative to T_f.

Table 2 lists the melting temperatures relative to the folding temperatures of the 16 different protein designs. The potentials without an explicit water term (Be and P0) show aggregation of model proteins around the folding temperatures, whereas the potentials with explicit water terms (P1 and P2) show aggregation of folded proteins at much lower temperatures.

Fig. 4 shows the difference in sequence design between potentials with and without explicit water terms. Without explicit water terms, polar residues cluster together on one side of the protein, leaving the other half for the hydrophobic residues. In the design with explicit water the polar residues sit on the outer layer of the protein, as they are attracted by the solvent in the design process. Typically the solvent terms contribute one-third of the total interaction energy in the folded state. Consequently these proteins also have better defined hydrophobic cores, and fewer hydrophobic patches making the proteins inherently less likely to aggregate.

Figure 4.

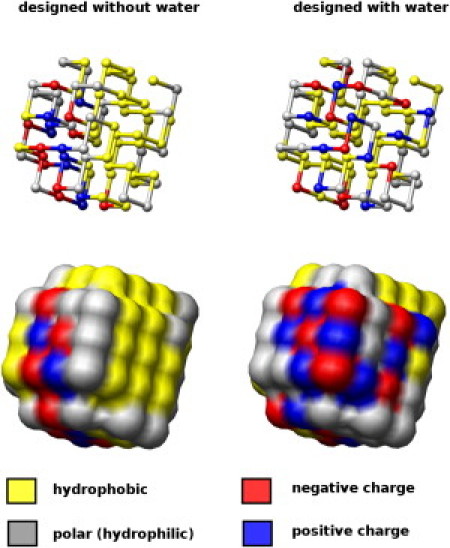
Surface and core of proteins designed with and without water in the pair-potential. In the model protein designed without water, all polar residues cluster together. In the model protein designed with water, the polar residues are at the surface of the protein. Note that the positively and negatively charged amino acids form alternating patterns at the interior (left) and surface (right). The structures used were 80 residues long and designed with the Be potential (left) and the P1 potential (right); see the Supporting Material for structures and sequences.

Concentration

The onset of aggregation is dependent on the monomer concentration of proteins in solution. To investigate the concentration range for which our results are valid, we performed grand canonical simulations at different concentrations of free chains (see Methods). Fig. 5 shows that all designed proteins aggregate around or above their folding temperature (T_f/T_m < 2) for concentrations of 5 × 10⁻⁵ free chains per lattice site or above. If we assume a lattice spacing of 3.8 Å, then this is comparable to millimolar concentrations. In vitro, single protein solutions tend to start gelating or precipitating above millimolar concentrations, a feature that is well reproduced by our simulations in this concentration range. Fig. 5 also shows that there is a significant difference in solubility at lower concentrations between the different model proteins: those designed and simulated with the solvent term aggregate at much lower temperatures, well below the folding temperature, than those without a solvent term.

Figure 5.

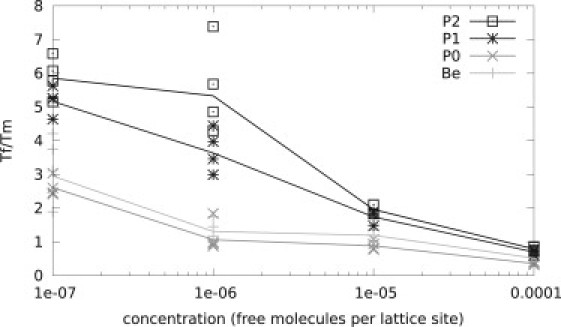
Aggregation at different concentrations. Concentration in molecules per lattice site versus the ratio of the folding temperature (T_f) over the melting temperature (T_m). The T_m/T_f ratio of the solid line is an average over the four different structures for each potential. At millimolar concentrations (3e-6 molecules per lattice site) all models show aggregation behavior at the folding temperature. At lower concentrations, the proteins designed and simulated with a water potential (P1 and P2) are significantly more soluble.

Discussion

Using simple pair-potentials between amino acids to design foldable model proteins leads to aggregation around the folding temperature. We show that, by including explicitly calculated solvent interactions in the pair-potentials, the designed proteins remain soluble at their folding temperatures and below.

Because most proteins should not aggregate under physiological conditions, a prerequisite to any modeling approach of pathological protein aggregation should be that the same type of model would not predict aggregation of normal globular proteins. The knowledge-based pair-potential that we propose here has precisely this feature.

Protein aggregation, in specific amyloid formation, is associated with several neurodegenerative diseases. It is therefore of considerable interest to model the onset of amyloid formation. Particularly, the early stages of amyloid formation are prohibitively expensive to simulate with an atomistic model. During these stages, prefibrillar aggregates are formed of 10–50 protein molecules (34) that undergo significant structural changes over time.

In this work, the lattice model provides a convenient and—importantly—cheap reference model to study the factors that make otherwise normal proteins aggregation-prone. On the other hand, off-lattice coarse-grained protein models show promising results for studying peptide aggregation (5–9), and generally use pairwise knowledge-based potentials (e.g., (35)) developed on-lattice (e.g., (23)). Therefore, such models could immediately benefit from the results obtained by this work, and become more appropriate for studying the competition between protein solubility and aggregation.

Most alternative interaction potentials are not suitable for studying the early stages of amyloid formation. Gō-like potentials may be adapted to study specific cases of aggregation (36), but are generally not applicable because they will not provide a low energy state for alternative configurations. Unfortunately it is unfeasible to simulate such systems with all-atomistic potentials, even though useful details of the process may be obtained (e.g., (37,38)).

The calculation of the potential is simple to implement, and the concept of adding solvent interactions is easily adaptable to more-complex interaction potentials and more-detailed protein structure models. Moreover, the proteins designed with the potential that includes a solvent term tend to have a better-defined hydrophobic core. In fact, solvent-exposure-specific amino-acid substitution terms have long been recognized as a powerful tool in distant homology detection between proteins (39). We suggest that it may also be useful to include solvent-amino acid interactions in pair-potentials for structure prediction and design.