Comparative Study of the Energetics of Ion Permeation in Kv1.2 and KcsA Potassium Channels

Abstract

Biological ion channels rely on a multi-ion transport mechanism for fast yet selective permeation of ions. The crystal structure of the KcsA potassium channel provided the first microscopic picture of this process. A similar mechanism is assumed to operate in all potassium channels, but the validity of this assumption has not been well investigated. Here, we examine the energetics of ion permeation in Shaker Kv1.2 and KcsA channels, which exemplify the six-transmembrane voltage-gated and two-transmembrane inward-rectifier channels. We study the feasibility of binding a third ion to the filter and the concerted motion of ions in the channel by constructing the potential of mean force for K⁺ ions in various configurations. For both channels, we find that a pair of K⁺ ions can move almost freely within the filter, but a relatively large free-energy barrier hinders the K⁺ ion from stepping outside the filter. We discuss the effect of the CMAP dihedral energy correction that was recently incorporated into the CHARMM force field on ion permeation dynamics.

Introduction

Selectivity and fast permeation of ions are two crucial properties of biological ion channels (1). The crystal structure of the KcsA potassium channel (2) provided the first microscopic picture of how nature reconciles these apparently conflicting demands by attracting multiple ions to binding sites in the selectivity filter and then exploiting the Coulomb repulsion among the ions to facilitate fast permeation. The high-resolution structure of KcsA (3,4) revealed six ion-binding sites in the channel: four in the filter (S1–S4), one outside the filter (S0), and one in the cavity (C; see Fig. 1). Subsequently, numerous molecular-dynamics (MD) simulations of potassium channels have demonstrated that two K⁺ ions occupying either the S1-S3 or S2-S4 binding sites in the filter and a third K⁺ ion in the cavity form a stable waiting state (5–13). Transitions between the S1-S3 and S2-S4 states have been observed to occur on a nanosecond timescale, indicating an almost barrierless diffusion of ions. An outward permeation event is triggered when the K⁺ ion in the cavity enters the filter, forming a three-ion complex at the S0-S2-S4 sites, separated by two water molecules at S1 and S3. This three-ion complex is semistable, and the presence of an electrochemical potential is sufficient to eject the outermost ion at S0, completing the permeation cycle. Inward permeation of K⁺ ions follows a similar cycle in the reverse direction. This recycling between two and three K⁺ ions during permeation has been confirmed by free-energy perturbation (14,15) and potential of mean force (PMF) (16,17) calculations in MD simulations, and has also been observed directly in Brownian dynamics (18,19) and MD simulations (20,21).

Figure 1.

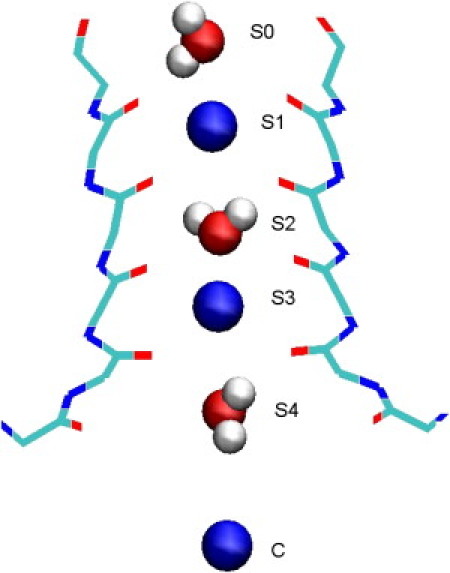
Snapshot of the selectivity filter in Kv1.2 potassium channel in the waiting state. Three K⁺ ions occupy the S1-S3 sites and the cavity (C). Three water molecules that occupy the S0-S2-S4 sites are also shown explicitly.

Most of the MD simulations of potassium channels performed to date have employed the bacterial KcsA and inward rectifier Kir channels, which have a two-transmembrane topology. The structural and functional similarities of these two types of channels were noted in several MD simulations (22–24). The voltage-gated potassium channels have the same TVGYG motif in the filter but differ in topology, in that they have four extra transmembrane helices that serve as voltage sensors. Of more importance, they exhibit some differences near the filter region. For example, the residue corresponding to E71 in KcsA is replaced with a nonpolar residue in voltage-gated potassium channels, which results in a more flexible filter structure. Thus, conservation of the TVGYG motif in itself does not guarantee that the ion permeation dynamics will be similar in all potassium channels. Despite the availability of several crystal structures (e.g., KvAP (25), Kv1.2 (26), and a Kv1.2 chimera (27)), only a few MD studies of ion permeation in voltage-gated K⁺ channels have been conducted (20,21,28,29). In particular, a comprehensive study of the energetics of ion permeation in Kv1.2 has not yet been performed.

In a recent MD study of the selectivity filter in Kv1.2 and KcsA channels (30) employing the CHARMM22 force field (31), it was found that the filter structure was less stable in Kv1.2 than in KcsA. The carbonyl oxygens were observed to flip back frequently in Kv1.2, and the filter was not selective for K⁺ ions. Only after the recently introduced CMAP dihedral energy correction term (32) was included in the CHARMM force field were investigators able to stabilize the carbonyl oxygens and obtain a filter structure consistent with the crystal structure. Inclusion of the CMAP correction was found to boost the K⁺/Na⁺ selectivity free energy by ∼11 kT in Kv1.2, bringing it into agreement with experimental data (30). Several other studies have confirmed the importance of the CMAP correction for maintaining the structural integrity of globular proteins in long MD simulations (33–36). A similar correction to the dihedral energy was also incorporated into the AMBER force field to provide a better description of the peptide backbone and improve the agreement between simulations and experiments (37). Because the CMAP correction was introduced relatively recently, it was not used in earlier MD simulations of the KcsA channel with the CHARMM force field. In view of its considerable impact on K⁺/Na⁺ selectivity, it is desirable to assess the effect of the CMAP correction on the energetics of ion permeation in KcsA as well.

Here, we address the issues raised above by constructing the PMFs of K⁺ ions in the Kv1.2 and KcsA channels. We focus on two critical events in the permeation cycle: 1), the binding of a third K⁺ ion to the filter while it is occupied by two other K⁺ ions; and 2), the feasibility of concerted motions of ions in the filter. For the former, we calculate the PMF of a single K⁺ ion as it is moved to the filter from either side. To investigate the feasibility of concerted motions of a pair of K⁺ ions between the binding sites S2-S4, S1-S3, and S0-S2, we construct the PMFs for their center of mass. A similar PMF for the center of mass of three K⁺ ions is constructed to study their concerted motions between the configurations S1-S3-C and S0-S2-S4.

Materials and Methods

Model system and MD simulations

The initial simulation systems for the Kv1.2 and KcsA channels were taken from a previous study (30) in which both channel proteins were relaxed carefully in the waiting state (S1-S3-C). The simulation protocols were explained in detail in that study; therefore, we give only a brief description of the model systems and the MD simulations here. The simulation systems with various ion configurations are constructed using the VMD suite of software (38). The pore domain of the crystal structure of Kv1.2 (PDB ID: 2A79, residues 312–421) is embedded in a lipid bilayer consisting of 96 1-palmitoyl-2-oleoyl-phosphatidylethanolamine (POPE) molecules and solvated with 8900 water molecules, and 8 K⁺ and 24 Cl⁻ ions. Equilibration is carried out in three stages: first the side chains are gradually relaxed in MD simulations lasting 2.7 ns, followed by relaxation of the backbone atoms in 6.5 ns MD simulations, and finally the ion positions are relaxed in 4.5 ns MD simulations. This is followed by a production run of 2 ns with no constraints, which is used to determine the average ion positions required in construction of the two-ion and three-ion PMFs. A snapshot of the waiting state indicating the positions of the K⁺ ions and water molecules in the filter regions is shown in Fig. 1. The last stage of this procedure is repeated after the three K⁺ ions are moved from S1-S3-C to S0-S2-S4. Again a 2 ns production run is performed to determine the equilibrium positions of the three K⁺ ions at the S0-S2-S4 sites. A similar protocol is employed to construct the two KcsA systems with three K⁺ ions at the S1-S3-C and S0-S2-S4 sites. In this case, the crystal structure (PDB ID: 1K4C) is embedded in a bilayer of 105 POPE molecules and solvated with 9640 water molecules, and 6 K⁺ and 18 Cl⁻ ions.

MD simulations are carried out using version 2.6 of the NAMD code (39), which includes the CMAP correction terms in the CHARMM22 force field (31). We did not attempt a parallel calculation without the CMAP correction here because it was previously shown (30) that it is not possible to achieve a stable filter structure for Kv1.2 without CMAP. The CHARMM22 force field provides a complete set of parameters for all atoms in the system and uses the TIP3P model for water molecules. An NPT ensemble is used with periodic boundary conditions. Pressure is kept at 1 atm using the Langevin piston method with a damping coefficient of 5 ps⁻¹. Similarly, temperature is maintained at 298 K by Langevin damping with a coefficient of 5 ps⁻¹. Electrostatic interactions are computed using the particle-mesh Ewald algorithm. The list of nonbonded interactions is truncated at 13.5 Å, and a switching cutoff distance of 10 Å is used for the Lennard-Jones interactions. A time step of 2 fs is employed in all simulations. Trajectory data are written at 1 ps intervals during both equilibration and production runs. Ion positions are recorded at every time step in the PMF production runs.

PMF calculations

We calculated the PMFs of K⁺ ions along the channel axis using umbrella sampling (40) together with the weighted histogram analysis method (WHAM) (41). Application of this method to ion channels was described in some detail in earlier studies (42–44); therefore, only a brief description of the method is given here. To construct a single-ion PMF, umbrella potentials are placed at equal intervals along the channel axis and the position of the ion is sampled during MD simulations of the system. In all cases, the ion position is measured with respect to the center of mass of the channel protein. The biased ion distributions obtained from the production runs are then unbiased and combined using WHAM. In the case of multi-ion PMFs, the umbrella potential is applied to the center of mass of the ions, and their center of mass is considered as the reaction coordinate. We stress that such a choice is possible only because the K⁺ ions move in tandem across the filter, and thus their relative distance is maintained. Otherwise, one would have to construct a two-dimensional PMF that takes into account the relative motion of the ions as well as their center of mass motion.

For single-ion PMFs, we employ umbrella potentials with a force constant of 10 kcal/mol/Ų at 0.5 Å intervals. We check the adequacy of this procedure by plotting the ion distributions at all windows and making sure that there is adequate overlap between the populations of the neighboring windows (see Fig. S2 in the Supporting Material for an example). If this is not the case, as happens when there is a sharp peak in the PMF, we employ additional windows at half intervals (0.25 Å) at the problem spots with the force constant doubled. Because pulling the ions for long distances tends to create equilibration problems, we populate the window positions first by exchanging the K⁺ ion with the nearest water molecule on the axis. Consequently, the ion has to be pulled at most by 1.5 Å to either side to populate all the windows.

For two-ion PMFs, the centers of mass of the equilibrium positions of two K⁺ ions at S0-S2, S1-S3, and S2-S4 are used as pivot points. The distance between two neighboring pivot points is divided into eight sections to create nine window positions, which are further extended beyond the pivot points to obtain a complete PMF profile. During construction of the PMF between two equilibrium configurations, the ions are moved from their respective positions toward the middle point, so that the maximum distance they need to be pulled is <2 Å. This step is very important to ensure faster convergence of the PMFs. In test calculations for which the ions were moved from one equilibrium position to a second one (e.g., from S1-S3 to S0-S2), the convergence of the PMF in the second pocket took a much longer time. The three-ion PMFs are constructed similarly using the center of mass of the three K⁺ ions at S0-S2-S4 and S1-S3-S5 as pivot points. Here, the S5 position corresponds to the closest stable position of a K⁺ ion to the K⁺-W-K⁺-W complex in the filter, where it neighbors the water molecule at S4. Use of this configuration is essential for maintaining the K⁺-W-K⁺-W-K⁺ complex while it is moved into the filter.

For single-ion PMF calculations, the system is equilibrated for 100 ps and the trajectory data for ion positions are collected for 500 ps for each window. This is five times longer than the simulation time used in previous PMF studies in the KcsA channel (16,17). The need for a longer simulation time was indicated by detailed studies of the convergence properties of PMFs in the gramicidin A channel (44,45), which has a narrow pore structure like the selectivity filter in potassium channels. The adequacy of the sampling and convergence of the PMFs are checked by dividing the production data into two equal blocks and comparing the PMFs constructed from each block. A difference between the two PMFs of <1 kcal/mol, which is the statistical accuracy of the calculations, is taken as a sign of convergence. A more detailed study of convergence, in which data were accumulated in 100 ps blocks, is presented in Fig. S1. Such checks revealed that a 100 ps equilibration is not sufficient for multi-ion PMFs; therefore, they are equilibrated for 500 ps followed by two 500 ps production runs. Congruence of the two PMFs constructed from the two data sets is used as a sign that the multi-ion PMFs have properly converged.

The absolute binding energy of a K⁺ ion to the S0 binding site of the potassium channel is estimated from the single-ion PMF in the extracellular region using the one-dimensional approximation for the binding constant (43).

Results

Configurations of K⁺ ions in the filter

To determine the ion-binding sites in the Kv1.2 and KcsA channels, we create two simulation systems for each channel with three K⁺ ions occupying the sites S1-S3-C and S0-S2-S4. After the equilibration is completed, 2 ns of data are collected for each channel and ion configuration for trajectory analysis. The time series of the positions of the K⁺ ions and water molecules in the filter show that they fluctuate around stable positions, indicating well-formed binding sites for both the S1-S3-C and S0-S2-S4 ion configurations. The average positions of the ions and water molecules in each case are listed in Table 1. Because the position of the cavity ion is not well determined, it is not listed. For the three-ion PMF, we determine the position of the S5 site using a small restraint force, given by z = −0.5 Å (Kv1.2) and z = 1 Å (KcsA). In KcsA, the K⁺ ion at S5 has an off-axis position, which allows it to come closer to the S4 site. A comparison of the ion-binding positions in Kv1.2 and KcsA shows that they match rather well, as one might expect from the conserved sequence of the filter residues. The S3 and S4 binding sites, in particular, are almost identical. One small difference that will be relevant in the discussion of PMFs further below is that the S0-S2 ion positions are shifted down in Kv1.2 relative to KcsA, whereas the position of the water molecule at S1 remains the same. As a result, the water molecule at S1 provides a better coordination for the K⁺ ion at S0 in Kv1.2 compared with KcsA.

Table 1.

Average positions of the K⁺ions and water molecules (underlined) in the filter after equilibration in MD simulations (in units of Å)

Channel	Kv1.2		KcsA
Binding site	S1-S3-C	S0-S2-S4	S1-S3-C	S0-S2-S4
S0		15.0		15.3
S1	12.0	12.6	12.3	12.6
S2	7.6	9.3	8.3	9.6

The second and fourth columns show the positions of the ions for the S1-S3-C configuration, and the third and fifth columns show those of S0-S2-S4. Because water molecules at the S0 site are frequently exchanged, their positions are not shown.

Binding of a K⁺ ion to the filter

The event that triggers the outward permeation of ions is the binding of a K⁺ ion from the cavity to the S4 site in the filter while it is occupied by two other K⁺ ions. The main question here is, can the third ion bind to S4 while the other two ions are at S1-S3, or is movement of the resident ions from S1-S3 to S0-S2 necessary? We first address this question in Kv1.2. The K⁺ PMF in Fig. 2 (top, dashed line) shows that there is no binding pocket for the third K⁺ ion at S4 while the S1-S3 sites are occupied by K⁺ ions (to obtain this PMF, the two ions at S1-S3 have to be restrained by 10 kcal/mol/Ų; otherwise, they move to S0-S2 while the third ion is moved to S4). The PMF rises steeply as the ion approaches the filter, reaching +40 kT at the S4 site (z = 3.8Å), which is due to the Coulomb repulsion of the ion at S3. This result indicates that simultaneous occupation of the S1-S3-S4 sites by three K⁺ ions is not feasible. An inspection of the ion and water densities in the S3-S4 region (Fig. S3) reveals that the S4 site can accommodate an ion and water simultaneously in off-axis positions. This is not feasible for the S1-S3 binding sites, which are formed by eight carbonyls. In contrast, the S4 site is formed by four carbonyls and four hydroxyl side chains of the Thr residues opening to the cavity, and thus is more flexible.

Figure 2.

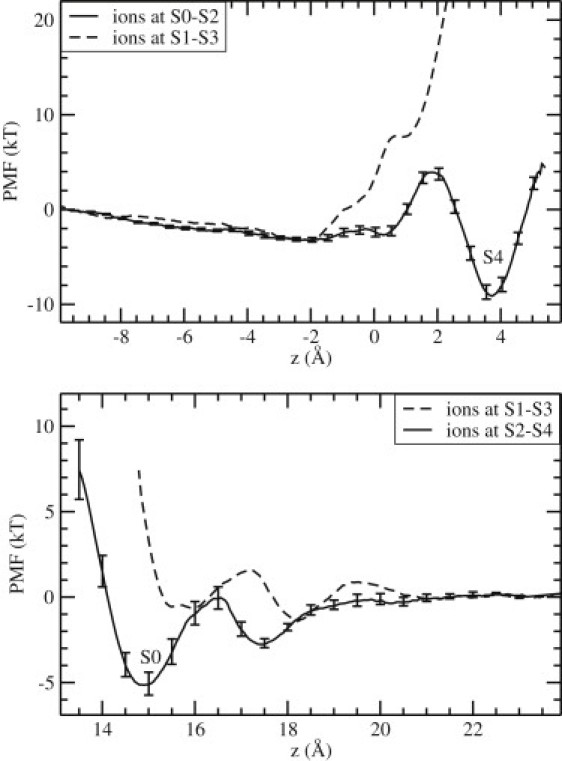
PMFs of a K⁺ ion in Kv1.2 as it is moved to the filter from the intracellular side (top) and the extracellular side (bottom). In both cases, the solid lines show the PMFs leading to the configuration with three K⁺ ions occupying the S0-S2-S4 sites separated by two water molecules at S1-S3. The dashed lines show the PMFs for the alternative configurations in which the two resident K⁺ ions are at S1-S3 while the third K⁺ ion moves from the cavity to S4 (top), or from the outside to S0 (bottom). The error bars on solid lines are estimated by constructing five PMFs from 100 ps blocks of data (similar errors are found in all other PMFs).

The second PMF (top, solid line) is constructed when the two resident ions are at S0-S2. In this case, a binding pocket of depth ∼9 kT is observed to form at S4, leading to a stable three-ion complex occupying the S0-S2-S4 sites separated by two water molecules at S1 and S3. The small energy barrier before the binding pocket arises during the exchange of the ion with the water molecule at S4, when the ion coordination is not optimal. The error bars on the solid line are estimated from a block data analysis.

A similar question arises for the inward permeation of ions, namely, can a K⁺ ion bind to the S0 site while the resident ions occupy S1-S3, or do they have to move to S2-S4 to enable the binding? This is answered in Fig. 2 (bottom), which shows the PMFs of a K⁺ ion for the two configurations. The PMF for the S1-S3 configuration (dashed line) indicates that the third K⁺ ion can approach the S0 site but cannot actually bind to this site. To quantify this statement, we calculate the binding energy of the K⁺ ion from the PMF, which yields ∼0 kT. In contrast, the second PMF with the resident ions at S2-S4 (solid line) exhibits a clear binding pocket at S0 with a depth of ∼5 kT. The binding energy of the K⁺ ion in this case is −2.6 kT. The formation of an external binding site at z = 17.5 Å with a depth of ∼3 kT is also evident from this PMF.

The results of a similar study in KcsA are presented in Fig. 3. A comparison of the PMFs in Figs. 2 and 3 shows that the conclusions derived from Kv1.2 about the binding of a third K⁺ ion to the filter apply equally well to KcsA: 1), binding of a K⁺ ion from the cavity to S4 is not possible when the resident ions are at S1-S3, but a shallow binding pocket forms at S4 when they are at S0-S2 (Fig. 3, top); and 2), there are no binding pockets at or near S0 while the resident ions are at S1-S3, but a fairly deep pocket with a depth of ∼9 kT is observed when they are at S2-S4 (Fig. 3, bottom). The binding energy of the K⁺ ion to the S0 site, calculated from the PMF (Fig. 3, bottom, solid line), is −5.7 kT. Thus, in both channels, stable binding of three K⁺ ions to the filter is only possible when they occupy the S0-S2-S4 sites separated by two water molecules at S1 and S3. One notable difference between Kv1.2 and KcsA is that in Kv1.2 the binding pocket at S4 is deeper than that at S0, whereas the opposite is true in KcsA. A deeper binding pocket at the entry of a channel helps to attract ions, and a shallower one at the exit enables their quick release, thus facilitating ion permeation in that direction. This suggests that Kv1.2 is primed for outward permeation, and KcsA is primed for inward permeation (1).

Figure 3.

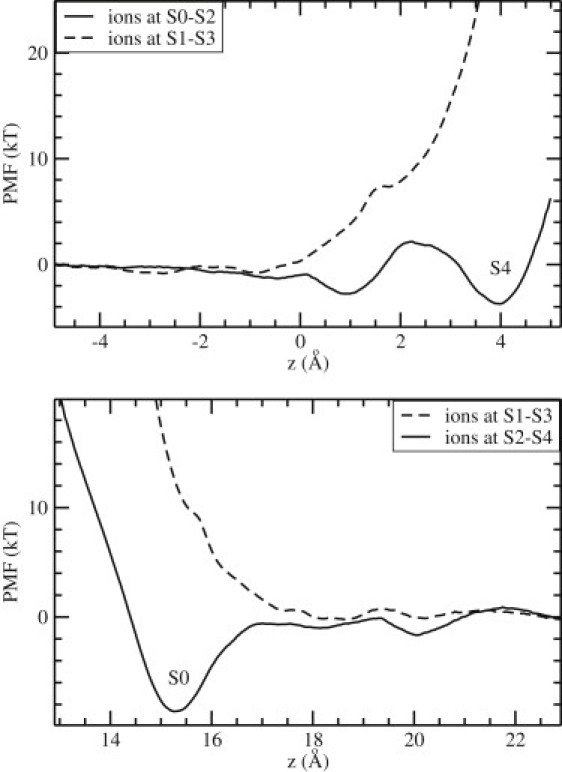
PMFs of a K⁺ ion as in Fig. 2, but for the KcsA potassium channel.

Concerted motion of ions

The above results for single-ion PMFs demonstrate the importance of the concerted motion of ions in the filter. Before a third K⁺ ion can bind from the cavity to S4, the resident ions at S1-S3 have to move to S0-S2. Similarly, binding of a third K⁺ion to S0 requires the transition of resident ions from S1-S3 to S2-S4. To investigate the feasibility of such motions occurring independently of the position of the third ion, we construct PMFs for the center of mass of two K⁺ ions resident in the filter while the third K⁺ ion remains in the cavity. The concerted motion of a pair of K⁺ ions in the filter was previously demonstrated in numerous MD simulations (5–9), providing an intuitive justification for such a choice for the reaction coordinate. A more rigorous justification for using the center of mass of the ions as the reaction coordinate can be obtained by inspecting the distribution of their relative coordinates (Fig. S4). These distributions exhibit sharply peaked Gaussians, confirming the correlated motion of the K⁺ ions.

The two-ion PMF results are shown in Fig. 4 for Kv1.2 (top) and KcsA (bottom). The three minima in the PMFs correspond to the configurations in which the pair of ions occupy S2-S4 (left), S1-S3 (middle), and S0-S2 (right). In Kv1.2, the free energies of the S1-S3 and S2-S4 configurations are almost the same, and they are separated by a small barrier (∼4kT). Thus, transitions between these two configurations can occur with little impediment. The free energy of the S0-S2 configuration is ∼5 kT deeper than that of the other two, which is consistent with the outward permeation function of Kv1.2. There is, however, a large energy barrier (>20kT) for the S1-S3 → S0-S2 transition, which would drastically hinder such a movement of ions. The large difference between the two barrier heights is presumably due to the different nature of S0: all other binding sites have eight carbonyl (or hydroxyl) oxygens coordinating the K⁺ ions, whereas S0 has only four carbonyls, and the ion has to rely on water molecules for full hydration.

Figure 4.

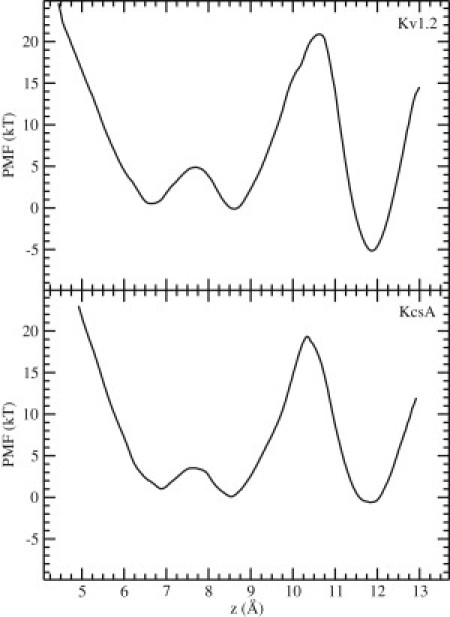
PMFs for the center of mass of two K⁺ ions in the filter of Kv1.2 (top) and KcsA (bottom). The three minima (from left to right) correspond to the configurations in which the two K⁺ ions occupy sites S2-S4, S1-S3, and S0-S2. The third K⁺ ion is in the cavity. A large free-energy barrier is observed for the S1-S3 → S0-S2 transition in both cases.

The situation in KcsA (Fig. 4, bottom) is broadly similar. The energy barriers are slightly smaller in KcsA than in Kv1.2, but the barrier for the S1-S3 → S0-S2 transition remains too high (∼19kT). One quantitative difference between the two PMFs is that the free energy of the S0-S2 configuration is almost the same as that of S1-S3 and S2-S4 in KcsA. The deeper energy pocket in Kv1.2 may result from the closer coordination of the K⁺ ion at S0 with the water molecule at S1, as mentioned above.

The two-ion PMFs indicate that the S1-S3 → S2-S4 transition can occur readily, enabling binding of a third K⁺ ion to S0. However, the S1-S3 → S0-S2 transition is substantially hindered, which makes it difficult for a third K⁺ ion to bind from the cavity to S4. To investigate whether this transition might be helped by a simultaneous movement of the K⁺ ion from the cavity to S4, we constructed three-ion PMFs using the center of mass of the three ions as the reaction coordinate. In constructing these PMFs, we placed the cavity K⁺ ion at the S5 site, as explained in Materials and Methods. These PMFs are shown in Fig. 5 for Kv1.2 (top) and KcsA (bottom). The minimum on the left corresponds to the three-ion configuration S1-S3-S5, and the one on the right corresponds to S0-S2-S4. In both cases, the barrier for the transition S1-S3-S5 → S0-S2-S4 changes very little compared with the S1-S3 → S0-S2 transition in Fig. 4. Thus, simultaneous movement of the cavity ion to S4 does not help reduce the energy barrier faced by the pair of K⁺ ions moving from S1-S3 to S0-S2.

Figure 5.

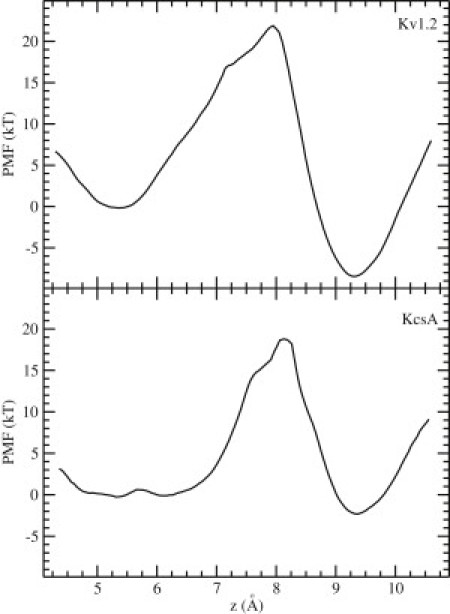
PMFs for the center of mass of three K⁺ ions in Kv1.2 (top) and KcsA (bottom). The minimum on the left corresponds to the configuration in which the three K⁺ ions occupy sites S1-S3-S5, and the one on the right corresponds to the occupation of S0-S2-S4.

Discussion and Conclusions

In this study, we attempted to assess the effect of the CMAP correction in the CHARMM force field on the energetics of ion permeation in Kv1.2 and KcsA channels. Our main findings, which differ from those obtained in previous PMF studies of K⁺ions in KcsA (16,17), are as follows:

• 1.Occupation of the S1-S3-S4 sites by three K⁺ ions is energetically infeasible in either channel. By far the most favorable conduction configuration is three K⁺ ions occupying the S0-S2-S4 sites, buffered by two water molecules at S1 and S3. The Coulomb repulsion between cations provides a strong disincentive for simultaneous occupation of neighboring sites by two K⁺ ions (>200 kT). This result is consistent with previous free-energy perturbation calculations that showed the infeasibility of three K⁺ ions binding to the S1-S3-S4 sites (14,15). Experimental evidence also supports the primacy of the S0-S2-S4 configuration. Measurements of ion-water flux coupling in potassium channels indicate that the flux ratio, n(water)/n(K⁺), is ≥1 (46–48). This is consistent with three K⁺ ions occupying S0-S2-S4 but not S1-S3-S4. Because ions and water move in single file in the filter, the water/ion flux ratio will necessarily be <1 in the S1-S3-S4 scenario. Finally, in recent 30 μs MD simulations of the Kv1.2 channel that included the CMAP correction, the S0-S2-S4 configuration (but not S1-S3-S4) was identified as one of the main steps in the permeation cycle (21).
• 2.A large energy barrier of height ∼20 kT is found in the two-ion PMF, which would hinder the transitions of K⁺ ions between the S1-S3 and S0-S2 sites and prevent barrierless diffusion of K⁺ ions across the filter. We attribute this barrier to the S1 → S0 transition of a K⁺ ion rather than to the S3 → S2 transition because there is no evidence of such a barrier in other transitions of K⁺ ions in the filter (that is, S4 → S3 and S2 → S1), which are similar in nature to S3 → S2. In a previous publication (30), we showed that the Tyr carbonyl oxygens between the S0-S1 sites are very flexible in the absence of the CMAP correction, but become quite rigid when it is included. Thus, it is very likely that the rigidity of the Tyr carbonyls contributes to the observed S0-S1 energy barrier. We previously showed that the CMAP correction is essential for describing the structure and function of the selectivity filter in Kv1.2 (30); therefore, we need to look elsewhere for the resolution of this problem. One possibility is to include the polarization interaction in the force field. What distinguishes the S0 site from the others in the filter is that a K⁺ ion at S0 is only partially hydrated by the carbonyl oxygens, and three water molecules are required to complete its coordination shell. If the polarization properties of these water molecules at the interface are different from the average, this may help to lower the energy barrier. Lack of polarization has been shown to lead to similar energy barriers in the gramicidin A channel (42–45). Ab initio calculations have demonstrated the importance of water polarization for ion permeation in gramicidin A (49), and indeed, inclusion of the polarization interaction in classical MD simulations has resolved the barrier problem in this channel (50).

Subsequent to the completion of the PMF calculations presented here, Jensen et al. (21) published an MD study of conduction of K⁺ ions in the Kv1.2 channel. Because similar structures and force fields were employed in the two studies, our PMF results may help to explain their conductance results, some of which are in apparent conflict with the experimental observations (e.g., outward conductance is delayed until the applied voltage becomes quite large and there is no inward conductance). There are plenty of data for Kv channels that show inward conductance (51,52). Our PMF results were obtained at zero voltage, but they would not change much at small applied voltages. Even if the ∼20 kT barrier at the S0-S1 transition point is reduced by a small amount, it will remain sufficiently high to prevent outward conduction at small voltages. As the outward driving force is increased, the S0-S1 energy barrier will naturally be decreased further. Of more importance, however, the K⁺ ions in the filter (at the S1-S3-S5 positions) will be pushed in further, which will help to push the K⁺ ion at S1 over the energy barrier. This could explain why the outward conductance is observed only at higher applied voltages. Lack of inward conduction can be explained similarly. In this case, a K⁺ ion at the S0 site faces a substantially higher barrier compared with an inward transition (see Figs. 4 and 5, top), and there are no ions behind to help push it across to S1. Jensen et al.'s (21) observation that K⁺ ions prefer S2-S4 sites to S1-S3 sites, in contrast to previously published data (3,4,25–27), may also be explained by our PMF results. It can be seen in Fig. 2 that the K⁺ ion at S0 is in a 5 kT energy well relative to the outside. Movement of the pair of K⁺ ions from S2-S4 to S1-S3 is contingent upon vacation of the S0 site by the third K⁺ ion, but this may be delayed due to the energy well it is in. Furthermore, the three-ion PMF (Fig. 5, top) shows that the S0-S2-S4 configuration is more stable than the S1-S3-S5 configuration, which directly confirms the dominance of the former.

In summary, our PMF results are broadly consistent with the conductance simulations reported by Jensen et al. (21), and highlight the need for further improvements in MD force fields so that the conduction properties of potassium channels can be described more accurately. Although we also observed some differences between the Kv1.2 and KcsA PMFs, they were relatively small, and it would be more prudent to discuss them only after the problem with the S0-S1 energy barrier is resolved.