Mechanisms of Protein-Ligand Association and Its Modulation by Protein Mutations

Abstract

Protein-ligand interactions are essential for nearly all biological processes, and yet the biophysical mechanism that enables potential binding partners to associate before specific binding occurs remains poorly understood. Fundamental questions include which factors influence the formation of protein-ligand encounter complexes, and whether designated association pathways exist. To address these questions, we developed a computational approach to systematically analyze the complete ensemble of association pathways. Here, we use this approach to study the binding of a phosphate ion to the Escherichia coli phosphate-binding protein. Various mutants of the protein are considered, and their effects on binding free-energy profiles, association rates, and association pathway distributions are quantified. The results reveal the existence of two anion attractors, i.e., regions that initially attract negatively charged particles and allow them to be efficiently screened for phosphate, which is subsequently specifically bound. Point mutations that affect the charge on these attractors modulate their attraction strength and speed up association to a factor of 10 of the diffusion limit, and thus change the association pathways of the phosphate ligand. It is demonstrated that a phosphate that prebinds to such an attractor neutralizes its attraction effect to the environment, making the simultaneous association of a second phosphate ion unlikely. This study suggests ways in which structural properties can be used to tune molecular association kinetics so as to optimize the efficiency of binding, and highlights the importance of kinetic properties.

Introduction

The ability of proteins to bind ligands, including ions, substrates, cofactors, and other proteins, is essential to all life processes. For example, protein-ligand interactions mediate the uptake and storage of cargo (e.g., oxygen uptake in hemoglobin), molecular recognition leading to information transfer (e.g., sensing of neurotransmitters or growth hormones), and the buildup of biological structures (e.g., in RNA-ribosome interactions) (1,2). Although most of the biochemical and pharmaceutical studies conducted to date have investigated protein-ligand interactions in terms of equilibrium binding affinities, it is becoming increasingly evident that the effectiveness of such interactions crucially depends on dynamical and kinetic properties (3). For example, a slow-binding/slow-releasing enzyme substrate might show the same affinity as a quick-binding/quick-releasing one while exhibiting a significantly smaller substrate turnover rate. The dynamical properties of binding are inherently linked to structural aspects such as the size, concentration, and spatial distribution of the binding partners, as well as their detailed atomic structures and changes that occur therein.

The structure-dynamics relationships for binding processes have been studied at the binding-site contact distance in terms of relevant energetics such as the detailed electrostatic complementarity of the binding surfaces and hydrophobic burial, as well as structural binding mechanisms such as induced fit versus conformational selection (4,5). However, the fundamental properties of the spatiotemporal mechanism underlying this first contact in the protein-ligand binding process are still elusive. For example, does binding occur via a single dominant pathway, via multiple separated pathways, or via a funnel-shaped ensemble of pathways? Is it directed to the binding site, or are there metastable states that trap the binding partners in nonfunctional states? Can diffusion-limited binding be sped up by rapid binding to the surface and a subsequent surface search?

From a theoretical point of view, the protein-ligand association process can be considered as diffusion in a high-dimensional energy landscape that usually has an energetically favorable minimum at the configuration of the protein-ligand complex. In situations in which the interaction process takes place in dilute media, this energy landscape is flat at large protein-ligand distances, resulting in a purely diffusive motion of the molecules. When the interaction partners approach each other, electrostatic forces become relevant, and for favorably interacting molecules, the energy landscape funnels down toward the complex formation configuration (6). Such a binding funnel may also possess complex features as local minimal or parallel pathways. Gaining an understanding of this binding funnel and the dynamics that govern the motion upon it will likely enhance our ability to answer many important mechanistic questions. Protein-ligand binding has many similarities to protein folding, and principles or methods worked out in the protein-folding field are also likely to be useful here.

Molecular simulations are increasingly being used to correlate structural and mechanistic information with experimental observations (7). A widely used computational approach to simulate protein-ligand association dynamics involves the use of Brownian dynamics (BD) and Langevin dynamics (LD) simulations (8) of the diffusional motion of internally rigid protein models in implicit solvent. The BD approach is useful for predicting bimolecular association rates (9–11) in situations where binding is diffusion limited, as well as to provide detailed insights into how protein-ligand encounter complexes are formed (12). However, it is often difficult to perform a systematic analysis of the obtained simulation data. In this work, we present a simulation and analysis approach that directly reveals the ensemble of pathways of a ligand to the binding pocket, thus allowing mechanistic questions to be answered. Using this approach, one can identify metastable states in the binding procedure and study how binding mechanisms and rates are altered by mutations in the protein.

There are two alternative approaches to simulate and analyze dynamics. Most commonly, one uses the direct simulation approach, in which long trajectory realizations of the dynamical equations (e.g., BD) are generated and then analyzed. This approach has the advantage that it allows simulation of complex geometries with many degrees of freedom, such as large heterogeneous protein mixtures (13). A disadvantage is that quantities computed from generated trajectories (e.g., association rates) may have statistical uncertainty, or may be systematically biased when some rare events have not been sampled at all. Moreover, trajectory data are often tedious to analyze and necessitate a search for interesting observables that involve human subjectivity. Alternatively, one can describe the ensemble dynamics of the system, where the transition probabilities or rates between configurational substates of the system are characterized. This approach has been successfully used to model the conformational dynamics of proteins with Markov models (14–18), where the interstate transition probabilities are estimated from many short simulations that are initialized from different substates. In diffusion processes such as BD and LD, the ensemble dynamics can be expressed directly via the Fokker-Planck equation. Based on this formulation, sampling of individual trajectories can be avoided and the sampling error can be made zero. However, the downside of this approach is that to solve the Fokker-Planck equation, the configuration space must be discretized. When using a rectangular lattice, this is currently feasible only for three-dimensional spaces. Nevertheless, with a three-dimensional space, one can address the biophysically interesting process of ion binding to proteins (19). Higher-dimensional problems such as protein-protein binding with internal dynamics can be addressed with the use of meshless discretization approaches (16,20,21).

Here, we show how the ensemble dynamics approach permits a straightforward and objective analysis of protein-ligand association pathways under the mathematical framework of transition path theory (TPT) (22,23), which provides a complete and quantitative description of association pathways that lead from a freely diffusing ligand toward a protein-ligand complex in a given molecular model. We apply this approach to systematically study the binding of inorganic phosphate (P_i) to the phosphate-binding protein (PBP) of Escherichia coli (24,25). This protein plays an important role in the phosphate supply of bacterial cells and is expressed when the intracellular concentration of P_i is low. After it is transported to the bacterial periplasm, it scavenges for free P_i to subsequently pass it on to a membrane protein that transports the phosphate into the cytoplasm. Previous work on the binding of P_i to PBP was mainly concerned with investigating the binding kinetics by experimental means (26,27) or direct simulation (28); therefore, to our knowledge, this work is the first to provide a systematic description of the P_i binding pathway ensemble. We show how various mutations modulate the phosphate binding rates and pathways. Furthermore, it is shown how a P_i bound to PBP influences the binding of a second anion.

The findings presented here highlight the importance of a positively charged patch of the PBP for attracting negatively charged ions. They also suggest that this prebinding site may be a general mechanism for efficiently organizing specific ion binding via a two-step mechanism that selects first by polarity and then by ion type.

Theory

Dynamical model

Without loss of generality, the protein-ligand association process can be divided into two phases that are dominated by different forces (29) (see Fig. 1 a). The association phase (phase I) is largely governed by electrostatic forces and thermal motion of solvent molecules that lead to a diffusive approach of the solutes studied, and does not depend on intramolecular flexibility. In the binding phase (phase II), the protein-ligand complex is formed, which involves more complex short-range forces, intramolecular flexibility, and the structural role of solvent molecules. This separation into two phases suggests the need for two different computational models to describe them. The second phase requires a more detailed approach, such as an all-atom molecular-dynamics (MD) simulation with full structural resolution and flexibility. Here, we restrict ourselves to phase I, where the motion of the ligand in the protein-ligand potential is described by rigid-body Brownian (or Smoluchowski) dynamics in implicit solvent:

$$d\mathbf{x}\left(t\right)=-\frac{D}{k_{B}T}\mathbf{\nabla }V\left(\mathbf{x}\right)dt+\sqrt{2D}d{\mathbf{W}}_t,$$ (1)

where x(t) is the position of the ligand at time t ≥ 0, D is the joint translational diffusion constant of PBP and P_i, T is the absolute temperature, k_B is the Boltzmann constant, V(x) is the potential energy of the ligand at position x(t), and W_t is a multivariate Wiener process (i.e., white noise with independent, normally distributed increments). We assume isotropic diffusion for both the protein and the ligand, and hence diffusion can be described by a scalar constant. The error introduced by neglecting hydrodynamic interactions between interaction partners is unlikely to affect the main findings of this work. However, in future studies, hydrodynamic interactions could also be included, in accordance with a recent study by Geyer and Winter (30). The change in particle position dx(t) in a time interval dt is thus the result of the force from the potential, −∇V(x), and a random displacement that implicitly models the collisions with solvent molecules. It is important to note that the solution x(t) of the stochastic differential equation (Eq. 1) is a random sequence. Hence, for a given initial position x(0) = x_o, each realization of x(t) describes a possible ligand trajectory.

Figure 1.

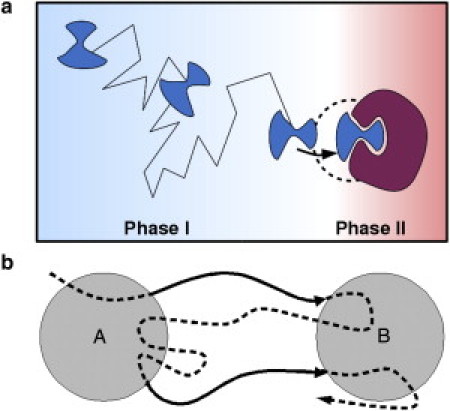
Phases of protein-ligand association. (a) Phase I is largely characterized by diffusional association and ends with formation of an encounter complex. Phase II involves actual binding of the ligand and may involve structural rearrangements in both interaction partners. (b) Reactive trajectory definition. The bold parts show reactive trajectory parts going from set A (unbound configurations) to set B (bound configurations).

Interaction potential

To compute the interaction potential between PBP and phosphate ion, only electrostatic forces are considered because they are the most important contributors during the association phase. An explicit modeling of Van der Waals forces can be omitted because the interaction partners can be thought of as being immersed in dense media (water) and therefore interacting equally with all surrounding atoms.

Furthermore, the structure of the diffusing ligand P_i is approximated by a point charge of −2e to represent the HPO₂⁻² form of phosphate. This allows one to calculate the energy of PBP-P_i configurations by multiplying the electrostatic potential induced by the protein with the phosphate charge (−2e) at the respective positions. The protein potential V(r) is computed according to the Poisson-Boltzmann theory (31), in which the solvent is modeled as a continuum with a specific dielectric constant. The Poisson-Boltzmann equation is given by

$$\mathbf{\nabla }\left[\epsilon \left(\mathbf{x}\right)\mathbf{\nabla }V\left(\mathbf{x}\right)\right]=-4\mathit{\pi \rho }\left(\mathbf{x}\right)-4\mathit{\pi }\sum _i{c}_i^{\mathrm{\infty }}{z}_i\exp \left(\frac{-z_{i}V\left(\mathbf{x}\right)}{k_{B}T}\right)\mathit{\lambda }\left(\mathbf{x}\right),$$ (2)

where ɛ(x) is the dielectric constant at position x, ρ indicates the charge density of the protein (given by assigning partial atom charges), c_i^∞ denotes the concentration of ion species i at an infinite distance from the molecule, z_i is its charge, k_B is the Boltzmann constant, T is the temperature, and λ(x) indicates the ion accessibility.

For the calculation of association rates to be correct, the volume considered around the protein has to be large enough that the gradient of the potential will approach zero at its outer boundaries. At the same time, for a correct calculation, it is crucial to ensure that the potential close to the protein surface is well described. To comply with the large volume and high resolution requirements, we use the manual focusing mechanism (mg-manual) provided by the Adaptive Poisson-Boltzmann Solver (APBS), and solve the PB equation on differently sized grids ranging from 33 × 33 × 33 with isotropic spacing of d = 16 Å to 193 × 193 × 193 with isotropic spacing of d = 0.35 Å. The respective coarser solutions are used as an outer boundary condition for the finer one.

Transition path theory

Although individual realizations of the stochastic dynamics (Eq. 1) are random, we are interested in the deterministic expectation values of this random process, such as transition rates, fluxes, and pathway probabilities. To obtain these quantities, we apply TPT (22,32,33) to the Markov jump process, which results from discretizing the Fokker-Planck equation associated with Eq. 1.

The main concepts of TPT are briefly restated here. Given an ergodic stochastic process, such as BD in a potential, LD, or Markov jump process (e.g., on a grid), TPT provides the statistical properties of the ensemble of reactive pathways between two disjoint subsets (A and B) of the state space. Consider a hypothetical, infinitely long trajectory. A trajectory fragment is called a reactive trajectory if it leaves A and subsequently enters B. In particular, trajectories that return to A before reaching B are not considered part of the reactive trajectory ensemble (see Fig. 1 b for an illustration).

To calculate TPT quantities in practice, one must discretize the configuration space. We consider that the configuration space is partitioned into small sets, here briefly called states. In the scenario of protein-ligand binding, set A is defined as comprising configurations in which the ligand can freely diffuse, here chosen to contain all states in space that are >250 Å away from the center of mass of the protein. In turn, set B is chosen to contain all states that correspond to bound or metastable precomplex protein-ligand configurations.

The essential quantity needed to compute the statistical properties of transition pathways between A and B is the forward committor, q_i⁺, defined as the probability that the process when being at state i will reach set B next, rather than returning to set A. In the context of protein-ligand association, q_i⁺ denotes the probability to associate to the binding site (at B) rather than to dissociate to set A. In the Materials and Methods section, we explain how the forward committor q_i⁺ can be efficiently calculated for a given dynamical model. Furthermore, we need the backward committor probability q_i⁻, which is the probability when being at state i that the process was previously in set A rather than in set B, i.e., it reached state i from the dissociated states A and had not been bound before. For reversible stochastic processes, as in the present case, it is simply given by q_i⁻ = 1 − q_i⁺. Let k_ij be the transition rate between states i and j, without taking into account the choice of A and B. To be able to infer information about the reactive parts of the trajectory, i.e., the parts that leave A and go to B, one must consider only the part of k_ij that involves trajectories that come from the dissociated A set and will go on to the associated B set, i.e., q_i⁻k_ijq_j⁺. The reactive probability flux is hence given by

$${\mathrm{f}}_{\mathrm{ij}}={\mathrm{\pi }}_{\mathrm{i}}{\mathrm{q}}_{\mathrm{i}}^{-}{\mathrm{k}}_{\mathrm{ij}}{\mathrm{q}}_{\mathrm{j}}^{+},$$ (3)

where π_i denotes the Boltzmann weight of state i, i.e., the overall probability for the process to be in the volume element represented by state i. This definition still contains recrossing events of reactive trajectories. To account only for the net reactive probability flux from A to B, the reactive flux f_ji associated with recrossings of the reactive trajectory is subtracted from the forward flux f_ij, leading the following expression for the net reactive probability flux:

$$f_{ij}^{+}=\max \{0,f_{ij}-f_{ij}\}.$$ (4)

It is important to note that the flux is conserved, i.e., the amount of flux leaving A equals the amount entering B, and for all intermediate states i the influx equals the outflux. This property leads directly to an expression for the transition rate from A to B, as explained in the next section. Refer to Fig. 2 for an illustration of TPT in a two-dimensional model of protein-ligand association.

Figure 2.

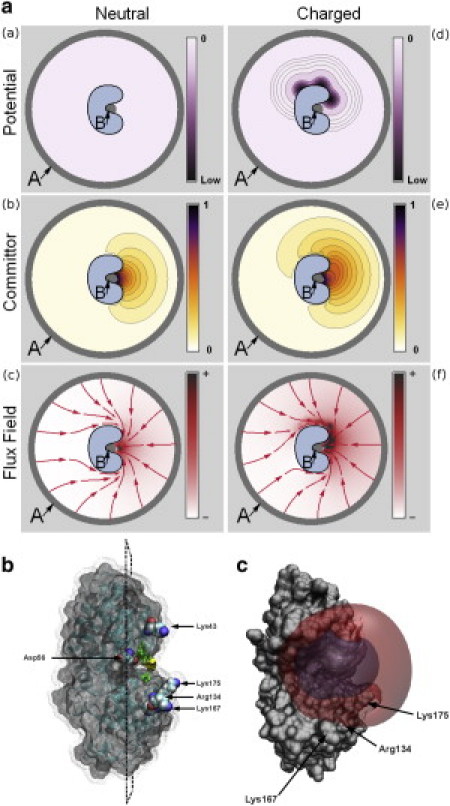
(a) Illustration of TPT in a simple two-dimensional protein-ligand binding model. The dissociated state of the ligand, state A, and the associated state B are shown. Panels a–c show a situation in which no potential is present and the ligand can diffuse freely until it associates to the protein. Panels d–f illustrate a situation where the protein has surface charges, generating energy minima that attract the ligand. (a and d) The different potentials. (b and e) The forward committor q⁺, revealing for areas on top of the charged protein a higher probability to reach the binding site compared with the uncharged protein. (c and f) The reactive flux density and integrated flux lines calculated from the flux field resulting from the fluxes f_ij⁺. For the neutral protein, it becomes apparent that the ligand diffuses freely and the binding pathways are restricted only by spatial constraints. In the charged scenario, the ligand is strongly attracted by the top side of the protein, creating a high reactive flux density in that area that distorts the pathway ensemble accordingly. (b) Transparent Connolly surface of the PBP (E. coli) showing secondary structure elements. The yellow region depicts the B set. A subset of mutated amino acids is shown in Van der Waals representation. The dotted surface represents points that are accessible by the phosphate ion. The indicated plane denotes the projection area used to visualize first hitting densities (as in Fig. 3). (c) Connolly surface representation of PBP with transparent intermediate 1 (red) and intermediate 2 (blue) committor isosurfaces.

Binding rate calculation

The expected number of $A\to B$ transitions per time unit is given by the total flux (33):

$$F_{AB}=\sum _{i\in A}\sum _{j\notin A}{f}_{ij}^{+}=\sum _{i\in A}\sum _{j\notin A}{\pi }_i{k}_{ij}{q}_j^{+}.$$ (5)

This quantity includes the fact that the ligand must diffuse back to the A area before another transition to B is considered. Hence, to calculate the $A\to B$ transition rate, we need to take the probability into account, that the ligand is moving from A to B, i.e., it was in A last:

$${\mathit{\pi }}_A=\sum _{i\in S}{\mathit{\pi }}_i{q}_i^{-},$$ (6)

where S is the set of all states. Therefore, the transition rate is given by (14)

$$k_{AB}=\frac{F_{AB}}{{\mathit{\pi }}_A},$$ (7)

where k_AB is the rate at which a ligand molecule binds starting from set A. To compute the bimolecular association rate of PBP and P_i, the rate at which ligand molecules arrive at the A sphere has to be taken into account. Based on the assumption that protein and ligand diffuse freely upon a distance r (i.e., in our scenario the ligand enters the A sphere), according to Erban and Chapman (34), the diffusion-limited association constant k_On can be obtained by

$$k_{\text{On}}=4\mathit{\pi }D\left(r-\sqrt{\frac{D}{k_{AB}}}\tanh \left(r\sqrt{\frac{k_{AB}}{D}}\right)\right),$$ (8)

where D is the diffusion constant, and r denotes the radius of the A sphere. Note that k_On is a concentration-dependent rate (e.g. in nm³s⁻¹), and k_AB is the rate of a single-molecule event (in s⁻¹).

Materials and Methods

Molecular model and simulation setup

The coordinates of the open form mutant T141D of the PBP from E. coli (Protein Data Bank (PDB) (35) code 1OIB, Chain A) served as a template to create several in silico mutants of the protein. The mutagenesis tool of PyMOL (version 0.99rc6) was used to create mutants D56N, D137T, K43M, K43Q, R134Q, R135Q, R134Q/K167Q/K175Q (3 mut.), R134Q/K167Q/K175Q/D21N/D51N/D61N (6 mut.), and T141D, chosen in agreement with previous work on PBP (28). The wild-type (wt) was modeled by replacing Asp-141 with Thr-141.

We carried out energy minimization of the structures in a TIP3P water box by running 2000 steps of the steepest-gradient algorithm using the Gromacs (version 4.5) program (36) with the CHARMM (37) force field. For continuum electrostatic calculations, we added partial charges and atom radii by using the PDB2PQR suite (38) with CHARMM force-field parameters. PDB2PQR makes use of PROPKA (39) to determine the protonation state of ionizable amino acids at a given pH, which was set to 7 here. Furthermore, the program automatically optimizes the hydrogen-bonding network of the structures by rotating residues when necessary. All calculated pKa values can be found in the Supporting Material. We calculated the electrostatic potential of the resulting structures at zero ionic strength using APBS (40), with dielectric constants of ɛ_P = 4.0 for the protein interior and ɛ_S = 78.0 for the solvent. As the joint diffusion constant, D = 8 × 10⁻⁶cm²s⁻¹ (41) was used.

Space discretization

To calculate the TPT quantities for the protein-ligand binding process, a finite volume space discretization is required that extends over a large volume and at the same time has a high resolution close to the protein surface. Therefore, we developed a simple adaptive discretization scheme based on the numerical gradient of the electrostatic potential. The procedure starts from a coarse cubic 33 × 33 × 33 grid with an edge length of 528 Å and refines interior grid points based on a local error criterion. By using central finite differences, one computes the potential derivatives in each Euclidean direction for each point, employing the discretization presented here as well as a finer discretization in which additional grids points have been added halfway between each pair of initial grid points. When at a given refinement point the two derivatives differ by more than a specified threshold (here 0.01 kT/Å), the refinement is accepted and another grid plane is added, intersecting with this refinement point and perpendicular to the connection between the two coarse grid points. This procedure is iterated until no more planes are added. Grid points that lie inside the protein (defined as having a minimal distance to protein atoms of <3.2 Å) are not taken into account, and are dismissed from the final grid. The resulting grids had an average size of 173 × 151 × 177 points (a total of 4,623,771 elements) with box lengths ranging from 16 Å for distant boxes to 0.5 Å in the vicinity of the protein.

Rate matrix computation

When considering BD (Eq. 1), one can compute the transition rates between volume elements of the regular grid defined above by using the discretization scheme introduced by Latorre et al. (42). The resulting matrix K is a discrete model of the entire ensemble dynamics of the protein-ligand association process, and all subsequent analysis can be conducted based on this matrix. A matrix element k_ij specifies the number of transitions per time unit to a volume element j conditional on starting at element i, and is computed as follows:

$$k_{ij}=\{\begin{array}{ll}\frac{D}{h_{i,j}{d}_{i\to j}}\exp \left(-\frac{1}{2k_{B}T}\left(V_j-V_i\right)\right)\hfill & j\in \left\{N_i\right\}\hfill \\ -\sum _j{k}_{ij},\hfill & j=i\hfill \\ 0\hfill & \text{otherwise},\hfill \end{array}$$ (9)

where N_i denotes the st of all volume elements that share a face with element i, D is the joint diffusion constant, V_i designates the potential at grid point i, h_i,j denotes the distance between grid points i and j, and $d_{i\to j}$ stands for the length of the ith volume cell in the direction of j.

A and B definition and committor computation

After obtaining the space discretization of the volume around the protein, we assign the A and B sets. For the set of free-diffusing configurations of the phosphate ion (A set of states), all volume elements whose center is farther than 250 Å away from the geometric center of the protein are chosen. Note that the choice of A is irrelevant as long as it is far enough away from the protein that the electrostatic forces will be zero in A. Defining A farther away from this minimal distance will increase r but decrease k_AB, resulting in the same concentration-dependent binding rate as in Eq. 8. Set B of the bound/precomplex configurations is chosen to include all volume elements that are within a 3 Å radius of the geometric center of Thr-10, Ser-38, and Ser-139 (shown as the yellow region in Fig. 2 b). The choice of B will affect the pathways and association rates because it defines the bound state.

With the discrete rate matrix (Eq. 9), the forward committor can be computed by solving the constrained linear problem:

$$\mathbf{Kq}=0$$

$$\mathrm{s}.\mathrm{t}.q_i=0\forall i\in A$$

$$q_i=1\forall i\in B,$$ (10)

where A and B are the sets of discrete states corresponding to dissociated and associated states, respectively. This problem is solved by reordering the states in the order (S, A, B), where S = (A ∪ B)^C, yielding the following structure in K and q:

$$\mathbf{K}=\left(\begin{array}{ccc}{\mathbf{K}}_{SS}& {\mathbf{K}}_{SA}& {\mathbf{K}}_{SB}\\ {\mathbf{K}}_{AS}& {\mathbf{K}}_{AA}& {\mathbf{K}}_{AB}\\ {\mathbf{K}}_{BS}& {\mathbf{K}}_{BA}& {\mathbf{K}}_{BB}\end{array}\right),q\left(\begin{array}{c}{\mathbf{q}}_S\\ {\mathbf{q}}_A=0\\ {\mathbf{q}}_B=1\end{array}\right),$$ (11)

This allows Eq. 10 to be rewritten as:

$${\mathrm{K}}_{SS}{\mathrm{q}}_S={\mathrm{K}}_{SB}$$ (12)

This can easily be solved by standard numerical methods to obtain the unknown q_S. In the present application, the number of unknowns is on the order of 10⁶. To solve this task, we use the implementation of the iterative BiCGStab algorithm provided by the Java Matrix Tookit (43). In scenarios where the rate matrix is obtained based on direct sampling of trajectories, the entries have a statistical error. In this case, the uncertainties of the rates and the corresponding uncertainties of molecular properties derived from K should be evaluated (44). However, in this study, no statistical error is involved because the rates k_ij are directly obtained from a discretization of the transport equation.

Free-energy profile of ligand association

Because the forward committor is the probability to associate rather than dissociate, it measures the progress of the reaction and thus represents a kinetic reaction coordinate (45), with 0 representing the dissociated configuration (A) and 1 representing the associated configuration (B). The free energy along this coordinate is given by

$$F\left(q\right)=-k_{B}T\ln \left(\rho \left(q\right)\right)+const,$$ (13)

where ρ(q) denotes the stationary density of the set of states having a committor value q and is calculated in our discrete model by

$$\rho \left(q\right)=\sum _{i,q_i\in \left[q-\frac{\Delta }{2},q+\frac{\Delta }{2}\right]}\exp \left(\frac{-V\left(x_i\right)}{k_{B}T}\right)$$ (14)

using a sliding window with width Δ = 0.005 over the range of $q\in \left[\frac{\Delta }{2},1-\frac{\Delta }{2}\right]$.

Binding flux field and visualization

To visualize the phosphate association pathways, we calculated a vector field of reactive fluxes. For this purpose, we assigned a total flux vector to each grid point i by vectorially summing all outgoing fluxes f_ij⁺. To visualize the resulting vector field, as shown in Figs. 3, we used the Mayavi2 program (46). Starting from a fixed number of points spherically distributed with distance 80 Å from the geometric center of the protein, the program follows the streamlines along the flux vectors, thus tracing out possible binding pathways. The streamlines are colored according to the local flux strength, i.e., the norm of the total flux vectors. The lighter the coloring, the stronger the encountered flux.

Figure 3.

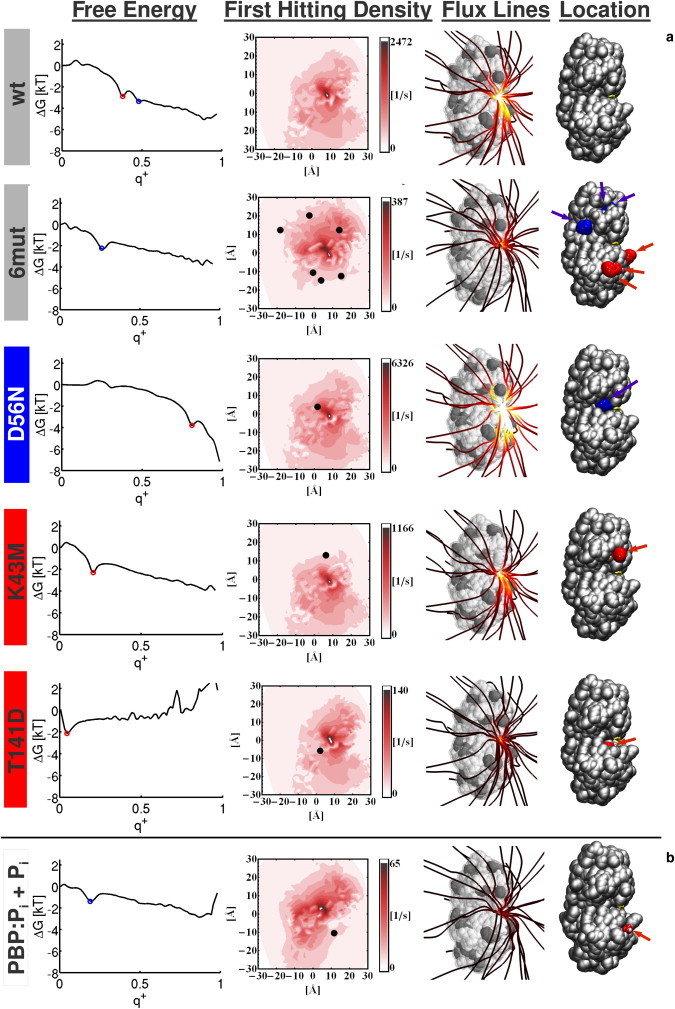
Free-energy profiles, first hitting densities, and pathways for selected mutants of P_i associating to the PBP. Text background coloring: gray, protein has neutral net charge; blue, positive net charge; red, negative net charge. First column: Free-energy profile of the ligand when it travels from the dissociated (q⁺ = 0) to the associated state (q⁺ = 1). A red or blue dot is shown whenever a minimum could be assigned to one of the two isosurfaces shown in Fig. 2c. Second column: Surface density of reactive trajectories that hit the extended protein surface per unit of time. In each plot, the black points represent projected C_α positions of mutated amino acids. Note that for clarity, the color axis is scaled separately for each mutant. Third column: Streamlines of the reactive flux of ligand association (see text) for the different mutants, which represent the ensemble of association pathways. A lighter streamline coloring corresponds to a higher local reactive flux. Here, the same color scheme is used for all pictures. Fourth column: The positions of mutated residues are shown. Red/blue corresponds to negative/positive charged mutations relative to the wt structure.

To better visualize how the association pathways behave near the protein, we calculated where they hit the protein surface for the first time. To this end, we defined a surface at a distance of 10 Å around the phosphate-accessible surface. At each surface element, the flux through the surface, quantified by the reactive TPT flux f_ij⁺ (Eq. 4), was calculated. For the sake of visualization, we calculated an orthogonal projection of surface elements onto a two-dimensional plane that divided the surface into two halves. The plane is depicted in Fig. 2 b. In the projection, only surface elements on the half of the binding site were taken into account.

Results and Discussion

The results of the modeling and analysis of P_i association to the PBP and various in silico mutants are presented below. Selected mutants are summarized in Fig. 3, and the results for the remaining structures are shown in the Supporting Material.

Free-energy profiles and association rates

The left column of Fig. 3 shows the free-energy profile of phosphate associations along the committor coordinate. For most of the investigated mutants, the free energy decreases with increasing committor value, indicating that binding of phosphate is energetically favorable. An inspection of the free-energy profiles of different mutants shows the existence of several minima along the committor coordinate. Such minima indicate that the phosphate ion is more likely to be found at certain positions in space with corresponding committor values, and these configurations may be metastable. Interestingly, the two committor isosurfaces shown in Fig. 2 c are especially relevant for the phosphate-binding process: for each mutant, at least one of these two isosurfaces describes configurations associated with a minimum in its free-energy profile. Whenever a minimum could be assigned to one of the isosurfaces, it is marked with a red or blue dot in the free-energy profile. Phosphate configurations represented by the outer isosurface (red) are termed intermediate 1, and configurations described by the inner isosurface (blue) are termed intermediate 2.

In the wt protein, both intermediate 1 and intermediate 2 free-energy minima indicate two metastable configurations of the phosphate before it reaches the binding site. The A197W mutant (see the Supporting Material) exhibits a very similar profile and an almost equal association rate of 26.4 M⁻¹s⁻¹ compared with 27.9 M⁻¹s⁻¹ for the wt, indicating that this mutation has little effect on the phosphate ion binding capability. For mutants R134Q/K167Q/K175Q (3mut.) and R134Q/K167Q/K175Q/D21N/D51N/D61N (6mut.), the intermediate 1 configuration is destabilized, and thus only the configurations corresponding to intermediate 2 are found to be metastable. Both mutants have the same three positively charged amino acids replaced by neutral substitutes, but in the 6mut. mutant the associated loss of charge is compensated for by additionally replacing three negatively charged amino acids with neutral substitutes. The destabilization of intermediate 1 indicates that residues Arg-134, Lys-167, and Lys-175 are necessary for holding the phosphate ion at the protein surface. Interestingly, losing this kinetic trap along the binding coordinate does not increase the association rate of phosphate; rather, it is decreased by a factor of 3 for the 6mut. mutant (9.3 M⁻¹s⁻¹) and by a factor of ∼10 for the negatively charged 3mut. mutant (2.5 M⁻¹s⁻¹). In consideration of its relevance for attracting phosphates and thereby enhancing the binding efficiency, we henceforth refer to the positive charge patch around residues Arg-134, Lys-167, and Lys-175 as the anion attractor.

To further assess the relevance of positive surface charges, we considered the single-point mutations R134Q and R135Q. R134Q neutralizes one residue of the anion attractor, whereas R135Q neutralizes a residue that is found between the anion attractor and the phosphate-binding site, thereby interfering with the phosphate transport route. Although both mutants show a reduced association rate, this reduction is fivefold for R135Q and only twofold for R134Q. The corresponding free-energy profile of R135Q also reveals this effect by showing smaller binding (committor) probabilities for intermediate 1 and 2 configurations compared with the R134Q mutant.

The mutants discussed so far mainly affected residues in the vicinity of the anion attractor. For a more comprehensive assessment of phosphate association, we also considered mutations D56N, D137T, K43Q, and K43M. Mutations D56N and D137T both neutralize a negative charge and increase the association rate by a factor of ∼3 compared with the wt. Due to the consequently stronger attraction of the negatively charged phosphate ion, the minimum associated with intermediate 2 configurations vanishes, whereas intermediate 1 trapping is still present, albeit with an increased probability to reach the binding site from these configurations. The intermediate 2 minimum also disappears for the negatively charged K43M/K43Q mutants. However, in contrast to the positively charged D56N/D137T mutants, the association rate is reduced by a factor of almost 3, and the binding probability associated with intermediate 1 configurations is strongly reduced, as evidenced by the left-shifted minimum in the free-energy profiles.

Finally, we discuss the T141D mutant. The free-energy profile of this mutant is remarkably different from other mutants that also introduce a negative net charge of −1e. In fact, a free-energy minimum can also be assigned to intermediate 1 configurations, but the associated binding probability is very small. Furthermore, the free-energy difference between unbound and bound phosphate is positive, rendering phosphate binding unfavorable. This can also be observed at the corresponding association rate, which is also drastically reduced and a factor of 5 smaller than the smallest association rate found for almost all other mutants with a negative net charge of −1e. This result may be explained be the location of the mutation, which introduces a negative charge very close to the phosphate-binding site, repelling the phosphate there. Unlike other mutations that introduce negative charges, in this case the phosphate ion cannot avoid the repulsive region via alternative pathways to reach the binding site. Consequently, this mutation has the largest effect on the association efficiency of the phosphate ion.

Streamlines and first hitting density

The free-energy profiles and rates described above provide information about the macroscopic or effective properties of the phosphate association process, but they provide little information about the fine details of phosphate association. Dynamical properties provide more information that can be accessed with the TPT approach: the shape of the binding pathways and the distribution of where they hit the protein surface. Fig. 3 shows representative pathways of the association pathway ensemble. These plotted pathways are streamlines that follow the reactive flux field of binding. The number of reactive trajectories that pass a volume element per unit of time is expressed by streamline coloring. The brighter the coloring, the more reactive trajectories pass through the surrounding volume elements. This manifests as almost white coloring in the vicinity of the binding site, where the increasing bundling of reactive trajectories leads to an increased flux density. To obtain additional information where the phosphate association pathways attack the protein, we measured how many reactive trajectories per unit of time hit surface elements in a distance of 10 Å around the protein. This hitting density is visualized by a planar projection in the second column of Fig. 3 along with the positions of the mutations.

The neutrally charged structures wt and A197W share a similar pattern in the first hitting density and distribution of pathways. The phosphate trajectories attack the protein on both sides of the phosphate-binding side, with a preference for the side where the anion attractor is located. The corresponding streamline illustrations show that some phosphates make the first contact with the anion attractor and then crawl over the surface to the binding site. This picture is not qualitatively different for the positive D56N and D137T mutants. Here again, both sides of the protein are approached by the phosphate and the surface crawling still occurs. However, due to the increased net charge of the protein, the number of reactive trajectories is strongly increased. A change in both hitting density and approach pathway distribution can be observed for K43M/K43Q. In this case, the number of pathways that attack the protein at the side of the mutation is reduced, and the streamlines show that the phosphate is no longer attracted to the surface at the respective position. An even stronger distortion is observed when the positive patch is neutralized as in the 6mut. and 3mut. mutants. The number of pathways that hit the extended protein surface above the positive patch is significantly reduced in both cases. Furthermore, the flux lines show that the pathways are not attracted to the positive patch, but rather straightly approach the phosphate-binding site from the bulk. Due to the negative net charge of the 3mut. mutant, the number of phosphates that reach the binding site per unit of time is reduced, as indicated by the darker flux lines. Although the T141D mutation strongly reduces the association rate, it does not exhibit a change in the first hitting density, and the topology of the association pathways is not affected. The surface attraction of the phosphate ion is still present; however, the number of phosphates that reach the binding site is strongly reduced, i.e., this mutation affects only the last step of association. Although mutations R134Q and R135Q do not show a pronounced effect on the first hitting density, they do show a difference in the flux line picture. The surface attraction at the positive patch is less pronounced in the R134Q mutant compared with R135Q.

In the studies discussed so far, we investigated the binding dynamics of a single phosphate ion in the dilute limit, i.e., in the absence of other solutes. In a biological scenario, the situation is much more complex, as the cytosol is densely filled with various species of different sizes, shapes, and charges. Although such heterogeneous complexity is of limited interest to the biophysicist, it is very interesting to work out some of the principles that contribute to the phosphate-binding dynamics (and, more generally, to all ion-binding dynamics) in the cell. For example, how does phosphate binding occur in a phosphate-rich environment, i.e., where phosphates compete for binding? To model this, we investigated P_i association in a model in which a phosphate ion was already trapped at the positively charged surface patch. An HPO₄⁻² ion was placed in the vicinity of Arg-134, Lys-167, and Lys-175, and the association dynamics were computed based on the resulting electrostatic potential. The computed free-energy profile, the first hitting density, and the binding pathways are depicted in Fig. 3 b. The free-energy profile shows that the trapping property of the positively charged patch is lost when it is already loaded with a negatively charged ion, and the minima corresponding to the intermediate 1 isocommittor surface are no longer present. Moreover, the overall binding free energy is nearly zero. The hitting density plot shows that the pathways avoid the protein at the bound phosphate location and are redirected farther down. The streamlines additionally reveal that the second phosphate does not crawl over the anion attractor; rather, it reaches the binding site from space.

Conclusion

In this study, we have presented a computational approach to systematically investigate protein-ligand association kinetics. Whereas existing computational approaches permit the calculation of binding energies and rates using a variety of molecular and dynamical models, our method provides an extensive analysis of the entire ensemble of association pathways by which a ligand approaches its target protein, and their relative probabilities. In this study we used a simple electrostatic interaction model in combination with rigid-body BD; however, our analysis approach can be readily applied to any MD model that allows one to calculate or estimate transition probabilities or rates between the substates of the protein-ligand configuration space.

We demonstrated the usefulness of our approach by studying the binding of P_i to the PBP from E. coli and several in silico mutants of it. The results of our analysis reveal that protein mutations that affect surface charges may have effects ranging from subtle to drastic on the association kinetics and association pathways. Some mutations affect only association rates without significantly altering the associating pathways, i.e., they scale the fluxes. Other mutations change the association pathways of P_i, and the associated change in the rate may be of very different magnitude depending on the exact location of the mutation. In this context, it is noteworthy that the association rates obtained here are in good agreement with rates calculated by Huang and Briggs (28) using BD sampling (see Supporting Material for comparison).

Overall, all of the systems studied here exhibit binding via a broad ensemble of parallel pathways, indicating a funnel-like energy landscape that narrows down toward the bound state. This is very similar to the situation in protein folding (47).

Consequently, only very few single-point mutations are able to effectively disable P_i binding. The only single-point mutation observed to do this was next to the binding site and thus affected nearly all binding pathways at the bottleneck where they converged. Most of the other constructed single-point mutations disabled only a subset of pathways, allowing other parts of the pathway ensemble to take over, and resulting in only a mild reduction of the association rate. Multiple mutations at critical positions, however, were much more effective and could efficiently disable binding.

Our analysis of the mutagenetic behavior revealed the importance of two anion attractors on the surface of PBP that unspecifically attract all negatively charged molecules. This unspecific attraction brings anions closer to the phosphate-binding site, thereby trapping them in a region of limited size. As a result, the PBP wt exhibits superdiffusive association, i.e., association with a rate that is about threefold greater than the free-diffusion association rate to the binding site, which is estimated to be 9.2 M⁻¹s⁻¹. With favorable mutations, the association rate may be sped up to about 10 times the free diffusion rate.

After an anion reaches the attractor, phosphate specificity is introduced in the subsequent step, i.e., the actual complex formation, where binding of phosphate is energetically favored over other anions by a detailed interaction (25,48). The resulting catch-and-select mechanism may be a general strategy that allows ions to be efficiently screened before being specifically selected. To experimentally verify our findings, it may be useful to assess the relevance of different pathways on the protein surface by labeling specific surface residues and P_i, and to investigate their contact dynamics using a technique such as NMR.

The grid-based discretization used here to define configurational substates is restricted to a few dimensions and is thus limited to study simple problems, e.g., a point-like ligand that approaches a rigid protein. However, in future work, the approach will be extended to gridless data-based discretization of configuration spaces, as they are frequently used in Markov model analyses of protein internal dynamics (14). With this extension, it will be possible to perform a flux analysis of association pathways for complex protein-ligand and protein-protein binding with a full dynamical treatment, such as all-atom MD in explicit solvent.