Comparative Genomics of the Vertebrate Insulin/TOR Signal Transduction Pathway: A Network-Level Analysis of Selective Pressures

Abstract

Complexity of biological function relies on large networks of interacting molecules. However, the evolutionary properties of these networks are not fully understood. It has been shown that selective pressures depend on the position of genes in the network. We have previously shown that in the Drosophila insulin/target of rapamycin (TOR) signal transduction pathway there is a correlation between the pathway position and the strength of purifying selection, with the downstream genes being most constrained. In this study, we investigated the evolutionary dynamics of this well-characterized pathway in vertebrates. More specifically, we determined the impact of natural selection on the evolution of 72 genes of this pathway. We found that in vertebrates there is a similar gradient of selective constraint in the insulin/TOR pathway to that found in Drosophila. This feature is neither the result of a polarity in the impact of positive selection nor of a series of factors affecting selective constraint levels (gene expression level and breadth, codon bias, protein length, and connectivity). We also found that pathway genes encoding physically interacting proteins tend to evolve under similar selective constraints. The results indicate that the architecture of the vertebrate insulin/TOR pathway constrains the molecular evolution of its components. Therefore, the polarity detected in Drosophila is neither specific nor incidental of this genus. Hence, although the underlying biological mechanisms remain unclear, these may be similar in both vertebrates and Drosophila.

Introduction

The neutral theory of molecular evolution predicts a negative correlation between the functional significance of genomic regions and the levels of polymorphism and divergence (Kimura 1983). Indeed, the level and pattern of selection vary widely across different genes and genomic regions. The evolutionary meaning of such variation is a major topic in evolutionary biology. A number of factors affect selective constraint levels acting on genes, including expression level and breadth (Duret and Mouchiroud 2000; Pál et al. 2001; Subramanian and Kumar 2004), codon bias (Sharp 1991; Pál et al. 2001), the length of the encoded proteins (Subramanian and Kumar 2004), or molecular function (Castillo-Davis et al. 2004). These factors, however, account for only a small fraction of the variation in selective constraint, particularly in higher eukaryotes (Ingvarsson 2007).

The role of natural selection in the evolution of complex biological systems is poorly understood (Cork and Purugganan 2004). Genes do not act in isolation but rather interact with numerous genes within complex networks. The recent availability of large-scale protein–protein interaction (PPI) and metabolic data allows studying the impact of a gene’s position in a network on its pattern of evolutionary change. Remarkably, elements with greater connectivity or centrality in a network tend to be highly constrained (Fraser et al. 2002; Hahn and Kern 2005), and physically interacting proteins show correlated evolutionary histories (Fryxell 1996; Fraser et al. 2002). These observations clearly indicate that network architecture constrains the molecular evolution of its components.

Compelling evidence exists in well-characterized pathways suggesting a relationship between network position and evolutionary change. Specific enzymes in a pathway can contribute differentially to overall pathway function (and, hence, to the associated phenotypes). Genes encoding enzymes with high control coefficients (those exerting a relatively high influence over flux; Kacser and Burns 1973), such as those acting at network branch points (LaPorte et al. 1984; Stephanopoulos and Vallino 1991) or those acting in the upstream part of linear metabolic pathways (Wright and Rausher 2010), are expected to evolve under stronger natural selection (Hartl et al. 1985; Eanes 1999; Watt and Dean 2000; Wright and Rausher 2010). For instance, in the Drosophila pathways involved in glucose metabolism, positive selection acts preferentially on genes encoding branch point enzymes (Flowers et al. 2007). Furthermore, it has been proposed that, as a result of the hierarchical structure of branched pathways, genes acting upstream evolve under stronger purifying selection than those acting downstream because mutations in the former may have more pleiotropic effects. In agreement, Rausher et al. (1999) found that in the plant anthocyanin biosynthetic pathway, the level of selective constraint correlated with gene position along the upstream/downstream axis of the pathway, with the upstream genes (involved in the biosynthesis of a greater number of compounds) being the most constrained. This polarity seems to be neither explained by differences in mutation rates (Lu and Rausher 2003) nor by positive selection (Rausher et al. 2008) along the pathway. A similar polarity of the selective constraint distribution has been observed along the plant isoprene, terpenoid, and carotenoid biosynthetic pathways (Sharkey et al. 2005; Livingstone and Anderson 2009; Ramsay et al. 2009) and in the Drosophila Ras signaling pathway (Riley et al. 2003). This feature, nevertheless, is not general (Olsen et al. 2002; Jovelin et al. 2009; Yang et al. 2009) but rather may depend among other factors on the architecture of the particular pathway. Indeed, we found a polarity in the opposite direction (i.e., purifying selection is greater for the downstream genes) in the insulin/target of rapamycin (TOR) (IT) signal transduction pathway of Drosophila (Alvarez-Ponce et al. 2009).

The IT pathway plays a central role in fundamental biological processes, such as growth, energetic metabolism, reproduction, and aging (Oldham and Hafen 2003; LeRoith et al. 2004; Taguchi and White 2008). In addition, a number of diseases, such as insulin resistance, diabetes, obesity, and cancer, are associated with dysregulation of genes involved in this pathway. The IT pathway is well characterized in a number of organisms, and both its structure and function are highly conserved from insects to vertebrates. Therefore, this molecular pathway provides an excellent opportunity for studying the relationship between pathway architecture and gene evolution across a wide range of phylogenetic groups.

In this study, we sought to determine whether the polarity in selective constraint levels detected in Drosophila is incidental and specific to this genus or whether it represents a more general feature. For that purpose, we characterized the molecular evolution of the IT pathway genes of six vertebrates. We identified and manually annotated the orthologs and paralogs of 72 genes involved in the human IT pathway and reconstructed their evolutionary history. We determined that, as previously observed in Drosophila, genes acting in the downstream part of the vertebrate IT pathway are the most evolutionarily constrained. Therefore, the polarity in the distribution of selective constraints along the pathway is neither incidental nor specific to the Drosophila genus, suggestive of a more general biological mechanism.

Materials and Methods

Selection of IT Pathway Genes for Analysis

We selected genes that encode the human IT signal transduction pathway for analysis by searching the literature for known human orthologs of those genes included in our prior analysis of the Drosophila IT pathway (Alvarez-Ponce et al. 2009). In addition, we included in our analysis the insulin receptor gene (INR) and its closest paralogs, which encode the IGF1 receptor (IGF1R) and the insulin receptor-related receptor (INSRR), as well as the nine protein kinase C genes (PRKC). We also studied the nearest annotated paralogs of the selected genes (Ensembl database version 50; Flicek et al. 2008).

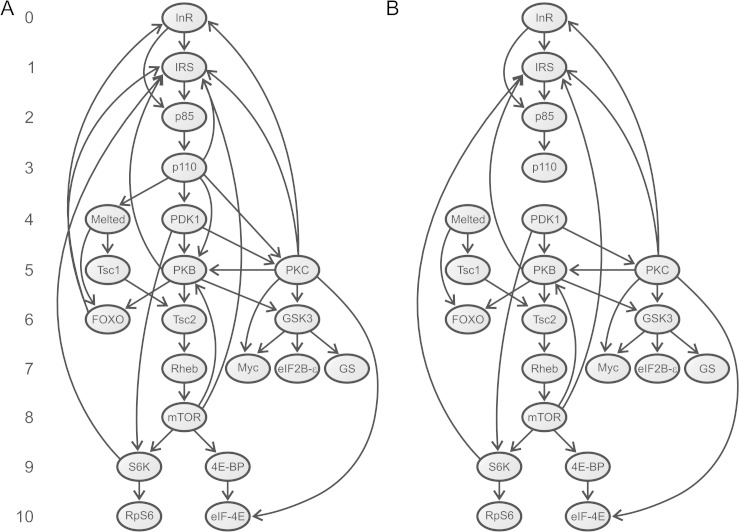
We attempted to identify unannotated paralogs using a two-round Blast search. We initially performed a TBlastN search (E value < 10⁻⁵) for each human IT pathway protein against the human genome (International Human Genome Sequencing Consortium 2004). The resulting hits were then used as query in a BlastP search against the human proteome. If the best hit corresponded to the original gene or one of its paralogs with a sequence identity higher than 60% and covering at least 50% of the sequence length, we manually annotated this sequence and included it in the analysis. The final set (supplementary table S1, Supplementary Material online) consisted of 72 genes, which belong to 23 paralogous groups, and 43 pseudogenes, 40 of which are intronless (likely processed copies). Twenty-one, out of these 23 paralogous groups, were used in the network-level analysis (fig. 1).

FIG. 1.

Directed graphs used in the network-level analyses. (A) Graph G containing all interactions (arcs) among human IT pathway proteins (nodes). This graph consists of 21 nodes and 39 arcs, of which 32 represent PPIs, five involve the membrane phospholipid PIP₃ (synthesized by p110 isoforms and activates the IRS, Melted, PDK1, PKB, and PKC proteins), and the other two represent the activation of the INR and IRS2 genes by the FOXO transcription factors (Puig and Tjian 2005). Numbers on the left indicate the position of each component in the pathway. Human proteins having orthologs in Drosophila (Alvarez-Ponce et al. 2009) were assigned the same position as their Drosophila counterpart. We assigned position 5 to PKC proteins because they are activated by PDK1 (position 4) (LeRoith et al. 2004). We excluded the phosphoinositide phosphatase PTEN from network-level analysis because it does not directly interact with any other element in the graph (for review, see Vinciguerra and Foti 2006). The cytohesins Cyh1–4 were also excluded because their specific function in the pathway remains unclear (Hafner et al. 2006). (B) Graph S, subgraph of G containing only the 32 physical interactions. Both graphs were constructed using information gleaned from the literature.

Identification and Annotation of IT Pathway Genes in Nonhuman Vertebrates

We searched for the IT pathway genes in the genomes of the mammals Mus musculus (Mouse Genome Sequencing Consortium 2002), Bos taurus (The Bovine Genome Sequencing and Analysis Consortium 2009), Monodelphis domestica (Mikkelsen et al. 2007) and Ornithorhynchus anatinus (Warren et al. 2008), and the bird Gallus gallus (International Chicken Genome Sequencing Consortium 2004). We retrieved the coding sequences (CDS) for the human genes and their predicted orthologs from the Ensembl database. For genes with alternative splicing, we chose the variant encoding the longest protein that was shared across the six species (supplementary table S1, Supplementary Material online).

Given that the Ensembl information is based mainly on computational gene predictions, we visually inspected and, when required, manually reannotated all sequences. To do so, we 1) removed exons that did not correspond with the human orthologs; 2) added exons that were missing in the original data set; and 3) merged gene model predictions from different portions of the same gene. In addition, we searched the GenBank database for incomplete or missing genes in our data set.

We performed a two-round Blast search to identify nonhuman unannotated sequences. Each human IT pathway protein was used as query in a TBlastN search (E value < 10⁻⁵) against all nonhuman genomes, and the resulting hits were used as query in a second TBlastN search against the human genome. Sequences that resulted in the original gene or one of its paralogs as the best hit were manually annotated and included in the analysis.

Sequences with premature stop codons or frameshifts were classified as putative pseudogenes. We confirmed these features by inspecting the corresponding trace archives. If there was a sequencing read that did not contain the disrupting feature or if the concerned chromatograms had low quality at the affected positions, these features were considered as sequencing errors. We also examined the trace archives to determine whether some paralogous copies were the result of erroneous genome assembly due to sequencing errors. For that purpose, we checked the quality of the sequencing traces at the mismatch positions; each group of putative paralogs that did not have a confirmed difference was considered as a single copy.

Multiple Sequence Alignment and Phylogenetic Analysis

We applied phylogenetic analysis to infer orthology/paralogy relationships among homologous genes. To do so, we generated a protein multiple sequence alignment (MSA) for each homology group using Probcons 1.11 (Do et al. 2005). These alignments were used to guide the alignment of the CDS sequences. We then built a neighbor-joining tree for each MSA based on either the CDS or the protein sequences (in function of the divergence level), using the MEGA4 software (Tamura et al. 2007) and applying either the Tamura–Nei (Tamura and Nei 1993) or the Jones, Taylor, and Thorton (Jones et al. 1992) evolution models.

We generated a separate MSA for each orthologous group. Sequences with pseudogenic features were excluded from these alignments, and only groups with putatively functional representatives in all six species were further considered. For those orthologous groups with multiple copies in a given genome (co-orthologs), we used the sequence that covered the largest fraction of the human ortholog. In order to avoid redundancy, if two orthologous groups shared a particular sequence due to gene duplication after the mammal/bird split, we only considered the most directly involved in the IT pathway according to the literature. All MSAs were manually curated using the BioEdit 7.0.5.2 software (Hall 1999), and poorly aligned positions were discarded from the analysis.

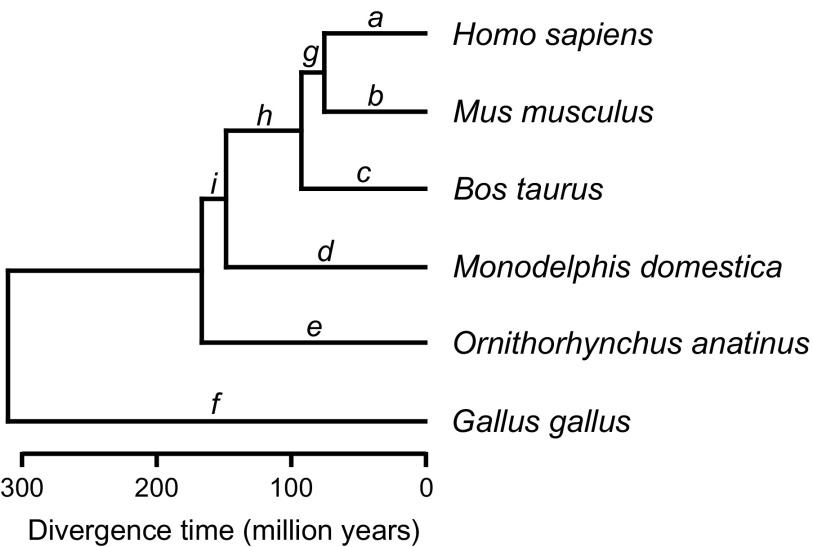
We evaluated the impact of natural selection on gene evolution using the nonsynonymous (d_N) to synonymous (d_S) divergence ratio (ω = d_N/d_S). Values of ω lower than 1 indicate the action of purifying selection, whereas ω = 1 and ω > 1 are indicative of strictly neutral and adaptive evolution, respectively. We obtained ω estimates by applying two evolutionary models implemented in the codeml program from the PAML 3.15 package (Yang 1997). The M0 model assumes a single ω value across all codons and phylogenetic branches, whereas the free-ratio (FR) model assumes an independent ω value for each branch. We tested for the presence of codons evolving under positive selection by contrasting the M1a and M2a models (Wong et al. 2004) and the M7 and M8 models (Yang et al. 2000) by the likelihood ratio test (Whelan and Goldman 1999). A significantly better fit to the data of models M2a or M8 was interpreted as evidence of positive selection. We controlled for the false discovery rate (FDR) associated with multiple testing at q = 0.05 (Benjamini and Hochberg 1995). We used the Bayes Empirical Bayes approach (Yang et al. 2005) to identify specific codons that evolved under positive selection (posterior probability ≥ 95%). All codon-based analyses were conducted using the accepted species tree topology (fig. 2), the F3×4 codon frequency model (Goldman and Yang 1994), complete deletion, and three different starting ω values (0.01, 0.1, and 1) to overcome the multiple local optima problem. Any set of FR estimates (d_N, d_S, and ω) with ω > 3, d_S > 5, or S × d_S < 1 (where S is the number of synonymous positions) was discarded from the analysis.

FIG. 2.

Phylogenetic relationships among the six vertebrate species used in this study. Tree topology and divergence times were taken from Ponting (2008).

Network-Level Analysis

The IT pathway structure (information extracted from the literature) was encoded into a directed graph (termed G; fig. 1A) with nodes and arcs representing proteins and activatory/inhibitory interactions, respectively. This graph consists of 21 nodes (representing paralogous groups) connected by 39 arcs (interactions), of which 32 represent physical PPIs (fig. 1B). We used this graph to assign the position of each pathway element, which was computed as the number of steps required to transduce the signal from the insulin/IGF1 receptor (position 0) to the remaining elements in the pathway (the maximum was ten steps). Paralogous genes share the same pathway position; however, paralogous copies not involved in insulin signaling (INSRR, PIK3CG, EIF4E2, and EIF4E3) were eliminated from network-level analysis. In the end, a total of 58 genes were assigned a pathway position but only 48 genes had copies in all six species and were therefore used in the analysis.

We contrasted whether physically interacting IT pathway proteins tend to exhibit similar d_N, d_S, or ω values by applying a Monte Carlo method (Fraser et al. 2002). For this analysis, we used a subgraph of G containing only physical interactions (denoted as S; fig. 1B), and the average absolute difference between the d_N, d_S, or ω values of pairs of physically interacting elements in the IT pathway (X) as statistic:

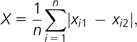where n = 32 is the number of interacting pairs in S, and x_i1 and x_i2 are the d_N, d_S, or ω values of genes encoding the two interacting proteins at pair i. We contrasted whether the observed X value is less than or equal to that expected at random by generating 100,000 randomizations of S. Each random network had the same 21 nodes and the same number of arcs (n = 32) connecting two different nodes (sampled without replacement). P values were computed as the proportion of simulated networks with an X value equal to or lower than the observed one. We also applied this Monte Carlo method to determine whether genes encoding physically interacting proteins exhibit similar values of expression level and breadth, codon bias, or connectivity.

Additionally, we conducted a modified Monte Carlo test controlling for the association between pathway position and selective constraint. For that purpose, we used linear regression to model the relationship between pathway position and either ω or d_N and used the residuals of the model (the difference between observed and predicted values) for the Monte Carlo analysis. We used a similar approach to factor out the effect of the putative associations between connectivity and selective constraint levels.

Statistical Tests of Association

We used the nonparametric Spearman’s rank correlation coefficient (ρ) to contrast whether d_N, d_S, and ω estimates correlated with pathway position along the IT pathway. We used the binomial test to contrast whether the number of branches with a negative sign in the correlation between the pathway position and the levels of selective constraint (values estimated under the FR model) is higher than expected at random (i.e., 50%). Additionally, we performed a Monte Carlo test using as statistic the weighted sum of P values of the correlation analysis across all phylogenetic branches:

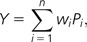where i is the phylogenetic branch, n is the number of branches in the phylogeny (either nine or seven, depending on whether or not O. anatinus is included in the analyses), w_i is the relative length of branch i (taken from Ponting 2008; fig. 1), and P_i is the P value of the correlation test for branch i. We assessed the statistical significance of Y from 10,000 randomized data sets; in each replicate, the pathway positions of ω, d_N, and d_S values in each phylogenetic branch were assigned at random. The P value was computed as the proportion of replicates with a Y value less than or equal to that observed.

Because selective constraint levels are affected by a number of factors, including gene expression level and breadth (Duret and Mouchiroud 2000; Pál et al. 2001; Subramanian and Kumar 2004), codon bias (Sharp 1991; Pál et al. 2001), protein length (Subramanian and Kumar 2004), and connectivity (Fraser et al. 2002), a polarity in these factors along the upstream/downstream IT pathway axis could potentially account for the distribution of d_N, d_S, and ω. Therefore, we included all these factors in the analyses to factor out their potential effect on sequence evolution. This information was gathered from multiple sources:

• Expression level and breadth: We used human gene expression data from Su et al. (2004) (U133A+ GNF1H data set, normalized using the MAS5 algorithm), which contain gene expression measures for 79 different tissues (or organs) with two replicates each. We excluded data from cancerous tissues because IT pathway elements are at times dysregulated in cancer. Furthermore, because some organs are represented by multiple entries in the data set (for instance, the brain is represented by multiple entries, including the whole brain and different portions), we only used a set of 25 nonredundant tissues (supplementary table S2, Supplementary Material online) to avoid biasing the results. For each gene and tissue, we took the average of both replicates. When multiple probes matched the same gene, we chose the entry with the highest average signal. For each gene, the expression level was estimated as the average of 25 selected tissues, and expression breadth was measured as the number of tissues where it is expressed (expression level ≥ 200; see Su et al. 2002).

• Connectivity: We obtained PPI data from the human interaction network of Bossi and Lehner (2009). This data set consists of 80,922 physical interactions gleaned from 21 different sources, of which 2,030 involve IT pathway components. The connectivity of each IT pathway protein was computed as the number of PPIs in which it is involved.

• Codon bias: For each orthologous group, codon bias was estimated as the median of the effective number of codons (ENC; Wright 1990) across all six studied species. ENC values were computed using the DnaSP 5.00.02 software (Librado and Rozas 2009).

• Protein length: Because many nonhuman sequences are incomplete and protein length is highly conserved across species (Wang et al. 2005), we used the length of the human protein.

We conducted a bivariate correlation analysis using these factors, the pathway position and the d_N, d_S, and ω estimates. Furthermore, we applied two multivariate analysis techniques (path analysis and partial correlation analysis) to better characterize the relationships among these factors. For path analysis, we used the causal model depicted in figure 3 and, when needed, variables were either log- or square root-transformed to improve normality. We conducted this analysis using the following packages: AMOS 17 (path analysis), PASW Statistics 17 (bivariate correlation analysis), and R (Ihaka and Gentleman 1996) (partial correlation analysis). Throughout this paper, we report two-tailed P values, except for the association between pathway position and d_N and ω, where we had an a priori hypothesis about the direction of the association (one-tailed tests).

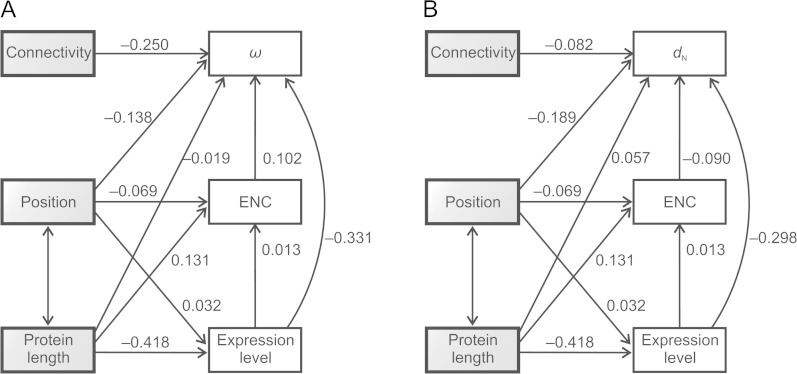
FIG. 3.

Path analysis for data set 2. Single- and double-headed arrows represent assumed causal dependencies and correlations, respectively. Numbers in each arrow represent the standardized path coefficients (β). None of the associations was significant. The analyses conducted using expression breadth instead of expression level yielded equivalent results. (A) Analysis for ω. (B) Analysis for d_N.

We used three data sets for the network-level analysis:

• Data set 1: This data set includes all 48 genes used for network-level analysis (elements with assigned pathway position and present in all six species; supplementary table S3, Supplementary Material online).

• Data set 2: This is a subset of data set 1 that includes only a single gene per paralogous group (n = 21; table 1). We used this data set to avoid the use of multiple paralogous copies, which may exhibit similar selective constraint levels and are, therefore, not suitable for correlation analysis (which assumes that all observations are independent). We chose a single paralog per group according to the available molecular function information (obtained from the literature). We chose, from the copies present in all six species: 1) the copy that plays the most direct role in the IT pathway (e.g., mutation of this copy most severely affects insulin signaling); 2) the copy whose activation is most affected by insulin signaling; 3) the embryonic lethal paralog; or 4) the archetypical copy that performs all functions (only partially undertaken by its paralogs). When the information on the differential molecular function of paralogs was insufficient, we chose the copy with a higher expression breadth.

• Data set 3: This data set was also derived from data set 1; for each paralogous group, values were averaged across all copies (n = 21; supplementary table S4, Supplementary Material online).

Table 1.

Summary Statistics Used in the Analysis (Data Set 2)

Gene	Pathway Position	Six Species					Five Speciesa					Gene Expression		Connectivity	Protein Lengthf
		dNb	dSb	ω	ENC	% Used Codonsc	dNb	dSb	ω	ENC	% Used Codonsc	Leveld	Breadthe
INSR	0	0.185	4.344	0.043	49.77	77.50	0.155	4.131	0.038	49.52	91.61	1,012.74	22	73	1,382
IRS1	1	0.068	4.688	0.015	41.98	23.19	0.081	3.096	0.026	42.95	48.07	340.74	18	66	1,242
PIK3R1	2	0.131	4.610	0.029	55.14	77.73	0.103	1.912	0.054	55.64	98.63	835.66	25	132	732
PIK3CB	3	0.129	2.430	0.053	52.82	95.05	0.107	2.146	0.050	52.71	99.25	419.30	24	7	1,070
VEPH1	4	0.338	2.774	0.122	53.15	92.80	0.278	2.235	0.124	52.62	92.80	80.54	2	4	833
PDPK1	4	0.025	2.916	0.009	52.72	44.06	0.077	2.064	0.038	52.54	80.04	1,338.84	25	36	556
AKT1	5	0.051	6.026	0.009	45.77	74.38	0.042	4.984	0.008	40.99	92.71	970.02	19	108	480
PRKCI	5	0.017	2.722	0.006	55.98	88.09	0.029	2.208	0.013	56.39	95.13	1,147.88	25	33	596
TSC1	5	0.275	1.970	0.140	54.69	91.49	0.228	1.708	0.134	54.54	91.49	715.78	25	15	1,164
FOXO1	6	0.202	3.688	0.055	47.50	74.35	0.157	2.419	0.065	49.32	87.63	868.36	25	23	655
GSK3B	6	0.003	1.551	0.002	53.88	62.59	0.027	0.974	0.027	53.99	99.77	561.56	25	88	433
TSC2	6	0.179	4.578	0.039	45.64	83.45	0.144	3.032	0.048	49.98	94.08	358.20	17	22	1,807
EIF2B5	7	0.285	3.861	0.074	53.98	86.82	0.235	2.876	0.082	54.04	91.40	711.14	25	68	721
GYS1	7	0.078	5.856	0.013	41.29	50.07	0.069	7.092	0.010	42.24	50.07	1,352.30	25	10	737
MYC	7	0.198	3.513	0.057	43.58	47.58	0.150	3.056	0.049	44.20	73.57	490.34	18	148	454
RHEB	7	0.017	1.481	0.011	45.33	90.22	0.018	1.115	0.016	46.09	100.00	2,303.66	25	7	184
MTOR	8	0.027	2.916	0.009	49.47	94.00	0.023	2.374	0.010	50.68	96.43	302.60	20	15	2,549
EIF4EBP1	9	0.171	3.370	0.051	43.46	38.14	0.116	2.849	0.041	45.02	68.64	558.70	19	15	118
RPS6KB1	9	0.019	1.188	0.016	53.83	89.90	0.014	1.020	0.013	53.44	94.48	164.44	7	21	525
EIF4E	10	0.036	1.081	0.033	54.81	94.93	0.031	0.815	0.038	54.20	94.93	—	—	106	217
RPS6	10	0.011	4.795	0.002	50.80	81.53	0.011	2.570	0.004	51.18	99.20	23,490.48	25	179	249

^aExcluding Ornithorhynchus anatinus from the analyses.

^bValues estimated as the sum across all branches of the phylogeny (M0 model).

^cPercent of used codons for estimating d_N, d_S, and ω values.

^dExpression levels averaged across 25 selected human tissues (supplementary table S2, Supplementary Material online).

^eNumber of tissues (out of 25) with expression level ≥ 200.

^fNumber of amino acids of the human protein.

Results

Distribution of IT Pathway Genes across Vertebrates

We applied a combination of automatic methods and manual curation to identify and annotate the orthologs of 115 human IT pathway sequences (72 genes and 43 pseudogenes; supplementary table S1, Supplementary Material online) in five nonhuman vertebrate genomes. We identified 617 putative orthologs of the human genes (332 putatively functional genes, 246 pseudogenes, and 39 intronless sequences; supplementary table S5, Supplementary Material online). Therefore, the current analysis encompasses a total of 732 sequences (129 of them were manually reannotated, and another 364 that were not in the Ensembl data set were identified by our search protocol). Because current genome data comprise unsequenced regions, this number should be considered as the minimum number of sequences. Moreover, recent duplicates might have been treated as a single copy during genome assembly. However, it should be noted that the six genomes have high-coverage sequence data (from 6× to 10×) and, therefore, putatively missing genes are most likely absent. Interestingly, we did not identify any pseudogene nor processed copy in the chicken genome, which agrees with the small number of processed copies detected in this organism (51 [International Chicken Genome Sequencing Consortium 2004], in contrast with the more than 15,000 genes detected in mammals [Torrents et al. 2003; Rat Genome Sequencing Project Consortium 2004]).

Two hundred and thirty-eight (out of 732) sequences belong to the ribosomal protein (RP) S6 (RPS6) homology group (6 genes, 212 pseudogenes, and 20 intronless sequences; supplementary table S5, Supplementary Material online). This is in agreement with previous observations in mammalian genomes showing that each RP is encoded by a single gene with introns that has several processed pseudogenes. Indeed, over 2,400 RP-processed pseudogenes have been identified in the human genome, in contrast to only 79 functional copies (Zhang et al. 2002). Consistent with our observations, multiple processed RPS6 pseudogenes have been described in both the human and the mouse genomes (Antoine and Fried 1992; Feo et al. 1992; Pata and Metspalu 1996; Zhang et al. 2002).

Sixty (out of 72) genes have putative functional copies in every genome, and all paralogous groups have at least one nonpseudogenic copy in each genome. Therefore, the function of missing genes may be undertaken by some of their functional paralogs. Consequently, our results suggest that all genomes encode a complete IT pathway.

Impact of Natural Selection on Gene Sequence Evolution

Estimates of ω under the M0 model range from 0.002 (for GSK3B and RPS6 genes) to 0.140 (TSC1) with a median value of 0.116 (supplementary table S3, Supplementary Material online). These values indicate that the IT pathway genes are under relatively strong purifying selection, suggesting that all genes are functional. We performed two maximum likelihood tests for positive selection (supplementary table S6, Supplementary Material online). Although there were no significant results in the M2a versus M1a comparison, the M8 versus M7 test identified three genes with the molecular signature of positive selection: IRS4, AKT3, and PRKCD (P < 0.05). However, after controlling for the FDR, none of these results remain significant.

Relationship between the Selective Constraints of Interacting Proteins

We used a Monte Carlo approach to determine whether genes that encode physically interacting proteins (fig. 1B) evolve under similar selective constraints (Fraser et al. 2002). Because current knowledge of the interactions among proteins encoded by different paralogous copies is very incomplete, we restricted the analysis to data sets 2 (which contains a single gene per paralogous group; table 1) and 3 (where values were averaged across paralogs; supplementary table S4, Supplementary Material online). We found that ω values of genes encoding physically interacting proteins are more similar than expected from a random network (data set 2: X_ω = 0.024, P = 0.003; data set 3: X_ω = 0.024, P = 0.012; supplementary table S7, Supplementary Material online). Separate analysis conducted for d_N and d_S yielded significant results for d_N (data set 2: X_N = 0.079, P = 0.005; data set 3: X_N = 0.084, P = 0.029; supplementary table S7, Supplementary Material online) but not for d_S (data set 2: X_S = 1.983, P = 0.872; data set 3: X_S = 1.316, P = 0.703; supplementary table S7, Supplementary Material online). These results indicate that amino acid changes are the main contributors to the similarity in selective constraint values between interacting proteins.

Levels of Selective Constraint along the IT Pathway

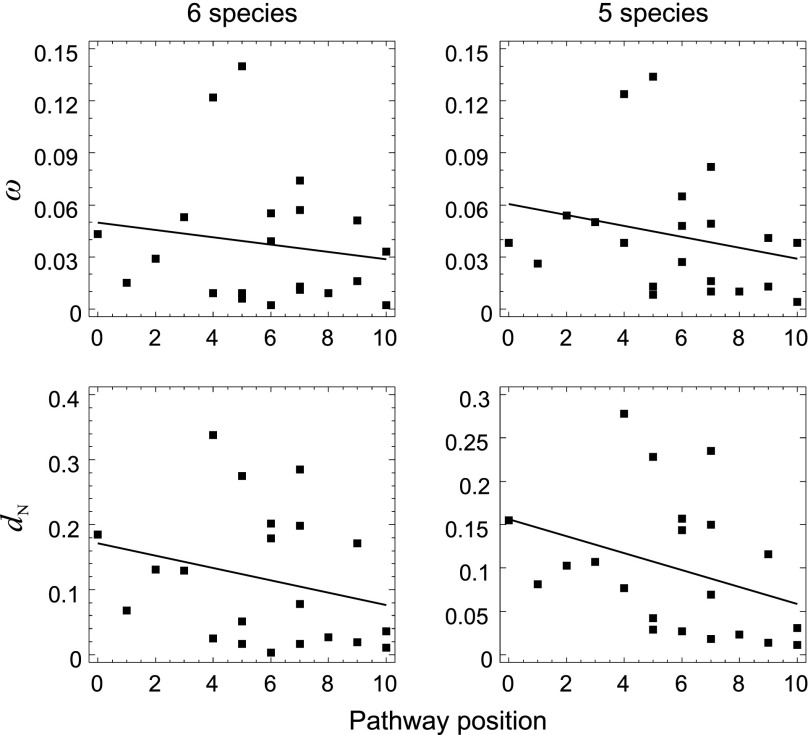
We tested whether a polarity exists in the selective constraint levels along the upstream/downstream IT pathway axis. Though not significant, a negative correlation between pathway position and ω was found for all three data sets (data set 1: Spearman’s rank correlation coefficient, ρ = −0.073, P = 0.312; data set 2: ρ = −0.136, P = 0.279; data set 3: ρ = −0.134, P = 0.281; table 2 and fig. 4; supplementary tables S8 and S9, Supplementary Material online). A similar, nonsignificant, trend was observed for d_N (table 2; supplementary tables S8 and S9, Supplementary Material online).

Table 2.

Bivariate Correlations (Data Set 2)

	Position		ωa		dNa		dSa		ENC		% Used Codons		Expression Level		Expression Breadth		Connectivity		Protein Length
	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P	ρ	P
Position	—	—	−0.304	0.090	−0.441	0.023*	−0.164	0.477	−0.050	0.828	0.110	0.636	0.032	0.894	0.011	0.962	0.040	0.862	−0.553	0.009**
ωa	−0.136	0.279	—	—	0.844	<0.001***	−0.190	0.410	0.353	0.116	−0.183	0.427	−0.355	0.125	−0.029	0.905	−0.173	0.453	0.230	0.316
dNa	−0.294	0.098	0.914	<0.001***	—	—	0.325	0.151	−0.005	0.982	−0.522	0.015*	−0.277	0.238	−0.156	0.511	−0.150	0.517	0.413	0.063
dSa	−0.229	0.318	−0.105	0.650	0.229	0.319	—	—	−0.714	<0.001***	−0.610	0.003**	0.087	0.715	−0.284	0.225	0.129	0.578	0.322	0.154
ENC	−0.107	0.646	0.027	0.907	−0.068	0.771	−0.473	0.030*	—	—	0.487	0.025*	−0.096	0.686	0.340	0.142	0.062	0.788	0.039	0.867
% Used  codons	0.144	0.532	0.200	0.385	0.004	0.987	−0.558	0.009**	0.542	0.011*	—	—	0.060	0.801	0.198	0.403	0.003	0.991	−0.156	0.500
Expression  level	0.032	0.894	−0.423	0.063	−0.337	0.146	0.280	0.232	−0.026	0.915	−0.232	0.326	—	—	0.762	<0.001***	0.273	0.243	−0.389	0.090
Expression  breadth	0.011	0.962	−0.274	0.242	−0.252	0.283	−0.014	0.952	0.337	0.146	−0.031	0.896	0.762	<0.001***	—	—	0.161	0.498	−0.224	0.342
Connectivity	0.040	0.862	−0.291	0.201	−0.175	0.448	0.367	0.101	0.183	0.426	−0.369	0.100	0.273	0.243	0.161	0.498	—	—	−0.291	0.200
Protein length	−0.553	0.009*	0.292	0.199	0.438	0.047*	0.261	0.253	−0.014	0.951	0.195	0.397	−0.389	0.090	−0.224	0.342	−0.291	0.200	—	—

Note.—Values below and above the principal diagonal are based on analyses using all six species or excluding Ornithorhynchus anatinus, respectively. All correlations are based on n = 21 observations except those involving gene expression level and breadth (n = 20). Two-tailed P values are provided except for the correlations between pathway position and ω and d_N (one tailed).

^aValues calculated under the M0 model.

*P < 0.05, **P < 0.01, and ***P < 0.001.

FIG. 4.

Correlation between pathway position and ω and d_N under the M0 model (data set 2) including (six species) and excluding (five species) Ornithorhynchus anatinus. Continuous lines represent regression lines. An extended version of this figure is provided as Supplementary Material (supplementary fig. S1, Supplementary Material online).

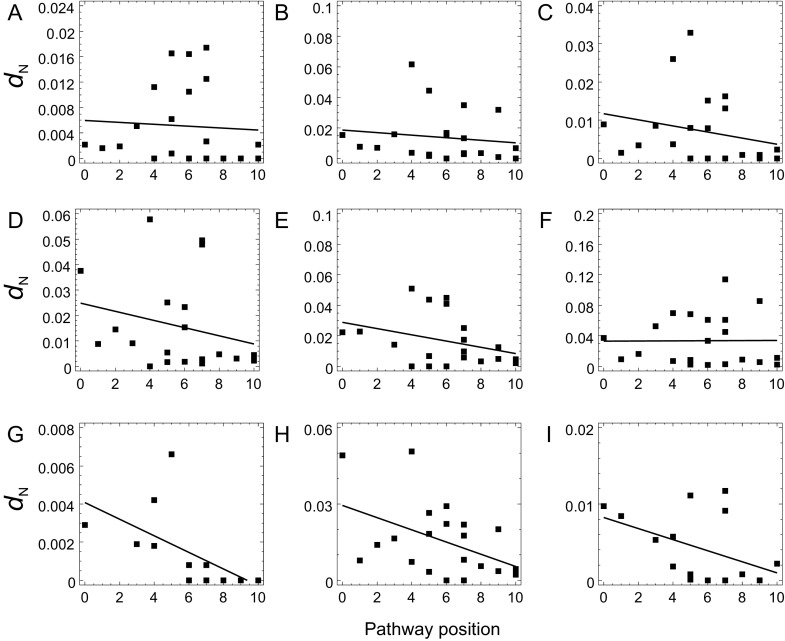
We conducted a separate correlation analysis for each of the nine phylogenetic branches (fig. 5 and table 3; supplementary tables S10 and S11, Supplementary Material online). For data sets 2 and 3, the correlation between ω or d_N and pathway position is negative in all nine branches (a number significantly higher than the 50% expected at random; binomial test, P = 0.002; supplementary table S12, Supplementary Material online). For data set 1, the correlation between ω and pathway position is negative for seven branches, which does not represent a significant departure from 50% (binomial test, P = 0.090; supplementary table S12, Supplementary Material online), whereas the correlation between d_N and pathway position is negative in eight branches (binomial test, P = 0.020; supplementary table S12, Supplementary Material online). Furthermore, the correlation between pathway position and ω is significant for two branches regardless of the data set, whereas for d_N, the correlation is significant for either two (data sets 1 and 3) or four branches (data set 2). The direction of the correlation between pathway position and d_S is negative in either seven (data sets 1 and 2) or six branches (data set 3), which does not represent a significant departure from 50% (binomial test, P = 0.090, P = 0.254, respectively; supplementary table S12, Supplementary Material online). This correlation is significantly negative for either one (data set 1) or two branches (data sets 2 and 3). The results of the Monte Carlo simulation analysis also support the overall association between pathway position and selective constraint (supplementary table S12, Supplementary Material online).

FIG. 5.

Correlation between pathway position and d_N (under the FR model) in all nine phylogenetic branches (data set 2). Panels A–I correspond to branches a–i in figure 2. Continuous lines represent regression lines.

Table 3.

Correlations between Pathway Position and ω, d_N, and d_S for Each Phylogenetic Branch (Data Set 2)

# Species	Brancha	n	ω		dN		dS
			ρ	Pb	ρ	Pb	ρ	Pc
6	Alld	21	−0.136	0.279	−0.294	0.098	−0.229	0.318
	a	21	−0.252	0.136	−0.255	0.133	−0.108	0.642
	b	21	−0.116	0.309	−0.314	0.083	−0.505	0.020*
	c	21	−0.382	0.044*	−0.422	0.028*	−0.409	0.065
	d	20	−0.115	0.315	−0.278	0.118	−0.190	0.422
	e	20	−0.198	0.201	−0.331	0.077	−0.183	0.439
	f	21	−0.101	0.332	−0.096	0.339	−0.190	0.409
	g	13	−0.828	<0.001***	−0.824	0.001***	0.030	0.922
	h	21	−0.316	0.082	−0.394	0.039*	−0.144	0.534
	i	16	−0.392	0.067	−0.439	0.045*	0.071	0.794
5e	Alld	21	−0.304	0.090	−0.441	0.023*	−0.164	0.477
	a	21	−0.434	0.025*	−0.455	0.019*	−0.254	0.267
	b	21	−0.279	0.111	−0.395	0.038*	−0.408	0.066
	c	21	−0.500	0.011*	−0.482	0.014*	−0.389	0.081
	d	20	−0.339	0.072	−0.426	0.031*	−0.080	0.739
	f + i	21	−0.196	0.197	−0.214	0.176	−0.193	0.402
	g	13	−0.797	0.001***	−0.766	0.001**	0.011	0.971
	h	21	−0.446	0.022*	−0.549	0.005*	−0.307	0.175

Note.—Unless noticed otherwise, all correlations are based on values estimated under the FR model.

^aBranch codes according to figure 2.

^bOne-tailed P values.

^cTwo-tailed P values.

^dUsing overall ω, d_N, and d_S values (M0 model).

^eExcluding Ornithorhynchus anatinus.

*P < 0.05, **P < 0.01, and ***P < 0.001.

Because the available genome sequence data for O. anatinus is highly fragmented, we reevaluated the correlations without this species. This involved an average increase of 11.13% in the number of analyzed codons (supplementary table S3, Supplementary Material online). Remarkably, this analysis uncovered a significant correlation between d_N and pathway position for data set 2 (ρ = −0.441, P = 0.023; table 2). The correlation between pathway position and ω is negative in either all seven (data sets 2 and 3; binomial test, P = 0.008; supplementary table S12, Supplementary Material online) or six branches (data set 1; binomial test, P = 0.063; supplementary table S12, Supplementary Material online) and is significant for either two (data sets 1 and 3) or four branches (data set 2). Furthermore, the correlation between pathway position and d_N is negative for all seven branches in each data set (binomial test, P = 0.008; supplementary table S12, Supplementary Material online) and significant for either two (data sets 1 and 3) or six phylogenetic branches (data set 2).

Effect of Expression Patterns, Codon Bias, Protein Length, and Connectivity on Gene Sequence Evolution

We evaluated whether gene expression level and breadth, codon bias, protein length, and connectivity correlate 1) with pathway position, 2) with the ω, d_N, and d_S values, or 3) among them. As shown in table 2 and supplementary tables S8 and S9 (Supplementary Material online), we found that 1) only protein length significantly correlates with pathway position, regardless of the data set used (ρ ≤ −0.365, P ≤ 0.026); 2) d_S correlates significantly with ENC for data sets 1 and 2 (ρ ≤ −0.473, P ≤ 0.030), ω and d_N correlate with expression level for data set 3 (ρ ≤ 0.498, P ≤ 0.026), and d_N correlates with protein length for data set 2 (ρ = 0.438, P = 0.047); and 3) gene expression breadth correlates with expression level in all data sets (ρ ≥ 0.606, P ≤ 0.005) and with ENC (ρ ≥ 0.650, P ≤ 0.002) and connectivity (ρ ≥ 0.631, P ≤ 0.003) in data set 3.

We applied two multivariate analysis techniques (path analysis and partial correlation analysis) to evaluate the association between the pathway position and the ω, d_N, and d_S values controlling for the factors discussed above. Both analyses showed that the association between pathway position and ω and d_N is always negative, regardless of the data set used and whether O. anatinus was included or not in the analysis (supplementary tables S13 and S14, Supplementary Material online). In addition, the path analysis revealed a significant association between pathway position and d_N for data set 1 (standardized path coefficient, β = −0.246; P = 0.041; supplementary table S13, Supplementary Material online). Moreover, this analysis showed a significant association between pathway position and ω and d_N for data set 3 when O. anatinus was not considered. Analysis conducted separately for each of the nine phylogenetic branches showed that the association between pathway position and both ω and d_N (but not d_S) is negative in a number of branches higher than the 50% expected by chance (table 4; supplementary tables S15 and S16, Supplementary Material online).

Table 4.

Partial Correlation and Path Analysis (Data Set 2)

# Species	Brancha	n	Partial Correlation Analysis						Path Analysis
			ω		dN		dS		ω		dN		dS
			ρ	Pb	ρ	Pb	ρ	Pc	β	Pb	β	Pb	β	Pc
6	Alld	20	−0.144	0.299	−0.117	0.335	0.084	0.762	−0.138	0.276	−0.189	0.213	−0.156	0.380
	a	20	−0.252	0.174	−0.173	0.264	0.457	0.064	−0.121	0.313	−0.076	0.379	−0.098	0.486
	b	20	−0.172	0.264	−0.210	0.219	−0.399	0.117	−0.102	0.330	−0.208	0.179	−0.276	0.122
	c	20	−0.121	0.330	−0.163	0.276	−0.118	0.667	−0.049	0.414	−0.071	0.379	−0.276	0.127
	d	19	−0.203	0.236	−0.102	0.361	0.141	0.622	−0.134	0.284	−0.106	0.317	0.047	0.834
	e	19	−0.141	0.310	−0.098	0.367	0.103	0.720	−0.126	0.301	−0.107	0.322	0.142	0.483
	f	20	−0.081	0.385	0.014	0.520	0.197	0.470	−0.015	0.476	0.003	0.505	0.020	0.934
	g	13	−0.817	<0.001***	−0.812	<0.001***	−0.124	0.760	−0.587	0.004**	−0.649	<0.001***	−0.265	0.370
	h	20	−0.190	0.243	−0.173	0.263	0.226	0.404	−0.184	0.200	−0.302	0.092	−0.154	0.487
	i	15	−0.025	0.472	−0.164	0.319	−0.007	0.984	−0.189	0.079	−0.381	0.041*	0.012	0.963
5e	Alld	20	−0.408	0.054	−0.321	0.111	0.236	0.381	−0.307	0.074	−0.307	0.090	−0.033	0.847
	a	20	−0.449	0.035*	−0.349	0.090	0.299	0.259	−0.315	0.085	−0.294	0.097	−0.085	0.566
	b	20	−0.393	0.062	−0.339	0.097	−0.085	0.759	−0.277	0.100	−0.366	0.042*	−0.255	0.144
	c	20	−0.414	0.051	−0.273	0.153	−0.121	0.659	−0.197	0.169	−0.214	0.164	−0.177	0.338
	d	19	−0.381	0.077	−0.256	0.180	0.242	0.388	−0.369	0.046*	−0.276	0.102	0.051	0.819
	f + i	20	−0.309	0.121	−0.145	0.298	0.025	0.929	−0.218	0.171	−0.135	0.293	−0.003	0.987
	g	13	−0.721	0.005**	−0.739	0.004**	−0.081	0.843	−0.561	0.018*	−0.736	0.001**	−0.164	0.492
	h	20	−0.263	0.163	−0.346	0.092	−0.097	0.726	−0.221	0.150	−0.358	0.039*	−0.165	0.407

Note.—Association between pathway position and ω, d_N, and d_S values after controlling for expression level and breadth, codon bias, protein length, and connectivity. Unless noticed otherwise, all correlations are based on values estimated under the FR model.

^aBranch codes according to figure 2.

^bOne-tailed P values.

^cTwo-tailed P values.

^dUsing overall ω, d_N, and d_S values (M0 model).

^eExcluding Ornithorhynchus anatinus.

^*P < 0.05, **P < 0.01, and ***P < 0.001.

Connections between IT Pathway Elements and Other Pathways

We studied the pattern of signaling interactions across the IT pathway proteins using the data set reported by Cui et al. (2007). This manually curated data set consists of a directed graph with 1,634 elements (nodes) connected by 5,089 interactions (arcs), of which 2,403 are activatory, 741 are inhibitory, 1,915 are undirected, and 30 are unspecified. Three hundred and fifty-six of these interactions (215 activatory, 74 inhibitory, and 67 undirected; supplementary table S17, Supplementary Material online) connect an IT pathway component with a non-IT pathway component. For each element, the number of inputs received from other pathways was computed as the number of arcs connecting an upstream (in the tail of the arc) IT pathway protein with a downstream (head) non-IT pathway protein; conversely, the number of outputs was computed as the number of interactions between a downstream IT pathway protein and an upstream non-IT pathway protein. In total, the IT pathway proteins receive 130 inputs (100 activatory and 30 inhibitory) and have 159 outputs (115 activatory and 44 inhibitory; supplementary table S17, Supplementary Material online).

Discussion

We have characterized the evolutionary forces acting on the vertebrate IT pathway genes. All ω estimates are lower than 1, with a maximum of 0.140 (supplementary table S3, Supplementary Material online), indicating that purifying selection is a major force acting on the IT pathway gene sequence evolution. This result, together with the fact that all genomes appear to encode at least one isoform of each IT pathway component, strongly supports that all organisms in this study have a complete and functional IT pathway.

Polarity in the Selective Constraint Level along the IT Pathway

In Drosophila, we detected a correlation between the strength of purifying selection and the position along the upstream/downstream axis of the IT pathway, with the downstream genes being the most constrained (Alvarez-Ponce et al. 2009). Even though this trend is not significant in vertebrates, the sign of the correlation coefficient is always negative regardless of the metrics of selective constraint (ω or d_N) or the data set used (table 2 and fig. 4; supplementary fig. S1 and tables S8 and S9, Supplementary Material online). When the correlation was analyzed in each phylogenetic branch separately (fig. 5), the correlation coefficient is negative in a number of branches significantly greater than the number expected by chance (i.e., 50%), independent of the data set used for d_N and for data sets 2 and 3 for ω. This consistency in the direction of the association between selective constraint and pathway position across the vertebrate phylogeny is not compatible with a random distribution of selective constraint levels along the IT pathway. Furthermore, after removing O. anatinus sequences from the analysis, the correlation between the pathway position and the overall d_N values is significantly negative for data set 2 (table 2).

Taken together, vertebrate results, as those in Drosophila, show a polarity in the level of selective constraint along the IT pathway, with downstream elements evolving under stronger purifying selection. Therefore, this feature is neither incidental nor specific to the Drosophila genus, but rather, it may indicate a more general mechanism. This observation indicates that the molecular evolution of the IT pathway components is affected by their specific position in the pathway. A correlation between the pathway position and the strength of purifying selection has also been observed in other pathways, including the anthocyanin, isoprene, terpenoid, and carotenoid biosynthetic pathways in plants (Rausher et al. 1999; Sharkey et al. 2005; Livingstone and Anderson 2009; Ramsay et al. 2009) and the Ras signal transduction pathway in Drosophila (Riley et al. 2003). However, the selective constraint polarity observed in these studies occurs in the opposite direction than in the IT pathway. Therefore, our results support the idea that the higher selective constraint observed in the upstream portion of molecular pathways is not universal.

The observed polarity of the selective constraint along the IT pathway might be due to a putative polarity in a number of factors affecting evolutionary rate. For instance, if positive selection acted preferentially in the upstream portion of the pathway, higher ω and d_N values would be expected at this part. However, we identified the footprint of positive selection in only three genes, IRS4, AKT3, and PRKCD (at pathway positions 1 and 5), and the significance was lost after correcting for multiple testing (supplementary table S6, Supplementary Material online). Therefore, positive selection would not account for the ω and d_N polarity along the IT pathway.

Genes with higher expression level or breadth, more biased codon usage, higher connectivity, or encoding shorter proteins tend to evolve under stronger purifying selection (Sharp 1991; Duret and Mouchiroud 2000; Pál et al. 2001; Fraser et al. 2002; Subramanian and Kumar 2004). Therefore, a putative polarity in any of these factors might contribute to the observed selective constraint polarity along the pathway. Indeed, we detected a negative correlation between protein length and pathway position, and d_N positively correlates with protein length for data set 2. However, both partial correlation and path analysis show that the departure from 50% in the number of phylogenetic branches with negative sign in the association between pathway position and ω and d_N remains significant after controlling for the above factors (table 4; supplementary tables S15 and S16, Supplementary Material online). These factors, therefore, are unlikely to explain the correlation between selective constraint and pathway position.

Given that mutations in genes involved in a large number of pathways likely have important pleiotropic effects, these genes may be under strong selective constraint. Accordingly, in a pathway that is able to modulate the activation of other pathways (i.e., with signaling outputs along the pathway), upstream genes will be involved in a higher number of pathways and, hence, will evolve under stronger purifying selection. Conversely, a pathway that receives signaling inputs from other pathways is expected to be more constrained in the downstream portion. The direction of the selective constraint polarity observed along the anthocyanin biosynthetic pathway (Rausher et al. 1999) is consistent with this model because upstream genes participate in the biosynthesis of a greater array of compounds than downstream genes, which are only involved in anthocyanins biosynthesis. The same reasoning applies to other biosynthetic pathways with a similar distribution of selective constraints (Sharkey et al. 2005; Livingstone and Anderson 2009; Ramsay et al. 2009).

Our results showing that downstream IT pathway genes evolve under stronger purifying selection than upstream genes might therefore be explained on the grounds of the IT pathway having more inputs than outputs. However, our analysis of the connection pattern of the IT pathway with other pathways shows that it in fact has more outputs than inputs (supplementary table S17, Supplementary Material online). Nevertheless, current knowledge of the IT pathway connection pattern is far from complete. Furthermore, given that the biological impact of signaling interactions are not necessarily equivalent, the number of inputs and outputs is most likely an inaccurate predictor of the distribution of selective constraints along the pathway. A more accurate predictor should take into account the relative biological significance of inputs and outputs in terms of fitness effects, which is, however, very difficult to evaluate. Consequently, it is premature to draw conclusions about the effect of the IT pathway connection pattern on the evolution of its components.

Proteins in a pathway can contribute differentially to the overall pathway function. Enzymes that greatly affect pathway function are expected to be under stronger natural selection than enzymes with limited effects (Hartl et al. 1985; Eanes 1999; Watt and Dean 2000; Wright and Rausher 2010). Enzymes acting at network branch points are expected to play a key role in flux control and, hence, to be preferentially targeted by natural selection (LaPorte et al. 1984; Stephanopoulos and Vallino 1991). Consistently, in the pathways involved in glucose metabolism in Drosophila, Flowers et al. (2007) observed that positive selection preferentially targets genes acting on pathway branch points. Interestingly, two of the three IT pathway genes showing some evidence of positive selection in vertebrates, AKT3, and PRKCD, act on major network branch points. Analysis of the sensitivity of the IT pathway function to the kinetic properties of each of its components may provide insight into the distribution of negative and positive selection along the pathway. Recent development of a mathematical model for the IT pathway (Zielinski et al. 2009) may serve as a starting point for this type of analysis.

Physically Interacting IT Pathway Proteins Tend to Evolve under Similar Selective Constraints

We found that the level of selective constraint of physically interacting proteins is more similar than expected from a random network (supplementary table S7, Supplementary Material online). Such a tendency has also been observed in interactome-wide analyses (Fraser et al. 2002; Lemos et al. 2005) and has been explained by a coevolution and/or similar strength of stabilizing selection between interacting proteins (Fraser et al. 2002; Lemos et al. 2005). In the IT pathway, however, this pattern might be a by-product of the polarity of the selective constraint along the pathway. Because proteins tend to interact with those occupying adjacent positions in the pathway, the detected selective constraint polarity might determine that interacting proteins also exhibit similar selective constraints. However, removing the influence of the association between pathway position and selective constraints yields equivalent results (supplementary table S18, Supplementary Material online). This similarity, therefore, is not a by-product of the selective constraint polarity along the pathway. Interestingly, connectivities of physically interacting IT pathway proteins are also more similar than expected by chance (data set 3, supplementary table S7, Supplementary Material online); this feature could explain the similarity in selective constraint values among interacting proteins. However, after discounting the effect of the association between connectivity and selective constraint, we obtain equivalent results (supplementary table S19, Supplementary Material online). This indicates that the selective constraint similarity among genes encoding interacting proteins is not a by-product of the similar connectivities of interacting partners. Therefore, the similarity in selective constraint levels among genes encoding interacting proteins may have the same underlying mechanism as proposed in interactome-wide analyses.

Current results contrast with our findings in Drosophila that the similarity in selective constraints among interacting IT pathway proteins vanishes after controlling for the association between pathway position and selective constraint (Alvarez-Ponce et al. 2009). However, the number of interactions remarkably differs between both studies (32 PPIs in vertebrates vs. only 20 in Drosophila). Hence, the lack of significance in Drosophila may have resulted from lower statistical power associated with the smaller number of interactions. Accordingly, when the analysis of the vertebrate IT pathway is restricted to the 20 interactions that were analyzed in Drosophila, we obtain equivalent results: the association is significant for ω in data set 2 (supplementary table S7, Supplementary Material online), but this significance disappears when controlling for the association between pathway position and selective constraint (supplementary table S18, Supplementary Material online).

Molecular Evolution of the Drosophila and Vertebrate IT Pathways

Even though both Drosophila and vertebrates show a polarity in selective constraints along the IT pathway, the trend is less apparent in vertebrates. The difference might be explained by a lower statistical power of the vertebrate analysis caused by a putative smaller number of substitutions. However, the number of synonymous changes across the phylogeny (and the d_S values) is, in fact, higher in vertebrates than in Drosophila (paired t-test, P = 0.004 for the number of synonymous changes; P < 0.001 for d_S [data set 2]). The lower effective population size of vertebrates, as compared with Drosophila (Lynch 2007), may also explain this difference. Indeed, the nearly neutral theory of molecular evolution predicts that natural selection will be more relaxed in populations with a small effective population size (Ohta 1973) and, in fact, purifying selection has been shown to be stronger in Drosophila than in mammals (e.g., Petit and Barbadilla 2009). Therefore, the putative biological mechanism maintaining the polarity of functional constraints along the IT pathway may be less efficient in vertebrates. However, we did not observe any reduction in the selective constraint levels among vertebrate genes (the ω values do not differ significantly between the IT pathway genes of vertebrates and Drosophila; paired t-test, P = 0.999 for data set 2).

Whereas in Drosophila most IT pathway genes are single copy (Alvarez-Ponce et al. 2009), most pathway genes exist in multiple copies in vertebrates (supplementary table S4, Supplementary Material online). Because the strength of purifying selection depends on the number of duplicates (Lynch and Conery 2000; Jordan et al. 2004), the polarity of selective constraints along the IT pathway in vertebrates may result from a gradient in the number of duplicates. Nevertheless, because the number of copies per paralogous group correlates with neither pathway position (ρ = −0.201, P = 0.383) nor the average ω (ρ = −0.021, P = 0.923) or d_N (ρ = 0.010, P = 0.963), this factor would not account for the selective constraint polarity.

Concluding Remarks

In summary, we provide evidence that the IT pathway architecture impacts the pattern of molecular evolution of its components. We found a gradient in selective constraint levels along the vertebrate IT pathway, with the downstream genes being the most constrained. This selective constraint polarity mirrors that observed in Drosophila (Alvarez-Ponce et al. 2009). Therefore, although the biological mechanism underlying this gradient distribution of selective constraints remains elusive, it is likely to be similar between Drosophila and vertebrates. The direction of the selective constraint polarity, however, differs from studies in a number of pathways showing that purifying selection is stronger in the upstream part (Rausher et al. 1999; Riley et al. 2003; Sharkey et al. 2005; Livingstone and Anderson 2009; Ramsay et al. 2009). Further understanding of the connection pattern of the IT pathway with other pathways and of how pathway function depends on the properties of each of its components will provide insight into the factors underlying the molecular evolution of the IT pathway genes. Furthermore, comprehensive analysis of pathways with different topologies will likely enhance our understanding of the effect of pathway architecture on the molecular evolution of its components.

Supplementary Material

Supplementary figure S1 and tables S1–S19 are available at Genome Biology and Evolution online (http://www.oxfordjournals.org/our_journals/gbe/).