SYSTEMICALLY MODELING THE DYNAMICS OF PLASMA INSULIN IN SUBCUTANEOUS INJECTION OF INSULIN ANALOGUES FOR TYPE 1 DIABETES

Abstract

Type 1 diabetics must inject exogenous insulin or insulin analogues one or more times daily. The timing and dosage of insulin administration have been a critical research area since the invention of insulin analogues. Several pharmacokinetical models have been proposed, and some are applied clinically in modeling various insulin therapies. However, their plasma insulin concentration must be computed separately from the models’ output. Furthermore, minimal analytical study was performed in these existing models. We propose two systemic and simplified ordinary differential equation models to model the subcutaneous injection of rapid-acting insulin analogues and long-acting insulin analogues, respectively. Our models explicitly model the plasma insulin and hence have the advantage of computing the plasma insulin directly. The profiles of plasma insulin concentrations obtained from these two models are in good agreement with the experimental data. We also study the dynamics of insulin analogues, plasma insulin concentrations, and, in particular, the shape of the dynamics of plasma insulin concentrations.

1. Introduction

Since their inventions, insulin analogues have made a dramatic evolution in diabetes management ([5], [12]). The diabetics’ lives are tremendously improved with newly developed insulin regimes using insulin analogues. There are approximately 20.8 million diabetics in the United States, accounting for 7% of the total population (American Diabetes Association, http://www.diabetes.org). The total worldwide diabetic population is estimated at 190 millions. The cause of diabetes is still not fully understood. But it is confirmed that diabetes mellitus can induce many complications, for example, cardiovascular disease, blindness (retinopathy), nerve damage (neuropathy), and kidney damage (nephropathy). ([9]). Many researchers have engaged in research in this area with the objectives of understanding how the system works ([19], [21], [35], [37]), what leads to the dysfunction of the system ([4], [38]), how to detect the onset of diabetes, how to prevent or postpone the onset ([3], [8], [20]), and ultimately providing more efficient, effective, and economic insulin therapies ([24], [36], [41]).

The real cure for diabetes, at least for type 1 diabetes ([11]), would be the transplantation of a pancreas or Langerhans islets in pancreas. However, due to immunological issues, the implantation is usually not successful. Approaches for β-cell neogenesis or cell differentiation from stem cells are still at the research stage ([11], [6]). So, the most widely used therapy is still the daily insulin subcutaneous injection. The purpose is simply to supply the need of insulin in one’s body exogenously, which mimics the physiological insulin secretion occurring in normal subjects. Normally, insulin is secreted from the pancreas in two time scales in an oscillatory manner: pulsatile oscillations accounting for the basal insulin, and ultradian oscillations controlled by plasma glucose concentration levels ([21], [25], [32], [35], [37]). Table 1 lists part of the currently available insulin analogue products for clinical uses.

TABLE 1.

Pharmacokinetics of Available Insulin Products ([7]).

Insulin	Onset	Peak	Duration
Lispro	5–15 minutes	30–90 minutes	3–5 hours
Aspart	10–20 minutes	1–3 hours	3–5 hours
Regular insulin	30–60 minutes	1–5 hours	6–10 hours
Buffered regular insulin	30–60 minutes	1–3 hours	8 hours
Lente	1–3 hours	6–14 hours	16–24 hours
NPH	1–2 hours	6–14 hours	16–24+ hours
Glargine	1.1 hours	None	24 hours
Ultralente	4–6 hours	8–20 hours	> 24 hours

To understand the dynamics of the insulin analogues from subcutaneous injection to absorption, several mathematical models have been proposed ([2], [16], [16], [23], [27], [31], [36], [39], [40]). A critical review of most of the models was given by [24], which omits only the most recent work, for example, Tarin et al. [36]. The partial differential equation (PDE) models proposed by Mosekilde et al. ([23]), which were simplified by Trajanoski et al. ([39]) and Wach et al. ([40]), are implemented in an internet-based decision support system, DiasNet, for patients and healthcare professionals ([26]). The siblings ([39], [40]) of the model proposed in [23] and the model in [36] quantitatively depict the dynamics of insulin analogues in different molecular forms at injection depot, which agrees with experimental data ([18], [24], [36]). The computations of plasma insulin concentrations fit the experimental data as well.

However, no analytical and qualitative studies were performed in these models. For example, under what conditions, does a positive and bounded solution of the PDE models exist? How many peaks can the plasma insulin concentration have? Apparently, the trivial solution is the unique homogeneous steady state of all these PDE models. Is it stable? In addition, according to the experiment performed in [39], the diameter of the boundary of the diffusion is about one half inch after 15 minutes, and about two inches after 24 hours (Figure 6 and Figure 7 in [39]). Thus the diffusion effect at the injection depot is relatively negligible when considering the plasma insulin concentration in systemic circulation. In this paper, to systemically model the behavior of the plasma insulin concentration, we incorporate the plasma insulin concentration as a variable and propose two ordinary differential equation (ODE) models to model the dynamics of the administration of rapid-acting insulin analogues and long-acting insulin analogues. We perform rigorous qualitative analysis first, followed by numerical simulations. This provides models that are more reasonable in physiology and molecular chemistry and simpler for computation of plasma insulin concentration. The profiles of plasma insulin concentrations produced from our models agree well with the experimental data. Potentially, the models proposed in this paper, together with the glucose-insulin regulation model proposed by [21] and [19], could form the foundation for artificial pancreas if integrated with a glucose monitoring system.

We arrange this paper as follows. In the next section, we discuss the background of insulin analogues; then in Section 3 we propose models of the exogenous injection of insulin analogues. In Section 4, we analyze the dynamics of the models, followed by numerical simulations of the models in Section 5. We will end this paper with a discussion section.

2. Background

Diabetes is a disease in which β-cells in the pancreas do not produce insulin or the cells in body do not utilize insulin properly. Insulin is a pancreatic hormone needed to convert glucose into energy needed for daily life. Glucose is the basic fuel for cells in the body. After insulin binds the insulin receptors of the cells (for example, adipose and muscle cells), the glucose transporter GLUT4 takes the glucose molecules from the plasma into the cells so that the glucose can be metabolized.

Diabetes is classified into type 1 diabetes, type 2 diabetes, and gestational diabetes. Type 1 diabetes is usually diagnosed in children and young adults, and so has also been called juvenile diabetes. In type 1 diabetes, β-cells in the pancreas do not produce insulin. The majority of diabetics have type 2 diabetes. In type 2 diabetes, either the β-cells do not produce enough insulin or so-called insulin resistance caused by the dysfunctional system prevents the cells to take up glucose efficiently. Pregnant women who have never had diabetes but develop high plasma glucose levels during pregnancy are said to have gestational diabetes. Glucose is toxic when its concentration is high, a condition known as hyperglycemia. Hyperglycemia is often accompanied with that the body cells are starving for energy, and over time, eyes, kidneys, nerves, or the heart can be hurt.

At the β-cell level, the propensity of insulin to self-associate into hexamers is crucial for the hormones’ processing and storage. The additions of zinc ions and phenolic compounds into human insulin can not only prevent undesirable chemical degradation and promote the hexamer conformation, but also prevent physical denaturation. This property of insulin has been exploited in pharmaceutical formulation to produce stable solution preparations and microcrystallines used for diabetes treatment. (Refer to [1]).

During the late 1980s, biotechnology provided the laborious techniques needed in chemical modifications or semisynthesis that results in the success of recombinant DNA (rDNA) technologies for the creation of new insulin analogues ([5]). Consequently, a new research area has been opened since then. Several different types of insulin analogues have been created and put in clinical practices ([5], [12], [29], [43]). In 1996, the first rapid-acting insulin analogue, lispro, was introduced into clinical application. It is an evolutionary development of genetically engineered human insulin with a short duration of action because of its weakened propensity to self-associate into dimers. The rapid-acting insulin analogue is designed and developed in making the pharmocokinetic profile of injection to be similar to its normal physiological counterpart to better help cells to utilize glucose postprandially. Lispro exists in its respective formulations as hexamers that are stabilized with zinc-ions and phenolic preservatives to assure two years of shelf life at 4°C. But, structurally, lispro’s formulation differs from other insulin analogues because its hexamer complex dissociates into monomeric subunits virtually instantaneously after subcutaneous injection, resulting in a plasma absorption profile indistinguishable from that of a pure monomeric insulin ([5]). The effectiveness of rapid-acting insulin analogues in controlling postprandial glycemia has been demonstrated. In addition, thanks to the rapid action, the use of the rapid-acting insulin analogues provides the convenience of injecting a few minutes before or after the meal ingestion. This prompt action has reduced frequency of both hyperglycemic and hypoglycemic episodes using conventional short-acting insulin ([43]).

Beginning in 2002, glargine, a new long-lasting insulin analogue that has the advantage of maintaining a twenty-four-hour effect with no peak, was put into clinical use. Glargine is also developed by rDNA technology. Comparing to human insulin, both A and B chains of the molecule contain amino acid changes. This change leads to a shift of the isoelectric point towards a neutral pH, which results in a molecule less soluble after injected. At the injection site, a molecule depot is subcutaneously formed, from which insulin is slowly released. The absorption is so slow that no peak of insulin concentration will occur during the long lasting twenty-four-hour release-absorption duration. Thus the long-acting insulin analogues are desirable to simulate the physiological pulsatile insulin secretion that occurs in nondiabetic subjects. ([12], [29].)

To mimic the behavior of insulin secretion in normal subjects by using insulin analogues, insulin pumps are designed to deliver rapid-acting or short-acting insulin twenty-four hours a day through a catheter placed under the skin. The insulin doses are separated into basal rates and bolus doses that simulate the insulin pulsatile secretion and ultradian secretion in oscillatory fashion, respectively. The dosage of basal insulin and bolus insulin delivery, however, can be adjusted manually according to different daily activities. Automated programmable corrections based on feedback information from glucose monitoring and more efficient and robust algorithms would be more desirable. Furthermore, the effect would be even better with the combined use of a rapid-acting insulin analogue to mimic the basal insulin and a rapid-acting insulin analogue to mimic the bolus insulin.

3. Modeling the subcutaneous injection of insulin analogues

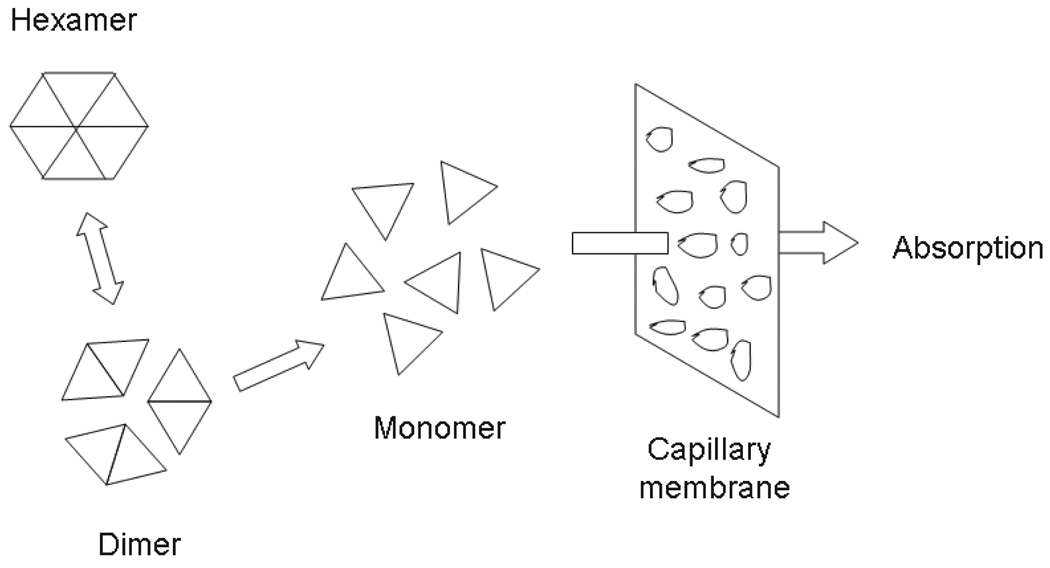
It is well accepted that subcutaneous insulin absorption is a complex process that can be influenced by many factors, e.g., insulin’s hexameric, dimeric and monomeric states; injection locations; volume; temperature; and blood flow near the injection site ([24]). Insulin analogue in its hexameric form is the predominant associated state after the subcutaneous injection of the soluble insulin preparation. The progressive dissociation of the hexamers into smaller units, dimers and monomers, is facilitated by the diffusion of the liganded phenolic molecules and zinc ions in the subcutis, which is caused by the diffusion in the intercellular dilution of the insulin concentration. Then the insulin in dimeric form and monomeric form can penetrate the capillary membrane and be absorbed into plasma ([1]). Figure 1 shows putative events occurring under the subcutis after the injection. The chemical molecular reaction diagram is given as

$$H\underset{\mathit{\text{pq}}}{\overset{p}{\rightleftharpoons }}3D,$$ (1)

where H (U/ml) stands for hexamer and D (U/ml) for dimer, p (min⁻¹) is the transform rate from one hexameric molecule to three dimeric molecules, and pq (q has unit ml²/U²) is the transform rate from three dimeric molecules to one hexameric molecule.

FIGURE 1.

Putative events occurring at subcutis after injection of insulin analogues. The hexamer is too big to penetrate the capillary membrane, while the dimer and monomer succeed, so that the absorption into plasma occurs.

Mosekilde et al. ([23]) proposed a model with the hypotheses that only the dimeric form of insulin can be absorbed into plasma and that the fraction of soluble insulin dissociating into a monomeric form is negligible. This model was simplified by Trajanoski et al. ([39]) under the assumption that the binding state in the model proposed by [23] can be negligible due to its short-acting time. This is reasonable for rapid-acting insulin analogues, and the resulting model contains the first and second equation without the binding term. Wach et al. ([40]) further simplified the model in [39]. To enable the computations of the models, a spherical depot centered at subcutaneous injection site is assumed and fifteen or more shells are spatially discretized with homogeneous concentration, so that the plasma insulin concentration can be calculated by integration of the concentration of dimers over the distribution volume. Based on the models in [23] and [39], Tarín et al. ([36]) reinforced the imaginary bound state with diffusion and proposed a model to study the dynamics of long-acting insulin analogues such as glargine. A similar approach is applied in computing the plasma insulin concentration by integrating the concentration of dimers over the subcutaneous discretized depot volume.

Notice that the diffusion effect of both hexamers and dimers applies to a small local scope of the injection site so the impact of the diffusion to the whole metabolic system is negligible according to the experiment performed in [39] (Figure 6 and Figure 7). Based on the molecular reaction diagram (1) and the law of mass action, and in light of the existing models ([24], [23], [39], [40]), we propose following model to simulate the dynamics of the rapid-acting insulin analogues of the whole metabolic system:

$$\{\begin{array}{c}H\prime (t)=-p(H(t)-{\mathit{\text{qD}}}^3(t))\hfill \\ D\prime (t)=p(H(t)-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t)\hfill \end{array}$$ (2)

with H(0) = H₀ > 0, D(0) = 0, and I(0) = I₀ ≥ 0, where H(t) (U/ml) stands for concentration of insulin analogue in hexameric form, D(t) (U/ml) for concentration of insulin analogue in dimeric form, and I(t) (U/ml) for plasma insulin concentration at time t ≥ 0. As no experimental study is observed, to create a bridge between the local injection of insulin analogue and plasma insulin concentration in the whole body, we hypothesize that the rate of dimers penetrating the capillary is inversely proportional to the plasma insulin concentration, which is depicted by the term bD(t)/(1 + I(t)) in the second equation and the term rbD(t)/(1 + I(t)) in the third equation of model (2), where b (U/min) is a constant parameter ([23], [40] and [36]), and r ≤ 1, as only fractional molecules can become plasma insulin ([36]). The constant d_i (min⁻¹) in the third equation is the insulin degradation rate that has been assumed as linear ([21], [35], [38]). We will analyze model (2) in Section 4.

While rapid-acting insulin analogues, when injected right before or after meal ingestion, can simulate the physiological insulin secretion triggered by elevated plasma glucose concentration, another type, so-called long-acting insulin analogue, is needed to mimic the physiological pulsatile insulin secretion in normal subjects, also known as basal insulin.

Since the depot releases insulin slowly, a continuous delay exists in the process of transforming insulin analogue in hexameric form to dimeric form. As in [36], we use an imaginary state, called bound state, to simulate the delay. The transformation is inverse-proportional to the concentration of the hexamer, so the change rate of the transformation can be determined by C_max/(1 + H(t)), where C_max (U/ml) is the maximum capacity of the transformation. Thus we obtain following model:

$$\{\begin{array}{c}B\prime (t)=-\mathit{\text{kB}}(t)\frac{C_{\mathit{\text{max}}}}{1+H(t)}\hfill \\ H\prime (t)=-p(H(t)-{\mathit{\text{qD}}}^3(t))+\mathit{\text{kB}}(t)\frac{C_{\mathit{\text{max}}}}{1+H(t)}\hfill \\ D\prime (t)=p(H(t)-{\mathit{\text{qD}}}^3(t))-\frac{\mathit{\text{bD}}(t)}{1+I(t)}\hfill \\ I\prime (t)=\frac{\mathit{\text{rbD}}(t)}{1+I(t)}-d_{i}I(t)\hfill \end{array}$$ (3)

with B(0) = B₀ > 0, H(0) = 0, D(0) = 0, and I(0) = I₀ ≥ 0, where B(t) (U/ml) stands for the concentration at the bound state for the insulin analogue in hexermeric form, H(t) (U/ml) for concentration of insulin analogue in hexameric form, D(t) (U/ml) for concentration of insulin analogue in dimeric form, and I(t) (U/ml) for Insulin concentration at time t ≥ 0. The term kB(t)C_max/(1 + H(t)) in the first and second equations is due to that the insulin analogue in the depot formed near the injection site is transformed into hexameric form gradually and the transform is inversely proportional to the concentration of the insulin in hexameric form with the maximum transformation capacity C_max ([23], [36]), where k (min⁻¹) is the constant absorption rate. This avoids the situation in which the behavior of the solutions are unpredictable even if H(t) > C_max, which is an issue in the existing models ([23], [36]). Other notations are the same as those in model (2).

Apparently model (2) is a special case of model (3) without the imaginary bound state. We will analyze model (3) in the next section.

4. Analysis of the models

In this section, we state the analytical results without proofs. The proofs of Proposition 1, Theorem 4.1, and Theorem 4.3 can be found in the appendices. We skip the proofs of Proposition 2 and Theorem 4.2 as the proofs can be carried out similarly. Results similar to that of Theorem 4.3 for model (3) can be obtained without further effort, so we also skip the statement.

It is clear that both model (2) and model (3) have unique equilibriums (0, 0, 0) and (0, 0, 0, 0), respectively. Furthermore, we have

Proposition 1. All solutions of model (2) with the initial condition H(0) = H₀ > 0, D(0) = 0, and I(0) = I₀ ≥ 0 are positive and bounded.

Theorem 4.1. The origin (0, 0, 0) of model (2) is a global attractor.

Proposition 2. All solutions of model (3) with the initial condition B(0) = 0, H(0) = H₀ > 0, D(0) = 0, and I(0) = I₀ ≥ 0 are positive and bounded.

Theorem 4.2. The origin (0, 0, 0, 0) of model (3) is a global attractor.

Below, we analyze the shapes of the solutions of model (2). Similar arguments can be applied to analyzing the shapes of the solutions of model (3), and the same results can be obtained.

Theorem 4.3. Let (H(t), D(t), I(t)) be a solution of model (2) with initial condition H(0) = H₀ > 0, D(0) = 0 and I(0) = I₀ ≥ 0. Then

1. H′(t) < 0.

   Furthermore, if p ≥ b(H₀ + I₀/r)r, then

2. There exists a t_D ∈ (0, ∞) such that D(t) is monotonically increasing in (0, t_D) and decreasing in (t_D, ∞).

3. If the initial condition I(0) = I₀ > 0, I(t) either has a unique local minimum in (0, t_D) and a unique local maximum in (t_D, ∞) or is monotonically decreasing in (0, ∞). If the initial condition I(0) = 0, I(t) has a unique local maximum in (t_D, ∞).

Remark 1. According to Theorem 4.3, if both D(t) and I(t) assume their maximums, then D(t) attains its peak before I(t) does. When the initial condition I(0) > 0, which is clinically realistic ([29], [34]), I(t) decreases in a very short time right after the insulin analogue is injected. This is due to that a short time is needed for insulin analogue to dissolve into smaller molecules and then absorbed into plasma. This case is not covered by previously existing models ([24], [27], [36], [39], [40], [42]). When the initial condition I(0) = 0, I(t) will assume a unique maximum value in (0, ∞). This is in agreement with the numerical simulations in existing models ([24], [27], [36], [39], [40], [42]).

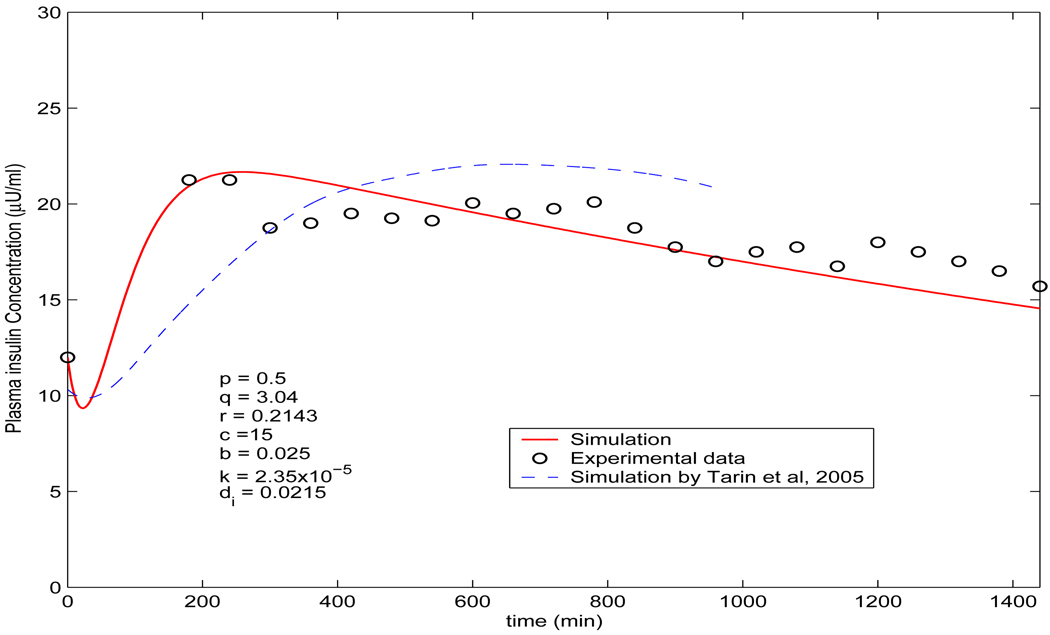
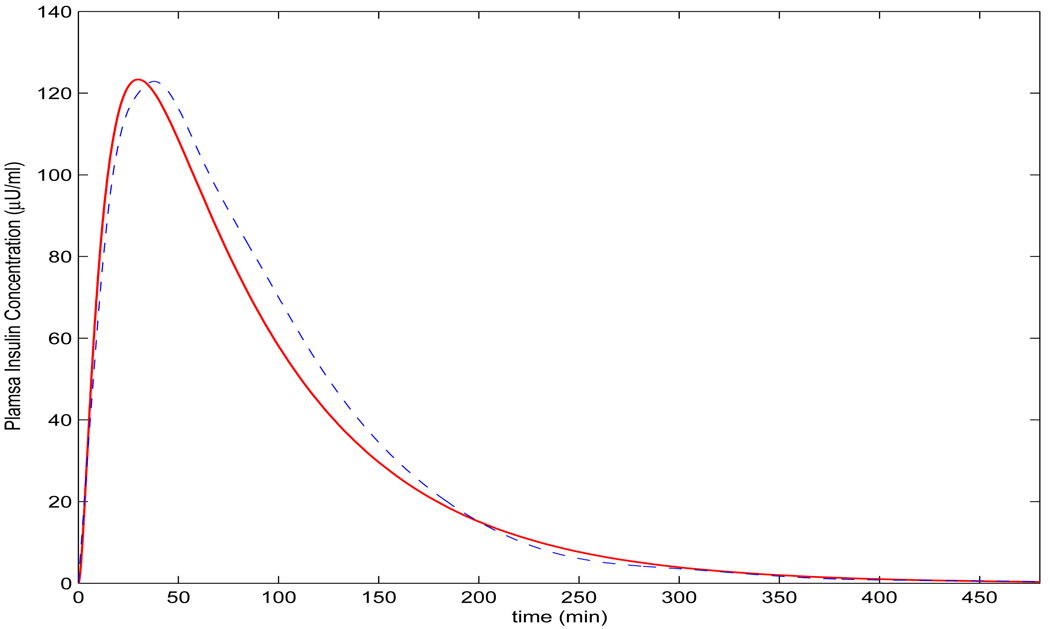
Remark 2. The condition in Theorem 4.3 for (b) and (c) is satisfied in the simulations of lispro and aspart in section 5 (Figure 5) according to the selection of the parameters based on [14] and [18].

FIGURE 5.

Comparison of the simulated plasma insulin concentration (solid line) by model (3) (p = 0.5, q = 3.04, r = 0.2143, c = 15, b = 0.025, k = 2.35 × 10⁻⁵ and d_i = 0.0215) with the measured data from [18] (circle ○). The dashed line is the simulation by the model in [36], which is adapted from [36] showing from 0 hour to 16 hours.

5. Numerical simulations

In this section we perform numerical simulations according to model (2) and model (3). Then we compare the profiles obtained with the measured data. The simulations are performed in Matlab, and the measured data are from [5], [18], and [36]. The plasma insulin concentration I(t) is a variable of the systems (2) and (3). So, no separate and additional effort is needed for calculations. The dynamics of the insulin concentrations are well in agreement with the measured data given in [5], [14], [18], and [36].

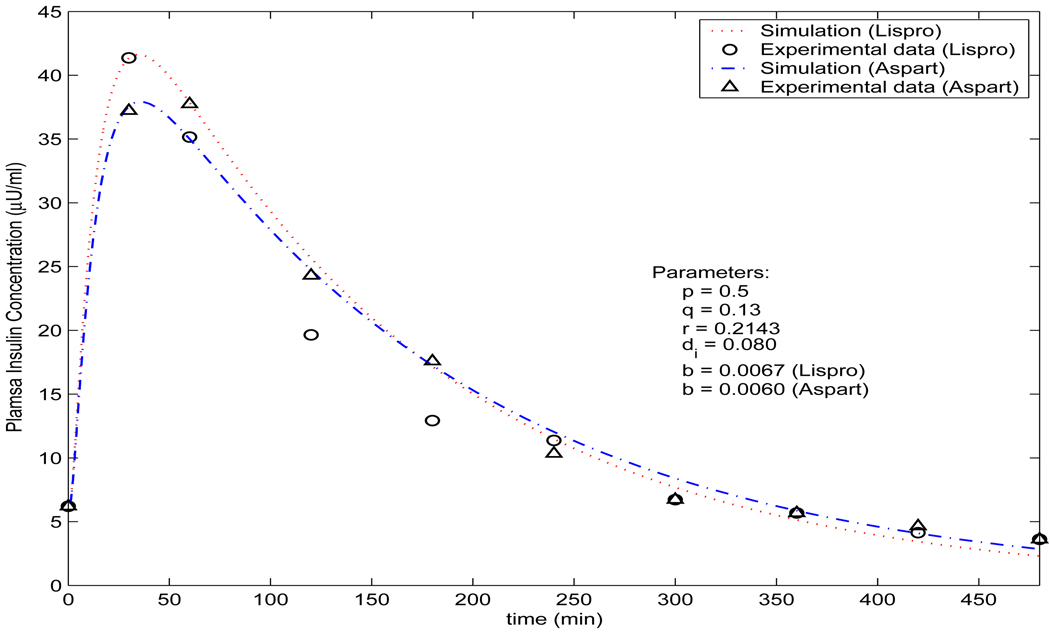
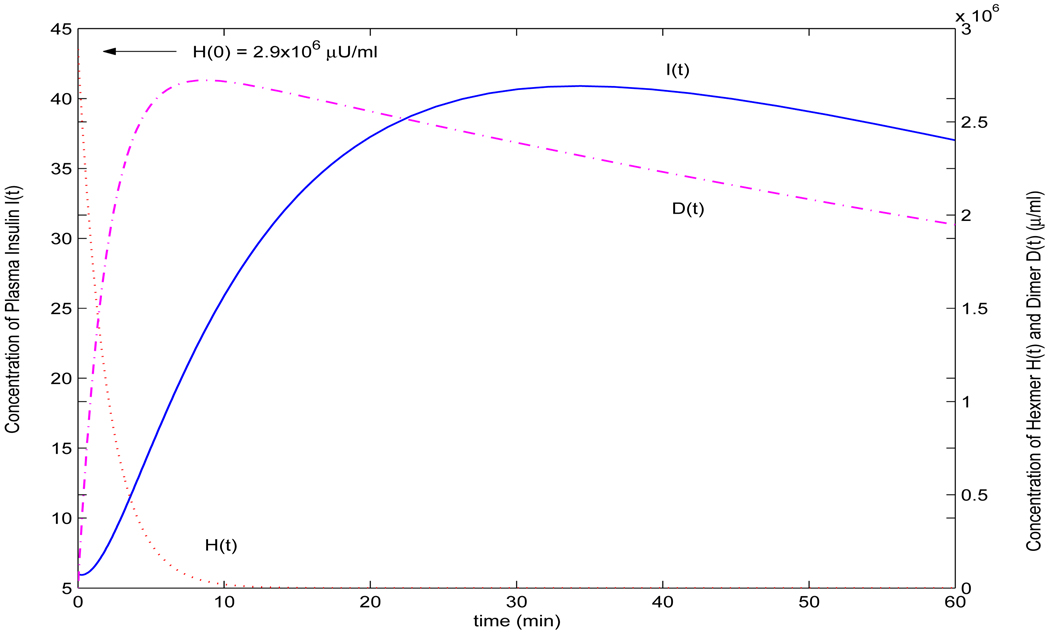
As observed by Trajanoski et al. ([39]), the changes of the parameter p in model does not alter the results significantly. So, we have used the same values of p = 0.5 and q = 0.13 as [39] and [40], and r = 0.2143. We choose r = 0.2143 because usually only part of an insulin analogue can be absorbed into plasma ([36]). To simulate insulin lispro, we choose the parameters b = 0.0068 and d_i = 0.081 for simulating insulin lispro, while choosing b = 0.0060 and d_i = 0.0775 for simulating insulin aspart. The values of d_i and b are selected in view of the interquartile range of the best model 10 and 9 proposed in [42] (Table III(a)). The initial value H(0) = H₀ is selected as follows: H₀ = 9.4U/72.3kg45ml/kg = 0.0029U/ml = 2.9 × 10³µU/ml, as 9.4U/kg lispro or aspart was injected subcutaneously in the experiments performed in [14] and the plasma volume is assumed to be 45 ml/kg by [36]. I₀ = 6µU/ml according to [14]. It is easy to verify the condition in Theorem 4.3 holds and thus all conclusions are true. Figure 2 reveals that the profiles for insulin analogues lispro and aspart produced from model (2) are very well in agreement with the clinically measured data given in [14]. Figure 3 shows the simultaneous profiles and overall relationships of each of the dynamic variables in the dynamical system. The calculation is simply achieved by the solver ode23 in Matlab while solving the ordinary differential equation system. This significantly simplified the computations in existing models ([24], [39], [40] for examples.) Notice that the existing models ([24], [39], [40]) were proposed before the first rapid-acting insulin analogue lispro was introduced (refer to the second section of this paper and [5]), and the models proposed in [36] are for bolus and continuous subcutaneous insulin injection (CSII). Model (2) proposed in this paper is for bolus injection only, and comparing with the profiles produced by these models is not valid. Nevertheless, with slightly tuned parameters ([39]), b = 0.0135, d_i = 0.076 and r = 0.35, the profile in Figure 4 produced by model (2) is compatible with the simulation in Figure 4 in [39] for the case of monomeric analogues.

FIGURE 2.

Comparison of the simulated plasma insulin concentration produced by model (2) and the measured data. The measured data of aspart and lispro are from [14].

FIGURE 3.

Dynamics of hexamer, dimer and insulin concentrations produced by model (2).

FIGURE 4.

Comparison of profile produced by model (2) (I(0) = 0, p = 0.5, q = 0.13, b = 0.0135, d_i = 0.076, r = 0.35) (solid line) and the simulation in Figure 4 in [39] (dashed line, adapted from [39]), illustrating the absorption of equimolar doses of monomeric insulin analogues.

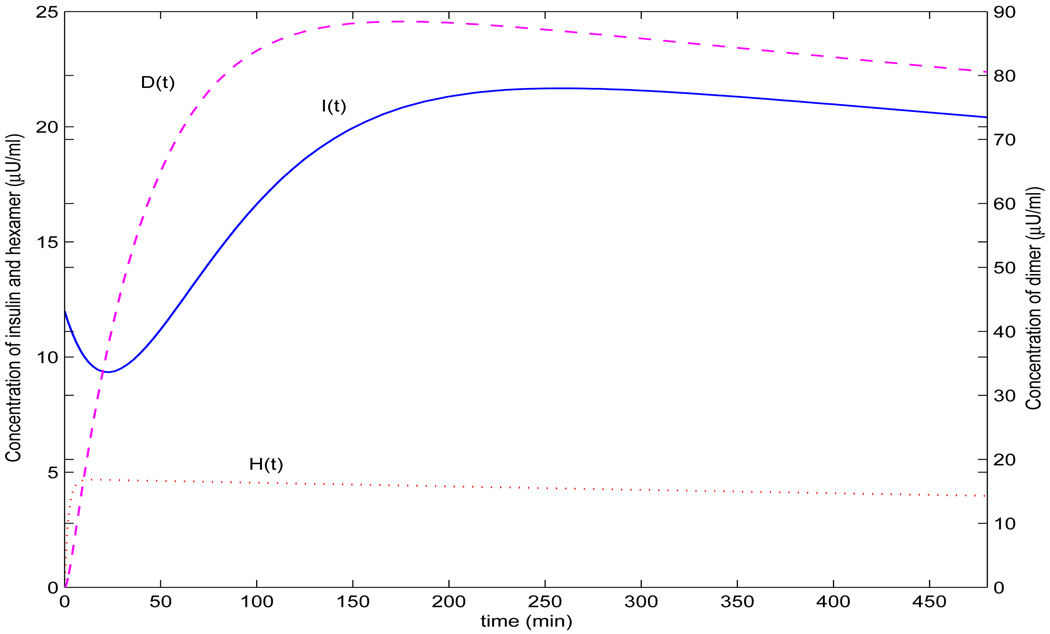
Model (3) involves more parameters than model (2), because of the imaginary bound state. We use the same p = 0.5 and r = 0.2143 as above when simulating rapid-acting insulin analogues by model (2). For other parameters, we choose q = 3.04, b = 0.02 and C_max = 15 as in [36]. We assume that d_i = 0.0215, given that the value is within the interquartile range shown in [42] (Table III(a)). The parameter k corresponds to the rate of disengagement of a hexamer from its bound state κ in [36]. Since we model the disengagement by the term −kB(t)C_max/(1 + H(t)), k shall be significantly smaller than κ in Tarin et al. (2005). Thus we choose k = 2.35 × 10⁻⁵. The initial value B(0) = B₀ is selected as follows: B₀ = 0.3U/kg/45ml/kg = 0.0067U/ml = 6.7 × 10³µU/ml as 0.3U/kg was injected subcutaneously in the experiments performed in [18] and the plasma volume is estimated to be 45 ml/kg by [36]. I₀ = 12µU/ml according to [18]. Figure 5 reveals that when compared with the clinical measurement ([18]) of plasma insulin concentration of a subject using insulin glargine, our simulated profile is in agreement with the measured data in [18] and shows significantly better fitting than the profile given by Figure 3 in [36]. Figure 6 demonstrates the simultaneous profiles and overall relationships of each of the dynamic variables in the dynamical system. Similar to model (2), the computation of the numerical solution of the plasma insulin concentration is greatly simplified as obtaining I(t) is part of solving the ordinary differential equation numerically. Involving a delay parameter in the model (3) to replace the imaginary bound state may result in a more accurate model. Additionally, it is well known that the delayed effect could cause oscillations, either damped or sustained. The apparent discrepencies in the experimental result could be more accurately modeled by a model involving an explicit delay. The apparent discrepencies of the data and the solution might also be due to stochastic factors. Applying a bias to the solution could improve the simulation ([28]). We will investigate this in a future study.

FIGURE 6.

Dynamics of concentrations of hexamer (dotted line), dimer (dashed line) and insulin (solid line) simulated by model (3) when p = 0.5, q = 3.04, c = 15, r = 0.2143, b = 0.025 and d_i = 0.0215

6. Discussions

Type 1 diabetics do not produce insulin. To maintain lifestyle close to normal, it is necessary to exogenously infuse insulin analogues and dynamically adjust the injection timing and dose. Some insulin analogues, e.g., lispro and aspart, take effect quickly. That is, after only a few minutes, the injected insulin analogue has been absorbed and starts to help the body’s cells to metabolize the glucose. Some insulin analogues, e.g., glargine and ultralente, take longer for absorption and then function to help the cells to take up glucose.

Basically, there are two types of therapies to administrate the injection. In the first, a diabetic takes one or two shots a day with long-acting insulin analogues. The insulin gradually absorbed into the plasma supplies the whole day’s need of the patient. The patient somehow must adjust his or her lifestyle to accommodate the way the exogenous insulin infusion works. The more advanced method is using a insulin pump. With an insulin pump, instead of adjusting his or her life style, the patient can match insulin levels to his or her daily activities by adjusting the doses and injection timing. All type 1 diabetics at all ages can use insulin pumps, and more and more people with type 2 diabetes are starting to use insulin pumps too. (refer to American Diabetes Association, http://www.diabetes.org). However, because of the expense, not all diabetics choose to use insulin pumps.

The regulation of glucose-insulin endocrine metabolism occurs in our daily life continuously. To mimic the normal physiological insulin secretion in type 1 diabetes, at least theoretically, the best way is to use glargine as the basal insulin for physiological pulsatile secretion, and apply lispro or aspart as the bolus insulin for the physiological secretion stimulated by elevated plasma glucose concentration level. With feedback information of plasma glucose concentration monitored periodically, dynamically adjusting the timing and doses of subcutaneous insulin injection is desirable. To this end, a more advanced, dynamical, and efficient algorithm for determining the timing and doses is needed. The two new systemic models proposed in this paper can be used for this purpose. These two models, (2) and (3), are systemic in pharmacology, simpler and reasonable in mathematics, and significantly simplify the computing procedures in clinical practices; thus, model (2), model (3) and the model proposed in [21] and [19] can form a foundation of an artificial pancreas if integrated with a glucose monitoring system.

Schlotthauer et al. ([30]) integrated three submodels to create a closed-loop control model, called nonlinear model-based predictive control (NMPC), to mimic the operation of normal pancreas. The three submodels include 1) a subcutaneous–plasma insulin absorption model to compute the plasma insulin; 2) a glucose regulation model; and 3) a subcutaneous glucose sensing model. When selecting the first sub-model, the authors evaluated the models proposed by [23], [39] and [40] and found that it is difficult to integrate these models in NMPC, as these models deal with single injections and it is hard to compute precise insulin concentration. Thus the authors used an autoregressive model for a substitute. The second submodel simulates the plasma glucose concentration. As stated by the authors of [30], NMPC lacks robustness and can have instability depending on the parameters. Neither model (2) nor the model in [21] and [19] has such issues as analytical analysis on both models assuring the desired dynamics. Apparently, it would be better choices to choose model (2) as the first submodel and the model in [21] and [19] as the second submodel.

Notice that the existing models ([24], [39], [40]) were proposed before the rapid-acting insulin analogue was put into clinical usage (refer to the second section of this paper and [5]), and the models proposed in [42] are for bolus and continuous subcutaneous insulin injection (CSII). So model (2) proposed in this paper is, to our knowledge, the first attempt for modeling bolus injection of rapid insulin analogues. Nevertheless, with parameters I(0) = 0, p = 0.5, q = 0.13, b = 0.0135, d_i = 0.076 and r = 0.35 (mostly from [39] but fine-tuned), model (2) produces a compatible profile (Figure 4) to the simulation in Figure 4 in [39], which illustrates the absorption of equimolar doses of monomeric analogues.

We should also notice that, at the small injection depot, the existing PDE models with diffusion terms will be more accurate than the newly proposed models in this paper. Thus the inverse relationship demonstrated by [39] between the absorption and doses at the depot is not observed. However, the aims of the new ODE models proposed in this paper are to analyze and simulate the dynamics of plasma insulin concentration at the whole systemic level and to avoid unexpected behaviors not being handled by the existing PDE models. Nevertheless, it might be plausible that Michaelis-Menten kinetics is imposed on insulin absorption as in model (3) and model (4) in [42], although the authors implied that these two models are not the best choice in applications ([42]). We will study this in the future.

A hypothesis is made when considering the rate of dimers penetrating the capillary membrane. Since the simulations are in agreement withwhile the experimental data, it might be worth to perform new experiments to verify this new hypothesis.

Appendix A. Proof of Proposition 1

Proof of Proposition 1. Observe that model (2) is monotone, hence an argument similar to the proof of Theorem 2.1 on page 81 of ([33]) can be applied to establish the following: if H(t) or D(t) is not always positive for all t > 0, then there exists t₀ > 0 such that H(t₀) = 0, D(t₀) = 0, and H(t) > 0, D(t) > 0 for 0 < t < t₀.

Now, assume that H(t) or D(t) is not always positive for t > 0. Then, there exists t₀ > 0 such that H(t₀) = 0, D(t₀) = 0, and H(t) > 0 and D(t) > 0 for 0 < t < t₀. So

$$H\prime (t)=-\mathit{\text{pH}}(t)+{\mathit{\text{pqD}}}^3(t)\ge -\mathit{\text{pH}}(t)\text{ for }0<t<t_0.$$

Therefore,

$$H(t)\ge H_0{e}^{-\mathit{\text{pt}}}\text{ for }0<t<t_0.$$

By continuity,

$$H(t_0)\ge H_0{e}^{-{\mathit{\text{pt}}}_0}>0.$$

So H(t) > 0, D(t) > 0 for t > 0.

If there exists t̂ > 0 such that I(t̂) = 0 and I(t) > 0 for 0 < t < t̂, then 0 ≥ I′(t̂) = rbD(t̂) > 0. This contradiction implies that I(t) > 0 for t > 0.

Now we show that all solutions are bounded. Let

$$F(t)=\mathit{\text{rH}}(t)+\mathit{\text{rD}}(t)+I(t),\text{for }t>0.$$ (4)

Then

$$F\prime (t)=-d_{i}I(t)<0.$$

So there exists a constant A ≥ 0 such that

$$\underset{t\to \infty }{\text{lim}}F(t)=A\ge 0.$$

This implies that H(t), D(t) and I(t) are uniformly bounded.

Appendix B. Proof of Theorem 4.1

The following fluctuation lemma, which is needed in the proof of Theorem 4.1, is elementary ([13]).

Lemma 6.1. Let f : R → R be a differentiable function. If l = lim inf_t→∞ f(t) < lim sup_t→∞ f(t) = L, then there are sequences {t_k} ↑ ∞, {s_k} ↑ ∞ such that for all k, f′(t_k) = f′(s_k) = 0, lim_k→∞ f(t_k) = L and lim_k→∞ f(s_k) = l.

Proof of Theorem 4.1. Consider F(t) defined in (4). All we need to show is that A = 0. Let

$$G(t)=\mathit{\text{rH}}(t)+\mathit{\text{rD}}(t),t>0.$$

Then

$$G\prime (t)=-\frac{\mathit{\text{rbD}}(t)}{1+I(t)}<0.$$

So lim_t→∞ G(t) = B ≥ 0 exists. Thus I(t) = F(t) − G(t) → A − B as t → ∞. So for any sequence {t_n} ↑ ∞, I(t_n) → A − B as n → ∞.

Denote

$$\begin{array}{c}\overline{H}=\underset{t\to \infty }{\text{lim sup}}H(t)\text{ and }\underset{¯}{H}=\underset{t\to \infty }{\text{lim inf}}H(t);\hfill \\ \overline{D}=\underset{t\to \infty }{\text{lim sup}}D(t)\text{ and }\underset{¯}{D}=\underset{t\to \infty }{\text{lim inf}}D(t).\hfill \end{array}$$

By the fluctuation lemma, there exists a sequence s_n → ∞ such that D′(s_n) = 0 for each n and lim_n→∞ D(s_n) = D̅. Then from the second equation in system (2),

$$0=D\prime (s_n)=p(H(s_n)={\mathit{\text{qD}}}^3(s_n))-\frac{\mathit{\text{bD}}(s_n)}{1+I(s_n)}.$$ (5)

Let ε > 0, then there exists T > 0 such that H(t) ≤ H̅ + ε when t ≥ T. Then, for n sufficiently large, H(s_n) ≤ H̅ + ε and (5) becomes

$$0\le p(\overline{H}+\epsilon -{\mathit{\text{qD}}}^3(s_n))-\frac{\mathit{\text{bD}}(s_n)}{1+I(s_n)}.$$

Letting n → ∞,

$$0\le p(\overline{H}+\epsilon -q{\overline{D}}^3)-\frac{b\overline{D}}{1+A-B}.$$

This is true for all ε > 0, therefore

$$0\le p(\overline{H}-q{\overline{D}}^3)-\frac{b\overline{D}}{1+A-B}$$

or

$$q{\overline{D}}^3+\frac{b\overline{D}}{p(1+A-B)}\le \overline{H}.$$

Similarly, there exists a sequence $s_n^{\prime }\to \infty$ such that $H\prime (s_n^{\prime })=0$ for each n and ${\text{lim}}_{n\to \infty }H(s_n^{\prime })=\overline{H}$. From the H equation in system (2),

$$0=H\prime (s_n^{\prime })=-p(H(s_n^{\prime })-q{D}^3(s_n^{\prime })).$$

Let ε > 0, then there exists T′ > 0 such that D(t) ≤ D̅ + ε for all t ≥ T′. For all n large, $D(s_n^{\prime })\le \overline{D}+\epsilon$ and therefore

$$0\le -\mathit{\text{pH}}(s_n^{\prime })+\mathit{\text{pq}}{(\overline{D}+\epsilon )}^3.$$

Letting n → ∞ and then ε → 0 gives

$$0\le -p\overline{H}+\mathit{\text{pq}}{\overline{D}}^3$$

or H̅ ≤ qD̅³. Therefore

$$q{\overline{D}}^3+\frac{b\overline{D}}{p(1+A-B)}\le q{\overline{D}}^3.$$

Hence D̅ = 0 and H̅ = 0, so that, since D(t) > 0 and H(t) > 0, lim_t→∞ D(t) = lim_t→∞ H(t) = 0. From the asymptotically autonomous limiting form of the equation for I(t) in (2), it follows that lim_t→∞ I(t) = 0.

Appendix C. Proof of Theorem 4.3

We need following lemma to prove Theorem 4.3.

Lemma 6.2. H(t) ≤ H₀+I₀/r, D(t) ≤ H₀+I₀/r, and I(t) ≤ rH₀+I₀ for all t ≥ 0.

Proof. Notice that rH′(t) + rD′(t) + I′(t) ≤ 0. Thus rH(t) + rD(t) + I(t) ≤ rH(0) + I(0).

Proof of Theorem 4.3. Notice that H′(0) < 0. First we prove part (a). If there exists t₀ > 0 such that H′(t₀) = 0, without loss of generality, we have H′(t) < 0 for 0 < t < t₀, and

$$H(t_0)={\mathit{\text{qD}}}^3(t_0)\text{\hspace{1em}\hspace{1em}and\hspace{1em}\hspace{1em}}D\prime (t_0)=-\frac{\mathit{\text{bD}}(t_0)}{1+I(t_0)}.$$

Thus

$$H″(t_0)=-\mathit{\text{pH}}\prime (t_0)+3{\mathit{\text{pqD}}}^2(t_0)D\prime (t_0)=3{\mathit{\text{pqD}}}^2(t_0)D\prime (t_0)<0.$$

Therefore, for small δ > 0, H′(t) > 0 when t ∈ (t₀ − δ, t₀). This is a contradiction.

Now we turn to proving part (b). Assume D′(t_D) = 0, t_D > 0. Notice that

$$D″(t)=\mathit{\text{pH}}\prime (t)-3{\mathit{\text{pqD}}}^2(t)D\prime (t)-\frac{b[D\prime (t)(1+I(t))-D(t)I\prime (t)]}{{(1+I(t))}^2}.$$

Thus at t_D,

$$D″(t_D)=\mathit{\text{pH}}\prime (t_D)+\frac{\mathit{\text{bD}}(t_D)I\prime (t_D)}{{(1+I(t_D))}^2}.$$

Clearly, if I′(t_D) ≤ 0, D″(t_D) ≤ pH′(t_D) < 0; otherwise, since p ≥ b(H₀ + I₀/r)r,

$$D″(t_D)\le \mathit{\text{pH}}\prime (t_D)+b(H_0+I_0/r)I\prime (t_D)\le b(H_0+I_0/r)(\mathit{\text{rH}}\prime (t_D)+\mathit{\text{rD}}\prime (t_D)+I\prime (t_D))<0.$$

So, for any extreme point t̂ of D(t), we have D″(t̂) < 0. Therefore it is a local maximum point. It is easy to see that t_D is the unique maximum point and thus the global maximum point since D(0) = 0 and lim_t→∞ D(t) = 0. In fact, assume $t_D^{\prime }$ is another local maximum point of D(t), without loss of generality, assume $t_D<t_D^{\prime }\text{ and }D(t_D)\ge D(t_D^{\prime })$. Thus $D\prime (t_D)=D\prime (t_D^{\prime })=0,\text{ and }D″(t_D)<0\text{ and }D″(t_D^{\prime })<0$. If $D(t_D)>D(t_D^{\prime })$, there exists a $t_0\in (t_D,t_D^{\prime })$ such that D(t₀) assumes a local minimum, which is a contradiction. If $D(t_D)=D(t_D^{\prime })$, similar argument shows that there must be a local minimum point in $(t_D,t_D^{\prime })$ if D(t) ≠ D(t_D) for some $t\in (t_D,t_D^{\prime })$. However, D(t) ≡ D(t_D) for $t\in (t_D,t_D^{\prime })$ implies that D′(t) = D″(t) = 0 for all $t\in (t_D,t_D^{\prime })$, which is a contradiction.

It follows that D′(t) ≠ 0 in (0, t_D) and (t_D, ∞). Since 0 = D(0) < D(t_D) and D(t_D) > 0 = lim_t→∞ D(t), it is clear that D′(t) > 0 for t ∈ (0, t_D) and D′(t) < 0 for t ∈ (t_D, ∞). We complete the proof of part (b).

For part (c), notice that D′(t) > 0 for t ∈ (0, t_D), D′(t) < 0 for t ∈ (t_D, ∞), D′(t_D) = 0, and

$$I″(t)=\frac{\mathit{\text{rbD}}\prime (t)}{1+I(t)}-[\frac{\mathit{\text{rbD}}(t)}{{(1+I(t))}^2}+d_i]I\prime (t).$$ (6)

We first show that I(t) does not assume a local extreme value at t_D. If I′(t_D) = 0, then I″(t_D) = 0 according to (6). Since I‴(t_D) = rbD″(t_D)/(1 + I(t_D)) < 0, there exists a δ > 0 such that I″(t) > 0 for t ∈ (t_D − δ, t_D) and I″(t) < 0 for t ∈ (t_D, t_D + δ). Since I′(t_D) = 0, I′(t) < 0 for t ∈ (t_D − δ, t_D), and I′(t) < 0 for t ∈ (t_D, t_D + δ). Thus I(t) does not assume a local extreme value at t = t_D.

Suppose that I(t) assumes a local extreme value at t₀ ∈ (0, ∞), then I′(t₀) = 0. By (6), I″(t₀) = rbD′(t)/(1 + I(t)) > 0 if t₀ ∈ (0, t_D), and I″(t₀) = rbD′(t)/(1 + I(t)) < 0 if t₀ ∈ (t_D, ∞). Using a similar argument to the proof of part (b), if I(t) assumes an extreme value in (0, t_D), then it must be a local minimum thus it is unique; if I(t) assumes an extreme value in (t_D, ∞), then it must be a local maximum so it is unique. Furthermore, because of their uniqueness, if they exist, they are the global minimum and global maximum.

When the initial condition I(0) > 0, since D(0) = 0, we have I(t) < I(0) for small t > 0. Thus, either I(t) does not attain any extreme value in (0, ∞), that is, I(t) decreases to vanish in (0, ∞); or I(t) has a local minimum point $t_I^{\prime }\in (0,t_D)$ first followed by a local maximum point $t_I^{″}\in (t_D,\infty )$ since lim_t→∞ I(t) = 0. That is, I(t) is monotonously decreasing for $t\in (0,t_I^{\prime })$, increasing for $t\in (t_I^{\prime },t_I^{″})$, and then decreasing to vanish in $(t_I^{″},\infty )$.

When the initial condition I(t) = 0, since I(t) = 0, lim_t→∞ I(t) = 0 and I(t) > 0 for t ∈ (0, ∞), I(t) must have a global maximum point $t_I^{″}\in (0,\infty )\text{ and }{t}_D<t_I^{″}$. If I(t) has a local minimum point $t_I^{\prime }\in (0,\infty ),\text{ then }{t}_I^{\prime }<t_D$ and thus I(t) must have a local maximum point between $(0,t_I^{\prime })$, which is a contradiction. That is, I(t) is increasing for t ∈ (0, t_I) and decreasing to vanish in (t_I, ∞). We complete the proof of Theorem 4.3.