Changes in Selective Effects Over Time Facilitate Turnover of Enhancer Sequences

Abstract

Correct gene expression is often critical and consequently stabilizing selection on expression is widespread. Yet few genes possess highly conserved regulatory DNA, and for the few enhancers that have been carefully characterized, substantial functional reorganization has often occurred. Given that natural selection removes mutations of even very small deleterious effect, how can transcription factor binding evolve so readily when it underlies a conserved phenotype? As a first step toward addressing this question, I combine a computational model for regulatory function that incorporates many aspects of our present biological knowledge with a model for the fitness effects of misexpression. I then use this model to study the evolution of enhancers. Several robust behaviors emerge: First, the selective effects of mutations at a site change dramatically over time due to substitutions elsewhere in the enhancer, and even the overall degree of constraint across the enhancer can change considerably. Second, many of the substitutions responsible for changes in binding occur at sites where previously the mutation would have been strongly deleterious, suggesting that fluctuations in selective effects at a site are important for functional turnover. Third, most substitutions contributing to the repatterning of binding and constraint are effectively neutral, highlighting the importance of genetic drift—even for enhancers underlying conserved phenotypes. These findings have important implications for phylogenetic inference of function and for interpretations of selection coefficients estimated for regulatory DNA.

CORRECT spatial and temporal gene expression is necessary for many developmental (Carroll et al. 2005; Davidson 2006; Prud'homme et al. 2007), cellular (Breeden 2003), and physiological (Gasch et al. 2000) processes. Pervasive conservation of gene expression across many evolutionary timescales (Rifkin et al. 2003; Denver et al. 2005; Gilad et al. 2006a,b; Hare et al. 2008; Visel et al. 2008) suggests that most genes are subject to stabilizing selection for an optimal expression pattern most of the time. Indeed, there are a number of vertebrate developmental enhancers that show near complete expression conservation and sequence conservation over the last 75 million years of evolution (Nobrega et al. 2003; Visel et al. 2008). On this basis, one may be tempted to equate functional conservation with evolutionary conservation of the sequence encoding that function.

A number of observations make clear that this equation is not strictly true, however, and raise important questions. In Drosophila melanogaster, for example, more intergenic sequence appears to be constrained than can be explained by known functions (Halligan et al. 2004; Andolfatto 2005; Halligan and Keightley 2006) and although less compact genomes show a correspondingly smaller fraction of the genome under constraint (Peterson et al. 2009), the amount of constrained DNA is still inexplicably high. As an illustration, the signal of conservation often extends beyond the regions bound by transcription factors in in vivo assays (Li et al. 2008). These observations either signal an important functional role for these conserved but apparently unbound regions [perhaps an important role for weak binding (Tanay 2006)] or suggest that the conservation is a vestige of a historical functional role (Dermitzakis et al. 2003), but is a poor predictor for present-day function (Li et al. 2008). These alternatives have practical implications. Indeed, a widely used method to identify functional regulatory elements, phylogenetic footprinting, looks for conserved sequences among many related species (Tagle et al. 1988; Cliften et al. 2003). This approach relies on the assumption that functional elements will be conserved and nonfunctional elements will not. When applied to noncoding DNA, this approach has fallen short of the success achieved in the identification of protein-coding genes (Cliften et al. 2003; Kellis et al. 2003). While it does well in the aggregate, identifying collections of genes enriched for motifs, it remains unclear how well any individual motif instance can be trusted (Tompa et al. 2005). The limited success of phylogenetic footprinting further suggests that conservation of regulatory sequence is not synonymous with conservation of regulatory function.

This uncoupling of function and conservation has also become clear from detailed characterizations of enhancers for the even-skipped (eve) gene in Drosophila, in which functional transcription factor (TF) binding sites have been gained or lost while maintaining enhancer output (Ludwig et al. 1998, 2000, 2005). More recently, turnover has been observed in other Drosophila developmental enhancers (Ho et al. 2009), with substantial reorganization possible over long evolutionary time frames (Hare et al. 2008). Turnover is also extensive when viewed at a genome-wide scale (e.g., Moses et al. 2006), consistent with genes tending to have a flexible regulatory architecture that is permissive of small-scale rewiring while largely maintaining functional output. Thus, qualitatively we know that both the functional organization (i.e., which nucleotides bind transcription factors) and the patterns of constraint (i.e., which nucleotides are under purifying selection) evolve. Yet, natural selection is effective in eliminating even deleterious mutations of very small effect [a few times the reciprocal of the effective population size (Crow and Kimura 1970)], raising the question of how the functional organization of an enhancer evolves when the expression phenotype is under stabilizing selection.

Here, I use a computational modeling approach that relies on simple, biologically motivated assumptions about how gene expression is implemented to examine the relationship between functional organization and patterns of selective constraint. My model consists of two components: (i) a mapping from sequence to gene expression using a computational model that was shown to have good predictive value for modeling expression in the Drosophila segmentation pathway (Segal et al. 2008) and (ii) a mapping from gene expression to fitness that provides a description of stabilizing selection around an optimum. The first component captures important mechanistic aspects of transcriptional regulation and the second component allows one to model evolution under a regime of stabilizing selection on gene expression, i.e., to assume that the phenotype is conserved. I then investigate the evolution of regulatory DNA by running forward population simulations. In this model, the fitness effect of each mutation is calculable and follows directly from the mechanistic model of transcription and the model for stabilizing selection.

This study differs from earlier efforts to model substitution processes on complex fitness landscapes in a number of respects (Kauffman and Levin 1987; Orr 2005, 2006; Kryazhimskiy et al. 2009; Draghi et al. 2010). First, these earlier models are general and do not consider constraints on the nature of the fitness landscape that result from modeling the biological function of the sequence. The preference for such abstracted models stems in part from how little is known about fitness landscapes (Kryazhimskiy et al. 2009) and in part from their simplicity, which makes them analytically approachable. In contrast, the structure of the fitness landscape in my model reflects a specific biological function, namely transcription. Second, these earlier efforts were concerned with the adaptive phase of the substitution process, focusing primarily on the dynamics of adaptive walks, such as walk length, adaptive step size, and time intervals between adaptive events (Kauffman and Levin 1987; Orr 2005, 2006; Kryazhimskiy et al. 2009), or more recently on questions of robustness (Draghi et al. 2010). In contrast, I model evolution under stabilizing (purifying) selection.

The most well-studied and biologically realistic sequence–phenotype mapping is that of RNA secondary structure. Computational predictions of secondary structure are a good approximation to the biological function of RNA, such that the evolution of these structures can be investigated using simulations. A number of important results have come out of this body of work. First and foremost is the existence and properties of neutral networks—connected sets of mutationally accessible sequences all yielding the same structure (Schuster et al. 1994). A population of sequences encoding a structure with a large neutral network is free to explore the network by drift. Thus structures with large neutral networks are more robust to mutation and may also be more evolvable (Huynen et al. 1996; Ancel and Fontana 2000; Wagner 2008). The focus of these studies has been primarily on the role that neutral networks play in facilitating adaptation, rather than on the process of turnover during the exploration of the neutral network. Another difference between these RNA landscapes and the landscapes that I consider is that the former are discrete—mutations either result in a different structure or not—and thus questions concerning the role of weakly deleterious mutations are not easily addressed. In contrast, in the case of regulatory sequence landscapes, fitness is mediated through expression, which is quantitative, and under the model I consider, very few, if any, sequences result in identical fitnesses.

In one study to focus on the effects of purifying selection and regulatory function, Lusk and Eisen (2010) simulated enhancer evolution using binding site composition as the measure of fitness. They considered the case in which having too few TF binding sites is lethal and all alleles above the threshold number of binding sites are functionally equivalent (Lusk and Eisen 2010). The authors required a binary classification of sequence into what is or is not a binding site. Instead, I determine the functional equivalency of alleles on the basis of their composite expression output by using the affinities of TFs to all parts of the sequence. Accordingly, my model allows the nature of turnover to be an emergent property not tied to a priori architectural requirements; for example, I do not necessarily view turnover as a two-step process, in which a new binding site arises, obviating an existing one. Such two-step models are forced to assume functional equivalency of alleles with redundant binding sites (Lusk and Eisen 2010) or to assume an arbitrary selection coefficient for the intermediate form (Durrett and Schmidt 2008). Binding-site–oriented models may portray the turnover process unrealistically because, in a population setting, even a fewfold variation in a selection coefficient can be the difference between having an appreciable or vanishingly small fixation probability. Mutations with small selection coefficients may not correspond to binding site creation or disruption, but could still determine which evolutionary paths are possible.

A recent analysis of promoter substitution rates incorporates continuous estimates of transcription factor binding, rather than discrete binding sites (Hoffman and Birney 2010). The authors' hidden Markov model-based estimates of TF binding are similar in spirit to part of the model that I employ; however, in assessing the effect of mutations, the authors focus strictly on the TF binding profile. In contrast, I model the expression resulting from TF binding and assume selection acts on the expression phenotype, rather than directly on binding.

By putting together a model for regulatory function and a model for stabilizing selection on gene expression, I can address the question of how functional turnover occurs despite strong stabilizing selection on expression output. I show that selective constraint on individual sites varies extensively over time and that this variation explains much of the functional turnover. Additionally, I show that both functional organization and selective constraint evolve with a high degree of historical contingency, whereby multiple realizations of the evolutionary process show markedly different degrees of turnover. Admittedly, the modeling assumptions are obvious simplifications, as is always the case with computational models of biology. But, importantly, assumptions similar to these are often made—implicitly or explicitly—when thinking about regulatory evolution (Kellis et al. 2003; Wray et al. 2003).

METHODS

Model overview:

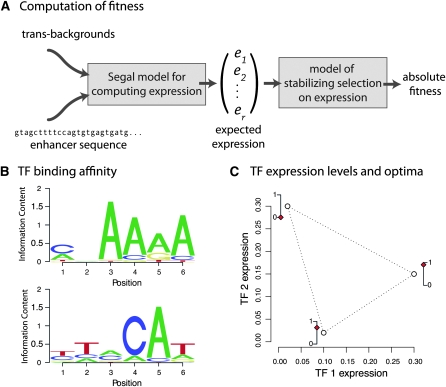
Modeling the evolution of regulatory DNA using forward population simulations requires computing the fitness for each haplotype that arises in the population. I break this computation down into two components: (i) a sequence-to-expression mapping and (ii) an expression-to-fitness mapping. I model a number of distinct regulatory problems, each of which can be thought of as the task faced by a particular gene or enhancer: to be expressed correctly in a small number of regulatory contexts, termed trans-backgrounds. In turn, each trans-background can be thought of as a cell type, a developmental time point, or a spatial position. Trans-backgrounds are characterized by the expression levels of the various input TFs in that background. Together, the set of trans-backgrounds and the optimal expression in those backgrounds, along with the nucleotide binding affinities and interaction properties of the TFs, define the complete regulatory problem (see Figure 1 for a simple schematic). Fitness is then a function of how close the expression pattern of an enhancer is to the optimal expression for that regulatory problem.

Figure 1.—

Schematic description of the model. (A) The expression of an enhancer sequence in each of the given trans-backgrounds is determined according to the Segal model. The fitness is then computed using a model of stabilizing selection, in which fitness is a function of the Euclidean distance between the realized and the optimal expression. (B) The binding specificities of the activator (top) and the repressor (bottom) are shown as position-weight matrices (PWMs), with the site-wise affinity of the TF to each nucleotide shown scaled by information content (in bits). These two PWMs are used for the nine primary regulatory problems. (C) Each regulatory problem is characterized by the expression levels of the two TFs (horizontal and vertical axes) in each of the three trans-backgrounds (points of the triangle) with the target expression (red diamond) shown on the adjacent 0–1 scale. The regulatory problem for enhancer 1 is shown. See Figure S1 for the other regulatory problems.

I compute the expected expression of an enhancer using a model proposed by Segal et al. (2008), the crux of which is a probabilistic computation that sums the contributions of all possible arrangements of TFs on the regulatory sequence. This model is designed to capture a number of important aspects of transcriptional regulation: (i) the locations of TF binding are determined primarily by TF–DNA affinities, (ii) higher TF concentrations result in more binding, (iii) multiple TFs cannot simultaneously bind the same stretch of DNA, and (iv) protein–protein interactions may influence binding (e.g., through cooperativity or quenching). This model is well suited for studying substitution processes in regulatory DNA because it performs a computation on the entire enhancer, potentially allowing mutations at any nucleotide to affect expression (Segal et al. 2008; Fakhouri et al. 2010).

The remainder of the methods section provides a detailed description of the Segal model, of how the regulatory problems were selected, and of the forward population simulations. Additional details are provided relating to mutational opportunities and the classification of functional mutations.

Details of the Segal model:

The Segal model (Segal et al. 2008) predicts expression from an enhancer sequence, given prior information about the binding specificities of TFs and the expression levels of the input TFs. In addition, there are number of free parameters, which were estimated in the original article for 44 enhancers involved in the Drosophila segmentation pathway using a training set of observed expression levels. Here I fix these parameters, which include the activity levels of the TFs and their interactions, assuming these are intrinsic aspects of the fully specified regulatory problem. Given the parameters appropriate for an enhancer, the model computes the expression of that enhancer and does not incorporate the temporal dynamics of expression, autoregulation, or other sorts of feedback.

According to the Segal model, at any given instant, and in a particular trans-background, transcription factors may occupy the enhancer DNA in any nonoverlapping fashion. The particular instantaneous arrangement of TFs bound to the DNA is termed a configuration. The probabilities of the configurations, denoted P(c_k) for configuration c_k, vary greatly, as determined by the affinities of the constituent TFs to their respective locations on the DNA, the expression levels of the TFs, and their interaction properties. Given that a particular configuration occurs, transcription of an mRNA occurs with probability P(E | c_k), which is a function only of the number and kinds of TFs in the configuration. The expression output of the enhancer is then assumed to be proportional to the overall probability of expression, P(E), in that trans-background, which is the sum of the contributions toward expression of all possible configurations, weighted by their probabilities:

P(E) can be interpreted as the expression level as a fraction of maximal expression (in a sense averaging over potential transcription events). The probability of configuration c_k, P(c_k), is the joint probability of its TFs binding to the DNA, which can be factored into conditional probabilities as follows:

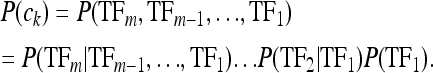By making the standard Markov assumption, whereby the probability of observing a TF bound at a certain location is contingent only on the adjacent TFs, one obtains the following factorization, where the TFs are numbered according to their appearance on the sequence (in either direction):

Let τ_TFi be the expression level of the ith bound TF and let 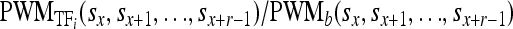be the affinity of the ith TF to the DNA sequence at sites s_x through s_x+r−1 relative to background [r is the width of the PWM and PWM_b() assumes equal affinity to each base]. Then, the conditional probability of a TF binding given that another TF is bound d nucleotides away is

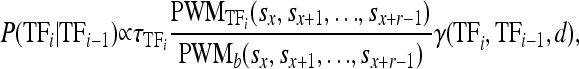where γ(tf_i, tf_i−1, d) accounts for the strength of the interaction between tf_i and tf_i−1. The product over all TFs, termed the weight (or energy) of the configuration, w(c_k), is proportional to the probability of interest

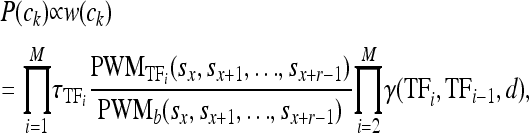where the constant of proportionality is simply the reciprocal of the sum of all weights:

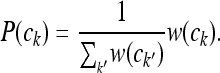In addition to homotypic interactions, present in the original Segal model, I also allow heterotypic interactions (i.e., between two distinct TFs) and I allow for both synergistic (e.g., cooperative binding) and antagonistic TF interactions (e.g., quenching). Let 1 + g_jk be the strength of the interaction when the ith TF, j, is bound adjacently to the (i – 1)th TF, k, where g_jk is positive for synergistic and negative for antagonistic interactions and g_jk ∈ (−1, ∞). The effect of the interaction then decays as a function of the number of intervening nucleotides, d:

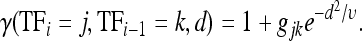Here, υ controls the rate of decay of the curve, which I set to 80, as this means that 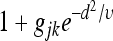approaches 1 by d ≈ 20 bp for modest g_jk [e.g., –0.9 < g_jk < 9, a range covering up to a 10-fold decrease or increase in P(c_k) due to the interaction]. I chose υ = 80 so that the interaction does not extend across the entire toy enhancer.

In addition to P(c_k), the computation of expression also requires the conditional probability of expression given the configuration, P(E | c_k). To capture saturation effects, whereby a little more or less binding does not alter P(E | c_k) when there is already either very little or extensive binding, the authors chose a logistic function of the sum of the contributions toward transcription of all the TFs in that configuration. The ith TF in the sequence, TF_i = k, has a parameter λ_k, which is positive for activators and negative for repressors. The logistic equation is

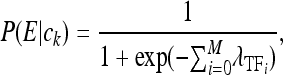where λ₀ is the basal activity of the enhancer.

For a more detailed description, see the original article (Segal et al. 2008). I made a few additional decisions in my implementation that I presume were similarly made by the original authors. These include symmetrically modeling both forward- and reverse-strand binding and modeling one empty configuration, with probability .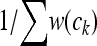

Computation of expression:

I computed P(E) by Monte Carlo integration. Obtaining independent and identically distributed samples from the configuration distribution can be accomplished by building a configuration progressively, sampling the TFs in the order in which they appear in the configuration, conditional on already sampled TFs. Despite a combinatorially large number of configurations, sampling from P(c_k) can be done efficiently using a dynamic programming algorithm.

For my application, very small errors in the estimation of expression could heavily influence the evolutionary dynamics, producing fluctuations in the selection coefficients of mutations at a site simply as a result of noise in the estimate of expression. I avoid this problem by ensuring that errors in the estimation of P(E) are more than an order of magnitude smaller than the reciprocal of the effective population size, 1/N, which is the magnitude at which the fate of mutations starts being influenced by natural selection (for most simulations I use N = 1000). I determined that sampling 200,000 configurations from P(c_k) is sufficient to achieve the desired precision. For the simulations involving N = 10,000, I sample 10⁶ configurations. The C++ source code of my implementation is available upon request.

Generation of regulatory problems:

I initially explored the parameter space of regulatory problems by generating hundreds of regulatory problems and varying regulatory problem parameters, including the number of TFs, TF binding affinities, target expression levels, input TF expression levels, TF–TF interaction parameters, and activity levels of the TFs. I then sampled 10,000 sequences uniformly under each of these regulatory problems, examining the fitness distribution for each problem. These distributions are primarily determined by the problem being solved, e.g., the input expression of the TFs and the target expression. For example, the following problem is impossible (i.e., no sequence produces the desired expression): two trans-backgrounds, one with only activator TFs expressed and for which the optimal expression level is silent, combined with another trans-background with only repressor TFs expressed and optimal expression at the maximum. In contrast, one trans-background consisting solely of high activator expression with a goal of maximal expression combined with another trans-background of only high repressor expression with a goal of no expression can be satisfied by a large fraction of random sequences. I chose to investigate a collection of nine regulatory problems with the property that only a small, but nonzero fraction of randomly sampled sequences have a high fitness (e.g., w ≥ 0.99) and such that these problems collectively offer a broad variety of input and target expression levels (supporting information, Figure S1).

To present comparable regulatory problems, I keep many of the parameters identical, including using two TFs (one activator, λ₁ = 2, and one repressor, λ₂ = −3, in a slightly repressive environment, λ₀ = −1) and employing the same TF–TF interaction matrix (g₁₂ = g₂₁ = −0.5 and g₁₁ = g₂₂ = 2) and the same pair of TF binding functions (Figure 1B). To assess whether the behaviors of the model are robust with respect to the choice of these parameters, I conducted additional simulations, systematically varying these parameters (see File S1 for details).

Definition of the expression–fitness function:

I penalize misexpression as a function of the Euclidean distance between the expression computed for a haplotype and the expression at the global fitness optimum for the regulatory problem. I use a Gaussian kernel as the fitness penalty for misexpression,

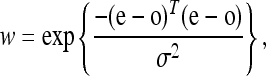where w is absolute fitness, e is the expression output vector (vector components are expression in each trans-background), o is the optimum expression vector, and σ² (equal to 0.6 in most simulations) is a scalar for the steepness of the misexpression penalty. In some ways, this specification is similar to parameterizations of Fisher's geometrical model (Fisher 1930), which can also be used to model purifying selection (Martin and Lenormand 2006); however, my mutational model is not at the level of the phenotype, and instead it describes the mutation process on the sequence with an explicit sequence-to-fitness mapping.

Forward population simulations:

I use standard Wright–Fisher multinomial sampling. The effective population size, N, is constant, and the population is haploid (equivalent to genic selection in a diploid population). Although I chose θ = 2Nμ = 0.001 to approximate humans, to speed up drift I used a population size of N = 1000 and a correspondingly high point mutation rate (as expected, results are comparable for simulations with N = 10,000 and 10,000N generations, but keeping θ = 0.001; not shown). Mutations occur uniformly on the sequence with equal mutation rates among all base pairs and all simulations are without recombination. All replicates for a particular regulatory problem are initiated with the same initial haplotype at frequency 1, which has initial fitness 1 and is therefore at the global fitness optimum. Parameters for the population simulations are shown in Table 1. For most analyses, 12 replicate simulations of each regulatory problem were run, an arbitrary number, but sufficient to consider variation among replicates. For select analyses requiring a larger number of observed mutations, 100 replicate simulations were run.

TABLE 1.

Parameters for forward population simulations

Parameter	Value	Description
N	1000	Population size
μ	5 × 10−7	Spontaneous point mutation rate per base pair per generation
θ	0.001	Population point mutation rate (2Nμ)
L	100 bp	Regulatory sequence length
G	2000N	Generations simulated

Computation of selection coefficients of mutation opportunities:

Mutation opportunities are those haplotypes that are accessible with a single mutation from an observed haplotype. To compute selection coefficients for these mutation opportunities, which I use in the analyses, I use the standard definition, 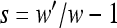, where w is the absolute fitness of the background upon which the mutation could occur and w′ is the absolute fitness of the haplotype generated by the mutation.

Classification of substitutions into large and small functional effect:

In classifying substitutions by functional effect size, I use the Euclidean distance (E_d) between the full occupancy profiles of the mutant and background haplotypes. For example, if there are two TFs and three trans-backgrounds and the enhancer is of length L, then I compute the Euclidean distance between the two vectors each of length 2 × 3 × L. For Figure 6, large-effect substitutions are defined as those with E_d > 2 and small-effect substitutions are those with E_d < 0.1.

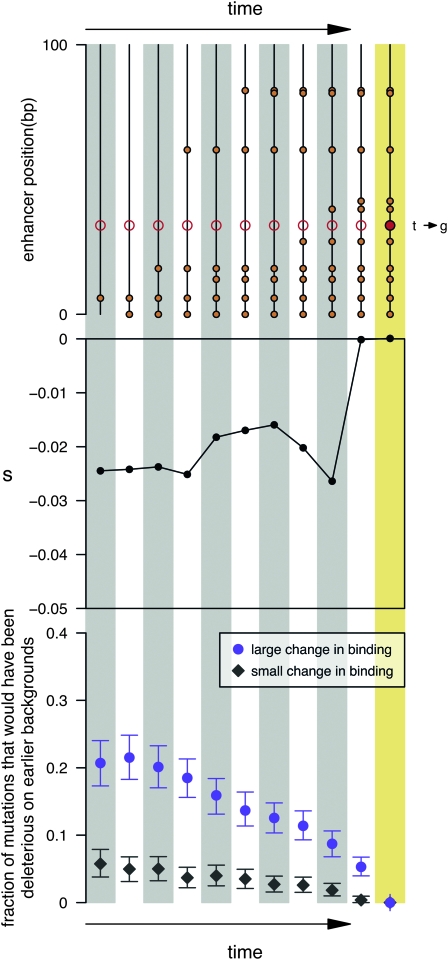
Figure 6.—

Large functional changes are facilitated by preceding substitutions. I consider two classes of substitutions: ones that substantially change TF occupancy and ones that produce little change (on the basis of the Euclidean distance between the full occupancy profiles; see methods). The top two plots illustrate a single, observed substitution of the large-effect class while the bottom plot is a collated summary of all substitutions falling into these two classes for 100 replicates of enhancer 3. (Top) For the particular T to G substitution (solid red dot) I consider each of the most recent 10 ancestral haplotypes (vertical lines) leading up to it. I then compute the selection coefficient associated with the haplotypes (middle) had that mutation occurred on that earlier background. As can be seen, had the mutation occurred only two haplotypes earlier, it would have been deleterious and highly unlikely to fix. (Bottom) I calculate the proportion of substitutions (vertical axis) that would have been deleterious had they occurred x substitutions in the past (horizontal axis). Mutations are considered deleterious if Ns < −4. Purple circles show the fraction of large-effect substitutions that would have been deleterious on ancestral haplotypes, and gray diamonds show these fractions for a comparably sized random subset of substitutions that did not alter TF binding. Notably, substitutions with large effects more often would have been deleterious, suggesting that in many cases, one or more of the preceding substitutions altered the selection coefficient of the mutation, making it effectively neutral and thus allowing it to substitute. Bars indicate the 90% interquantile range of the fractions based on subsampling with replacement.

RESULTS

Simulations of enhancer evolution:

I investigate the substitution processes during regulatory evolution and the dynamics of turnover by running forward population simulations in which the fitness of each enhancer sequence is computed using a computational model for expression, combined with a model for stabilizing selection on that expression phenotype (see Figure 1 for a simple schematic). In the methods section Model overview provides an overview of the model, defines terminology, and is followed by sections offering additional detail.

In brief, I combine the Segal model, which provides a sequence-to-expression mapping, with a model of stabilizing selection, which provides an expression-to-fitness mapping. The bulk of the regulatory problems that I investigate involve two TFs (an activator and a repressor) and three trans-backgrounds (see Figure 1 for an example and Figure S1 for the full set). These regulatory problems differ in their optimal expression and the expression levels of the input TFs. All regulatory problems that I investigate are nontrivial; i.e., few random sequences encode an expression profile very near the optimum.

I simulate the evolution of a constant-size population by sampling alleles according to their fitnesses. This provides a model of drift and selection, which is essential for modeling the substitution processes of enhancers because many mutations are likely affected by both. I selected the simulation parameters to optimize the trade-off between simulation efficiency and realism (shown in Table 1). The bulk of the results involve nine regulatory problems. For each regulatory problem I ran 12 replicate simulations starting from the same initial sequence. The simulation duration of 2 million generations (2000N) corresponds to a relatively long evolutionary time: between 0.25 and 0.46 substitutions per site, which is about the divergence observed between human and mouse in the vicinity of transcription start sites (Taylor et al. 2006). The population mutation rate, θ, corresponds to a plausible value for humans. Although regulatory modules are often on the order of 1 kb, numerous developmental regulatory modules in mouse and Drosophila are as small as 100 bp (Kirchhamer et al. 1996). I chose to model 100-bp enhancers as these are large enough to allow an investigation of the dynamics of turnover and are easily visualized and efficiently simulated (simulations of 500-bp enhancers yield similar results; not shown). I chose not to model recombination given the short enhancers, and consequently the entire sequence shares the same, single evolutionary history. I sample the most common haplotype at the end of the simulation and consider the succession of haplotypes leading from the initial haplotype to this final one. Although much of what I report involves simulations without insertions or deletions (indels), I also investigated regulatory evolution with indels, as these may be important mechanisms by which regulatory regions evolve (Rockman and Wray 2002; Lusk and Eisen 2010). All of the behaviors that I report here are also seen when including indels (see File S1 and Figure S23, Figure S24, Figure S25, Figure S26, Figure S27, Figure S28, Figure S29, Figure S30, and Figure S31).

I ensure that the population starts at the global fitness optimum by setting the optimum to the expression produced by the initial haplotype. In my simulations, populations invariably stay very close to this global optimum, and thus adaptation is not seen other than mutations compensating for weakly deleterious substitutions (the lowest absolute fitness among all runs was 0.990 with a mean of 0.999 across runs; given the optimum is at 1, the maximum selection coefficient was thus Ns = +10). By choosing to model a population near the global fitness optimum, I consider the effects of stabilizing selection alone, without confounding these with those of adaptive processes.

Selective constraint on individual sites varies greatly over time:

To consider how selective constraint within an enhancer varies over time, I compute selection coefficients of each mutation that can occur at each site in the observed enhancer sequences. More specifically, for each haplotype ancestral to the most common one at the end of a simulation, I compute the selection coefficient for each of the 3L mutation opportunities (i.e., opportunities to mutate to one of the alternative 3 bases in a sequence of length L). Nearly all of these potential point mutations occur during the simulations—many occurring multiple times—although only a tiny fraction reach any appreciable frequency in the population. Computing these 3L selection coefficients provides a snapshot of the constraint facing a haplotype at a given time and is informative about feasible substitutions. I then consider two summaries: the maximum selection coefficient at each site among the three alternative nucleotides (s_max) and the average (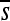, also at each site). The former is suitable for considering whether any of the substitutions are feasible whereas the latter better summarizes the overall constraint on the site.

Perhaps the most striking finding is the large extent to which the selection coefficients associated with mutation opportunities fluctuate over time (Figure 2; Figure S13, Figure S14, Figure S15, Figure S16, Figure S17, Figure S18, Figure S19, Figure S20, Figure S21, and Figure S22 show the corresponding plots for other enhancers/replicates). Large vertical stretches of dark colors in Figure 2 show regions of enhancer sequence in which deleterious mutations are possible, such that 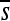is low. Patches of light gray are sites where, on average, point mutations are neutral. One can see from this plot that, although there are regions in which mutations are consistently (on average) deleterious, 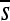differs between successive haplotypes at a substantial number of sites.

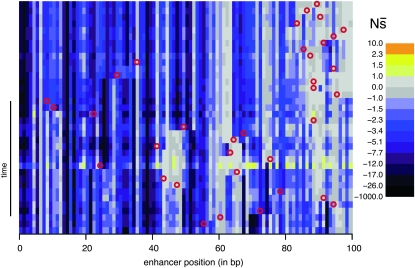
Figure 2.—

Evolution of constraint. Rows correspond to the haplotypes formed by each successive substitution during the 2000N generation evolutionary history. The initial haplotype is at the top and the final one, which is the most frequent haplotype at the end of the simulation, is at the bottom. For each haplotype, the positions (along the horizontal axis) are colored according to 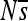: the mean population selection coefficient of point mutations at that site (were they to occur), averaged over the three possible alternative bases. 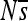is on a nonlinear scale that moves away from zero in both directions logarithmically, which expands the range sensitive to genetic drift. The locations of substitutions (red circles) are indicated on the background haplotype on which they occurred (with the resulting haplotype in the next row). This simulation is without indels. Enhancer 7, replicate 3 is shown; plots for other enhancers and replicates can be found in Figure S13, Figure S14, Figure S15, Figure S16, Figure S17, Figure S18, Figure S19, Figure S20, Figure S21, and Figure S22.

Figure 3 highlights one example site (position 2 of enhancer 6, replicate 7) that switches from having a rather modest deleterious 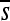to a highly deleterious one. In this particular case, a substitution at position 3 causes this dramatic change at position 2; it is followed by a second substitution at position 5 nearly 500N generations later, which largely restores at position 2. Interestingly, the two substitutions at positions 3 and 5 were approximately neutral yet they dramatically altered the selection coefficients of mutations at position 2 (see Figure S22 for a plot of 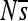over time for all sites). Such fluctuations in selection coefficients of mutations are the rule rather than the exception, as the majority of sites show substantial changes in the mean selection coefficient (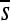) in one or more replicate simulations (small panels in Figure 3). While in this example the critical sites (2, 3, and 5) are all highly clustered, this is not always the case, with appreciable changes in selective effects at more distance sites (see Figure S2).

Figure 3.—

Change in selective pressures at single sites over time in replicate simulations of enhancer 6. Each of the 100 small plots corresponds to one position in the 100-bp enhancer. 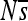(vertical axis) is shown over the 2000N generations (horizontal axis) for each of the 12 replicate simulations (different colors). Replicate 7 of position 2 (red) is also shown in the large plot (top right). See Figure S22 for a depiction similar to Figure 2 of 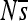for all sites for replicate 7. The range plotted is 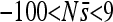, although 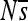is sometimes entirely below this range, resulting in plots appearing empty. Simulations are without indels.

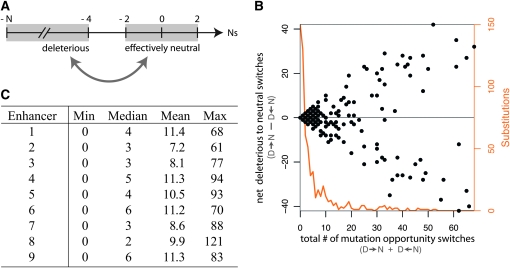
Patterns of selective constraint change when sites that were previously constrained become candidates for substitution and conversely, when previously unconstrained sites come under increased purifying selection. This process requires that the selection coefficient associated with a mutation opportunity switch between being deleterious and being effectively neutral (i.e., the fixation probability is within a fewfold of the neutral fixation probability). As detailed in Figure 4, the number of mutation opportunities whose selective effects are altered by substitutions elsewhere in the enhancer has a highly skewed distribution, with the majority of substitutions opening or closing only a few opportunities for turnover. Yet not infrequently, a sizable number of mutation opportunities switch from having deleterious to effectively neutral selection coefficients (or the reverse). Thus most substitutions are responsible for some change in constraint and a subset of substitutions causes substantial selective repatterning. This fluctuation in selection coefficients over time has important implications for how one interprets constraint. For example, on average only 55% of the sites of enhancer 7 (replicate 8) have nondeleterious mutational opportunities (Ns > −2), yet at some point or another during that simulation all sites have one or more nondeleterious opportunities—in other words, despite high overall constraint, none or few of the sites are always constrained (see Table S1).

Figure 4.—

Counts of mutations that switch from effectively neutral to deleterious (or deleterious to neutral) after a single substitution at another site. As a result of each substitution, each of the 3(L − 1) = 297 mutation opportunities at other sites may have a selection coefficient that is different from what it was on the old haplotype. Most substitutions affect a small number of mutation opportunities at other sites, while some affect a considerable number of mutation opportunities, often with a substantial overall net increase or decrease in effectively neutral mutation opportunities. (A) The number line showing the two categories of selection coefficients: deleterious (Ns < −4) and effectively neutral (|Ns| < 2). I consider switches between these two ranges, excluding −4 < Ns < −2, so that the transitions represent substantial changes in the probability of fixation (at least a 4-fold difference, but typically larger, e.g., 75% have a >15-fold difference, pooling across enhancers). (B) The effects of substitutions observed in simulations of enhancer 1. Each dot corresponds to a substitution, with its position given by the number of mutation opportunities that switch categories in either direction (horizontal axis) and the net number of mutation opportunities that switch from deleterious to neutral (subtracting out neutral to deleterious switches; left vertical axis). Points scatter away from the horizontal line (at zero) when there are more mutation opportunities switching one way than the other (i.e., points above the line indicate a net increase in neutral mutation opportunities). The orange line shows the counts (right vertical axis) of substitutions with the given number of mutation opportunities that switch. The 12 replicate simulations of enhancer 1 are pooled to produce this. (C) Summaries of the distributions of mutation opportunities that switch categories for each enhancer (replicates pooled).

Functional turnover is in a large part due to shifting constraint:

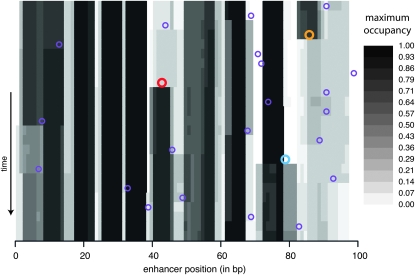
To consider the implications of changing constraint for the evolution of function, I use maximum occupancy as a measure of the functional importance of a nucleotide. The occupancy of a nucleotide by a TF is the expected fraction of time during which the TF binds, overlapping the nucleotide, in a given trans-background; maximum occupancy of a nucleotide is the maximum occupancy over TFs and trans-backgrounds. Figure 5 shows how maximum occupancy evolves during one simulation. The vertical banding illustrates functional conservation of TF binding. Although most bands remain intact, there are cases where the binding site is essentially knocked out (yellow circle in Figure 5), newly created (red circle), split into two (blue circle), or shifted (see Figure S13, Figure S14, Figure S15, Figure S16, Figure S17, Figure S18, Figure S19, Figure S20, Figure S21, and Figure S22 for other enhancers/replicates). Although many sites show similar binding between the beginning and the end of the simulations, there is a subset that experiences radical changes in occupancy levels; for example, among the 12 replicate simulations of enhancer 3, 6% of sites see either an increase or a decrease in maximum occupancy of >0.5 between the beginning and the end of the simulation (see Figure S3). How, then, do these changes in occupancy occur?

Figure 5.—

Evolution of TF binding over time. Rows correspond to the haplotypes formed by each successive substitution in the 2000 N-generation evolutionary history. The initial haplotype is at the top and the final one is at the bottom. For each haplotype, the positions (along the horizontal axis) are shaded according to maximum occupancy (i.e., the largest fraction of time bound by any TF among the various trans-backgrounds). The locations of substitutions (purple circles) are indicated on the background haplotype on which they occurred. Larger colored circles are cases where a binding site disappears (red, left), arises (orange, right), or splits into two overlapping sites (blue, center). This simulation is without indels. Enhancer 6, replicate 6 is shown; for more examples see Figure S13, Figure S14, Figure S15, Figure S16, Figure S17, Figure S18, Figure S19, Figure S20, Figure S21, and Figure S22.

The substitutions that most dramatically alter the TF occupancy profile of the enhancer (i.e., contribute most to functional repatterning) are often mutations that would have been deleterious had they occurred on an earlier allelic background (see Figure 6 and Figure S11). In contrast, substitutions that do not substantially repattern TF binding are much less often deleterious on earlier allelic backgrounds. In other words, many of the function-repatterning substitutions were able to substitute only because the pattern of constraint shifted. This result exemplifies the extensive context dependence [sometimes referred to as physiological or functional epistasis (Brodie 2000)] of this enhancer and suggests that such context dependence is of particular importance to mutations that lead to functional repatterning. More generally, a substantial fraction of substitutions occur at sites that at one point in time could have mutated only to deleterious alleles (Ns_max < –4). For example, using the final haplotype as a proxy for present-day constraint, a sizable subset of substitutions occurred at sites that are presently constrained (see Figure S4). Thus, observing a substitution at a site does not necessarily imply that the site is currently unconstrained. Conversely, a site that is presently constrained will not necessarily remain constrained.

Fixation by drift of nearly neutral mutations underlies variability among evolutionary realizations:

To gain insight into the variability among evolutionary realizations, I consider the change in constraint over time for 12 replicate simulations of each enhancer. I measure change in constraint by the correlation between the mean selection coefficients, 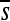, of the initial haplotype and those of each subsequent haplotype. Strikingly, distinct realizations of the same evolutionary process often result in dramatically different amounts of turnover in the pattern of constraint (Figure 7). Like the evolution of constraint, the evolution of functional organization (i.e., TF occupancy) exhibits variation in the extent of departure from the original functional organization (Figure S5).

Figure 7.—

Change in the organization of selective constraint over time. Each row of plots corresponds to a distinct regulatory problem with 12 replicates arranged horizontally (shown in alternating shades of gray). For each simulation, only the haplotypes ancestral to the most common haplotype at 2000N generations are considered. For each haplotype, the pattern of constraint is summarized by 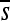at each site (so that a given haplotype is represented by a vector of length 100 bp). The Pearson correlation between the 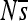vectors for the initial haplotype and the haplotype x substitutions later is shown as a single bar; the vertical axis is [0, 1]. Correlations for each successive haplotype relative to the first are arrayed in sequence along the horizontal axis. Thus the width of each small plot is the number of substitutions on that lineage in 2000N generations.

While variation among regulatory problems may be due to the distinct regulatory problem solved by each enhancer, variation within replicates of the same enhancer reflects the chance fixation of repatterning mutations by genetic drift. The probability of a mutation fixing by genetic drift is a well-known function of the selection coefficient (Ewens 2004), with mutations quickly becoming unlikely to fix as Ns becomes increasingly negative (e.g., for Ns = −10, the probability of fixation is 1/2200 that of a neutral mutation). One explanation for variation among replicate simulations is that repatterning is largely the result of the chance fixation of large-effect, deleterious mutations, which occur rarely, and hence inconsistently across replicate simulations. While there is clearly a relationship between the selection coefficient of a substitution and how much that substitution repatterns constraint or binding, the relationship is weak. There are very few deleterious substitutions, and many effectively neutral substitutions have large repatterning effects (Figure S6 and Figure S7). So although clearly an important factor, the chance fixation of large-effect, deleterious mutations may be insufficient to explain the full extent of the variation among replicates.

Another process that appears to underlie the variation among replicate simulations is that some substitutions can open opportunities for repatterning, leading to more repatterning in some replicates than in others. Supporting this hypothesis is the observation that a large fraction of substitutions alter the amount of repatterning of TF binding that is likely to subsequently occur (e.g., after such a substitution occurs, the pattern of TF binding evolves more, on average, over the next 500N generations than if the substitution had not occurred). Interestingly, even effectively neutral mutations are capable of altering the amount of patterning expected (Figure S8).

Chance may thus play an important role (e.g., Lenormand et al. 2009) in shaping regulatory evolution in two ways: directly, through the occasional fixation of large-effect repatterning mutations by genetic drift, and indirectly, because drift may fix mutations that do not themselves cause much functional repatterning, but that open opportunities for repatterning. For both the direct and the indirect effects of drift, nearly neutral mutations play an important role. In light of how much the turnover in function and constraint varies among evolutionary realizations, the divergence among orthologous regulatory sequences—which might be thought of as distinct realizations of the evolutionary process—may therefore not be due solely to changes in the underlying regulatory problem, but also to the stochastic nature of drift and how substitutions alter the opportunities for future repatterning.

DISCUSSION

As models of regulatory function become more predictive (Jaeger et al. 2004; Segal et al. 2008; Fakhouri et al. 2010), it is plausible that they also better reflect the underlying biology. It is then worth asking whether such models offer insight into the evolution of regulatory DNA. To my knowledge, the present simulation study is the first of its kind to combine a model of regulatory function shown to have substantial predictive value in a real biological setting (Segal et al. 2008) with a model of fitness to gain insight into the evolution of regulatory DNA.

Although I model only toy enhancers, the behaviors of the simulations are hopefully informative because the small number of assumptions was chosen to reflect important aspects of regulatory function. Most notably, these simulations suggest that even under a regime consisting solely of stabilizing selection on the expression phenotype, substantial functional reorganization is possible. Both the evolution of functional organization and that of selective constraint show extensive context dependence and involve a large fraction of sites and substitutions. Pervasive context dependence means that when a mutation arises at a particular site, it may have a different selection coefficient from previous mutations to the same base at that site. This fluctuation in the selection coefficients of mutation opportunities is a primary avenue for functional turnover. Thus, rather than seeming puzzling, the observations that functional sequence does not always appear conserved and conserved sequence may not be functional should be expected from simple assumptions. Together, these findings have important implications both for the use of phylogenetic comparisons to infer function (or lack thereof) and for population genetic analyses, notably the inference of selection coefficients.

Challenges posed by markedly changing selection coefficients:

Much of our intuition for thinking about selection on DNA stems from work modeling mutations in protein-coding genes. The redundant nature of the genetic code and the high ratio of synonymous to nonsynonymous substitutions led Kimura to make the simplifying assumption that mutations fall into two categories, those that are neutral and those that are “definitely deleterious” (Kimura 1977), and that, because of the genetic code, the category to which a site belongs is easily determined. This basic premise [even if approximate (Kreitman 1996)] has been hugely important for estimating neutral rates of evolution (Bromham and Penny 2003), understanding the histories of duplicate genes and gene families (Gu et al. 2002), measuring constraint (Eyre-Walker and Keightley 1999), and detecting adaptively evolving proteins using either McDonald–Kreitman-style tests (McDonald and Kreitman 1991) or PAML-style tests (Yang and Bielawski 2000). This assumption is also employed in the widely used Poisson random field methods for estimating selection coefficients (Sawyer and Hartl 1992; Bustamante et al. 2005).

Implicit in this categorization is that mutations at a site are considered independent of the background on which they arise. While originally developed for protein-coding genes, these methods have been used to detect positive selection in noncoding regions (Torgerson et al. 2009) and similar assumptions have been employed to estimate the constraint in intergenic regions (e.g., Shabalina et al. 2001) and estimate the distribution of selective effects in noncoding regions (Kryukov et al. 2005). Studies interested in constraint on TF binding sites make this type of assumption in using the position-specific substitution rates in TF binding motifs as a proxy for constraint (Moses et al. 2003; Kim et al. 2009).

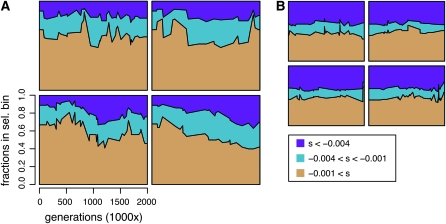
As shown here, however, the regulatory code has a more complex architecture (Wray et al. 2003), with marked context dependence. Selection coefficients associated with mutation opportunities change dramatically over time as substitutions occur in the background, and thus one cannot safely assume the selection coefficient is a fixed property of the site. In fact, the overall fraction of constrained sites across the whole enhancer changes substantially over time, as do the fractions of weakly constrained and neutral sites (Figure 8). For example, the fraction of the sequence that experiences only neutral mutations shifts from ∼70% to <40% (seven of the nine regulatory problems show changes in constraint at least this large in one or more replicates, for a total of 30 replicates of 108). Thus, even the distribution of s across sites changes over time, suggesting that it may not be appropriate to think of assigning s from a fixed distribution, let alone ascribing a fixed value to an entire class of sites.

Figure 8.—

The distribution of selective effects over time. Each plot shows the proportion (over time) of the enhancer sequence in each of three selective classes: neutral (tan), weak purifying selection (blue), and strong purifying selection (purple). The selective bin into which a site is placed is determined by the maximum selection coefficient, s_max, among the three possible point mutations at that site, relative to the observed base. The vertical axis indicates the cumulative fraction of sites in the three bins. The bins are chosen to reflect three categories of sites (neutral, weakly deleterious, and deleterious), which have markedly different fixation probabilities. Time is indicated on the horizontal axis in units of 1000 generations (for a total of 2 million generations). Four replicates are shown for each of two regulatory problems: enhancer 2 (A) and enhancer 6 (B). Binning by s_max rather than 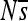ensures that sites are considered strongly constrained only when indeed all substitutions are highly unlikely.

Phylogenetic interpretations:

Replicate simulations can be interpreted as independent evolutionary trajectories from the same ancestral sequence and are thus equivalent to an idealized star phylogeny. During the evolution of this phylogeny, stabilizing selection for a particular optimum expression pattern is unchanging. Yet different replicates exhibit markedly different amounts of turnover in functional organization and selective constraint. In a phylogenetic context, one may be tempted to infer that the selective pressures themselves have changed, and yet these simulations show this need not be a valid conclusion. Instead, the varying levels of turnover reflect the high degree of historical contingency apparent in this model, combined with the stochastic nature of genetic drift.

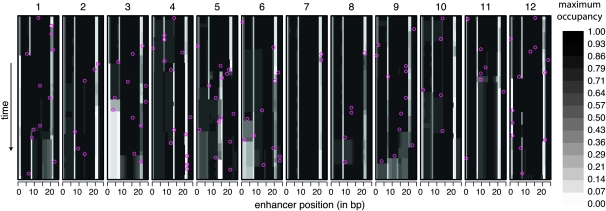
This variability among replicate simulations is also important for interpreting particular functional changes. As an illustration, Figure 9 shows maximum occupancy over time for the 12 replicate simulations of the left quarter of enhancer 4. This part of enhancer 4 has high maximum occupancy, and yet several of the replicate simulations show substantial decreases in maximum occupancy. Thus, were one to observe an evolutionary realization after which nucleotides 3–8 still showed strong binding at the end, one might be inclined to assume this site is highly conserved and necessary for proper expression; alternatively, observing replicate 3 or 6 might suggest binding was dispensable. A more nuanced perspective is that few binding sites are completely necessary or completely dispensable and that the evolutionary outcome is simply one realization among many possible ones. Thus, differences in the rate of turnover are not necessarily indicative of changes in selective pressures or function, but may result simply from which particular mutations fix by drift: not only those that directly repattern function, but also those that open up new opportunities to repattern function.

Figure 9.—

The evolution of TF binding varies markedly over replicate evolutionary realizations. Each of the 12 plots corresponds to a replicate simulation of enhancer 4, showing TF binding (maximum occupancy) for the leftmost 25 nucleotides of each haplotype (rows) on the lineage leading to the most common haplotype at 2000N generations (bottom). For a complete description of this style of plot, see Figure 5. Pink circles show the locations of substitutions. These simulations were run without indels.

Limitations to the model of regulatory function:

The informativeness of this approach hinges on the validity of the model; although the Segal model showed an impressive fit to data in one context (Segal et al. 2008), it is unclear how well it captures the evolutionary processes that I investigate here, after incorporating my model of fitness effects of misexpressison. Also, there are a number of important departures of my model from known regulatory biology. First, I am not modeling nucleosome binding or other aspects of chromatin organization, such as methylation or histone modifications. These features of regulatory biology are known to affect gene regulation (Li et al. 2007) and are important to regulatory evolution (Field et al. 2009).

Nucleosomes, for example, compete with transcription factors for DNA (Workman and Kingston 1992) and have been suggested to also induce synergistic TF–TF binding (Mirny 2009; Wasson and Hartemink 2009), compartmentalize enhancers (Raveh-Sadka et al. 2009), and affect the variability of gene expression (Tirosh and Barkai 2008). Although nucleosome binding is comparatively well understood and can be accurately modeled (Kaplan et al. 2009) and integrated into models such as the one I am using (Raveh-Sadka et al. 2009), I chose to forgo this layer of complexity in favor of focusing on a smaller set of features of transcription, which suffices to address a preliminary set of questions about turnover.

Second, the regulatory problems that I investigate do not necessarily correspond to those faced by real enhancers. Instead I rely on the observation that the behaviors I characterize are general, depending little on the number of TFs or regulatory contexts modeled (not shown), the entropy of the TF binding functions (Figure S9 and Figure S12), and the TF–TF interaction parameterizations (not shown). Additionally, the qualitative patterns are apparent for a broad spectrum of strengths of stabilizing selection on the expression phenotype (Figure S10 and Figure S11).

Third, I do not model recombination within the enhancer. This is probably a reasonable approximation for small enhancers, like those I investigate. Given this short enhancer size (100 bp) and the relatively small population mutation rate (θ = 0.001), the majority of substitutions are sequential (i.e., the mutations did not cosegregate), suggesting the results would not differ substantially in the presence of recombination. For larger enhancers or particularly high rates (like in Drosophila), intraenhancer recombination may have important effects on enhancer evolution, and thus this remains an important topic for future work.

On the whole, the observations resulting from this model of regulatory evolution appear to be quite robust and should help better guide the interpretation of comparative genomic approaches as well as the design of methods to infer selection on regulatory DNA.

The relevance of nearly neutral mutations:

A nice feature of this modeling approach is that it offers insight into aspects of the evolutionary process for which there is not much information in available or readily obtainable data. For example, measurements of selection coefficients can at best detect effects of size |s| > 0.01 in yeast (DeLuna et al. 2008). Yet it may be that many of the important dynamics of regulatory evolution under stabilizing selection involve mutations of small functional effects and even smaller fitness effects. By using a computational model, quantities such as selection coefficients and the amount of binding at each position in the enhancer are directly computable and can be related to the few assumptions underlying the model.

Indeed, this model of regulatory evolution reveals the role that neutral mutations play in remodeling function and constraint. The label of “neutral” ascribed to a mutation is simply a statement about the fitnesses of individuals carrying the allele relative to those that do not. If one assumes mutations have substantial functional consequences only when they also have substantial fitness consequences, then turnover may be possible only if combinations of weakly deleterious mutations and compensatory mutations substitute jointly (Kimura 1985). Such a process is highly dependent on the effective population size—and for parameters relevant to humans, may not be common (Durrett and Schmidt 2008). Yet one need not presume that a mutation that is neutral with respect to fitness is neutral with respect to function. As shown here, effectively (or nearly) neutral mutations can not only alter the functional organization of the enhancer directly; they can also shift the pattern of selective constraint at other sites, opening up opportunities for subsequent functional change. Importantly, this process is prevalent at even modest population sizes and levels of diversity.