Biophysical mechanisms underlying olfactory receptor neuron dynamics

Abstract

Odor responses of olfactory receptor neurons (ORNs) exhibit complex dynamics. Using genetics and pharmacology, we show that these dynamics in Drosophila ORNs can be separated into sequential steps, corresponding to transduction and spike generation. Each of these steps contributes distinct dynamics. Transduction dynamics can be largely explained by a simple kinetic model of ligand-receptor interactions, together with an adaptive feedback mechanism that slows transduction onset. Spiking dynamics are well-described by a differentiating linear filter that is stereotyped across odors and cells. Genetic knock-down of sodium channels reshapes this filter, implying that it arises from the regulated balance of intrinsic conductances in ORNs. Complex responses can be understood as a consequence of how the stereotyped spike filter interacts with odor- and receptor-specific transduction dynamics. However, in the presence of rapidly fluctuating natural stimuli, spiking simply increases the speed and sensitivity of encoding.

INTRODUCTION

The fluctuations created by a turbulent odor plume can carry useful information about the chemical environment, and there is evidence that insects use this information to help locate odor sources^1,2. Yet olfactory systems appear to be poorly suited to encoding fluctuations, because even simple odor pulses generally elicit prolonged temporal patterns of activity in olfactory receptor neurons (ORNs). These patterns include epochs of excitation and inhibition, and vary with ORN type, odor identity, and odor concentration^3-6, often somewhat unpredictably. A key question in olfactory coding is thus how these first-order neurons transform and encode the dynamics of fluctuating stimuli.

Many mechanisms have been proposed to shape the dynamics of ORN responses. These include second-messenger pathways^7,8, neuromodulators⁹, or buffering by odorant binding proteins^10,11. However, recent discoveries suggest that olfactory transduction in insects may be simpler than previously thought. First, swapping odorant receptors between Drosophila ORNs produces a swap in their odor-evoked temporal patterns¹¹. This implies that the differences between these temporal patterns are a property of the receptor itself. Second, there is evidence that Drosophila odorant receptors do not couple to G-proteins, and instead function as ligand-gated ion channels^12-14. This argues against a major role for second-messenger pathways in shaping ORN response dynamics, although the issue remains controversial¹⁵. Third, recent findings suggest that odor-evoked inhibition in Drosophila ORNs represents inverse agonism, meaning the odor stabilizes an inactive state of the receptor¹¹. This explains why the same odor can be either excitatory or inhibitory depending on the receptor⁶, and why swapping receptors can produce a swap in the polarity of an ORN’s response to an odor¹¹.

In light of these discoveries, we set out to understand the origins of dynamical spike patterns in Drosophila ORNs, and how these dynamics affect responses to rapid odor fluctuations. We found that these dynamics can be understood in terms of two elementary biophysical processes acting in sequence: transduction and spike generation. Both shape the dynamics of neural activity, and the interaction between the two can give rise to complex patterns. However, in the presence of rapidly-fluctuating odor plumes, ORN responses are surprisingly simple: transduction acts as an odor- and receptor-specific low-pass filter, while spike generation accentuates high-frequency fluctuations that were diminished during transduction.

RESULTS

ORN spiking dynamics are odor- and receptor-dependent

Previous studies have shown that odor-evoked spike trains in Drosophila ORNs have odor- and receptor-specific dynamics^4,6,16. Two odors can drive similar mean levels of firing in an ORN, but with distinct time courses. In an example shown here, one odor produces a transient peak at onset and inhibition at offset, while another produces only a modest peak at onset and no offset inhibition (Fig. 1a,b). A single odor can also produce distinct temporal patterns in different neurons: for example, a tonic response in one neuron (Fig. 1b) but a phasic response in another (Fig. 1c).

Figure 1. Temporal patterns of ORN spiking are cell- and odor-dependent.

Rasters and peristimulus-time histograms (PSTHs, mean ± s.d.) show ORN spiking responses to an odor pulse (1.7 s duration, odors diluted in paraffin oil as labeled). The time course of the odor pulse (top) is not square because it is slightly smoothed by our odor delivery device (see Supplementary Fig. 1). (a) An example of a response with a strong onset transient and offset inhibition. (b) In the same ORN type, a different stimulus drives a similar steady-state firing rate, but the onset transient is weaker and there is no offset inhibition. (c) This same stimulus drives a strong onset transient and offset inhibition in a different ORN type. (d) A more complex response, with an onset transient, then offset inhibition, then more excitation. (e) An example of inhibition followed by excitation. Each trace represents the mean of 5-6 sensillum recordings, each in a different fly.

We also observed more complex responses. For example, responses can exhibit a transient peak at odor onset, followed by inhibition at odor offset, followed by another period of elevated spiking (Fig. 1d). Other odor-receptor combinations produce inhibition during the odor pulse, followed by elevated firing after odor offset (Fig. 1e). In this study, we set out to understand the origins of these dynamics and their implications for encoding fluctuating stimuli.

Measuring transduction and spiking in single ORNs

We hypothesized that some aspects of these dynamics reflect transduction events, while others reflect events that link transduction to spiking. We therefore set out to obtain independent measures of transduction and spiking in single ORNs. Transduction occurs in the dendrites of ORNs, where olfactory receptor (OR) proteins are localized^13,17, with one OR type per cell. ORN dendrites are packaged into finger-like sensilla on the antenna and the maxillary palp. In this study, we focused on the palp, which contains only six ORN types, arranged as stereotyped pairs in three types of sensilla^4,18 (Fig. 2a). Spikes arising from the two ORNs in a sensillum can be sorted based on their size⁴, or by genetically ablating one type of ORN (see Methods).

Figure 2. Field potentials and spikes can be isolated from single ORNs.

(a) Three sensillum types in the maxillary palp (de Bruyne et al., 1999; Goldman and Carlson, 2005). (b) A typical extracellular recording from a pb1 sensillum (stimulus is 2-butanone 0.1×). Enlarged segment at the peak of the response shows individual spikes (inset); taking the first derivative (inset lower trace) facilitates spike detection. (c) TTX (50 μM) injected into the palp abolishes spikes, leaving the LFP largely unaffected. We fit exponentials to the rising and falling phases of the LFP, and we also computed the overshoot after odor offset; none of these parameters changed significantly (data not shown). (d) In Or42a^–/– flies, this sensillum type no longer responds to this stimulus, although some spontaneous spikes persist. (e) Mean pb1 LFP responses to selected stimuli are largely unaffected by TTX but are abolished by mutating Or42a. This mutation does not affect responses to these stimuli in a different sensillum type (pb3, Supplementary Fig. 2). (f) In another sensillum type (pb2), responses to fenchone (0.25×) and cyclohexanone (1×) are abolished by ablating the A neuron in a genetic background where B is already ablated. In a background where A is ablated, 1-octen-1-ol (1×) elicits an inhibitory (upward) LFP which is abolished by killing the B neuron. (The small remaining downward response reflects activity in other sensilla.) (g) In pb3 sensilla, LFP responses to isoamyl acetate (1×) are abolished by a mutation in Or85d. Here, the A neuron has been ablated genetically. Data in (e-g) represent mean ± s.d., n = 4-7 recordings each.

In extracellular recordings from single palp sensilla, odors evoke both a change in spike rate and a deflection in the local field potential (LFP, Fig. 2b). The time course of the LFP reflects the time course of the local transmembrane current¹⁹ (see Methods) and a downward deflection in the LFP indicates a depolarization of local dendrites²⁰. The sensillar LFP is thought to arise mainly from transduction currents²¹. To confirm this, we verified that spikes do not affect LFP dynamics. Injecting a Na⁺ channel antagonist (TTX, 50 μM) into the palp abolished spiking, but had no effect on LFP time course (Fig. 2c,e). Control injections of saline had no effect. These data are consistent with the idea that the LFP is a proxy for transduction currents, although we cannot exclude a contribution from conductances downstream of transduction but upstream of spiking.

Next, we asked whether under certain conditions, the LFP response can be attributed to a single ORN. First, we chose concentrations of specific odors that drive robust responses in a particular ORN type (pb1A). The pb1A ORN normally expresses the receptor gene Or42a. We found that a mutation in Or42a eliminated most pb1 responses to these odors (Fig. 2d,e), indicating that they are due to this single receptor type. Some of these odors also drove responses in a second sensillum type (pb3) which were unaffected by mutating Or42a (Supplementary Fig. 2). This result indicates that palp sensilla can be electrically isolated from one another, because responses arising from pb3 sensilla are either absent or strongly attenuated in intermingled pb1 sensilla.

Under other conditions, we observed that LFP responses can propagate between nearby sensilla. In particular, LFP responses in antennal sensilla were not well-isolated (data not shown), probably because they are packed more densely than palp sensilla. For this study, we recorded only from palp sensilla, and we used genetic ablation of one ORN in a sensillum, or careful choice of odors, to insure that the LFPs we recorded arose from single ORNs. In each case, we confirmed that the LFP response was largely abolished when the cognate OR was mutated and/or the cognate ORN was killed genetically (Fig. 2f,g).

Dynamics of transduction and spike generation

The LFP and spike rate have distinct dynamics (Fig. 3a). The LFP time course is similar to the time course of the odor. By contrast, the spike rate is highest when the LFP response is growing and lowest when the LFP is recovering. This implies that the spike rate is sensitive to the slope of the LFP.

Figure 3. Filter models describe transformations between stimulus, LFP, and spikes.

(a) Time course of odor stimulus and neural response (pb1, stimulus is 2-butanone 0.01×). Note that spike rate is highest when the LFP is growing but suppressed when the LFP is recovering. (b) Linear filter describing the relationship between the stimulus and the LFP (pb1A, 2-butanone 0.01×, ± s.d.). Arrow indicates single filter lobe. (c) The prediction of the filter (blue) is simply an inverted and slightly smoothed version of the odor time course, as expected for a filter with a single lobe. Comparison to the recorded LFP (black, mean of 5 recordings in 5 flies) shows that the linear model is an adequate coarse description but underestimates onset rate and overestimates offset rate. (d) Actual versus predicted LFP for the stimulus segment shown in (c). Note that the model underestimates responses during onset (open arrow) and overestimates responses during offset (filled arrow). (e) Linear filter describing the relationship between LFP and spike rate. Arrows indicate two filter lobes. The biphasic filter means the spike rate increases when the LFP is growing more negative, and is inhibited when the LFP is recovering. Because the negative lobe is larger than the positive lobe, the spike rate remains elevated above baseline during a maintained negative LFP deflection. (f) The prediction of the filter (magenta) agrees well with the data (black). (g) Actual versus predicted spike rate.

To describe these relationships quantitatively, we calculated the linear filters that best summarizes each transformation. To calculate the linear filter relating the odor to the LFP, we presented a fluctuating odor waveform while recording the LFP, then cross-correlated the odor waveform with the LFP waveform, and finally corrected for correlations in the odor waveform. Similarly, we also calculated the linear filter that relates the LFP to the spike rate. We did this by cross-correlating the LFP with the spike rate, and then correcting for correlations in the LFP.

We found that the filter describing the transformation from odor to LFP had a single lobe (Fig. 3b), indicating that the LFP tends to smooth odor fluctuations. The lobe is negative because odor increases elicit downward deflections in the LFP. The width of this lobe (105 ms half-width) indicates that the LFP faithfully tracks odor fluctuations up to ~6Hz (20 dB attenuation). The interval between the lobe and zero indicates the absolute latency of the response, which is less than 10 ms.

To test the filter model, we used it to predict the response to a novel odor waveform (Fig. 3c). The prediction was made by convolving the filter with the odor time course. It accurately captured the coarse features of the LFP response (correlation coefficient 0.94 ± 0.006). However, plotting the predicted versus the actual LFP revealed two separate curves (Fig.3d), indicating that LFP onset and offset are asymmetric in a way that cannot be captured by a linear model. We investigate these asymmetries in a later section.

The filter relating the LFP to the spike rate was biphasic (Fig. 3e), indicating that the spike rate is sensitive to the LFP slope. The order of the lobes (positive followed by negative) indicates that spiking is promoted by downward deflections in the LFP, and inhibited by upward deflections. The slightly larger negative lobe indicates that the spike rate remains above baseline as long as a steady negative LFP deflection persists. Convolving the spike filter with the LFP produced an excellent prediction of the actual spike response (correlation coefficient 0.97 ± 0.003; Fig. 3f). The spike filter was equally good at predicting responses to fast and slow LFP events, and to short and long odor pulses (data not shown). Plotting the predicted versus actual spike rate revealed a small nonlinearity which is typical of neural responses: the curve flattens near zero because the actual spike rate cannot be negative, and saturates at high values (Fig. 3g).

We note that this filter has structure to the right of the zero time point, whereas the true filter should not, because spikes are caused by the LFP. This is an artifact of the slow time course of the LFP, which limits how narrow the calculated filter can be (see Methods). An idealized filter that is realistically narrow and has no structure to the right of zero can perform as well as the recovered filter, whereas a monophasic filter cannot (Supplementary Fig. 3). This implies that the general biphasic shape of the filter is correct, but that its width is over-estimated.

Odor- and cell-dependent transduction and spiking dynamics

We next asked how the dynamics of these two transformations—transduction and spiking—depend on the odor and the receptor. We recorded LFPs and spikes for several different ligand/receptor combinations. For each combination, we calculated filters describing transduction and spiking.

Filters describing transduction were generally monophasic (Fig. 4a), but their width and polarity depended on both the stimulus and the receptor (compare Fig. 4, rows 1-3), corresponding to differences in the speed and polarity of the LFP responses (Fig. 4b). Overall, these filters predicted the shape of the LFP well (Fig. 4b), implying that transduction can be approximately described as a low-pass filter with a stimulus- and receptor-dependent width and polarity. As in the example above, there were systematic discrepancies at odor onset and offset.

Figure 4. Odor- and cell-dependence of transduction and spiking dynamics.

(a) Linear filters describing the relationship between the stimulus and the LFP for five different stimulus/cell combinations. Note that the filter depends on both ligand and receptor. Mean ± s.d. across recordings, n = 5-6 each. Units of y-axes are mV per unit odor. (b) Mean LFP responses for these ligand/receptor combinations (black). Colored lines show the prediction of the linear model, obtained by convolving the corresponding filter in (A) with the stimulus waveform (shown at top). Mean correlation coefficient 0.93 ± 0.04. (c) Linear filters describing the relationship between the LFP and spike rate. Note that these filters have a relatively stereotyped shape, unlike the transduction filters. Units of y-axes are spikes/s per mV. (d) Mean spiking responses (black) in units of spikes/s. Colored lines show the prediction of the linear model, obtained by convolving the corresponding filter in (c) with the recorded LFP. Mean correlation coefficient 0.92 ± 0.06.

By contrast, filters describing the LFP-to-spiking transformation had a biphasic shape that was relatively similar across stimuli and receptors (Fig. 4c). The magnitude of the filter was generally smaller for larger LFP fluctuations, consistent with the idea that neurons adapt to the scale of their inputs^22-24. This filter accurately predicted many details of the spike response (Fig. 4d). For example, this filter predicts which responses show onset transients and offset inhibition (Fig. 4 first two rows). It also predicts that when the LFP decays with multiple slopes (Supplementary Fig. 4), there will be distinct phases of inhibited and elevated spiking during odor offset (Fig. 4, fourth row). Finally, it predicts elevated spiking after offset of an inhibitory odor (Fig. 4 bottom row). The success of this model implies that the transformation of transduction currents into spike rates can be described by a universal biphasic filter.

Genetic manipulation of the differentiating spike filter

What accounts for the biphasic shape of the filter relating LFP to spike rate? Hodgkin-Huxley models predict that the relationship between input current and spike rate depends on the balance of voltage-dependent Na⁺ and K⁺ conductances²⁵. When the Na⁺/K⁺ ratio is high, the spike rate reflects a running average of recent input (“integrator” behavior). When this ratio is low, the spike rate responds preferentially to the slope of the input (“differentiator” behavior). To test whether the differentiating shape of the ORN spike filter reflects a specific balance of intrinsic conductances, we asked whether we could reshape the filter by genetically manipulating Na⁺ conductances. We chose Na⁺ conductances as our target because there is only one Na⁺ channel α-subunit in the Drosophila genome (DmNa_v).

We knocked down DmNa_v in ORNs using transgenic RNA interference (RNAi). This produced a general decrease in spike rate (Fig. 5a,b) and a change in spike rate dynamics. Specifically, the spiking response became more transient (Fig. 5c,d). DmNa_v knockdown did not affect LFP dynamics, although it slightly reduced LFP magnitude (Fig. 5e).

Figure 5. Knocking down DmNa_v makes the LFP-to-spiking transformation more differentiating.

(a) Firing rates in ORNs with reduced expression of voltage-dependent Na⁺ channels (pb1A, stimulus is 2-butanone 0.1×). Thin lines are trial-averaged responses from different recordings (n = 20-22 sensilla in 10-11 flies of each genotype); thick lines indicate the mean. Mean firing rate during the odor is significantly reduced (p<0.01, t-test). (b) Spontaneous spike rate is also significantly reduced by Na⁺ channel knockdown (p<0.01, t-test). (c) Rate of decay from the peak odor-evoked firing rate was speeded by Na⁺ channel knockdown, measured here by fitting an exponential to the trace from peak to 200 ms after odor offset (p<0.01, t-test). (d) The ratio of peak to steady-state rate firing rate is significantly increased by Na⁺ channel knockdown (p<0.01, t-test). (e) Knockdown has no effect on the time course of the LFP response, although the amplitude is slightly reduced. (f) Filters describing the LFP-to-spiking transformation (mean ± s.d., n = 4). Note that knockdown produces more symmetrical positive and negative lobes, indicating a more differentiating transformation. (g) Filters describing the stimulus-to-LFP transformation were unaffected by Na⁺ channel knockdown, as expected.

The more transient spiking response suggests that the spike filter has become more differentiating. To examine this directly, we calculated LFP-to-spike filters for a small number of neurons showing a knockdown phenotype (peak to steady-state firing rate ratio = 1.7-2.3). In these ORNs, the positive and negative lobes of the spike filter were more symmetric— and thus more purely differentiating— than in controls (Fig. 5f), while the filter describing transduction was not significantly altered (Fig. 5g). Together these data suggest that the differentiating spike transformation in ORNs is specified by the regulated expression of voltage-dependent channels in these cells.

A kinetic model can explain asymmetry in transduction

We observed that linear filters approximately describe the time course of transduction. However, filter predictions consistently underestimated the speed of transduction onset and overestimated the speed of offset (Figs. 3c and 4b). This is because transduction onset was always faster than offset. A filter, having a single time scale, predicts an average of these two rates.

One model that can account for both of these phenomena is a kinetic model of ligand receptor interactions. In the simplest case, the level of transduction current is related to the number of activated receptors (OR*), described by

$$\mathrm{R}\stackrel{\mathrm{R}}{\leftrightarrow }\mathrm{OR}\leftrightarrow {\mathrm{OR}}^{\ast }$$ (1)

where O is the ligand, R is the receptor, and R* is activated receptor. This model accounts for odor-specific transduction rates because the binding and activation constants depend on the identity of both the receptor and the ligand. This model also accounts for the asymmetry we observed between onset and offset rates, because the forward reaction rate depends on the concentration of odorant available, while the reverse reaction rate depends only on the amount of bound receptor.

One prediction of this model is that onset rates should grow with concentration, while offset rates should not. To test this prediction, we recorded LFP responses to several concentrations of two odors. For both odors, we found that the onset rate grew with increasing concentration, whereas the offset rate was much less sensitive to concentration (Fig. 6a,b). These data imply that some of the nonlinear features of transduction dynamics arise from elementary properties of receptor binding and activation.

Figure 6. Dynamics of transduction and adaptation.

(a) LFP recordings from pb1A ORNs illustrate how transduction dynamics depend on odor concentration. Top is 2-butanone (dilutions of 0.1×, 0.02, 0.004, 0.0008, 0.00016, 0.000032). Bottom is isoamyl acetate (1×, 0.2, 0.04, 0.008, 0.0016). Traces are means of 5-6 recordings. Traces at right are normalized to the same maximum negative deflection. Dashed blue line shows one exponential fit to response offset; note that only the initial segment was fit and no attempt was made to fit the overshooting later portion. (b) On- and off-rates as a function of odor concentration, mean ± s.d. across recordings. Rates were calculated by fitting exponential curves to the onset and offset phases of the normalized mean LFP. (c) A typical recording showing that a long adapting pulse of 2-butanone (0.1×) reduced the amplitude and onset slope of the LFP response to a weak test odor pulse (2-butanone 0.004×, green) but not the response to a strong test odor pulse (2-butanone 0.2×, orange). (d) Mean responses to test pulse 1 (solid) and test pulse 2 (dashed) for the two test odors shown in (c), n = 6 recordings. Inset shows the onset phase of these traces normalized to the same amplitude. (e) Mean response amplitude (± s.d.) as a function of concentration for test pulse 1 (filled) and test pulse 2 (open). Arrows indicate the two concentrations shown in (c) and (d). (f) Onset slope as a function of concentration for initial (filled) and adapted (open) responses.

Adaptation slows response kinetics

Another prominent nonlinearity in some responses was a slow decrease in LFP amplitude during the odor pulse (adaptation) which was most prevalent when responses were strong (Fig. 6a,b). Adaptation was often followed by an overshoot after odor offset (Fig. 6a, see also Supplementary Fig. 4). This type of adaptation persisted in TTX (Fig. 2b,c), and so arises upstream from spiking.

To probe the mechanisms underlying adaptation, we compared the response to two short test pulses, before and after a long adapting pulse (Fig. 6c). Adaptation reduced the amplitude of the test pulse response. This effect was reduced as the test pulse concentration increased (Fig. 6c,d). Thus, adaptation produces a rightward shift in the concentration-response function (Fig. 6e). Similarly, adaptation reduced the onset rate of the test pulse (Fig. 6d,f), and this was also mitigated by high test pulse concentrations. This suggests that adaptation acts on the activation of transduction, for example by reducing the affinity of the receptor for ligand or making it more difficult to open the transduction channel (see Discussion).

Adaptation is not intrinsic to the receptor

In a simple scenario, adaptation might reflect inactivation of the odorant receptors themselves. If so, then responses mediated by two receptors in the same ORN should not cross-adapt. To test whether adaptation is intrinsic to the receptor, we ectopically expressed a second receptor (Or47a) in one palp ORN type (pb1A, which natively expresses Or42a). To drive the two receptors independently, we found two stimuli (2-butanone <0.1× and pentyl acetate <0.02×) that were specific to each receptor (see Supplementary Fig. 5).

Next, we asked whether transduction cross-adapts. We found that responses of either receptor type could be adapted by driving the other receptor for a prolonged period (Fig. 7a,b). Cross-adaptation was similar to self-adaptation, in that adapted responses were smaller and had slower onset rates. Similar to self-adaptation, we found that cross-adaptation could be overcome by using a high test pulse concentration (data not shown). These results imply the self- and cross-adaptation are due to the same phenomenon. Thus, adaptation must involve processes that are shared between receptors, either up- or downstream from the receptor.

Figure 7. Cross-adaptation between co-expressed odorant receptors.

(a) A typical recording showing that a long pulse of 2-butanone (0.1×) acting on OR42a adapts the LFP response to a test pulse of another odor (pentyl acetate, 0.02×) acting on OR47a. Group data (right) shows that both the amplitude and the onset rate of the second test pulse response are significantly reduced compared to the first test pulse response (p<0.01 , n=6 , paired t-test). (b) Same experiment, but in reverse: a long pulse of pentyl acetate (0.02×) adapts the response to a test pulse of 2-butanone (0.004×). The amplitude of the test pulse response is significantly reduced (p<0.01 , n=5, paired t-test). The onset rate is reduced but not significantly (p=0.14, paired t-test). (c) A long pulse of 1-octanol (0.1×) acting on OR47b de-adapts the response to a test pulse of 2-butanone (0.1×) acting on OR42a. Both the amplitude and the onset rate of the test pulse response are significantly increased (p<0.01 , n=9, paired t-test). (d) A long pulse of 2-butanone (0.1×) adapts the response to a test pulse of 1-octanol (0.1×). The amplitude of the test pulse response is significantly reduced (p<0.01 , n=8, paired t-test).

Adaptation is induced as a consequence of transduction

If adaptation is initiated by events upstream from ligand binding (for example, if adaptation is caused by depletion of a chaperone that delivers ligand to the receptor) then it should be triggered equally well by odors that inhibit transduction. In contrast, if adaptation is initiated downstream of transduction, then an inhibitory odor should not produce adaptation. To ask whether adaptation is initiated up- or downstream of ligand binding, we ectopically expressed a receptor that produces an inhibitory response in pb1A ORNs (OR47b). As before, we used stimuli that act specifically on the native receptor (2-butanone 0.1×) and the ectopic receptor (1-octanol 0.1×, Supplementary Fig. 5).

In these ORNs, we observed that the inhibitory response did not produce adaptation of the excitatory response. To the contrary, a prolonged inhibitory response appeared to de-adapt the cell: the response to the excitatory test pulse became larger and had a faster onset rate (Fig. 7c). This implies that adaptation does not depend on odor merely binding to the receptor. Rather, adaptation depends on transduction. In the same ORNs, we observed that the excitatory response reduced the inhibitory response (Fig. 7d). (Any effects on onset rate were unclear in this case, because the test pulse coincided with the overshoot produced by the adapting pulse.)

ORNs ectopically expressing OR47b had significantly higher rates of spontaneous activity than normal ORNs of the same type (36.4 ± 17.9 versus 12.8 ± 2.6 spikes/s s.d., p<0.01, t-test, n=6-9, see Methods), consistent with a previous report that OR47b confers high spontaneous firing rates when mis-expressed³⁰. Interestingly, ORNs with the ectopic receptor also had significantly smaller initial responses to 2-butanone (0.1×) (11.0 ± 5.2 versus 20.3 ± 2.5 mV s.d., p<0.01), consistent with the idea that a high basal level of transduction places the cell in a more adapted initial state. These results further support the idea that adaptation is induced as a result of the transduction channel opening, or something downstream. The finding that adaptation alters onset kinetics implies that adaptation targets the pathway leading up to transduction channel opening. Because the target of adaptation is upstream of where adaptation is induced, adaptation likely requires a negative feedback signal.

Responses to natural odor plumes

Our results demonstrate that ORN response dynamics arise from the interaction of two dynamical steps, transduction and spike generation. How do natural plumes engage these two distinct steps? To create plumes, we used a fan to produce an air current, and we placed a vial of odor upwind from the fly (Fig. 8a). Plumes reaching the fly were monitored using a photoionization detector. Consistent with previous reports^1,2, wind-borne odor signals were intermittent. Odor fluctuations were rapid at high windspeeds and slower at low windspeeds (Fig. 8a). When the odor source was displaced laterally, the frequency of odor encounters decreased, and when the source was moved away, encounters became less discrete (Fig. 8a). Thus, odor fluctuations provide information about odor source location. Because fluctuations are slowest at low windspeeds, adaptation is likely to be most relevant in this regime.

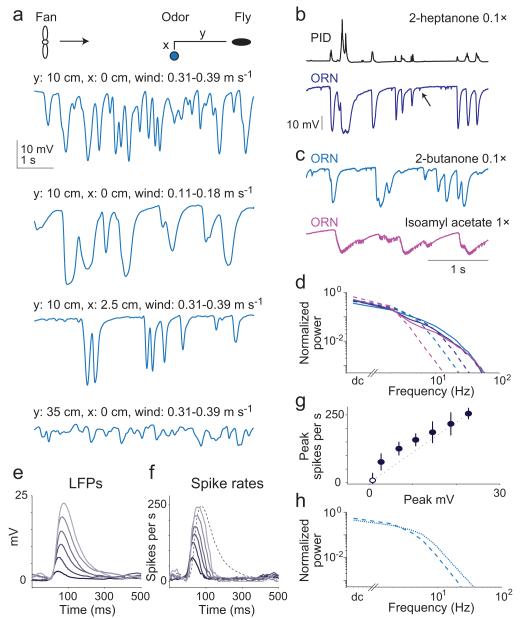
Figure 8. Encoding the dynamics of natural odor plumes.

(a) Plume dynamics depend on windspeed and odor location. Cartoon schematizes upwind distance (y) and crosswind distance (x). Traces are LFP recordings from a pb1A ORN responding to 2-butanone (0.1×). (b) Simultaneous recordings from a PID and a pb1A ORN (1.5 mm from the PID). Note spontaneous spikes (arrow); odor-evoked spikes are not visible at this scale. (c) Responses from the same sensillum in the same configuration, now with different odors. (d) Power spectra of simultaneously-measured PID signals (solid lines) and LFP responses (dashed lines). Spectra are normalized to have the same total power. ORN is pb1A, stimuli are color-coded as above (y = 5 cm, x = 0 cm). (e) LFP events sorted and averaged by amplitude (inverted here for display). The range of rise times (time from 10% to 90% of peak) was 28-32 ms. Stimulus is 2-butanone 0.1×. Same configuration as in (b,c). (f) Average spike rates corresponding to the LFP events in (e). Dashed trace represents the largest average LFP response, normalized to the same amplitude as the largest average spike rate. (g) Peak LFP amplitude versus peak spike rate for the data in (e) and (f), ± s.e.m. Open symbol is baseline (defined as the 30 ms starting 100 ms before event onset); dashed line is a linear extrapolation from this to the largest response. (h) Power spectra of LFP (dashed line) and spike rate (dotted line) for responses shown in (c). Stimulus is 2-butanone 0.1×.

Consistent with our filter calculations, transduction filtered plumes in a ligand- and receptor-dependent manner. For some ligand-receptor combinations, the LFP faithfully tracked every plume, even at high wind speeds (Fig. 8b). For other ligand-receptor combinations, LFP signals were much slower (Fig. 8c). To quantify this, we compared the power spectra of these signals. While the power spectra of plume fluctuations (as reported by the photoionization detector) were similar across ligands, LFP signals were low-pass filtered with a cutoff frequency that depended on the odor-receptor combination (Fig. 8d).

To examine how LFP dynamics depend on LFP amplitude, we identified isolated LFP events, and we binned and averaged these events by amplitude (Fig. 8e). This analysis was performed under conditions that increased the incidence of discrete odor encounters (close odor source, high windspeed). We found that the shape of these LFP events was similar for small and large amplitudes, indicating that complex transduction dynamics (like adaptation and overshoot) are not strongly engaged in these conditions. Rather, every plume hit generates an LFP response with similar dynamics.

Finally, we asked how spike generation shapes the response to natural plumes. For each LFP event, we identified the associated spike train, and computed the average spike rate associated with each average LFP amplitude. Small LFP events produced disproportionately large spike rates (Fig. 8f,g), meaning that spike generation tends to emphasize encounters with weak stimuli. The spike response consistently peaked before the LFP response (Fig. 8f), indicating that spike generation increases the speed of encoding. Accordingly, we found that the power spectrum of the spike rate contained comparatively more power at high frequencies than the power spectrum of the associated LFP (Fig. 8h). Thus, the transformation from transduction to spiking promotes rapid and sensitive encoding of natural stimuli.

DISCUSSION

Input currents and spiking as distinct dynamical processes

Many studies have described the early stages of neural encoding in terms of linear filters, sometimes followed by a static nonlinearity^22,23. Recently, these techniques have been applied to olfactory systems as well^16,24,26. The general approach of these studies is to summarize all the dynamical steps between the stimulus and spiking in a single filter.

Here we have adopted a different approach, motivated by the observation that input currents and spikes have different dynamics. After separating input currents from spiking using genetic and pharmacological tools, we characterized their dynamics independently. We found that transduction was described by an integrating filter. In contrast, spiking was described by a differentiating filter. Thus, transduction smoothes the input signal, while spike generation differentiates the transduction response, thereby emphasizing some of the high-frequency fluctuations that were diminished during transduction.

Transduction dynamics depend on the odor and receptor

Olfaction differs from vision in that the dynamics of the primary transduction event depend on the quality of the stimulus. A photoreceptor’s response depends only on the number of absorbed photons and the state of the cell, not the wavelength of those photons²⁷. In contrast, ORN responses depend on both the receptor the neuron expresses and the identity of the ligand. Explaining why this is true required us to move from a linear model to a kinetic model. Because different ligand-receptor combinations involve different rate constants, a kinetic model accounts for the odor- and receptor dependence of transduction rates. Because forward rates increase with odor concentration and reverse rates do not, a kinetic model also correctly predicts that transduction onset, but not offset, depends on odor concentration.

Like ORNs, central neurons in the insect brain also exhibit cell- and odor-dependent dynamics^26,28-30. In particular, changes in odor concentration affects the on- and offset portions of these responses in different ways³¹. The finding that qualitatively similar dynamics are observed in ORNs^4,6 suggests that these dynamics are partly inherited from the periphery³². Our results demonstrate that these dynamics arise at the level of transduction and are a necessary consequence of the most basic kinetic features of chemosensory transduction.

Slow transduction dynamics

In response to strong and prolonged stimuli, odor responses adapt and show overshoot after odor offset. Our results show that these slow dynamics originate at the level of transduction, not spiking. Our results also pinpoint where these dynamics arise.

First, we find that adaptation depends on transduction channel opening. Whereas an excitatory odor response increased adaptation, an inhibitory response decreased adaptation. Because the effect of an odor on the adaptation state of a cell depends on how the odor affects transduction, adaptation cannot be induced prior to transduction.

Second, we find that adapted responses look like unadapted responses to a lower odor concentration. . Specifically, onset rates are slowed. This result rules out a mechanism where adaptation increases the rate of transduction shut-off, because this would produce faster rather than slower kinetics³³. It also rules out a mechanism where adaptation targets an intrinsic conductance downstream of transduction, because this would not slow the rate of transduction onset. Finally, adaptation is unlikely to be due to a change in the driving force for transduction currents, because adaptation outlasts the LFP response to the adapting pulse by several seconds. Adaptation is most likely to involve a decrease in ligand binding affinity, and/or a decrease in the efficacy of channel gating, both of which slow onset kinetics.

Third, adaptation likely involves a diffusible factor. Adaptation is induced as a consequence of transduction channel opening, but targets the activation of transduction, implying a negative feedback signal. What might this signal be? Previous studies reported that mutations in either IP₃ receptors or the TRP channel can reduce adaptation in Drosophila ORNs^7,34, suggesting a role for cytoplasmic calcium. Furthermore, odors induce calcium influx in heterologous cells expressing Drosophila odorant receptors¹². Resting calcium in these cells is decreased by an extracellular chelator, consistent with our conclusion that transduction and adaptation can occur spontaneously. Thus, calcium is a good candidate for a diffusible adaptation factor.

The transduction channel in Drosophila ORNs probably contains the Or83b gene product, because a mutation in the putative pore domain of this gene changes the ionic selectivity of the channel¹⁵. Odorant receptors are thought to form heteromeric complexes with OR83b^12,13,35. Alternatively, odorant receptors may gate OR83b through a direct but transient association¹⁵. Our results are broadly consistent with either alternative.

If the receptor forms a stable heteromer with OR83b (Supplementary Figure 6, Model 1), then adaptation likely involves changes in both affinity and efficacy. Decreasing affinity is necessary to explain the rightward shift in the concentration-response function (Fig. 6e), while decreasing efficacy is necessary to explain the overshoot after odor offset (Figure 6a). Alternatively, if the activated receptor gates OR83b through an additional step (Supplementary Figure 6, Model 2), both overshoot and the rightward shift can be explained by a decrease in the efficacy of channel gating. In this model, overshoot arises because both spontaneously-active receptors (R*) and odor-activated receptors (OR*) have a diminished ability to open the channel. A rightward shift in the concentration-response function occurs so long as the pool of activated receptors can fully activate most of the available transduction channels at high odor concentrations (see Supplementary Figure 6).

In mammalian ORNs, adaptation is due to calcium-calmodulin acting as an allosteric inhibitor which reduces channel gating. This process reduces the apparent affinity of the transduction channel for ligand³⁶. Although olfactory transduction is fundamentally different in Drosophila versus mammals, olfactory adaptation is qualitatively similar: in both cases, adapted responses resemble responses to lower odor concentrations. Similar observations have been reported in moth ORNs³⁷.

In most sensory systems, adaptation helps extend the dynamic range of encoding by adjusting the range of neural responses to the current range of stimulus intensities. This idea is consistent with our finding that adaptation in Drosophila ORNs represents a negative feedback loop which adjusts the apparent affinity of the receptor for the odor. Because adaptation strongly reduces weak responses but weakly reduces strong responses, it should make ORNs relatively insensitive to small fluctuations in the level of background odor, without compromising the ability of ORNs to encode large fluctuations.

The shape of the differentiating spike filter

A recent study has shown that ORN spikes encode both the concentration of an odor stimulus and its rate of change²⁴. Our results indicate that sensitivity to the rate of change arises mostly at the level of spiking, rather than transduction. Moreover we found that the same differentiating spike filter described the transformation between input current and spiking in different ORN types, and when the same ORN was presented with different odors.

The shape of this filter explains many of the distinctive features of ORN responses. It can account for why some odors produce transient responses while others do not, and for why inhibitory stimuli produce excitation after odor offset (Supplementary Figure 7). Finally, it helps explain the results of receptor swap experiments. Namely, if all ORNs impose the same differentiating spiking transformation on their input currents, then receptor swap will recapitulate not only the simpler dynamics of transduction, but also the more complex dynamics of spiking.

ORN spiking dynamics fall on a continuum of behaviors observed in other neurons. Some neurons in the early auditory system behave as nearly pure differentiators³⁸, while cortical pyramidal neurons behave as nearly pure integrators³⁹. A Hodgkin-Huxley neuron can produce behaviors ranging from differentiation to integration, depending on the Na⁺/K⁺ conductance ratio²⁵. As predicted by this model, we were able to shift the spike response of ORNs from mixed differentiation-integration toward pure differentiation by reducing Na⁺ conductance genetically. This result implies that the ORN spike filter is specified by the regulated expression of voltage-dependent conductances, and does not require any additional biophysical mechanisms.

Although the shapes of the spike filters we measured were similar across odors and ORNs, we did observe that filter size was inversely related to the magnitude of fluctuations in the transduction current. This type of adaptive rescaling occurs in simulated integrate-and-fire neurons simply as consequence of the nonlinearities inherent in voltage-dependent conductances⁴⁰. This result is thus consistent with the idea that the spike filter reflects the balance of intrinsic conductances in the cell.

Transduction and spiking shape responses to odor plumes

Consistent with previous findings¹, we observed that the time course of odor encounters in a wind-borne plume provides information about the location of the odor source. Here we demonstrate that both transduction and spike generation shape the way these turbulent stimuli are encoded.

First, we found that transduction low-pass filters responses to turbulent stimuli with a different time constant for each ligand-receptor pair. ORNs thus act as a set of temporal filters which collectively analyze an odor filament on many time scales. However, unlike neurons in the auditory system, which are dedicated to encoding information about a specific frequency range, a single ORN encodes temporal information on different time scales depending on the ligand.

Second, we found that the spike transformation increases the speed and sensitivity with which odor fluctuations are encoded. A similar transformation occurs between ORN spike rates and the spike rates of their postsynaptic targets in the brain⁴¹. This suggests that one function of the ascending olfactory system may be to make neural responses as fast as possible, given the limits of transduction. A similar iterative speeding has been observed in successive layers of the retina⁴² and may be a general feature of many sensory systems.

Comparisons with olfactory dynamics in vertebrates

Our results support the idea that the diverse dynamics of olfactory transduction reflect diverse kinetic rate constants for different receptor-ligand pairs. This concept should generalize to vertebrates, even though vertebrate transduction is mediated by G-proteins. Consistent with this idea, recent imaging studies in the rodent olfactory bulb show that the time course of ORN activity is ligand-, receptor- and concentration-dependent^43,44.

However, vertebrate transduction is much slower than insect transduction. For example, in dissociated frog ORNs, the response to a brief pulse of odor (25 ms) requires about 400 ms to peak and almost 1000 ms to terminate⁴⁵. By contrast, we found that the fastest responses could peak in <30 ms and terminate in <200 ms (Fig. 8e). Our results are consistent with other measurements in Drosophila¹⁶ and moth⁴⁶. The difference in speed between vertebrate and insect transduction may reflect the slower speed of metabotropic as compared to ionotropic signaling.

It is also worth noting that the “natural temporal statistics” of odors are probably different for different organisms. In terrestrial vertebrates, olfaction is linked to respiration, which imposes a slow oscillation on olfactory signals⁴⁴. Respiration may also tend to enforce laminar flow and disperse odor filaments prior to odorant receptor binding. By contrast, insect odorant receptors encounter odor filaments more directly. It is tempting to speculate that this difference in the natural temporal statistics of odors might have driven the divergence between ionotropic and metabotropic transduction.

ONLINE METHODS

Fly Stocks and Genetic Strategies

Flies were reared at 25°C on conventional cornmeal agar medium. All experiments were performed on adult female flies 2-7 days post-eclosion. Stocks are described elsewhere as follows: Or42a^f04305 (ref ⁴⁷), Or85d^–/– (ref ⁴⁷), Or85e^–/– (ref ⁴⁷), pebbled-Gal4 (ref ⁴⁸), UAS-DTl (L.M. Stevens, http://flybase.org, personal communication to FlyBase FBrf0204962), Or33c-Gal4 (ref ¹⁸), Or46a-Gal4 (ref ¹⁸), Or59c-Gal4 (ref ⁴⁹), UAS-DmNa_v-IR (Vienna Drosophila RNAi Center, http://stockcenter.vdrc.at, stocks 6131 and 6132), Or42a-Gal4 (ref ⁴⁹), UAS-OR47a (ref ¹⁷), UAS-OR47b (ref ¹¹). We used the following genotypes to produce flies with one active neuron in a sensillum, and to verify that LFP responses from this sensillum type were due to a single type of OR:

Sensillum pb1

To record from pb1A, we primarily used a strain (w¹¹¹⁸) where the pb1B neuron is silent because this strain harbors a mutation in Or71a (Goldman et al., 2005). (Some pilot recordings were performed in the genotype NP3481-Gal4;UAS-CD8:GFP, where pb1B is functional; we found that pb1 recordings in this genotype were not different from w¹¹¹⁸, due to the fact that pb1B is narrowly selective for an odor that we did not use.) To silence pb1A, we used a mutation in Or42a (Or42a^f04305). Some pilot experiments were performed in the genotype Or42a^f04305; TM3/TM6b; here TM3 supplies a functional copy of Or71a (Goldman et al., 2005) which was useful in helping us identify the pb1 sensillum. These data were not included in the manuscript.

Sensillum pb2

To record from pb2A, we killed pb2B by expressing diphtheria toxin light chain under Gal4/UAS control (Or46a-Gal4/UAS-DTl;UAS-DTl/+). To record from pb2B, we killed pb2A (Or33c-Gal4/UAS-DTl;UAS-DTl/+). To silence both pb2 neurons, we killed them both (Or46a-Gal4/Or33c-Gal4;UAS-DTl/+), or else we killed pb2B and silenced pb2A by mutating Or85e (Or46a-Gal4/UAS-DTl;Or85e^–/–).

Sensillum pb3

To record from pb3B, we killed pb3A (Or59c-Gal4/+,UAS-DTl/+;UAS-DTl/+). To silence both pb3 neurons, we killed pb3A and silenced pb3B by mutating Or85d (Or59c-Gal4/+;UAS-DTl/+;Or85d^–/–).

The lines designated Or85d^–/– and Or85e^–/– in this study represent the same genotype, which is called Δ85 in Olsen et al., 2007. This mutation abolishes odor responses in both pb2A and pb3B, and likely represents a genetic lesion that eliminates both of these receptors.

To knock down Na⁺ channel expression in ORNs, we used flies of the following genotype: pebbled-Gal4/+;;UAS-DmNa_v-IR/+. Control flies lacked the inverted-repeat transgene (pebbled-Gal4/+;;TM3/+). The two UAS- DmNa_v-IR stocks produced similar results, and so data from both genotypes was combined.

Self-adaptation experiments in Figure 6c,d and cross-adaptation experiments in Figure 7a,b were performed in the same genotype (Or42a-Gal4/+;UAS-Or47a/+). Similar results for self-adaptation were obtained in two control genotypes (w¹¹¹⁸ and pebbled-Gal4, data not shown). Cross-adaptation experiments in Figure 7c,d were performed in the genotype UAS-Or47b/+;Or42-Gal4/+. Control experiments to verify that each cross-adaptation stimulus was specific to just one of the two odorant receptors are described in Supplementary Figure 5. The self-adaptation experiment used a higher concentration of 2-butanone than any of our other experiments (0.2×), so we also did additional control experiments to verify that this stimulus produced very little LFP deflection in Or42a mutants (genotype Or42a^f04305, mean LFP response = −0.5 5± 0.30 mV). Spontaneous firing rates in pb1A neurons mis-expressing OR47b (UAS-Or47b/+;Or42-Gal4/+) were significantly higher than spontaneous firing rates in normal pb1A neurons (Or42a-Gal4/CyO, p<0.01) or pb1A neurons mis-expressing OR47a (Or42a-Gal4/+;UAS-Or47a/+, p<0.01). The comparison of spontaneous firing rates and initial response amplitudes to 2-butanone in pb1A neurons in the text refers to a comparison between UAS-Or47b/+;Or42-Gal4/+ and Or42a-Gal4/+;UAS-OR47a/+.

Electrophysiology

The fly was cold-anesthetized and wedged into the tip of a modified plastic pipette with the body, head, and proboscis waxed into place. The fly was then fixed under an upright compound microscope with a 50× air objective (Olympus BX51). The palp was stabilized between a glass pipette and a glass coverslip. A reference electrode filled with saline was placed in the eye while a silver chloride electrode inside a saline-filled sharp glass micropipette was inserted into the sensillum lymph.

Within the sensillum lymph, the resting potential was higher than within the surrounding hemolymph²⁰, and odor-induced LFPs were larger, presumably because the path between recording and reference electrodes has higher resistance within versus outside the sensillum. Spike waveforms recorded inside the sensillum had the shape characteristic of extracellular recordings, indicating that our electrodes did not penetrate ORN dendrites. Sensillum types were identified by their characteristic responses to a panel of odors⁴ or as described in the text. Electrical signals were acquired using a Model 2400 amplifier (A-M Systems) and low-pass filtered at 2 kHz with a LPF202A signal conditioner (Warner Instruments) before digitization at 10 kHz. Where filters for multiple odors were calculated for the same neuron type, each recorded individual neuron was generally tested with all these odors.

Spikes were identified using custom routines written in MATLAB that filtered, differentiated, and thresholded the raw signal. For pb1 and ab5 recordings, the two spike types were easily identified on the basis of spike size. For the other sensilla, we recorded from flies where one neuron was killed so only a single spike type remained. LFP signals were extracted from the raw trace by low-pass filtering at 15 Hz with a digital 2-pole Butterworth filter implemented in MATLAB. Spike times and LFPs were down-sampled to 1 kHz for display and analysis. For the experiments in Figure 2 using TTX, the drug was dissolved in saline (50 μM) and injected into the body of the palp using a syringe-driven glass micropipette. After 2-3 pulses of pressure we observed the injected liquid move into the palp. Recordings were made starting 5 minutes after injection. TTX and saline injections were randomly interleaved and in most experiments the experimenter was blind to the contents of the injection. Post-hoc analysis revealed that spiking was completely abolished after all TTX injections and no saline injections.

Note that all recordings (except for ab5 and trichoid recordings shown in Supplementary Figure 5) were performed from palp sensilla. This is because sensilla are less densely-packed on the palp as compared to the antenna, which permits better isolation of LFP signals arising from single sensilla. However, we observed that the time course of ORN spiking responses was not systematically different in antennal versus palp sensilla (data not shown). Thus, our major conclusions are likely to generalize to these ORNs as well.

Odor Delivery

In Figures 1-8, odors were delivered using a custom-built device designed to allow stable and repeated presentation of long-duration odor stimuli (Supplementary Figure 1). The design of this device means that odors were delivered at an effective concentration which is substantially lower than what would be delivered using a more conventional device and the same nominal odor dilutions in solvent. A 1-mL vial was filled with 900 μL of pure odorant or odorant diluted in paraffin oil (J.T. Baker, VWR #JTS894). A continuous stream of air (100 mL/min) passed over the vial and was diluted in a second air stream (100 mL/min) before venting into a vacuum tube. In order to allow the head space of the vial to equilibrate with the air flowing over it, an odor vial was placed in the device at least 20 min before odor was first delivered to the fly, during which time the odor concentration in the air stream reached a steady state (Supplementary Figure 1). For experiments where several odors were presented briefly (test pulse odors in Figures 6-7 and control experiments to verify the privacy of these odors in Supplementary Figure 5), odor vials were placed in the device for only 5 minutes before presentation. In general, experiments using a single odor were completed before switching to a different odor. During an experiment, a three-way solenoid valve allowed us to rapidly switch the odor stream from the vacuum tube into a delivery air stream (1 L/min) directed at the fly. The air flow rates in the vacuum and delivery tubes were equalized to minimize transients during switching. In some of the LFP traces displayed in the paper, a brief electrical artifact caused by the solenoid was deleted for display purposes and the trace was mended by linear extrapolation between the cut ends; the maximum time blanked was 200 msec. Adaptation experiments (Figures 6-7) were performed using a modified olfactometer with two parallel sets of valves, mixing tubes, and odor vials. We used a photoionization detector to verify that each channel could deliver odor independently.

In Figure 8, an open vial of odor was placed 5-35 cm downwind of a small fan (Rosewill DFS802512M or Caframo Tiny Tornado 827 BL) and upwind of the fly (or PID). The windspeed at the fly was measured using a hot wire anemometer (Kanomax A004) and ranged from 0.11 to 0.39 m/s. This is within the range of windspeeds encountered by Drosophila in its native habitat, according to a study that measured a mean of 0.37 m/s and a range of ± 0.35 m/s in an orange orchard where Drosophila were active⁵⁰. In order to vary crosswind distance (x), the vial was moved perpendicular to the line connecting the fan and the fly. In order to vary upwind distance (y), the fly was moved away from the vial along this line. When the odor vial was removed, LFP events disappeared and only spontaneous spikes remained.

Data Analysis

Peristimulus-time histograms (PSTHs) were calculated by taking the mean spike train across trials, then convolving spike times with a 50-ms Hanning window. Spontaneous firing rates were calculated over the 4 s preceding stimulus presentation. In Figure 2, mean LFP amplitude was computed over a 1200-ms window beginning 300 ms after stimulus onset and ending 500 ms after offset. In Figure 5c, we fit an exponential function with a variable decay rate and variable steady-state value to each PSTH, beginning from its peak and ending 200 ms after nominal stimulus offset (i.e., valve closing). In Figure 5d, we calculated the peak-to-steady-state ratio by comparing the maximum of each PSTH to the mean firing rate over a 400-ms period beginning 800 ms after nominal stimulus onset (valve opening). In Figure 6b, on- and off-rates were computed by fitting an exponential function with a variable decay rate and latency to the normalized mean LFP. To compute on-rates, we fit a 1-s period from nominal stimulus onset to offset. To compute off-rates, we fit the remainder of the trial (10 s) beginning at nominal stimulus offset. Mean response amplitudes in Figures 6e and 7a-c were calculated over a 400 ms period starting 300 ms after nominal stimulus onset. For 7d, mean response amplitude was calculated over 1300 ms. Onset rate for Figures 6f and 7a-c were calculated by fitting an exponential function as in Figure 6b, but for the 500-ms period from nominal stimulus onset to offset. In Figure 8e, we detected discrete events in the LFP by low-pass filtering the raw voltage trace at 15 Hz, differentiating, and looking for threshold crossings in the resulting signal. Events were binned by peak amplitude in bins of 4 mV over the range from 2-26 mV. Compound events were identified by having values above 10 mV during a window 50 ms before or 300 ms after initiation, and were eliminated from the analysis. In Figure 8g, peak spike rate was computed over 30 ms preceding the LFP peak.

Filter Analysis

To estimate linear filters, we delivered odor with a slowly-varying random time course. The time course was created from binary random values sampled at 20 Hz, passed through an exponential low-pass filter with a time constant of 3 s, then rounded to obtain a binary signal. We used offline simulations to verify that this stimulus could be used to correctly estimate the shape of a linear filter. LFPs and spike times were further down-sampled to 100Hz for filter analysis.

In general, the linear filter that transforms an input I into a response R, can be calculated in the frequency domain according to

$$\mathrm{F}\left(\omega \right)=<{\mathrm{I}}^{\ast }\left(\omega \right)\mathrm{R}\left(\omega \right)>∕<{\mathrm{I}}^{\ast }\left(\omega \right)\mathrm{I}\left(\omega \right)>$$

where F(ω), I(ω), and R(ω) are the Fourier transforms of the filter, input, and response respectively. The variable ω represents frequency and * represents the complex conjugate. The numerator of this equation is equal to the Fourier transform of the cross-correlogram of input and response:

$$\mathrm{C}\left(\tau \right)=\int dt\mathrm{R}\left(t\right)\mathrm{I}(t-\tau )$$

while the denominator is the power spectrum of the input.

For all the filters we calculated, both the input and output signals have relatively little high-frequency content, and so the filter is poorly estimated at high frequencies. Moreover, because the input signal has little power at high frequencies, normalizing by the power spectrum of the input signal tends to boost this high-frequency noise in the filter. Therefore, to obtain a reasonable filter, we gradually attenuated the frequency representation of the filter above a cutoff frequency (f_cut) according to

$$\mathrm{c}\left(\omega \right)=\exp (-\mid \omega -f_{\mathit{cut}}\mid ∕f_{\tau })\text{for}\mid \omega \mid >=f_{\mathit{cut}}$$

prior to transforming it back into the time domain. Gradual attenuation was used to reduce ripples in the filter that arise from a sharp frequency cutoff. For odor-to-LFP filters we chose f_cut = 5 Hz, f_τ = 20 Hz, and for LFP-to-spike rate filters we chose f_cut = 5 Hz, f_τ = 200 Hz. For filters relating the theoretical command signal to the PID response, we used f_cut = 10 Hz, f_τ = 50 Hz. In general, we chose the largest values of f_cut and f_τ that did not introduce excessive noise into the resulting filter. Qualitatively similar results were obtained with higher absolute cutoffs and sharper attenuation, though this produced more ripples at the edges of the filter.

In general, the power spectrum of the input signal limits the power spectrum of the calculated filter. In our case, the fact that the LFP has little power at high frequencies means that the calculated spike filter cannot contain high frequencies. The true spike filter is almost certainly quite narrow, and so the calculated spike filter is likely a smoothed version of the true spike filter (see Supplementary Figure 3). This smoothing is what gives rise to the fact that the calculated spike filter has some structure to the right of the zero time point. In addition, the calculated spike filter may include a small contribution from the spike waveform itself.

Data used to test the filter was kept separate from data used to calculate the filter. MATLAB (Mathworks, Natick, MA) was used to produce stimulus waveforms, analyze the data, and perform simulations.