Lipopolymer gradient diffusion in supported bilayer membranes

Abstract

We measure the gradient diffusion coefficient of a model lipopolymer in supported lipid bilayer membranes from Fourier-transform post-electrophoresis relaxation. The experiments and accompanying quantitative interpretation furnish the concentration dependence of the gradient diffusion coefficient. In striking contrast to the recent measurements of the self-diffusion coefficient from fluorescence recovery after photobleaching, the lipopolymer gradient diffusion coefficient increases with concentration. We interpret the enhancement at small but finite concentrations using the Scalettar–Abney–Owicki (SAO) statistical mechanical theory (1988) and the Bussell–Koch–Hammer (BKH) hydrodynamic theory (1995), which are customarily adopted to model membrane protein dynamics. The SAO theory furnishes an effective disc radius and soft repulsive interaction radius that are comparable to the Flory radius of the unperturbed polyethylene glycol chains. On the other hand, the BKH theory predicts a gradient diffusion coefficient that decreases with disc/membrane protein concentration. Thus, in contrast to membrane proteins, we conclude that lipopolymer hydrodynamic interactions are weak because the principal disturbances are in the low-viscosity aqueous phase. Accordingly, lipopolymer interactions are dominated by thermodynamic interactions among polymer chains. Interestingly, our experiments suggest that increasing (decreasing) the polymer molecular weight should increase (decrease) the relaxation rate of lipopolymer concentration fluctuations.

1. Introduction

An extensive literature is devoted to understanding the physics of diffusion in cell membranes [1–8]. The relationship between the diffusion coefficient D₀ of a single transmembrane protein and physical properties of the membrane is well described by the theory of Saffman & Delbrück [9]. In concentrated systems, however, where protein interactions are important, the Saffman–Delbrück equation breaks down, giving way to two distinct diffusion phenomena [10,11].

Self-diffusion (also termed tracer diffusion) describes the fluctuating trajectory of a Brownian tracer particle, with a self-diffusion coefficient D_s that quantifies the rate at which the mean-squared displacement of a tracer increases with time. On the other hand, gradient diffusion (also termed mutual diffusion) is the macroscopic flux of Brownian particles due to a concentration gradient. The accompanying gradient diffusion coefficient D_g is the one that appears in Fick's law of diffusion. While both the processes can have qualitatively different behaviours at finite concentrations, the self- and gradient diffusion coefficients at infinite dilution become equal to D₀ [10,12].

The concentration dependence of the self- and gradient diffusion coefficients reflects the balance of thermodynamic and hydrodynamic interactions. According to the statistical mechanical theory of fluids [10,13], direct repulsive (attractive) interactions are predicted to increase (decrease) the gradient diffusion coefficient, whereas the hydrodynamic interaction theory of Bussell et al. [14], which specifically deals with hard cylinders in continuum phospholipid membranes, predicts that hydrodynamic interactions hinder gradient diffusion. Thus, the gradient diffusion coefficient in two-dimensional fluid systems may increase or decrease with concentration, depending on the strength of thermodynamic and hydrodynamic interaction forces.

For lipopolymers, the thermodynamic and hydrodynamic size of the polymer can be considerably larger than the anchoring lipid tail and, indeed, comparable to or larger than membrane proteins. Thus, thermodynamic and hydrodynamic interactions are expected to impart a concentration dependence to the diffusion coefficient, which may be significant at very low lipopolymer mole fractions. Moreover, it is not clear whether these influences should hinder or enhance gradient diffusion. Despite extensive biotechnological applications, there are few studies reporting the concentration dependence of lipopolymer self-diffusion. Even more surprising, perhaps, is that there are no studies of lipopolymer gradient diffusion and its concentration dependence.

We recently reported the concentration dependence of the self-diffusion coefficient of the model lipopolymer 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[poly(ethylene glycol)2000-N′-carboxyfluorescein] (DSPE-PEG2k-CF) in glass-supported 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC) lipid bilayers [15]. Similar lipopolymer systems have been widely adopted as model cell membranes and as bio-sensing platforms [16–19]. These experiments quantified how the self-diffusion coefficient of this lipopolymer decreases nonlinearly with increasing concentration. By drawing upon theories developed in the literature for membrane proteins, we attributed the dominant interaction to thermodynamic repulsion of the polyethylene glycol (PEG) chains. A stronger conclusion regarding the roles of thermodynamic and hydrodynamic interactions rests on the concentration dependence of the gradient diffusion coefficient.

Accordingly, in this work we developed an independent, but complementary, experimental methodology to measure the lipopolymer gradient diffusion coefficient. This so-called Fourier-transform post-electrophoresis relaxation (PER) analysis reveals a lipopolymer gradient diffusion coefficient that increases linearly with concentration. Such behaviour is contrary to theoretical expectations for membrane proteins modelled as hard discs with hydrodynamic interactions. This striking observation may influence the design of micro-fluidic technologies involving lipopolymer gradients; for example, for purifying bio-macromolecules using electrophoresis within patterned bilayers [20]. From a fundamental perspective, however, we believe that this is the first systematic measurement of D_g to test pioneering theoretical studies of gradient diffusion in lipid bilayer membranes [10,11,13,14,21,22].

The paper is organized as follows. Section 2 details bilayer synthesis, PER experiments and the Fourier-transform PER analysis. In §3, we apply the PER methodology and report the concentration dependence of D_g for the lipopolymer DSPE-PEG2k-CF in glass-supported DOPC bilayers. This section also presents the results for a non-PEG-bearing lipid tracer: 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-(7-nitro-2-1,3-benzoxadiazol-4-yl) (ammonium salt; DOPE-NBD) in DOPC. Section 4 theoretically interprets the lipopolymer data—drawing upon existing theories for membrane proteins—and discusses the influences of thermodynamic and hydrodynamic interactions. We conclude in §5 with a brief summary.

2. Material and methods

2.1. Patterned bilayer synthesis

Since Groves & Boxer [23] patterned the first supported lipid bilayers by scratching with tweezers, other methods have been developed to produce more precise patterns [24–26]. Here, we use micro-contact printing [27]. The master was synthesized using standard photolithographic techniques with SU-8 negative photoresist (approx. 120 µm thick) on silicon wafers. The stamp was synthesized by curing polydimethylsiloxane (PDMS, Sylgard 184, Dow Corning, Hemlock, MI, USA) on the master for 8 h at 60°C. The stamp was peeled off and oxidized for approximately 30 s in a plasma cleaner (Harrick Plasma, Ithaca, NY, USA), then immediately incubated in a solution containing 250 µg ml⁻¹ Texas-Red-conjugated albumin from bovine serum (TR-BSA, Molecular Probes, Carlsbad, CA, USA) for 1 h, and dried under a stream of nitrogen gas to remove excess protein solution.The stamp was then placed in contact with a pre-cleaned coverslip for 1 h. Finally, a dispersion of small unilamellar vesicles (SUVs) was deposited onto the patterned glass surface to form lipid bilayers by vesicle fusion. The coverslips were first boiled in 7X solution (MP Biomedical, Solon, OH, USA) for 30 min, rinsed excessively with reverse osmosis (RO) water, dried under a stream of nitrogen gas, and further cleaned by piranha etching for 20 min in a solution of 3:1 (v/v) concentrated sulphuric acid (H₂SO₄) and 30 per cent hydrogen peroxide (H₂O₂). The coverslips were then rinsed excessively with RO water, dried under a stream of nitrogen gas and used immediately. SUVs were prepared following literature procedures [23] with minor modifications. First, a mixture of lipids containing 2 mg of DOPC (Avanti Polar Lipids, Alabaster, AL, USA) and a desired concentration of lipopolymer DSPE-PEG2k-CF (Avanti Polar Lipids) in chloroform was dried under a stream of nitrogen gas, followed by desiccation under vacuum for 2 h before reconstituting in buffer (10 mM phosphate, 100 mM NaCl, pH 7.4) to 2 mg ml⁻¹. The lipid mixture was extruded 20 times through a 100 nm polycarbonate membrane, and then another 20 times through a 50 nm polycarbonate membrane (Avanti Polar Lipids) to form SUVs. Control experiments were performed with DOPE-NBD (Avanti Polar Lipids) in DOPC. All chemicals, except where otherwise stated, were used as purchased (Sigma Aldrich, Oakville, ON, Canada).

2.2. PER experiments

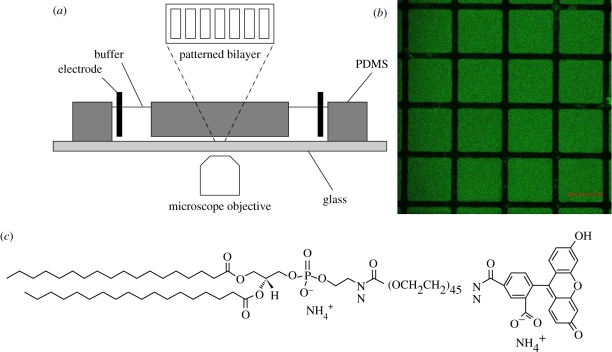
Bilayers were imaged with a Zeiss LSM510 confocal laser-scanning microscope (Carl Zeiss, AG, Germany) with a 20 × 0.50 dry objective and a 488 nm argon ion laser (25 mW) with 0.1–0.5% intensity. PER experiments were undertaken in fluid channels with dimensions of 30 × 6 × 0.3 mm. A schematic of the experiment is shown in figure 1. Channels were synthesized from PDMS using a custom-made glass mould, and mounted onto a patterned coverslip as the bilayer support. Two platinum (Pt) electrodes were placed in PBS buffer reservoirs at the ends of the channel. A low ionic strength buffer solution containing 0.5 mM Na₂HPO₄ and 0.25 mM NaH₂PO₄ was used during electrophoresis to minimize Joule heating. For electric field strengths less than 100 V cm⁻¹, the temperature increase, calculated with zero heat loss, is less than 0.5°C min⁻¹. Accordingly, we neglected heating influences during the short (<5 min) periods of electrophoresis. The electric field strength was calculated from measurements of the current, buffer conductivity and channel cross section. Current was recorded from the power supply (PS325, Stanford Research Systems, Sunnyvale, CA, USA), conductivity was measured using a Zetasizer Nano Series instrument (Malvern Instruments, Malvern, UK) and the channel cross section was estimated from the mould used to synthesize the PDMS channel. The channel was carefully aligned with the electric field to achieve concentration gradients that are perpendicular to the corrals. Our analysis of the relaxation by one-dimensional diffusion is described in §2.4.

Figure 1.

(a) Schematic of the PER experiment. (b) Representative laser-scanning confocal micrograph of micro-contact-printed corrals in DSPE-PEG2k-CF decorated DOPC SLBs. These corrals are 250 µm square, whereas the stripes used in our PER experiments were 250 µm wide (figure 4). (c) Molecular structure of lipopolymer DSPE-PEG2k-CF. Scale bar, (b) 200 µm.

2.3. Photobleaching correction

Quantitative analysis of fluorescence intensity requires the intensity to be proportional to the fluorochrome (lipopolymer) concentration. This cannot be achieved at high fluorochrome concentrations due to self-quenching. We previously demonstrated that a linear relationship prevails for the two tracers (DSPE-PEG2k-CF and DOPC-NBD) used in this work when the mole fraction c ≲ 0.05. Furthermore, we adjusted the experimental parameters such as illumination intensity and frequency to minimize photobleaching. Nevertheless, to compensate for acquisition photobleaching, we assume first-order photobleaching kinetics

2.1

where I is the fluorescence intensity and k is the first-order rate coefficient. With diffusion exclusively in the x-direction, the corrected intensity is

2.2

where I_m(x, t) and I_c(x, t), respectively, are the measured and corrected intensity profiles at time t. To ascertain k, we integrate equation (2.2) over x, giving the total intensity

2.3

where, again, subscripts denote the corrected and measured intensities. Since I_c^T(t) = I₀^T, the total intensity before applying an electric field and imaging, it follows that e^kt = I₀^T/I_m^T(t) and, hence, equation (2.2) becomes

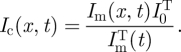2.4

2.4. PER diffusion model

Interpretation of PER experiments with a concentration-dependent diffusion coefficient has proved to be difficult [10,28]. By drawing upon numerical solutions of the diffusion equation with a concentration-dependent diffusion coefficient, one can, in principle, fit model concentration profiles to PER experiments. However, this approach is time-consuming, requires an a priori functional form for D_g(c), and is adversely sensitive to noise in the experimental data.

To overcome the foregoing difficulties, we consider the electric field-induced concentration perturbation

2.5

where c₀ is the initially uniform lipopolymer concentration. The diffusion equation governing the relaxation of the perturbation following electrophoresis is

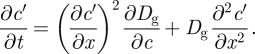2.6

Expanding D_c(c) as a Taylor series about D_g(c₀), the leading-order approximation of equation (2.6) is

2.7

Next, expanding c′ as a Fourier series that satisfies no-flux boundary conditions at x = 0 and L gives

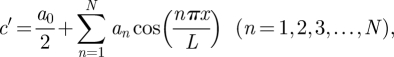2.8

where L is the corral length, and the Fourier coefficients

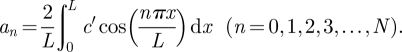2.9

Substituting equation (2.8) into equation (2.7) gives

2.10

so

2.11

with

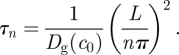2.12

Thus, by Fourier transforming the corrected fluorescence intensity and plotting the amplitude of the slowest decaying mode a_l(t), we obtain the diffusion coefficient D_g(c₀) from the least-squares fit of equation (2.11).

3. Gradient diffusion coefficient from PER

We compute the Fourier transform of fluorescence intensity profiles of fluorescent lipid tracers in glass-supported DOPC bilayers synthesized by vesicle fusion. Bilayers are corralled with protein barriers deposited by micro-contact printing. Application of a longitudinal electric field, oriented perpendicular to the barriers, induces a non-uniform tracer concentration that relaxes by gradient diffusion to the uniform state upon turning off the field. We image the spatial and temporal relaxation of the fluorescence intensity, assuming a linear relation between fluorescence intensity, also correcting for image-acquisition photobleaching. The exponential relaxation of the slowest decaying Fourier mode furnishes the gradient diffusion coefficient at the bulk lipopolymer concentration. By performing experiments on bilayers synthesized with various bulk lipopolymer concentrations c₀, we obtain the concentration dependence of the gradient diffusion coefficient D_g(c₀) at mole fractions up to about 3 per cent. We tested this quantitative methodology using numerically generated PER profiles (see appendix A), finding it to be robust and accurate, whereas nonlinear least-squares fitting of the diffusion model to PER data produces erroneous results.

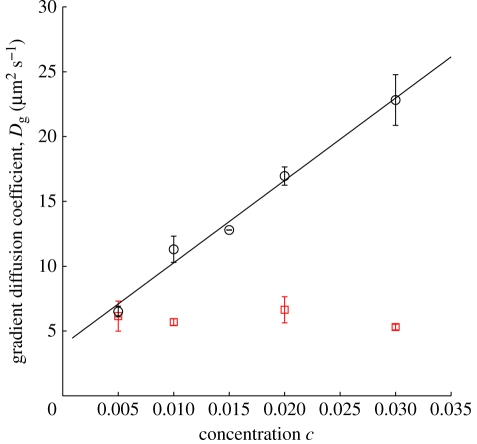
From experiments with various average concentrations of lipopolymer DSPE-PEG2k-CF in DOPC, the concentration dependence of the gradient diffusion coefficient is shown in figure 2 (circles). As a control, we obtained—using the same methodology—the gradient diffusion coefficient of DOPE-NBD in DOPC at various concentrations of DOPE-NBD; these data are also plotted in figure 2 (squares). There is distinctive, significant linear increase of the lipopolymer gradient diffusion coefficient with concentration, whereas the gradient diffusion coefficient of the control is practically independent of its concentration at the prevailing (low) mole fractions. A least-squares fit of the linear relationship

3.1

to the lipopolymer data yields D₀ ≈ (3.7 ± 0.4) µm² s⁻¹ and β ≈ 180 ± 30 with concentration c expressed as a mole fraction.¹ We now turn to comparing the gradient diffusion coefficient with its counterpart for self-diffusion, also theoretically interpreting β, which reflects thermodynamic and hydrodynamic interactions among the lipopolymers.

Figure 2.

Gradient diffusion coefficient D_g from PER experiments with lipopolymer DSPE-PEG2k-CF (circles) and a control DOPE-NBD (squares) in glass-supported DOPC. The solid line is a least-squares fit of equation (3.1) to the lipopolymer data, furnishing D₀ ≈ 3.7 µm² s⁻¹ and β ≈ 180 (see text for details). Error bars are the standard deviation of at least three PER measurements at each tracer concentration.

The gradient diffusion coefficient reflects the competition between thermodynamic and hydrodynamic influences [12], quantified by the generalized Stokes–Einstein equation

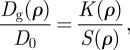3.2

where K(ρ) and S(ρ) are termed, respectively, the hydrodynamic and thermodynamic interaction coefficients [29], and ρ is the tracer number density.

Bussel and co-workers [14,21] showed that hydrodynamic interactions among hard cylinders hinder self- and gradient diffusion. Similarly, Scalettar et al. [10] showed that thermodynamic interactions—whether attractive or repulsive—hinder self-diffusion. More importantly, they showed that attraction (repulsion) hinders (enhances) gradient diffusion. Thus, for lipopolymers with D_g increasing markedly with c, the principal interactions are repulsive thermodynamic forces.

The thermodynamic coefficient S(ρ) may be directly determined from the osmotic pressure Π(ρ), which has contributions from electrostatic repulsion, van der Waals attraction and configurational entropy [30]. The lipopolymer DSPE-PEG2k-CF bears a charge –e at the PEG–lipid junction, and a charge –e at the PEG–CF junction. Interestingly, DOPE-NBD used in this study as a control, because it bears no polymer and has a charge –e at the lipid–NBD junction, does not exhibit an appreciable change in its self- and gradient diffusion coefficients with concentration. This suggests that electrostatic repulsion has a weak influence on lipopolymer diffusion, or, possibly, that electrostatic interactions, which should enhance gradient diffusion and hinder self-diffusion, might be balanced by hydrodynamic influences. On the other hand, the osmotic pressure of aqueous PEG solutions increases with a power-law dependence on PEG concentration [31], suggesting that PEG2k-excluded volume and configurational entropy play dominant roles.

Our earlier measurements of the concentration dependence of the self-diffusion coefficient D_s of DSPE-PEG2k-CF in DOPC bilayers furnish D_s ≈ D₀/(1 + αc), where D₀ ≈ (3.4 ± 0.1) µm² s⁻¹ and α ≈ 56 ± 6 with concentration c expressed as a mole fraction [15].² Self- and gradient diffusion coefficients should coincide at infinite dilution [10]. Here, the limiting self- and gradient diffusion coefficients, D₀ ≈ 3.36 and 3.68 µm² s⁻¹, respectively, are within about 10 per cent of each other. This difference probably reflects a systematic error in the experiments. Because the self- and gradient diffusion coefficients decrease and increase, respectively, with concentration, the values (D_s ≈ 2.78 µm² s⁻¹ and D_g ≈ 6.50 µm² s⁻¹) at the lowest experimentally accessible mole fraction in this study (c₀ ≈ 0.005) differ substantially because of interactions.

For DOPE-NBD in DOPC, the self- and gradient diffusion coefficients are practically independent of concentration at the low concentrations investigated. Interestingly, the relative magnitude of the self- and gradient diffusion coefficients of DOPE-NBD in DOPC at mole fraction c ≈ 0.005, D_s ≈ 2.85 µm² s⁻¹ and D_g ≈ 6.15 µm² s⁻¹, are similar to the differences between these quantities reported for λ-DNA solutions by Scalettar et al. [12]. They measured a larger D₀ ≈ (0.54 ± 0.15) µm² s⁻¹ from self-diffusion when compared with D₀ ≈ (0.42 ± 0.02) µm² s⁻¹ from gradient diffusion, attributing the discrepancy to a divergence of the laser beam in the fluorescence correlation spectroscopy (FCS) that they adopted for measuring gradient diffusion. Note, however, that scaling diffusion coefficients with the respective values at infinite dilution is generally understood not to influence the concentration dependence of D_s/D₀ or D_g/D₀ [12,32].

We recently reported the self-diffusion coefficient of the lipopolymer at infinite dilution to be somewhat higher than that of its DOPE-NBD control, suggesting that there is a stronger hydrodynamic coupling of DOPE-NBD to the glass support [15]. In striking contrast, the gradient diffusion coefficient of the lipopolymer at infinite dilution is ostensibly lower than that of its DOPE-NBD control. Note also that the gradient diffusion coefficient of DOPE-NBD is systematically and substantially higher than its self-diffusion coefficient. Interestingly, the DOPE-NBD diffusion coefficients have a similar non-monotonic dependence on concentration. The self- and gradient diffusion coefficients of DOPE-NBD are listed in table 1 with their ratio, which is a constant D_g/D_s ≈ 2.2 ± 0.3 to within the experimental error. Together, our results for lipopolymers and the DOPE-NBD control suggest the experiments are robust, and that the surprising differences between the self- and gradient diffusion coefficients of the DOPE-NBD are due to a fundamental change in the bilayer–support interaction upon applying an electric field prior to PER.

Table 1.

Summary of self- and gradient diffusion coefficients for DOPE-NBD in glass-supported DOPC bilayers.

c (mol %)	Dg (µm2 s−1)	Ds (µm2 s−1)	Dg/Ds
0.5	6 ± 1	2.8 ± 0.2	2.2 ± 0.5
1	5.7 ± 0.3	2.79 ± 0.05	2.0 ± 0.1
2	6.6 ± 1	2.86 ± 0.06	2.3 ± 0.4
3	5.3 ± 0.2	2.6 ± 0.1	2.1 ± 0.2

The higher gradient diffusion coefficient of DOPE-NBD in DOPC (D_g ∼ 5.9 µm² s⁻¹) suggests that the bilayers are further separated from the glass. Supporting this hypothesis are independent measurements of the diffusion coefficient of BODIPY tail-labelled lipids (2-(4,4-difluoro-5-octyl-4-bora-3a,4a-diaza-s-indacene-3-pentanoyl)-1-hexadecanoyl-sn-glycero-3 phosphocholine (C8-BODIPY 500/510 C5-HPC)) from FCS. Using the Z-scan method, Przybylo et al. [33] measured D_s ≈ (7.8 ± 0.8) µm² s⁻¹ in giant unilamellar vesicles (free-standing bilayers) and D_s ≈ (3.1 ± 0.3) µm² s⁻¹ when supported on mica. The absolute values and the ratio of these are similar to the values obtained by ourselves for self- and gradient diffusion, suggesting that our gradient diffusion experiments bring the supported bilayers closer to a free-standing state. Note also that the diffusion coefficient of BODIPY lipids on a mica support is similar to the self-diffusion coefficient of DOPE-NBD that we measured on glass.

Stone & Ajdari [34] extended the Saffman & Delbrück [9] analysis of a disc with radius a embedded in a continuum membrane with viscosity μ_l and thickness h to include the influence of a solid support at a distance H from the membrane. For example, with h = 3 nm, a = 0.5 nm, and μ_l/μ_f = 100, 50, 20 and 10, their theory gives D₀(H → ∞)/D₀(H = 1 nm) ≈ 1.78, 1.76, 1.72 and 1.68, respectively.³ Thus, the increase in the diffusion coefficient that comes from increasing the membrane–support separation from h = 1 nm to the free-standing state yields a fractional increase of approximately 1.8, which is only approximately 20 per cent smaller than the ratios D_g/D_s ≈ 2.2 that we measured for DOPE-NBD as c → 0. Note that the absolute values of the diffusion coefficients predicted by Stone & Ajdari are very different from the measured values for DOPE-NBD. This is because their theory addresses discs (transmembrane proteins) whose radius is much larger than the lipid-head radius—to justify an accurate continuum approximation—and whose length spans the entire membrane, whereas lipid tracers (DOPE-NBD) have a small radius and span only one bilayer leaflet.

4. Theoretical interpretation

For a two-dimensional fluid of hard discs, Scalettar et al. [10] theoretically predict

4.1

where ϕ ≪ 1 is the disc area fraction. To our best knowledge, the linear increase in D_g with concentration has not been corroborated by experiments. Quantitative comparison of theory and experiments with proteins in lipid bilayers is complicated by the difficulty in specifying the protein size [11,13,22]. For lipopolymers, the area fraction is even more difficult to specify, because the tracers comprise a large polymer coil grafted to a small lipid anchor. Nevertheless, we proceed by approximating lipopolymers as discs with an effective radius a_e, giving an effective area fraction ϕ_e = cπa_e²/A_l, where, again, c is the lipopolymer mole fraction, and A_l ≈ 0.65 nm² is the lipid cross-sectional area corresponding to a lipid head radius a_l ≈ 0.46 nm. Accordingly, equation (4.1) becomes

4.2

hence, comparing with our empirical equation (3.1) furnishes 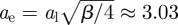(β ≈ 178; figure 2).

By including hydrodynamic interactions, Bussell et al. [14] predict a gradient diffusion coefficient for hard cylinders

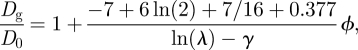4.3

where γ ≈ 0.5772 is Euler's constant, and λ = hμ_f/(aμ_l) with a the disc radius, h the bilayer thickness, μ_l the bilayer viscosity and μ_f the fluid viscosity. Quantitative comparison of equation (4.3) with our experiments is clearly not possible, because hydrodynamic interactions for a dilute, two-dimensional fluid of hard cylinders evidently hinder gradient diffusion. This suggests that hydrodynamic interactions in lipopolymer systems have a negligible influence when compared with the thermodynamic (excluded volume) interactions of the polymer chains. From our previous analysis of the self-diffusion coefficient at small but finite lipopolymer concentrations, the theory of Scalettar et al. [10] yields a lipopolymer effective radius a_e ≈ 2.41 nm, whereas the hydrodynamic theory of Bussell et al. [14] furnishes a_e ≈ 2.92 nm. These values are comparable to, but ostensibly smaller than, the value of a_e ≈ 3.03 nm obtained in this study of gradient diffusion.

The influence of lipopolymer thermodynamic interactions on the diffusion coefficient can be modelled in the manner undertaken for transmembrane proteins at small but finite concentrations. Under these conditions, the leading-order friction coefficient is dominated by a constant lipid-tail friction coefficient k_BT/D₀. Accordingly, we consider the model of Scalettar et al. [10] for particles in the plane of a membrane interacting via a soft repulsive potential. The specific potential adopted by Scalettar et al. is

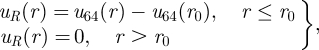where

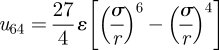4.4

is zero at radial separation r = σ, and has minimum value −ε at r = r₀ = (3/2)^1/2σ.

Setting ε = k_BT, where k_BT is the thermal energy, Scalettar and co-workers obtain

4.5

and

4.6

where ρ* = ρσ² with ρ = c/(πa_l²) the disc (surface) number density and c the mole fraction.

Our earlier measurements of the self-diffusion coefficient at small but finite concentrations [15] yield σ ≈ 5.40 nm, corresponding to an effective (soft) lipopolymer radius a_e = σ/2 ≈ 2.70 nm. From our reported gradient diffusion coefficient, we find σ ≈ 5.95 nm, which corresponds to an effective radius a_e ≈ 2.98 nm.

The foregoing effective radii are summarized in table 2. In contrast to the foregoing hard-disc model, the soft interaction potential provides much improved consistency between self- and gradient diffusion. Note that equation (4.3) explicitly addresses hydrodynamic interactions among discs that reside entirely within a membrane that is generally considered one to two orders of magnitude more viscous than water. Thus, because the hydrodynamic interactions between lipopolymers are likely to be dominated by disturbances within the the aqueous phase, equation (4.3) should not even qualitatively describe lipopolymer hydrodynamic interactions. Moreover, because the lipid tail has a small hydrodynamic radius, and the fluid viscosity is much lower than that of the bilayer, hydrodynamic interactions should indeed be weak. These arguments are supported by our earlier interpretation of the self-diffusion coefficient at low concentrations [15], and by the present interpretation of the gradient diffusion coefficient based solely on thermodynamic interactions.

Table 2.

Effective lipopolymer radii a_e (nm) obtained from theoretical interpretations of the measured concentration dependence of self- and gradient diffusion coefficients of lipopolymer DSPE-PEG2k-CF in DOPC. Note that the PEG2k Flory radius R_F ≈ 3.83 nm and the lipid head radius a_l ≈ 0.46 nm (see text for details). HC, hard cylinders; SR, soft repulsion; HI, hydrodynamic interaction.

model	Ds	Dg
HC [10]	2.41	3.03
SR [10]	2.92	2.98
HC and HI [14]	2.70	—

Note that the Flory radius of a polymer coil

4.7

where a_m is the size of a monomer and n_p is the degree of polymerization [17]. According to Hristova et al. [35] and Nagle & Tristram-Nagle [36], a_m ≈ 0.35–0.43 nm. Therefore, setting a_m = 0.39 nm gives R_F ≈ 3.83 nm, which is considerably larger than the foregoing effective soft radius a_e ≈ 2.70–2.98 nm. Of course, there is no reason why these should be the same. Nevertheless, as expected, the effective radius is significantly larger than the hard cylinder radius of a lipid head, a_l ≈ 0.46 nm.

Note that the root mean-squared end-to-end distance of an unperturbed PEG2k chain R = lN^0.5 ≈ 3.76 nm is comparable to the foregoing Flory radius. Here, the statistical segment size l = 0.71 nm and the number of statistical segments N = 28 nm [37]. Moreover, self-consistent mean-field calculations of the segment density profiles for end-grafted PEG2k chains indicate that the layer thickness L ≈ 2R ≈ 7.6 nm at all the grafting densities encountered in our experiments. Thus, even when the PEG2k chains overlap, the mean segment densities are low enough for the chains to be only weakly perturbed from their end-tethered conformation at infinite dilution.

The reasonableness and consistency of the molecular sizes that we have extracted from independent, quantitative studies of lipopolymer self- and gradient diffusion support the underlying assumption that the tracer concentration in the membranes is equal to the bulk concentration of the lipid mixtures used to synthesize them. Moreover, the interpretations furnish a valuable quantitative guide for engineering these membranes for technological applications.

5. Summary

In summary, we applied Fourier-transform PER to measure the concentration dependence of the gradient diffusion coefficient of model lipopolymer DSPE-PEG2k-CF in glass-supported DOPC bilayers. From experiments with various bulk lipopolymer concentrations, we found the gradient diffusion coefficient to increase linearly with lipopolymer mole fraction. This is in striking contrast to the self-diffusion coefficient, previously found to decrease nonlinearly with increasing concentration. From statistical mechanical models for small but finite tracer concentrations, we demonstrated consistency between the self- and gradient diffusion coefficients by neglecting hydrodynamic interactions and attributing thermodynamic interactions to a soft repulsive potential corresponding to an effective lipopolymer radius of approximately 2.70–2.98 nm, which is modestly smaller than the Flory radius of the PEG2k chains. Thus, the physical picture of lipopolymer dynamics emerging from our complementary studies of self- and gradient diffusion is one where membrane hydrodynamic interactions are negligible because of the small radius of the lipid anchor, but thermodynamic interactions are significant because of the large excluded volume and configurational entropy of the PEG2k chains. Together, the experiments and theoretical interpretation suggest that lipopolymer gradient diffusion can be controlled by PEG molecular weight. Interestingly, increasing (decreasing) the polymer molecular weight should increase (decrease) the rate of relaxation by gradient diffusion.

Appendix A. Testing the Fourier-transform PER methodology

To test the Fourier-transform PER methodology, we numerically integrated the diffusion equation⁴

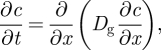A 1

with no-flux boundary conditions at x = 0 and L, and an initial condition

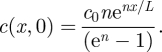A 2

This initial perturbation qualitatively mimics the nonlinear concentration profile that prevails in experiments with the application of an electric field. Note that the parameter n controls the initial degree of perturbation—depending on the strength and duration of the applied electric field—from c₀. With this functional form, we define a dimensionless scalar perturbation index

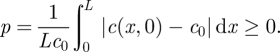A 3

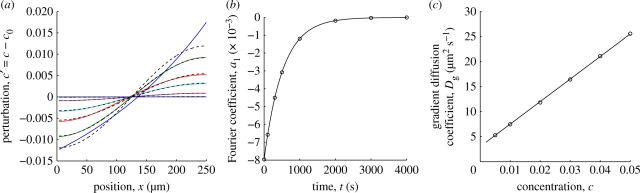
A representative example is shown in figure 3 with mole fraction c₀ = 0.03 and n = 1 giving p ≈ 0.23. Here, the gradient diffusion coefficient is specified as D_g = 3(1 + 150c) µm² s⁻¹ giving D_g(c₀) = 16.5 µm² s⁻¹. Figure 3a shows profiles of c′ according to equation (A 1) (solid lines) at the times identified with symbols in figure 3b. Dashed lines in figure 3a are the first Fourier mode whose amplitude a_l(t) is plotted in figure 3b. A least-squares fit to the exponentially decaying amplitude recovers D_g ≈ 16.54 µm² s⁻¹, which is very close to the exact value. Repeating the foregoing procedure with several values of c₀ yields the concentration dependence of D_g shown in figure 3c (circles). Least-squares fitting yields D_g ≈ 3.01(1 + 149c) µm² s⁻¹ (solid line), which is again in excellent agreement with the specified D_g = 3(1 + 150c) µm² s⁻¹. We have found that the perturbation index p and random noise have little influence on the accuracy of the methodology. In our experiments, p is in the range of 0.1–1, and the corresponding errors are small (≲5%) when compared with the other sources of experimental error.

Figure 3.

Fourier transform methodology to obtain D_g(c₀) from PER lipopolymer concentration profiles with corral length L = 250 µm and gradient diffusion coefficient D_g = 3(1 + 150c) µm² s⁻¹. (a) Concentration profiles from numerical solutions of the diffusion equation (A 1) with average mole fraction c₀ = 0.03 and n = 1 (solid lines). Dashed lines are the first Fourier mode, whose exponentially decaying amplitude is plotted in panel (b) (circles) giving D_g ≈ 16.54 µm² s⁻¹. (c) Least-squares fitted values of D_g(c₀) obtained from computations (to mimic experimental data) with various c₀ and D_g = 3(1 + 150c) µm² s⁻¹ (circles). The solid line is a least-squares fit recovering D_g ≈ 3.01(1 + 149c) µm² s⁻¹.

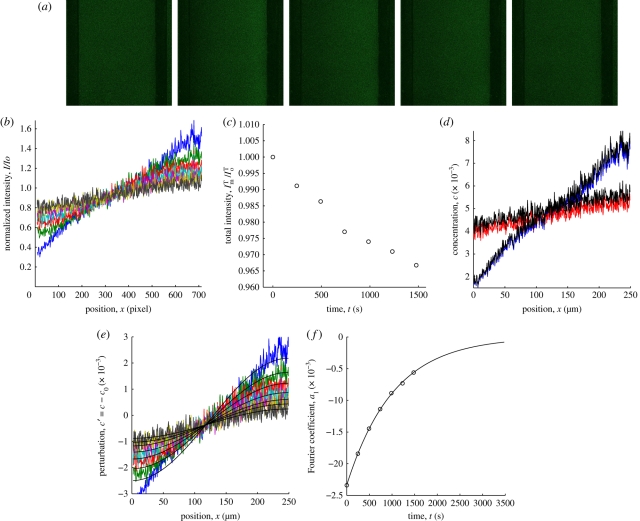
Representative experimental data and analysis are shown in figure 4. Figure 4a shows raw fluorescence images of a lipid bilayer with lipopolymer DSPE-PEG2k-CF mole fraction c₀ = 0.005 before applying an electric field (left image) and during PER. Figure 4b shows intensity profiles I(x, t)/I₀(x, 0), where, recall, I₀ is the initial intensity profile. The normalized total intensity I_m^T(t)/I₀^T is plotted in figure 4c. Note that the approximately exponential decay confirms that the photobleaching kinetics are first order with a rate constant k that reflects the imaging intensity and exposure. Note that the total acquisition intensity loss is less than about 10 per cent. Here, the ostensible intensity loss during electrophoresis is because images were acquired prior to PER (t ≤ 0). Figure 4d shows representative concentration profiles c(x, t) from corrected (solid line) and uncorrected (dotted line) intensity profiles I(x, t), assuming a linear relationship between concentration and intensity. Note that the concentration profiles after compensating for acquisition photobleaching yield a perturbation index p ≈ 0.29. Figure 4e shows the concentration perturbation profiles c′ = c(x, t) − c₀ and first Fourier modes whose amplitudes a_l(t) are plotted in figure 4f (circles) with a least-squares exponential fit (solid line) giving a decay time τ₁ ≈ 1043 s and a gradient diffusion coefficient D_g(c₀) ≈ 5.73 µm² s⁻¹. Without compensating for photobleaching, the Fourier transform methodology yields D_g(c₀) ≈ 5.89 µm² s⁻¹, indicating that photobleaching intensity loss yields a faster apparent relaxation of the concentration perturbation and, hence, a larger apparent gradient diffusion coefficient.

Figure 4.

A representative PER experiment and analysis to obtain the gradient diffusion coefficient at the average lipopolymer concentration. (a) Fluorescence images of DSPE-PEG2k-CF in a DOPC bilayer with lipopolymer mole fraction c₀ = 0.005 before electrophoresis (left) and during PER: t = 0, 246, 493, and 1478 s (left to right). Scale bar, 100 µm. (b) Intensity profiles normalized with the pre-electrophoresis intensity profile. (c) Total intensity I_m^T scaled with the total intensity I₀^T at time t = 0. Circles correspond with the time series in panel (b). (d) Concentration profiles with (black) and without correction for acquisition photobleaching. For clarity, only the first (t = 0) and last series (t = 1478 s) in panel (b) are shown. (e) Concentration profiles with correction for acquisition photobleaching, and the accompanying first-Fourier mode (black lines). Colours correspond with the time series in panel (b). (f) Amplitude of the first-Fourier mode a₁(t) (circles) and the least-squares exponential fit (solid line) giving τ₁ ≈ 1043 s and D_g ≈ 5.73 µm² s⁻¹.