maxAlike: maximum likelihood-based sequence reconstruction with application to improved primer design for unknown sequences

Abstract

Motivation: The task of reconstructing a genomic sequence from a particular species is gaining more and more importance in the light of the rapid development of high-throughput sequencing technologies and their limitations. Applications include not only compensation for missing data in unsequenced genomic regions and the design of oligonucleotide primers for target genes in species with lacking sequence information but also the preparation of customized queries for homology searches.

Results: We introduce the maxAlike algorithm, which reconstructs a genomic sequence for a specific taxon based on sequence homologs in other species. The input is a multiple sequence alignment and a phylogenetic tree that also contains the target species. For this target species, the algorithm computes nucleotide probabilities at each sequence position. Consensus sequences are then reconstructed based on a certain confidence level. For 37 out of 44 target species in a test dataset, we obtain a significant increase of the reconstruction accuracy compared to both the consensus sequence from the alignment and the sequence of the nearest phylogenetic neighbor. When considering only nucleotides above a confidence limit, maxAlike is significantly better (up to 10%) in all 44 species. The improved sequence reconstruction also leads to an increase of the quality of PCR primer design for yet unsequenced genes: the differences between the expected T_m and real T_m of the primer-template duplex can be reduced by ~26% compared with other reconstruction approaches. We also show that the prediction accuracy is robust to common distortions of the input trees. The prediction accuracy drops by only 1% on average across all species for 77% of trees derived from random genomic loci in a test dataset.

Availability: maxAlike is available for download and web server at: http://rth.dk/resources/maxAlike.

Contact: gorodkin@rth.dk

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

With increased opportunities for high-throughput sequencing, a large number of additional genomes will be sequenced in the near future. Given the limitations of these sequencing technologies, however, it is likely that routinely produced genomic sequences will be incomplete at various levels. Also, the genomic information for less ‘popular’ model organisms or economically important species might remain unavailable for a long time. It is still essential to infer as much knowledge as possible about incomplete or missing genomic data in relation to specific analyses, such as studying the distribution of gene families across the phylogeny of species. The relative position of the target species in the evolutionary tree is typically known or can be inferred from the partial sequence information that is already available. With the rapidly growing collection of sequence data from diverse organisms, homologs for a certain region of interest can be utilized, together with their inherent pattern of evolutionary variation. We present an algorithm—maxAlike—-that aims at reconstructing sequences in a particular target species, based on a species phylogeny and sequence homologs from other species.

The maxAlike algorithm uses a multiple sequence alignment and a corresponding phylogenetic tree, annotated with phylogenetic distances on the branches, to estimate mutation rates for each alignment column. It then infers nucleotide probabilities for each site in the theoretical homologous sequence in the target species. From the estimated nucleotide probabilities, the entire sequence can be reconstructed, given a certain level of confidence. The reconstructed sequence can then be utilized for several applications.

The sensitivity and specificity of homology search methods that are based either on primary sequence alone or on profile alignment algorithms can be increased by employing a search query that is optimized for the target species of the homology search (Menzel et al., 2009).

A very important application of (partially) reconstructed sequences is the design of oligonucleotide primers for a PCR experiment, e.g. for analysis of expression of the targeted (re-)sequencing of a particular region that is not or incompletely represented in a genome assembly. The successful amplification of a gene sequence depends on a careful selection of a pair of short primers, which, besides certain thermodynamic properties, should have the highest possible sequence identity to their target site. Designing these primers for yet unsequenced genes is still a difficult problem, often based on trial and error. One of the first approaches that comes to mind is to derive primers from an available homologous sequence in a phylogenetically proximal species. Alternatively, if more than one homolog is known, primers can be derived from a consensus sequence, based on a multiple sequence alignment of the homologs. However, the nearest-neighbor approach might be substantially biased toward one end in the phylogeny and does not take sequence conservation into account, whereas the multiple-alignment approach usually does not consider the exact phylogenetic position of the target species and a careful selection of the seed sequences is an additional parameter. Another issue is the handling of ambiguous sites in the alignment. Restricting the consensus sequence to only perfectly conserved sites might limit the available nucleotides too much in order to derive a primer pair with the desired properties, e.g. thermodynamics, length or base composition. A common remedy is the selection of the most frequent nucleotide at each alignment position to derive the consensus sequence. These problems are inherently solved by the maxAlike reconstruction algorithm, which takes the phylogenetic position of the target species as well as all possibly available homologs into account.

Primer design by including phylogenetic information has been addressed earlier, but with a more narrow scope. In particular, the primers4clades approach (Contreras-Moreira et al., 2009) derives a phylogenetic tree from a multiple sequence alignment of protein-coding genes. From this, the user can, through manual intervention though, restrict the input sequences to a phylogenetic group that is considered for primer design based on a CODEHOP algorithm. However, it does not compute nucleotide probabilities and is not suitable for reconstructing arbitrary non-protein-coding sequences, which potentially can occupy an even larger portion of the genome than the ~1.2% occupied by the protein-coding genes (Mattick and Makunin, 2006). In fact, in the light of the ENCODE project (ENCODE Project Consortium, 2007), which showed that more than 90% of the human genome is transcribed, it may become relevant to design primers on a genome-wide scale. The restriction to protein-coding regions and the limited availability as a web server makes a comparison with other methods difficult for a genome-wide benchmark. The uniprime2 web server (Boutros et al., 2009) employs a pipeline with homology search, multiple alignment and primer design software to derive primers from conserved parts of a given gene. However, no phylogenetic information is taken into account. Methods for designing degenerate primers start by finding highly conserved regions across a sequence alignment, e.g. by solving a Set Covering Problem (Jabado et al., 2006). Depending on the input alignment, this often limits the number of available alignment positions for the primer design considerably. The maxAlike algorithm, however, not only highlights conserved regions by creating sequence profiles but also makes all possible sequence positions available for primer design with a certain confidence threshold. Using a probability threshold for each nucleotide is similar to exploiting base quality scores for selecting regions for primer design (Li et al., 1997). The output of maxAlike can also be used for designing degenerate primers, where two or more nucleotides are allowed at one position, by choosing the most likely occurring nucleotides for this site. By relying on the highly probable nucleotide for a site, however, the total number of degenerate sites can be reduced, which in turn increases the specificity of the primer sequence. This makes maxAlike the optimal choice for designing primers, when the sequence of the target gene is not known, but homologous sequences of other species and a phylogenetic tree including the target species are available. These data serve as input to the maxAlike web server, which in turn allows for estimation of primers using Primer3 from the reconstructed sequence in the target species.

The principle of the maxAlike sequence reconstruction is similar to the reconstruction of genes from ancestral species from their extant offspring, but maxAlike reconstructs a gene sequence on a leaf node of the, possibly unrooted, species tree. Using the information from the extant offspring, this has been shown to be a powerful tool for testing hypotheses on the function and evolution of genes from extinct species, see e.g. Thornton (2004) for a review. Ancestral sequence reconstruction programs infer the sequences at the interior nodes of the tree from their descendants in a rooted phylogeny. In contrast to these, maxAlike reconstructs the most likely sequence at an additional leaf node in the possibly unrooted species tree. Therefore, the sequence information of all taxa influence the reconstruction of the target sequence. Several methods for reconstructing ancestral sequences from their descendants have been developed so far, of which methods based on the maximum likelihood principle have been shown most successful (Zhang, 1997). Recent applications include the ancestors web server (Diallo et al., 2010) or the Ortheus program (Paten et al., 2008). Not only in the case of procaryotes, the ancestral relationships between species might not be clear, but the phylogenetic relationship among the taxa can often be derived from the available sequence data. In these cases, the maxAlike algorithm is still applicable, without necessarily rooting the tree.

2 MATERIALS AND METHODS

2.1 Sequence reconstruction algorithm

The maxAlike algorithm aims at reconstructing the nucleotides of a DNA sequence homolog in a given target species by employing a maximum likelihood computation over a phylogenetic tree, which results in residue probabilities for each position in the target sequence.

The input for maxAlike is a multiple sequence alignment M and a phylogenetic tree T, which represents the phylogenetic relationships and distances among the species. Additionally, one of the species in the tree (but absent in the multiple alignment) is chosen as the target species for the reconstruction.

Maximum likelihood (ML) methods require an explicit residue substitution model for calculating substitution probabilities given a certain branch length. For each alignment position, the ML algorithm performs a post-order traversal of the tree, starting from the root. From the known residues found at the leaves of the tree, it then computes likelihoods for each nucleotide at the interior nodes of the tree, based on the substitution model and the branch lengths between the tree nodes (Felsenstein, 1981).

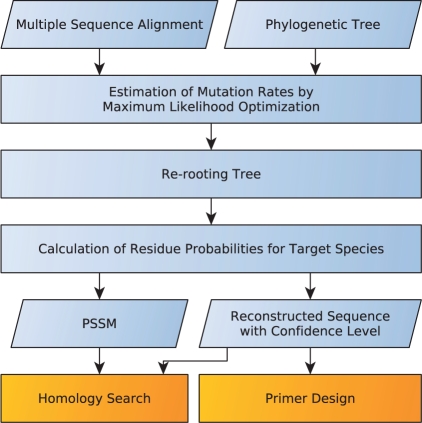
The maxAlike algorithm follows two steps, see Figure 1. In the first step, T is restricted to the species contained in the alignment, and for each alignment column i, a relative substitution rate 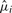is estimated by numerically optimizing the likelihood of the tree: . An extended HKY85 (Hasegawa et al., 1985; Young and Healy, 2003) substitution model (4 nt + gap) is used for computing nucleotide substitution probabilities given a branch length t: P_xy(t, μ)=[e^tμQ]_xy, where x and y are the two nucleotides and Q is the substitution rate matrix. The transversion bias parameter κ is estimated beforehand from T and M.

Fig. 1.

The steps of the maxAlike algorithm. From the input, consisting of a multiple alignment and a phylogenetic tree, the algorithm computes PSSMs and reconstructed sequences for the target species. The output can readily be applied to primer design and homology search.

In the second step, we use the estimated values 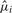to compute the probabilities for each residue at the i-th position of the target sequence. We re-root the original tree T to the target species and calculate the likelihoods 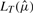for each nucleotide at the root of the tree. From these likelihoods, we directly obtain the residue probabilities in each alignment column i. In our substitution model, gaps are treated as an additional state rather than missing information. Thus, we can also assign a probability of observing a gap for each sequence position in the target species, which in turn depends on the distribution of gaps in the other species.

The calculated probabilities depend explicitly on the relative position of the target species to the other species in T. If the target is in close proximity to one or several other species with known homologs, then high probabilities will be assigned to the nucleotides present in these neighboring species. On the other hand, a single substitution in the sequence of a close neighbor has little impact on the target species, if it is not shared by other closely related sequences. With increasing distance to its neighbors, the residue probabilities in the target species will converge to an equilibrium distribution based on the nucleotide frequencies of the substitution model, which are derived from the base composition of the input alignment. The higher the substitution rate 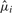is the faster the equilibrium is reached. The algorithm thus tells us which alignment columns or regions can be expected to be informative for a particular target sequence. To this end, we also compute the Shannon information content at each site, from which in turn, we can derive subsequences with a minimum length that have a certain minimum average information content, e.g. for constructing homology search patterns based on position-specific scoring matrices (PSSSs). From the nucleotide probabilities at each site, we then can reconstruct the entire sequence homolog in the target species. At the lower end, we choose the most likely nucleotide at each position. For sites with increasing mutation rates, however, the probabilities for each nucleotide will decrease faster and the information content also decreases. Thus, for a more precise reconstruction, only positions with nucleotide probabilities above a certain, user-defined, probability threshold are considered for the reconstructed sequence, while the remaining nucleotides will be denoted as unknown ‘N’ characters.

The algorithm is available via a web server or as download of the entire source code. The user submits a multiple sequence alignment of homologous DNA or RNA sequences and a phylogenetic tree and chooses one of the species in the tree as the target for reconstruction. The output contains the predicted nucleotide probabilities for each column as well as a sequence logo (Schneider and Stephens, 1990) and two reconstructed sequences: with and without a user-defined probability threshold. These reconstructed sequences can then be used as input to primer design software or directly submitted to the Primer3 web server (Rozen and Skaletsky, 2000). In addition, the information content and the estimated relative substitution rates 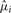are printed for each alignment column i. These values can be used for identifying slowly or rapidly evolving sites or for finding those characters that evolve at rates according to the phylogenetic tree (Townsend and Lopez-Giraldez, 2010). The last part of the output contains a list of PSSMs with average information content and length defined by the user. These PSSMs can directly be used with homology search programs, e.g. fragrep2 (Mosig et al., 2006).

2.2 Data and benchmarking

An example application of the algorithm for constructing PSSMs for homology searches was discussed in Menzel et al., (2009). Here, we go beyond the proof of concept and extend the algorithm to the reconstruction of sequences and explore the application to the design of oligonucleotide primers for PCR.

For evaluation of the reconstruction performance, we use two datasets from multiple alignments of vertebrates. The datasets are derived from human genome (hg18) alignments to 43 vertebrate species (multiz44way) (Browser, 2010). These genome-wide alignments contain both protein-coding and non-coding regions. The first dataset contains alignments with higher sequence conservation, MZ44-1: multiz score from 1M to 4M, at least 20 species per alignment with minimum length 200 nt, and with n=3431 alignments. The second set contains alignments with lower sequence conservation, MZ44-2: multiz score from 10k to 1M, at least 20 species per alignment and n=13524. Gapped columns were removed from the alignments.

From each alignment, we removed one species at a time and used the remaining sequences to reconstruct the homolog in the removed species (target species) with the maxAlike algorithm using the phylogenetic tree from the multiz phastCons model (see Supplementary Fig. S13). The transition bias parameter κ for the HKY85 substitution model is estimated using PAML (Yang, 2007). The predicted nucleotide probabilities were converted into PSSMs for each predicted sequence. In addition, sequences were reconstructed by considering the one nucleotide at each site with a probability greater than a threshold of 0.5 and by considering the most probable nucleotide without using a threshold. We also created PSSMs by counting the nucleotide frequencies in each input alignment and derived consensus sequences, again using either a relative frequency threshold of 0.5 or no threshold, respectively. In order to evaluate the effect of including phylogenetic information into the PSSM and sequence reconstruction, we compared the predictions from the maxAlike probabilities (ML) and the nucleotide frequencies (Freq). Additionally, for each target species, we took the sequence of the phylogenetically closest neighbor (NN) as another prediction for the target sequence. Depending on the alignment, this neighbor is not necessarily constant for each species, thus we measured the average distance to the nearest neighbor for each target species.

The five reconstructions for each target sequence (ML and Freq, each with and without threshold, and NN) were evaluated in terms of the percentage of correctly predicted nucleotides (recovery rate) by comparing the reconstructed sequences to the previously removed homolog in the target species. We excluded absolutely conserved sites from the evaluation, since all methods perform identically on this subset. For the comparison of the ML and Freq PSSMs, we calculate the MATCH scores (Kel et al., 2003) for both the ML and Freq PSSMs using the previously removed sequence as reference. The MATCH algorithm is designed for matching matrix profiles to a primary sequence and the score takes values between 0.0 and 1.0, with 1.0 denoting a perfect match of the matrix to the sequence. For both the recovery rate and MATCH score comparison, we calculated P-values using the Wilcoxon rank sum test.

The species tree, which is estimated from whole-genome alignments and thus represents an average across many different loci and genes, is naturally different from gene trees made from a single set of homologous sequences of one gene family. Gene trees can be used as input for maxAlike, if some sequence information for the target sequence is already available, e.g. for filling gaps. An optimized gene tree should lead to more accurate predictions and thus to a higher recovery rate for the sequence reconstruction. Thus, we measure the possible gain of using gene trees over the species tree. To this end, we estimate a tree for each alignment in both datasets using the fasttree program (Price et al., 2010), remove and reconstruct the target sequences using the estimated tree again and calculate the recovery rates. Since we already know the sequence of the target species beforehand, the gene tree estimated from a particular alignment thus represents the most ‘perfect’ phylogeny for this set of sequences.

If no species tree is available in the first place, the phylogenetic tree needs to be inferred first from other available sequence information, typically from other genes or genomic loci. These trees typically have a different topology and different branch lengths than the reference species tree. While the overall topology might be similar, i.e. major clades can be distinguished, leaves within clades are locally rearranged. To measure the robustness of the maxAlike predictions to erroneous input trees, we selected all the 479 alignments of minimum length 100 nt that contain all 44 species (average alignment length is 178 nt). From each of these alignments, we inferred a phylogenetic tree using fasttree, resulting in 214 binary trees. Additionally, we created 200 trees each by concatenating 3, 5 and 7 randomly selected alignments (from those 479) and retained the binary trees, giving us 808 trees in total. We then used the program sdist (http://www.daimi.au.dk/~mailund/split-dist.html) to measure the split distance (Gusfield, 1991) of each estimated tree to the reference species tree. The split distance is a measure of the topological similarity between two trees, which we used to broadly classify the tree distortion. However, also pairwise distances between all pairs of species vary between the species tree and the estimated trees. The distances range from 5 to 36 with median 17. We then binned the trees according to their distance in 10 bins (see Supplementary Fig. 4a for the distribution of the bins). For each bin, we copied each dataset (only half of the data in MZ44-2), randomly chose one of the trees in the bin for each alignment as input for maxAlike, and reconstructed the target sequences again. This gives us a measure how the maxAlike reconstruction performance responds to suboptimal tree inputs.

Another issue that one has to consider is that two loci often evolve at different rates, which affects the branch lengths of the estimated trees. Therefore, we also measured the impact of branch length distortion in the input tree on the maxAlike prediction accuracy. We created another five datasets corresponding to five bins, each containing 20 trees with a certain ‘relative normal’ error on the branch lengths [adapted from (Diaz-Uriarte and Garland, 1998)]. For each branch with length b, we added an amount drawn from a normal distribution with mean 0 and SD equal to the specified relative normal error e multiplied by the branch length: b=b+norm(0, eb). By scaling the distribution of the error to the length of each branch, branches of different lengths are all subject to the same relative error. We used five relative normal errors: 0.05, 0.1, 0.25, 0.5 and 1.0.

2.3 Application to primer design

For a successful PCR reaction, the chosen primer pair needs to follow certain restrictions regarding thermodynamics, self-complementarity and base composition. It is also very important, that the primer sequence matches its complementary sequence in the target gene sufficiently. Mismatching nucleotides in the primer sequence (by wrong estimation of the target sequence) increase the chance of non-specific binding, leading to possible undesired by-products (Cha and Thilly, 1993). Mismatches between a primer and its complementary sequence decrease the melting temperature T_m of the primer–template duplex. To compensate for this, the annealing temperature in the PCR cycle can be reduced to excite the formation of the duplex. Even though the destabilizing effect of single mismatches on oligo hybridization decreases with increasing oligo length, a higher number of mismatches cause a large decrease in the melting temperature with constant oligo length (Koehler and Peyret, 2005). The T_m of the forward and reverse primer should be similar to avoid different annealing behaviors, since usually both primers have equal concentration in the reaction mix. Thus, a reduction of the number of mismatches would be beneficial for the process of designing primers and for an efficient PCR reaction. To study the impact of an improved sequence reconstruction rate on the hybridization properties of oligonucleotide primers, we measured the difference between the T_m of the predicted primers to their complementary target sequences and the hypothetical perfectly binding primer. For each of the five reconstructions for a target sequence (ML and Freq, each with and without threshold, and NN), we used Primer3 to obtain a pair of primer sequences (Primer length: 15–25 nt, product length 75–300 nt, Primer T_m 45−65^○C, T_m difference between forward and reverse primer: maximum 5^○C) and calculated the expected T_m for both primers. We extracted the complement of each primer (template) from the known target sequence and counted the number of mismatches compared with the predicted primers. In addition, we used the melting program (Novère, 2001) to compute the melting temperature between the predicted primer and its complement from the target sequence. If mismatches are present, this ‘real’ T_m will be lower than the expected T_m, calculated by Primer3. Neighboring mismatches and mismatches at the two extreme positions of the oligo have a higher destabilizing effect than single mismatches (Kwok et al., 1990). However, these mismatch types are not supported in the T_m calculation by melting and there is also no other publicly available software for download that supports these mismatch types. Therefore, we counted the occurrences of these cases separately and compared the numbers for each of the five reconstruction methods. Especially for phylogenetically distant species, the number of mismatches increases so much, that the T_m could not be computed by melting in most cases. Thus, we considered only values that are averaged from at least 20 measurements, in order to compare the numbers between the different methods. Note, however, that there is still a bias toward the lower end in the absolute values for the T_m difference, because all the cases where the T_m could not be calculated are not included in the average.

3 RESULTS

3.1 Sequence reconstruction

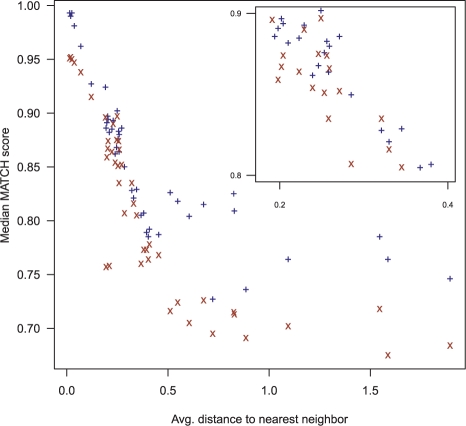
To test the prediction performance of maxAlike, we compared the MATCH scores of the maxAlike (ML) and Freq PSSMs for each of the species. Figure 2 shows the median MATCH scores (dataset MZ44-2) of both methods for each species compared with the average tree distance to its closest neighbor. Supplementary Tables S4 and S5 list all scores for both datasets. For almost all species, we see a significant improvement of the MATCH scores when using the ML PSSMs compared with the Freq PSSMs. On the one hand, species with one or more phylogenetically proximal neighbors will have very high nucleotide probabilities at each position and in turn yield a high overall score. On the other hand, ML PSSMs for more distant target species gain most from the inclusion of phylogenetic information: the difference between ML and Freq increases systematically with the average distance to the nearest neighbor. In these species, high probabilities will only be assigned to highly conserved nucleotide. All bony fishes (teleostei) show improved scores, since the sequences from the tetrapoda have much less impact on the ML probabilities than in the Freq PSSMs. Here, the large fraction of mammals in the overall set of species causes a substantial bias. Conversely, the impact of bony fish sequences on mammalian targets is overestimated in Freq PSSMs compared with the ML PSSMs.

Fig. 2.

Dataset MZ44-2: median MATCH scores for maxAlike (ML) and nucleotide frequency (Freq) PSSMs for each species compared with the average distance to its phylogenetically closest neighbor.

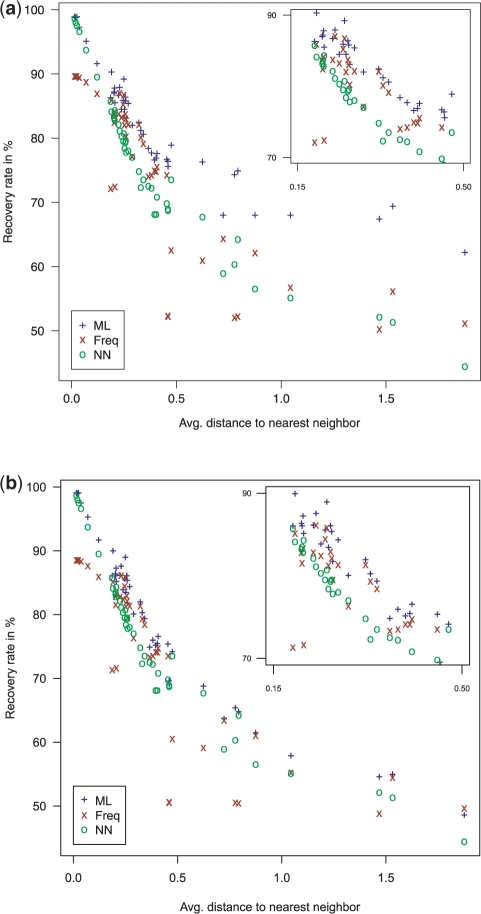
Table 1 shows the total recovery rates in percent across all alignments of both the maxAlike (ML) and the Freq reconstructed sequences for threshold 0.5 and no threshold, respectively, and the recovery rates of the nearest neighbor sequence (NN) for dataset MZ44-1 (see Supplementary Table S1 for MZ44-2). In almost all species, the amount of correctly predicted positions is significantly higher in the maxAlike reconstructions compared with the Freq consensus sequences. As expected, for target species with phylogenetically close neighbors, e.g. in the primates, the improvement between ML and NN is small, but still significant. However, with increasing phylogenetic distance, the difference between the reconstruction rates of both methods becomes bigger. When requiring a nucleotide probability of at least 0.5, the prediction quality increases on average for both ML and Freq and the difference between ML and Freq/NN is much higher than without the probability threshold. Similarly to the PSSM comparison, the difference between ML and Freq/NN recovery rates becomes higher for increasingly more distant species. The mean recovery rates across all species are 82.1% for ML, 74.7% for Freq and 75.3% for NN. In dataset MZ44-1, the ML recovery rates reach a plateau of about 65% for more distant species, while Freq and NN drop down to 55% when using a 50% threshold (Fig. 3a). Here, maxAlike can have up to 10% higher recovery rates than Freq/NN. When no threshold is used, the recovery rates for all methods drop more with increasing tree distance, while ML still has a slight, but yet significantly better performance on average (Fig. 3b). The mean recovery rates without threshold across all species are 79% for ML and 73.7% for Freq. In the MZ44-2 dataset, the prediction performance is lower for all methods compared with MZ44-1. However, the difference between ML and both Freq and NN is slightly higher in MZ44-2. This is due to the lower overall sequence conservation in the alignments, which increases the impact of phylogenetic tree information on the predictions.

Table 1.

Dataset MZ44-1: recovery rates in percent for reconstructed sequences by maxAlike probabilities and nucleotide frequencies (Freq), and the nearest neighbor sequence (NN) for each species

Species	Dist.	Total nt	maxAlike			Freq			NN
			T0.5	n/T	T%	T0.5	n/T	T%
hg18	0.014	779 477	98.9	98.9	99	89.6	88.5	97	98.6
gorGor1	0.019	529 462	98.8	98.8	99	89.6	88.5	97	98.0
panTro2	0.025	761 670	98.9	98.9	99	89.6	88.5	97	97.5
ponAbe2	0.037	747 827	97.3	97.3	99	89.4	88.3	97	96.6
rheMac2	0.069	743 113	95.1	95.1	99	88.7	87.6	97	93.7
calJac1	0.121	706 714	91.6	91.5	99	86.9	85.9	97	89.5
rn4	0.186	491 913	86.3	85.9	98	72.1	71.3	97	85.7
turTru1	0.190	604 007	90.3	89.8	99	85.9	85.1	98	84.1
felCat3	0.202	437 037	87.0	86.2	98	83.6	82.8	97	83.2
bosTau4	0.203	661 325	87.2	85.9	97	82.4	81.5	97	83.5
vicPac1	0.205	514 301	87.8	87.1	98	84.1	83.3	98	82.8
mm9	0.206	529 929	85.5	85.0	98	72.4	71.6	97	84.3
canFam2	0.224	719 731	86.7	86.0	98	83.7	82.8	97	82.1
micMur1	0.229	539 424	87.9	87.4	98	87.0	86.1	97	81.1
otoGar1	0.238	512 427	84.5	83.7	98	83.2	82.4	97	80.3
tarSyr1	0.246	557 077	85.9	85.4	98	85.2	84.4	97	79.5
equCab2	0.249	741 529	89.2	88.8	99	86.7	85.8	97	80.7
choHof1	0.252	402 430	84.5	83.3	97	82.0	81.2	97	78.4
pteVam1	0.256	585 413	86.4	85.9	98	83.7	82.9	98	79.3
myoLuc1	0.258	405 078	85.8	85.2	98	83.0	82.1	97	79.5
dasNov2	0.260	404 201	83.1	81.6	96	80.2	79.5	97	77.8
loxAfr2	0.270	413 718	85.4	84.2	97	82.1	81.3	97	78.0
proCap1	0.289	375 311	82.0	79.9	94	77.1	76.3	97	77.0
tupBel1	0.321	461 072	82.4	81.8	98	82.1	81.3	97	74.8
speTri1	0.330	437 202	81.2	80.1	97	80.1	79.3	97	72.3
oryCun1	0.342	401 696	80.6	79.2	96	79.1	78.4	98	73.5
ochPri2	0.366	340 724	78.4	74.7	90	74.0	73.3	98	72.5
echTel1	0.381	269 011	77.7	75.8	94	74.2	73.5	98	72.2
cavPor3	0.395	608 398	76.6	75.0	95	74.9	74.1	97	68.1
dipOrd1	0.403	349 724	76.9	75.3	95	74.8	74.1	97	68.1
eriEur1	0.407	208 092	77.6	76.4	96	75.5	74.7	97	70.8
sorAra1	0.454	218 519	76.7	75.2	94	74.2	73.5	97	69.8
fr2	0.459	69 842	76.4	69.4	81	52.3	50.6	94	68.9
tetNig1	0.460	69 423	75.6	68.9	81	52.2	50.5	94	68.7
taeGut1	0.475	25 380	78.9	74.0	88	62.5	60.5	94	73.5
galGal3	0.624	35 632	76.3	68.6	82	60.9	59.1	94	67.7
monDom4	0.723	170 184	68.0	63.5	82	64.3	63.4	97	58.9
gasAcu1	0.777	72 157	74.3	65.2	77	52.0	50.5	94	60.3
oryLat2	0.793	67 953	74.9	64.6	74	52.2	50.4	94	64.2
ornAna1	0.875	84 976	68.0	61.3	74	62.1	61.0	96	56.5
anoCar1	1.044	39 206	68.0	57.7	68	56.7	55.2	94	55.1
danRer5	1.468	75 481	67.4	54.4	61	50.2	48.8	94	52.1
xenTro2	1.532	73 440	69.4	54.8	61	56.1	54.4	94	51.3
petMar1	1.876	48 714	62.2	48.4	57	51.1	49.6	94	44.4

A value of, e.g. 70 means that 70% of the nucleotides were predicted correctly. The T_.5 columns show recovery rates for only those sites with a nucleotide probability/relative frequency above a 0.5 threshold, the ‘n/T’ columns show the recovery rates for reconstructed sequences with highest probability/frequency nucleotides at each site (no threshold). The ‘Dist.’ column shows the average distance to the nearest neighbor in the tree. ‘Total nt’ shows the total number of reconstructed nucleotides for each species and the ‘T_%’ columns denote the percentage of sites exceeding the threshold. Bold-faced maxAlike values are significantly better (P < 0.05) than both values of Freq with corresponding threshold and NN.

Fig. 3.

Dataset MZ44-1: recovery rates in percent for sequences reconstructed by maxAlike (ML), frequency-based consensus (Freq) and nearest neighbor (NN). Each point is one species plotted as its average distance to the phylogenetically nearest neighbor. (a) threshold 0.5. (b) no threshold.

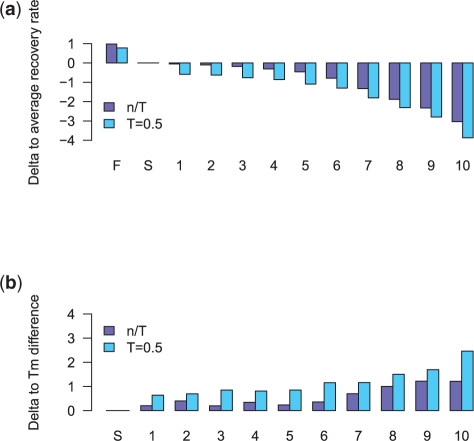
As expected, most of the species show an improved recovery rate when using an alignment-specific gene tree compared with the species tree. However, the improvement is very small for most species. The largest increase observed is about 4% (see Supplementary Tables S2 and S3), while the average increase of the recovery rate is 0.78% (threshold 0.5) and 0.98 (no threshold) across all species for MZ44-1. On the other hand, maxAlike reconstruction performance decreases with increasing error levels in the input trees. Figure 4a shows the average change of the total recovery rates in MZ44-1 for sequence reconstructions using trees with increasing bin number, i.e. split distance to the reference species tree (S). For trees in bins 1–5 (containing 70% of all trees), the average change is below 1% for both threshold 0.5/no threshold, but with increasing bin number, the recovery rate drops by maximum 4% on average across all species in bin 10. Supplementary Figure S5 shows the total recovery rates in each bin for all 44 species for dataset MZ44-1. The horizontal bars indicate the recovery rates of Freq (0.5 and no threshold). Supplementary Figure S6 shows the distribution of changes in the recovery rates for all species in each bin. These results show that for trees having an increasingly disturbed topology compared with the reference tree, the maxAlike prediction rate drops to the level of the frequency consensus sequence or even below for some of the species and this occurs on average for trees having a split distance of 23 or higher (bin 7). See Supplementary Figures S8 and S9 for the results of MZ44-2. However, when using enough sequence data for the tree inference in the first place, the estimated trees are sufficiently precise, so that maxAlike can make use of the information in the tree for a better reconstruction performance and so outperforms nearest-neighbor and frequency consensus sequences. Supplementary Figure S4b shows the distribution of the split distances for inferred trees. Even when using only three loci instead of one for the tree construction, there is a significant shift toward a smaller split distance, i.e. a more accurate tree topology. This becomes even more apparent as more sequences are used for the tree inference. The majority of the trees we estimated from randomly chosen loci have a split distance to the species tree of less than 23 (bins 1–6).

Fig. 4.

Dataset MZ44-1: (a) Average change of total recovery rates across all species for different sets of input trees: gene tree (F); reference species tree (S); (1–10) bins with trees estimated from other genomic loci; increasing bin number corresponds to higher topological distance to reference tree. (b) Change in the T_m difference due to increased number of mismatches in the primer sequence.

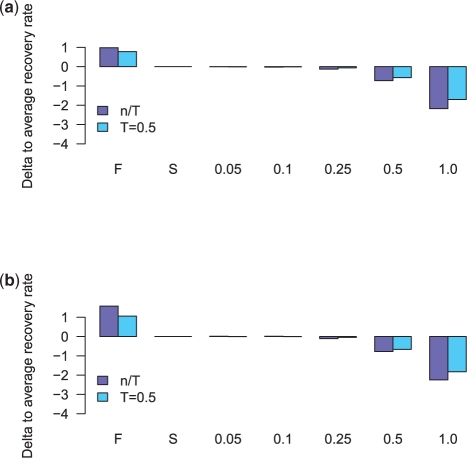
Similar results were observed for the datasets containing trees with increasingly distorted branch lengths. For input trees in the first three bins with relative normal errors of 0.05, 0.1 and 0.25 only a very small decrease in the total recovery rates is visible in all species for maxAlike (see Supplementary Figures S11 and S12 for the results of both datasets). When increasing the error to 0.5, the recovery rates drop by 0.7% (threshold 0.5) and 0.5% (no threshold) on average across all species. A relative error rate of 1.0 decreases the average recovery rate by 2.2% (threshold 0.5) and 1.7% (no threshold) in MZ44-1, see Figure 5. In this last scenario, maxAlike's performance drops down to the level of the frequency consensus for 6 of the 44 species (threshold 0.5) and 16 of 44 (no threshold) in MZ44-1.

Fig. 5.

Average change of total recovery rates across all species for different sets of input trees: gene tree (F); reference species tree (S); bins with trees having distorted branch lengths using the specified relative normal errors. (a) MZ44-1. (b) MZ44-2.

3.2 Primer design for unknown sequences

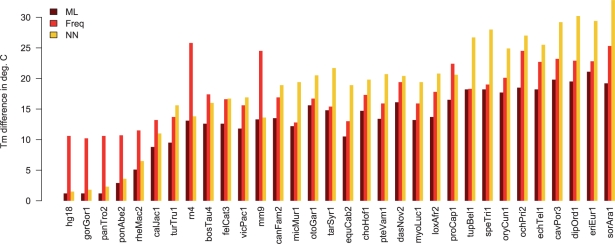
To measure the impact of an improved sequence reconstruction on the quality of PCR primers, we compared the expected melting temperature of the primer–template duplex to the actual melting temperature depending on mismatches between the primer and the template. Figure 6 shows the average difference of the expected T_m and the T_m of the actually formed duplex for the primers derived from maxAlike and Freq reconstructed sequences (both threshold 0.5) and the nearest neighbor sequence (NN) for dataset MZ44-1. Supplementary Tables S6 and S7 contain the average number of mismatches per primer sequence and the averaged T_m difference in each species for both datasets. For most species, the number of mismatches is much lower for the primers derived from the maxAlike reconstruction using the 0.5 threshold, compared with sequence reconstructions without threshold. Correspondingly, the T_m difference is also smaller. This difference is not as high between the threshold and no threshold reconstructions of the Freq method. In most species, the average T_m difference of the primers from the maxAlike predictions is significantly lower, compared with primers from Freq and NN, in particular when using reconstructed sequences with a threshold of 0.5. Across all species, the average T_m difference is ~26% (~4.6^○C) lower with the primers from maxAlike compared with Freq, and ~30% (~5.6^○C) lower compared with NN. The higher the phylogenetic distance to the target species, the larger the T_m difference becomes on average for all methods, but also the gap between maxAlike and Freq/NN increases. The T_m difference can be reduced up to 30%. In the closely related primates, the difference between all methods is smaller, with NN being almost as good as maxAlike, while Freq performs worse (~9.5^○C higher T_m difference than maxAlike). This observation follows the results from the sequence reconstruction. While NN performs well for target species with close neighbors, Freq is better for more distant target species. maxAlike outperforms both since it takes both the nearest neighbor and all other sequences into account for the reconstruction. Note, however, that the reported averaged T_m differences are biased toward lower values, since the cases of dinucleotide/extreme position mismatches, which would again reduce the melting temperature of the duplex, were not included in the T_m calculation. This bias increases with a higher phylogenetic distance of the target species and correspondingly a higher number of mismatches in the primer sequence. One would expect an ever higher gap between the maxAlike and the Freq/NN T_m differences, since the latter have significantly more of these mismatch types. In some cases, it was not possible for Primer3 to select a primer pair according to our specifications, when using the reconstructed sequences with the 0.5 threshold, because of a high number of unpredicted (‘N’) nucleotides. This was usually only a problem in short alignments and for species with a high branch length to its nearest neighbor, e.g. Pteropus vampyrus or Danio rerio. A reduced sequence reconstruction performance due to less accurate tree topologies of the input trees translates also into more mismatches in the selected primer sequences and thus in an increased difference between actual and expected primer T_m. Figure 4b shows the average increase of the T_m difference for primers derived from reconstructed sequences across all species using trees with increasing bin number, i.e. split distance to the reference species tree (S). Supplementary Figures S7 and S10 show the distribution of the changes in T_m difference for all species in each bin for both datasets. We observe a maximum 1^○C (9%) increase of the average T_m difference in the first 6 bins for MZ44-1. For input trees with large topological errors (bin 10), the T_m difference increases by 2.5^○C (30%) on average across all species. These results are similar to the sequence reconstruction, in that the change is moderate for trees in the first 5 bins, but becomes higher with increasingly erroneous trees.

Fig. 6.

Dataset MZ44-2: average differences of the expected and actual melting temperature T_m of the primer–template duplex for primers derived from maxAlike (threshold 0.5) and Freq (threshold 0.5) reconstructed sequences and nearest neighbor (NN) sequence for each species, sorted by average distance to its phylogenetically nearest neighbor.

4 DISCUSSION

The maxAlike algorithm estimates the nucleotide probabilities at each sequence position for an unknown sequence in a target species using a combination of homology information from a multiple sequence alignment and a phylogenetic tree. The calculated nucleotide probabilities can be used for homology search or for reconstruction of sequences on which primer design can be made.

In a benchmark dataset, we demonstrated that the inclusion of phylogenetic information in sequence reconstruction significantly improves the reconstruction accuracy compared with two standard approaches. For the comparison to the first standard approach, frequency-based consensus sequences, the maxAlike reconstruction rate is up to 10% higher in most target species, when using a suitable probability threshold. Taking the closest available phylogenetic neighbor (the second standard approach) as a prediction for the target species yields poor results in many cases and is often worse than the frequency consensus. Taking the sequence of the closest available phylogenetic neighbor as a prediction for the the target species is often worse than the frequency consensus (26 out of 44 species, Table 1). However, the difference to maxAlike is not large for sequence homologs in very proximate species.

On the other hand, the sequence reconstruction with maxAlike also improves when homologs of closely related taxa are available. In those cases, the reconstruction rate can reach as much as 99% accuracy, and is better than both the nearest neighbor and frequency consensus sequences. The better the reconstruction rate is, the better the precision of homology search programs becomes, e.g. when using PSSMs. Additionally, maxAlike provides information about highly variable sites through the estimation of mutation rates for each position. These positions could therefore be easily excluded from the homology search or primer design. When using a nucleotide probability threshold in the sequence reconstruction, the primers generated from these reconstructed sequences have significantly less mismatches to their target complement, compared with both the frequency consensus sequences as well as the nearest neighbor sequences. From that follows a reduced deviation from the expected melting temperature of the primer–template duplex, which increases the chance of a successful PCR. In some cases, e.g. for short sequences or distant target species, a suitable primer pair could not be found, because not enough positions exceed the chosen probability threshold. To compensate for this, the threshold can successively be lowered or the length of the primers could be reduced. Compared with primer design using the two standard methods, frequency consensus and nearest neighbor, primers designed from sequences reconstructed by maxAlike on average exhibit a reduction of the difference between the expected and real melting temperatures by 26%. As expected in the regime of short evolutionary distances, we observe that the nearest neighbor method is significantly more accurate than the frequency-based methods. Nevertheless, maxAlike yields slightly better results. In the regime of large distances, where the overall accuracy of all methods drop, the frequency-based approach outperforms the nearest neighbor approach. Again maxAlike performs best.

Our results show, that a general species tree already yields good reconstruction results, but a slightly higher reconstruction rate can still be obtained by using an optimized gene tree for the particular gene family under study. If a gene tree is available, e.g. for filling gaps in an otherwise complete sequence, the gene tree should be preferred in order to maximize the number of correctly predicted nucleotides. However, the exact position of the target species in a certain gene tree is usually unknown, and the reconstruction of the homolog is based on a general species tree or a tree inferred from other genomic loci. Ideally, this tree is constructed by all available sequence data from the target species, combined with the homologs of these sequences in other closely related organisms. Even if no general species tree is available, we observe that the prediction performance of maxAlike is robust against the variations in the input tree generated by randomly selecting genomic loci for estimating the tree. Furthermore, we demonstrated that more accurate tree topologies can easily be obtained by a small increase in the number of loci that are used for the tree inference. The more accurate the tree topology is, the more information from the tree can be used for the sequence reconstruction by maxAlike and the higher the prediction performance becomes, e.g. the accuracy of the sequence reconstruction only decreases by 1% on average across all species for 70% of the input trees in MZ44-1. The general robustness against erroneous tree topologies in the sequence reconstruction translates to the design of PCR primers, which in turn leads to more accurately predicted primer sequences compared with the other methods. The prediction accuracy has also been shown to be robust against distortions in the branch lengths of the input tree. Of course, maxAlike can also be used with phylogenetic trees from databases, such as treebase (Piel et al., 2003) or TreeFam (Li et al., 2006).

Future directions include taking RNA structure explicitly into account. Several studies showed that potential ncRNAs in genomic sequence have altered their primary sequence while maintaining their secondary structure and the sequence-based alignments are insufficient to represent the RNA structure across related species (Torarinsson et al., 2006, 2008). This calls for an RNA version of maxAlike, in which RNA structural alignments are used rather than primary sequence alignments.