Principal network analysis: identification of subnetworks representing major dynamics using gene expression data

Abstract

Motivation: Systems biology attempts to describe complex systems behaviors in terms of dynamic operations of biological networks. However, there is lack of tools that can effectively decode complex network dynamics over multiple conditions.

Results: We present principal network analysis (PNA) that can automatically capture major dynamic activation patterns over multiple conditions and then generate protein and metabolic subnetworks for the captured patterns. We first demonstrated the utility of this method by applying it to a synthetic dataset. The results showed that PNA correctly captured the subnetworks representing dynamics in the data. We further applied PNA to two time-course gene expression profiles collected from (i) MCF7 cells after treatments of HRG at multiple doses and (ii) brain samples of four strains of mice infected with two prion strains. The resulting subnetworks and their interactions revealed network dynamics associated with HRG dose-dependent regulation of cell proliferation and differentiation and early PrPSc accumulation during prion infection.

Availability: The web-based software is available at: http://sbm.postech.ac.kr/pna.

Contact: dhhwang@postech.ac.kr; seungjin@postech.ac.kr

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Systems biology attempts to describe systems behaviors in terms of dynamic operations of biological networks (Hood et al., 2004). A number of gene expression studies have been performed to understand network dynamics over multiple conditions (Hwang et al., 2009). However, it is challenging to decode network dynamics from the multi-conditional gene expression data due to (i) diverse activation patterns of nodes over multiple conditions; (ii) dense interactions (edges) among the nodes; and (iii) the large size of the global network.

To understand complex network dynamics, it is common in systems approaches to extract major subnetworks (Hwang et al., 2009). The common tasks for generation of such subnetworks include: (i) identification of differentially expressed genes (DEGs) between various conditions, (ii) clustering of the DEGs based on their differential expression patterns and (iii) reconstruction of subnetworks using the genes belonging to major clusters and their interaction partners from the global interactome. However, as the numbers of both time points and conditions increase, the generation of major subnetworks using this approach often becomes intractable due to the complexity in the above tasks.

There have been several methods for automatically generating active subnetworks (ASs) that are composed of (i) active nodes showing significant changes over conditions (node-based methods) or (ii) active edges having the interacting nodes whose gene expression levels were co-varied over conditions (edge-based methods). Most of node-based methods (Ideker et al., 2002; Scott et al., 2005; Sohler et al., 2004) generate ASs by identifying subnetworks including mainly the active nodes, but they do not consider the correlation between activation patterns of the interacting nodes. An edge-based method (Guo et al., 2007) results in a subnetwork composed of the active edges for which the interacting nodes are co-varied in their gene expression levels. However, both node- and edge-based methods generate the subnetworks with a mixture of different activation patterns, which makes it inefficient to sort out complex network dynamics in terms of the resulting subnetworks.

We propose a new concept of ‘principal subnetwork’ for analyzing complex network dynamics. We define a principal subnetwork (PS) by an AS including both nodes and edges that share a particular major (or principal) activation pattern. Several PSs showing a number of major activation patterns can be generated from a single dataset. Thus, analyzing the individual PSs and their interactions can allow us to efficiently sort out complex network dynamics. In this study, we developed principal network analysis (PNA) that can automatically (i) capture principal activation patterns over multiple conditions and (ii) generate the corresponding protein and metabolic subnetworks (PSs) to the captured patterns based on the orthogonal non-negative matrix factorization (ONMF). We demonstrated the utility of PNA by applying it to three datasets. The results showed that the collective analysis of PSs and their interactions can effectively generate network-driven hypotheses for given problems.

2 MATERIALS AND METHODS

2.1 A synthetic network and synthetic gene expression data

2.1.1 Development of a synthetic network model

A geometric random graph has been used as a protein network model (Higham et al., 2008). To build the network model, we produced a geometric random graph by distributing nodes at random uniformly on the unit square and assigning an edge to every pair of nodes for which the corresponding nodes are close enough according to the Euclidean distance (in this study, we used 0.25 as a cutoff). Using this procedure, we generated a network model including 100 nodes and 748 edges (Supplementary Figure S1A).

2.1.2 Generation of synthetic gene expression data

We then generated synthetic time-course gene expression for the network model. We used 13 different time points at two different conditions. For the 60 nodes among 100 nodes in the network model, we categorized them into six groups, each of which includes ten nodes and then assigned one of the following six gene expression patterns to each group (Supplementary Figure S1B and Figure 2A): (i and ii) time-dependent up-regulation (log2-fold change = 1) during the early and late stages, respectively, (iii) condition-dependent up-regulation, and (iv–vi) the same patterns as in (i–iii) but for down-regulation (log2-fold change = −1). The remaining 40 nodes were set to have no change (log2-fold change = 0) over time. Finally, we added the Gaussian noise [mean = 0 and standard deviation (SD) = 0.2]. As a result, we generated a 100 × 13 × 2 three-dimensional array containing log2-fold changes ranging from −1.5606 to 1.6542 (note that log2-fold change = 0 at time zero for all genes).

2.2 Interactome and gene expression data

2.2.1 Human interaction data

We gathered human interaction data from NCBI and KEGG (Kanehisa and Goto, 2000) database. There are (i) 37 811 non-redundant protein–protein and protein–DNA interactions (upper panel in Figure 1C; 33 370 from NCBI and 10 092 from KEGG) and (ii) 6752 synthetic pseudo-interactions, pairs of metabolic enzymes involved in two consecutive metabolic reactions (bottom panel in Figure 1C; 5739 reactions from KEGG) for 9663 proteins.

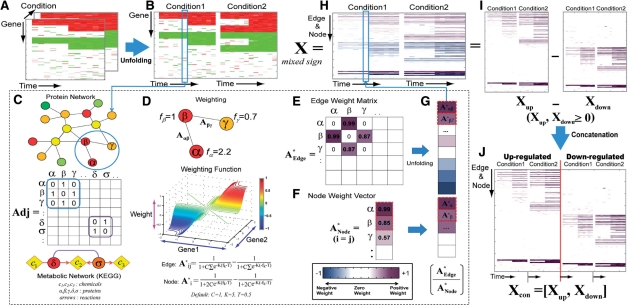
Fig. 1.

Construction of an activation weight matrix. PNA first transforms multi-dimensional expression data into log2-fold changes (A) and unfolds it into a two-dimensional matrix (B). We then represent the edges with the adjacency matrix Adj (C). Using a weighting function (D), the PNA then computes both edge (A^*_Edge) and node (A^*_Node) activity weights (E and F), unfolds the A^*_Edge into a vector and concatenates it with A^*_Node, resulting in a weight vector for each condition (G and H). For the ONMF analysis, we represented the activity weight matrix (X) with X = X_up−X_down (I) and then concatenated X_up and X_down to result in X_con = [X_up, X_down] (J).

2.2.2 Gene expression profiles of heregulin-treated MCF7 cells

We obtained time-course gene expression data from GEO database (GSE6462). The data were collected from MCF7 breast cancer cells that were treated with a growth hormone, heregulin (HRG), at four different doses of 0.1, 0.5, 1 and 10 nM (Nagashima et al., 2007). The mRNA expression levels for 22 277 probes (12 791 genes) were measured at seven time points (5, 10, 15, 30, 45, 60 and 90 min) after treatment of HRG at each dose, resulting in a 22 277 × 7 × 4 dataset, as well as a control with no HRG treatment.

2.2.3 Gene expression profiles of prion-infected brain tissues

We obtained seven time-course gene expression profiles from ArrayExpress (E-MTAB-76). The data were collected from five strains of mice (B6, B6.I, FVB, Prnp0/1, and Tg4053) infected with two prion strains (RML and 301V; Hwang et al., 2009): (i) B6-RML, (ii) B6-301V, (iii) B6.I-RML, (iv) B6.I-301V, (v) FVB-RML, (vi) Prnp0/1-RML and (vii) Tg4053-RML. See Supplementary Table S1.

3 PNA FRAMEWORK

3.1 Generation of an activity weight matrix

3.1.1 Evaluation of activity of edges and nodes

We represented the synthetic time-course gene expression data as a 100 × 7 × 4 three-dimensional array including mRNA levels in 13 time points at two different conditions (Figure 1A). This array was then unfolded in condition-wise to form a 100 × 28 matrix (Figure 1B). The fold changes in each time point (the blue box in Figure 1B) were used to evaluate the activities of both nodes and edges. For this evaluation, we represented the edges (protein–protein, protein–DNA and pseudo-metabolic interactions) in an adjacency matrix Adj where Adj(i, j) = 1 when elements i and j interact with each other and Adj(i, j) = 0 otherwise (Figure 1C).

The activities of all these edges were computed as the edge weights using a weighting function (Figure 1D) including two multivariate logistic functions (Henrick and Bovas, 1973):

where f_i and f_j are the log2-fold change values of the genes corresponding to the interacting proteins i and j. Also, C and K (C = 1 and K = 5 by default) are the parameters controlling the shape of the multivariate logistic distribution, and T is a shifting parameter (0.5 by default) added to produce zero when f_i and f_j are both zeros. In the above equation, the first term captures co-activation of genes while the second term, the origin symmetry of the first term, captures co-repression. This logistic function-based weighting of the edges effectively prevents ONMF from being biased toward the samples with large fold change value. This function results in (i) a positive weight (up to 1) if both f_i and f_j have positive log2-fold changes (e.g. A_αβ = 0.99 for the α − β edge with f_α = 2.2 and f_β = 1 in Figure 1D), suggesting that the interaction is likely to be active in the condition; (ii) zero either when both f_i and f_j are zero, or when f_i and f_j have the opposite signs; and (iii) a negative weight (up to −1) if both f_i and f_j have negative log2-fold changes. These activities of edges are then deposited into the edge weight matrix (Figure 1E). Similarly, the node weights were computed using the same weighting function, assuming that each node forms a homodimer, and then arranged into a 100 × 1 node weight vector A_Node(k) (Figure 1F). The edge weight matrix was then unfolded into a vector and concatenated with the node weight vector, resulting in a weight vector for each condition (Figure 1G). Finally, this weight vector is added as a column to the whole weight matrix (Figure 1H). Thus, the resulting weight matrix (X) contains the activity information of nodes and edges over all the conditions.

3.1.2 Conversion of the weight matrix to a non-negative matrix

A non-negative matrix factorization (NMF; Lee and Seung, 1999) requires the input matrix to be non-negative. To generate a non-negative matrix, we first represented the weight matrix as X = X_up − X_down · X_up is the weight matrix (X) whose negative elements were replaced with zeros, whereas X_down is X whose positive elements were replaced with zeros and the negative elements were changed into their absolute values (Figure 1I). These two matrices were then concatenated to generate a non-negative matrix (X_con = |X_up, X_down|; Figure 1J). NMF can now capture relationships between up- (X_up) and down-regulation (X_down). See Supplementary information 1 for details.

3.2 Application of Orthogonal NMF to the weight matrix

3.2.1 Orthogonal non-negative matrix factorization (ONMF)

Given a non-negative matrix X_con (N × M), the NMF (Lee and Seung, 1999) iteratively computes N × k basis matrix (W) and k × M activation matrix (H) so that ||X_con − WH||₂ is minimized, where ||·||₂ represents the Frobenious norm. NMF has been successfully applied to various data including gene expression data (Brunet et al., 2004; Kim et al., 2003). Several variants of NMF have been developed by adding extra-constraints for their own purposes. For example, non-smooth NMF (nsNMF) employed a constraint to ensure the sparseness in the bases and activations (Pascual-Montano et al., 2006).

Among various NMF methods, we employed orthogonal NMF (ONMF) to generate non-redundant subnetworks. ONMF (Yoo and Choi, 2008) imposes an orthogonality constraint on either W or H (W in this study):

where I is an identity matrix. The orthogonality constraint on W results in as non-redundant weights of nodes and edges in each pattern as possible, thus resulting in non-redundant subnetworks. Non-redundancy among subnetworks is useful for interpreting the networks. For the discussion on determination of the number of basis, see Supplementary information 2.

3.2.2 Summarization of ONMF solutions

Like other NMF methods, ONMF also suffers from the local minima problem. To resolve this problem, we applied ONMF to the same weight matrix (X_con) n times (n = 30 was used in this study) with different initialization and then used (i) a metaclustering method (Badea, 2005) and (ii) a template-based method to summarize the resulting n Hs and Ws (Supplementary information 3 for details). We implemented metaclustering, as described in Badea (2005), except that we used ONMF instead of the standard NMF. To summarize the n Hs and Ws, metaclustering performs another NMF including a random initialization, which tends to result in a different solution depending on the initialization.

Thus, we developed an alternative template-based method that can result in a unique solution given n Hs (templates) and Ws. This method selects the most representative H and W among the n templates as a solution. For a pair of templates, they are rewarded by one whenever a pair of rows (activations) from the two Hs is the same (correlation coefficient >0.99): thus, the maximum score between the two Hs is the number of bases when the two Hs share all the patterns. Using this scheme, for each template, we computed the scores between the template and n − 1 others and then added up the scores to generate a cumulative score. This procedure was repeated for all n templates. Finally, the representative template (H_f), as well as the corresponding W_f, was chosen as the one with the largest cumulative score. Both summarization methods are implemented in PNA software. After obtaining W_f and H_f from these methods, we ordered the columns of W_f and rows of H_f in the descendent manner of Euclidean norms of the rows of H_f to prioritize the activation patterns according to their significance (Figure 2B).

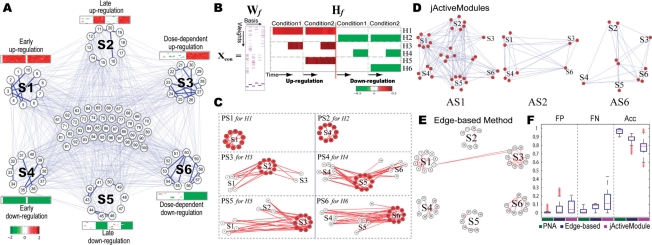
Fig. 2.

A PNA application to the synthetic data. Six differential expression patterns were assigned to the nodes in the synthetic network (A). ONMF correctly captured the six differential expression patterns (B). The resulting PSs successfully represented the activation patterns in the synthetic data (C). We also obtained the active subnetworks using jActiveModules (D) and the edge-based method (E) and then compared the performance of PNA with those of the other two methods using FP, FN and accuracy (Acc) (F). See the text for details.

3.3 Reconstruction of the principal subnetworks (PSs)

3.3.1 Generation of the PSs from ONMF results

We reconstructed the PS (e.g. Figure 3) for each activation pattern resulting from ONMF by selecting both nodes and edges significantly contributing to the pattern. Such nodes and edges were selected as the ones with P-values of bases values (W_f) less than a cutoff value (e.g. 0.01 or 0.05). To compute the P-value for each basis value, we first randomly permuted the elements of X_con to generate X_rand and then applied ONMF to X_rand, resulting in W_f−rand and H_f−rand. Unlike W_f resulted from the original X_con, which would include systematic activation patterns in the data, W_f−rand and H_f−rand should include random activation patterns. We then computed an empirical distribution of such random basis values (W_f−rand; Supplementary Figures S2A and S2C). Finally, we computed a P-value of the observed basis value (an element of W_f) for each node (or edge) by the right-sided test using the empirical distribution. Due to the difference between the distributions of basis values for nodes and edges, the above procedure including: (i) randomization of X_con, (ii) estimation of the empirical distribution and (iii) computation of P-values was done separately for nodes and edges (Supplementary Figure S2). See Supplementary information 4 for details. Using the selected nodes and edges, initial PSs are constructed. Note that PNA separately reconstructs protein and metabolic PSs by using protein–protein/protein–DNA interactions and pseudo-metabolic interactions, respectively.

Fig. 3.

Application of PNA to the gene expression data from HRG-treated MCF cells. ONMF captured six activation patterns in the data (A). Differential expression of the top 20 genes is well-correlated with the activation patterns in A (B). To investigate HRG dose dependent dynamics, we reconstructed the PS for H5 (HRG dose-dependent activation) using the selected nodes (red) and edges (C). The blue boundary indicates that the corresponding node also belongs to PS1. We then explored the interactions between two PSs for H6 (low-dose specific down-regulation; red nodes) and H4 (high-dose specific up-regulation; red boundary) (D). See the text for details.

3.3.2 Removal of false positive nodes and edges

After constructing the initial PS for each activation pattern, we further removed the insignificant nodes (e.g. node P-value >0.05) that do not densely interact with the significant nodes. They tend to be included due to the edges for which interacting nodes have partially shared expression patterns (e.g. early up-regulation in S1 of Figure 2A) with the activation pattern (e.g. late up-regulation in S2 of Figure 2A). First, we identified all nodes with P-values larger than a cutoff value (e.g. 0.05; white nodes in Supplementary Figure S3). Then, for each identified node, we counted the number of significant interactors (e.g. node P-value <0.05). Finally, we removed those nodes (e.g. small white nodes in Supplementary Figure S3) having the number of significant interactors less than another user-defined cutoff value l (l = 2 by default for protein networks and l = 1 for metabolic networks).

4 RESULTS AND DISCUSSION

4.1 Application of PNA to synthetic gene expression data

To demonstrate the utility of PNA, we first applied it to the synthetic gene expression data (see Section 2.1.2). Figure 2A shows six differential expression patterns each of which was assigned to the ten nodes in a subnetwork: (i) early up-regulation to the 10 nodes in S1; (ii) late up-regulation in S2; (iii) condition-dependent up-regulation in S3; and (iv–vi) the same patterns as in i–iii) but for down-regulation in S4–S6. Note that ‘zero’ exists at time zero for every pattern including early up and down-regulated genes (S1 and S2 in Figure 2A; same in Figures 2C and 3A and B). For the PNA application, we used the following parameters and cutoff values: C = 1, K = 5 and T = 0.5 for the weight matrix construction, the number of basis (k) = 6 for ONMF, P-value cutoff = 0.05, and the reduction cutoff (l) = 2. The rows of H_f in Figure 2B show that ONMF successfully captured the six differential expression patterns in the synthetic expression data (e.g. H1 captured the early up-regulation in S1 while H4 captured late down-regulation in S5). Six principal subnetworks (PSs) corresponding to H1–H6 are shown in Figure 2C. The red nodes and edges represent the selected ones with P-values <0.05 (see Section 3.3.1). Each PS (e.g. PS1) correctly captured the 10 nodes (e.g. the nodes in S1) and all the edges among the 10 nodes (e.g. thick lines in S1 of Figure 2A) in the subnetwork showing the corresponding activation pattern (e.g. H1). Other than PS1 and PS2, the PSs included the white nodes that were selected by their edge P-values (<0.05), not by their node P-values (≥0.05), and for which the numbers of significant interactors (red nodes) were larger than or equal to the reduction cutoff (l = 2). For example, PS3 that represents S2 having late up-regulation included the white nodes in S1 due to (i) the partially shared activation patterns (i.e. their edge P-values <0.05) between the late (S2) and early up-regulation (S1) and (ii) their intense interactions (l ≥ 2) with the red nodes in S2. Note that PNA attempts to include such white nodes, which can be removed by using their node P-values, because they can improve the interpretation of PS3 by providing the information of interactions between S1 and S2.

We then compared the PSs from PNA with the active subnetworks (ASs) from jActiveModule (Ideker et al., 2002) and an edge-based method (Guo et al., 2007). To generate the ASs using jActiveModule, we first computed P-values of all the genes being differentially expressed by chance at each time point and then used them as the input to jActiveModule plugin (ver 2.23) in Cytoscape (ver 2.6). We used the following parameters: overlap threshold = 0.8, enabled ‘adjust score for size’ and ‘regional scoring’, search depth = 1 and max depth from start nodes = 2. For the edge-based method, we developed background models, as described in Guo et al. (2007), and then performed simulated annealing with the following parameters: the number of iteration = 30 000, starting temperature = 1, and ending temperature = 0.001. Figure 2D shows the three ASs from jActiveModule (see the other ASs in Supplementary Figure S4). Each AS includes the nodes (red) selected by jActiveModule and all the edges existing between the selected nodes. jActiveModule does not discriminate the six differential expression patterns in terms of the ASs (e.g. AS1 includes the nodes from all subnetworks S1–S6). Figure 2E shows the AS resulting from the edge-based method. Similarly to jActiveModuel, the AS tends to include all the nodes with the six differential expression patterns and the edges within the individual subnetworks (e.g. the edges in S1). Furthermore, it appears to fail to include the significant nodes (e.g. nodes 13, 17 and 18 in S2) with no interactions in the corresponding subnetwork. To compare the three methods in their performance, we performed a number of experiments for each method using different combinations of parameters (Figure 2F; Supplementary information 5). False positives (FPs) were defined by the nodes selected from the 40 nodes with no change (see the nodes in the middle of Fig. 2A) while false negatives (FNs) were defined by the nodes not selected from the 60 nodes in S1–S6. PNA outperformed the other two methods by achieving significantly higher accuracy than jActiveModule and the edge-based method (P = 2.568 × 10⁻⁶⁴ and 2.104 × 10⁻¹⁶² from KS test for PNA versus jActiveModule and PNA versus edge-based method, respectively). Note that Figures 2C–E were the results obtained by using one of parameter sets generating the median accuracy in the individual methods.

4.2 Application of PNA to gene expression data from HRG-treated MCF cells

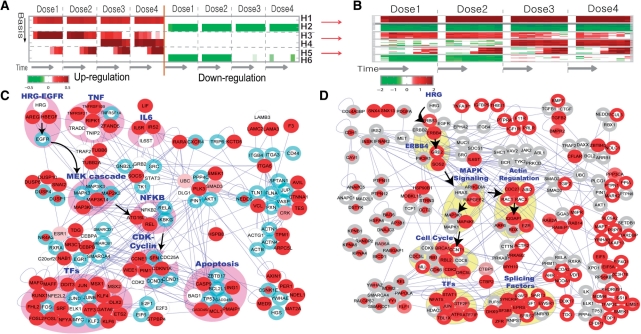
We also applied PNA to gene expression data collected from HRG-treated MCF7 cells to understand HRG dose-dependent dynamics in terms of PSs. In this application, we excluded pseudo-metabolic interactions to focus on the reconstruction of protein subnetworks using 37 811 protein interactions and used the same parameters and cutoff values used in 4.1. PNA resulted in the six activation patterns (the rows of H_f, sorted by their significance, in Figure 3A) including (i–ii) dose-independent early up- (H1) and down-regulation (H2); (iii) high-dose specific up-regulation (H4); and (iv) low-dose specific down-regulation (H6) and (v–vi) other dose-dependent regulations (H3 and H5). Differential expression patterns of top 20 nodes with the smallest node P-values (Figure 3B) together with those in Supplementary Figure S5 show that PNA captured consistent patterns in the data (Supplementary information 6).

Figure 3C shows the PS that describes biological processes with slow activation after the HRG treatment in a dose-dependent manner (H5). The same node coloring scheme was used as in Figure 2C. The PS shows several modules associated with (i) HRG-EGFR, (ii) TNF and (iii) IL6 signaling, (iv) their downstream pathways (e.g. MAPK and NFKB), (v) transcriptional regulators (e.g. JUN, FOSL1/2 and SRF), (vi) CDK-cyclin module (e.g. CDKN1A and CCNE1) and (vii) apoptosis related module (e.g. CASP9, MCL1, GADD45 and PMAIP1). The PS reveals these modules closely interact with each other: EGFR to which HRG binds interacts with MAPK pathways, which then interacts with the NFKB pathway (Belich et al., 1999) via MAP kinases (MAP3k14 and MAP3K8) (see the arrows in Figure 3C). This association is consistent with previous findings that HRG can promote cell proliferation by inducing CDKN1A and Cyclins (e.g. CCNE1) via MAPK-NFKB pathways (Foehr et al., 2000; Yang et al., 2008).

PNA provides two ways to explore the interactions among the PSs. First, we can indicate the shared nodes and edges between two PSs (e.g. PS1 and PS5 for H1 and H5, respectively) using either PS as a reference PS (e.g. PS5), thus permitting to explore the interaction between PSs in the context of the reference PS. Figure 3C shows the interactions between PS1 (dose-independent early up-regulation) and PS5 (dose-dependent late up-regulations) using the PS5 as a reference PS. The nodes belonging to PS1 are indicated by the blue boundaries. Interestingly, most of white nodes (EGFR, TNFRs, MAPKs and NFKB) have blue boundaries, indicating dose-dependent functional links between PS5 and PS1.

Second, we can reconstruct different PSs and then combine them to explore their interactions. Figure 3D shows the combined PS of two PSs for H6 (low-dose specific down-regulation) and H4 (high-dose specific up-regulation). The selected nodes for PS6 and PS4 were indicated by red node and boundary colors, respectively. Interestingly, the combined PS shows a number of shared nodes between PS4 and PS6 that were down-regulated in low dose of HRG but up-regulated in high dose. Focusing on these shared nodes, the combined PS shows two groups of network modules associated with HRG-dependent anti-proliferation and differentiation, which is consistent with previous findings (see Supplementary information 7). The PS further shows that these modules closely interact with each other: ERBB4 to which HRG binds interacts with MAPK pathways, which then interact with both cell cycle inhibitors (BRCA1 and RBL2) and actin regulation related modules (IQGAP1) (see the arrows in Figure 3D). Interestingly, both TGFB (TGFB2 and BMPR2) and splicing related molecules (SF3B1, DHX9, EPRS and ZFR) were shared in both PSs, suggesting their potential association with anti-proliferation and differentiation (see also Supplementary information 7). Note that each PS represents an averaged view of protein interactions most of which are expected to be transient and also includes an incomplete set of edges due to the yet incomplete interactome data.

4.3 Comparison of PSs from PNA with ASs from jActiveModule and an edge-based method

We then compared the PSs from PNA with the ASs from jActiveModule and the edge-based method. Both jActiveModule and edge-based method were applied as described in Section 4.1. Supplementary Figure S6A summarizes the results. Combining the numbers of nodes and edges in all subnetworks generated from each method (i.e. six PSs from PNA, six ASs from jActiveModule, and one AS from the edge-based method), PNA resulted in the subnetworks with the largest number of nodes (2714 nodes), compared to jActiveModule (1568 nodes) and the edge-based method (1793 nodes), while jActiveModule resulted in a larger number of edges (7801 edges) than PNA (5527 edges) and the edge-based method (2790 edges). Supplementary Figure S6B shows that 707 nodes were shared by the three methods, whereas 571 (jActiveModule), 189 (edge-based method), 992 nodes (PNA) were specifically identified by each method.

We compared the performance of the three methods by counting the number low-fold-change nodes (fold change ≤1.5 in all conditions) in their resulting subnetworks. The nodes selected by PNA but not by either jActiveModule or edge-based method (Supplementary Figure S6C) showed clear differential expression patterns (Supplementary Figure S6D), which are well-correlated with Hs in Figure 3A, thus indicating a small number of low-fold-change nodes (56 out of 2714). The nodes in the boxes were included in the corresponding PSs because of their composite differential expression. For example, the nodes in the box of PS6 showed both low-dose specific down-regulation (H6 in Figure 3A) and high-dose specific up-regulation (H4 in Figure 3A) and thus included in both PS4 and PS6 (the shared nodes in Figure 3D). For jActiveModule and the edge-based method, we counted low-fold-change nodes among the nodes selected by either of two methods but not by PNA. Supplementary Figures S6E and S6F show a large number of low-fold-change nodes selected by jActiveModule (465 out of 657) and edge-based method (107 out of 275), respectively.

Finally, we compared the performance of ONMF in identifying principal activation patterns with that of non-smooth NMF (nsNMF), another NMF variant. From this comparison, we found that ONMF generated non-redundant PSs while nsNMF generated redundant subnetworks and further that the differential expression patterns of the selected nodes by nsNMF were not correlated with the corresponding activation patterns (see Supplementary Figures S5 and S7).

4.4 Application of PNA to gene expression data from prion infected brain tissues

We also applied PNA to gene expression data collected from prion-infected brain tissues during the course of prion disease (see Section 2.2.3). Before applying PNA, we performed an additional normalization on the log₂-fold changes (see Supplementary information 8). In this application, we included pseudo-metabolic interactions together with protein interactions to generate both protein and metabolic subnetworks. We used the same parameters except for the number of bases (k) = 20 and P-value cutoff = 0.01. Among the 20 activation patterns resulted from PNA (Supplementary Figure S8), Figure 4A shows top four activation patterns. Differential expression patterns of top 20 genes with the smallest P-values are well-correlated with the four activation patterns (Figure 4B). The most significant activation pattern (H1) shows up-regulation specific to the four conditions having early accumulation of PrP^Sc after prion inoculation (see Supplementary information 9).

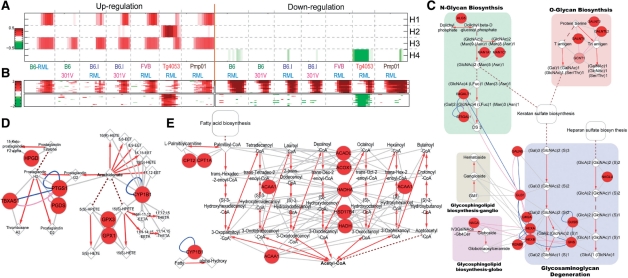
Fig. 4.

Application of PNA to gene expression data from prion-infected tissues. The results show four strain-combination-dependent activation patterns (A), as well as differential expression patterns of top 20 genes in each basis (B). Both PS (Supplementary Figure S9) and PMS (Supplementary Figure S10) for basis 1 (early PrP^sc accumulation) using the significant nodes (red) and edges were reconstructed. Three pathways of the PMS (GAGs, fatty acids and arachidonates to prostaliandins; C–E), previously reported to be associated with PrP^sc accumulation are shown. The round, diamond and octagon nodes indicate proteins, metabolitess and glycans, respectively. Red arrows indicate metabolic reactions, and gray edges indicate interactions between enzymes and either substrates or products. See the text for details.

To investigate cellular processes associated with early PrP^Sc accumulation, we then reconstructed PS1 (Supplementary Figure S9). The PS1 includes the modules related to (i) microglial/astrocytic activation (complement activation, cell adhesion, cell motility, anti-apoptosis and several signaling pathways including FcR-PLC, MAPK, Tnf-NFkB, ILs-Jak-Stat and Tgf-Smad pathways), (ii) ECM reorganization (e.g. MMPs and TIMP2) and cell-ECM interactions (collagens, integrins and cytoskeleton) and (iii) lipid homeostasis. The PS1 suggests that these cellular processes have potential association with early PrP^Sc accumulation. To explore the interactions between these processes and the ones commonly activated in all of the seven conditions (H3 in Figure 4A), we added blue boundaries to the nodes selected by PS3 for H3. The shared nodes (red node and blue boundary colors) between PS1 and PS3 indicate that they are commonly activated in all seven combinations and further activated in the four conditions with early accumulation of PrP^Sc, suggesting that the additional activation may be responsible for the early accumulation.

Supplementary Figure S10 shows a principal metabolic subnetwork (PMS) for H1. Three pathways of the PMS, previously reported to be associated with early PrP^Sc accumulation (Hwang et al., 2009), were shown in Figures 4C–E. The three pathways indicated the increased degradation of GAGs (potential PrP^Sc receptors; Figure 4C), fatty acids (components of sphingolipids; Figure 4D) and arachidonates to prostaliandins (inflammation mediators; Figure 4E).

5 CONCLUSION

This study presents PNA that can efficiently identify activation patterns from the data showing complex dynamics and can also generate their associated subnetworks (PSs). We demonstrated the utility of this method by applying it to three datasets. The results showed that PNA effectively captured major activation patterns in the data and generated their associated PSs. As a result, the collective analysis of these PSs and their interactions allowed us to generate a couple of network-driven hypotheses regarding (i) dose-dependent dynamic effects of HRG on cell proliferation and differentiation and (ii) key processes controlling early PrP^Sc accumulation. These hypotheses can be the subjects of detailed functional studies. In summary, the collective analysis of PSs and their interactions would support effectively generating network-driven hypotheses for various problems in systems biology.

Funding: Korean MEST grants (FPR08A1-050, R15-2004-033-07002-0 and 2010-0028453), Korean MOHW grants (A080768), NRF grants (No. 2010-0014306), WCU Program (R31-2008-000-10100-0 and R31-2008-000-10105-0); Biogreen 21(grant 20080401-034-041-008-02-00); NIH grant NS41997, and ISB-University of Luxemburg program.

Conflict of Interest: none declared.