Switch and template pattern formation in a discrete reaction-diffusion system inspired by the Drosophila eye

Abstract

We examine a spatially discrete reaction diffusion model based on the interactions that create a periodic pattern in the Drosophila eye imaginal disc. This model is known to be capable of generating a regular hexagonal pattern of gene expression behind a moving front, as observed in the fly system. In order to better understand the novel “switch and template” mechanism behind this pattern formation, we present here a detailed study of the model's behavior in one dimension, using a combination of analytic methods and numerical searches of parameter space. We find that patterns are created robustly provided that there is an appropriate separation of timescales and that self-activation is sufficiently strong, and we derive expressions in this limit for the front speed and the pattern wavelength. Moving fronts in pattern-forming systems near an initial linear instability generically select a unique pattern, but our model operates in a strongly nonlinear regime where the final pattern depends on the initial conditions as well as on parameter values. Our work highlights the important role that cellularization and cell-autonomous feedback can play in biological pattern formation.

1. Introduction

Scientists have long been fascinated by the ability of biological systems to organize themselves into complex structures. The appearance of periodic patterns of gene expression and cell fate during animal development, in particular, has been studied for some time; starting with the famous work of Turing [1], a number of elegant mechanisms have been suggested that might underlie such pattern formation [2-5]. Only relatively recently, however, has it become possible to subject these ideas to direct experimental tests and to reconcile them with descriptions more firmly grounded in known genetic and molecular interactions. While confirming the utility of many of the classic proposals, this ongoing work has also made clear that further insights will be required to explain the richness and robustness of pattern formation during development [6-8]. In one example of the newer generation of models informed by detailed genetic studies, we argue in a separate communication that a novel switch and template mechanism is responsible for the hexagonal pattern of gene expression seen in the eye imaginal disc of the fruit fly Drosophila melanogaster [9]. Here, we give a detailed analysis of this new mode of pattern formation in its simplest, one-dimensional form.

The Drosophila eye imaginal disc is a monolayer epithelium—that is, a roughly two-dimensional sheet of cells—found in the fly larva and destined to develop into the adult fly's retina [10]. During the larval stage, a moving front of differentiation sweeps across the disc, leaving in its wake a regular lattice of single cells expressing the gene atonal (ato) and fated to become R8 photoreceptors [11-14]. These R8 cells then induce surrounding cells to attain other photoreceptor and support cell fates. The support cells surrounding a given R8 in turn secrete one of the ∼750 lenses on the surface of the compound eye, which are arranged in a startlingly regular two-dimensional hexagonal packing (Fig. 1). The ordered packing of the lenses thus reflects the original pattern of ato expression. A large body of genetic experiments gives a qualitative picture of the regulatory network responsible for creating this expression pattern, making the eye disc an excellent model system in which to study biological pattern formation.

Figure 1.

Scanning electron micrograph of the adult Drosophila eye. Each round facet is the lens of a photoreceptor cluster called an ommatidium. Each ommatidium is founded by a single photoreceptor neuron, the R8 cell, which is specified during larval development. The dramatic hexagonal order visible here is first observed in the spatial arrangement of these R8 cells. (Public domain image courtesy of Dartmouth Electron Microscope Facility.)

In this paper, we consider a model abstracted from the experimentally determined interactions controlling ato expression. This model distills the regulatory network down to its essential features by lumping superficially redundant genes into single dynamical variables, each of which can be thought of as representing a given sort of regulatory feedback: cell-autonomous auto-activation (i.e. activation of gene expression in a given cell by high concentrations of the same gene's products within that cell, without any cell-to-cell communication); short-ranged, but cell-non-autonomous, inhibition; and longer-ranged activation. Together, these interactions are sufficient to generate a stable, stationary pattern behind a moving front, as seen in the fly eye disc. In the one-dimensional case that is our focus here, this pattern takes the form of single, regularly spaced cells with high ato expression separated by a number n ≥ 1 of cells with negligible ato levels. (In two dimensions the same model yields the observed hexagonal pattern and further makes testable predictions about the physiological patterning process in flies; these predictions, and their experimental confirmation, are discussed elsewhere [9].) The pattern is generated through the interaction of a bistable switch created by the cell-autonomous positive feedback with a spatially-varying template of diffusible inhibitor produced by cells behind the front. As the front—driven by the long-ranged activator—progresses, individual cells at the leading edge are induced to flip from the low to the high ato state. These cells then inhibit ato expression in their neighbors, creating a space between successive high ato cells whose size is determined by the range of the inhibitory signal.

Unlike many standard patterning scenarios, this switch and template mechanism does not involve any Turing-like instability [5], and the final pattern is not related in any simple way to a bifurcation of an initially uniform state. In particular, in contrast to patterns that can be described by an amplitude equation [15, 16], the pattern that appears behind the front in our model can depend on the initial conditions. This final pattern has some similarities with those found in other bistable activator-inhibitor systems [17-19], but differs from them in that it was selected by a moving front and that ato's strictly cell-autonomous self-activation greatly increases the variety of allowed patterns. Our model thus suggests a new, robust route to pattern formation in biological systems.

In the remainder of this paper, we first give an overview of the biology of the eye imaginal disc (Sec. 2) and then introduce our simplified mathematical model of pattern formation in this system (Sec. 3). In Sec. 4, we construct front solutions to our model in the limit that front propagation is much slower than the dynamics of ato expression and inhibitor secretion. In this limit, cells flip from low to high ato concentration almost instantaneously on the timescale of the long-ranged activator, and it is thus possible to calculate the activator profile created by a given pattern growing with a given speed; similarly, given an activator field, one can determine which cells will flip and when. The full solution is then found by self-consistently matching the behavior on these two different scales. Sec. 5 compares these predicted solutions to the results of simulating the full model for 640,000 randomly selected parameter sets and finds generally good agreement. The parameter scan shows that the behavior of the model is predictable and extremely robust to parameter variation, as long as the assumptions informing our analytic understanding are met. Finally, in Sec. 6 we compare our picture to other models of pattern formation in biology and discuss some broader implications of our results.

2. Biological background

Like all insects, Drosophila melanogaster has a compound eye composed of about 750 facets called ommatidia [20]. Each ommatidium in the adult eye is centered on a suite of 8 photoreceptor neurons (R1-8) and comprises a total of 20 cells [21]. The ommatidia are remarkable for their identical appearance and for the fact that they are packed into a perfectly crystalline hexagonal array in the adult eye (Fig. 1). These clusters of cells are not clonally derived, but begin differentiating from the unpatterned epithelium of the eye imaginal disc during the third instar of larval development [22]. Ommatidia are founded by single cells expressing the gene atonal which will eventually become R8 photoreceptors [23, 24]. These cells are specified and begin differentiating at the same time that a front of physical distortion (the morphogenetic furrow, MF) moves across the epithelium from posterior to anterior. In front of the MF the cells are unpatterned, while immediately behind the MF one finds a characteristic hexagonal pattern of single cells expressing ato against a background of undifferentiated cells. This process has been reviewed by several authors [11, 13, 14, 25]. In subsequent steps, each R8 cell interacts with the surrounding epithelium, inducing adjacent uncommitted cells to differentiate into the other neurons and support cells observed in the adult eye [23, 24, 26-31].

The progress of the MF is driven by the morphogen Hedgehog (Hh) secreted by the differentiating neurons behind the MF, and by the secreted factor Decapentaplegic (Dpp) expressed in the MF itself, both of which activate ato expression [32-34]. ato encodes a basic helix-loop-helix (bHLH) transcription factor and is the characteristic proneural gene for R8 specification [23, 24]. Its expression is initially diffuse, but is refined to single (future R8) cells as the MF passes [25, 35-37]. As ato expression becomes confined to a subset of cells, Ato also activates the zinc finger transcription factor Senseless (Sens), which in turn further activates ato expression and which continues to be expressed in R8 cells into adulthood [31, 38-40].

Because they appear at a moving front, the columns of R8 cells are specified sequentially (By convention, lines of cells running parallel to the MF are called columns, and those running perpendicular are called rows.). The positions of R8 cells in successive columns are found to be strongly correlated—each column is staggered along its long axis by one-half a row spacing, producing a hexagonal packing of R8s. It thus seems reasonable that each column might be specified using the previous one as a template, and several authors have suggested that inhibitory signals might serve to carry the needed information from one column to the next [25]. The idea that each ato-expressing cell is able to repress its neighbors, preventing or suppressing their ato production, is termed lateral inhibition. The molecular mechanism of this inhibition in eye discs is not known in detail, though the Notch (N) receptor is certainly integral to it, as is the Notch ligand Delta (Dl) [41-44]. Loss-of-function (LOF) of either of these genes results in an overpopulation of R8 photoreceptors [28, 37]. There are also other genes involved in the patterning process with more subtle phenotypes, among them scabrous [45, 46].

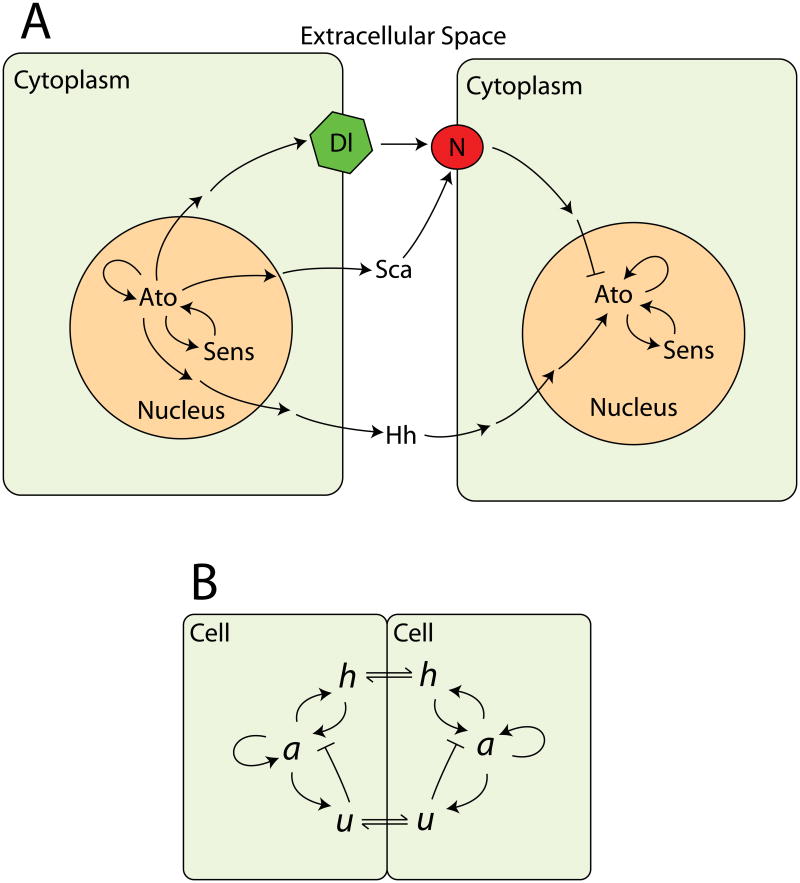
Fig. 2A summarizes the genetic interactions just described. Together, they conspire to create a moving front behind which single cells expressing ato appear in a regular pattern. With this genetic network in place, we now turn our attention to the construction of a model that captures its essential features.

Figure 2.

(Color online) Some interactions involved in patterning R8 photoreceptors in the Drosophila eye. (A) Intercellular and intracellular regulation involved in fate specification in the epithelium of the eye imaginal disc. Only signals originating at the left cell and being received by the right cell are shown, but all interactions may be assumed to be reciprocal. Pointed arrows show a positive, activating influence; blunt arrows signify inhibition. The locations of gene names reflect the subcellular localization of the gene product. This diagram is necessarily incomplete, and most of the signals transmitted really on other genes during their production and transduction. N, Notch; Dl, Delta, Hh, Hedgehog; Sca, Scabrous; Ato, Atonal; and Sens, Senseless. (B) The simplified model studied in this paper. Diffusible activation is represented by h, with inhibitory activity lumped into u. The variable a takes the place of the proneural genes ato and sens. The multitude of different compartments present in a tissue are ignored, with each cell being treated as a lattice site, and intercellular signals moving on this lattice by diffusion (signified by the bi-directional arrows).

3. The model

The network diagram of Fig. 2A incorporates three distinct sorts of feedback loops, mediated by secreted activators (Hh and Dpp), by cell-non-autonomous inhibitors (Dl, Sca, and others), and by strictly cell-autonomous interactions (direct Ato self-regulation and positive feedback through Sens). Presumably, there are functional reasons that the fly has a regulatory network that includes more than one representative of each sort of interaction. In making a first attempt to understand the basic pattern formation mechanism in the eye imaginal disc, however, it seems reasonable to elide these distinctions and to consider a model with only three variables, each representative of one of the three types of feedback. Indeed, such a simplified model, summarized in Fig. 2B, can capture many features of R8 patterning. The variable a plays roughly the role of atonal and directly activates its own expression, while h and u provide, respectively, non-autonomous activation and non-autonomous inhibition. (Elsewhere, we have considered a model with a fourth variable reminiscent of sens; the delay in the positive feedback that is thus introduced is important for accurately recapitulating all of the stages in the refinement of ato expression to a single cell, including the transient presence of so-called proneural clusters of ato-expressing cells, but it has little effect on the ability of the system to form a pattern [9].) Because of the central role played by cell-autonomous interactions in the eye disc, it is important that any model respect the discrete nature of the cells that make up the epithelium. Our model thus takes the form of a set of coupled lattice differential equations, with each lattice site representing a single cell. After non-dimensionalization, the governing equations in any spatial dimension take the form

$$\begin{array}{l}\frac{\partial a_x}{\partial t}=f_{n_a}\left(\frac{a_x}{A_a}\right)-a_x+G\cdot g_{m_h,m_u}\left(\frac{h_x}{H},\frac{u_x}{U}\right)\hfill \\ {\tau }_h\frac{\partial h_x}{\partial t}=f_{n_h}\left(\frac{a_x}{A_h}\right)-h_x+D_h\Delta h\hfill \\ {\tau }_u\frac{\partial u_x}{\partial t}=f_{n_u}\left(\frac{a_x}{A_u}\right)-h_x+D_u\Delta u\hfill \end{array}$$ (1)

Here, the subscript x indexes the lattice site, and Δ is the lattice Laplacian operator, which is dependent on lattice geometry. Each variable has been rescaled so that its natural scale is of order unity. We have chosen to non-dimensionalize time by the decay rate of a; τ_h and τ_u give the decay times of h and u in these units. The source term $f_{n_{\alpha }}\left(\frac{a}{A_{\alpha }}\right)$ in each equation is a dimensionless function with 0 ≤ f_nα ≤ 1 for 0 ≤ a < ∞. This restriction reflects the fundamental limits to the rate of production of any biomolecule. For simplicity, we take f_nα to have the sigmoidal form

$$f_{n_{\alpha }}\left(\frac{a}{A_{\alpha }}\right)=\frac{a^{n_{\alpha }}}{A_{\alpha }^{n_a}+a^{n_{\alpha }}}.$$ (2)

This introduces the three dimensionless parameters A_a, A_h, and A_u that characterize the scale at which a activates production of itself, of h, and of u, and the three Hill coefficients n_a, n_h, and n_u. D_h and D_u are diffusion coefficients. We non-dimensionalize length by setting the lattice spacing to 1.

There are two terms in the equation for $\frac{\partial a}{\partial t}$, beyond its linear decay. They can be thought of as reflecting the presence of two enhancers at the ato gene, one responsible for auto-activation and the other for responding to the diffusible activators Hh and Dpp [9]. We assume here that inhibition acts primarily on this latter enhancer. The corresponding term in Eq. (1) has a maximum strength (relative to self-activation) G; the function g varies between 0 and 1. A Hill-like functional form for this interaction offers, once more, the desired behavior in a simple package. Based on the fact that negative signaling through a pathway involving Delta, Notch, and Scabrous seems able to dominate any quantity of Hedgehog-mediated enhancement, we used a non-competitive model for the interaction of these signals:

$$g_{m_h,m_u}\left(\frac{h}{H},\frac{u}{U}\right)=\frac{{\left(\stackrel{h}{}/\underset{H}{}\right)}^{m_h}}{1+{\left(\stackrel{h}{}/\underset{H}{}\right)}^{m_h}}\left(\frac{1}{1+{\left(\stackrel{u}{}/\underset{U}{}\right)}^{m_u}}\right).$$ (3)

The remaining model parameters (H, U, m_h, and m_u) are thus defined as the scales at which h and u become effective and the associated Hill coefficients.

Eq. (1) as written can describe a model in any dimension, but in this paper our primary interest is the one-dimensional version. On a regular 1D grid with nearest-neighbor interactions, the system reduces to a tridiagonal system of ODEs, where the integer-valued variable x indexes cells by their location in the grid. Exhibiting this spatial dependence explicitly and substituting the Hill-like forms for the functions f and g, we arrive at the basic system of equations that we will study for the remainder of this paper:

$$\begin{array}{l}\frac{\partial a_x}{\partial t}=\left(\frac{{a_x}^{n_a}}{{a_x}^{n_a}+{A_a}^{n_a}}\right)-a_x+G\left(\frac{{\left(\frac{h_x}{H}\right)}^{m_h}}{{\left(\frac{h_x}{H}\right)}^{m_h}+1}\right)\left(\frac{1}{{\left(\frac{u_x}{U}\right)}^{m_u}+1}\right)\hfill \\ {\tau }_h\frac{\partial h_x}{\partial t}=\left(\frac{{a_x}^{n_h}}{{a_x}^{n_h}+{A_h}^{n_h}}\right)-h_x+D_h(h_{x+1}-2h_x+h_{x-1})\hfill \\ {\tau }_u\frac{\partial u_x}{\partial t}=\left(\frac{{a_x}^{n_u}}{{a_x}^{n_u}+{A_u}^{n_u}}\right)-u_x+D_u(u_{x+1}-2u_x+h_{x-1})\hfill \end{array}.$$ (4)

Our main interest in this work is the formation of patterns in which only single, isolated cells retain high a levels. This requires that these cells be able either to keep their neighbors from becoming activated, inhibiting them before their concentrations begin to rise, or to force them back down after their a levels have begun to move upwards. The former scenario turns out to hold for the parameter sets we have found that consistently form patterns. In this case, levels of the inhibitor u must respond quickly to changes in a, and we thus expect τ_u to be small. It is then natural to simplify our analysis by taking the limit τ_u → 0, replacing Eq. (4) by

$$\begin{array}{l}\frac{\partial a_x}{\partial t}=\left(\frac{{a_x}^{n_a}}{{a_x}^{n_a}+{A_a}^{n_a}}\right)-a_x+G\left(\frac{{\left(\frac{h_x}{H}\right)}^{m_h}}{{\left(\frac{h_x}{H}\right)}^{m_h}+1}\right)\left(\frac{1}{{\left(\frac{u_x}{U}\right)}^{m_u}+1}\right)\hfill \\ {\tau }_h\frac{\partial h_x}{\partial t}=\left(\frac{{a_x}^{n_h}}{{a_x}^{n_h}+{A_h}^{n_h}}\right)-h_x+D_h(h_{x+1}-2h_x+h_{x-1})\hfill \\ 0=\left(\frac{{a_x}^{n_u}}{{a_x}^{n_u}+{A_u}^{n_u}}\right)-u_x+D_u(u_{x+1}-2u_x+u_{x-1})\hfill \end{array}$$ (5)

In effect, in this limit, a can be regarded as having a local, cell-autonomous effect which may be activating or inhibitory, and a non-local effect that is always inhibitory. The substitution of Eq. (5) for Eq. (4) further prohibits cell-autonomous oscillations that could be spawned from the relaxation-oscillator-like structure of the activator-inhibitor system.

4. Front solutions

In this section, we construct solutions to Eq. (5) in the limit τ_h ≫ land D_h ≫ 1 that have the form of a front that moves with constant velocity and leaves a regular periodic pattern in its wake. This limit is consistent with the properties of the activators present in the fly system: Hh, in particular, diffuses forward from differentiating cells behind the MF and thus must be quite long-ranged. In order for the front velocity to remain of order unity, τ_h must then also be large. Our strategy makes use of this separation of scales to determine the behavior of a and u on short scales—and, in particular, which cells flip from the low to the high a state—given an imposed h_x (t) and, separately, to find the h front created by a lattice of sources (i.e. cells with high a) that adds a new cell at regular intervals. These solutions on two different scales are then matched self-consistently to arrive at the full front solution. Fig. 3 illustrates some observed behaviors of our one-dimensional system, while Fig. 4 gives a spatiotemporal portrait of the regular, patterning solutions that are our primary interest here. Before turning, in Sec. 4.2, to the construction of the front solution, we first, in Sec. 4.1, establish some notation and introduce a few elementary results on the behavior of the cell-autonomous bistable switches.

Figure 3.

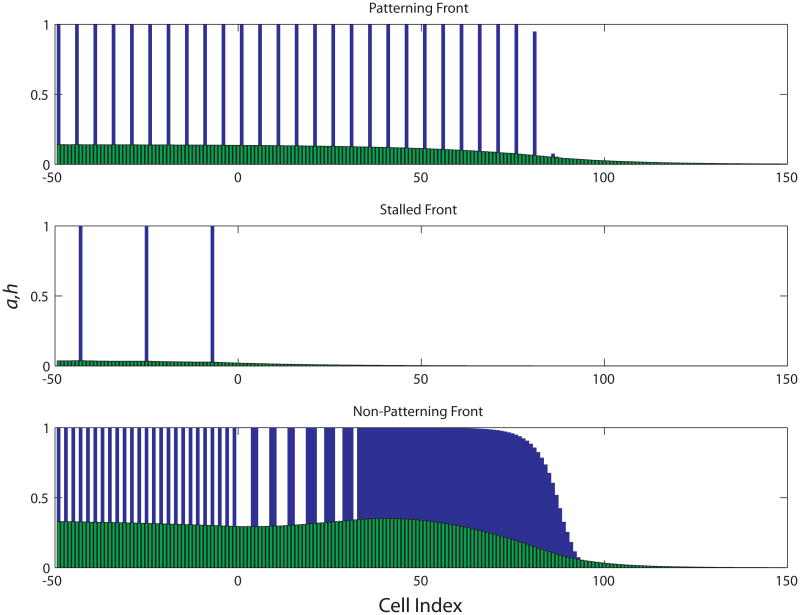
(Color online) Typical simulation results. In each plot, the activation of cells with negative indices was specified by initial conditions, but any cells activated with indices greater than zero represent propagation of a moving front. All simulations were conducted on lattices of 2048 cells by integrating Eq. (5) with the same set of parameters, varying only the wavelength of the initial pattern. A) A propagating front of h (light, green) that produces a stable, regular pattern of a (dark, blue). B) Propagation can fail if the h produced by the initial localized pattern is insufficient to activate a in additional cells. This always occurs for a sparse-enough prepattern. C) If the evolution of a and u is too slow for a recently activated cell to inhibit its neighbors before the h front gets to them, a propagating, unpatterned front of activation may exist. This solution can exist for parameter sets that otherwise have only stalled solutions and for ones that also have patterning solutions. In this case it is induced by supplying a too dense prepattern.

Figure 4.

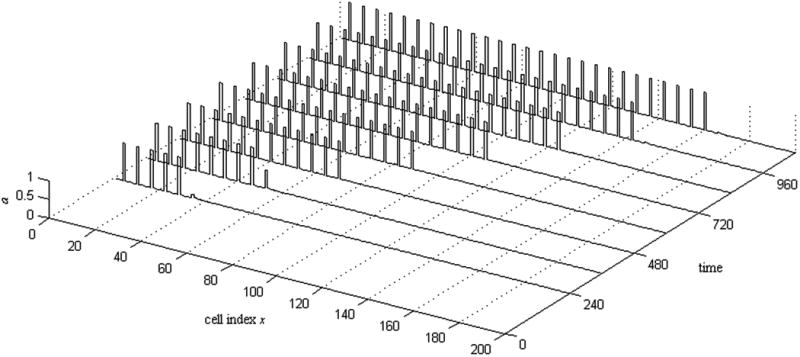
Spatiotemporal portrait of a patterning solution of our model, Eq. (5). The variable a is plotted as a function of spatial position (or cell index x) for 8 regularly spaced time points. As time progresses, the pattern expands with a constant speed while maintaining the same period. Each rectangular spike in the plot corresponds to a single activated cell. Parameters: A_a = 0.25; A_h = 0.75; A_u = 0.9; H = 0.021; U = 5.4×10⁻⁶; G = 11.7; D_h = 640; D_u = 0.16; τ_h = 428; m_h = 8; m_u = 8; n_a = 4; n_h = 4; n_u = 8.

4.1. Cell-autonomous switching

We begin by studying the behavior of a single cell, considering separately the effects of cell-autonomous and non-autonomous interactions. To this end we first solve for the steady-state u field due to a source of strength s at x = 0:

$$\begin{array}{l}0=s{\delta }_x-u_x+D_u(u_{x-1}-2u_x+u_{x+1})\hfill \\ u_{\pm \infty }=0\hfill \end{array}.$$ (6)

The solution is elementary and is given by

$$\begin{array}{l}{u}_x=c_0{\lambda }^{\left|x\right|}\hfill \\ \lambda =\frac{1+2D_u-\sqrt{1+4D_u}}{2D_u}\hfill \\ c_0=s\cdot \frac{-1+\sqrt{1+4D_u}}{1+4D_u-\sqrt{1+4D_u}}\hfill \end{array}.$$ (7)

The quantity c₀ is the contribution of a cell producing u to the local amount of that substance at the same cell.

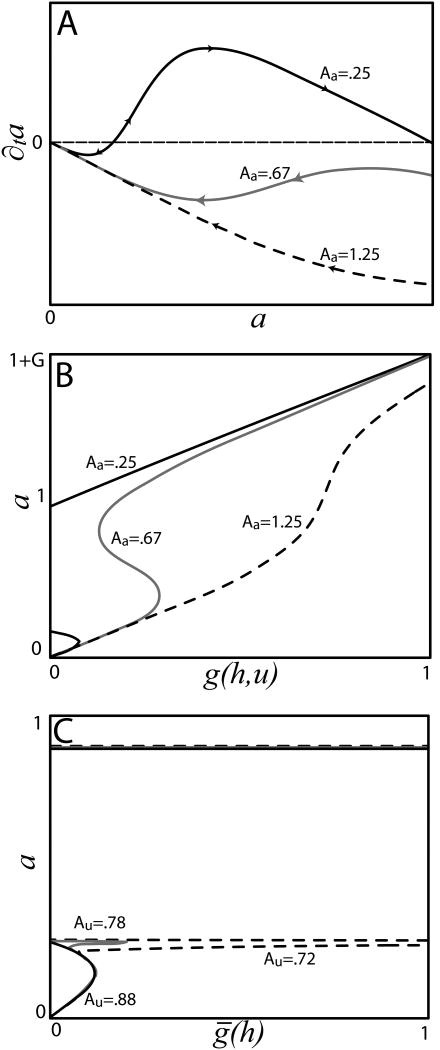
Neglecting autoinhibition, the amount of a at a lattice site can be bistable through autoactivation (Fig. 5). Here, we focus primarily on the simple case in which cells starting at the low a stable fixed point can switch to the high a fixed point in response to signals from h, but a cell with high a cannot go back down. That is, we require that a be bistable even when the activating input $g_{m_h,m_u}\left(\frac{h}{H},\frac{u}{U}\right)$ [which, in a slight abuse of notation, we will often abbreviate as g (h,u)] is zero and that the low stable steady state vanish in a saddle-node bifurcation as g (h,u)—viewed, for the moment, as a bifurcation parameter that does not change with time—increases past a critical value g_crit (Fig. 5B). The first condition holds whenever

Figure 5.

(A) ∂a/∂t versus a for an isolated cell with h = 0 or u ≫ U. At low A_a bistability exists even when h=0. At high A_a there is no bistability. At intermediate values bistability can exist for some amount of external activation. (B) Steady states of a as a function of the input $g(h,u)=g_{m_h,m_u}\left(\frac{h}{H},\frac{u}{U}\right)$. (C) Steady states of a including the effects of self-u (see Eq. 9), plotted as a function of the activating input ḡ(h). The cell is assumed to receive negligible u from other cells. As A_u decreases, the high steady state eventually becomes completely inaccessible to cells starting from a=0, even when h is very large. Parameters: G = 1; n_a = 4. In (C), A_a = 0.35; U = 0.0001; n_u = 8; m_u = 8.

$$\begin{array}{l}{A}_a<\frac{{(n_a-1)}^{\frac{n_a-1}{n_a}}}{n_a}\hfill \\ n_a>1\hfill \end{array}.$$ (8)

For n_a = 4, we must thus have A_a < .569 for bistability when g(h,u) = 0.

The next step in treating a single cell is to include the u that was produced by the cell itself, which we call the self-u. A cell with activator concentration a creates a self-u concentration c₀ (Eq. 7) with $s=f_{n_u}\left(\frac{a}{A_u}\right)$. We introduce the variable u_ns (meaning u - non-self) to represent inhibitor produced elsewhere that has diffused to the current location. With h and u_ns again viewed as fixed parameters, the a concentration in a given cell then obeys

$${\partial }_{t}a=\frac{a^{n_a}}{{A_a}^{n_a}+a^{n_a}}-a+G\cdot \overline{g}(h){[1+{\left(\frac{u_{ns}+c_o\left(\frac{a^{n_u}}{{A_u}^{n_u}+a^{n_u}}\right)}{U}\right)}^{m_u}]}^{-1}.$$ (9)

Here, the function ḡ(h) = h^m_h/(H^m_h + h^m_h) keeps track of the activating contributions to $g_{m_h,m_u}\left(\frac{h}{H},\frac{u}{U}\right)$, while we have shown the inhibitory contributions explicitly.

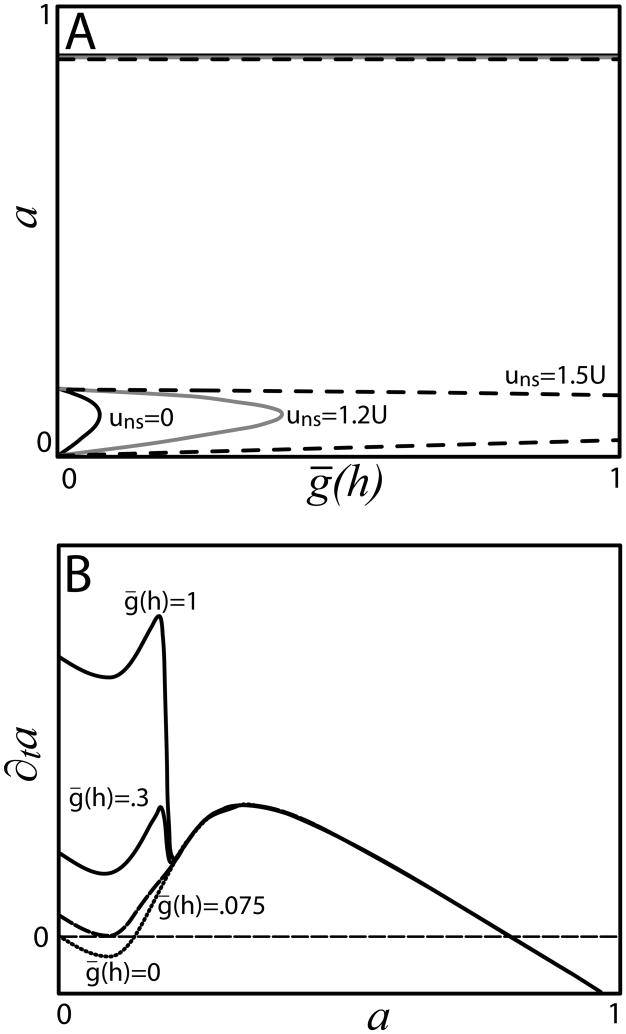
Figs. 5C and 6A illustrate the behavior of an isolated cell with autoinhibition governed by Eq. (9). If A_u or U is too small, autoinhibition will be strong enough that a cell initially in the low state will remain there forever. Similarly, enough u_ns can make the high steady state completely inaccessible from the low steady state. That is, there is a threshold value u_threshold for u_ns above which g(h,u) < g_crit, where g_crit is the critical value to flip the switch, for any h. For typical parameter values, the value of a in the high steady state is nearly independent of h because autoinhibition effectively blocks all activation through the 3′ enhancer when a is high. Indeed, Fig. 6B shows that self-u typically makes a's dynamics insensitive to g over a considerable range of a values. As a result, there is a minimum risetime for a to go from the low to the high steady state, no matter how large h becomes; on the other hand, the risetime depends very little on u_ns unless ḡ(h) passes through the bifurcation value quite slowly. These effects will be important when we consider templating in Sec. 4.2.2.

Figure 6.

(A) The response of a's bifurcation diagram to increasing amounts of externally generated u (i.e. u_ns). The value of the activating input ḡ(h) at which the low (stable) and middle (unstable) steady states collide increases with increasing u_ns until this bifurcation eventually becomes inaccessible for any finite h. (B) The dynamics of a with no external inhibition and various fixed activations. Because of autoinhibition, ∂_ta is insensitive to h for a above a certain threshold, and there is thus well-defined minimum amount of time, independent of h, between a cell's activation and its reaching the high a state. Parameters: A_a = 0.25; A_u = 0.75; U = 0.0001; G = 1; m_u = 8; n_a = 4; n_u = 8.

4.2. Propagating solutions

Inspired by the behavior observed in imaginal discs, we are interested in solutions to Eq. (5) propagating with constant speed that produce a regular pattern of isolated active (high a) cells separated by an integer number of inactive (low a) cells (one-up-integer-down patterning, or OUID, Fig. 4). In the limit τ_h ≫ 1 and D_h ≫ 1, such solutions involve two competing processes occurring on different time and length scales: Immediately after one cell flips from inactive to active, it produces a u gradient that maintains nearby cells in the inactive, low a state. Then, on a slower timescale, the h field builds up in front of the existing pattern until it is able to flip the next cell into the active state, at which point the process repeats itself. Which cell will flip is determined by the interaction between h and the static, short-ranged u gradient, which acts as a sort of template determining which cells are most susceptible to activation; the h field, in turn, depends on the density of active cells, which is set by this short-ranged templating process. More specifically, given the spacings of the active cells that are sources of h and the rate at which new ones appear as the pattern expands, we can calculate h at any point (Sec. 4.2.1). Similarly, given h as a function of x and t, we can find the next cell to be activated, and thus the pattern produced (Sec. 4.2.2). One can then look for self-consistent solutions where the h produced by a pattern of active cells interacts with the template produced by those same cells in such a way that the original pattern is extended (Sec. 4.2.3). A solution of this sort, if stable, represents an observable asymptotic longtime behavior of the model.

4.2.1. The h field due to a periodic pattern

We would like to solve the problem

$$\begin{array}{l}{\tau }_h{\partial }_t{h}_x=s_x(t)-h_x+D_h(h_{x-1}-2h_x+h_{x+1})\hfill \\ s_x(t)=\overline{s}(vt-x){\delta }_{x,q\cdot j}\hfill \\ j\in \mathbb{Z}\hfill \end{array}.$$ (10)

Here s̄(t) gives the stereotyped dynamics of a single cell being activated. s_x(t) thus corresponds to a pattern with integer period q growing with speed v. When τ_h ≫ 1, cells flip from low to high a almost instantaneously on h's timescale. The explicit time dependence of s then takes the simpler form

$$s_x(t)=s_0\Theta (vt-x){\delta }_{x,q\cdot j},$$ (11)

where Θ is the Heaviside step function. Because of our choice of non-dimensionalization and the strong effect of auto-inhibition in active cells, s₀ is generally very near 1. The impulse response of Eq. (10) is known exactly [47], so we can immediately write down the solution

$$h_x(t)=\frac{1}{{\tau }_h}\sum _{x^{\prime }=-\infty }^{\infty }\underset{-\infty }{\overset{t}{\int }}{s}_{x^{\prime }}(t^{\prime })e^{-(t-t^{\prime })-2D_h(t-t^{\prime })/{\tau }_h}{I}_{\left|x-x^{\prime }\right|}\left[\frac{2D_h}{{\tau }_h}\left(t-t^{\prime }\right)\right]d{t}^{\prime },$$ (12)

where I is an associated Bessel function of the first kind. Substituting the idealized form of s_x (t) from Eq. (11) leads to the simplified expression:

$$h_x(t)=\frac{s_0}{{\tau }_h}\sum _{x^{\prime }<vt,x^{\prime }=q\cdot j}^{\infty }\underset{0}{\overset{t-x^{\prime }/v}{\int }}{e}^{-(1+2D_h)t^{\prime }/{\tau }_h}{I}_{\left|x-x^{\prime }\right|}\left(\frac{2D_h}{{\tau }_h}{t}^{\prime }\right)d{t}^{\prime }.$$ (13)

To better understand this formula, it helps to look at the analogous continuum problem, where the source term is not patterned and x is a continuous spatial variable, namely,

$${\tau }_h{\partial }_{t}h(x,t)=s_0\Theta (vt-x)-h+D_h{\partial }_x^{2}h,$$ (14)

which has the solution

$$\begin{array}{l}h(x,t)=s_0\{\begin{array}{c}1-\left(\frac{v{\tau }_h+c_1}{2c_1}\right)exp\left[\frac{-v{\tau }_h+c_1}{2D_h}(x-vt)\right],x<vt\\ \left(\frac{-v{\tau }_h+c_1}{2c_1}\right)exp\left[\frac{-v{\tau }_h-c_1}{2D_h}(x-vt)\right],x\ge vt\end{array}\hfill \\ c_1=\sqrt{v^2{\tau }_h^2+4D_h}\hfill \end{array}.$$ (15)

We expect that the discrete expression of Eq. 13 will approach this continuum limit when the spatial scale over which h typically varies is much larger than the pattern wavelength q [48-52]. For our typical parameter values, D_h ≫ τ_h²v², and h's scale is thus roughly $\sqrt{D_h}$, or about 25 for the reference parameter choice D_h = 640 at which we do many of our simulations. The biology of the eye disc suggests we are interested in q ∼ 5, indicating that the continuum approximation h_x (t) ≈ h(x,t) is reasonably accurate. We use this approximation to impose boundary conditions that allow us to approach the long-time asymptotic front solution in simulations on finite-sized grids (Sec. 5 and Appendix A, below).

4.2.2. Templates and the selection of the next activated cell

In the previous section we assumed the existence of a large-amplitude periodic pattern of a which acts as a source for h. We now turn to the question of whether such a pattern will indeed form in response to a moving front of h of the form of Eqs. (13) or (15). We first discuss in detail a simple limiting case in which smoothly varying h_x (t) is replaced by a step function and then develop analogous arguments for the more general case. Some further technical details are found in Appendix B.

With u slaved to a, the total u concentration at point x follows directly from Eq. (7) and is

$$\begin{array}{l}{u}_x=\sum _{x^{\prime }}{c}_{0,x^{\prime }}{\lambda }^{\left|x-x^{\prime }\right|}\hfill \\ \lambda =\frac{1+2D_u-\sqrt{1+4D_u}}{2D_u}\hfill \\ c_{0,x^{\prime }}=\left(\frac{{a_{x^{\prime }}}^{n_u}}{{A_u}^{n_u}+{a_{x^{\prime }}}^{n_u}}\right)\cdot \frac{-1+\sqrt{1+4D_u}}{1+4D_u-\sqrt{1+4D_u}}\hfill \end{array}.$$ (16)

Consider a simple pattern with period q in the left halfspace, so that active cells are found at x′ = 0,−q,−2q,−3q…. With identical u production at each active cell (as will be the case if the u production term f_na (a_x′/A_u) is saturated or if a_x′ varies little among the active cells), we have

$$u_x=c_0\frac{{\lambda }^x}{1-{\lambda }^q}\text{for}x\ge 0,$$ (17)

where c₀ is given by c_0,x′ in Eq. (16) with x′ = 0,−q,−2q,−3q…. Here, and throughout this section, we assume that cells that have not been activated produce negligible u.

In the section on cell-autonomous behavior, we noted that there is, in general, an amount of exogenous u, u_threshold, that can absolutely prevent a from leaving the low steady state, regardless of activation from h. Suppose first that the role of inhibition is solely to put some cells above this threshold, so that when the h front progresses, the next cell to be activated is just the first one it encounters with u_x < u_threshold. That is, the first cell that possibly can be activated by h is the one that actually does come up.

A self-extending pattern in these conditions is subject to two inequalities which ensure that the next cell to come up is spaced a distance from the previous cell that is the same as the period q of the existing pattern:

$$c_0\frac{{\lambda }^q}{1-{\lambda }^q}<u_{\mathit{\text{threshold}}}<c_0\frac{{\lambda }^{q-1}}{1-{\lambda }^q}.$$ (18)

For given constants c₀, λ, and u_threshold, there is at most one integer q that satisfies these conditions. We understand the physical meaning of the two cases (integer solution exists or does not) in terms of a one-dimensional map that gives u in each newly activated cell in terms of the value of u in the previous activated cell. Let the previously activated cell be located at x = 0 with inhibitor concentration û_m immediately after activation and the newly activated cell have inhibitor concentration û_m+1 immediately after its own activation, where m indexes the active cells and plays the role of time in the map. If the newly activated cell is at spatial position x′ > 0, we have a map of û_m onto û_m+1, where c₀ accounts for the inhibitor produced by the newly activated cell itself:

$${\widehat{u}}_{m+1}={\widehat{u}}_m{\lambda }^{x^{\prime }}+c_0.$$ (19)

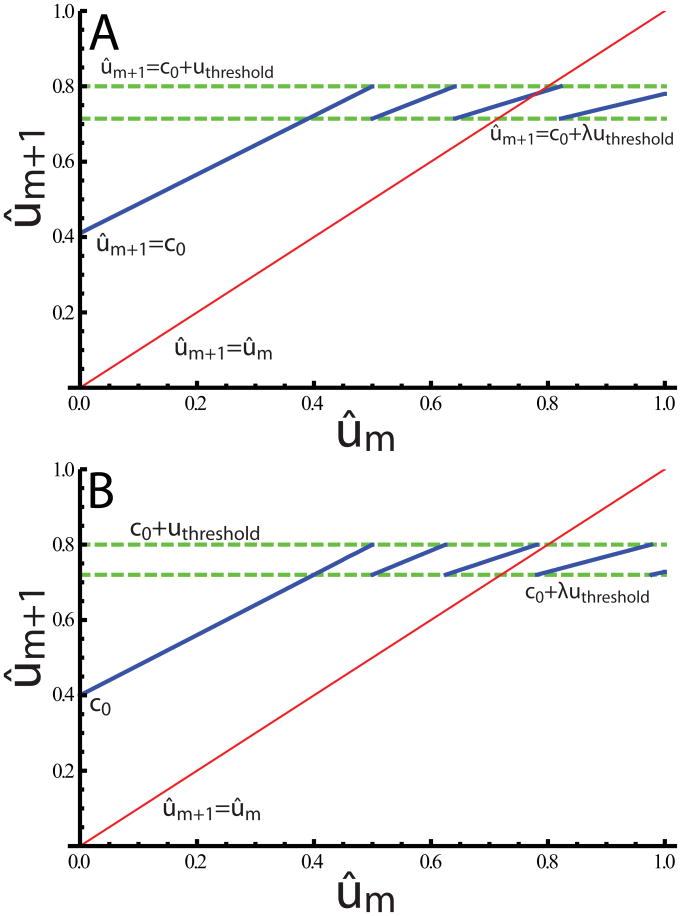
For the cell at x′ to indeed be the next one activated (and thus the first one that can be activated), the non-self u at x′ must satisfy u_ns,x′ = û_mλ^x′ < u_thresold < u_ns,x′−1 =û_mλ^x′−1. The full map giving the value of u at the cell that is actually activated is thus the union of segments of the form of Eq. (19) for each successive x′ in the range where it satisfies these inequalities, and is consequently piecewise linear and discontinuous. All the linear segments have positive slope less than one (since λ < 1), and all the segments with x′ > 1 lie within a finite band of allowed û_m+1, as shown in Fig. 7. There are two possible behaviors: The identity line passes either through a line segment, such that there is one point of intersection (i.e. one integer x′ satisfying Eq. (19) with û_m+1 = û_m and the inequalities [Fig. 7A]), or through a discontinuity between two line segments (no integer x′ satisfying Eq. (19) with û_m+1 = û_m and the inequalities [Fig. 7B]). The two situations are separated by a discontinuous border collision bifurcation [53]. At such a bifurcation, a single, stable fixed point is replaced by a stable limit cycle with period greater than one. Fig. 8 illustrates a case with a period-3 solution. These limit cycle solutions can reach arbitrarily high periods and are arranged in parameter space in a complex geometry.

Figure 7.

(Color online) The map relating u at a newly patterned cell immediately after its activation to the amount of u at the previous activated cell. The heavy, solid blue lines represent the map function, as given by Eq. (19). The top dashed line indicates the maximum amount of u that still permits cell activation. The lower dashed line shows the minimum amount of u at a point that also implies its neighboring point cannot be activated. In (A), the identity line (light solid line, in red) intersects the fourth line segment of the map function, implying the existence a single, stable 1-up-2-down pattern. In (B), the identity goes through a discontinuity, so that asymptotically the pattern will alternately have gaps of 2 or 3 cells between active cells. Parameters: (A) c₀ = 0.4; λ = 0.78. (B) c₀ = 0.4; λ = 0.8.

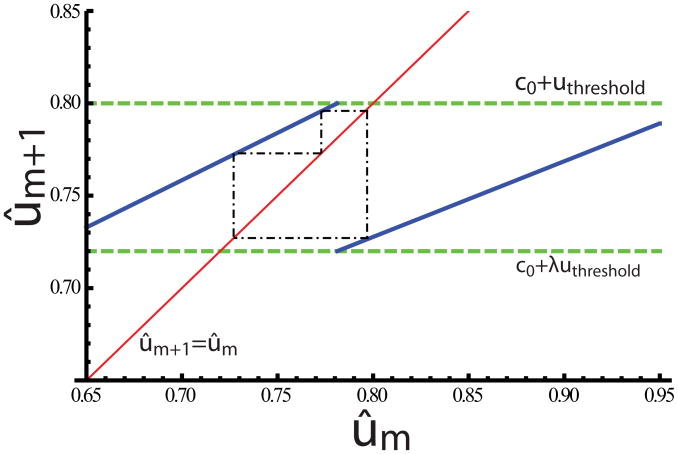
Figure 8.

(Color online) A detail of the higher-period solution in Fig. 7(B). The attractive orbit of the map is shown as the dash-dotted line. In this case, the overall period is 10 cells, and consists of repetitions of the motif 1-up-2-down-1-up-2-down-1-up-3-down.

Translating our results on the map back into the language of spatial patterns, we find that if one varies parameters continuously in such a way as to go from a stable OUID pattern of period q to a period q + 1 pattern—which, in terms of the map û_m ↦ û_m+1 correspond, respectively, to fixed points on the q^th and q + 1^th line segments—one must pass through a region characterized by more complex high-period patterns. These patterns correspond to limit cycles in the map that oscillate between the q^th and q + 1^th line segments, as illustrated in Figs. 7 and 8. The unit cell of the pattern thus consists of a set of single active cells separated by either q − 1 or q inactive cells, with the sequence of q and q − 1 dictated by the limit cycle in the map. Notably, in this simplified picture the patterning solution is globally attractive given any initial prepattern, and is unique up to an overall translation [53].

These results can be generalized for significantly relaxed assumptions. In the original model of Eqs. (4) and (5), h varies continuously (whereas in the preceding paragraphs we have, in effect, taken it to be a step function in space), and the effect of u is not necessarily negligible for u < u_threshold. To address these concerns, we first note that, in a cell with inhibitor concentration u, there is a critical value of h, h_crit(u), at which the low a steady state disappears through a saddle-node bifurcation. u_threshold in the previous analysis is defined so that $\underset{u\to u_{\mathit{\text{threshold}}}}{lim}{h}_{\mathit{\text{crit}}}(u)=\infty$, and, more generally, h_crit satisfies g_crit = g[h_crit(u),u]. h_crit(u_x) decreases monotonically with increasing x toward a finite, positive limiting value. Additionally, its second derivative in space (and discrete approximations thereto) is always positive. These general characteristics of h_crit are dictated by the functional form of u_x in our model.

Let us approximate the advancing h front with a linear function of z = x − vt with slope −c₃, cut off at h = 0. This is reasonable when $\sqrt{D_h}\gg 1$ so that h varies slowly in space compared to the scale of the pattern. We then have

$$h=max[-c_{3}z,0].$$ (20)

Unlike in our earlier treatment of a continuum model of h production (Eqs. 14-15), here z = 0 does not necessarily correspond exactly to the point where an active cell first appears. As before, assume that there is a semi-infinite regular pattern of active cells on x ≤ 0 and ask where the next cell is activated. As t increases, the first cell where h exceeds h_crit (u_x′) is, again, found at a point x′ governed by two inequalities (see also Appendix B),

$$h_{\mathit{\text{crit}}}(u_{x^{\prime }+1})-h_{\mathit{\text{crit}}}(u_{x^{\prime }})<c_3<h_{\mathit{\text{crit}}}(u_{x^{\prime }})-h_{\mathit{\text{crit}}}(u_{x^{\prime }-1}).$$ (21)

These are analogous to the simpler inequalities for u of Eq. (18), and they determine the locations of the discontinuities in a similar map of û_m onto û_m+1. One can show that the existence of a unique, globally attractive fixed point or limit cycle for the map is guaranteed by the positive second derivative of h_crit(u_x′), except in the non-generic case of equality in one of the relationships in Eq. (21), which indicates simultaneous activation of two cells. Appendix B argues that this same qualitative behavior persists whenever h_x (t) is a function only of x − vt —which we have already pointed out is true to very good approximation for our system when $\sqrt{D_h}$ is large—and u_x decays sufficiently fast that u_ns at cells that are about to be activated comes almost entirely from the most recently activated cell.

We thus conclude that an imposed h_x (t) of the form (16), with τ_h, $\sqrt{D_h\gg 1}$ leads to a unique pattern that consists of single activated cells; the only exception occurs when h_x (t) is too weak ever to activate any cells, even in the complete absence of inhibition. The resulting pattern has either a simple OUID form or a more complex periodic pattern consisting of single active cells separated by some admixture of two integer numbers of inactive cells. The former includes the possibility, when each cell produces a very small amount of inhibitor, of active cells separated by 0 inactive cells, in which case the resulting pattern of course consists entirely of cells with high a; we will see, however, that such a pattern in practice more often arises because our assumption of a separation of timescales between h and a is violated.

4.2.3. Self-consistent solutions

Armed with these ideas for understanding front propagation and pattern templating, we are now in a position to construct solutions to the full model. Specifically, we restrict ourselves to OUID patterns and look for values of the front speed v and the pattern wavelength q that allow us to match a large-scale h front (Sec. 4.2.1) to a short-scale templating solution (Sec. 4.2.2). For any v and q, Eq. (13) immediately gives h_x (t), and from this knowledge of the long-ranged activator field, we can find the time and place where the next cell will flip from inactive to active. For a given v and q to correspond to a self-consistent solution, this newly activated cell must be a distance q from the last-activated cell, and it must flip to the active state a time q/v after the previous cell flipped. We examine these two conditions in turn, starting with the second.

A cell at a position x flips from inactive to active when h_x (t) exceeds the critical value h_crit (u_x). Consider a pattern of wavelength q growing with speed v, and assume that the cell at x = 0 flips to active at t = 0. The next cell to flip should then be located at x = q. For t > 0, u_q is independent of t, but h_q (t) increases monotonically with time (Eq. 13), approaching a finite value h_q (∞) as t → ∞; this value depends on q but not on v. If h (∞) < h_crit (u_q), then a semi-infinite OUID pattern of wavelength q can never produce enough h to activate the next cell in the pattern, and no OUID pattern is possible with this wavelength. Because h_q (∞) decreases monotonically to zero for large q, while h_crit (u_q) approaches a finite value in the same limit, such stalling must always occur for large enough q (that is, for patterns with a low enough density of active cells that are sources of h), and we need only consider patterns with a wavelength up to some maximum value q₀.

It is not hard to see that, for 1 ≤ q ≤ q₀, there can be at most one front speed v_q corresponding to each wavelength q. Indeed, for the new cell at x = q to flip a time q/v_q after the previous cell (at x = 0 and t = 0), we must have

$$h_q\left(t=\stackrel{q}{}/\underset{v_q}{}\right)=h_{\mathit{\text{crit}}}(u_q).$$ (22)

The left-hand side of this equation decreases monotonically with increasing v_q, so it can have no more than one solution. If this solution v_q exists, it is readily found with standard numerical techniques (Sec. 5).

Thus, it is possible, for some set of wavelengths, to find a velocity v_q such that the long-ranged activator field h flips the next cell at exactly the correct time. Not all of these (q, v_q) pairs, however, give rise to self-consistent solutions of the full problem. For this to be the case, the new active cell at position q must not only flip at the right time, it must also flip before any other cells in the wrong location. (For any reasonable parameter values, the correct cell, once it has flipped, makes enough inhibitor that there is no danger that cells at positions, say, q − 1 or q − 2 will flip after the cell at position q.) Numerically, we impose this requirement by checking, for any given pattern expanding at its self-consistent speed v_q, whether, at the moment of activation of the appropriate next cell, h at any other cell is greater than that cell's h_crit. This question should be asked for every potential wavelength q.

It is possible to pick parameters for which the number of self consistent OUID patterns, satisfying both conditions given in the first paragraph of this section is, 0, 1, or more than one. Cases with one self-consistent solution and no self-consistent OUID solutions correspond, respectively, to circumstances where the simple map of Sec. 4.2.2 has a single fixed point or a limit cycle of period greater than one. Parameter sets with more than a single self consistent solution, on the other hand, correspond to cases where the change in the shape of the propagating h front due to a change in the pattern density is enough to substantially change how h interacts with the inhibitor template; such a situation is not possible when, as in Sec. 4.2.2, h_x (t) is a given, fixed function, but can arise from the self-consistent matching procedure described in this section. Such cases are relatively rare, but we have verified numerically that they do indeed exist.

5. Simulations

It remains to check how well the analytic results of Sec. 4, obtained in the limit τ_h ≫ 1 and D_h ≫ 1, apply to the original system of Eq. (5) over a range of parameter values. In this section, we use a random numerical search of parameter space to show that these results do indeed provide qualitatively, and in many cases quantitatively, correct predictions for the behavior of the full model. Equally importantly, the analytic predictions break down in the expected manner: Regardless of the other parameter values, almost all parameter sets in which a and h have sufficiently different timescales adhere to the behavior described in Sec. 4. In addition to testing our analytic results, our random parameter scan further serves to explore the full range of behaviors that our model can exhibit and to gather data on how robust various behaviors are to parameter variation.

5.1. Parameter scan

We tested 640,000 independent, random parameter sets chosen from a region known to contain at least some parameters capable of producing OUID patterns. For every parameter set, each of the parameters A_a, A_h, A_u, U, H, G, D_u, D_h, m_h, and τ_h was chosen independently from a distribution centered on the reference values p_ref:

$$p_{\mathit{\text{ref}}}=\{\begin{array}{l}{A}_a=.25\hfill \\ G=3.475\hfill \\ H=.0193\hfill \\ m_h=8\hfill \\ U=.00001048\hfill \\ {\tau }_h=371.65\hfill \\ A_h=.75\hfill \\ D_h=640\hfill \\ A_u=.9\hfill \\ D_u=.16\hfill \end{array}.$$ (23)

In each case, we took either the parameter or its logarithm to be uniformly distributed on an interval given in Table I. We did not vary the Hill coefficients for functions of a and u. These are summarized in p_static.

Table I.

Scanned parameters and ranges. Each model parameter was chosen randomly and independently from within a given range. The minimum and maximum values were set by the indicated ratios with the reference parameter set. For most parameters, the distribution that was sampled was $p\left[ln\left(\stackrel{\mathit{\text{parameter}}}{}/\underset{p_{\mathit{\text{ref}}}}{}\right)\right]\propto \text{constant}$, the distribution identified in the table as “Log.” The exponent m_h was sampled uniformly over its range.

Parameter	Min/pref	Max/pref	Distribution
Aa	.01	10	Log
G	.01	100	Log
H	.01	100	Log
mh	.0625	1.25	Linear
U	.01	100	Log
τh	.01	10	Log
Ah	.01	5	Log
Dh	.01	100	Log
Au	.01	5	Log
Du	.01	100	Log

$$p_{\mathit{\text{static}}}=\{\begin{array}{l}{n}_a=4\hfill \\ n_u=8\hfill \\ n_h=4\hfill \\ m_u=8\hfill \end{array}$$ (24)

The sampling limits for this work are necessarily a bit arbitrary; we took our target to be two orders of magnitude up and down from each reference value. This limit did not make sense for A_a, A_u, and A_h, as the model does little of interest if they exceed the high steady state value of a, which is typically near 1. We limited the maximum value of τ_h for the practical reason that this plays a very direct role in how long an equation system must be integrated to examine its asymptotic behavior. That asymptotic behavior is expected to become independent of τ_h (up to an overall rescaling of time) for large enough τ_h.

For each parameter set, we integrated the differential equations (5) on a 1D grid using random initial conditions chosen from an appropriate distribution, as well as initial conditions specifically meant to mimic the predicted asymptotic pattern-forming attractor, as described in Appendix A. Using an automated pattern detection scheme, we compared the result of each integration both qualitatively and quantitatively to analytic predictions based on the results of Sec. 4.

5.2. Analyzing patterns

The first, qualitative, stage of looking at patterns involved classifying parameter sets among 5 basic types of behavior based on the results of simulating Eq. (5): Patterning (Fig. 4A), stalled (Fig. 4B), poorly-patterning, non-patterning (Fig. 4C), and impermanent fronts. The first two cases, where a solution consisting of a self-extending periodic pattern of isolated active cells exists or where the system cannot sustain a moving front of any sort, are addressed by our theory, and we expect predictions of period and speed to be accurate in the limit that a is much faster than h. The other cases are categories of behavior we observed in the course of running simulations that are not explained in detail by our theory. Briefly, a poorly-patterning front consists of a solution in which a propagating front results in some active cells and some inactive cells, but where these cells are not arranged in a periodic pattern with isolated active cells. Non-patterning fronts occur when an initial pattern leads to a propagating front where all the cells become active. Some instances of this behavior fall within the purview of our theory—we predict such a solution when an active cell does not produce enough inhibitor to prevent the activation of any of its neighbors—but many do not. Impermanent fronts are any solutions in which a cell we determine to be active becomes inactive again at a later time. Such solutions violate one of our fundamental assumptions, namely the irreversibility of activation, and can be found only when A_a is large enough to violate the inequality of Eq. (8).

5.3. Results

5.3.1. Qualitative results

The results of our parameter scan were entirely consistent with the predictions of Sec. 4; behaviors we did not find analytically began to appear only when the assumptions behind the analytics—specifically, that activation of a cell is irreversible, that inactive cells produce negligible u and h, and, most importantly, that h is much slower than a—no longer held.

Of the 640,000 parameter sets scanned, 137,235 had A_a ≥ .569, meaning that a activation can be transient. Any parameter sets in which a was transiently high, but fell back to a value near the low fixed point (an impermanent front) were in this set. Additionally, persistent activation of any sort was exceedingly rare for these parameter sets, confined to those where A_a was very close to the cutoff of .569 or u was never produced in significant amounts. Most of the parameter sets≈(95%) with the offending values of A_a can be described as stalled solutions, given reasonable initial conditions. The balance show complicated dynamical behavior.

Of the remaining 502,765 parameter sets, we predicted 241,572 (or 48%) would have no propagating solution. Of these, 208,348 (86%) were unequivocally stalled. About three-quarters of the remaining 33,224 displayed some sort of fairly well-behaved front solution. Most of these parameter sets gave patterns that either had multiple adjacent active cells, or propagated very quickly, in clear violation of the assumptions of Sec. 4. The remainder showed behavior suggesting pathologies in the numerical integration itself. We examined a subset of these pathological cases individually, pursuing them with tighter error tolerances, and all resolved cleanly into one of the well-behaved classifications. We should mention that a prediction in Sec. 4 of a OUID front solution does not necessarily imply that other attractors cannot exist. Indeed, there is always an attractor representing propagation failure for a sparse-enough initial pattern. Less universally, there can be an attractor representing a fast-propagating front with no patterning if the maximum source-density is high enough to push the important h dynamics faster than a.

Our theory predicts that the other 261,192 parameters sets have some sort of propagating solution that can be understood within our analytical framework, provided the slow-h assumption holds. Of these, 89% had an easily-classified propagating solution, and about 1% seemed truly stalled. The remainder yielded easy-to-classify behavior only when given “special treatment,” i.e. when integrated with tighter tolerances, for longer times, and over larger domains. For 24,213 parameter sets the predicted self-consistent pattern was a front of uniform activation, which was observed in 82% of cases. We pursued quantitative pattern analysis on those 236,932 parameter sets where there was a predicted pattern, other than uniformly high a.

It should be clear that our predictions about the model's behavior are, in broad, qualitative terms, correct. Most of the bad predictions, moreover, can be traced to the fact that our parameter search cast a very wide net, including some parameter values that are at the very edge of anything physiologically plausible.

5.3.2. Quantitative results

We now turn our attention to the analysis of the simulation data from the 236,932 parameter sets where we predicted a pattern-forming, propagating front. These we further culled in several ways. First, we checked whether the u and h produced by inactive cells could be neglected (as is almost certainly the case for the real fly system): We demanded that, when a was at its unstable steady state for ḡ (h) = 0 (which is the “point of no return” beyond which self-activation will, no matter what the inputs from u and h, drive the cell to the high fixed point), the amount of self-u produced by the cell was less than half u_threshold; we also required that, if all cells were held at the unstable fixed point, the steady-state h concentration that resulted was less than h_crit (u = 0). 151,450 parameter sets met both these criteria. Of these, we predicted that 136,620 have a single OUID solution, 537 have multiple OUID solutions, and 14,293 have no OUID solution, but may have solutions where the spacing between active cells varies between 2 values; we chose not to further explore this last possibility.

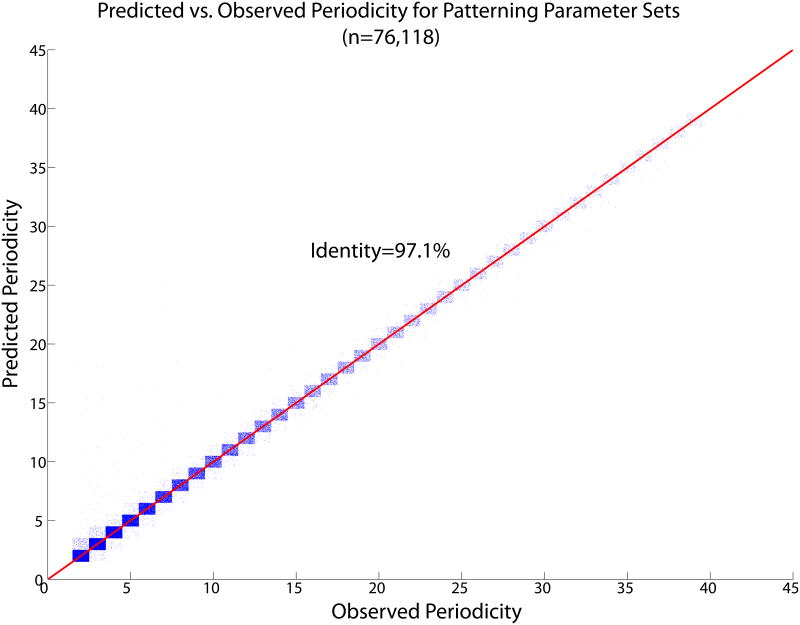
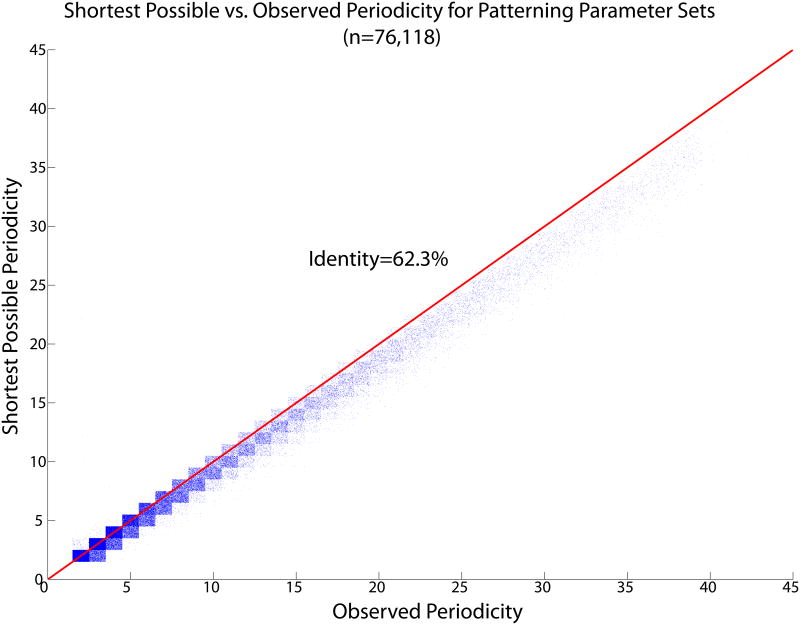
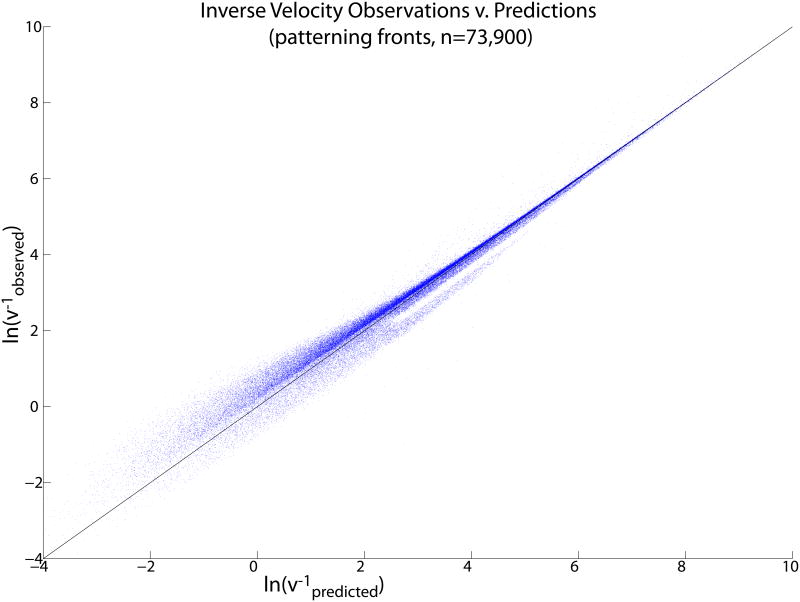
76,118 (56%) of the 136,620 parameter sets predicted to have a single, attractive patterning solution made a propagating pattern with single, isolated activated points. Of these, we predicted the correct spatial period, q, for 97.1% (Fig. 9). This striking agreement is much better than that achieved using the simpler approximation in which the h front is given a step function profile, which is only 62.1% accurate, and clearly systematically biased (Fig. 10). Its bias towards predicting a period that is too short is not surprising: the step function model assumes that the first cell that could possibly be activated is the one that is actually activated, even when it sees a much higher u_ns than subsequent cells. It remained to check whether violation of the slow-h assumption could account for the 44% of parameter sets that did not violate any of the criteria already applied but that nonetheless did not agree with our analytic prediction.

Figure 9.

(Color online) Predicted vs. observed pattern period for parameter sets showing regular OUID patterns. Each blue dot represents a parameter set. The points described by a particular ordered pair of integers ([observed, predicted], for instance [5,3]) are assigned a random location within a square box of side 1 centered on those coordinates, to give an indication of the density of points. The points are densely concentrated along the identity line. More than 97% of parameter sets show perfect agreement.

Figure 10.

(Color online) Same Fig. 9, but with period predicted by the simpler step-function activator model of Sec. 4.2.2. The overall correlation of prediction and observation is still clear, but, as expected, there is a bias towards predicting periods that are too short.

In general, these parameter sets yielded behavior in which multiple adjacent cells were activated in the final pattern. The actual behavior in these cases ranged from unpatterned propagating fronts, in which every cell was activated (recall that some of the parameter sets that were predicted to stall also showed this behavior), to complex patterns of activated cells not obeying any obvious periodicity, to regular-appearing patterns of multiple active cells separated by multiple inactive cells. While measures of the “average” expressed pattern period and spacing (in non-uniform solutions) showed significant correlation with the predictions, the absolute accuracy of the predictions was much lower than for parameters that showed basic OUID patterning.

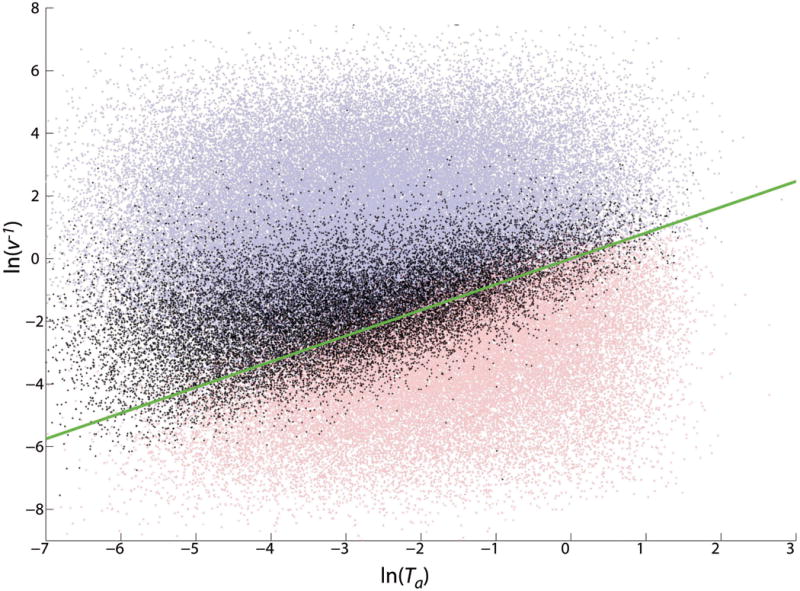
To test quantitatively whether our assumption of a separation of timescales holds, the specific time scales requiring comparison are: A) the time T_a it takes a recently activated cell to reach the a level necessary to inhibit its nearest neighbor (which is effectively set to zero in the analysis of Sec. 4), and B) the time it takes the propagating front of h to progress 1 lattice site. These timescales are not strictly independent, and evaluating them separately, without careful integration of the full model, requires further approximation. We use the self-consistently calculated front velocity to estimate the second timescale, which we take to be 1/v. The first timescale we approximate as the time it takes an isolated, uninhibited cell to progress from the a value at the bifurcation that destroys the low fixed point to the level where its nearest neighbors are completely inhibited. This value in principle depends on h, but, as previously noted (Fig. 6B), this dependence is largely washed out by the strong effect of self-u.

A scatter plot of parameter sets on axes reflecting these two time scales shows a clear separation between simple OUID patterns and more complicated cases (Figs. 11 and 12). To determine more precisely how well the time scales T_a and 1/v alone predict a parameter set's behavior, we looked for the line in the ln(T_a), ln(1/v) plane that best separates parameters yielding patterns where only isolated active cells appear from those for which every cell is activated by the passing front (Appendix C). This line is shown in Figs. 11 and 12; it discriminates between these two cases with a sensitivity, specificity, positive predictive value, and negative predictive value all substantially above 90% [54], indicating that a parameter set's qualitative behavior is indeed largely determined by the timescales of front motion and of cell activation.

Figure 11.

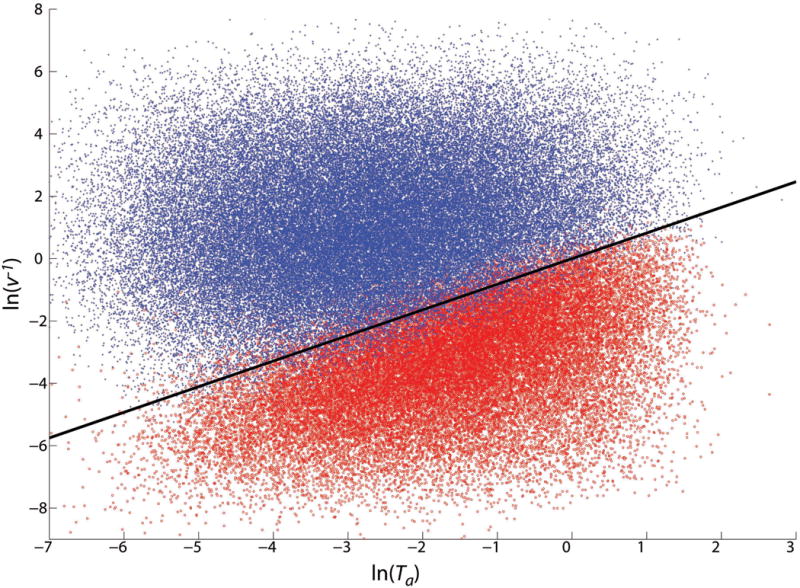
(Color online) Each point represents a parameter set for which pattern formation was predicted. The pattern was either observed as predicted (dark, blue), or an unpatterned (i.e. all cells active) propagating front was observed (light, red); parameter sets with other behaviors are not shown (see Fig. 12). Horizontal axis, shortest possible time for a cell experiencing maximum activation to reach high enough a to fully inhibit its nearest neighbor. Vertical axis, inverse front velocity. This approximates the amount of time it takes the average h-front to advance one lattice site. The black line optimally separates the two possible outcomes. It successfully classifies about 95% of these parameter sets. The switch and template pattern formation mechanism begins to fail when the internal dynamics of a cell can no longer be considered fast compared to front propagation.

Figure 12.

(Color online) Same as Fig. 11, but with the addition of the points for which a pattern was predicted, but neither that pattern nor a uniform propagating front was observed (black). Very complicated behavior was observed in this set, and these parameter sets are particularly prone to very long transients. Whether these solutions are in the process of settling down to one of the better-known behaviors (patterning or non-patterning) or are approaching other, more complicated limiting behavior is an open question. It is clear, however, that they tend to fall between parameters that lead to patterning and those that lead to uniform high a.

The classifier just described ignores the minority of parameter sets that yield patterns containing both inactive cells and blocks of more than one adjacent active cells. As Fig. 12 shows, parameter sets showing such behavior cluster around our separating line, in the region of parameter space in between the more easily classified patterns. This suggests that as one reduces the timescale separation between a and h, one will go from a simple OUID pattern, to a region where only more complex patterns are supported, to, finally, a limit where the only propagating solution is one for which all the cells end up activated. The exact nature of this transitional region, unlike that of the zone between OUID patterns of different periodicity described in Sec. 4, is likely quite complex. It is also difficult to study, in part because of the very slow transients that can occur before the truly asymptotic long-time pattern appears in simulations. It is clear, however, that the transitional region holds parameter sets that can produce not only relatively exotic patterns, but also multiple patterns for a single parameter set as initial conditions are varied. In essence this multistability stems from the fact that the front speed depends not only on parameter values, but also on the density of active cells (and thus of h sources) in the pattern; it is possible, for one choice of parameters, to have relatively good separation of timescales when the density is low but to lose the timescale separation completely when the system is initiated with a high active cell density. It is finally worth noting that a similar transition (with similar complexities in the transition region) is found, as h is sped up, between parameter regimes where no propagating fronts are possible and those where rapidly propagating, poorly patterned fronts occur.

The analytic theory of Sec. 4 predicts not only the spatial pattern period, but also the front speed. We would expect that the quality of these predictions should increase with longer times between the activation of cells, since the (comparatively) invariant activation time of a single cell, which our calculations effectively set to zero, will have a relatively smaller effect on the overall front speed under these conditions. For the parameter sets where we correctly predict the presence of an OUID pattern and its period, this is the case (Fig. 13).

Figure 13.

(Color online) Comparison of observed front velocity from integration of Eq. (5) to analytic predictions based on the fast-a approximation, for parameter sets that lead to stably propagating patterns with the predicted wavelength. Each dot is a parameter set. The prediction becomes relatively better as the front slows down, as expected.

6. Discussion

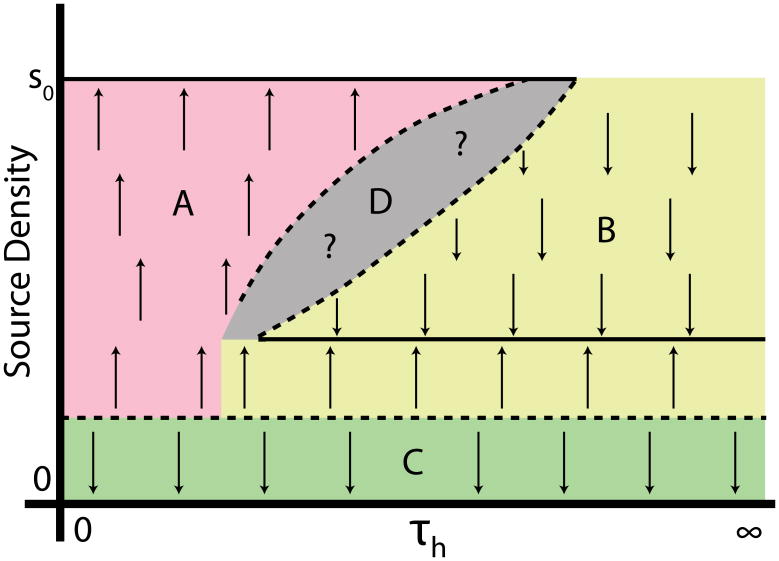
Although they have now been the subject of serious study for decades, activator-inhibitor systems continue to demonstrate new and unexpected behavior. Here, we have shown how coupling a simple activator-inhibitor subsystem to a longer-ranged diffusible activator can lead to front-driven pattern formation by a novel switch and template mechanism. The defining feature of this mechanism is its reliance on bistable switches which are flipped from a low to a high state in certain cells based on inputs from longer-ranged diffusible signals. Such behavior appears naturally in models in which cells are treated as discrete objects and certain genes self-activate cell-autonomously, with the concentrations of the self-activating species in one cell not depending directly on their concentrations in adjacent cells. Our dissection of the simplest, one-dimensional version of switch and template pattern formation has emphasized the essential role of a separation of timescales between the activator-inhibitor subsystem and the longer-ranged activator that drives front motion. Specifically, we have demonstrated that our model can be solved analytically in the limit that the former is much faster than the latter and that our solution in this limit correctly predicts the behavior of the full model for a substantial range of parameter values. As one might expect, however, our analytic predictions begin to fail as the two timescales approach each other; simple patterns built up from repeating units containing only a single active cell can then give way to far more intricate behavior. The exact structure of this boundary region remains obscure, but our analysis does make predictions about the qualitative arrangement of solutions in parameter space; these are summarized in the schematic bifurcation diagram of Fig. 14.

Figure 14.

(Color online) Schematic one-parameter bifurcation diagram for front propagation and pattern formation, showing the stable solution types discussed in this paper and their basins of attraction. Solid lines, stable long-time behaviors; dotted lines, unstable behaviors. Arrows indicate the direction in which the system evolves over time. We take the source density for h (i.e. the fraction of cells in an active, or high a state) as the output state; it can range from 0 (stalled) to s₀, the maximum activity of a single cell. The bifurcation parameter τ_h controls the relative timescales of front motion and of activation of a single cell. Our analytic predictions (Sec. 4) apply for large τ_h, and thus for regions B and C, which correspond, respectively, to stalled fronts and to OUID patterns. If the initial pattern density is too low, front propagation cannot occur, and the system lies in region C. A system that produces enough h, and where h dynamics are slow enough compared to a (region B), is attracted to a regular patterning solution. If h dynamics are not slow, then many cells can be activated before any is able to inhibit another, and a propagating front characterized by a maximum-density pattern is observed (region A). The structure of the boundary between regions A and B is unknown (gray, region D), but there are parameter sets where stable patterning and unpatterned front propagation are observed for different initial conditions (see Fig. 3).

Although many of the features found in our model have appeared individually in previous models, the consequences of coupling them together have not previously been described. Starting with Turing, one major theme in the study of reaction-diffusion systems has been the possibility of steady states that are unstable to finite-wavelength perturbations [1, 55, 56]. While the continuum has been examined most extensively, there have also been many studies that have concentrated on discretized systems where isolated cells become active [57-59]. In particular, more than one system has been described in which a patterned field expands into a region in an unstable state; in this case, the linear instability of the unstable state largely determines what final pattern is selected [60, 61]. The patterning system we have discussed here, in contrast, does not have a finite-wavelength linear instability. In its reliance instead on a bistable activator-inhibitor subsystem, our mechanism bears some resemblance to the formation of domain patterns in the Fitzhugh-Nagumo and related models [17-19], but the fact that auto-activation is strictly cell-autonomous leads to much more pronounced multistability among different patterns, while the presence of the long-ranged activator allows for front-driven pattern formation of a sort not usually associated with domain patterns. This prominence of lattice effects and front motion is somewhat reminiscent of work on front pinning (or propagation failure) in discrete systems [49, 50, 62-64] and of the well-known clock and wavefront mechanism [4, 65]. Our model differs from these, respectively, in its ability to generate stationary spatial patterns and in the absence of any oscillations. Importantly, in classic clock-and-wavefront patterning, the spatial period depends both on the frequency of the cell-autonomous oscillators and on the speed of front propagation, whereas in our system it is set directly by the range of the inhibitory signal and is largely independent of the details of the dynamics of other components of the system.

A feature of our model related to the existence of multiple stable, stationary patterns is the initial-condition-dependence of the pattern selected by the moving front. Most trivially, no growing pattern at all is possible in our model if the initial condition does not provide enough h (or enough active cells that can then make h) to start front motion. This makes sense in a biological context, where it is likely important to guard against accidentally starting the patterning process at the wrong place or time; indeed, it is known that in the eye disc a separate genetic circuit provides an initial burst of Hh to initiate MF motion at the posterior margin [14]. For some parameter values, our model also supports more than one front solution, each of which selects a different pattern; the basins of attraction of these different solutions seem to be determined largely by how much h an initial condition can generate. It is in the variety of different patterning fronts that we expect the greatest difference between the one-dimensional model studied here and a more realistic two-dimensional model. While the 1-D version allows more than one solution for a given parameter set, the number of distinct propagating patterns should be far larger in two dimensions, where the potential for near-simultaneous activation of two or more cells is greater; we imagine that pattern defects observed in real eye discs may well be related to interactions between these various idealized, regular solutions. We of course also expect that richer phenomenology may become possible as more of the complexities of the real biological circuitry are added to the model. We have already noted, for example, that adding a delay to a's self-activation can lead to the creation of short-lived proneural clusters. Another interesting extension might consider the difference between secreted inhibitory signals, like u in our model, for which auto-inhibition is possible, and juxtacrine signals where this is not allowed [57-59]; both types of signals appear to be present in the eye disc [13, 14, 25]. Our careful study of one of the simplest possible models should lay the groundwork for systematic examinations of these and other extensions.

Although the basic model we have studied, Eq. (4), is a set of ordinary differential equations, our ultimate understanding of its behavior is more akin to what one might expect for a finite state machine or a Boolean model. This is significant on at least two counts. First, it reinforces the growing evidence that switch-like behavior plays a major role in fate specification during development [66-69]. Indeed, our analysis underlines the robustness to parameter variation that a switch-based mechanism can provide. Second, our ability to pass from a continuous differential equation model to a hybrid object with a more discrete flavor gives an intriguing hint of how one might begin to analyze more complicated developmental models, involving multiple interacting genetic circuits. In such situations, an ability to coarse-grain the initial, detailed network model is essential; one way to do this is to identify functional modules consisting of several genes and to replace them with a single coarse-grained circuit element. Here, we have carried out just such a program for a simple model and have shown that it leads to robust pattern formation through a novel switch and template mechanism.

Appendix A: Numerical Procedures

Each of the 640,000 random parameter sets (Sec. 5.1) was subjected to several numerical and analytical tests. First, as an undirected exploration of the system's behavior, Eq. (5) was solved for each parameter set on an array of 1024 cells with periodic boundary conditions. All three fields (a, h, and u) were initially set to zero, except for a on 100 adjacent cells where a was chosen randomly and independently for each cell from a uniform distribution on [0, 0.25]. The equations were then integrated forward in time using an Euler integrator that treated the diffusive interaction terms fully implicitly. Each model was integrated forward in time 5000 time steps with dt = .06. All of the basic behaviors discussed in the paper (non-patterning fronts, stalled patterns, patterning fronts, fronts producing complicated patterns and transient activation—see Sec. 5.2) were observed in this test. Patterns were analyzed by eye to get a sense for the scope of the problem, and algorithmically to systematically classify the results. Another, similar test was conducted on a subset of stalled fronts using random uniform variants up to 0.35 instead of 0.25 for the initial a values on 100 cells. With these initial conditions, some of the stalled solutions became moving-front solutions, demonstrating this simple predicted initial condition dependence.

The first step in automatically classifying patterns was to apply a threshold to a corresponding to halfway between the zero-activation high steady state and the zero-activation intermediate unstable steady state (the “point of no return”). Cells with a above this threshold were considered active. For parameter sets where these steady states do not exist (A_a > .569) an arbitrary threshold of 0.5 was used. The easiest behavior to classify, in general, is transient activation, as it requires only that one see a point that was once above threshold go below threshold. It is easy to classify the non-patterning fronts next. Because the range of the inhibitor is typically short, we decided to classify as non-patterning any front that showed at least 20 consecutive cells above threshold behind the most recently activated cell at the end of 5000 time steps. If the front overran the entire 1024 cell field in the allotted integration time, the front was additionally classified as “fast,” and the last saved time point where the front had not yet crossed the entire field was used to evaluate the pattern. The vast majority of “fast” fronts were unpatterned, but there were exceptions. For a parameter set to be considered regularly patterning, the most recently created five groups of adjacent active cells had to consist of single active cells, and 3 of the 4 intervening gaps had to be equal in size. The solutions producing complicated patterns were subdivided into those with multiple adjacent cells in one of the most recent 5 groups, and those without. The first group dominated this category. To be considered stalled, a front had to produce no new active cells between time steps 2500 and 5000. Slipping through the cracks in this analysis are parameter sets that form very slowly propagating fronts. Indeed, parameter sets not conforming to any of the descriptions above were provisionally labeled “unknown behavior,” but upon detailed examination most proved to produce solutions that activated <5 cells, but did activate at least 1 in the interval 2500dt – 5000dt, thus failing the test for being stalled.

To compare these numerical results with the analytic theory of sec. 4, we followed the steps outlined in that section. We needed to calculate the amount of inhibitor at the points ahead of a patterned halfspace (which simply requires summing a geometric series) and the time when h_crit (u_x) is exceeded for each of these points, which entails solving for the self-consistent velocity of the pattern, v_q. Once that is calculated, the priority of the point representing continued patterning must be established by calculating h and h_crit (u_x) at its neighbors. h_crit (u_x) is easily calculated by setting ∂_ta to zero, finding g (h) as the root of the resulting polynomial, and then inverting that function if it is less than 1. h_x (t) was constructed numerically, and a standard root-finding algorithm was used to solve the relationship h_x (t) − h_crit (u_x) = 0 for t at all integer x up to the maximum value of x where h_x(∞) − h_crit (u_x) > 0. The numerical approximation for h_x (t) involved summing contributions from more and more distant active patterned sites according to Eq. (13), using a Runge-Kutta integrator with adaptive step size (because of the presence of more than one time-scale in the integrand) for the time integral, until one of two truncation conditions was met. The first truncation criterion was rarely used and involved a simple truncation if the contribution from the last patterned site was less than 10^-11 of the running total. The second truncation method involved evaluated the ratios of contributions of consecutive sites, and, in the event the relative change in these became less than .01, extrapolating the further contributions as the total of an infinite geometric series with the appropriate decay constant, which gives excellent results.

With this new information, a second pass over the parameter sets was made, setting initial conditions and integration parameters according to the predicted patterning behavior. The initial conditions for all cells and all fields were zero, except for one cell at the end of the (no longer periodic) array which had a at the high steady state. h was put into the system as a time-dependent boundary condition based on the solution to the unpatterned continuum problem with the appropriate constants, and corrected to account for the h produced by the initial 1-cell prepattern. The time-step, dt, was set to be .02 times the amount of time the front was expected to take to propagate 1 lattice unit, or .06, whichever was smaller, and the equations were integrated for twice as long as we anticipated it would take to produce 5 active cells. This led to some very long integrations. The time of each cell's activation was recorded and used to calculate the front speed. Pattern classification was conducted by methods similar to those described above. The main differences in the classification between these parameter sets were that some parameter sets that yielded non-patterning fronts originally yielded patterning ones, and those that were too slow to classify in the previous test were shown to propagate and pattern as expected.

Appendix B: The Interaction of Front and Template

We consider a uniformly translating front of h interacting with an inhibitor template exponentially decaying in space, u.

$$\begin{array}{l}{h}_x(t)=h(z)\\ z=x-vt\\ u_x=u_0{\lambda }^x\end{array}$$ (25)

The critical value of h, h_crit, at which the switch in each cell is flipped from low to high depends on u:

$$\begin{array}{l}{h}_{\mathit{\text{crit}}}(u_x)=H{\left[\frac{1-h_c-h_c{\left(\stackrel{u_x}{}/\underset{U}{}\right)}^{m_u}}{h_c\left(1+{\left(\stackrel{u_x}{}/\underset{U}{}\right)}^{m_u}\right)}\right]}^{-\stackrel{1}{}/\underset{m_h}{}}\hfill \\ h_c=h_{\mathit{\text{crit}}}(0)\hfill \end{array}$$ (26)

Here, we have introduced the variable h_c to denote the critical value with no inhibitor. The continuum approximation for h(z) was given in Sec. 4.2.1 and is

$$\begin{array}{l}h(z)=s_0\{\begin{array}{l}1-\left(\frac{v+c_1}{2c_1}\right)e^{\frac{-v+c_1}{2D_h}(z)},z<0.\hfill \\ \left(\frac{v+c_1}{2c_1}\right)e^{\frac{-v-c_1}{2D_h}(z)},z\ge 0\hfill \end{array}\hfill \\ c_1=\sqrt{v^2+4D_h}\hfill \end{array}$$ (27)

Since the function is actually only sampled at integer x, we expect the first cell where h_x (t) exceeds h_crit (u_x) as time goes forward to be one of the integers flanking the value of x at which the continuum h (z) first surpasses the continuum h_crit (u_x). At this first crossing of the two curves, both the functions themselves and their tangents must coincide:

$$\begin{array}{l}h(x-vt)=h_{\mathit{\text{crit}}}(u_x)\hfill \\ {\partial }_{x}h(x-vt)={\partial }_x{h}_{\mathit{\text{crit}}}(u_x)\hfill \end{array}.$$ (28)

We want to know two things about this point of intersection. First, how sensitive is it to changes in template patterns given a particular h (z)? If it changes by less than one, then only stable OUID patterns, or high-period patterns as discussed in Sec. 4.2.2 can exist. Second, sensitive is it to changes in h (z), as if, for instance, some random errors had occurred in the templating process? If it changes by very much less than 1 for the h (z) that would be produced by patterns that differ in wavelength by one, then having more than one stable OUID pattern supported by the same parameter set will be proportionally unlikely.

We proceed by expanding h_crit (u_x) and h (z) in Taylor series up to second order in x about their point of most likely contact, i.e. where the following relationships are satisfied:

$$\begin{array}{l}{u}_x=U\\ z=0\end{array}$$ (29)

This gives the following formulae:

$$\begin{array}{ll}{h}_{\mathit{\text{crit}}}(x)\hfill & \approx H{\left(\frac{2h_c}{1-2h_c}\right)}^{\frac{1}{m_h}}-\hfill \\ \hfill & H{\left(\frac{2h_c}{1-2h_c}\right)}^{\frac{1}{m_h}}\left(\frac{m_{u}log[\lambda ]}{-2m_h+4h_c{m}_h}\right)\left(x-\frac{log\left[U\right]-log\left[u_0\right]}{log[\lambda ]}\right)+\hfill \\ \hfill & \frac{H}{2}{\left(\frac{2h_c}{1-2h_c}\right)}^{\frac{1}{m_h}}{\left(\frac{(1+m_h)m_{u}log[\lambda ]}{-2m_h+4h_c{m}_h}\right)}^2{\left(x-\frac{log\left[U\right]-log\left[u_0\right]}{log[\lambda ]}\right)}^2+\hfill \\ \hfill & O{\left(x-\frac{log\left[U\right]-log\left[u_0\right]}{log[\lambda ]}\right)}^3\hfill \end{array}$$ (30)

and

$$\begin{array}{ll}h(x)\hfill & \approx \frac{1}{2}{s}_0\left(1-\frac{v}{c_1}\right)+\hfill \\ \hfill & s_0\frac{(v^2-{c_1}^2)(x-\mathit{\text{vt}})}{4c_1{D}_h}+\hfill \\ \hfill & s_0\frac{(c_1-v){(c_1+v)}^2{(x-\mathit{\text{vt}})}^2}{16c_1{D_h}^2}+\hfill \\ \hfill & O{(x-\mathit{\text{vt}})}^3\hfill \end{array},$$ (31)

where we have opted to use the steeper branch of h, which was defined piecewise. The relative magnitude of the two second order terms, here, is significant, as we are interested in tangential contact. For small velocities, the magnitude of the second order term in the expression for h(x) falls off as ¹/_Dh whereas the first order term falls off as $\stackrel{1}{}/\underset{\sqrt{D_h}}{}$, meaning that for higher D_h the approximation becomes better, and the dependence on x more linear, which is unsurprising. By comparison, the second order term for h_crit (x) is dependent mainly on the steepness of the u gradient, and the Hill coefficients m_u and m_h. For typical parameters, this second order term is hundreds of times larger than that for h (x).

We want to solve for tangential intersection of these two approximations, as mentioned. In general, the tangential intersection of two quadratics is easily calculated. For convenience, here, we apply the further simplification that h (x) is linear,

$$\begin{array}{ll}{h}_{\mathit{\text{crit}}}(x)\hfill & =r_2\left(x-\frac{log\left[U\right]-log\left[u_0\right]}{log\left[\lambda \right]}\right)+\hfill \\ \hfill & r_1\left(x-\frac{log\left[U\right]-log\left[u_0\right]}{log\left[\lambda \right]}\right)+r_0,\hfill \\ \hfill & h(x)=w_1(x-\mathit{\text{vt}})+w_0\hfill \end{array}$$ (32)

where the r and w coefficients are the appropriate terms from the Taylor series. The linear approximation is unnecessary if one does not mind the cumbersome equations it produces. Solving for tangential intersection yields

$$x=\frac{-r_1+w_1+2r_2\left(\frac{log\left[U\right]-log\left[u_0\right]}{log\left[\lambda \right]}\right)}{2r_2}$$ (33)

Taking the partial derivatives of x with respect to u₀ and s₀ gives the sensitivity of this intersection point to, respectively, template source strength and pattern density,

$$\begin{array}{l}{\partial }_{u_0}x=-\frac{1}{u_{0}log\left[\lambda \right]}\hfill \\ {\partial }_{s_0}x=\frac{{\left(1-2h_c\right)}^{\stackrel{1}{}/\underset{m_h}{}}\left(-{c_1}^2+v^2\right)\left(m_h-2h_c{m}_h\right)}{{\left(2h_c\right)}^{\stackrel{1}{}/\underset{m_h}{}}{c}_1{D}_{h}H\left(1+m_h\right){m_u}^{2}log{\left[\lambda \right]}^2}\hfill \end{array}.$$ (34)

The first derivative is, unsurprisingly, dependent on the source strength of the inhibitor and its length scale u. It is of order unity or less for typical parameters. The variation one can expect in x, then, from a template pattern of q + 1, instead of the preferred period q is given approximately by

$$|({\lambda }^{q+1}-{\lambda }^q){\partial }_{u_0}x|\ll 1.$$ (35)

The expression for the source-strength sensitivity is more complicated, but it is notable that there is a net factor of $\sqrt{D_h}$ in the denominator, as well as a net factor of m_u² log[λ]², the first of which is high when h is smooth, the second of which is high when the template is steep. This implies that for parameters that typify our assumptions, this derivative can be quite small. Multiplying it by a change in source density that is also much less than 1 (the maximum source density) suggests that the first point to be activated is relatively independent of small changes in source density, and thus, generically, only one patterning solution is supported in this limit, with two patterns supported infrequently, in proportion to the shift in x.

Appendix C: Binary classification based on timescales

In this appendix, we describe how we obtained the line in Figs. 11 and 12 separating OUID patterns from patterns in which all cells are active; the basic motivation for finding such a separating line is discussed in sec. 5.3.2.

Given a line ln(1/v) = m ln(T_a) + b in the ln(T_a), ln(1/v) plane, we can determine whether each point in Fig. 11 falls above or below that line. We already know whether the point corresponds to parameters that give an OUID or an all-up pattern. Based on these two binary decisions, each point can thus be assigned to one of four groups. Let A be the number of points above the line with an OUID pattern, B the number above the line but with an all-up pattern, C the number below the line but with an OUID pattern, and D the number below the line with an all-up pattern. If the line perfectly separated the OUID from the all-up patterns, we would have B = C = 0, and we can say that the line does a good job of classifying the patterns if B and C are small. More specifically, a good classifier should have a sensitivity A/(A + C), specificity D/(D + B), positive predictive value A/(A + B), and negative predictive value D/(D + C) all as close to unity as possible [54]. We thus defined the line that best separated the two sorts of patterns to be the one with the slope m and intercept b that maximized the product A²B²/(A+B)(A+C)(D+B)(D+C) of these four measures. More standard choices, like the phi statistic AD-BC/[(A+B)(A+C)(D+B)(D+C)]^(1/2), are also available, but we found that these performed slightly worse on our data (for which A and D are large and of the same order while B and C are small).