Nonlinear time course of brain volume loss in cognitively normal and impaired elders

Abstract

The goal was to elucidate the time course of regional brain atrophy rates relative to age in cognitively normal (CN) aging, mild cognitively impairment (MCI) and Alzheimer’s disease (AD), without a-priori models for atrophy progression. Regional brain volumes from 147 CN subjects, 164 stable MCI, 93 MCI-to-AD converters and 111 AD patients, between 51 to 91 years old and who had repeated 1.5T magnetic resonance imaging (MRI) scans over 30 months, were analyzed. Relations between regional brain volume change and age were determined using generalized additive models, an established non-parametric concept for approximating nonlinear relations. Brain atrophy rates varied nonlinearly with age, predominantly in regions of the temporal lobe. Moreover, the atrophy rates of some regions leveled off with increasing age in control and stable MCI subjects whereas those rates progressed further in MCI-to-AD converters and AD patients. The approach has potential uses for early detection of AD and differentiation between stable and progressing MCI.

1. INTRODUCTION

Alzheimer’s disease (AD) is associated with higher rates of brain tissue loss than normal aging, as demonstrated by longitudinal studies with magnetic resonance imaging (MRI) (Frisoni, et al.). Higher rates of brain tissue loss are also seen in mild cognitive impairment (MCI), a clinical concept to characterize subjects who lie cognitively between dementia and normal aging and who have an increased risk for AD (Petersen, et al., 2009). MRI studies further showed that the regional distribution of high brain tissue loss in AD and MCI patients exhibits a characteristic pattern that involves predominantly regions in the medial temporal lobe, including the entorhinal cortex (ERC) and hippocampus, mirroring the known distribution of plaques, tangles and neurodegeneration, the hallmarks of AD (Braak and Braak, 1996, Leow, et al., 2009,Morra, et al., 2009). MRI measurements of increased rates of brain tissue loss have therefore been proposed as a potential imaging marker of AD. However, critical issues about the time course of regional tissue loss relative to age remain.

Although many MRI studies have provided an incredible amount of information about rates of brain tissue loss in normal aging, MCI and AD, a fundamental limitation has been the difficulty in deriving the time course of brain atrophy over the adult age range. This information is essential to determine, for example, whether some areas in the brain lose tissue earlier than others and how compounding losses relate to cognitive decline. Variations in brain atrophy rates over the adult age range could also be the reason behind some startling observations in sporadic AD that some patients with late onset of clinical symptoms progress more slowly than those with earlier onsets (Wilson, et al., 2000). Several longitudinal MRI studies attempted to elucidate the time course of brain atrophy by testing whether rates of tissue loss accelerate (Davatzikos, et al., 2009,Driscoll, et al., 2009,Jack, et al., 2008b,McDonald, et al., 2009,Schuff, et al., 2009). Other studies derived information of brain atrophy from cross-sectional observations, which are inherently limited by distinguishing between secular and age-related changes (Raz, et al., 2004). The approaches all have used a-priori models for the time course of brain atrophy to extract information. However, to find an a-priori reason for using a particular model is difficult and therefore, the time course of brain atrophy relative to age remains elusive, especially across the cognitive spectrum.

In this study, we abolished modeling explicitly the time course of brain atrophy and aimed at achieving a more data driven approach, while simultaneously controlling effectively for variations across subjects at different ages and cognitive conditions. To accomplish this goal, we employed generalized additive models (GAM) (Hastie and Tibshirani, 1986), an extension of the better known generalized linear models used in statistical parametric mapping (Ashburner and Friston, 2000) and an established approximation of nonlinear functions. Because the flexibility of GAM allows combining parametric model components, i.e. brain volume changes between MRI scan intervals, and non-parametric components, i.e. brain volume variations across the age range of the subjects, the method is particularly suited for the purpose of this study. Specifically, we tested first whether brain atrophy rates vary non-linearly with age across the cognitive spectrum, i.e. in normal aging, MCI and AD and second, whether the time course of brain atrophy with age is regionally dependent such that regions known to be impacted early in AD, i.e. the hippocampus, will exhibit higher rates earlier than regions affected later by AD. In addition, we explored– based on the estimated rates - which brain regions in MCI and AD provide hypothetically the best differentiation between young patients and controls, i.e. those not older than 65 years.

2. METHODS

Subjects

The participants in this study were recruited between 2005 and 2008 through the Alzheimer’s Disease Neuroimaging Initiative (ADNI), a longitudinal study of about 800 individuals from 56 centers in the U.S. and Canada, designed to identify biomarkers of early AD for clinical trials (Mueller, et al., 2005a,Mueller, et al., 2005b). Further details of the ADNI study design as well as inclusion and exclusion criteria of subjects can be found at www.adni-info.org. Written consent was obtained from all subjects participating in the study, and the study was approved by the institutional review board at each participating site.

At the time of this investigation, regional brain volumes were available from 155 cognitively normal subjects, 266 subjects diagnosed with MCI and 115 patients diagnosed with AD, who all completed at least 2 and up to 5 longitudinal MRI scans at 1.5Tesla as well as a battery of clinical and cognitive assessments parallel to MRI over a period of 2 ½ years. We further divided the MCI group into those who converted to AD at a later visit (cMCI, n=93) and those who remained stable (sMCI, n = 164). We also ensured that the control group included stable subjects only and excluded 8 controls, who either converted to MCI or had a change in the clinical dementia rating (CDR) score from 0 to 0.5. This converter group was too small for any further meaningful analysis. We also excluded 13 subjects whose diagnosis was reversed during the course of the study (either from MCI to controls (n=9) or from AD to MCI (n=4) because of the uncertainty about these subjects’ cognitive status. The final size of each group is summarized in Table 1, together with other demographic data at baseline. The subjects were between 56 and 91 years old. Each subject’s cognitive evaluation included: 1) the Mini-Mental State Examination (MMSE) (Folstein, et al., 1975) to provide a global measure of mental status; 2) and the Alzheimer’s disease Assessment Scale – Cognitive Subscale (ADAS-Cog) (Mohs, et al., 1997), which is the most used cognitive assessment battery in clinical dementia trials. The participants were also examined for depression using the Geriatric Depression Scale (GDS) questionnaire (Yesavage, et al., 1982), in which subjects are asked to respond to 30-items with yes or no in reference to how they felt over the past week. In addition, the genetic profile of the apolipoprotein E (APOE) gene of each subject was determined. More details about the tests can be found on the ADNI website www.loni.ucla.edu/ADNI. A summary of the demographic and clinical data is provided in Table 1, separately for each group. Finally, to exclude the possibility of selection bias, we compared age, ADAS-Cog score and ApoE profile of the subjects in this study with those from all subjects enrolled in ADNI but found no significant differences (p > 0.3).

Table 1.

Demographic and clinical data summary

Variable	Control Stable	MCI Stable	MCI Converter	AD	P-value
Number of subjects	147	164	93	111
Female %	50	38	38	46	0.1*
APOE-ε4 carriers %	22	45	68	60	< 0.001*
Baseline
Age (years)	76 ± 5	75 ± 7	74 ± 7	75 ± 8	0.2
	[61 - 91]	[56 - 90]	[56 - 88]	[56 - 90]
MMSE(1)	29 ± 1	27 ± 3	25 ± 3	21 ± 4	< 0.001
	[25 - 30]	[21 - 30]	[18 - 30]	[5 - 27]
ADAS-Cog(2)	6 ± 3	11 ± 6	15 ± 6	22 ± 9	< 0.001
	[0 -14]	[2 - 25]	[4 - 35]	[6 - 50]
GDS(3)	1.0 ± 1.3	1.9 ± 1.4	2.1 ± 1.8	1.9 ± 1.8	< 0.001
	[0 - 5]	[0 - 11]	[0 - 9]	[0 - 6]
Change from baseline(4)
MMSE	0 ± 0.8	-0.4 ± 1.4	-7.0 ± 1.8	-10.5 ± 2.6	< 0.001
ADAS-Cog 11	0 ± 2.1	+5.7 ± 2.8	+20.3 ± 3.6	+25.2 ± 5.1	< 0.001
GDS	+13.1 ± 0.9	+13.4 ± 1.1	+8.5 ± 1.1	+8.0 ± 1.3	0.2

Values are in mean ± standard deviation; Ranges are listed in square brackets; P-values indicate effects across the groups;

^*Using Fisher exact test; all other tests using analysis of variance (ANOVA);

⁽¹⁾Mini-Mental State Examination; maximal range 0 to 30 points;

⁽²⁾Alzheimer’s disease Assessment Scale – Cognitive Subscale; maximal range 0 to 70 points;

⁽³⁾Geriatric Depression Scale; maximal range 0 to 15 points;

⁽⁴⁾Change is expressed as annualized percent change from baseline

MRI acquisition and brain volumetry

The subjects underwent at each site the standardized 1.5 T MRI protocol of ADNI (see http://www.loni.ucla.edu/ADNI/Research/Cores/index.shtml), which included T₁-weighted MRI based on a sagittal volumetric magnetization prepared rapid gradient echo (MP-RAGE) sequence with an echo time of 4 ms, a repetition time of 9 ms, a flip angle of 8°, and acquisition matrix size of 256 × 256 × 166, yielding a nominal resolution of 0.94 × 0.94 × 1.2 mm per voxel. Image quality and pre-processing was performed at a designated MRI center, as described in (Jack, et al., 2008a). The raw Digital Imaging and Communications in Medicine (DICOM) MRI data for this study were downloaded from the Laboratory of Neuro Imaging (LONI) Image Database Archive (http://www.loni.ucla.edu/ADNI/Data/index.shtml). The images were intensity-normalized, aligned to a brain atlas, skull-stripped, and segmented into 70 regional volumes using the freely available FreeSurfer software package, version 4.4 (http://surfer.nmr.mgh.harvard.edu/). In version 4.4 of FreeSurfer, the confounding effect of intra-subject morphological variability was reduced by using a longitudinal workflow that estimated brain morphometry measurements unbiased with respect to any time point in each subjects’ longitudinal MRI data. Specifically, instead of using data obtained at a specific time point (e.g. baseline MRI) as a prior for the longitudinal morphometric deformations, a template image volume from all time points was created first as an unbiased prior before the morphometric deformations were computed for data at all time points. For a full description of the FreeSurfer processing steps, see (Fischl, et al., 2002,Fischl, et al., 2004), and for a full description of the longitudinal workflow, see http://surfer.nmr.mgh.harvard.edu/fswiki/LongitudinalProcessing. The outcome measures of the Freesurfer workflow were segmented maps with anatomical labels of 70 brain regions, yielding the volume of each region for each time point and each subject. (In all, 40 regions are reported after averaging those regions which showed strong correlations between the left and right hemisphere). The segmented maps were visually rated for accuracy by experienced staff and excluded from the analysis if quality criteria were not met.

Generalized additive models (GAM)

Here, we briefly describe the application of GAM for the prediction of brain atrophy rates. GAM were proposed in 1986 by Hastie and Tibshirani (Hastie and Tibshirani, 1990) as an effective method to tackle the problem of rapidly increasing variance of estimates when there is a large number of variables to model. GAM assume that the expected value of the dependent variable is related to the predictor variables through a smooth (and not necessary linear) link function and furthermore that the probability distribution of the dependent variable is described by the family of exponential functions. Applying GAM for this study, we sought to relate changes in brain volume V_ij of each subject i across MRI scans j to the age distribution of the subjects m(age_i) The age distribution can induce variations in both magnitude α₁m(age) and time m(γ_iage), where m is of unknown shape. The volume changes can then be modeled according to:

$$V_{\mathit{ij}}(\mathit{age})={\beta }_0+{\beta }_1{t}_{\mathit{ij}}+m({\alpha }_i+{\gamma }_i\mathit{age}).$$ EQ (1)

The first two terms on the right hand side of EQ (1) represent the conventional parametric model for brain volume at baseline and linear volume change over time, respectively. The third term represents the unknown age-dependent shape of volume change in amplitude and time. The goal is to estimate the age-dependence of volume change, i.e. E(V_ij | age) without explicitly knowing the shape of m. Utilizing the concept of GAM, we approximate m by smooth basis functions with coefficients S_ϕi for magnitude and T_ϕi for time, which leads to:

$$E\left(V_{\mathit{ij}}\mid \mathit{age}\right)={\beta }_0+{\beta }_1{t}_{\mathit{ij}}+g\left(S_{{\varphi }_i}m\left(T_{{\varphi }_i}\mathit{age}\right)\right).$$ EQ (2)

Here, g (•) is a smooth link function, relating the unknown shape of m to the volumes and E(V_ij |age) stands for the expected age-dependent values of V_ij .We used the GAM library in R (http://www.r-project.org/, (Wood, 2004)) for fitting. For smoothing, we used thin plate spline basis functions, which do not require selecting explicitly knot positions, and we controlled smoothness by a second derivative penalty function (Wood, 2004). To obtain the optimal smoothing parameters and avoid overfitting, we used numerical iterations of penalized least squares toward minimizing the generalized cross-validation score, an index for optimal smoothness (Woods, 2006). This procedure is implicitly embedded in the GAM library in R for automatic smoothing parameter estimations (http://stat.ethz.ch/R-manual/R-patched/library/mgcv/html/00Index.html). To reassure an optimum selection of smoothing parameters, we also performed the numerical iterations with maximum likelihood estimations. In the few cases where iterative least squares and maximum likelihood tests yielded discordant results, we selected the smoothing terms manually until we found the minimum generalized cross-validation score. Finally, to further reduce the risk of overfitting, we forced the effective degree of freedom in the model to count as 1.4 degrees of freedom, which is an ad-hoc approach against overfitting (Kim and Gu, 2004). We augmented the model by parametric functions to account for covariates, such as head size, gender, and each subject’s genetic APOE profile.

Statistic

Changes in regional brain volumes as a function of age were fitted separately for each diagnostic group and for 40 regional brain volumes (and CSF spaces) defined with Freesurfer. (A total of 70 brain regions were evaluated initially but regions showing strong correlations between the left and right hemisphere were averaged, resulting ultimately in 40 regional tests). To test the significance of nonlinearity between volume and age relations, we compared the fits from GAM with fits derived using a non-penalized generalized linear model (GLM), in which age was included as a linear variable while all other variables in GAM and GLM were the same. An F-statistic was used to determine if differences between the fits are significant and the Akaike information criterion was used to determine which fit was better. The p-values of such comparisons, however, are not exact and can be biased since the tests are based on pretending that a penalized fit is equivalent to an unpenalized fit with the same effective degrees of freedom and neglect the uncertainty associated with smoothing parameter estimations. To determine the potential statistical bias in such comparisons, we evaluated the procedure using simulated linear and nonlinear data with a range of noise levels and found a slight bias toward nonlinearity of p = 0.01 (finding nonlinearity in simulated data when there was none). We therefore adjusted the significance threshold in tests of nonlinearity to an alpha level of less than 0.01. Lastly, we estimated - based on the GAM results of age-dependent brain atrophy - which brain regions provide hypothetically the best effect size to differentiate between young MCI and AD patients, who are presumably in an early disease stage and controls. This was accomplished by comparing estimates of brain tissue loss based on GAM across the groups using 1000 fold bootstrap of the GAM residuals and by computing effect sizes, expressed as Cohen’s d. All statistics was performed with R (http://www.r-project.org/). P-values are adjusted conservatively for multiple comparisons of brain regions using Bonferroni correction.

3. RESULTS

Table 1 lists demographic and clinical characteristics of the subjects at baseline and follow-up. At baseline, the four groups did not differ significantly in age (p = 0.2, ANOVA) and gender ratio (p = 0.1 Fisher exact test) but - as expected – cMCI and AD patients carried the APOE-ε4 gene more frequently (p < 0.001) than control subjects and also scored worse on cognitive performance (p < 0.001 for MMSE and ADAS-cog) as well as on depression (p < 0.001). sMCI subjects had values that lay in the middle between those of control and cMCI subjects. With respect to change from baseline, cMCI and AD patients declined cognitively much faster than the control and sMCI subjects, as expected (p < 0.001), whereas the groups did not differ significantly in changes in depression over time (p = 0.2). Differences in age distributions across the groups were also not significant (p > 0.09 by Kolmogorov-Smirnov tests), implying that variations in age sampling should not bias the analysis of age-dependent brain tissue loss in favor of any group.

A representative example of the time course of brain tissue loss as a function of age is shown in Figure 1 for the hippocampus. In the top row are shown raw data of individual trajectories of hippocampal volume change as a function of age from 75% randomly selected subjects. In the bottom row are shown the trajectories of estimated volume change from the same subjects after a GAM analysis, including parametric corrections for variations in intracranial volume and ApoE4 status. The figure illustrates first that the relationship between hippocampal volume loss and age is generally nonlinear and second that nonlinearity varies substantially across the groups.

Figure 1.

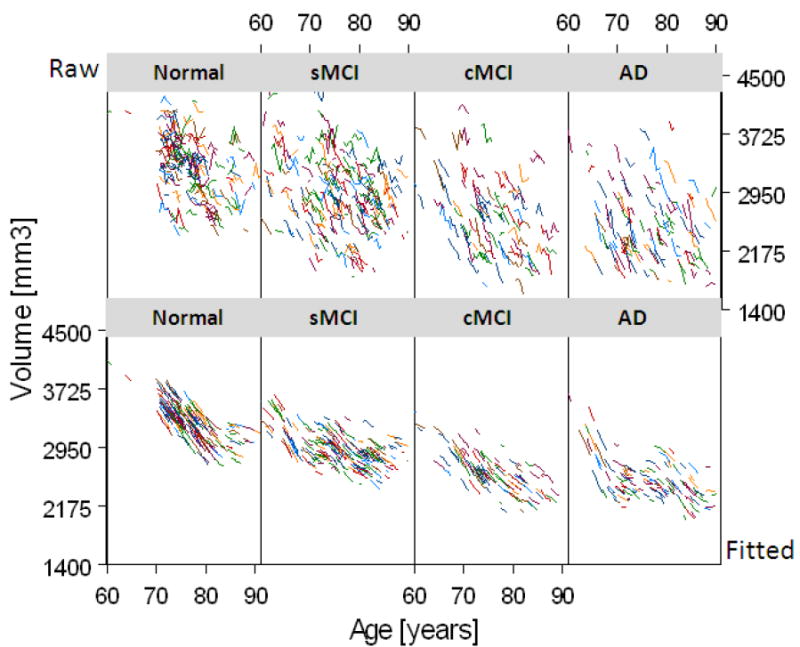
Individual trajectories of hippocampal volumes as a function of age from 385 (75%) randomly selected subjects of the study. Raw data are shown in the top row and fitted data in the bottom row. The data is shown separately for cognitive normal subjects, subjects with stable mild cognitive impairments (sMCI), subjects with MCI who converted to Alzheimer’s disease (cMCI), and patients with a diagnosis of Alzheimer’s disease (AD).

Group mean brain volume changes as a function of age are illustrated for global measures (e.g.lateral ventricle (VL) dilatation, white matter (WM), and cortical gray matter (GM)) in Figure 2, for temporal lobe regions in Figure 3 and for parietal/frontal lobe regions in Figure 4, separately for each group and ranked by significance of nonlinearity. The mean volume change of each brain region and each group is referenced to the overall mean volume of the corresponding brain region in the control group, where positive values indicate a larger size and negative values indicate a smaller size than the reference volume. The mean volumes are represented as solid lines, the 95% confidence bands are indicated by shaded areas, and the age sampling is indicated by rugs at the bottom of each plot. For each plot in Figures 2-4, the corresponding statistical test results of age dependence and significance of nonlinearity in are summarized in Table 2. Figure 2 illustrates that the well established ventricular expansion with age, an indirect measure of global brain atrophy, levels off significantly at increasing age in normal and sMCI subjects (significance of nonlinearity p_nonlinear = 0.008) whereas the expansion continues in cMCI and AD patients. The shape of ventricular expansion is mirrored in each group by atrophy of WM (p_nonlinear = 0.009) and cortical GM, though nonlinearity in GM changes was only a trend (p_nonlinear = 0.011). A more regionally selective analysis of GM change revealed significant nonlinear changes with age primarily in the temporal lobe, as illustrated in Figure 3. Specifically, the time course of GM atrophy is leveling off with increasing age in the parahippocampal gyrus (PG, p_nonlinear = 0.00004) and the hippocampus (HP, p_nonlinear = 0.0005) and more prominently so in normal subjects than in sMCI, cMCI and AD subjects, where GM volume is markedly reduced already. In contrast to the parahippocampal gyrus and hippocampus, the time course of GM atrophy of the fusiform gyrus and transverse temporal lobe accelerates with increasing age (FG: p_nonlinear = 0.0007 ; TT: p_nonlinear = 0.002) and this is seen primarily in controls while sMCI, cMCI and AD subjects already have reduced GM volumes. The entorhinal cortex (ERC, p_nonlinear = 0.01) largely exhibits a linear time course of GM loss with age across all groups with a progressively increasing atrophy rate from controls to sMCI, cMCI and AD patients. GM loss in parietal and frontal lobe regions progressed largely linear with advanced age across the groups (all p_nonlinear > 0.01), as illustrated in Figure 4. Similarly, a linear time course of tissue loss was found in most other brain regions, including subcortical structures (see supplementary material for details).

Figure 2.

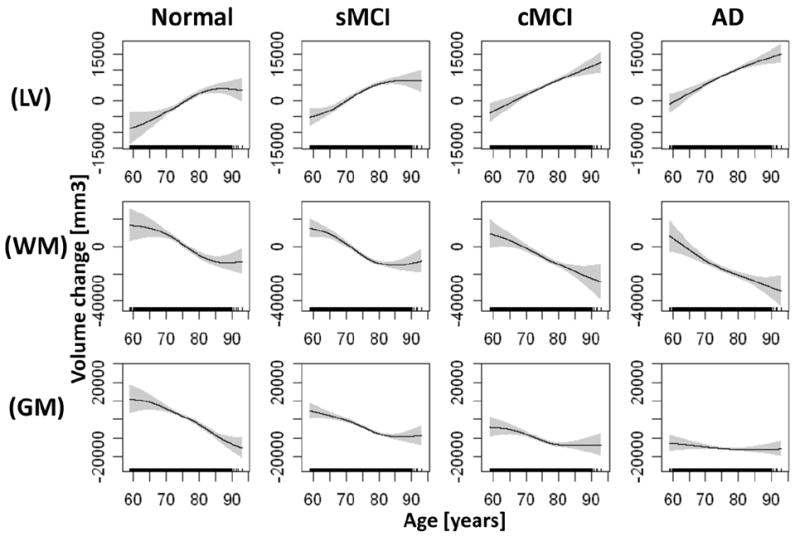
Estimations of brain volume loss and ventricular dilation as a function of age by diagnostic group. Shown are dilation of the lateral ventricles (LV) and volume loss of white matter (WM) and cortical gray matter (GM), in order of significance of nonlinearity (see table 2). Solid lines represent mean volume loss, shaded areas indicate the 95% confidence bands, and rugs at the bottom of each plot indicate the age sampling. Volume loss in each group is referenced relative to the overall mean volume of the corresponding brain region in the control group. Hence, positive values indicate larger volumes and negative values indicate smaller volumes than the overall reference mean volume.

Figure 3.

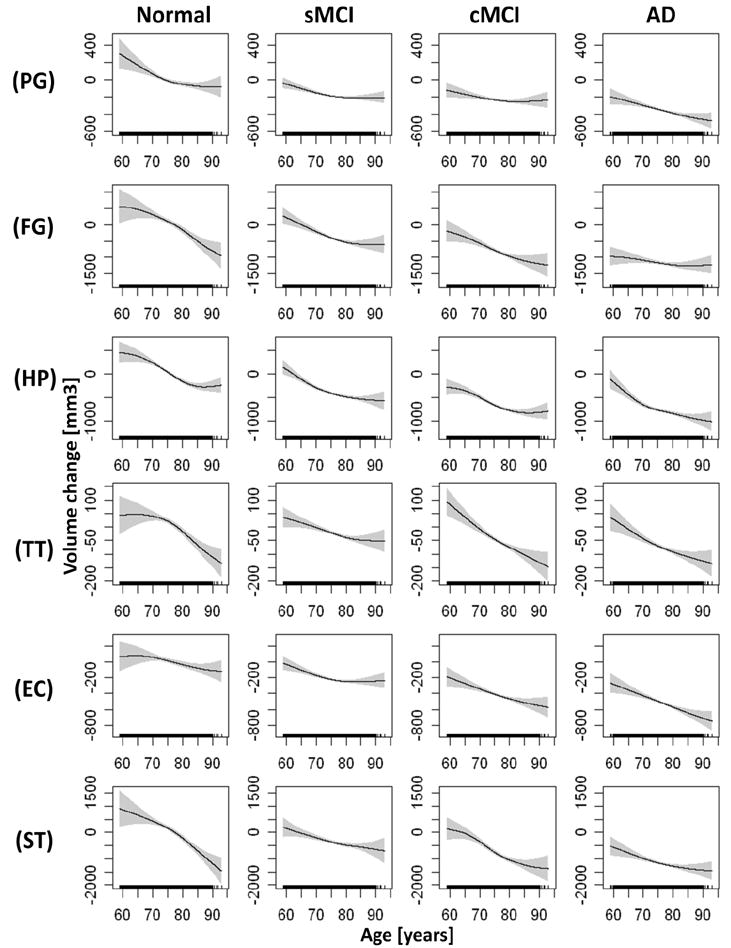
Estimations of brain volume loss as a function of age by diagnostic group for temporal lobe regions. Shown are volume loss of the parahippocampal gyrus (PG), fusiform gyrus (FG), hippocampus (HP), transverse temporal lobe gray matter (TT), entorhinal cortex (EC), and superior temporal lobe gray matter (ST), in order of the significance of nonlinearity (see table 2). The figure representations of volume loss are the same than those in Figure 2.

Figure 4.

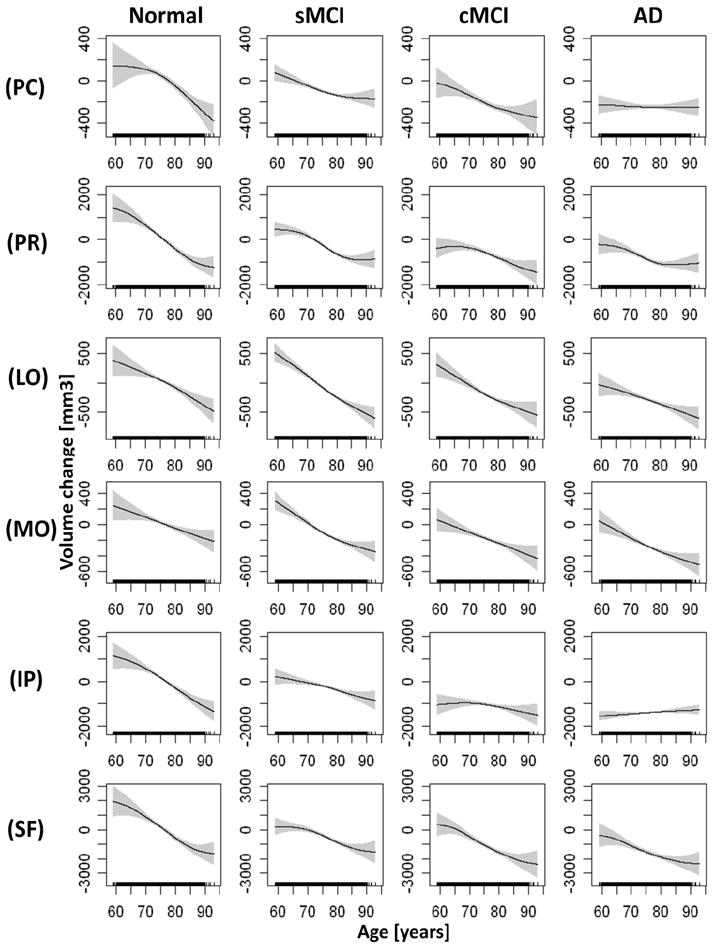
Estimations of brain volume loss as a function of age by diagnostic group for frontal and parietal lobe regions. Shown are volume loss of the posterior cingulate gray matter (PC), precentral gray matter (PR), lateral orbitofrontal lobe gray matter (LO), medial orbitofrontal lobe gray matter (MO), inferior parietal lobe gray matter (IP), and superior frontal lobe gray matter (SF). The figure representations of volume loss are the same than those in Figure 2.

Table 2.

Relationship between brain volumes and age as well as significance of nonlinearity using generalized additive modeling

Brain Regions	Control		sMCI		cMCI		AD		Nonlinearity
	eDF	Fage	eDF	Fage	eDF	Fage	eDF	Fage	Fnonlinear	pnonlinear
Lateral ventricles	1.9	22.2‡	2.3	45.2‡	1.3	33.5‡	1.5	35.7‡	7.1	8.0 × 10-3
Total white matter	1.7	23.5‡	2.2	40.2‡	1.9	18.7†	2.0	18.3†	5.5	9.2 × 10-3
Total gray matter	1.8	45.9‡	2.0	30.7‡	1.9	9.1$	1.2	0.6ns	5.3	1.1 × 10-2
Parahippocampal gyrus	1.9	9.3$	1.6	18.7$	1.3	2.4ns	1.4	14.4†	14.9	3.6 × 10-5
Fusiform gyrus	1.6	31.2‡	1.3	17.1†	1.2	16.8†	1.0	2.6ns	14.1	7.0 × 10-4
Hippocampus	1.7	44.5‡	2.4	37.8‡	1.8	25.6‡	2.1	27.3‡	12.2	4.6 × 10-4
Transverse temporal GM(a)	1.9	20.5‡	2.2	9.7†	2.0	20.7‡	1.3	12.2†	9.9	1.9 × 10-3
Entorhinal cortex	1.7	5.5ns	1.4	18.8†	1.3	12.9†	1.4	22.6‡	9.2	1.0 × 10-2
Superior temporal GM(a)	1.9	33.6‡	1.4	9.6†	1.9	27.0‡	1.3	6.9ns	4.3	ns
Posterior cingulate	1.9	31.1‡	1.4	13.7‡	1.9	9.4†	1.0	0.1ns	5.0	ns
Precentral GM(a)	1.8	60.0‡	2.1	50.1‡	1.8	14.6‡	1.7	10.1†	5.0	ns
Lateral orbitofrontal GM(a)	1.3	25.9‡	1.7	82.3‡	1.4	21.7‡	1.4	13.2†	4.9	ns
Medial orbitofrontal GM(a)	1.3	12.1†	1.6	58.2‡	1.4	13.6†	1.4	19.3†	4.5	ns
Inferior parietal GM(a)	1.2	48.9‡	1.6	14.6†	1.3	3.2ns	1.0	2.0ns	1.5	ns
Superior frontal GM(a)	1.8	41.1‡	1.9	22.2‡	1.8	23.7‡	1.7	11.9†	0.9	ns

eDF: extra degrees of freedom, an index of nonlinearity where a value larger than unity indicates the deviation from linearity.

F_age: F-value of age dependence test;

P-value levels of age tests: ns = not significant;

^$p = 0.05;

^†p = 0.01;

^‡p = 0.001;

F_nonlinear: F-value of nonlinearity test;

p_nonlinear = p-value of nonlinearity test;

GM: Gray matter;

To address the issue of overfitting, which could mimic nonlinearity, we also fitted the data using non-penalized generalized linear models (GLM) with a quadratic term for age to approximate nonlinear age dependence. In each case, where GAM implied a significant nonlinear relationship between volume loss and age, GLM also yielded significant results for the quadratic term of age, suggesting that findings of nonlinearity in some brain regions are not simply an artifact of overfitting.

Lastly, we determined - based on the GAM estimations - which brain regions provide hypothetically the best effect size to differentiate between young patients and controls, i.e. those no older than 65 years. The results are summarized in Table 3, listing volume change as annualized percentage change from baseline, separately for each group as well as the corresponding effect sizes to separate sMCI, cMCI and AD patients from control subjects. ERC atrophy rates provided the best effect size to separate AD patients from control subjects early, followed by atrophy rates of the hippocampus and ventricular expansion. Interestingly, the same measures and in the same order were also effective (effect size > 1.0) to differentiate between young cMCI and control subjects. No measure differentiated between sMCI and control subjects at a young age.

Table 3.

Hypothetical annualized rates of percent brain volume change and corresponding effect sizes for subjects not older than 65 years based on estimations using generalized additive models.

Region	Control	sMCI	cMCI	AD	Effect size(1)
					sMCI	cMCI	AD
ERC(2)	-1.1 ± 2.8	-2.3 ± 3.1	-5.0 ± 3.6	-5.9 ± 3.9	0.4	1.3	1.4
HP(3)	-1.0 ± 1.9	-2.0 ± 2.1	-3.5 ± 2.2	-4.0 ± 2.3	0.5	1.2	1.3
LV(4)	+4.2 ± 3.6	+5.2 ± 4.3	+8.2 ± 4.7	+9.9 ± 5.3	0.2	1.1	1.3
FG(5)	-0.8 ± 2.0	-1.6 ± 2.2	-3.9 ± 2.3	-4.0 ± 2.9	0.3	0.9	1.3
PG(6)	-1.0 ± 2.3	-1.8 ± 2.7	-3.6 ± 2.8	-4.2 ± 2.8	0.3	1.1	1.2
ST(7)	-0.9 ± 1.8	-1.4 ± 2.0	-3.0 ± 2.5	-3.4 ± 2.9	0.2	0.9	1.0

Annualized rates listed as mean ± standard deviation;

⁽¹⁾Effect sizes computed as Cohen’s d, which is defined as the difference between the two means divided by the pooled standard deviation of the data;

⁽²⁾entorhinal cortex;

⁽³⁾hippocampus;

⁽⁴⁾lateral ventricles;

⁽⁵⁾fusiform gyrus;

⁽⁶⁾parahippocampal gyrus;

⁽⁷⁾superior temporal lobe gray matter;

4. DISCUSSION

We have two major findings: First, we demonstrated that the time course of brain tissue loss can vary nonlinearly with age, depending on the brain region and cognitive status. While our results are consistent with other MRI studies, we did not explicitly model the shape of change but let the data drive the results. Second, we found atrophy rates of certain brain regions (and similarly ventricular expansion rates, which basically reflects global brain tissue loss) level off with increasing age and this is seen primarily in control and sMCI subjects whereas in cMCI and AD patients the atrophy rates (and equivalently ventricular expansion rates) progress further. A leveling-off of brain atrophy is consistent with the concept that age related neurodegeneration is statistically distributed such that the tissue dying first is the one with low vitality. The time course in cMCI and AD is consistent with the idea that disease related neurodegeneration accumulates over years. In conclusion, the new approach using GAM has uses for early detection of AD and the differentiation between stable and progressing MCI.

Many MRI studies investigated the time course of brain atrophy relative to age (McDonald, et al., 2009,Pfefferbaum, et al., 1994,Thompson, et al., 2003) and several reported nonlinear variations (Driscoll, et al., 2009,Jack, et al., 2008b,McDonald, et al., 2009,Schuff, et al., 2009). In contrast to most other studies, however, we did not model the relationship between brain volume change and age a-priori, and therefore the findings of nonlinear relationships are more insightful. Investigations before were hampered by the complexity of modeling progression of brain atrophy in AD and aging as well as by the huge biological variability across patients that limits sensitivity to detect trends. We reduced these problems by abolishing explicit models for atrophy progression while simultaneously accounting for variations across subjects. To accomplish this goal we took advantage of the fact that brain atrophy varies slowly and smoothly over time and used generalized additive models, a well-established approximation of nonlinear functions, to predict the course of brain atrophy changes with age. The cost we paid is that the sensitivity to detect fast variations in brain change over short periods, i.e. on and off medication, is diminished. However, this should not be a major limitation for studies which focus on brain aging and prediction of disease progression where long time periods matter.

The finding that CN and AD have different time courses of brain atrophy with age is not surprising, because age is by far the most important risk factor for sporadic AD (Chen, et al., 2009) and the mechanisms of neurodegeneration in AD are thought to differ fundamentally from those in normal aging (Shagam, 2009). However, it is fascinating to see that a GAM analysis captured the leveling-off of brain volume loss in certain brain regions in CN and partly also in sMCI without a-priori models for atrophy progression. The leveling-off of brain atrophy progression cannot be explained by a floor effect of brain volume because the rates continued to decline in cMCI and AD patients, who both have on average smaller brain volumes than CN and sMCI subjects. One explanation is that brain damage in aging is statistically distributed such that brain tissue with low vitality degenerates first. Thereafter, only tissue with high vitality remains and neurodegeneration levels off with advanced age. This explanation is also consistent with modern theories of biological survival that show a decline in mortality rates in old age (Piantanelli, 1986). A decline in mortality rate with increasing age may also explain why older patients with late onset of sporadic AD may progress clinically slower than patients with early disease onset. While it remains unclear which mechanism may lead reduced mortality rates, possible scenarios at the cellular level include polymorphisms in mitochondrial function, oxidative stress, and protein denaturation (Drachman, 2006). In contrast to aging, our findings in AD of a continuation and even acceleration of brain atrophy in old age is consistent with the concept that neurodegeneration due to AD accumulates over years. It is also striking to see that the leveling off of atrophy rates in CN and MCI is predominantly seen in medial temporal lobe structures, including the hippocampus, and less in the other brain lobes, implying that less vital brain tissue in the medial temporal lobe is dying faster than in other brain regions while vital tissue survives. However, another explanation for the leveling off of rates is that the older group of CN and sMCI subjects included fewer individuals with asymptomatic AD.

In some temporal lobe regions in controls, GM atrophy appeared to be limited initially but then accelerated with increasing age. Whether this time course indicates a particular resistance of these brain regions to damage until late life is unclear. It may also be possible that the time course of accelerated atrophy represents control subjects who have elevated brain amyloid, which is sometimes seen in controls on PET amyloid imaging and which has been shown to correlate with high atrophy rates (Apostolova, et al.,Jack, et al., 2009). More studies are warranted to investigate the relationship of atrophy rates with age, especially with respect to the brain amyloid burden.

We also estimated- based on the GAM results – which brain regions would hypothetically provide a sufficiently high effect size to differentiate between patient and controls not older than 65 years. We determined that atrophy rates of the ERC yield the best effect size to separate young AD patients from control subjects early, followed by rates of hippocampal atrophy and ventricular expansion. Interestingly, the atrophy rates of ERC also yielded the highest effect sizes to differentiate between young cMCI and control subjects, followed - in the same order as for AD - by hippocampal volume and ventricular expansion. In practice, however, segmenting reliably the ERC, which is a small structure and located in a convoluted area of the cortex, is not without complication and larger structures, such as the hippocampus and ventricles, might provide better precision. In general, our estimations indicate that mesial temporal lobe structures provide larger effect sizes than other brain regions, in line with general observations that mesial temporal lobe atrophy is the most prominent feature of AD seen on MRI.

The GAM method is not limited to analysis of age-related variations in MRI. In principle, GAM should also be useful to explore relationships between brain changes and other distributed measures, such as cognitive scores, CSF biomarkers, and brain amyloid load.

Several limitations of this study ought to be mentioned: First, since this is still largely a cross-sectional study, secular effects across subjects may have mimicked age variations. A mixed effects GAM model, which is available in R, might have relaxed the impact of secular effects by allowing a decomposition of errors into between and within subject variations. However, an exact statistic for significance tests of nonlinearity, as required in this study, has not yet been formulated for mixed effects GAM models. It is possible that we overestimated nonlinear relationships between brain changes and age by not considering mixed effects. Another limitation is that we evaluated rate variations with age separately by region without including relationship between them. This resulted likely in a loss of sensitivity as most brain regions are more or less affected by age and exploiting spatial relations across regions might increase power. More development is needed to incorporate the GAM framework into image analysis. Another limitation is that our investigations were limited by study design to the last 4-5 decades of life but excluded earlier decades. We therefore cannot rule out that some of our findings are modulated by prior lifetime events that are unrelated to age as well as cognitive status.