A quantitative model of the phase behavior of recombinant pH-responsive elastin-like polypeptides

Abstract

Quantitative models are required to engineer biomaterials with environmentally responsive properties. With this goal in mind, we developed a model that describes the pH dependent phase behavior of a class of stimulus responsive elastin-like polypeptides (ELPs) that undergo reversible phase separation in response to their solution environment. Under isothermal conditions, charged ELPs can undergo phase separation when their charge is neutralized. Optimization of this behavior has been challenging because the pH at which they phase separate, pH_t, depends on their composition, molecular weight, concentration, and temperature. To address this problem, we developed a quantitative model to describe the phase behavior of charged ELPs that uses the Henderson-Hasselbalch relationship to describe the effect of side-chain ionization on the phase transition temperature of an ELP. The model was validated with pH-responsive ELPs that contained either acidic (Glu) or basic (His) residues. The phase separation of both ELPs fit this model across a range of pH. These results have important implications for applications of pH-responsive elastin-like polypeptides, because they provide a quantitative model for the rational design of pH responsive polypeptides whose transition can be triggered at a specified pH.

Introduction

New materials capable of undergoing bioresponsive self-assembly and higher-order supramolecular organization are required to build the next generation of biomaterials. Genetic engineering is a promising approach to synthesize such materials, and guided by this belief, we have been exploring recombinant elastin-like polypeptides (ELPs) as building blocks for self-assembled nanoparticles for drug delivery^1–3, hydrogels for local drug delivery ⁴, and tissue engineering ^5–8. ELPs are recombinant protein-polymers composed of pentapeptide (Val-Pro-Gly-Xaa-Gly)_L repeat units, and are so named because this pentamer and its analogs are recurring motifs in tropoelastin in a wide range of species ⁹. ELPs undergo an inverse phase transition – also called a lower critical solution temperature (LCST) transition– at a characteristic temperature, T_t, above which they phase separate from bulk water. At the molecular level, the identity of Xaa and L control this phase behavior ¹⁰. When pH-sensitive acidic or basic amino acids are placed at some of the Xaa positions, the T_t of these ELPs becomes dependent on pH.

Polymers that show LCST behavior are one class of materials that can be used as the building blocks for bioresponsive systems ¹¹, and we have chosen to focus on ELPs for the following reasons: ELPs are genetically encodable, so they can be produced in heterologous expression systems with high yield and purity. The ability to produce ELPs recombinantly has several important ramifications. First, we have found that ELP fusion proteins also retain stimulus responsive behavior. The ability to impart stimulus responsiveness to proteins and peptides by gene-level fusion of an ELP tail is a simple method to create proteins and peptides whose physical behavior (e.g., solubility) can be externally modulated by a small change in solution conditions. This attribute is extraordinarily useful as it generates a range of applications in biotechnology, ranging from non-chromatographic purification of ELP fusions ^12–14 to the development of affinity capture reagents ^15–17 and interfaces ^18–20. ELPs are also attractive for biomedical applications ^21–24 including drug delivery ^{11, 23, 25–29} and tissue engineering ^5–8 because they are biocompatible ^{30, 31}, non-toxic, and biodegradable ^{3, 27}. For biomedical applications in which ELPs are injected or implanted in vivo, genetically encoded synthesis provides significant advantages over synthetic polymers that display LCST behavior, as it provides precise control over their composition, molecular weight (MW), and polydispersity, features that control their in vivo biodistribution, biodegradation and disposition ^{25, 32}.

In an effort to diversify the range of applications of ELPs, we have recently focused on the use of pH as a trigger of their phase transition behavior ³³. This effort was motivated by the recognition that pH plays a role in many biological processes and is hence a useful trigger to develop bioresponsive therapeutics. For example, the extravascular space within tumors has a reduced pH compared to that found in blood or many healthy tissues due to tumor hypoxia and production of lactate by anaerobic glycolysis. A large percentage of aggressive clinical tumors display regions with elevated levels of lactic acid³⁴, and areas of lactic acid production can be diffusely spread across large regions of the tumor. The elevation in lactic acid level correlates with the lower pH of tumors³⁵. There is, however, considerable variability between tumor types; sarcoma and adenocarcinoma have pHs as low as 5.6, squamous cell carcinoma have pHs as low as 6.3, and melanoma have been measured as low as pH 6.8 ³⁵.

Because ELPs undergo a sharp phase change that can be isothermally triggered by a small change in pH, and because this pH responsiveness is controlled by the type and number of ionizable residues and MW of the ELP, in principle it should be possible to synthesize ELPs that are designed to undergo their phase transition within a narrow, physiologically relevant range of pH that is optimized for delivery to a specific tumor type. This level of control of the pH responsiveness of ELPs or other stimulus-responsive polymers requires a biophysical model that is capable of predicting the pH responsiveness of these polymers with great precision. However, to the best of our knowledge, a quantitative model that allows prediction of the pH at which a charged ELP will undergo its phase transition does not exist. In an effort to address this limitation, we report herein a quantitative model that incorporates the effect of pH with MW and solution concentration, the two other primary variables that control the phase transition behavior of an ELP, to quantitatively predict the T_t of ionizable ELPs.

Materials and methods

ELP biosynthesis and purification

ELPs were synthesized by heterologous expression of a plasmid-borne synthetic gene in E. coli as described previously (Supplementary Fig. 1) ²⁵. Genes encoding ELPs were constructed using recursive directional ligation (RDL) in pUC19 plasmids grown in TOP10™ cells (Invitrogen Corporation, Carlsbad, CA) and then transferred to modified pET25b+ expression vectors (Novagen, Madison, WI). 5’ phosphorylated oligonucleotides were purchased from Integrated DNA technologies (Coralville, IA). All DNA plasmids were purified using QIAprep™ spin miniprep kits (Qiagen; Germantown, MD). To generate the acidic ELPs containing glutamic acid guest residues (Glu), an annealed oligonucleotide cassette was prepared from a sense 99 base oligonucleotide (5’-AATTCATATGGGCCACGGCGTGGGCGTTCCGGGTATCGGTGTTCCGGGTATCGGTGTTCCGGGTGAAGGTGTTCCGGGTATCGGTGTGCCGGGCTGGCA-3’) and an antisense 99 base oligonucleotide (5’-AGCTTGCCAGCCCGGCACACCGATACCCGGAACACCTTCACCCGGAACACCGATACCCGGAACACCGATACCCGGAACGCCCACGCCGTGGCCCATATG-3’). To generate basic ELPs containing histidine (His) guest residues, an annealed oligonucleotide cassette was prepared from a sense 99 base oligonucleotide (5’-AATTCATATGGGCCACGGCGTGGGTGTTCCGGGCCACGGTGTCCCAGGTGGCGGCGTACCGGGCCACGGTGTTCCTGGTGCTGGCGTGCCGGGCTGGCA-3’) and an antisense 99 base oligonucleotide (5’-TGCCAGCCCGGCACGCCAGCACCAGGAACACCGTGGCCCGGTACGCCGCCACCTGGGACACCGTGGCCCGGAACACCCACGCCGTGGCCCATATGAATT-3’). For each ELP, the pUC19 vector was digested with EcoR I and Hind III (New England Biolabs; Ipswich MA), and the digest was purified using a QIAquick™ PCR purification kit (Qiagen; Germantown, MD). The vector and annealed oligonucleotide cassette were ligated using T4 DNA ligase (Invitrogen; Carlsbad, CA), transformed into chemically competent cells, and selected on Terrific Broth (TB)-agar plates with ampicillin (100 µg/mL). Colonies were screened by diagnostic digestion and positive clones were confirmed by DNA sequencing. To oligomerize the “monomer” gene of each ELP to create a library of genes that span the MW range of interest, recursive directional ligation was carried out as previously described ²⁵. In a typical round of RDL, linear inserts were generated by restriction digestion of plasmid DNA with Pflm I and Bgl I, and the correct insert was purified by gel extraction. Linearized vector was generated by incubation with Pflm I, the linearized vector was dephosphorylated using calf intestinal phosphatase (CIP) and then purified using a PCR purification kit. The linearized vector and insert were then ligated to obtain successively longer synthetic genes. After the desired number of rounds of RDL to oligomerize the monomer gene to the desired number of repeats, the insert gene was obtained by restriction digestion as described above and ligated into a modified pET25b+ expression vector that was linearized by digestion with SfiI ²⁵. This approach produced synthetic genes (Supplementary Table 1) that express acidic ELPs with the sequence MSKGPG[XGVPG]_L=40,80,160WPC with X = V:I:E [1:3:1] and basic ELPs with the sequence MSKGPG[XGVPG]_{L=40,60,100,120}WP with the ratio of X = V:H:G:A [1:2:1:1]. Successful ligation products were transformed into chemically competent BLR(DE3) (Novagen, Madison, WI) cells for ELP expression.

To express ELPs, 1 liter cultures of TB (MoBio; Carlsbad, CA) were seeded from 50 mL overnight cultures (100 µg/mL ampicillin) and incubated for 24 h at 37 °C and ~210 RPM. Bacterial cultures were centrifuged, resuspended in ~20 mL PBS, and disrupted by probe ultrasonication (Misonix; Farmingdale, NY). To precipitate DNA with the insoluble debris, the lysate was supplemented with polyethyleneimine to a concentration of about 1% and centrifuged at 16,100 RCF at 4 °C. The clarified supernatant was removed, supplemented with up to 3 M NaCl as required to induce the ELP transition, and purified by inverse transition cycling (ITC) ^{9, 12}. Briefly, ITC consists of raising the NaCl concentration as needed (0 to 3 M) to induce ELP phase separation. The ELP pellet was collected by hot centrifugation at 16,100 RCF (37 °C). The enriched pellet was resuspended in buffer and centrifuged in the cold (4 °C) to remove aggregated contaminants. The enriched ELP solution was subjected to this cycle of hot and cold centrifugation 4–6 times until sufficient purity was obtained. ELP purity was confirmed using SDS-PAGE (Supplementary Fig. 2). The ELP concentration was determined using UV-Vis spectrophotometry and an estimated molar extinction coefficient for the sole tryptophan³⁶ in each ELP of 5,690 cm⁻¹ M⁻¹ at 280 nm. Yields of purified ELP were ~100 mg/L culture.

To determine the pH dependent transition temperature, concentrated ELPs were dialyzed into buffer solutions containing pH-adjusted solutions of sodium succinate (pH < 6.4) or sodium phosphate (pH >= 6.4). Both buffers were selected based on the relative insensitivity of their pKa to temperature. For the acidic ELPs, buffers were prepared with 10 mM buffer and 140 mM of NaCl. The basic ELPs were prepared with 100 mM buffer and 50 mM of NaCl because they have a higher linear charge density than the acidic ELPs and hence required additional buffering capacity to maintain their pH. ELP transition temperatures were determined on a CARY 300Bio UV-VIS spectrophotometer (Varian; Palo Alto, CA) by scanning the temperature at 1°C per minute. The transition temperature was defined as the solution temperature that corresponded to the maximum first derivative of the optical density at 350 nm (Supplementary Fig. 3).

Results

pH dependence of the ELP phase transition

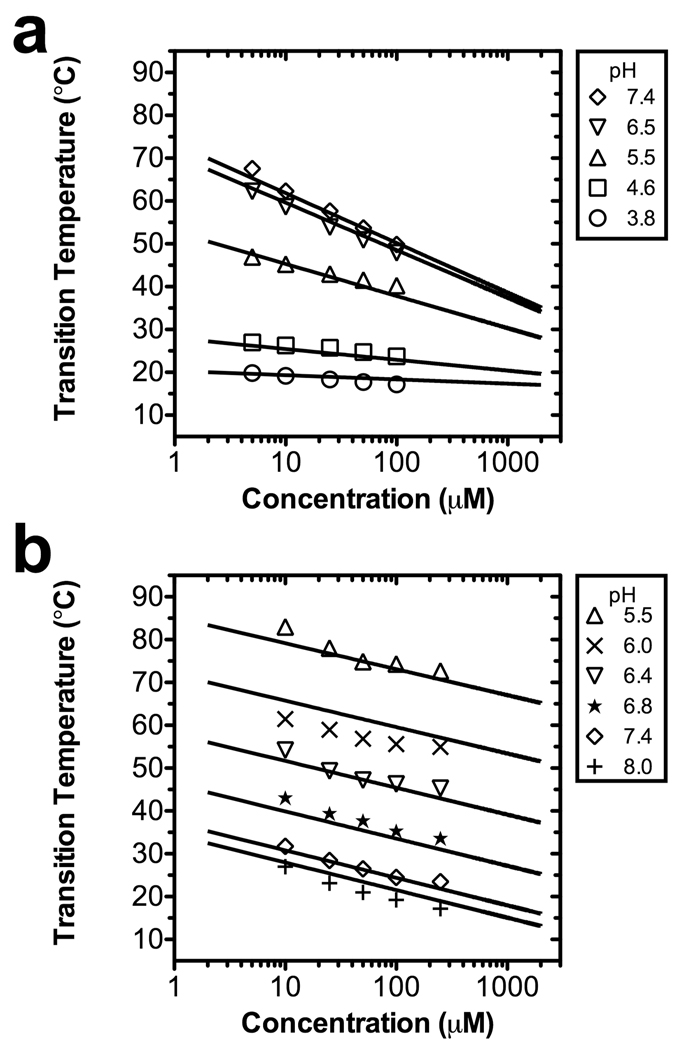
We synthesized two ELP libraries with a range of molecular weights that have pH sensitive phase behavior. The first library comprises acidic ELPs that contain multiple glutamic acid residues that repeat along the ELP sequence. Above their pKa, these ELPs are charged and have a high phase transition temperature, but a decrease in pH below their pKa leads their glutamic acid residues to be protonated and become neutral, which dramatically reduces their phase transition temperature. The second library contains the basic amino acid histidine interspersed periodically along the ELP sequence. At low pH these basic ELPs are charged and soluble; however, when the pH rises above their pKa, they become neutralized and their phase transition temperatures decreases. Thus, these two ELP libraries exhibit opposing pH dependent phase transition behavior across a range of pH (Fig. 1). These pH-triggered ELPs exhibit a phase transition over a wide range of pH, which were deliberately chosen to test the robustness of a quantitative model.

Figure 1.

The pH and concentration dependence of ELP phase behavior. ELP transition temperatures are plotted as a function of the logarithm of the polymer concentration. For each pH, a best-fit line to Eq. 7 is presented (Table 1). (a) An acidic ELP of 160 pentamers containing guest residues V:I:E [1:3:1] with a pKa of 5.29. (b) A basic ELP of 120 pentamers containing guest residues V:H:G:A [1:2:1:1] with a pKa of 6.22.

As has been reported previously, the phase transition temperature for non-ionic ELPs strongly depends upon both the ELP chain length and its solution concentration ³², so that these orthogonal variables allow the phase transition temperature to be finely tuned. We observed that this relationship also holds upon introducing pH-sensitive guest residues into an ELP, but that the effect of the pH on the phase transition temperature dominates over the ELP chain length or its solution concentration. To describe this finding within a quantitative framework, we developed an empirical analytical model that fit the observed pH dependence of the transition temperature (T_t, in °C) of the ELP phase transition of both ELP libraries as a function of their concentration (C, in µM) and length (L, in pentamers). This model explicitly accommodates the pH dependent behavior of both the acidic and basic ELP libraries. A key assumption of this model is that the transition temperature at an intermediate pH can be linearly interpolated between the transition temperature of a fully deprotonated ELP at a high pH, T_depro, and a fully protonated ELP at a low pH, T_pro, as follows:

$$T_t=f_{\mathit{\text{depro}}}{T}_{\mathit{\text{depro}}}+(1-f_{\mathit{\text{depro}}})T_{\mathit{\text{pro}}}$$ Eq. 1

where f_depro is the fraction of total ELP guest residues that is deprotonated. This linear approximation is strongly supported by previous observations, which showed that the transition temperature depends linearly upon the mixture of both charged and neutral guest residues ⁹.

To determine f_depro, the Henderson-Hasselbalch equation can be used to estimate the relative concentration of protonated, C_pro, vs. deprotonated, C_depro, guest residues in a polymer solution as follows:

$$\mathit{\text{pH}}=\mathit{\text{pKa}}+\mathit{\text{Log}}\left[\frac{C_{\mathit{\text{depro}}}}{C_{\mathit{\text{pro}}}}\right]$$ Eq. 2

By conservation of total ionizable residues, C_total:

$$C_{\mathit{\text{total}}}=C_{\mathit{\text{depro}}}+C_{\mathit{\text{pro}}}$$ Eq. 3

Substituting Eq. 3 into Eq. 2 and rearranging provides an expression for the fraction of guest residues protonated in the ELP polymer solution.

$$f_{\mathit{\text{depro}}}=\frac{C_{\mathit{\text{depro}}}}{C_{\mathit{\text{total}}}}=\frac{1}{1+{10}^{(\mathit{\text{pKa}}-\mathit{\text{pH}})}}$$ Eq. 4

By substituting Eq. 4 into Eq. 1 and rearranging, the following approximation is obtained:

$$T_t=T_{\mathit{\text{pro}}}+\frac{T_{\mathit{\text{depro}}}-T_{\mathit{\text{pro}}}}{1+{10}^{(\mathit{\text{pKa}}-\mathit{\text{pH}})}}$$ Eq. 5

The above equation linearly interpolates between the transition temperature of a fully protonated or a fully deprotonated ELP as a function of pH, and was explored in combination with other variables that influence the transition temperature. Note that Eq. 5 is valid for fitting the behavior of ELPs with either acidic or basic guest residues. Basic amino acids such as histidine are charged in their protonated form; therefore, their transition temperature decreases above their pKa. In contrast, acidic amino acids such as glutamic acid are neutral in their protonated state; therefore, their transition temperature increases above their pKa. Thus, Eq. 5 describes the pH-dependent phase transition behavior of both basic and acidic ELPs.

T_t dependence on concentration at fixed length

Prior to developing a single multivariate model that relates transition temperature to pH, length, and concentration, we first verified that Eq. 5 is valid at fixed length; furthermore, this step was necessary to confirm our assumption that the pKa is roughly independent of ELP length. Empirical observation has shown that the ELP transition temperature depends on the natural logarithm of the polymer concentration; furthermore, the degree of this dependence is strongly influenced by the selection of guest residues and polymer length³². The following relationship has been previously derived to quantify the concentration dependence for ELPs ³²:

$$T_t=T^{\mathit{\text{ref}}}-b\text{ ln}[C]$$ Eq. 6

where T^ref is the transition temperature at a reference concentration (1 µM here) and ELP concentration, C, is in units of µM. The slope, b, represents the concentration dependence of the transition temperature. When Eq. 6 is written for the protonated (T^ref_pro, b_pro) and deprotonated (T^ref_depro, b_depro) form of the ELP and inserted into Eq. 5, the following relationship is obtained:

$$T_t=T_{\mathit{\text{pro}}}^{\mathit{\text{ref}}}-b_{\mathit{\text{pro}}}\text{ ln}[C]+\frac{T_{\mathit{\text{depro}}}^{\mathit{\text{ref}}}-T_{\mathit{\text{pro}}}^{\mathit{\text{ref}}}-(b_{\mathit{\text{depro}}}-b_{\mathit{\text{pro}}})\text{ln}[C]}{1+{10}^{(\mathit{\text{pKa}}-\mathit{\text{pH}})}}.$$ Eq. 7

The above equation was used to fit each ELP analyzed in our dataset (Fig. 1) to obtain the best-fit parameters (Table 1). Interestingly, these data suggest that all the parameters of Eq. 7 depend on length except for the pKa. The observation that the pKa of an ionizable ELP is independent of its chain length leads us to propose the assumption that the pKa of an ELP is constant within its compositional library.

Table 1.

The ^adependence of the transition temperature on pH and concentration for ELPs with fixed lengths and guest residues.

ELP guest residues	Length, L (pentamers)	pKa	Trefpro (°C)	Trefdepro (°C)	bpro (°C / Ln [µM])	bdepro (°C / Ln [µM])	R2	n
bV:I:E [1:3:1]	40	5.50 (0.05)	35.2 (1.8)	148 (11)	2.48 (0.53)	15.5 (2.4)	0.990	21
	80	5.51 (0.05)	21.6 (2.3)	81.0 (2.0)	0.42 (0.67)	5.04 (0.54)	0.985	36
	160	5.29 (0.03)	18.6 (1.1)	73.9 (0.8)	0.28 (0.32)	5.09 (0.23)	0.997	30
cV:H:G:A [1:2:1:1]	40	6.59 (0.09)	137 (12)	103 (4)	8.4 (2.0)	11.8 (0.9)	0.979	20
	60	6.26 (0.06)	116 (6.7)	62.1 (2.8)	4.3 (1.1)	6.3 (0.6)	0.978	33
	100	6.25 (0.05)	98.0 (4.6)	38.5 (2.9)	2.9 (1.0)	3.1 (0.7)	0.982	30
	120	6.22 (0.05)	95.1 (4.4)	33.4 (2.8)	2.6 (1.0)	2.8 (0.7)	0.985	30

^adata fit to Eq 7 and parameters reported as the estimate (standard error).

^bacidic ELP at pH 2.5–7.8, and concentrations from 5–100 µM.

^cbasic ELP at pH 5.5–8.0, and concentrations from 10–500 µM.

T_t dependence on concentration and length at fixed pH

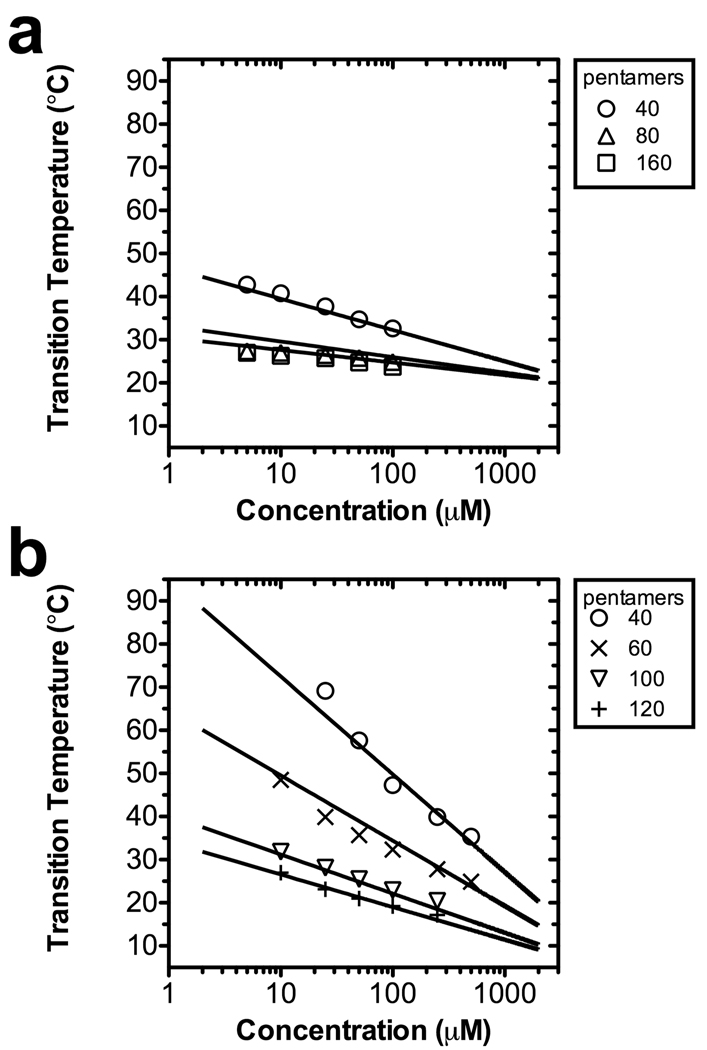
Having demonstrated that the ELP phase transition temperature can be modeled by the Henderson-Hasselbalch equation (Fig. 1), we next investigated the dependence of ELP chain length and its solution concentration at a fixed pH. ELP transition temperatures depend on the polymer molecular weight, related here to the number of pentameric repeats, L (Fig. 2). For an ELP library at constant pH, the dependence of the transition temperature on concentration and length was expected to follow the empirical relationship previously developed by Meyer and Chilkoti³²:

$$T_t=T_c+\frac{k}{L}\text{ln}\left[\frac{C_c}{C}\right]$$ Eq. 8

where T_c is a critical transition temperature described by the extrapolated intersection of the concentration-dependent transition temperatures from ELPs of different lengths, L. These curves intersect at a critical concentration, C_c; furthermore, an interaction parameter k is included to modulate the dependence of T_t on length and concentration. To verify that both acidic and basic ELPs follow this principle, both libraries were fit to Eq. 8 at a number of fixed pHs (Table 2). The fit parameters demonstrate that T_c and k both depend on pH; however, C_c does not substantially change with pH. This is partly due to the fact that C_c is an extrapolated value, far above the concentration that is achievable in a dilute, buffered solution. Despite this, it appears that at constant pH, Eq. 8 accurately describes the transition behavior of both acidic and basic ELPs (Fig. 2).

Figure 2.

The length and concentration dependence of ELP phase behavior. For each length, a best-fit line to Eq. 8 is presented (Table 2). (a) The acidic ELP library at pH 4.6 containing guest residues V:I:E [1:3:1]. (b) The basic ELP library at pH 8.0 containing guest residues V:H:G:A [1:2:1:1].

Table 2.

The ^adependence of the transition temperature on length and concentration at fixed pH.

ELP guest residues	pH	Tc (°C)	K (°C pentamers)	Cc (mM)	R2	n
bV:I:E [1:3:1]	6.5	39.5 (2.7)	363 (72)	3.1 (2.7)	0.786	22
	5.5	32.8 (2.5)	278 (80)	1.8 (2.2)	0.841	14
	4.6	19.7 (1.0)	126 (27)	5.4 (6.7)	0.927	15
	3.7	13.3 (0.9)	106 (23)	7.8 (10.5)	0.929	15
cV:H:G:A [1:2:1:1]	8.0	3.6 (1.2)	394 (24)	10.9 (3.4)	0.978	21
	7.4	8.5 (1.5)	403 (29)	9.9 (3.6)	0.968	21
	6.8	20.5 (1.2)	354 (26)	16.5 (6.0)	0.972	20
	6.4	30.9 (1.4)	348 (29)	20.9 (8.3)	0.964	19
	6.0	39.9 (1.5)	308 (31)	42.0 (22.7)	0.958	19
	5.5	58.7 (1.4)	340 (30)	24.8 (9.8)	0.958	13

^adata fit to Eq. 8 and parameters reported as the estimate (standard error).

^bacidic ELP lengths from 40–160 pentamers and concentrations from 5–100 µM.

^cbasic ELP lengths from 40–120 pentamers and concentrations from 10–500 µM.

T_t co-dependence on concentration, length, and pH

Having demonstrated that the ELP phase behavior is simultaneously pH, length, and concentration dependent, it is now possible to develop a single equation that accounts for each of these behaviors. To do this, a form of Eq. 8 that represents both the protonated and deprotonated ELP can be substituted into Eq. 5 and rearranged, yielding:

$$T_t=T_{c,\mathit{\text{pro}}}+\frac{k_{\mathit{\text{pro}}}}{L}\text{ ln}\left[\frac{C_{c,\mathit{\text{pro}}}}{C}\right]+\frac{T_{c,\mathit{\text{depro}}}-T_{c,\mathit{\text{pro}}}+\frac{1}{L}\left(k_{\mathit{\text{depro}}}\text{ ln}\left[\frac{C_{c,\mathit{\text{depro}}}}{C}\right]-k_{\mathit{\text{pro}}}\text{ln}\left[\frac{C_{c,\mathit{\text{pro}}}}{C}\right]\right)}{1+{10}^{(\mathit{\text{pKa}}-\mathit{\text{pH}})}}$$ Eq. 9

where C_c,depro and C_c,pro are the critical concentrations for the deprotonated and protonated polymers, respectively, T_c,depro and T_c,pro are the critical transition temperatures for the deprotonated and protonated polymers, respectively, and k_depro and k_pro are the parameters for the length-concentration interaction for the deprotonated and protonated polymers, respectively. Eq. 9 assumes that pKa is independent of concentration and length, as supported by Table 1. Including pKa, Eq. 9 has 7 parameters, so some simplification of this equation was considered desirable. The critical concentration, C_c, is an extrapolated value, and it does not appear to have a significant dependence on pH (Table 2). Thus, we simplified Eq. 9 by assuming that the critical concentrations are roughly equal between the protonated and deprotonated forms. After substitution of C_c,pro and C_c,depro with C_c into Eq. 9, we obtain:

$$T_t=T_{c,\mathit{\text{pro}}}+\frac{k_{\mathit{\text{pro}}}}{L}\text{ln}\left[\frac{C_c}{C}\right]+\frac{T_{c,\mathit{\text{depro}}}-T_{c,\mathit{\text{pro}}}+\frac{(k_{\mathit{\text{depro}}}-k_{\mathit{\text{pro}}})}{L}\left(\text{ln}\left[\frac{C_c}{C}\right]\right)}{1+{10}^{(\mathit{\text{pKa}}-\mathit{\text{pH}})}}.$$ Eq. 10

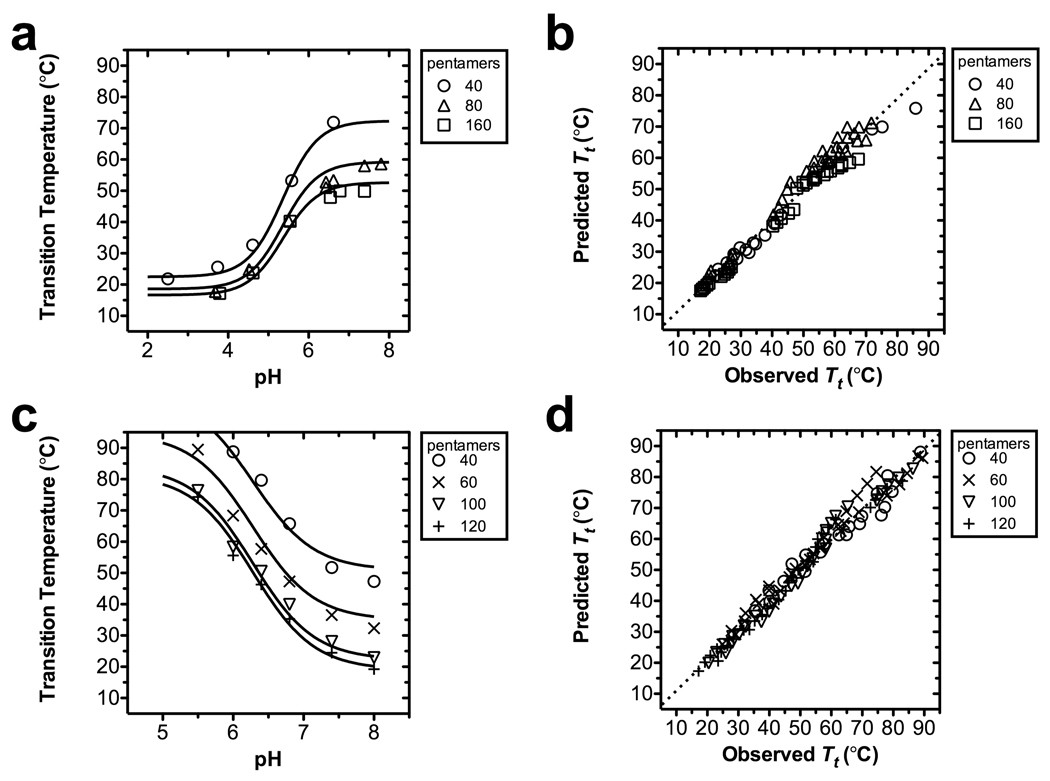
The above relationship was fit to both the acidic and basic ELP libraries, spanning a range of concentration, C, polymer length, L, and pH to determine the 6 parameters (Table 3). These parameters have been used to fit data as a function of pH (Fig. 3). Impressively, the global model fit describes ~97% of the observed variability in the transition temperature for both libraries.

Table 3.

Multiple nonlinear regression parameters describing the ^adependence of the transition temperature on pH, length, and concentration.

ELP guest residues	pKa	Tc,pro (°C)	Tc,depro (°C)	kpro (°C pentamers)	kdepro (°C pentamers)	Cc (mM)	R2	n
bV:I:E [1:3:1]	5.36 (0.04)	14.7 (1.2)	46.1 (1.2)	118 (17)	398 (42)	1.4 (0.5)	0.97	87
cV:H:G:A [1:2:1:1]	6.28 (0.03)	68.4 (2.1)	3.1 (1.2)	309 (32)	376 (18)	16.1 (3.7)	0.98	113

^adata fit to Eq 10 and parameters reported as estimate (standard error).

^bacidic ELP lengths from 40–160 pentamers, pH 2.5–7.8, and concentrations from 5–100 µM.

^cbasic ELP lengths from 40–120 pentamers, pH 5.5–8.0, and concentrations from 10–500 µM.

Figure 3.

The pH dependence of the ELP phase behavior. ELP transition temperatures plotted as a function of pH. For each ELP chain length, a best-fit curve following Eq. 10 has been indicated (Table 3). (a–b) An acidic ELP library containing guest residues V:I:E [1:3:1]. (a) Transition temperatures as a function of pH at 100 µM. (b) Predicted vs. observed transition temperatures for global fit (R² = 0.98, n=87). (c–d) A basic ELP library containing guest residues V:H:G:A [1:2:1:1]. (b) Transition temperatures as a function of pH at 100 µM. (b) Predicted vs. observed transition temperatures for global fit (R² = 0.98, n=113).

Development of an isothermal ELP phase diagram

Some of the most interesting applications for pH responsive ELPs are to develop smart biomaterials that respond to physiologically relevant pH gradients. Thus, we note that a rearrangement of Eq. 10 can be used to estimate the isothermal transition pH_t at which these ELPs undergo their phase transition as a function of ELP concentration and chain length. The following re-arrangement of Eq. 10 is solved for the inverse phase transition pH, pH_t:

$${\mathit{\text{pH}}}_t=\mathit{\text{pKa}}+\mathit{\text{Log}}\left[\frac{T-T_{c,\mathit{\text{pro}}}-\frac{k_{\mathit{\text{pro}}}}{L}\text{ln}\left[\frac{C_c}{C}\right]}{T_{c,\mathit{\text{depro}}}-T+\frac{k_{\mathit{\text{depro}}}}{L}\text{ln}\left[\frac{C_c}{C}\right]}\right]$$ Eq. 11

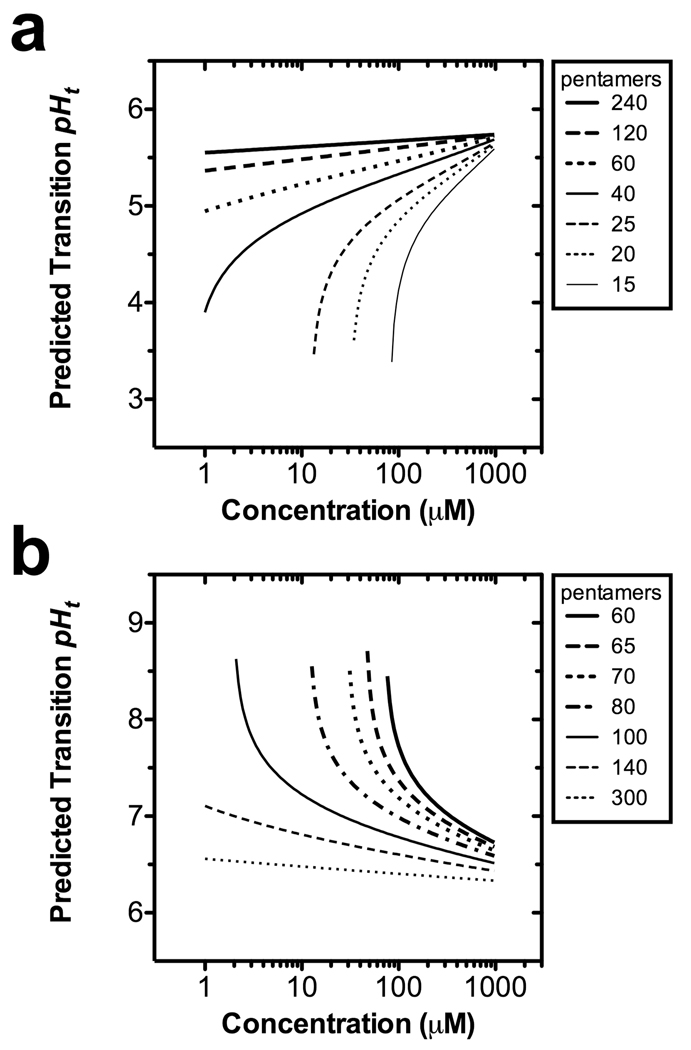
ELP chain length and concentration are simple to control; furthermore, the data presented in Table 3 can be used to select optimal conditions to optimize pH_t within several pH units of the observed pKa (acidic: pKa = 5.36; basic pKa = 6.28). By plugging in the best-fit parameters obtained in Table 3, Eq. 11 can be used to estimate the pH at which a given ELP may transition at body temperature (Fig. 4).

Figure 4.

The transition pH isotherms for acidic and basic ELPs. Isothermal transition pH_t have been calculated for ELPs at a constant temperature of 37 °C for a variety of accessible lengths and concentrations (Eq. 11; Table 3). This phase diagram permits selection of a suitable length and concentration for achieving a transition at the target pH. (a) A predicted library of acidic ELPs containing guest residues V:I:E [1:3:1], which are water soluble above the indicated boundaries. (b) A predicted library of basic ELPs containing guest residues V:H:G:A [1:2:1:1], which are soluble below the indicated boundaries.

The above relationship permits the selection of the best length and mixture of guest residues to either trigger the aggregation or disaggregation of ELP at physiologically relevant pH. For example, acidic ELPs may remain soluble in the blood, but aggregate when they encounter the low pH in the extracellular tumor fraction or some intracellular compartments. Such a polymer could be useful to induce local retention of bulk aggregates, or polypeptide block copolymers could be designed that form multivalent micelles. The 60 pentamer acidic ELP depicted in Fig. 4a is perfectly tuned to drive the assembly of aggregates in intracellular compartments, as they are highly soluble at pH 7.4, but have a pH_t of 5.5 (at 100 µM). To target the extracellular tumor pH, a phase diagram like Fig. 4 could be used to guide the design of new mixtures of guest residues that have a higher pH_t.

In contrast, block copolymers that contain the basic ELP are well suited to engineer multivalent micelles that remain assembled in the blood at pH 7.4. Basic ELPs can serve as the hydrophobic components of block copolymers designed to disassemble and release their cargo in response to either the stimulus of low extracellular pH, improving the interstitial penetration of the released drug, or endosomal pH, potentially leading to endosomal disruption for intracellular drug release. Taking 100 µM as an approximation of the ELP concentration, the phase diagram constructed in Fig. 4b suggests that a micelle core segment of roughly 80 pentamers has a pH_t of 7.0, which would disaggregate between pH 7.4 and the tumor extracellular pH 6.8. Alternatively, a basic ELP with a different mixture of guest residues might be used to target micelle disruption to the endosomal pH 5.0. Thus, these phase diagrams will allow us to tailor the design of new polypeptide biomaterials with optimal physiological response.

We successfully developed two novel libraries of ELPs that phase separate near physiological temperature and pH; furthermore, one library (histidine) is soluble only at acidic pH and the other (glutamic acid) at basic pH. These amino acids were selected because they have titratable chemistries and pKas within the physiologically relevant range. When the amino acids become either cationic or anionic, the phase transition temperature and solubility are increased. Histidine becomes protonated under acidic conditions, producing a cationic ELP with high solubility. In contrast, glutamic acid becomes deprotonated under basic conditions, conferring an anionic charge and enhancing ELP solubility. Lysine, aspartic acid, and tyrosine also have titratable chemistries, which may be useful to target phenomena that occur at pHs near their pKas. Presumably, lysine-containing ELPs would behave qualitatively similarly to histidine-containing ELPs, albeit at a much higher pH. In contrast, aspartic acid and tyrosine guest residues are expected to behave qualitatively similarly to the glutamic acid-containing ELPs. Glutamic acid and histidine were chosen as the ionizable residues of interest as their pKas (4.3 and 6.1, respectively) are closest to the physiologically relevant range. The high pKas of tyrosine and lysine (10 and 10.5, respectively) place those responses outside of the relevant range, and while the pKa of aspartic acid is similar to that of glutamic acid, the uncharged aspartic acid is less hydrophobic, meaning that protonation of this residue under acidic conditions would have less of an effect on the ELP T_t. Even though they have opposite responses to pH, our proposed model perfectly describes the behavior of both acidic and basic ELPs. Variations on this model may be applicable to other biopolymer phase transitions that depend on concentration or molecular weight. Many other polypeptide assembly mechanisms depend on ionizable amino acids³⁷. For example, leucine zipper assemblies are pH-dependent because they are partially stabilized by electrostatic interactions between titratable amino acid side chains. These models may enable precise engineering of recombinant biopolymers that assemble at target physiological pH and temperature.

Conclusions

Herein, we have described two libraries of ELPs with basic or acidic guest residues that have pH responsive phase behavior. We observed that their concentration and molecular weight influence their phase transition behavior, and then developed an empirical model that describes the ELP phase transition temperature as a function of concentration, chain length, and pH. This approach is valid for ELPs that undergo phase separation at high pH (histidine-containing ELPs) and low pH (glutamic acid-containing ELPs). These results are useful, as they will enable the rational design of ELPs that are capable of exhibiting phase transition behavior in response to a specified change in pH as the trigger. Future work will examine the generality of this model with respect to ELPs that contain other ionizable residues not used to develop the model (e.g., Asp, Lys), as well as the validity of this model in predicting the pH-triggered self-assembly of diblock ELPs that contain one ionizable block, with the goal of rational design of ELPs that exhibit self-assembly into nano-mesoscale structures such as micelles or vesicles, or conversely exhibit pH-triggered disassembly in response to pH gradients that exist in physiological systems.

Abbreviations

ELP

Elastin-like polypeptide