Approximate Entropy Used to Assess Sitting Postural Sway of Infants with Developmental Delay

Abstract

Infant sitting postural sway provides a window into motor development at an early age. The approximate entropy, a measure of randomness, in the postural sway was used to assess developmental delay, as occurs in cerebral palsy. Parameters used for the calculation of approximate entropy were investigated, and approximate entropy of postural sway in early sitting was found to be lower for infants with developmental delay in the anterior-posterior axis, but not in the medial-lateral axis. Spectral analysis showed higher frequency features in the postural sway of early sitting of infants with typical development, suggesting a faster control mechanism is active in infants with typical development as compared to infants with delayed development, perhaps activated by near-fall events.

1. Introduction

Cerebral palsy occurs because of brain injury sustained very early in life, either before, during, or shortly after birth, and is characterized by motor dysfunction. Identifying affected infants when they are very young allows for physical therapy to be started early when brain plasticity is maximal (Ballantyne, Spilkin, Hesselink, Trauner, 2008), with the goal of improving the long-term outcome for these infants (Blauw-Hospers, Hadders-Algra, 2005; Blauw-Hospers, de Graaf-Peters, Dirks, Bos, Hadders-Algra, 2007; de Graaf-Peters, Blauw-Hospers, Dirks, Bakker, Bos, & Hadders-Algra, 2007). Sitting is a motor skill acquired early in life, typically at about age 4–9 months, and thus can serve as a window into the development of motor skills in very young infants (Harbourne & Stergiou, 2003). Studying sitting dynamics affords the possibility of objectively quantifying motor coordination in order to identify infants who might benefit from physical therapy, and to assess improvements as therapy progresses, even in infants who cannot yet stand. Because cerebral palsy is difficult to diagnose in young infants, we have described the infants in our study as “developmentally delayed” since we can confirm they were developmentally delayed. However, the developmentally delayed infants in our study were either diagnosed with cerebral palsy or at risk for cerebral palsy, and not a general sampling of infants with all types of developmental delay.

Lack of general movement complexity in young infants may be a useful indicator of cerebral palsy and that therapeutic intervention is appropriate (Hadders-Algra, 2004), but it is not yet clear how best to objectively quantify movement complexity in very young infants. Hadders-Algra’s (2004) discussion of complexity is focused on the quality of general movements, which are the frequent and varied movements of all parts of the body, and that the healthy infant produces highly varied movement patterns. Conversely, infants with cerebral palsy display less complex movement patterns, perhaps as a result of damage to the cortical subplate (Hadders-Algra, 2007). Hadders-Algra’s (2004) method of quantifying general movement complexity from video recordings requires two days of training, and requires further practice to become a skilled observer. Another way to quantify body movements is to record time series data from a force plate. However, to quantify the dynamics of infant sitting postural sway using force plate data, a measure of time series dynamics is needed that is sensitive to differences between affected and unaffected infants. This measure needs to be robust to experimental noise and robust to shorter time series segments since many infants cannot sit for extended periods of time. The long term goal of this work is to develop a measure that can assess developmental delay early in life, is sensitive enough that it can be used to monitor the effectiveness of a course of therapy, and is robust enough to real-world data limitations such as noise and limited time for analysis, that it could someday be applied in a clinical setting.

Approximate entropy was developed by Pincus (1991) as a measure of “complexity” for time series data, where “complexity” is defined as being low for time series with a repetitive pattern such as a sine function, high for a random variable, and intermediate for systems with chaotic dynamics. Alternatively, it can be described as a measure of “regularity” where time series data with repeated patterns have low approximate entropy and high regularity (Pincus & Goldberger, 1994), i.e. approximate entropy is a measure of lack of regularity. Because approximate entropy is sensitive to the system dynamics, it is a potentially useful measure for a wide range of medical conditions that alter physiological or motor control dynamics. There are a number of medical fields where the use of approximate entropy has been investigated, including cardiology (Pincus & Goldberger, 1994; Kaplan, Furman, Pincus, Ryan, Lipsitz & Goldberger, 1991), endocrinology (Liu, Iranmanesh, Keenan, Pincus, and Veldhuis, 2007; Veldhuis, Keenan, & Pincus, 2008), anesthesiology (Kumar, Anand, Chari, Yaddanapudi, & Srivastava, 2007), traumatic brain injury (Cavanaugh, Guskiewicz, Giuliani, Marshall, Mercer, & Stergiou, 2005, Cavanaugh, Guskiewicz, Giuliani, Marshall, Mercer, & Stergiou, 2006), Parkinson’s disease (Morrison, Kerr, Newell, & Silburn, 2008), and orthopedics (Georgoulis, Moraiti, Ristanis, Stergiou, 2006). Two hypotheses that have been advanced to explain the impact of pathology on control dynamics in humans, the loss of complexity hypothesis, which suggests that complexity will decrease with pathology, (Goldberger, Peng, & Lipsitz, 2002), and the optimal movement variability hypothesis, which suggests that complexity may either increase or decrease from an intermediate optimal value (Stergiou, Harbourne, & Cavanaugh, 2006). Both the loss of complexity hypothesis (Goldberger, Peng, & Lipsitz, 2002) and the optimal movement variability hypothesis (Stergiou, Harbourne, & Cavanaugh, 2006) suggest that approximate entropy of time series data from physiological systems may be clinically useful, as pathology can shift the regularity of system dynamics away from the optimal values. A measure like approximate entropy, with the ability to quantify regularity of system dynamics, may someday be used clinically to discriminate typically developing children from those with pathology, help assess severity of pathology, and assess efficacy of treatment.

One interpretation of approximate entropy as applied to postural sway is as an indication of the level of attention directed at postural control, with low attention automatic control having higher entropy (Donker, Ledebt, Roerdink, Savelsbergh, & Beck, 2008). If attention is diverted to another task, then postural control becomes more automatic and entropy increases (Cavanaugh, Mercer, & Stergiou, 2007; Donker, Roerdink, Greven, & Beek, 2007). Conversely if neurological injury makes postural control more difficult, then more attention is required to be focused on control and postural sway becomes more regular, as in stroke (Roerdink, De Haart, Daffertshofer, Donker, Geurts, & Beek, 2006) or in mild traumatic brain injury (Cavanaugh, Guskiewicz, Giuliani, Marshall, Mercer, & Stergiou, 2005; Cavanaugh, Guskiewicz, Giuliani, Marshall, Mercer, & Stergiou, 2006)). Based on this precedence, we hypothesize that cerebral palsy, being a neurological injury, would result in less automatic control of posture, and thus a lower entropy.

Despite the wide range of research applications of approximate entropy, the methodology of application of the approximate entropy algorithm to experimental data has yet to be fully optimized for widespread clinical implementation. Experimentally measured time series data is necessarily of limited length, and often, if not always, corrupted by experimental noise of unknown dynamics. Experimental noise is often assumed to be white noise, or independent and identically distributed error, allowing for statistical treatment based on these assumptions. The reality is that the measurement noise is generated by physical processes that have certain dynamics associated with them, which may lead to noise dynamics being something other than the statistical ideal of white noise. For example, time series data acquired at high enough frequency will often have a 60 Hz noise component due to electrical power distribution using 60 Hz frequency (or 50 Hz in Europe). The 60 Hz noise is certainly not well represented as white noise. The dynamics of the noise may not be important if the measure used on the time series data is range or standard deviation, but in using measures of the dynamics of the time series, including approximate entropy, the dynamics of the noise may interfere with the measurement of the dynamics of the system under study. One way the impact of noise can be studied is to add in computer generated white noise to time series data, and investigate the impact that the added white noise has on the approximate entropy analysis. However, this method leaves open the possibility that real experimental noise, which is not pure white noise, may have a different effect on the analysis.

Another approach to understanding the impact of experimental noise on measures of system dynamics is to use a model system that has known dynamics, and see if the dynamical analysis gives a result in reasonable agreement with the known dynamics. For example, a mechanical single pendulum has limit cycle dynamics, and thus would be expected to have a low value for the approximate entropy. Higher values of approximate entropy from experimental measurements of the dynamics of a single pendulum are likely a result of contamination of the measured signal with experimental noise with more complex dynamics. Data acquired from the single pendulum with the same experimental equipment as the infant sitting data would be contaminated with noise having the same dynamics as noise contaminating the infant sitting data. Thus it is possible to select analysis parameters for the approximate entropy analysis using pendulum data that minimize the impact of experimental noise on the analysis. A double pendulum is a pendulum with two linked segments that are each free to rotate, giving a system with enough degrees of freedom to display chaotic dynamics (Shinbrot, Grebogi, Wisdom, & Yorke, 1992). If the experimental limitations of the data are minor enough to not interfere with the analysis, then approximate entropy should be able to distinguish between data from these two mechanical systems. Thus mechanical pendulums can act as model systems to investigate the effect of the experimental noise on the analysis of system dynamics.

The approximate entropy algorithm has been described in detail elsewhere (Pincus, 1991; Pincus & Goldberger, 1994). As implemented (Kaplan & Staffin, 1996), the algorithm creates vectors of length m, and length m+1. The points in the vector are drawn from the time series with a specific lag value. For example, lag=1 indicates the points are consecutive, whereas lag=2 indicates that every other point is skipped in creating the length m vector. It then counts vectors of time series data of length m that are similar to each of the vectors of length m. Subsequently, counts how many of those similar m length vectors are also similar at length m+1 and normalizes based on the number of vectors being compared (N-m-1 vectors of length m, and N-m vectors of length m_1).

$${\mathrm{\Phi }}^m=\frac{1}{N-m+1}\sum _{i=1}^{N-m+1}log{C}_i^m{\mathrm{\Phi }}^{m+1}=\frac{1}{N-m}\sum _{i=1}^{N-m}log{C}_i^{m+1}$$

Where N is the length of the time series, m is the length of the comparison vector, and C^m_i is the count of vectors of length m similar to vector i, and C^m+1_i is the count of vectors of length m+1 similar to vector i. Similarity is defined below. Approximate entropy is then the difference between the two normalized log counts.

$$\text{Approximate}\text{Entropy}={\mathrm{\Phi }}^{\text{m}}-{\mathrm{\Phi }}^{\text{m}1}$$

Thus repeated patterns in the data give rise to lower approximate entropy values, because two vectors similar at length m will also be similar at length m+1 due to the repeating pattern, resulting in a ratio near 1, the log of which is then near zero. For this reason, time series with repeated patterns have approximate entropy near zero.

An important aspect of the approximate entropy calculation is determining how similar vectors are defined. The approximate entropy algorithm uses a parameter r to define similar vectors. If each point in a vector is within a distance r of the corresponding point in the other vector, then the two vectors are counted as similar. If r is too large, vectors are counted as being similar when they are not; if r is too small, then vectors that should be considered as similar are not counted as being similar. The time series data will have some measurement error, as is typical of experimentally derived data, and the r parameter allows for two vectors to be counted as similar, even if the experimental noise results in the values not being identical. A value for “R” is selected for all the time series in the analysis, and this value is multiplied by the standard deviation of each individual time series data in order to define the r for that time series; r_i=R*std(Data_i) for each time series i. While a range of 0.1 to 0.25 for R is suggested in early work (Pincus & Goldberger, 1994), Veldhuis, Keenan, and Pincus (2008) suggest that R be set at 0.2 for biological applications, i.e. r_i=0.2*std(Data_i). While the r parameter may serve to filter experimental noise, it also filters the biological signal, and thus serves to select the length scale of the system dynamics that is being probed by the approximate entropy analysis. It is not clear whether the most important function of the r parameter is simply to reduce the sensitivity of the analysis to experimental noise, or if it has a more important function relevant to the length scale of the dynamics of biological system.

If the function of the r value is simply to reduce the sensitivity of the analysis to experimental noise, then basing the r value on the noise, r_i=R*std(Noise_i), might be preferred. Pincus and Goldberger (1994) suggest that r must be chosen to be larger than the noise, but fail to give exact guidelines other than to suggest that a value of three times the estimated mean noise has worked well in their clinical studies. Thus one might expect that selecting the r value based on some estimation of the noise in the data might be a useful approach. Alternatively, other authors have suggested that r should be selected to maximize the entropy result (Castiglioni & Di Rienzo, 2008; Lu, Chen, Kanters, Soloman, & Chon, 2008). Both of these possibilities were investigated in this work. Understanding the impact of experimental noise (i.e. measurement error) on results is often difficult, since the actual signal and noise are not known a priori. One method to address this is to use the measurement technique on a known system, i.e. on a model system with known dynamics. Because we are making mechanical measurements on the infant postural sway, we used mechanical systems with known dynamics to test the analysis. Two such mechanical systems were used, 1) the single pendulum, which exhibits simple limit-cycle dynamics, and 2) the double pendulum, which exhibits chaotic dynamics when launched from appropriate initial conditions.

The purpose of this work is to examine the impact of the parameters used in the approximate entropy analysis to better understand the dynamics of infant sitting postural sway. We utilized COP data from single and double pendulums, in order to guide us in the analysis of the infant sitting data. The long-term goal of the work is to discover differences between postural sway of infants with typical development and infants with delayed development. Measures sensitive to these differences might be useful in a clinical setting to help assess alterations in infants motor control skills due to pathologies such as cerebral palsy, and to assess progress due to various therapeutic interventions.

2. Methods

2.1. Infant Participants

Thirty infants with developmental delay (age = 14.05 months, std = 5.33 months, for early sitting and age = 18.06 months, std = 5.09 months, for advanced sitting), with a third being born prematurely, and age corrected for premature birth. Additionally, 33 infants with typical development (age = 4.92 months, std = 0.57 months, for early sitting, and age = 7.92 months, std = 0.60 months, for advanced sitting) participated in the study. Recruitment was done through newsletters, flyers, and pediatric physical therapists employed at the University. Infants in the developmentally delayed group were diagnosed with cerebral palsy, or else were developmentally delayed and at risk for cerebral palsy. Obtaining a firm diagnosis of cerebral palsy at this young age is often not possible. Because a definitive diagnosis of cerebral palsy had not been made, we refer to these infants as developmentally delayed, because all scored below 1.5 standard deviations below the mean for their corrected age on the Peabody Gross Motor Scale (Folio & Fewell, 2000). However, the development is likely not just delayed, but also atypical (Chen & Woollacott, 2007). A consent form was signed by a parent or guardian of all infant participants, and all procedures were approved by the University of Nebraska Medical Center Institutional Review Board.

Inclusion criteria for entry into the study for the typically developing infants were: a score on the Peabody Gross Motor Scale of greater than 0.5 SD below the mean, age of five months at the time of initial data collection, and sitting skills as described below in early sitting. Exclusion criteria for the sample of infants who are typically developing were: a score on the Peabody Gross Motor Scales less than 0.5 SD below the mean, diagnosed visual deficits, or diagnosed musculoskeletal problems. If a typically developing infant was found to be less than 0.5 SD below the mean, and did not qualify for the study, the parents were informed of the score, the possibility of error in the measurement, and advised to have the infant re-evaluated within the next 3 months. Operational definitions of early sitting were used to determine the child’s readiness for entry into the study. Early sitting was defined as (a) head control such that when trunk is supported at the mid-trunk, head is maintained for over one minute without bobbing; (b) infant can track an object across midline without losing head control; (c) infant may prop hands on floor or legs to lean on arms, but should not be able to reach and maintain balance in the prop sit position; (d) when supported in sitting can reach for toy; (e) can prop on elbows in the prone position for at least 30 seconds. Each infant was tested when they entered into the study based on the ability to sit for about 10 s, and then again 3–4 months later.

For the infants with developmental delay the inclusion and exclusion criteria were as follows. Inclusion criteria were: age from five months to two years, score less than 1.5 SD below the mean for their corrected age on the Peabody Gross Motor Scales, and sitting skills as described above for early sitting. Exclusion criteria were: age over two years, a score greater than 1.5 SD below the mean for their corrected age on the Peabody Gross Motor Scale, a diagnosed visual impairment, or a diagnosed hip dislocation or subluxation greater than 50%.

The study design was longitudinal, with the infants returning 3–4 months after the initial data collection to assess development that occurred in that time. Note that “early” and “advanced” sitting are labels indicating that the sitting was either close to the time the infant was able to achieve about 10 seconds of upright sitting (early), or the sitting behavior that was displayed 3–4 months later (advanced). The “early” label means that the infants had just achieved ability to sit for 10 seconds, so the comparison between groups was between infants at a similar stage of development, not at a similar age. The “advanced” label means that the sitting skills had advanced by several months, and is not an indication of either similar skill level or similar age in the two groups. For the infants with typical development, the advanced sitting was also well controlled sitting. For the infants with developmental delay, the sitting behavior studied as advanced sitting was not necessarily well controlled sitting behavior, especially in infants who were more severely affected. The comparison between “early” and “advanced” should be understood as advancement in behavior with time, and not that the skill level had improved equally between the two groups. Thus the change in the measures of posture control might be expected to change less for the infants with delayed development than for those with typical development.

2.2. Pendulums

Two pendulums were used in the study (Figure 1). The first was a single pendulum, constructed from steel bar (1″ × .125″ × 3′) and mounted to swing freely on a rigid structure, using Bones Reds 608 Precision Skate Bearings (Bones Bearings, Santa Barbara, CA) to reduce friction as the pendulum swings. The pendulum arm length was selected to give the pendulum a frequency of approximately 0.7 Hz, because maximum power in the power spectra of the infant sitting was of a similar frequency. Weights were clamped on the pendulum arm to simulate the weight of an infant. Amplitude of the pendulum swing was varied from trial to trial. The second pendulum was a double pendulum, purchased commercially (www.chaoticpendulums.com), and could be mounted on the same mounting structure as the single pendulum. The double pendulum also had metal bearings to reduce friction.

Figure 1.

All data acquisition used the same force plate, which is built into the floor as is typical in a gait laboratory. a. single pendulum, b. double pendulum, c. infant sitting.

2.3. Data Collections

Data collections for both infants and pendulums were performed with the same equipment, using all the same data acquisition parameters. For data acquisition (Figure 1), a pendulum or infant was placed on an AMTI force plate (Watertown, MA), interfaced to a computer system running Vicon data acquisition software (Lake Forest, CA). Markers can be seen on the back of the pelvis and thorax of the infant in Figure 1, and kinematic data was also collected, but is not discussed in this paper. The time series data collected is center of pressure (COP) data, which is the position of the resultant vector where it intersects the surface of the force plate. Thus the time series data is position data, although it is derived from the forces measured by the force plate. The COP time series were acquired through the Vicon software at 240 Hz, in order to have a sampling frequency 10 times above the highest frequency found the time series from in a pilot study.

For all data collection sessions, the infants were allowed time to get used to the laboratory setting, and were at their parent’s side or on their lap for preparation and data collection. Infants were provided with a standard set of infant toys for distraction and comfort. All attempts were made to maintain a calm, alert state by allowing the infant to eat if hungry, be held by a parent for comforting, or adapting the temperature of the room to the infant’s comfort level. Testing was only proceeded when the infant was in a calm and relaxed state, not crying or otherwise making extended vocalization. A soft cloth was placed over the plate for warmth and was securely adhered with tape on the force plate. The investigator and the parent remained at one side and in front of the infant respectively during all data collection, to assure the infant did not fall or became insecure. The child was held at the trunk for support, and gradually the infant was guided into a prop sitting position while being distracted by toys presented by the parent. Once the examiner could completely let go of the infant, data were collected for 10 seconds while the child attempted to maintain sitting postural control. Trials were performed until we had collected three trials that are acceptable for our criteria, or until the infant was indicating that they were done. At any time the child became irritated; the session was halted for comforting by the parent or a chance for feeding, and then resumed only when the child was again in a calm state. In some cases, if the infant was crying for a long period of time, then data was not collected at that session. Infants came to the lab twice within a single week, and we attempted to get three trials in each of the two sessions.

Segments of usable (described below) data were analyzed using custom MatLab software (MathWorks, Nantick, MA). No filtering was performed on the data in order to not alter the nonlinear results (Rapp, Albano, Schmah, & Farwell, 1993). Trials were recorded including force plate data and video data from the back and side views. Afterwards segments were selected by viewing the corresponding video. Segments of data with 2000 time steps (8.3 seconds at 240 Hz) were selected from these trials by examination of the video. Acceptable segments were required to have no crying or long vocalization, no extraneous items (e.g. toys) on the force platform, neither the assistant nor the mother were touching the infant, the infant was not engaged in rhythmic behavior (e.g. flapping arms), and the infant had to be sitting and could not be in the process of falling.

For the single pendulum, long time series could be collected (limited by the storage capacity of the computer), and then these were divided into 2000 time step segments (i.e. N=2001) to match the infant sitting data. Segments matching the infant sitting based on signal-to-noise (discussed below) were selected for analysis. For the data collection with the double pendulum, to ensure initial conditions that would lead to chaotic motion, the double pendulum was restarted before each data collection. The first 8.3 seconds of data (2000 time steps, N=2001) were selected for analysis.

2.4. Data Analysis

Signal-to-noise

During the course of data analysis, it became apparent that some time series had better signal-to-noise than other time series, and that this was affecting the approximate entropy analysis. For the single pendulum, the equation of motion can be solved using the small angle approximation, resulting in a sine function for the solution to the equation of motion. As expected, the COP data obtained from the single pendulum appeared to be a sine function for small amplitudes of displacement, but appeared to have a noise component in addition to the expected sine wave. Based on this observation, we estimated the signal-to-noise for our time series data. Here “signal” refers to the true data if no experimental noise were present in the time series data. Signal-to-noise is defined as the ratio of the variances of the signal and noise (Manolakis, Ingle, & Kogon, 2005); signal-to-noise = s_s²/s_n², where s_s indicates the standard deviation calculated from the smoothed time series (estimated signal), and s_n is the standard deviation of the difference between the unsmoothed time series and smoothed time series (estimated noise).

Because we wanted to estimate the signal-to-noise in both periodic data and chaotic data, we used a sine function and a numerical solution to the Lorenz attractor, each with different levels of added random noise, as test pseudo-data sets, where “pseudo-” indicates data was generated in MatLab, not acquired with the force plate. By generating pseudo-signal and pseudo-noise separately before adding them to make pseudo-data, time series pseudo-data were generated with known signal-to-noise, allowing the result of the signal-to-noise detection algorithm to be verified. Sampling rate, spectral frequencies, and apparent signal-to-noise of the pseudo-data were chosen to be similar to the infant sitting data. An estimate of the signal in each of the pseudo-data sets was made by smoothing the noisy data, and then the noise was estimated by the difference of the pseudo-data and the estimated signal. Smoothing was accomplished with a Savitsky-Golay polynomial smooth, using the parameters of a polynomial order = 8, and window size = 121 (0.5 s). The double pendulum has much higher signal-to-noise than the other data types, and these parameters for estimation of signal-to-noise did not appear to work for the double pendulum data. Application of this method to single pendulum data and infant sitting data appeared to give reasonable results (Deffeyes, 2009), and the result from the single pendulum is especially encouraging because the solution to the equation of motion is expected to be a sine function, and the estimated signal, i.e. the smoothed data, closely resembles a sine function.

Approximate entropy

The approximate entropy calculation was described in the introduction. Pincus (1991), Pincus and Goldberger (1994), and Kaplan & Staffin (1996) are good resources for additional discussion of the method. Approximate entropy, and all other calculations for this work, were done using MatLab (version R2007a).

Spectral analysis

Periodograms were calculated using MatLab to estimate the power spectrum for each trial using a Hann window function. Periodograms were averaged for all trials in each of 4 categories, 2 subject types (infants with typical or delayed development), at 2 sitting ages (early or advanced sitting). Sharp peaks were observed at 30 Hz, 60 Hz, and 90 Hz, the largest of which was at 60 Hz, and were thought to be related to power transmission at 60 Hz, and not features of the infant sitting postural sway.

Statistical analysis

A statistic of interest in this analysis is the effect size in comparing two populations. Many estimators of effect size assume a normally distributed data, but the approximate entropy values in this study were observed to have a non-symmetric distribution, and the distribution was skewed to high side. Thus, we used the nonparametric Wilcoxon rank sum test (Mann-Whitney U test) to perform comparisons. This has the advantage of allowing comparison of the p value obtained to a critical p value to assess if the approximate entropy (ApEn) analysis were likely significant (p<p_critical), or if the difference in approximate entropy values were likely not significant (p>p_critical). The reported p values are for three different comparisons: 1) comparisons of the n=30 infants with developmental delay compared with the n=33 infants with typical development, for approximate entropy analysis of postural sway in the anterior-posterior (front-to-back) axis, 2) comparisons of the n=30 infants with developmental delay compared with the n=33 infants with typical development, for approximate entropy analysis of postural sway in the medial-lateral (side-to-side) axis, and 3) comparisons of n=100 trials of single pendulum with n=100 trials of double pendulum. For comparisons 1 and 2 (infant sitting) up to 3 trials for each infant were averaged (sometimes the infant was crying, and fewer than 3 trials were collected). Hundreds of comparisons were made using different parameters for the approximate entropy calculation, but these are not independent comparisons, e.g. the ApEn (m=2, r=1, N=2001) is correlated with ApEn (m=2, r=1, N=1001). Thus in correcting our significance level for multiple comparisons, we used a Bonferroni type correction considering three independent comparisons (infant sitting anterior-posterior axis, infant sitting medial-lateral axis, and pendulum comparisons), and set the significance level at alpha=0.05/3=0.017.

Repeated measures ANOVA analysis, comparing ApEn (m=1, r=std(Data), t=8.33s@240Hz, lag=8) of sitting postural sway for infants with typical development and delayed development (between subjects), for early sitting and advanced sitting (within subjects) was performed using SPSS Statistics (GradPack 17.0). Post-hoc paired t-tests were performed comparing early and advanced sitting, for infants with typical development and also for infants with delayed development.

3. Results

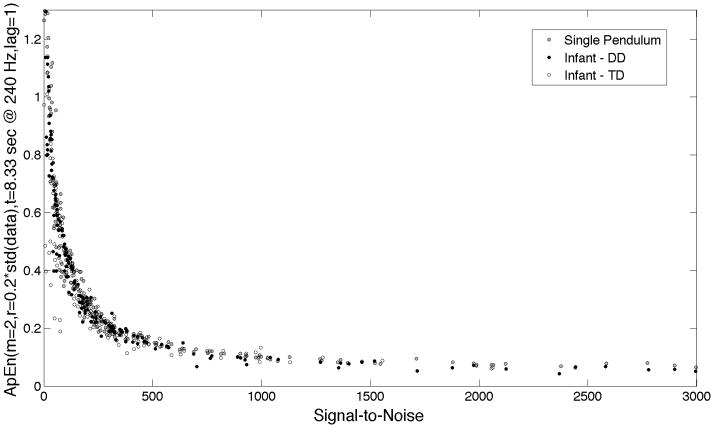
Typical parameters used in many studies for calculating approximate entropy are m=2, r=0.2* std(data), and lag=1; so we used these parameters as our starting point. To see the effect of noise on the approximate entropy result, we examined the relationship between approximate entropy using standard parameters ApEn(m=2, r=.2*std(data), N=8.33 s acquired at 240 Hz, lag=1), and estimated signal-to-noise (Figure 2), and found that approximate entropy is systematically higher for poor signal-to-noise for single pendulum data, as well as infant sitting in both anterior-posterior (front-to-back) and medial-lateral (side-to-side) directions. Compensating for the effect of poor signal-to-noise is critical, because most of the variability in the approximate entropy is due to signal-to-noise.

Figure 2.

Plot of approximate entropy using “standard” parameters (m=2, r=0.2*std(Data), N=8.3 sec @240 Hz, lag=1) versus estimated signal-to-noise. Signal-to-noise is the ratio of the variances of the estimated signal and estimated noise (σ_s²/σ_n²).

Proper selection of the r parameter would be expected to improve the performance of the algorithm on data contaminated by experimental noise, since this parameter is thought to act as a filter parameter (Pincus, 1991; Pincus & Goldberger, 1994). Conceptually, if the r parameter is larger than the experimental noise, then the effect of the experimental noise on the analysis should be reduced. Thus we investigated the performance of the approximate entropy algorithm as a function of the r parameter. Typically, r is defined for each time series as some multiple of the standard deviation of the time series data, r_i=R*std(data_i), where R is constant for a given analysis, but r varies for each time series i in the analysis because the standard deviation of each time series is different. Some authors have suggested that the best choice for the r parameter is to select one that maximizes the entropy calculated (Castiglioni & Di Rienzo, 2008; Lu, Chen, Kanters, Solomon, and Chon, 2008). Using r=R*std(data) for each time series, and varying R, we found that infant sitting and single pendulum data have maximum entropy with lowest values of r (Deffeyes, 2009). For these data, there is no maximum in entropy with changes in R, so that selecting R based on maximizing the time series is not feasible. The maximum in entropy for the double pendulum data down-sampled to 60 Hz, lag=1, occurs at R=0.25 (Lower left plot) and at R=0.15 for the 240 Hz data, lag=4. Perhaps the reason that the double pendulum has a maximum other than at the lowest R value is because the double pendulum data had better signal-to-noise than the infant sitting data and better than the single pendulum data, since trials of single pendulum data were chosen to match the infant sitting data in signal-to-noise. If maximizing the entropy were the best criteria, then the standard selection of R=0.2 appears to be near optimal for this better signal-to-noise data of the double pendulum.

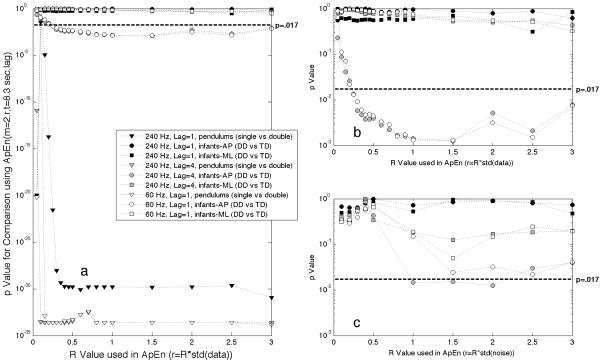
However, the goal of the approximate entropy analysis on the infant postural sway data is to distinguish between infants with delayed motor development and the infants with typical development, with the notion that pathologic development could lead to more regularity in postural sway (Goldberger, Peng, & Lipsitz, 2002; Stergiou, Harbourne, & Cavanaugh, 2006). The corresponding goal of the pendulum analysis is to take a system with known high regularity (the single pendulum), and a system with known chaotic behavior (the double pendulum), and see how well the approximate entropy algorithm can be tuned to distinguish between these two systems. Thus the measure of interest is a measure of comparison between two groups, and we have used the p value from a Wilcoxon rank sum comparison. To investigate the effect of the r parameter on the analysis, three types of comparisons were made: 1) infant sitting anterior-posterior postural sway (delayed development versus typical development), 2) infant sitting medial-lateral postural sway (delayed development versus typical development), and 3) pendulum reaction forces (single versus double pendulums). These 3 comparisons were repeated for various R values in the approximate entropy calculation, and for the data sampled at 240 Hz using lag=1, data sampled at 240 Hz using lag=4, and the 240 Hz down-sampled to 60 Hz using lag=1 (Figure 3a). The comparison of single and double pendulum data showed that the dynamics are significantly different between these two systems, and that for the pendulum comparison, the difference is statistically significant for a wide range of parameters. For the comparisons of infant sitting postural sway data, choice of analysis parameters was more critical, with the data acquired at 240 Hz and analyzed at lag=1 (Black symbols in Figure 3a and 3b), no value of R was successful in producing a significant p value for the comparisons of infants with typical development and infants with delayed development. For the infant sitting postural sway comparisons, no comparisons in the medial-lateral axis (squares) were significant. For the postural sway in the anterior-posterior axis (circles), and for the time series data down-sampled to 60 Hz (white symbols) and for the 240 Hz data analyzed using lag=4 (grey symbols), the comparison was statistically significant, with minimum p values in the range R=1 to R=1.5.

Figure 3.

Effect of R-parameter. Wilcoxon rank sum (Mann-Whitney U test) p values for comparison of approximate entropy(m=2,r,t=8.3 sec, lag) for single versus double pendulums (triangles), infants with cerebral palsy versus typical development in anterior-posterior axis (circles) and in medial-lateral axis (squares), plotted versus R value used in the calculation of approximate entropy. Similarity of points in comparison vectors r is determined by R*std(Data) in plots a and b, and by R*std(estimated noise) in plot c. Plot b is an expanded plot of the infant sitting data in a, for comparison with plot c using the same y axis scale as plot c, but note x axes differ between plots b and c.

Since it has been suggested that the function of the r parameter is to act as a noise filter (Pincus, 1991; Pincus & Goldberger, 1994), and since we have an estimate of the noise for each time series in our analysis, we investigated the use of the noise estimate to calculate the r parameter for each analysis. In this analysis, r_i=R*std(Noise_i), where Noise_i is the estimated noise time series based on subtracting the Savitsky-Golay fit to the data, as described in “signal-to-noise” methods section. Comparisons were again made using the infant sitting postural sway data (Figure 3c), but even though the result can be considered significant for the anterior-posterior sway (circles) for the 240 Hz data using lag=4 analysis, the p values obtained were an order of magnitude higher than for the analysis based on r_i=R*std(Data_i). Thus even though one function of the r parameter is to act as filter parameter and to reduce the sensitivity of the analysis to experimental noise, basing the value of the r parameter on the estimated experimental noise does not work as well as basing the r parameter on the standard deviation of the time series data. This result shows the importance of the r parameter as length scale for the system dynamics, not merely a filter for experimental noise. Based on these results, we have chosen to use r_i=R*std(Data_i) where R=1, for the rest of our analyses.

While the r parameter is related to the y axis of the time series (amplitude of data), several parameters affect the approximate entropy analysis in the x axis (time axis of data). The length of data acquisition, sampling rate, and length of the comparison vectors (m parameter) all potentially interact to affect the results of the analysis. Using similar methodology to the investigation of the r parameter above, we investigated the effects of other parameters on the analysis, and found the combination of approximate entropy parameters that provides the best distinction between postural sway of early sitting for infants with typical development versus infants with delayed development. The importance of lag=4, and multiples of 4, in lag values or sampling rate is likely due to 60 Hz electrical noise and sampling at 240 Hz, so that the 60 Hz noise cycles once every 4 data points. The longer time series are better, as these give a more complete sampling of the sitting dynamics. We found that ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) works best for our data set for distinguishing between the two groups using the early sitting postural sway data (Deffeyes, 2009).

Repeated measures 2×2 ANOVA analysis was performed on the infant sitting data using ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) with data from the early sitting and advanced sitting. In the anterior-posterior axis, the development comparison was significant (F=15.623, p<.001), the group difference was significant (F=6.908, p=.034), and the interaction was significant (F=4.723, p=.011). Post hoc paired t-tests showed that approximate entropy of anterior-posterior sitting postural sway decreases significantly with development for infants with typical development (p<.001), while the change with development for infants with delayed development was not significant (p=.33) (Figure 4). The post hoc paired comparisons for postural sway in the medial-lateral axis were not significant (p=.098 for typical development; p=0.783 for delayed development).

Figure 4.

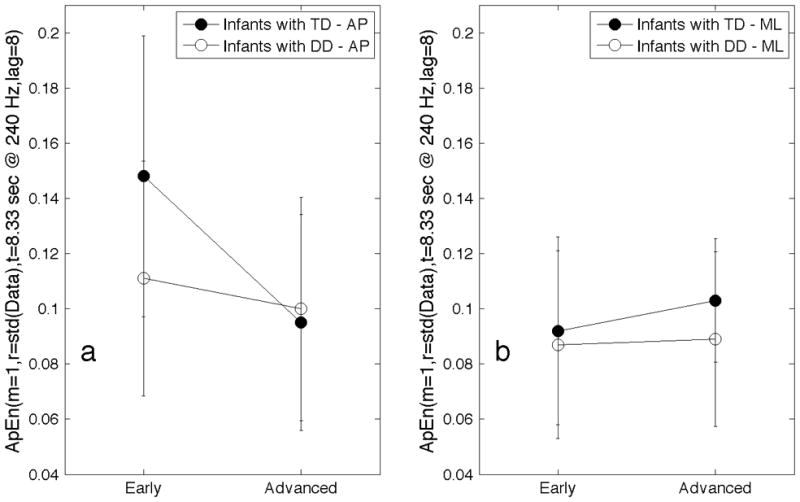
Mean values of ApEn(m=1, r=std(Data), t=8.33sec@240Hz, lag=8) for postural sway of early and advanced infant sitting in the anterior-posterior(AP) axis (a) and in the medial-lateral(ML) axis (b). Groups were infants with typical development (TD) and infants with delayed development (DD). Error bars indicate +/− 1 std.

The finding that approximate entropy calculations using m=1 and lag=8 found differences between the two groups suggested that events must be occurring on a short time scale on the order of 33 milliseconds (lag 8 * 1/240 Hz = 33 ms). To investigate this, spectral analysis was performed on the same time series data as the approximate entropy analyses. Spectral analysis confirms there are differences in the 10–30 Hz range, especially in the anterior-posterior axis data (Figure 5). The broad features seen in the power spectra from early sitting postural sway of infants with typical development in the 10–30 Hz region (Figure 5c) are greatly reduced in intensity in the advanced sitting of these infants (Figure 5d), and are not seen in the power spectra of postural sway from infants with delayed development, for either early (Figure 5a) or advanced (Figure 5b) sitting. The higher intensity seen in the power spectrum between 10–30 Hz is also seen in the medial-lateral postural sway of infants with typical development (Figure 6c,d) as compared to infants with delayed development (Figure 6,a,b), but it appears to lower in the medal later axis than in the anterior posterior axis (Figure 5c,d). The narrow peak at 30 Hz in these spectra is an artifact related to the 60 Hz power, as a larger narrow peak is seen at 60 Hz. Note that the power spectra are plotted on a semi-log axis, so the intensity in these high frequency features is small compared to the intensity of the lower frequency features.

Figure 5.

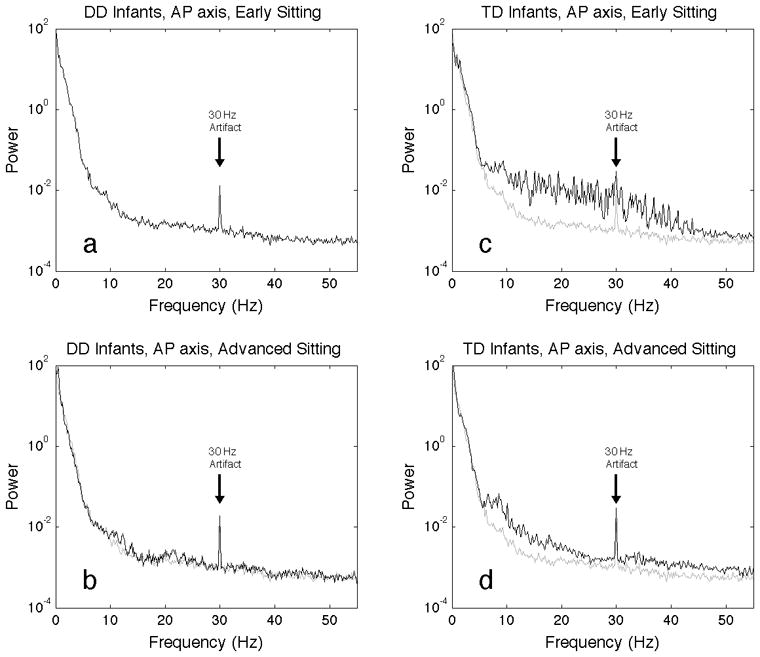
Spectral analysis of infant sitting postural sway in the anterior-posterior axis. Plotted in black is the average periodogram for all trials for infants with developmental delay, early sitting (a), advanced sitting (b), and infants with typical development, early sitting (c) and advanced sitting (d). To aid in visual comparison, plotted in grey on all four plots is the average periodogram for all trials of the developmentally delayed, early sitting. Artifacts seen at 30 Hz are due to electrical power distribution, and are not related to infant sitting.

Figure 6.

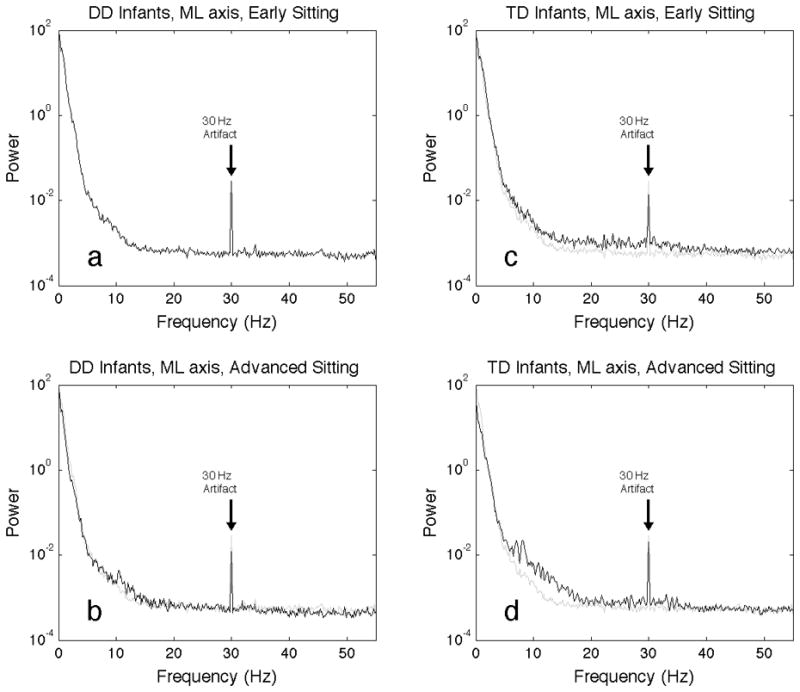
Spectral analysis of infant sitting postural sway in the medial-lateral axis. Plotted in black is the average periodogram for all trials for infants with developmental delay, early sitting (a), advanced sitting (b), and infants with typical development, early sitting (c) and advanced sitting (d). To aid in visual comparison, plotted in grey on all four plots is the average periodogram for all trials of the developmentally delayed, early sitting. Artifacts seen at 30 Hz are due to electrical power distribution, and are not related to infant sitting.

4. Discussion

The use of measures of nonlinear dynamics in medicine and physiology research is appealing because there are pathologies that alter system dynamics (Goldberger, Peng, & Lipsitz, 2002; Stergiou, Harbourne & Cavanaugh, 2006), and these measures have the capability to quantify the changes in dynamics. Approximate entropy was developed to be robust when applied to experimental data, but appropriate choice of parameters used in the algorithm needs to be made. Methods for selection of the r parameter based on experimental noise and on maximizing the approximate entropy value did not prove to be useful in our analysis. Use of a single and double pendulum as model systems provided to be of limited benefit, as the difference in the dynamics between these systems was so large, that the analysis was not sensitive to the choice of parameters used in the approximate entropy analysis. The analysis of infant postural sway, on the other hand, did depend on the choice of parameters. The discussion below is in two sections, one on the implementation of the approximate entropy algorithm, followed by a discussion infant sitting postural sway.

4.1 Discussion of implementation of the approximate entropy algorithm

For comparing systems with vastly different dynamics, such as the single and double pendulum, approximate entropy is not terribly sensitive to the choice of analysis parameters. Statistically significant differences between the single pendulum, a strictly periodic system, and the double pendulum, a known chaotic system, were found for a wide variety of parameters. However, for comparing systems with similar dynamics, such as infants with typical development and infants with motor development delay, the analysis benefits from more careful attention to the parameters used. Based on our results, we made some practical recommendations for performing approximate entropy analysis on flow data:

1. The r parameter in the approximate entropy algorithm is designed to compensate for experimental noise in the measured time series data, and many authors set the r parameter as r=0.2 * std(Data), i.e. 0.2 times the standard deviation of the time series. With our data set, use of the standard parameters ApEn(m=2, r=.2*std(Data), t @ 240 Hz, lag=1) leads to the conclusion that there is no significant difference between these two groups of infants, and use of ApEn(m=1, r=1.0*std(Data), t @ 240 Hz, lag=8) leads to the conclusion that there are significant differences between these two groups of infants in early sitting in the anterior-posterior axis. In previous work (Deffeyes, Harbourne, DeJong, Kyvelidou, Stuberg, & Stergiou, 2009) we found that the use of ApEn(m=2, r=3.0*std(Data), t @ 240 Hz, lag=4) leads to the conclusion that there are significant differences between these two groups of infants in advanced sitting in the medial-lateral axis. The r parameter is not simply a filter for experimental noise, but also adjusts the analysis to be sensitive to the magnitude of changes that are characteristic of the dynamics of the system. An a priori prediction of the most useful r value is difficult, and we suggest exploring the effect of this parameter on the analysis. Using the standard approach of .2*std(Data) may not be the best choice for certain types of data, such as our infant sitting postural sway data, but for systems with large differences in the dynamics, such as the periodic single pendulum and the chaotic double pendulum, the standard choice of r may be appropriate.

2. The sampling frequency and lag are two ways to adjust the time constant to which the analysis is sensitive. A lag value of 1 is often used, and this may be a good choice for many data sets. However, for our postural sway data, the adjustment of the lag parameter can improve the analysis. For our analysis, 33–50 milliseconds between data points had the best sensitivity to differences between the infants with typical versus delayed development. Selection of a sampling frequency and lag value that makes comparisons on this time scale provided the best separation between the two groups. Spectral analysis can be done first to help determine frequencies at which there are differences between populations of interest, and lag values of interest can be determined. If periodic noise is present, then selection of the lag value based on the repeat of the periodic noise may be beneficial. For example, we sampled at 240 Hz, and have 60 Hz noise from the power distribution frequency, which means the 60 Hz noise repeats every 4 data points. Thus selecting a lag value of 4, 8, 12, 16, etc. results in all the points in the comparison vector being acquired at the same point in the noise cycle, to help reduce the impact of the periodic noise on the analysis.

3. The m parameter is the length of the comparison vectors formed from the time series data. A comparison vector length of m=2 is commonly used, meaning that similar vectors of length 2 are tested to see if they are still similar at length 3. For more intricate patterns, longer comparison vectors may be beneficial to include in the analysis, but for our analysis, the m value was less critical than some of the other parameters. One reason to choose a smaller m value is that approximate entropy analysis with larger m values takes more time to run.

4. The length of the time series is important to the analysis, but verification that the length of the time series is appropriate is not as easy as we might have assumed at the outset. A commonly used criterion for the length of the time series data for approximate entropy analysis is that N, the number of data points in the time series, needs to be N> 10^m, or N>30^m if possible (Pincus, 1991; Pincus & Goldberger, 1994). For our choice of m=1, in theory we would only need 10 to 30 data points. One issue is that N does not give the complete answer about the necessary length of the time series because the sampling rate also needs to be considered. For example, with our sampling at 240 Hz, we could have met the N> 30^m criteria with a data collection of 125 ms. However, we found that at least 3 seconds of data was needed to find significant differences between infants with typical versus delayed development, and that the analysis improved for even longer data sets (Deffeyes, 2009). Thus the length of the time series needs to be set based on sampling the complete dynamics of the system, and not set based on getting a certain number of data points. One way to examine if the time series is long enough is to perform the analysis on increasingly longer lengths of time series data, and see if increasing the length of the time series used in the analysis changes the results.

5. Specify the parameters used in the analysis in discussing the results. The parameters that were selected for calculation of the approximate entropy in this study were based on maximizing the p value for a rank sum test involving early infant sitting. In this study, we found no significant effect in the data from the medial-lateral direction, only in the anterior-posterior direction, using ApEn(m=1, r=1.0*std(Data), t @ 240 Hz, lag=8). These parameters were optimized for comparing the early sitting data. A somewhat similar approximate entropy analysis was performed using a subset of this data, but the parameters were optimized using the data from advanced sitting (Deffeyes, Harbourne, DeJong, Kyvelidou, Stuberg, & Stergiou, 2009). This analysis found a significant difference between ApEn(m=2, r=3*std(Data), t=8.33s@240Hz, lag=4) sitting postural sway for infants with developmental delay and infants with typical development, but in the medial-lateral direction and not in the anterior-posterior direction. A third study with a subset of this data used nearly standard parameters ApEn(m=2, r=0.2*std(Data), t=8.33s@240Hz, lag=4) and found no significant difference between postural sway of infants with delayed development and infants with typical development (Deffeyes, Harbourne, Kyvelidou, Stuberg, & Stergiou, 2009). Because of the different results with different parameters, it is incorrect to say that the approximate entropy of one condition/group is different than another condition/group, but rather the parameters must be specified, i.e. that the ApEn(r,m,t @ Hz, lag) is different for the condition/group. Pincus (1991) has described the approximate entropy as a family of statistics, with members varying by r and m values. We point out that different family members may on occasion arrive at different conclusions.

4.2. Discussion of the infant sitting postural sway results

An important result from this work is that using a lag value of 8 or 12 in the approximate entropy analysis gave the best separation of early sitting between infants with typical development and infants with delayed development, and that the difference was only for postural sway in the anterior-posterior direction. ANOVA analysis of the ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) results found a significant interaction between sitting development and subject group only for the anterior-posterior axis. A lag value of 8 corresponds to a time lag of 33 ms, or a frequency of 30 Hz; a lag value of 12 corresponds to a time lag of 50 ms, or a frequency of 20 Hz. Spectral analysis confirmed that there are features in the 20–30 Hz range in the early sitting of infants with typical development that are greatly reduced in mature sitting, and these features are not seen in either early or advanced sitting of infants with delayed development. These features are apparent in the anterior-posterior data, but not in the medial-lateral data. The importance of these 20–30 Hz features is not that they are the largest features in the power spectra, but rather that they are more prominent for postural sway in the anterior-posterior axis in infants with typical development in early sitting, the same group/condition where the ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) was higher. As discussed in more detail below, our results suggest a contribution from a fast acting (20–30 Hz) control mechanism in early (~4.9 months of age) sitting of typical infants. This fast mechanism is greatly reduced in their postural control in advanced (~7.9 months) sitting, presumably because better control from other mechanisms has become active.

Our sitting postural sway results in typically developing infants fit well with results reported of infant sitting by Hadders-Algra (2005), as the author reported a change in postural variability that occurs at about 6 months of age, so that our early sitting is before the transition and the advanced sitting is after the transition. The transition that occurs at 6 months of age (Hadders-Algra, 2005) is a transition from “primary variability” in postural activity characterized by high variability and only poorly adapted to environmental constraints, to a more well-coordinated “secondary variability.” The “secondary variability” that emerges in infants at about age 6 months Hadders-Algra (2005) describes as being related to the infants refining the ability to successfully incorporate multiple sensory systems, such as somatosensory, visual, and vestibular, into the postural control (Hadders-Algra, 2005). Muscle response to external perturbations while sitting becomes better tuned to correcting for the perturbation from ages 5–6 months to ages 9–10 months (Hadders-Algra, Brogen, & Forssberg, 1996). In our study, higher entropy postural sway in early sitting corresponds to the more poorly controlled “primary variability” described by Hadders-Algra (2005), which the author says it serves the function of using trial and error to explore different patterns to establish better control head position in space. As the ability to incorporate more types of sensory information into the postural control improves, the apparent contribution of this control mechanism to postural sway declines and the advanced sitting with the lower contribution corresponds to the “secondary variability” described by Hadders-Algra (2005).

There are a number of changes occurring developmentally that may alter postural control. For example, muscle fibers are inherently fast twitch, but convert to slow twitch with development, polyinnervation of muscles converts to monoinnervation, and dendrites organize into dendritic bundles (Ijkema-Paassen & Gramsbergen, 2005). Additionally, myelination in the brain is ongoing (Paus, Collins, Evans, Leonard, Pike, & Zijdenbos, 2001). In the vocabulary of dynamic systems theory as a control parameter changes, the attractor changes resulting in the emergence of a new behavior, such as the emergence of sitting. While we have not elucidated the control parameter for the transition in infant sitting, candidates include improved neurological control, as described above, physical growth, muscle strength gains, or learning due to interaction with the environment that alters central nervous system connectivity based on neural plasticity mechanisms. While certainly neural myelination is an ongoing process during infancy, and physical growth and strength gains are apparent, Hadders-Aldra (2005) describes the emergence of the secondary variability from primary variability in infant sitting as being related to motor learning, and the increased use of appropriate motor synergies, while acknowledging that some of the other control parameters may also be contributing. If an important control parameter is increased experience, how is that translated into more appropriate motor synergies? What is it that an infant learns when learning to sit? One possibility is that the internal model of the infant is refined to the point that correct control decisions can be made, allowing the emergence of the new behavior (Chen, Metcalfe, Jeka, & Clark, 2007). The description of an improved internal model is somewhat of a mechanistic description of the changing attractor landscape, where the internal model is thought to be associated with cerebellar function (Ebner & Pasalar, 2008). Development of the internal model can alternatively be described as training networks to respond to environmental stimuli based on statistical inference (Fiser, Berkes, Orban, & Lengyel, 2010). Hadders-Algra (2005) studied the response to postural perturbations to arrive at these conclusions that the transition allows better response to external perturbations with “secondary variability” in postural control than with the “primary variability” found in younger infants. Our study did not include perturbations in the protocol, but internal perturbations, such as breathing movements, are present. If the infant’s internal model of the body is not well refined, then response to a perturbation, even if it is simply the breathing of the infants, will not be as well controlled as it would be with a better internal model. Sitting postural sway in infants has been shown to increase with the acquisition of walking skills, which was interpreted as being due to changes of the infant’s internal model of the body with walking (Chen, Metcalfe, Jeka, & Clark, 2007), showing that infants are actively refining their internal model, and that sitting postural sway can change based on changes in the internal model. To the extent that the younger infant’s internal model of their own body is not yet well developed, the movement of any part of their body may act as an unexpected perturbation to sitting posture. The infants in our study at age 7.9 months likely have not only a better ability to deal with unexpected perturbations than the infants at age 4.9 months, as Hadders-Algra (2005) data on response to external perturbations would suggest, but also a more refined internal model of their body so that they would be expected to encounter fewer unexpected internal perturbations.

Our data comparing sitting behavior of infants with typical development to infants with delayed development also fits well with other reported entropy results. We found differences between early sitting postural sway of infants with typical development compared to infants with delayed development, with the ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) being lower in the postural sway of infants with delayed development. Our result of higher approximate entropy for postural sway of infants with typical development is consistent with the results of Donker, Ledebt, Roerdink, Savelsbergh & Beek (2008) who found lower sample entropy, a measure very similar to approximate entropy, for standing postural sway in infants with cerebral palsy. Approximate entropy has been described as a measure of complexity (Pincus, 1991). Infants with typical development have been described as having more complex movements than infants with cerebral palsy, perhaps due to impaired cerebral connectivity (Hadders-Algra, 2008). If approximate entropy is a measure of complexity, then the higher ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) values we found for postural sway of infants with typical development are consistent with the reported higher complexity. We see the high values for ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) decrease with development, whereas Hadders-Algra (2008) hypothesizes that complexity should always be higher for infants with typical development, regardless of age. However, Hadders-Algra (2007) reports different types of movement complexity, including “pre-term”, “writhing”, and “fidgety”, depending upon the age of the infant. Our particular analysis may only be sensitive to one particular type of movement complexity that is prevalent in infants when they are 5 months old, i.e. the early sitting in our study. Infants with cerebral palsy may have inappropriate muscle sequencing, even in older children (Wollacott & Shumway-Cook, 2005; van der Heide & Hadders-Algra, 2005), which we can believe may result in more periodic movement if a series of corrections are needed after an incorrect movement. Future work is needed to address how different measures of complexity are related, and explore if our approximate entropy measure relates with other types of complexity assessments.

The development of motor skills has also been considered from a developmental psychology perspective, where the development of locomotion has been described as initiating a psychological reorganization that is wide ranging and impacts perception, spatial cognition, and social and emotional development (Campos, Anderson, Barbu-Roth, Hubbard, Hertenstein, & Witherington, 2000). While locomotor development may occur in synchrony with cognitive performance, the unilateral focus of Campos, Anderson, Barbu-Roth, Hubbard, Hertenstein, and Witherington (2000) on motor skills as the cause of cognitive change is unfortunate given that cognitive change is likely driving motor skill acquisition just as much as motor skill acquisition is driving cognitive change (Bushnell, 2000). However, Campos, Anderson, Barbu-Roth, Hubbard, Hertenstein, and Witherington (2000) make an interesting point that locomotion allows the infant to explore the environment by moving to and exploring objects of interest, thereby engaging cognitive function that might not otherwise be active. Relating this speculation to our study, sitting likely affords some of the same cognitive benefits as locomotion because the visual exploration of the environment is enabled by a stable sitting posture, and reaching to nearby objects is enabled by a stable sitting posture.

While we found infants with typical development have less periodic, more random movement, what benefit is there to moving in a random manner? Fractal movements, such as Lévy flights, are more random than periodic movements, and are a good search method. For example, such flights are used by animals for searching an area for food or mates (Reynolds & Rhodes, 2009). Infants sitting postural sway has been shown to be fractal (Deffeyes, Kochi, Harbourne, Kyvelidou, Stuberg, & Stergiou, 2009). Highly varied movements that give rise to higher entropy postural sway may be an adaptive method for exploring various postural positions. It seems counterintuitive that a young infant with poor postural control skills would attempt to use a wide range of different postures, as adopting new challenging postures may result in falls. However, unlike falling in adults that may cause injury, infants’ falling is typically inconsequential from an injury standpoint, and is instead part of the exploratory behavior of an infant as they learn new motor skills such as sitting, crawling, cruising, and walking, and learn to use these skills in novel environments (Adolph, 2008). The biological interpretation of the large value of the r parameter used in the analysis is that large excursions of the COP are required to be counted as non-matches by the approximate entropy algorithm. Near fall events, where the infant nearly falls but then recovers balance, might give rise to large excursions in the COP. Actual falling events were not included in the data, the infant must be sitting in order for the trial to be used. Higher entropy for early sitting infants with typical development might then reflect more near fall events, as compared to more developed and thus more skilled sitting. Higher entropy for infants with typical development as compared to infants with delayed development may indicate an increased willingness to engage in behaviors that result in near fall events as they explore various control strategies. The linear measures of variability, including range of motion and sway path length found no significant differences between the two groups (Deffeyes, Harbourne, Kyvelidou, Stuberg, & Stergiou, 2009). This is probably because one infant may have movement due to poor control, while another has movement due to wanting to explore the environment. It is the temporal organization of the movement, rather than the amount of movement, that is different between these two groups.

Adults have difficulty in producing random movement patterns even when requested to do so (Newell, Deutsch, & Morrision, 2000), so it is perhaps not surprising that the typical infants sitting behavior loses much, but not all, of its random quality in becoming more adult-like. The optimal movement variability theory (Stergiou, Harbourne, & Cavanaugh, 2006) suggests that there is an optimal randomness in human movement variability. Movement that is too rigidly structured does not allow for adaptability to changes in the environment, where as movement that is too random does not achieve the intended goal. Early sitting in infants with typical development may have too high a randomness compared to optimal adult values, with a subsequent loss of variability with development. However, this study only assesses infant sitting at two points in time, and there is no reason to believe that the development of infant sitting is a linear progression towards adult sitting (Adolph, Young, Robinson, Gill-Alvarez, 2008; Harbourne & Stergiou, 2003). While some authors suggest daily evaluation of a motor skill in order to assess developmental nuances (Adolph, Young, Robinson, Gill-Alvarez, 2008), a major goal of this work was to understand the parameters necessary for the approximate entropy analysis, rather than mapping out the shape of the developmental trajectory.

An interesting aspect of the postural sway features that we found are the high frequencies of the COP movements. The features in the 20–30 Hz range are at a higher frequency than is typically found in postural sway data, or even in other types of human movement data. Human clapping can be maintained as fast as 7 to 8 Hz (Morrison, Hong, & Newell, 2009), and the world’s fastest drummer can perform tapping movements no faster than 10 Hz (Fujii, Kudo, Ohtsuki, & Oda, 2009). Because of their high frequency, these COP movements are not thought to be related to any type of voluntary movement of the infants, and trials with observable repetitive movements, such as clapping or flapping the arms, were excluded from our analysis. Faster movements may be accomplished by reflexes, in particular the short latency reflexes that result from stretch reflex mechanism. Although different authors adopt different definitions of short latency, one definition is a latency less than 60 ms is short latency (Taube, Schubert, Gruber, Beck, Faist, & Gollhofer, 2006), and we would classify the features 33 to 50 ms as being short latency, if they are in fact due to reflex activity. For comparison, in adult sitting the stretch reflex of the paraspinal muscles, which help stabilize the spine in upright sitting, has a mean latency of 30.7 (+/− 21.3) ms in response to external perturbations (Granata, Slota, & Bennett, 2004). The response latency is the time from the perturbation until electromyography detects activation of the muscle. It does not include time for the muscle to reach full activation, which in adults was an additional 71.3 (27.7) ms (Granata, Slota, & Bennett, 2004). Thus the fastest reflex response might be fast enough to contribute to the 20–30 Hz, 50–33 ms features that we found in the anterior-posterior sitting postural sway of typically developing infant. As a comparison, normal finger tremor includes a 20–25 Hz component that is produced by the stretch reflex loop (Deutsch & Newell, 2006). However, for this tremor the frequency depends on the inertial properties and the stiffness properties of the limb, and to the best of our knowledge, the frequency for infant trunk movements has not been reported, but might be considerably different than the reported 20–25 Hz range for finger movement. It is possible that the near-fall events, where the infant nearly falls but recovers (discussed above), result in high frequency components of the COP. Perhaps this occurs by exciting a stretch reflex, or from high accelerations associated with the fall and/or recovery resulting in tissue vibrations in the high frequency range.

Is it reasonable to propose stretch reflexes are active in unperturbed infant sitting? Historically, reflexes were thought to be the main posture control mechanism, but more recent work has shown posture control is a more complex sensory motor integration problem (Horak, 2006). Additionally, the small movements in well-controlled postural balance do not seem capable of exciting a stretch reflex. Proposing stretch reflexes in a sitting posture study seems unlikely from this perspective, but sitting in young infants is not as well controlled as in adults. Postural control in adult standing has been much more widely studied than infant sitting, and one might hypothesize that similar control mechanisms are operative in infant sitting. Because stretch reflexes likely play only a small role in unperturbed adult standing postural control (Bove, Trompetto, Abbruzzese, & Schieppati, 2006), it might be argued that stretch reflexes are not active in early infant sitting. However, while stretch reflexes are not the main mechanism for control of sitting posture, evidence for stretch reflexes making some contribution to infant sitting postural sway has also been reported by Hadders-Algra, Brogren, and Forssberg (1996). Stretch reflexes are certainly important in generating a quick response to an external perturbation in adult sitting (Granata, Slota, & Bennett, 2004), but may not be activated in unperturbed sitting in adults. There are some important differences between adult postural control and young infants postural control. Adult postural control can potentially use information from a wide array of different sensory modalities, including visual information, vestibular information, joint proprioceptive information, cutaneous information from the plantar surface of the feet, as well as sensory information from the muscles. Some of these sensory modalities are not as well developed in the infant compared to adults or even older infants, and sensory integration capabilities are not as well developed. Children do not achieve fully adult-like sensory integration until they are 12 years old (Peterson, Christou, Rosengren, 2006). Using an oscillating moving-room experimental paradigm, infants’ sitting postural sway was found to become more strongly entrained to the visual stimuli as they reached the age where they learned to sit (Bertenthal, Rose, & Bai, 1997), and infant sensitivity to optic flow in contraction (meaning the image appears to be moving away from the infant) increased from 2 to 8 months, but still had not attained adult values (Brosseau-Lachaine, Casanova, & Faubert, 2008). The vestibular-ocular reflex matures as infants learn to walk (Wiener-Vacher, Toupet, & Narcy, 1996). Thus the younger, typically developing infants in our study did not have the full spectrum of sensory information to use for posture control. One might speculate that, as a result of not having fully developed sensory input to the postural control, postural sway carries the body to more extreme positions, sufficient to trigger stretch reflexes. Additionally, infants in early sitting more often adopt a posture where they lean forward and place their hands on the ground or on their legs, and support some of their upper body weight with their arms. Perhaps because of the forward leaning, the hamstring muscles are closer to being stretched to the threshold that can trigger a stretch reflex, and thus smaller amounts of postural sway in the anterior direction may be capable of triggering a stretch reflex. The differences found in our study were only significant in the anterior-posterior direction, not in the medial lateral direction, consistent with a stretch reflex of the hamstring muscles being triggered more often from a forward leaning posture. These results do not indicate that stretch reflexes are the main control mechanism for the infant controlling postural sway, but merely that the differences between the infants with developmental delay and those with typical development are more pronounced on time scales that are associated with reflex control.

If the features are related to a stretch reflex, why then would higher ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) values be associated with the movement? The stretch reflex in adults is well tuned, with the muscle stretch inducing contraction in the muscle that was stretched, and inhibition of the antagonist muscle. However, in infants the stretch reflex sensory neurons project to a number of different motor muscles, as the connections have not yet been optimally tuned (Myklebust & Gottlieb, 1993; Lichtman & Colman, 2000). Thus when any given muscle is stretched, a variety of muscles contract, generating movement in a direction that is not entirely appropriate. Thus the higher entropy values in postural sway of early sitting of typically developing infants are consistent with the occasional occurrence of a movement that triggers a stretch reflex, in conjunction with the poorly organized postural sway as result of reflex irradiation that is present in these younger infants. ApEn(m=1, r=std(Data), t=8.33s@240Hz, lag=8) decreases as the infants develop, consistent with better coordinated reflex activity.

If the features we observe in the early sitting postural sway data from infants with typical development are indeed due to a stretch reflex, then why do the infants with delayed development not have these features in their postural sway data? One potential reason for not seeing stretch reflexes in the data from infants with delayed development is that if the infant moves enough to trigger a stretch reflex, the reflex may be poorly coordinated and cause the infant to lose balance and fall. We did not use data in our analysis where the infant was falling, which may have resulted in not including data where stretch reflex was activated in infants with delayed development.

A second potential reason is that the emergent behavior in infants with cerebral palsy is different than in infants with typical development because the neuromuscular control constraints are different, and the optimal behavior for each system is different. For example, muscle firing patterns in walking that emerge in infants with Down’s syndrome are longer than in infants with typical development, and this emergent pattern is thought to be adaptive in these infants in order to help stabilize lax joints (Chang, Kubo, & Ulrich, 2009). In some cases, spasticity in limbs associated with cerebral palsy may be a result of an altered stretch reflex (van Doornik, Kukke, & Sanger, 2009). Children with cerebral palsy have hyperactive stretch reflexes (Poon & Hui-Chan, 2009), although the functional implications of the altered reflexes are not entirely clear (Matiello & Wollacott, 1997). Movement tends to be controlled by agonist/antagonist pairs. If one is stretched and then overcompensates by contacting too much (i.e. is hyperactive), then the resulting movement will be to stretch the antagonist, which if it also over compensates, leads to the first being stretched, and an oscillation ensues. This oscillation would be periodic, and thus have low entropy. This type of oscillation is a common problem in negative feedback controllers, for example if the gain is set too high. The infants with delayed development use a more forward leaning sitting posture in early sitting, as do many of the infants with typical development. However, unlike the infants with typical development, some infants with delayed development maintain this posture in advanced sitting. It may be that these high frequency features are not seen in the sitting postural of infants with delayed development because the infants with developmental delay do not exhibit as much movement as those with typical development, and therefore are less likely to trigger a stretch reflex. A previous analysis of this data set, minus a few subjects who had not yet finished the study, found the infants with typical development had slightly more postural sway than infants with delayed development, although the difference was not statistically significant (Deffeyes, Harbourne, Kyvelidou, Stuberg, & Stergiou, 2009). Given the nonlinear response of the stretch reflex, that small difference measured in amount of movement may be more important than the linear statistical analysis used in that study would indicate. Additionally, if the infant has learned through experience that certain behavior triggers a stretch reflex, and if that poorly coordinated stretch reflex results in a fall, the infant may adapt their behavior to avoid triggering a stretch reflex. Sitting still may be an adaptive response to an altered stretch reflex in these infants. Children with CP are reported to use more of a top-down postural control (van der Heide & Hadders-Algra, 2005), perhaps because reflexive control is less functional in these children.

A third potential reason for not seeing a stretch reflex response in the postural sway data is that it may be related to some unknown parameter that changes with normal development of the infants, rather than to typical or delayed developmental. As an example, the stepping reflex seen in young infants appears to disappear with development. If young infants are held over a moving treadmill, their feet will make stepping motions on the treadmill surface (Thelen, Fisher, & Ridley-Johnson, 1984). As the infants developed, they no longer make these stepping movements. Thelen, Fisher, and Ridley-Johnson (1984) found the reflex had not disappeared, but rather the infants had gained mass due to growth, and the muscle strength had not yet caught up. If the infants’ legs were submerged in water, such that the buoyancy force helped support the infant’s mass, the stepping movements were again observed. A weakness of our experimental design is that, even though both the infants with typical development and the infants with delayed development were just learning to sit, the infants with delayed development were necessarily older than the infants with typical development. Typically developing infants in our study had an average age of 4.9 months at early sitting and an average age of 7.9 months at advanced sitting, as compared to the infants with delayed development, who had an average age of 14.1 months at early sitting and an average age of 18.1 months at advanced sitting. So, these infants were delayed in their development, but they were also older than the typically developing infants.

There is also the possibility that the high frequency features are due to some cause other than a stretch reflex. While stretch reflexes are fast for control of movement, the fast movements we see in our study may not be controlled movements. Often gait data is low pass filtered in order to remove high frequency contributions from tissue vibrations that occur on impact of foot with the ground. There is a possibility that the high frequency features found in this study are some type of tissue vibration. Perhaps a rapid change of direction might be able to cause enough vibration of soft tissue for the vibration to be detectable. However, in sitting there are no impacts with the ground to excite tissue vibrations. Vibrations could be excited by quick movements in the anterior-posterior axis, accounting for the high frequency features in the anterior-posterior COP data. However, root-mean-square and range of movement did not differ significantly between infants with developmental delay and infants with typical development in the anterior-posterior axis (Deffeyes, Harbourne, Kyvelidou, Stuberg, & Stergiou, 2009), so differences in vibration would perhaps be due to differences in mass distribution or tissue elasticity between the two groups. Infants with cerebral palsy may have eating difficulties (Sleigh, Sullivan, & Thomas, 2004), prevented adequate nutrient intake during development and thereby reducing the adipose tissue compared to infants with typical development (Kuzawa, 1998).

4.3 Opportunities for further work

One area that was not investigated was the use of filtering to remove noise. Filtering data for linear analysis or spectral analysis is a well developed area of signal processing, but filtering for nonlinear analysis is not as well developed. Use of filters designed for linear or spectral analysis prior to nonlinear analysis may be problematic (Rapp, Albano, Schmah, & Farwell, 1993; Schreiber & Katz, 1995; Theiler & Eubank, 1993) as the filters have been designed to preserve certain linear and spectral aspects of the data, and may not preserve nonlinear features that are of interest in nonlinear analysis. However, many researchers use standard filter techniques on standing postural sway data, such as a low pass Butterworth filter (Donker, Ledebt, Roerdink, Savelsbergh, & Beek, 2008; Hong, James, & Newell, 2008; Stins, Michielson, Roerdink, & Beek, 2009; ), Savitsky-Golay smoothing (Hong, Manor, & Li, (2007), and some authors use detrending methods which effectively serve as filters for the data (Costa, Priplata, Lipsitz, Wu, Huang, Goldberger, & Peng, 2007). Our results suggest that down-sampling or appropriate choice of a lag value may be a good alternative to filtering noisy data, but we did not investigate filtering, so a test of this hypothesis is needed. Another approach to removing noise from the data is to use equipment for data collection that gives high signal-to-noise data, so that the dynamics of the system under study can be more readily quantified without filtering. Future studies from our laboratory on infant sitting will use force plate equipment with a dynamic range selected specifically for infant sitting postural analysis.

There are a number opportunities for further exploration of the approximate entropy algorithm and related measures. Attempting to select the one best set of parameters for approximate entropy misses the opportunity to use multiple sets of parameters to characterize a data set. For example, values of approximate entropy both using low and high values for the r parameter may provide a useful contrast, if the data has different dynamics at different length scales, such as our data that has differences with r=1*std(Data) versus r=3*std(Data). Similarly, differences could exist on different time scales, and multiscale entropy could be used to more rigorously investigate the entropy of dynamics that occur on multiple time scales (Costa, Goldberger, & Peng, 2002; Costa, Priplata, Lipsitz, Wu, Huang, Goldberger, & Peng, 2007). Postural sway data is not necessarily stationary (Schumann, Redfern, Furman, el-Jaroudi, Chaparro, 1995), and these high frequency features are likely not occurring all the time, but may be occurring only sporadically in the sitting position. Time frequency analysis (Schumann, Redfern, Furman, el-Jaroudi, Chaparro, 1995) or wavelet analysis might give more insight into the occurrence of these features. Additionally, using techniques such as electromyography to monitor muscle reflex activity after perturbation of sitting, and accelerometers to monitor tissue vibration, might shed light on the origins of the 20–30 Hz spectral features. There are other measures of complexity in infant movement (e.g. Hadders-Algra, 2008), and while we believe them to be related, analysis of a common data set with these multiple techniques would allow comparison of the results.

4.4. Summary

The use of standard parameters, ApEn(r=.2*std(Data),m=2, N, lag=1), for the approximate entropy analysis may work well for comparing systems with very different dynamics, but to detect more subtle differences, the standard parameters may not be optimal. A useful pragmatic finding of this work for researchers who use nonlinear measures is that spectral analysis can be used as a guide to select lag parameters for approximate entropy analysis. From a clinical perspective, this work is of interest because the design of an infant postural analysis system, coupled with computer for data analysis, may one day bring this technology to the clinical setting for a more sensitive analysis of postural control than is currently available. From a developmental neuroscience perspective, this work is of interest because it suggests the possibility that a short latency reflex for control of sitting posture is operative, perhaps triggered by near-falls. However, we did not measure reflex response, and thus can only speculate about source of the higher frequency, short time scale response, in our data. More work is needed to elucidate the importance of the specific control mechanisms identified in early sitting postural control, and to understand the differences in postural control between infants with developmental delay and those with typical development.