Principal-Component Analysis for Assessment of Population Stratification in Mitochondrial Medical Genetics

Abstract

Although inherited mitochondrial genetic variation can cause human disease, no validated methods exist for control of confounding due to mitochondrial population stratification (PS). We sought to identify a reliable method for PS assessment in mitochondrial medical genetics. We analyzed mitochondrial SNP data from 1513 European American individuals concomitantly genotyped with the use of a previously validated panel of 144 mitochondrial markers as well as the Affymetrix 6.0 (n = 432), Illumina 610-Quad (n = 458), or Illumina 660 (n = 623) platforms. Additional analyses were performed in 938 participants in the Human Genome Diversity Panel (HGDP) (Illumina 650). We compared the following methods for controlling for PS: haplogroup-stratified analyses, mitochondrial principal-component analysis (PCA), and combined autosomal-mitochondrial PCA. We computed mitochondrial genomic inflation factors (mtGIFs) and test statistics for simulated case-control and continuous phenotypes (10,000 simulations each) with varying degrees of correlation with mitochondrial ancestry. Results were then compared across adjustment methods. We also calculated power for discovery of true associations under each method, using a simulation approach. Mitochondrial PCA recapitulated haplogroup information, but haplogroup-stratified analyses were inferior to mitochondrial PCA in controlling for PS. Correlation between nuclear and mitochondrial principal components (PCs) was very limited. Adjustment for nuclear PCs had no effect on mitochondrial analysis of simulated phenotypes. Mitochondrial PCA performed with the use of data from commercially available genome-wide arrays correlated strongly with PCA performed with the use of an exhaustive mitochondrial marker panel. Finally, we demonstrate, through simulation, no loss in power for detection of true associations with the use of mitochondrial PCA.

Introduction

Sequence variants within the mitochondrial genome have been extensively investigated for association with medical conditions,^1–3 given the central role of mitochondria in energy metabolism and cell survival.^4–6 Population stratification (PS), the phenomenon by which variation in minor allele frequency (MAF) due to ancestry influences association with medical phenotypes of interest, is a common confounder in genetic-association studies.⁷ Although several tools have been developed to adjust for genetic ancestry in autosomal GWAS,⁸ the efficiency and effectiveness of different PS adjustment methods for mitochondrial genetic-association studies have not been empirically evaluated.

Adequate control for PS is crucial for mitochondrial medical genetics, given the large influence of ancestry and genealogy on the MAF of mitochondrial variants. In fact, all common variants in the mitochondrial genome possess some degree of information on genetic ancestry.⁹ Prior studies have focused on specific ancestral mitochondrial haplogroups to limit confounding due to population structure.¹⁰ This approach restricts generalizability of results to individuals carrying the analyzed haplogroup, thereby limiting its applicability to the field of common disease genetics. Other approaches have relied on case-control matching for geographic origin.^6,11 This method capitalizes on an assumed association between mitochondrial haplogroups and geography within continents. However, neither of these methods has ever been tested against any alternatives, particularly with respect to efficiency (retention of statistical power after adjustment) and effectiveness (reduction in proportion of false-positive results generated after adjustment).

We sought to evaluate the effectiveness and efficiency of different methods of PS assessment in mitochondrial medical genetics by using both autosomal (from commercial GWAS platforms) and mitochondrial (from comprehensive genotyping) genome-wide data provided by investigators within the International Stroke Genetics Consortium (ISGC). We compared the utility of mitochondrial principal-component analysis (PCA) with haplogroup-based adjustment in association tests of mitochondrial variants. Furthermore, given the correlation between autosomal population structure and geography,^12,13 we hypothesized that genome-wide autosomal data might assist in adjustment for mitochondrial PS. We therefore evaluated effectiveness and efficiency of combined mitochondrial-autosomal PCA (compared to mitochondrial PCA only) in adjusting for confounding due to mitochondrial PS. Finally, we investigated whether consistent PCA results could be obtained with the use of comprehensive mitochondrial genotyping or mitochondrial variants captured by commercially available GWAS platforms.

Subjects and Methods

Samples

Samples were contributed by the Massachusetts General Hospital Ischemic Stroke GWAS (MGH-AIS),¹⁴ by the Massachusetts General Hospital Intracerebral Hemorrhage Stroke GWAS (MGH-ICH),¹⁵ and by investigators participating in the Ischemic Stroke Genetics Study (ISGS)¹⁶ and the Siblings With Ischemic Stroke Study (SWISS).¹⁷ MGH-AIS GWAS samples were genotyped on the Affymetrix 6.0 platform (n = 432), MGH-ICH samples (n = 458) on the Illumina 610-Quad platform, and ISGS-SWISS samples (n = 623) on the Illumina 660 platform. All institutional review boards of participating institutions approved the aforementioned studies, and all participants gave written informed consent for participation. In order to compare results from our US cohorts with those from European and non-European individuals, we analyzed individuals genotyped as part of the Human Genome Diversity Panel (HGDP) and obtained from publicly available resources.^18,19 The HGDP comprises 938 unrelated individuals successfully genotyped (call rate > 98.5%) on Illumina HumanHap650K Beadchips, representing 51 population groups in every continent but Antarctica.²⁰ Detailed information on participating studies and populations is presented in Table 1.

Table 1.

Participating Studies and Populations

Study	No. of Samples	Continent	Population	Geographical Location	Mitochondrial Genotyping	Autosomal Genotyping
MGH-AIS	432	American	European American	USA	Comprehensive panel / Affymetrix 6.0	Affymetrix 6.0
MGH-ICH	458	American	European American	USA	Comprehensive panel / Illumina 610	Illumina 610
ISGS-SWISS	623	American	European American	USA	Comprehensive panel / Illumina 660	Illumina 660
HGDP	157	Europe	French	France	Illumina 650	Illumina 650
			Sardinian	Italy (Sardinia)	Illumina 650	Illumina 650
			Orcadian	Orkney Islands	Illumina 650	Illumina 650
			Russian	Russia	Illumina 650	Illumina 650
			Northern Italian	Italy (Lombardy)	Illumina 650	Illumina 650
			Central Italian	Italy (Tuscany)	Illumina 650	Illumina 650
			Basque	Spain	Illumina 650	Illumina 650
			Adygei	Caucasus	Illumina 650	Illumina 650
HGDP	64	America	Colombian	Colombia	Illumina 650	Illumina 650
			Surui	Brazil	Illumina 650	Illumina 650
			Maya	Mexico	Illumina 650	Illumina 650
			Kairitiana	Brazil	Illumina 650	Illumina 650
			Pima	Mexico	Illumina 650	Illumina 650
HGDP		Africa	Mbuti-Pigmy	Congo	Illumina 650	Illumina 650
			Biaka-Pigmy	Central African Republic	Illumina 650	Illumina 650
			Mandenka	Senegal	Illumina 650	Illumina 650
			Yoruba	Nigeria	Illumina 650	Illumina 650
			San	Namibia	Illumina 650	Illumina 650
			Bantu	Lesotho / Botswana	Illumina 650	Illumina 650
			Bantu	South Africa	Illumina 650	Illumina 650
			Bantu	Kenya	Illumina 650	Illumina 650
HGDP		Asia (Central / South)	Brahui	Pakistan	Illumina 650	Illumina 650
			Balochi	Pakistan	Illumina 650	Illumina 650
			Hazara	Pakistan	Illumina 650	Illumina 650
			Makrani	Pakistan	Illumina 650	Illumina 650
			Sindhi	Pakistan	Illumina 650	Illumina 650
			Pathan	Pakistan	Illumina 650	Illumina 650
			Kalash	Pakistan	Illumina 650	Illumina 650
			Burush	Pakistan	Illumina 650	Illumina 650
			Uygur	China	Illumina 650	Illumina 650
HGDP	228	Asia (Eastern)	Cambodian	Cambodia	Illumina 650	Illumina 650
			Japanese	Japan	Illumina 650	Illumina 650
			Jakut	Siberia	Illumina 650	Illumina 650
			Han	China	Illumina 650	Illumina 650
			Tujia	China	Illumina 650	Illumina 650
			Chin	China	Illumina 650	Illumina 650
			Yi	China	Illumina 650	Illumina 650
			Miao	China	Illumina 650	Illumina 650
			Oroqen	China	Illumina 650	Illumina 650
			Daur	China	Illumina 650	Illumina 650
			Mongolian	China	Illumina 650	Illumina 650
			Hezhen	China	Illumina 650	Illumina 650
			Xibo	China	Illumina 650	Illumina 650
			Dai	China	Illumina 650	Illumina 650
			Lahu	China	Illumina 650	Illumina 650
			She	China	Illumina 650	Illumina 650
			Naxi	China	Illumina 650	Illumina 650
			Tu	China	Illumina 650	Illumina 650
HGDP	163	Asia (Middle East)	Druze	Israel (Carmel)	Illumina 650	Illumina 650
			Bedouin	Israel (Negev)	Illumina 650	Illumina 650
			Palestinian	Israel (Central)	Illumina 650	Illumina 650
			Mozabite	Algeria (Mzab)	Illumina 650	Illumina 650
HGDP	27	Oceania	Papuan	New Guinea	Illumina 650	Illumina 650
			Melanesian	Bougainville	Illumina 650	Illumina 650

HGDP, Human Genome Diversity Panel; MGH-AIS, Massachusetts General Hospital Ischemic Stroke Study; MGH-ICH, Massachusetts General Hospital Intracerebral Hemorrhage Study; ISGS, Ischemic Stroke Genetics Study; SWISS, Siblings With Ischemic Stroke Study.

Comprehensive Genotyping of Mitochondrial Common Variants

Mitochondrial common variants were genotyped according to a published protocol.² In brief, we identified all 144 variants with frequency > 1% in Europeans from > 900 publicly available European mtDNA sequences and selected 64 tagging SNPs that efficiently capture all common variation (except the hypervariable D-loop). Genotyping was performed on the Sequenom platform (San Diego, CA, USA).

Imputation was performed for identification of the pre-HV, H1, H2, J, K, T, U, WX, and I haplogroups in all samples in accordance with previously published methods.²¹ In brief, a total of 1074 complete sequences from the ten most common European haplogroups (H, I, J, K, M, T, U, V, W, and X) were downloaded from mtDB. From these sequences, the genotypes at tagging-SNP loci were determined and used as predictors in a linear discriminant function analysis in the R v 2.10.0 statistical package. The accuracy of haplogroup prediction was determined via a bootstrap crossvalidation approach. For each of 1000 replicates, a bootstrap sample of sequences was chosen to form the prediction model, and the unsampled sequences had their haplogroups predicted. The prediction accuracy was then determined simply as the proportions of sequences whose haplogroups were correctly predicted. In line with previously reported results,²¹ 95% of all crossvalidation replicates had a prediction accuracy of > 98.5%.

Population-Structure Assessment

We performed PCA separately (methods detailed below) on mitochondrial and autosomal SNP data to determine genetic ancestry and to compare information on population structures between the autosomal and mitochondrial genomes.^22–24 We extracted the first ten principal components (PCs) for both mitochondrial and autosomal data and assessed all possible correlations by computing Spearman's correlation coefficients. We also evaluated the relationship between haplogroups (as determined by exhaustive mitochondrial SNP data) and population structure. Specifically, correlation coefficients (Spearman) were calculated for correlations between haplogroup assignments and PCs (both autosomal and mitochondrial).

Autosomal Genome PCA

For both Illumina and Affymetrix genome-wide data sets, nuclear genomic population structure was assessed by the performance of PCA with the use of the EIGENSTRAT program in the EIGENSOFT v 3.0 software package.^23,24 Analyses were performed separately via the multidimensional scaling (MDS) procedure implemented in PLINK v 1.07.²⁵ Results from separate analyses performed with these two software tools were then compared and found to be highly correlated (correlation coefficient > 0.99).

Nuclear PCAs were performed on a subset of all SNPs selected with the use of the following criteria: percentage of missing genotypes < 0.001, MAF > 0.05, and Hardy-Weinberg equilibrium (HWE) p value > 0.0001. For the avoidance of confounding due to linkage disequilibrium (LD), only SNPs with r² < 0.2 with all other SNPs within a 1 Mb sliding window (sliding: 250 Kb) were entered into the PCA. Furthermore, we removed SNPs in known extensive regions of LD (chromosome [chr.] 5: 44–51.5 Mb; chr. 6: 25–33.5 Mb; chr. 8: 8–12 Mb; chr. 11: 45–57 Mb),²⁶ as well as all mitochondrial SNPs.

We assigned genotype-determined ancestry by performing PCA on study subjects and reference populations from HapMap Phase 3 data: CEU (European-ancestry residents of UT, USA), TSI (Tuscans in Italy), MEX (Mexicans in Los Angeles, CA, USA), CHD (Chinese in Denver, CO, USA), and ASW (African Americans and individuals from Southwestern USA). As a measure of controlling for PS, only individuals clustering with CEU and/or TSI populations were considered to be of European ancestry. Clustering-inferred genetic ancestry was compared with haplogroup-determined ancestry. We subsequently reclustered European-ancestry individuals by using the same criteria and procedures and compared results with those of mitochondrial PCA.

Mitochondrial Genome PCA

We assessed mitochondrial population structure by performing PCA on all SNPs genotyped to capture mitochondrial common genetic variation, after applying filters for genotype missingness < 0.10 and MAF > 0.01. We performed sensitivity analyses to identify possible confounding effects of LD on ancestry determination, but we found that different LD-pruning criteria did not alter PCA results significantly (all PC correlations across different sensitivity analyses > 0.95, p < 0.0001). Furthermore, we observed that mitochondrial PCs (mtPCs) returned for PCA performed with the use of the 64 tagging SNPs and the full panel of 144 SNPs were highly concordant (all PC correlations > 0.99, p < 0.0001).

The effect of each SNP on PCA was evaluated by removing it from the list of markers determining genetic ancestry and comparing analyses using this modified adjustment with the full SNP-panel PC-adjusted analysis. We observed no differences when comparing these different analytical procedures for all mitochondrial SNPs (all correlation coefficients > 0.99, all p values < 0.0001).

Controlling for Confounding Due to PS

We compared three different methods for mitochondrial PS control: haplogroup-based stratified analysis, mitochondrial PCA, and combined autosomal-mitochondrial PCA. To do so, we generated 10,000 iterations of both case-control and quantitative trait locus (QTL) phenotypes. These phenotypes were generated to simulate the null hypothesis (i.e., no association with any mitochondrial variant) and to display varying degrees of correlation with mtPC1, with the following Spearman correlation coefficients: 0.00, 0.10, 0.20, 0.30, 0.40, 0.50, 0.60.

For phenotype simulation, available samples within each data set were grouped into deciles on the basis of their mtPC1 values. In case-control simulation, an unsupervised algorithm randomly generated ten increasing probability values (p₁–p₁₀), ranging from 0.0 to 1.0, and assigned them to individuals in each mtPC1 decile group. Each individual was then assigned a random probability value, p_rand, ranging from 0.0 to 1.0 and based on random number generation. Individuals in mtPC1 decile i (with i ranging from 1 to 10) with p_rand > p_i were defined as cases, and the remaining individuals were defined as controls. Simulated phenotypes that were generated by this algorithm and met the required correlation criteria with mtPC1 (tolerance: ± 2.5%), were retained for in silico association testing, and the remainder were discarded. For QTL phenotypes, the unsupervised algorithm identified for each individual ω, such that: $\varphi =\rho \cdot mtPC1+\sqrt{1-{\rho }^2}\cdot \omega$, in which ϕ is the desired QTL phenotype value and ρ is the desired Spearman's correlation coefficient. As for case-control simulations, phenotypes that met correlation criteria with mtPC1 (tolerance: ± 2.5%) were retained for in silico association testing.

Quality-control checks were performed for the elimination of simulated phenotypes that (1) were perfect duplicates (case-control status or QTL values identical for all subjects) of previously generated phenotypes; (2) did not achieve a case:control ratio of 1.0 ± 0.05 (for case-control simulations); 3) displayed nonnormal distributions, as identified by p < 0.05 for the Shapiro-Wilk normality test (for QTL phenotypes); and (4) displayed significant associations with any mitochondrial variant. For this quality-control filter, significant associations were defined as those returning p values beating the Bonferroni multiple-testing correction for 144 independent tests, i.e., p < 0.00035. Additional analyses removing phenotypes at a more lenient threshold imposed by counting only tagging SNPs as independent tests (p < 0.0008) did not alter results (data not shown).

We also performed sensitivity analyses by generating similarly stratified phenotypes, both case-control and QTL, according to mtPCs 2–10 and to haplogroup assignment and compared results. Phenotype generation for mtPCs 2–10 was identical to methods described above. For haplogroups, an unsupervised algorithm randomly generated case-control (random sampling from binomial distribution) or QTL (random normally distributed variable generation) phenotypes. For all generated phenotypes, logistic or linear regression was performed, with age, sex, and haplogroup assignment (multilevel categorical covariate) as predictors. Phenotypes displaying association with one or more haplogroups at p < 0.05 and passing previously described quality-control checks were retained for analysis.

Both autosomal PCs and mtPCs were entered as covariates in logistic- or linear-regression models for PS. We entered additional PCs until no further reduction of the empirical estimate of the mtGIF (see below) could be achieved. Autosomal PCs and mtPCs were entered separately in the combined PCA method analyses, and their impact on mtGIF was assessed independently. Haplogroup-based PS control was achieved with the use of three different analytical strategies: (1) regression analyses were performed within strata defined by each haplogroup, with the use of either the Cochran-Mantel-Haenszel test (case-control) or the combination of results from a Z-score-based (Liptak-Stouffer) method (QTL); (2) haplogroup assignment was introduced in regression analyses as a categorical multilevel covariate, with the average effect across all categories assumed as reference for computation of effect sizes; (3) regression analyses were performed within each haplogroup and combined with the use of a random-effects inverse-variance-weighted metaanalysis (DerSimonian-Laird method). Heterogeneity metrics²⁷ were computed for the assessment of uniformity of effect sizes comparing haplogroups: specifically, we computed the heterogeneity Q statistic (and associated p value) and I², i.e., the proportion of effect size attributable to between-study heterogeneity. We defined significant heterogeneity as p < 0.10 (because of the underpowered nature of the Cochrane heterogeneity test) and I² > 0.20.²⁷

Effectiveness of PS control was assessed by computing mitochondrial genomic inflation factors (mtGIFs) for all analyses. As for the GIF in GWAS,²⁸ the mtGIF was computed by dividing the median observed test statistic (as returned by association testing with the use of different PS-adjustment methods) by the expected test statistic under the null. The mtGIF was computed for each simulation, and values from each analytical scenario were grouped, thus yielding an empirical estimate and 95% confidence interval of mitochondrial genomic inflation. MtGIF distributions for different adjustment methods were compared with the use of an ANOVA (followed by Tukey's post hoc test) or the Wilcoxon-Mann-Whitney test, as appropriate.

Comparison of Mitochondrial PCA Derived from Commercial Arrays and Comprehensive Genotyping

Using 10,000 simulated stratified case-control and QTL phenotypes exhibiting varying degrees of correlation with mtPC1 (generated via methods described above), we performed mitochondrial PCA, using comprehensive genotyping data as well as mitochondrial SNP data derived from Affymetrix 6.0 or Illumina 610-Quad for the same subjects. Mitochondrial PCA on array data was performed with the use of identical quality-control filters and procedures as those described above. SNPs available for mitochondrial PCA for each tested platform are listed in Tables S1 and S2, available online. We also used previously described methods to assign haplogroups to individuals, using commercial array data. All major European haplogroups (H, JT, UK) could be assigned on the basis of available SNPs, as could major African (L, L1, L2, L3) and Asian (A, D) haplogroups.

After adjustment for mitochondrial PCA results, we then compared test statistics and mtGIF between comprehensive genotyping and Affymetrix 6.0 (MGH-AIS), as well as between comprehensive genotyping and Illumina 610-Quad (MGH-ICH and ISGS-SWISS). We also measured correlation coefficients between these two sets of results to examine the consistency of PCA adjustment between the two platforms.

Statistical Power

To compare the efficiency of different mitochondrial PS tools on statistical power for discovery of true association, we performed simulations according to a previously published and validated method for power calculation of mitochondrial common variants.²¹ In brief, we generated case-control and QTL phenotypes displaying association with each of the 144 SNPs in the total combined data set obtained by merging MGH-AIS, MGH-ICH, and ISGS-SWISS studies (n = 1513). We performed 10,000 simulations for each SNP, separately assessing case-control and QTL phenotypes. This yielded a total of 2,880,000 simulations (10,000 × 144 SNPs × 2 analytical scenarios). For case-control simulations, power was calculated for a SNP-conferred relative risk of 1.2, 1.5, and 2.0 at a sample size of 500, 1000, 1500, and 3000 case-control pairs. For QTL analyses, we estimated power for discovery of a SNP-related effect explaining 0.25%, 0.5%, and 1% of the total trait variance for sample sizes of 500, 1000, 1500, and 3000 samples.

In the case-control setting, the control pool was generated by random selection of samples with replacement from the 1513 individuals in order to achieve the desired sample size. For the case pool, MAF at the causal SNP was determined on the basis of genetic relative risk (GRR). Assuming that the disease under study is rare, GRR at a mitochondrial locus can be expressed as GRR ≈ (p_cases(1 − p_controls)) / (p_controls(1 − p_cases)), in which p_controls is the allele frequency in controls and p_cases is the frequency in cases. With the use of the calculated MAF in cases, the number of individuals with each allele at the causal SNP is determined with the use of a random draw from a binomial distribution. The case sample is then generated by sampling with replacement from the subset of individuals with the relevant allele at the causal SNP in order to achieve the previously determined number of samples with each allele.

The power to detect a locus affecting a quantitative trait was examined by randomly drawing a sample of individuals with replacement. A quantitative trait was then simulated by calculating the required effect at the causal SNP through rearranging the formula σ_a² = p(1 − p)a², in which σ_a² is the genetic variance explained by the causal SNP, p is the allele frequency at that SNP, and a is the effect of the SNP in phenotypic standard-deviation units. Genetic variance explained by mitochondrial variants represents half the value of an autosomal locus with the same additive effect and MAF, due to the haploid nature of the mitochondria. Because the samples are considered to be unrelated, the remaining phenotypic variance was simulated as random normal deviations.

The effect of each SNP was tested with the use of logistic regression in the case-control setting and linear regression for QTL traits. All analyses were adjusted for age and sex. Significance was determined at the 0.05 experiment-wide level, defined with the use of a threshold obtained with 10,000 simulation replicates under the null hypothesis. We also calculated the noncentrality parameter for all tests; i.e., the difference in the mean of the distribution of the −log₁₀ of the minimum p value across all SNPs under the alternative and null hypotheses. Statistical power for discovery of simulated association was then compared across different adjustment methods, both at the single-SNP level and the whole-mitochondrial-panel level, with the use of an ANOVA and Tukey's post-hoc test (where appropriate).

Mitochondrial Stroke Genetics

To confirm the utility of an efficient and effective method for PS control in mitochondrial medical genetics, we analyzed data collected as part of the MGH-AIS (660 cases and 749 controls of European American ancestry). All participants were recruited at a single institution in the USA (MGH, Boston, MA) with the use of previously described enrollment and exclusion criteria.¹⁴ Clinical diagnosis of ischemic stroke (supported by neuroimaging at admission) was the defining criterion for case-control assignment. Results surpassing the mitochondrial genome-wide threshold for significance (p < 0.05 after Bonferroni adjustment for 144 independent tests) were further investigated in the ISGS-SWISS data set, comprising 602 cases and 444 controls enrolled in a multicenter genetic study of ischemic stroke, with identical enrollment procedures followed.¹⁶ Statistical power for replication was computed with the use of previously described methods assuming α = 0.05 and effect size and MAF observed in the discovery analysis.

All samples were genotyped with the use of the exhaustive panel mentioned in the “Comprehensive Genotyping of Mitochondrial Common Variants” section.² A subset of enrolled individuals in each study were also genotyped on genome-wide arrays (Affymetrix 6.0 for MGH-AIS or Illumina 610 Quad for ISGS-SWISS) and have been used in all previous analyses. We computed mtGIF and test-statistic concordance for unadjusted analysis, haplogroup-adjusted analysis, and mitochondrial PCA as described above. For haplogroup-adjusted analyses, results are reported only for the approach returning the lowest mtGIF of the three tested (see above).

Results

PCA of Autosomal and Mitochondrial Genomes

We first examined the information on population structure yielded by the mitochondrial genome and compared it with that reflected in the autosomal genome. Ancestry information in the mitochondrial genome was extracted in two ways: traditional halplogroup assignments and PCA. We hypothesized that PCA could be applied to the mitochondrial genome as well and could provide a reliable, easily applicable method for dissection of mitochondrial ancestry, in a manner similar to its application in recent GWAS.

Haplogroup assignment and ancestry assignment according to PCA of the autosomal genome did not consistently correlate. As expected from prior studies of PCA analyses for the nuclear genome in European American populations,²² the MGH-AIS cohort of US individuals is composed mainly of subjects of European ancestry (clustering with the CEU and TSI samples), with a minority of samples being of African American (clustering with ASW), Mexican American (clustering with MEX), and Chinese American (clustering with CHB) origins (Figure 1). Comparison with mitochondrial haplogroup information in this cohort confirms that individuals of African American and Chinese American ancestry are efficiently identified by the African and Asian haplogroups (correlation coefficient = 0.99, p < 0.0001). In contrast, Mexican American ancestry could not be efficiently resolved on the basis of haplogroup (Figure 2A). There was no correlation between autosomal PCs and haplogroups when individuals of European ancestry were analyzed (Figure 2B, all p values > 0.20). Identical results emerged from analysis of the MGH-ICH and ISGS-SWISS cohorts (data not shown).

Figure 1.

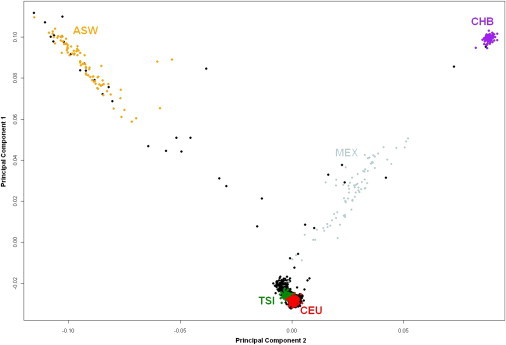
Autosomal Population Structure for the MGH-AIS Study

Population structure of the MGH-AIS subjects (black dots), based on autosomal PCs 1 and 2, compared with reference populations from Phase 3 of the HapMap Project. CEU (red dots): residents of Northwestern European ancestry residing in Utah, US; TSI (green dots): Tuscans in Italy; ASW (yellow dots): African Americans in Southwestern USA; MEX (gray dots): Mexicans in Mexico City; CHB (purple dots): Han Chinese in Beijing.

Figure 2.

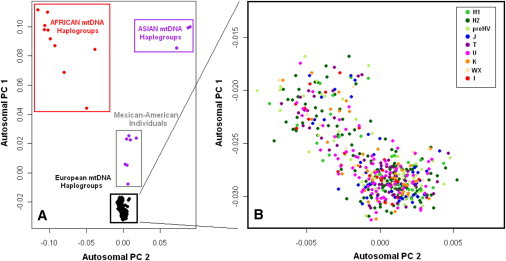
Autosomal Population Structure and Mitochondrial Haplogroups in the MGH-AIS Cohort

(A) Autosomal population structure as represented by plotting autosomal PCs 1 and 2 and corresponding individual mitochondrial haplogroup assignment in the MGH-AIS cohort. Mitochondrial haplogroups clearly distinguish individuals of Asian and African ancestry from European American individuals, but they fail to correctly identify Mexican American individuals (identified as Asian haplogroup carriers).

(B) Autosomal population structure and mitochondrial haplogroup assignment in the European American MGH-AIS subjects. No intracontinental distribution of haplogroups is discernible within the European-ancestry cluster. Autosomal PCA was performed separately after the removal of individuals of non-European ancestry.

PCA of the mitochondrial genome recapitulated the population structure reflected in haplogroup assignment (Figures 3A and 3B), with haplogroup-identical individuals clustering together in a plot of PC1 and PC2. Subclades of the same haplogroup (e.g., H1 and H2) also clustered in the same region of the MDS plot, as did haplogroups descended from a common precursor (e.g., J and T, or K, U, WX, and I). Plotting the third PC from the mitochondrial PCA (Figures 3C and 3D) further resolved and separated these tightly clustered haplogroups.

Figure 3.

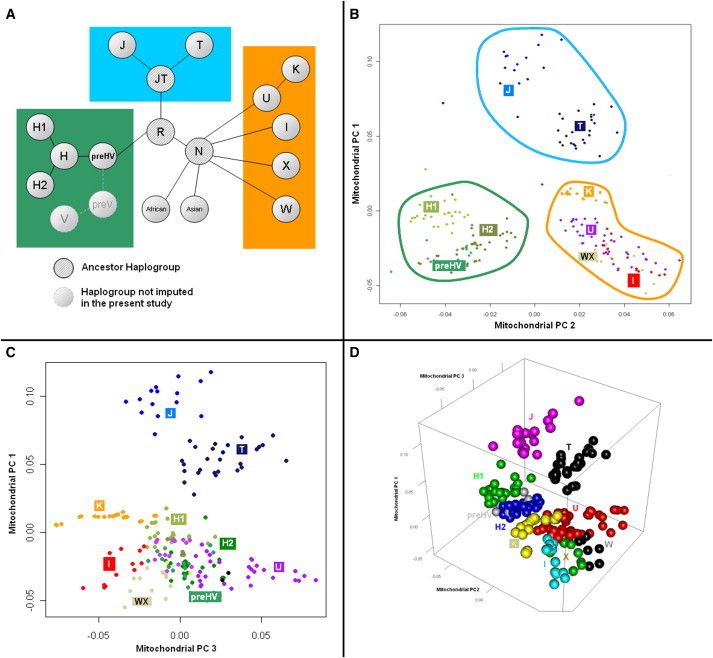
Mitochondrial Population Structure in MGH-AIS

(A) Relationship between European mitochondrial haplogroups. Different colors identify haplogroups descending from the same ancestral haplogroup (preHV = green, JT = light blue, N = orange).

(B) mtPCs 1 and 2 recapitulate haplogroup information in European Americans enrolled in the MGH-AIS. Colored contours identify haplogroups as in (A). Colored dots convey information about haplogroup assignment for each individual.

(C) Plotting mtPCs 1 and 3 further separates haplogroups K, I, and WX from U as compared to the plot in (B). Colored dots convey information about haplogroup assignment for each individual as in (B).

(D) Tridimensional plot of mtPCs 1–3 in European Americans enrolled in MGH-AIS assigns individuals to clusters that recapitulate mitochondrial haplogroup assignment.

Following up on qualitative exploration of the relationship between mtPCs and haplogroups via visual inspection of PCA output, we sought to quantify the correlation between PCs and haplogroups. Our analyses uncovered that all ten extracted mtPCs derived were associated with haplogroup assignment (median correlation coefficient: 0.87, range: 0.62–0.93, all p values < 0.001).

Limited Correlation between Mitochondrial and Autosomal PCAs

We assessed associations between mitochondrial and autosomal population structure in individuals of European ancestry by correlating nuclear PCs and mtPCs from the two analyses. Given the strong association between autosomal population structure and geography, both within and across continents,^12,18 we were interested in identifying patterns of covariance as signatures of PS. We identified very limited correlation between mitochondrial and autosomal PCs in MGH-AIS (correlation coefficient range: −0.09 to 0.15, all p values > 0.05), MGH-ICH (correlation range: −0.09 to 0.014, all p values > 0.05), and ISGS-SWISS (correlation range: −0.06 to 0.14, all p values > 0.05) (Figure 4).

Figure 4.

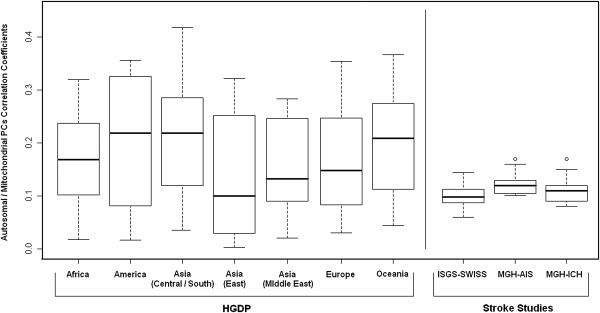
Correlation Coefficients for Autosomal PCs and mtPCs

Correlation between autosomal PCs and mtPCs is visualized as the distribution of correlation coefficients (absolute values) for each population enrolled in the participating studies. HGDP, Human Genome Diversity Panel; MGH-AIS, Massachusetts General Hospital Ischemic Stroke Study; MGH-ICH, Massachusetts General Hospital Intracerebral Hemorrhage Study; ISGS, Ischemic Stroke Genetics Study; SWISS, Siblings With Ischemic Stroke Study

Given the known correlation between autosomal PCs and geographical origin in European and European American populations,^12,22 we hypothesized that only limited correlation exists between mitochondrial population structure and geographical genetic ancestry (i.e., geographical origin of ancestors within Europe) in our European American cohort. Non-US European populations have not experienced the same degree of admixture as that of North American ones. Similarly, ethnic groups within other continents might have experienced lower admixture than European-ancestry US populations. A stronger relationship between autosomal and mitochondrial population structure might therefore be present, based on a similar correlation with geography.

In order to test this hypothesis, we performed a similar analysis on autosomal and mitochondrial SNP data from participants in the HGDP, separately correlating autosomal and mitochondrial PCs for individuals enrolled within each continent. Correlation factors between autosomal and mtPCs 1–5 were in fact higher in HGDP populations (correlation coefficient range: −0.38 to 0.26, Figure 4).

Simulation of Mitochondrial Stratified Phenotypes

To quantify the effect of PS on mitochondrial genetic-association analyses, we generated simulated case-control and QTL phenotypes at different levels of association with mtPC1 (10,000 iterations for each analysis). We then computed mtGIFs without any adjustment for population structure. We observed a wide range of mtGIFs for case-control simulated phenotypes, from 1.2 (95% confidence interval [CI]: 1.0–1.3) for uncorrelated phenotypes to 2.8 (95% CI: 2.7 –3.0) for strongly correlated phenotypes (correlation coefficient: 0.60). MtGIF for QTL phenotypes ranged from an average of 1.1 (95% CI: 0.99–1.25) for nonstratified phenotypes to 2.6 (95% CI: 2.5–2.8) for phenotypes strongly correlated with PC1 (correlation coefficient: 0.60). Observed mtGIF distributions for case-control and QTL simulations under different parameters are presented in Figure S1.

Controlling for PS in Mitochondrial Medical Genetics

On the basis of our analysis of mitochondrial population structure, we next hypothesized that haplogroup information would be crucial in controlling for confounding due to PS for association studies of common mitochondrial variants. We therefore evaluated the performance of haplogroup-stratified analyses in minimizing genomic inflation. Having observed that mitochondrial PCA recapitulates haplogroup information, we also assessed performance of PCA in PS control. We first simulated 10,000 case-control phenotypes stratified according to varying degrees of association with mtPC1. Logistic-regression analyses of each phenotype (adjusted for age and gender) were performed separately, both adjusting by haplogroups (using all three procedures detailed in Subjects and Methods) and after introduction of mtPCs.

Mitochondrial PCA was more effective than haplogroup stratification in controlling mtGIF for analysis of case-control and QTL phenotypes that are confounded by mitochondrial PS. We observed significantly (p = 0.001) smaller mtGIF values for PCA-adjusted analyses (median: 1.00, 95% CI: 0.99–1.02) in comparison with haplogroup-adjusted results (median: 1.8, 95% CI: 1.4–2.0) in MGH-AIS. We obtained similar results in MGH-ICH (PCA mtGIF: median 1.01, 95%CI: 1.00–1.02; haplogroup mtGIF: median 1.6, 95% CI: 1.45–1.82; comparison p = 0.0021) and ISGS-SWISS (PCA mtGIF—median: 1.00, 95%CI: 1.00–1.01; haplogroup mtGIF—median: 1.55, 95% CI: 1.30–1.64; comparison p = 0.002). A significant degree of metaanalysis heterogeneity between haplogroups was identified when the haplogroup-stratification method was used: the median heterogeneity p value across all three data sets was 0.01 (95% CI: 0.008–0.02), and the median I² (between-study heterogeneity in effect sizes; I² > 20% represents a significant degree of heterogeneity) was 0.32 (95% CI: 0.17–0.48). Additional analyses using haplogroup-based strata or haplogroup assignment as a categorical covariate also showed significantly higher mtGIFs (data not shown).

A similar analysis was carried out on 10,000 simulated QTL phenotypes, again exhibiting varying degrees of association with mtPC1. We again observed significantly (p = 0.01) lower mtGIF for PCA-adjusted analyses (median mtGIF: 0.99, 95% CI: 0.98–1.01) as compared to meta-analyses of haplogroup-stratified results (median mtGIF: 1.5, 95% CI: 1.4–1.9). We obtained similar results in MGH-ICH (PCA mtGIF—median: 1.00, 95%CI: 0.99–1.02; haplogroup mtGIF—median: 1.35, 95% CI: 1.15–1.43; comparison p = 0.009) and ISGS-SWISS (PCA mtGIF—median: 1.02, 95% CI: 1.01–1.04; haplogroup mtGIF—median: 1.75, 95% CI: 1.56–1.83; comparison p = 0.001). Across all three data sets, the median heterogeneity p value in QTL analyses for haplogroup-based adjustment was 0.04 (95% CI: 0.02–0.10), and the median I² was 0.23 (95% CI: 0.11–0.36). Similar results were obtained for haplogroup-stratified analyses or with the use of haplogroup assignment as a categorical covariate (data not shown).

To test the robustness of these findings, we reran all simulations by generating a phenotype associated with mitochondrial haplogroups. For case-control analyses across all three data sets, PCA adjustment yielded significantly (p = 0.022) lower mtGIFs (median: 1.01, 95% CI: 1.00–1.03) as compared to haplogroup-based adjustment (median mtGIF: 1.32, 95% CI: 1.15–1.46). For QTL analyses, PCA yielded significantly (p = 0.013) lower mtGIFs (median mtGIF: 1.00, 95% CI: 0.99–1.02) as compared to haplogroup-based adjustment (median mtGIF: 1.28, 95% CI: 1.09–1.45).

In order to determine why haplogroup-based adjustment for PS of simulated phenotypes stratified according to haplogroup assignment yielded such inflated mtGIF distributions, we tested the heterogeneity of the effect sizes across haplogroups. Between-haplogroup effect-size heterogeneity was elevated in both case-control (median heterogeneity p value: 0.05, 95% CI: 0.03–0.11; median I²: 0.22, 95% CI: 0.16–0.31) and QTL (median heterogeneity p value: 0.07, 95% CI: 0.04–0.12; median I²: 0.19, 95% CI: 0.13–0.26) simulations. These findings reflect systematic inconsistency in effect-size estimates across haplogroups. When we repeated these analyses using haplogroup-stratified adjustment or using haplogroup assignment as a categorical covariate, we obtained similar results (data not shown).

These results are notable in that they reveal a limited correlation between test statistics obtained with the use of different methods for controlling for confounding due to PS. Concordance analysis for case-control test statistics (mitochondrial PCA versus haplogroup stratification) across all three data sets returned a mean correlation coefficient of 0.41 (95% CI: 0.35–0.46, all p values > 0.05). Analysis of QTL phenotypes showed similar results, with a mean correlation coefficient of 0.52 (95% CI: 0.48–0.57, all p values > 0.05).

We also assessed the effect of incorporating autosomal PCs along with mtPCs when analyzing simulated phenotypes associated with mtPC1. Comparing test statistics obtained from analysis including and excluding autosomal PCs 1–5, we observed a high degree of correlation for both case-control and QTL simulations (mean correlation coefficient 0.99, 95% CI: 0.98–0.99), with no significant difference in mtGIF (p = 0.41). Even in the HGDP data sets, despite the higher correlation between mitochondrial and autosomal PCs, the autosomal population structure information did not alter test statistics (mean correlation coefficient: 0.99, 95% CI: 0.97–0.99) or modify mtGIF distribution (median mtGIF for mitochondrial PCA: 1.00, 95% CI: 0.98–1.02; median mtGIF for combined mitochondrial-autosomal PCA: 1.00, 95% CI: 0.98–1.01; p = 0.72 for comparison of distributions). Incorporation of autosomal population structure therefore appears to offer little improvement in the efficiency or effectiveness of mitochondrial PCA in controlling for confounding due to mitochondrial PS.

Autosomal PS Does Not Impact Mitochondrial Association Testing

In order to assess the effect of autosomal PS on mitochondrial association testing, we generated 10,000 simulated stratified case-control phenotypes displaying varying degrees of correlation with autosomal PC1. We subsequently examined the effect of this confounding variable on mitochondrial association testing. To this end, we analyzed mitochondrial common variants both before and after adjustment for autosomal PCs 1–5. Both analyses used logistic-regression models adjusted for gender and age.

Test statistics were compared across all 10,000 analyses and found to be highly correlated in MGH-AIS (median correlation coefficient: 0.98, empirical 95% CI: 0.97–0.99), MGH-ICH (median correlation coefficient: 0.99, empirical 95% CI: 0.98–0.99), and ISGS-SWISS (median correlation coefficient: 0.99, empirical 95% CI: 0.98–0.99). We separately assessed the difference in mtGIF values before and after adjustment for autosomal PCs. There was little evidence of mitochondrial genomic inflation (MGH-AIS—median mtGIF: 1.08, 95% CI: 1.05–1.11; MGH-ICH—median mtGIF: 1.03, 95% CI: 1.00–1.05; ISGS-SWISS—median mtGIF: 1.06, 95% CI: 1.02–1.08), and no difference was present after adjustment for autosomal PCs (p = 0.38). Generating simulated phenotypes stratified according to nuclear PCs 2–10 yielded similar results (data not shown).

We then performed a similar analysis using 10,000 simulated QTL continuous phenotypes, stratified on the basis of varying degrees of correlation with autosomal PC1. These phenotypes were analyzed with the use of a linear-regression model (adjusted for age and sex), both before and after adjustment for autosomal PCs 1–5. Mitochondrial association analysis of the QTL phenotypes confounded by autosomal PS was again not dependent on adjustment for nuclear PCA. Concordance for the two analyses across all three data sets was high (median correlation coefficient: 0.94, 95% empirical CI: 0.92–0.96) across all levels of phenotype stratification. Distribution of mtGIFs did not reflect significant inflation in all data sets (MGH-AIS—median mtGIF: 1.08, 95% CI: 1.04–1.10; MGH-ICH—median mtGIF: 1.06, 95% CI: 1.03–1.08; ISGS-SWISS—median mtGIF: 1.06, 95% CI: 1.04–1.10), and mtGIF distribution was not altered by the introduction of autosomal PCs (p = 0.72). Generating simulated phenotypes stratified according to nuclear PCs 2–10 yielded similar results (data not shown).

In summary, neither case-control nor QTL phenotypes exhibiting autosomal PS were affected by nuclear PCA adjustment in mitochondrial association testing. Even more important, analysis of these autosomally stratified phenotypes showed little evidence of mitochondrial genomic inflation, thereby consistent with a lack of influence of autosomal genetic structure on mitochondrial association testing.

Comparison of Array-Based and Comprehensive Genotyping for Mitochondrial PCA

Because mitochondrial PCA was most efficient in controlling mitochondrial PS in the prior analysis, we next set out to determine the sensitivity of mitochondrial PS adjustment using data derived from different genotyping platforms. We compared mtGIFs and test statistics for case-control and QTL analyses of simulated phenotypes stratified according to varying degrees of correlation with mtPC1. For this analysis, we compared results after introduction of mtPCs 1–5, obtained from PCA performed on either commercially available genome-wide arrays (Affymetrix 6.0 and Illumina 610 Quad) or custom exhaustive mitochondrial genotyping data.

We observed good correlation between these two methods for both mtGIFs (correlation coefficient: 0.93, 95% CI: 0.90–0.95, mtGIF range for array-based PCA: 0.99–1.01) and test statistics (correlation coefficient: 0.89, 95% CI: 0.88–0.92). We performed a similar analysis comparing Illumina 610-Quad mitochondrial SNPs from the MGH-ICH and ISGS-SWISS cohorts and comprehensive mitochondrial genotyping from these cohorts. We again observed a good correlation between both mtGIFs (correlation coefficient: 0.90, 95% CI: 0.89–0.91, mtGIF range for array-based PCA: 1.00–1.02) and test statistics (correlation coefficient: 0.87, 95% CI: 0.84–0.90).

Regardless of platform, correlation coefficients were not associated with increasing degrees of mitochondrial phenotype stratification; i.e., correlation between phenotype and mtPC1 (p = 0.43). When directly the two genome-wide platforms were directly compared (Affymetrix 6.0 and Illumina 610 Quad), there was no discernible difference in their ability to control for mitochondrial PS using the mitochondrial SNPs available on each platform (p = 0.21 for comparison of mtGIF distributions). Mitochondrial SNPs captured by commercially available genome-wide platforms appear to be adequate for implementation of mitochondrial PCA for control of confounding due to PS.

Statistical Power

Using a previously published²¹ simulation-based method, we empirically calculated power for discovery of associations in case-control and QTL analyses using a combined data set obtained from pooling mitochondrial genotype data from MGH-AIS, MGH-ICH, and ISGS-SWISS. Calculations were performed at different effect sizes (case-control: relative risk of 1.2, 1.5, and 2.0; QTL: 2.5%, 0.5%, and 1.0% of total variance explained) and for different sample sizes (case-control: 500, 1000, 1500, and 3000 case-control pairs; QTL: 500, 1000, 1500, and 3000 individuals). Statistical significance was determined at 5% experiment-wide empirical significance, and results for different methods were compared.

In the case-control analysis, empirically determined power was not different in a comparison of haplogroup-based or mitochondrial PCA adjustments to the baseline analysis (adjusted only for age and sex): all SNPs had similar power for discovery of associations in a comparison of the three methods (all p values > 0.05), and the average mitochondrial-wide power was also not different among all simulation scenarios (Table 2).

Table 2.

Statistical Power Calculation Results

Phenotype	Sample Size	Effect Size	Unadjusted Analyses	Haplogroup-Based Adjustment	mtPCA Adjustment	Comparison p Value
Case-Control	500	OR = 1.2	0.03 (0.01–0.05)	0.03 (0.01–0.04)	0.03 (0.01–0.05)	0.87
		OR = 1.5	0.11 (0.08–0.13)	0.10 (0.08–0.14)	0.11 (0.09–0.12)	0.64
		OR = 2.0	0.33 (0.27–0.35)	0.34 (0.28–0.34)	0.32 (0.28–0.35)	0.71
Case-Control	1000	OR = 1.2	0.04 (0.02–0.05)	0.04 (0.02–0.06)	0.05 (0.02–0.07)	0.44
		OR = 1.5	0.21 (0.18–0.23)	0.20 (0.18–0.220	0.21 (0.19–0.23)	0.27
		OR = 2.0	0.48 (0.46–0.51)	0.48 (0.45–0.53)	0.47 (0.45–0.51)	0.78
Case-Control	1500	OR = 1.2	0.05 (0.04–0.07)	0.04 (0.03–0.06)	0.04 (0.03–0.07)	0.25
		OR = 1.5	0.27 (0.25–0.31)	0.27 (0.24–0.30)	0.26 (0.25–0.31)	0.89
		OR = 2.0	0.64 (0.58–0.69)	0.65 (0.58–0.70)	0.64 (0.58–0.69)	0.60
Case-Control	3000	OR = 1.2	0.07 (0.05–0.10)	0.06 (0.05–0.09)	0.07 (0.05–0.10)	0.32
		OR = 1.5	0.41 (0.37–0.44)	0.41 (0.36–0.42)	0.42 (0.38–0.44)	0.24
		OR = 2.0	0.83 (0.77–0.88)	0.81 (0.75–0.87)	0.82 (0.77–0.86)	0.67
QTL	500	var. expl. = 0.25%	0.01 (0.00–0.02)	0.01 (0.01–0.02)	0.01 (0.00–0.02)	0.31
		var. expl. = 0.50%	0.12 (0.07–0.15)	0.11 (0.08–0.14)	0.11 (0.07–0.14)	0.28
		var. expl. = 1.00%	0.22 (0.18–0.26)	0.22 (0.17–0.25)	0.23 (0.18–0.25)	0.78
QTL	1000	var. expl. = 0.25%	0.03 (0.01–0.04)	0.02 (0.01–0.04)	0.03 (0.01–0.04)	0.81
		var. expl. = 0.50%	0.23 (0.17–0.28)	0.23 (0.17–0.29)	0.22 (0.16–0.27)	0.22
		var. expl. = 1.00%	0.48 (0.44–0.53)	0.47 (0.45–0.52)	0.49 (0.45–0.51)	0.48
QTL	1500	var. expl. = 0.25%	0.07 (0.04–0.10)	0.07 (0.03–0.11)	0.06 (0.05–0.10)	0.43
		var. expl. = 0.50%	0.34 (0.28–0.37)	0.34 (0.27–0.36)	0.34 (0.28–0.35)	0.52
		var. expl. = 1.00%	0.64 (0.58–0.70)	0.64 (0.58–0.70)	0.64 (0.57–0.70)	0.99
QTL	3000	var. expl. = 0.25%	0.32 (0.28–0.35)	0.30 (0.27–0.34)	0.32 (0.25–0.37)	0.42
		var. expl. = 0.50%	0.66 (0.59–0.72)	0.65 (0.57–0.71)	0.66 (0.60–0.71)	0.66
		var. expl. = 1.00%	0.92 (0.84–0.97)	0.93 (0.85–0.96)	0.91 (0.84–0.97)	0.56

For each simulation scenario, the average statistical power across the entire distribution of MAF for mitochondrial SNPs is shown, with interquartile ranges of observed distributions in parentheses. Sample size refers to the number of case-control pairs (case-control setting) or of individuals with QTL data available (QTL setting). Effect size is defined as odds ratio (case-control) or proportion of phenotypic variance explained (QTL). Empirical power estimates for different adjustment methods were compared with an ANOVA. For haplogroup-based adjustment, the highest power estimate for all three analytical methods tested (see Subjects and Methods) is reported. OR, odds ratio; var. expl., percentage of phenotypic variance explained; QTL, quantitative trait locus.

Similarly, we observed no differences in statistical power for discovery of associations with QTL phenotypes. In comparing to the baseline analysis (adjusted only for age and sex), we observed no differences in power for both the haplogroup-based and the mitochondrial PCA adjustments (all p values for single-SNP analyses > 0.05). The average mitochondrial-wide statistical power for association discovery was also not different (Table 2).

Mitochondrial Stroke Genetics

To confirm the utility of an efficient and effective method for PS control in mitochondrial medical genetics, we analyzed data collected as part of the MGH-AIS (660 cases and 749 controls of European American ancestry). We observed an mtGIF of 2.46 for the case-control analysis adjusted only for age and sex. Haplogroup-adjusted analyses returned an mtGIF of 2.32, whereas adjustment using PCs 1–5 from mitochondrial PCA returned an mtGIF of 0.99 (Figure 5). There was very limited correlation between test statistics returned by the haplogroup-based adjustment and those returned by the PCA-based adjustment (correlation coefficient: 0.48, p = 0.56).

Figure 5.

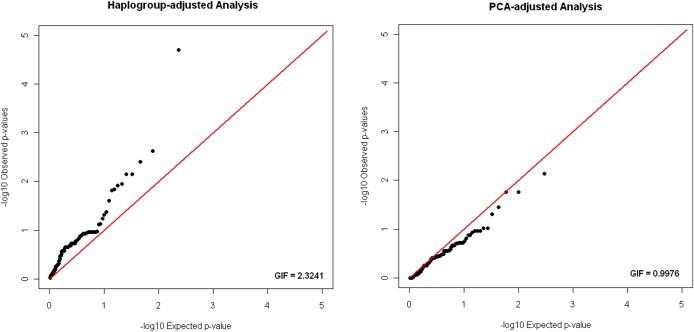
Comparison of Haplogroup-Based and PCA-Based Control for PS in the MGH Mitochondrial Stroke Genetics Study

Quantile-quantile plots for the mitochondrial GWAS of ischemic stroke in the MGH-AIS cohort and for corresponding mtGIF are shown for analyses adjusted for PS with the use of either haplogroup-based or mitochondrial PCA-based methods.

Control of mtPCA effectively removed a false-positive association that emerged in a haplogroup-adjusted analysis. Upon analysis of data from the MGH-AIS cohort, one variant surpassed the mitochondrial genome-wide significance threshold (Bonferroni correction for 144 independent tests) in the haplogroup-adjusted analysis (odds ratio [OR]: 0.42, 95% CI: 0.23–0.78, uncorrected p = 1.9 × 10⁻⁵, Bonferroni-corrected p = 0.00023). PCA-adjusted analysis, however, yielded no significant association (OR: 0.43, 95% CI: 0.23–0.80, uncorrected p = 0.006, Bonferroni-corrected p = 0.87). When attempting replication of the observed association in the ISGS-SWISS data set (602 cases and 444 controls), we found no association in unadjusted (p = 0.95), haplogroup-adjusted (p = 0.94), and PCA-adjusted (p = 0.94) analyses, despite statistical power for replication of 0.83 based on parameters from the discovery data set (α = 0.05, OR = 0.42, MAF = 0.02).

These results highlight the real-world importance of adequate control for PS in mitochondrial association studies, and they confirm the effectiveness of mitochondrial PCA.

Discussion

Our analysis has demonstrated the potential effect of PS on mitochondrial-genetics studies. We have presented a PCA-based method that summarizes haplogroup information and provides robust correction for PS, regardless of the degree of confounding between phenotype and genotype data. Although association analyses comparing haplogroup frequencies between cases and controls can account for confounding due to PS, their ability to identify specific disease-associated variants is limited. Our PCA-based method represents an efficient and effective approach that can identify disease associations for specific SNPs. This PCA-based method appears to be superior to haplogroup-adjusted analyses because it more efficiently controlled inflation of association statistics for mitochondrial variants, as determined by mtGIFs. We have further shown that correction for confounding by PS can be attained without corresponding autosomal PCs and that mitochondrial SNPs encoded on commercial GWAS platforms can provide adequate information for the recapitulation of PCA information obtained from comprehensive genotyping.

Multiple prior studies in mitochondrial medical genetics either have not addressed PS or have limited analysis to specific haplogroups in an attempt to control for it. Our data suggest that a minimal degree of inflation in significance for unadjusted analyses (as measured by the mtGIF) is present even for phenotypes displaying no degree of correlation with mitochondrial population structure. This finding is most likely explained by the presence of several SNPs with widely varying MAFs within each haplogroup. Indeed, prior studies have also identified this phenomenon in unrelated cohorts.²⁹ These outliers create inflated results based on differential assignment of individuals to haplogroups.

Mitochondrial PCA controlled for PS more effectively than haplogroup-based methods in our analyses. Indeed, we were able to eliminate a false-positive association that emerged from an initial analysis using a haplogroup-based approach. This finding supports results from our simulations, which demonstrated high heterogeneity in effect-size estimates across haplogroup-defined strata. Haplogroup assignment thus appears to offer lower information content for mitochondrial ancestry than does PCA, which leverages linkage disequilibrium to utilize almost all information on common variation contained in the mitochondrial genome.

In our analyses, the addition of information on autosomal population structure (in the form of PCs) did not alter mitochondrial genetic-association tests, and it provided no benefit in controlling for mitochondrial PS. This finding is consistent with our results on limited correlation existing between nuclear and population structure within European American populations, as determined either by haplogroups or by PCs. Even analysis of non-US populations with lower levels of intracontinental admixture are unlikely to be able to rely solely on autosomal PCA (or case-control geographic matching) for control of confounding due to mitochondrial PS. Although we did observe higher correlation between autosomal and mtPCs in HGDP individuals, autosomal PCs did not affect the mitochondrial analysis in this second data set or influence mtGIF distribution.

In the evaluation of widely available methods for mitochondrial genotyping, we compared the efficiency of PCA performed with the use of data from commercially available genome-wide platforms and that performed with the use of comprehensive genotyping data. Although genome-wide arrays do not necessarily capture the entirety of common genetic variation within the mitochondrial genome, we observed good concordance between these two strategies. This should allow merging of results from arrays and comprehensive genotyping with the use of the same PCA-based method for PS control. It should also allow mitochondrial association testing to be performed with the use of GWAS arrays, with a reasonable degree of control for underlying population structure.

Our study has limitations. We used mtGIF to measure the degree of inflation of results for mitochondrial association studies. This metric, given the limited number of SNPs being analyzed, is more sensitive to the influence of outlying association values than to that of the corresponding autosomal inflation factors for which the metric was initially designed. The application of GIF to mitochondrial association testing could be viewed as overly conservative, particularly given the presence of minimal inflation even for uncorrelated phenotypes. However, this phenomenon reflects fundamental characteristics of the mitochondrial genome, such as the uniparental inheritance and lack of recombination, resulting in a generally stronger LD than that found in the autosomal genome. These characteristics explain the association between relatively few markers and population structure arising from wide fluctuations in MAF across different haplogroups. These fluctuations could create spurious associations if not controlled. Another limitation is that the majority of our results were generated with the use of simulated phenotypes. Simulated phenotypes allow the precise control of experimental conditions for varying degrees of stratification using either case-control or QTL phenotypes. We were careful to perform 10,000 iterations of each stratified simulation in order to exclude random fluctuations from outlying data points. We also compared our in silico results to those obtained with clinical data from mitochondrial association studies of stroke, to ensure that our simulation-derived results were consistent with actual medical-genetics data sets. We excluded from analysis the limited number of samples of non-European ancestry in our clinical data sets. Additional studies will be required to evaluate the effectiveness and efficiency of mitochondrial PCA in non-European individuals, as well as to confirm that commercial arrays represent a viable alternative to targeted genotyping for other continental populations.

In summary, we present a PCA-based method for control of confounding due to PS in mitochondrial medical-genetics studies. This method, while highlighting the importance of haplogroups in determining mitochondrial population structure, is superior to haplogroup-based methods in controlling for confounding by PS. This PCA-based technique does not require autosomal genotype information in order to correctly adjust for mitochondrial population structure, but it is comparably effective if using a genome-wide array or comprehensive genotyping data as input. Future association studies in mitochondrial medical genetics will likely benefit from the application of this method to control for PS.

Web Resources

The URLs for data presented herein are as follows:

• EIGENSOFT, http://genepath.med.harvard.edu/∼reich/Software.htm

• HapMap, http://www.hapmap.org

• HGDP, http://shgc.stanford.edu/hgdp, ftp://ftp.cephb.fr/hgdp_supp1

• mtDB, http://www.genpat.uu.se/mtDB

• PLINK, http://pngu.mgh.harvard.edu/∼purcell/plink/

• R statistical package, http://www.r-project.org