Benefits and risks of transforming data from dynamic positron emission tomography, with an application to hepatic encephalopathy

Abstract

Transforming data sets to bring out expected model features can be valuable within limits and misleading outside them. Here we establish such limits for the widely used Gjedde–Patlak representation of dynamic PET data, with an application to hepatic encephalopathy.

1. Introduction

A representation of data acquired in dynamic positron emission tomography (PET), introduced by Gjedde (1982) and extended by Patlak et al. (1983), has been widely used since. This Gjedde–Patlak (GP) representation, pertaining to a class of models exemplified below, lends itself to an illuminating graphical analysis of the transformed data.

In the simplest of the relevant models, a PET tracer introduced into plasma with a time-dependent activity c(t) enters tissue in a region of interest (ROI) with clearance K₁. There it forms a pool of precursor with activity M₁(t), which is metabolized irreversibly into the pool M₂(t) with the rate constant k₃, while also returning to plasma with the rate constant k₂:

$$\frac{{\text{d}M}_1}{\text{d}t}=K_{1}c-(k_2+k_3)M_1$$ (1)

$$\frac{{\text{d}M}_2}{\text{d}t}=k_3{M}_1$$ (2)

The initial conditions are

$$M_1(0)=M_2(0)=0$$ (3)

at t = 0 when tracer injection begins. The pools M₁(t) and M₂(t) may represent more complicated processes (Bender et al., 2001).

The activity of the ROI observed by PET is

$$M(t)=V_{0}c(t)+M_1(t)+M_2(t)$$ (4)

where V₀ is the vascular volume in the ROI. Plasma activity c(t) is usually sampled upstream of the organ of interest, but it is commonly taken to equal vascular activity throughout the ROI. Corrections to this convenient but unphysiological assumption have been developed (Munk et al., 2003), but they do not affect the present considerations.

The two observed quantities M(t) and c(t) are recorded typically for 1 h. Nonlinear regression analysis of the resulting data aims at determining the kinetic constants V₀, K₁, k₂, k₃ in each ROI from Eqs. (1)–(4). In contrast, by introducing the ratio M/c and a transformed time as new variables, the GP representation permits the determination of certain combinations of the kinetic parameters from a more robust linear regression involving M(t) only at late times.

In what follows we consider properties of the new variables and their effects on the data analysis.

2. Time reversal on plasma upslope

The GP-transformed time variable is

$$\theta (t)=\frac{{\int }_0^{t}c(t^{\prime })\text{d}{t}^{\prime }}{c(t)}$$ (5)

for all positive t and c(t). Clearly, to each time t there corresponds just one value for θ; but is the converse true? Multiplying Eq. (5) through with c, differentiating with respect to time and rearranging, we find

$$\frac{\text{d}\theta }{\text{d}t}=1-\frac{\theta \frac{\text{d}c}{\text{d}t}}{c}$$ (6)

On the downslope of the plasma curve (negative dc/dt) we have positive dθ/dt, so that θ varies monotonically with t. But on the upslope there can occur temporary time-reversal, dθ/dt negative, for sufficiently steep dc/dt, as we show by an explicit example.

Let the earliest upslope of plasma activity be given by

$$c(t)=bt{\text{e}}^{{\alpha }^2{t}^2}$$ (7)

where b and α are positive constants. Substituting in Eq. (5) and integrating we find

$$\theta =\frac{1-{\text{e}}^{-{\alpha }^2{t}^2}}{2{\alpha }^{2}t}$$ (8)

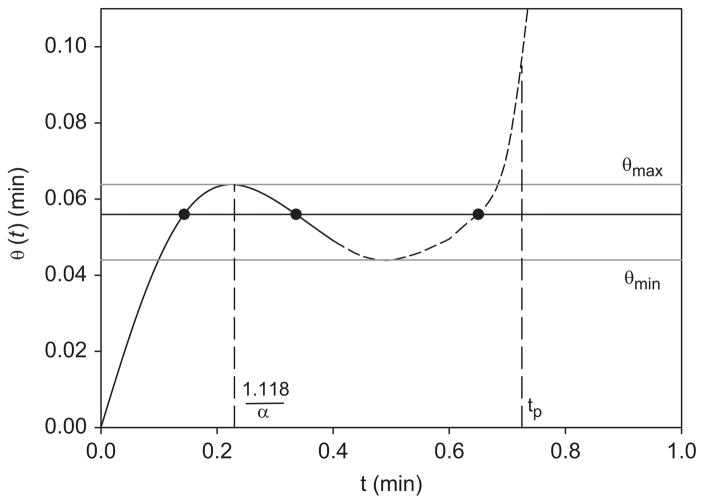
This θ grows as t/2 for small αt, reaches a local maximum θ_max (0.319/α at 1.118/α approximately), and then declines as 1/(2α²t) (Fig. 1, solid line). As t increases, θ(t) must pass through a minimum θ_min (dotted line in Fig. 1) in order to attain a positive slope which reaches dθ/dt = 1 at the time t_p of the peak of plasma activity (dc/dt = 0). Thus the transformed time θ elapses in the opposite direction to t between θ_min and θ_max. We believe this to be the first time-reversal seen in the biosciences.

Fig. 1.

Time-reversal seen in the falling part of the plot of transformed time θ against ordinary time t. The plot was made using Eq. (8) and α = 5min⁻¹ describing the early plasma upslope (solid line). The remaining part of the plasma curve up to its peak at t_p is also shown (dashed line). Three different values of t (solid circles) correspond to any one value of θ in the interval θ_min<θ<θ_max.

For any f(t) (such as M/c)

$$\frac{\text{d}f(t)}{\text{d}t}=\frac{\text{d}f(\theta )}{\text{d}\theta }\left(\frac{\text{d}\theta }{\text{d}t}\right)$$ (9)

so that, whenever dθ/dt<0, a function rising (falling) with t is falling (rising) with θ. To every θ between θ_min and θ_max in Fig. 1 there correspond three values of t, each with its ordinate f(t). The GP representation thus transforms a monotonic f(t) into an S-shaped f(θ), which is three-valued in the interval θ_min<θ<θ_max. When f(t) stands for M(t)/c(t), it is apparent that the GP representation is not helpful on a steep plasma upslope.

Time-reversal is prevented by plasma activity rising sufficiently slowly. Thus, reducing α in the foregoing example so that

$$\frac{1.118}{\alpha }>t_p$$ (10)

is sufficient to remove the domain of time-reversal in Fig. 1. This will be so for boluses that pass through the heart before reaching a brain ROI (Keiding et al., 2006), but may not be so when a 0.2 ml bolus is injected directly into the carotid artery (Phelps et al., 1977). Data points on multiple-valued M(θ)/c(θ) seen in GP plots at early times would probably be attributed to experimental errors.

Thus the inclusion of early data in GP plots requires injections which are sufficiently slow, as in Eq. (10). Rapid injections (e.g., intracarotid) succeed, without GP or related plots, at the exceptional extreme when the total amount of injected tracer that enters the ROI is present within the detector field of view at the instant at which the maximum count rate occurs (Raichle and Larson, 1981).

3. Spurious metabolism on plasma downslope

The GP plot of M/c against θ can have an asymptote at late times (Gjedde, 1982):

$$\frac{M}{c}=V_0+K_1\frac{k_2}{{(k_2+k_3)}^2}+K_1\frac{k_3}{k_2+k_3}\theta$$ (11)

which holds under conditions outlined below. The widest use of the GP representation Eq. (11) is the determination of the metabolic clearance, the coefficient of θ, (slope K) and of the sum of the first two terms (intercept V) by linear regression. This avoids the use of problematic early data, which must be included in non-linear regressions determining, from Eqs. (1)–(4), all the kinetic parameters.

A non-metabolized diffusible PET tracer, such as (¹¹C)methyl-glucose, has k₃ = 0 and M₂ = 0, which reduces Eq. (11) to

$$\frac{M(t)}{c(t)}-V_0=\frac{M_1(t)}{c(t)}=\frac{K_1}{k_2}$$ (12)

This special case suffices to focus on the quasi-steady assumption underlying all GP asymptotics. In the domain of the asymptote, M₁(t) must depend on time in the same way as c(t) (and approach zero in the same way) for M/c to tend to the constant in Eq. (12). On the other hand, substituting Eq. (12) in Eq. (1) we deduce that M₁ is independent of time (dM₁/dt = 0). The use of θ in place of t does not change these considerations on the downslope (Section 2).

To resolve this contradiction as simply as possible we represent c(t) asymptotically by a “final exponential” (Lassen and Sejrsen, 1971; Bass et al., 1984): −(dc/dt)/c = β = constant, take the time-derivative of M₁/c and use Eq. (1) with k₃ = 0:

$$\frac{\text{d}}{\text{d}t}\left(\frac{M_1}{c}\right)=K_1-(k_2-\beta )\frac{M_1}{c}$$ (13)

With M₁(0) = 0 from Eq. (3), integration of Eq. (13) gives

$$\frac{M_1}{c}=\frac{K_1}{k_2-\beta }[1-{\text{e}}^{-(k_2-\beta )t}]$$ (14)

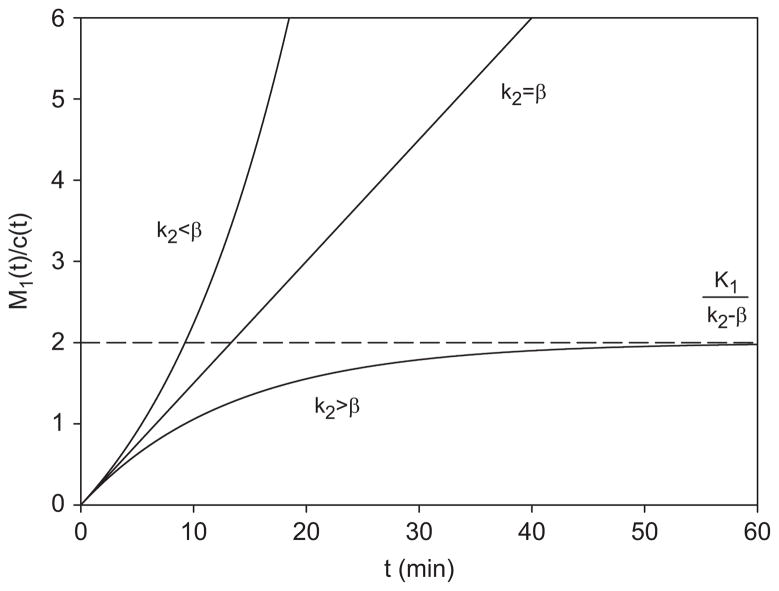
For k₂>β we find a horizontal asymptote with ordinate K₁/(k₂−β) (Fig. 2, lowest line), which is more accurate than Eq. (12) but approaches it when β is small compared with k₂. Here the inequality k₂>β ensures that c(t) falls slowly enough to match (and co-determine) the efflux k₂M₁ by the influx K₁c, whereby a quasi-steady state is maintained. This is the domain of validity of GP asymptotics.

Fig. 2.

Non-metabolized tracer with kinetic parameters K₁ = 0.15 ml ml⁻¹ min⁻¹, k₂ = 0.25 min⁻¹. The Gjedde–Patlak (GP) ordinate is plotted against ordinary time for slow plasma downslope (lower curve) using β = 0.175min⁻¹; rapid plasma downslope (upper curve) using β = 0.325 min⁻¹. GP asymptotics holds for k₂>β, and the two domains are separated by the line M₁/c = K₁t corresponding to k₂ = β.

For k₂<β we re-write Eq. (14):

$$\frac{M_1}{c}=\frac{K_1}{\beta -k_2}[{\text{e}}^{(\beta -k_2)t}-1]$$ (15)

As shown in Fig. 2 (upper curve), this M₁/c rises monotonically to infinity with t (and so with θ: Section 2). In this kinetic domain c(t) falls ahead of M₁ so that K₁c cannot match k₂M₁ to maintain proportionality of M₁(t) to c(t): the denominator of the GP ordinate M/c approaches zero faster than the numerator. The resulting growth of M/c with θ is unrelated to metabolism. In this domain the GP representation cannot be recommended for data analysis (Section 4). In Fig. 2 the two kinetic domains are separated by the line M₁/c = K₁t (case k₂ = β).

In the presence of metabolism the domain of validity of GP asymptotics and hence Eq. (11) is defined by k₂+k₃>β in place of k₂>β (see however end of Section 4). When k₂+k₃<β, the rise of M/c to infinity with t (and θ) is non-linear. The absence of the familiar asymptote in the presence of k₃ is due to non-metabolic terms (as in Eq. (15)), but it is apt to inspire modifications of the model Eqs. (1)–(4) rather than a re-examination of its kinetics.

Exact calculations, in which the “final exponential” is replaced by a form c(t) which is realistic at all times, reiterate the foregoing analysis.

4. Discussion

The possibility of time-reversal on the upslope of the plasma curve depends on experimental design (the site and rate of infusion: Section 2). In contrast, the validity of asymptotic GP analysis is not in the hands of the experimenter, but is determined by the interaction of each tracer with the ROI of the target organ (kinetic constants) as well as on its whole-body kinetics (down-slope of c(t)).

The popularity of determining metabolic clearance K by linear regression to the GP asymptote Eq. (11) rests on its avoidance of determining all kinetic constants by non-linear regression requiring the inclusion of problematic early data: but then k₂+k₃ is not available for comparison with β. If GP asymptotics such as Eq. (11) was used outside its domain of validity, the slope of the late rise of M/c with θ would simulate spurious metabolism (k₃ = 0) or miscalculate the rate of actual metabolism (see Appendix A).

The widely used glucose analog PET tracers (such as ¹¹C-methylglucose and ¹⁸F-fluorodeoxyglucose) appear to be safely in the domain of validity of GP asymptotics, their kinetic constants and biological plasma activity decay having been established for organs such as the brain and the liver in humans and animals. In contrast, the magnitude (and even the existence) of a backflux of ¹³N-ammonia from human brain is controversial (Ott and Larsen, 2004; Keiding et al., 2006), while avid uptake of ammonia in the body increases β after correcting c(t) for metabolites (see Appendix B).

If k₂ is negligible as compared with k₃, then k₃ cannot be determined from M(t), c(t): without an appreciable backflux, dynamic PET loses its grip on metabolism. To see this, we add Eqs. (1) and (2), set k₂ = 0 and integrate:

$$M(t)=V_{0}c(t)+K_1{\int }_0^{t}c\text{d}t$$ (16)

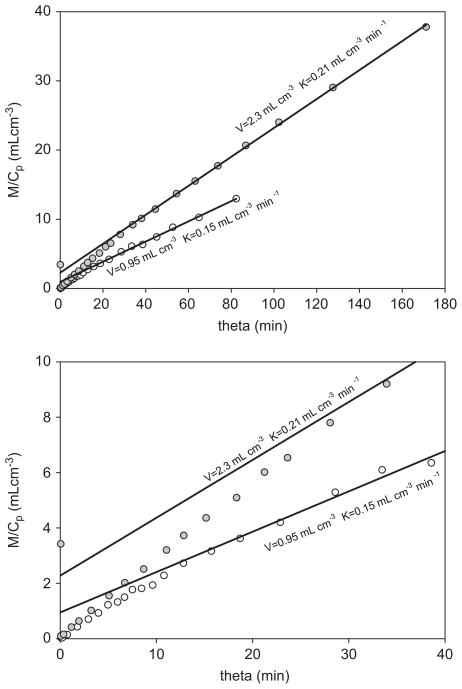
which is independent of k₃. Dividing Eq. (16) by c(t) we see that Eq. (11) has become one straight line for all time, not merely an asymptote. Its intercept is the vascular volume V₀, which in humans is of the order 0.2 mlcm⁻³ in the liver but less than 0.05 mlcm⁻³ in the brain. The intercepts in Fig. 3, and in all our corresponding cases, are more than 20 times greater, putting the backflux of ammonia from the brain beyond doubt.

Fig. 3.

Gjedde–Patlak (GP) plots of cerebral kinetics of ammonia tracer in a case of hepatic encephalopathy (lower curve) and in a normal subject (upper curve). The solid lines are GP asymptotes. The lower frame expands the early part of the upper frame. Both sets of measurements (circles) extend over 30 min of ordinary time. Within this time interval no reversal of the metabolizing step (which would have been seen as a concavity of the asymptote) is detectable.

When k₂ is positive, Eq. (16) holds for early data before the onset of backflux (while k₂M₁ is negligible: recall M₂(0) = 0 in Eq. (3)). Apart from microvascular heterogeneity, this time domain allows the simplest determination of K₁. However, in dynamic PET the data sets c(t), M(t) are determined by two disparate experimental procedures: the times pertaining to blood samples must be synchronized on a joint time axis with the times of ROI activities recorded by the PET camera (Munk et al., 2003). Any asynchronism induces a spurious (positive or negative) increment of K₁ in response to a temporal mismatch of c(t) and M(t). The resulting errors are maximal when these observables are changing rapidly during the first passage of the tracer bolus through the ROI, but are greatly attenuated in later downslope processes (hence a robust GP asymptote).

The insensitivity of GP asymptotics to early data is particularly valuable in PET studies of the human liver with its dual blood supply. As sampling of the portal vein is not admissible in humans, the true input c(t) is not available until hepatic arterial and portal venous tracer inputs are equalized by several recirculations. The quantitative effect of this circumstance on complete kinetic analyzes has been demonstrated in animal experiments (Munk et al., 2001).

When k₂<β, non-compartmental effects set in on the down-slope of c(t). Thus, in the course of washout from a once-through preparation of cat gastrocnemius muscle, k₂ dropped after 5 min to 1/5 of its initial value for sucrose, and to 1/2 for labeled water (Crone and Garlick, 1970). This phenomenon occurs when uncompensated efflux depletes tracer in the tissue close to the capillary membrane, so that rate-determination of the efflux is shifted increasingly from membrane permeability to transport along tissue concentration gradients of the tracer. To ensure that this non-compartmental time-dependence of k₂ does not invalidate the fitting of kinetic “constants” using Eqs. (1)–(4), the inequality k₂>β must hold. This in turn implies the validity of the condition k₂+k₃>β for the validity of GP asymptotics. However, these conditions may not be sufficient to ensure constancy of k₂ when the ROI extends over slow and fast non-vascular subcompartments (Lassen and Perl, 1979).

Nomenclature

α, b

positive constants describing early plasma upslope in Eq. (7)

β

exponential decay of c(t)

c(t)

input function i.e., activity concentration of blood entering the region (Bq ml⁻¹)

K

slope of the Gjedde–Patlak asymptote (ml ml⁻¹ min⁻¹). In Eq. (11), K is K₁k₃/(k₂+k₃)

K₁

clearance of tracer from blood to M₁ (ml ml⁻¹ min⁻¹)

k₂

rate constant for the efflux of tracer from M₁ (min⁻¹)

k₃

rate constant for the transformation of tracer from M₁ to M₂ (min⁻¹)

M(t)

total regional activity concentration as recorded externally by PET (Bq ml⁻¹)

M₁(t)

regional activity concentration in precursor pool (Bq ml⁻¹)

M₂(t)

regional activity concentration in metabolized pool (Bq ml⁻¹)

t

time (min)

t_p

time of the peak plasma activity (min)

θ(t)

the Gjedde–Patlak transformed time variable (min)

V

V = V₀+V_r is the intercept of the Gjedde–Patlak asymptote (ml ml⁻¹)

V₀

vascular volume in the region (ml ml⁻¹)

V_l

is V₀+V_r (GP intercept) estimated by linear regression (ml ml⁻¹)

V_nl

is V₀+V_r (GP intercept) calculated from parameters estimated by non-linear regression (ml ml⁻¹)

V_r

volume of reversible components in the region (ml ml⁻¹) given by Eq. (A.4) or, with β = 0 by K₁k₂/(k₂+k₃)² in Eq. (11)

Appendix A. Exactly soluble case

A.1. Derivation

To elucidate the GP representation of metabolism by an exactly soluble case, we choose a simple c(t) declining along a single exponential after an initial step-rise:

$$\begin{array}{ll}c(t)=0\hfill & \text{for}t<0\hfill \\ c(t)={b\text{e}}^{-\beta t}\hfill & \text{for}t\ge 0\hfill \end{array}$$ (A.1)

where b and β are positive constants.

Then, from Eq. (5),

$$\theta =\frac{{\text{e}}^{\beta t}-1}{\beta }$$ (A.2)

Using Eq. (A.1) in Eqs. (1)–(4), we calculate M(t), and after replacing t with θ by means of Eq. (A.2) we find

$$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +V_r[1-{(1+\beta \theta )}^{(1-(k_2+k_3)/\beta )}]$$ (A.3)

where

$$V_r=\frac{K_1{k}_2}{(k_2+k_3)(k_2+k_3-\beta )}$$ (A.4)

which may be interpreted as the a reversible extravascular volume of distribution of a tracer. This is the GP representation of the kinetics Eqs. (1)–(4) with input Eq. (A.1), valid exactly for all θ≥0. From it we deduce rigorously the late-time GP asymptotics including a corrected form of Eq. (11).

1. Slow plasma decay: (k₂+k₃)/β>1.

   As θ grows to infinity, the last term in Eq. (A.3) tends to zero because the exponent of (1+βθ) is negative. Thus we recover the GP asymptote Eq. (11) with the intercept corrected by the presence of β:

   $$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +V_r$$ (A.5)
   with V_r given by Eq. (A.4), so that the intercept is V = V₀+V_r. The approach to the asymptote depends on (k₂+k₃)/β. For example, if k₂+k₃ = 2β, then Eqs. (A.3) and (A.4) becomes

   $$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +\frac{2K_1{k}_2}{k_2+k_3}\left[1-\frac{1}{1+\frac{k_2+k_3}{2}\theta }\right]$$ (A.6)

   the square bracket tends to one from below, and V_r = 2K₁k₂/(k₂+k₃)² as θ becomes large.

2. Fast plasma decay: (k₂+k₃)/β<1.

   Here the exponent in Eq. (A.3) is positive, and both the square bracket in Eq. (A.3) and V_r in Eq. (A.4) change sign:

   $$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +\frac{K_1{k}_2}{(k_2+k_3)(\beta -k_2-k_3)}\times [{(1+\beta \theta )}^{(1-(k_2+k_3)/\beta )}-1]$$ (A.7)
   The last term increases non-linearly with θ: there is no asymptote. The form of increase depends on (k₂+k₃)/β. For example, if (k₂+k₃) = β/2, then Eq. (A.7) becomes

   $$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +\frac{K_1{k}_2}{{(k_2+k_3)}^2}[\sqrt{1+2(k_2+k_3)\theta }-1]$$ (A.8)

   so that the “intercept” grows with large θ as θ^1/2.

3. The limiting case: k₂+k₃ = β divides the regimes (a) and (b). From Eqs. (A.3) and (A.4), we obtain:

   $$\frac{M}{c}-V_0=K_1\frac{k_3}{k_2+k_3}\theta +\frac{K_1{k}_2}{{(k_2+k_3)}^2}ln[1+(k_2+k_3)\theta ]$$ (A.9)
   At small θ all cases reduce to

   $$\frac{M}{c}-V_0=K_1\theta$$ (A.10)

   When k₃ = 0, we recover Eqs. (14) and (15) with t replaced with θ by means of Eq. (A.2).

Appendix B. Application to hepatic encephalopathy

An important aspect of this disease is high plasma concentration of cold ammonia and slow biological decay of a bolus of ammonia tracer (small β), both resulting from deficient hepatic elimination of ammonia. Healthy subjects have distinctly lower plasma ammonia and faster biological decay of a tracer bolus (higher β).

When GP asymptotics is found to hold for cerebral kinetics of ammonia (k₂+k₃>β: Keiding et al., 2006), then the kinetic parameters K₁, k₂, k₃, V₀ obtained from Eqs. (1)–(4) by non-linear regression to all data determine the slope and the intercept of the asymptote Eq. (11) by full calculation. The same asymptote determined by linear regression to late data (Fig. 3) yields the slope and intercept more directly (and robustly). The resulting slope is the same, but the intercept is higher than that calculated from Eq. (11).

For mono-exponential c(t) this is apparent from the enhancement of V_r in Eq. (A.4) by the subtraction of β in the denominator. This non-equilibrium effect persists for more realistic forms of c(t). Denoting by V_nl the intercept obtained by non-linear regression, and by V_l that obtained by linear regression, we find in all subjects a systematic inequality V_l>V_nl such that the ratio V_nl/V_l quantifies the degree of hepatic encephalopathy. This diagnostic coupling between hepatic and cerebral ammonia kinetics may be conveniently (though only approximately) thought of in terms of the magnitude of β in Eq. (A.4): the time-course of ammonia tracer in plasma is itself diagnostic (Sørensen and Keiding, 2006).

Fig. 3 shows GP representation of cerebral ammonia kinetics for a normal subject with arterial ammonia concentration of 20 >mol/L and V_l = 2.3 mlcm⁻³ (upper curve), and for a patient with arterial ammonia concentration elevated to 41 >mol/L and V_l = 0.9 mlcm⁻³ (lower curve). The smaller slope of the patient’s asymptote is probably due to the relatively higher partial saturation of k₃ (glutamine synthetase: Ott and Larsen, 2004). The ratio V_nl/V_l in the patient is 0.65 in cortex, 0.74 in the basal region, and 0.68 in the cerebellum, with corresponding values 0.27, 0.35, 0.30 in the normal subject. A similar distinction is seen in all subjects who had c(t) carefully corrected for metabolites of the tracer (Keiding et al., 2006), but not enough of these are currently available for standard tests of statistical significance.