Voltage- and cold-dependent gating of single TRPM8 ion channels

Abstract

Transient receptor potential (TRP) channels play critical roles in cell signaling by coupling various environmental factors to changes in membrane potential that modulate calcium influx. TRP channels are typically activated in a polymodal manner, thus integrating multiple stimuli. Although much progress has been made, the underlying mechanisms of TRP channel activation are largely unknown. The TRPM8 cation channel has been extensively investigated as a major neuronal cold sensor but is also activated by voltage, calcium store depletion, and some lipids as well as by compounds that produce cooling sensations, such as menthol or icilin. Several models of TRPM8 activation have been proposed to explain the interaction between these diverse stimuli. However, a kinetic scheme is not yet available that can describe the detailed single-channel kinetics to gain further insight into the underlying gating mechanism. To work toward this goal, we investigated voltage-dependent single-channel gating in cell-attached patches at two different temperatures (20 and 30°C) using HEK293 cells stably expressing TRPM8. Both membrane depolarization and cooling increased channel open probability (P_o) mainly by decreasing the duration of closed intervals, with a smaller increase in the duration of open intervals. Maximum likelihood analysis of dwell times at both temperatures indicated gating in a minimum of five closed and two open states, and global fitting over a wide range of voltages identified a seven-state model that described the voltage dependence of P_o, the single-channel kinetics, and the response of whole-cell currents to voltage ramps and steps. The major action of depolarization and cooling was to accelerate forward transitions between the same two sets of adjacent closed states. The seven-state model provides a general mechanism to account for TRPM8 activation by membrane depolarization at two temperatures and can serve as a starting point for further investigations of multimodal TRP activation.

INTRODUCTION

Transient receptor potential (TRP) channels are nonselective cation channels, most of which are Ca²⁺ permeable. When activated, they produce calcium influx and membrane depolarization in virtually all cell types by responding to diverse stimuli in a multimodal manner (Venkatachalam and Montell, 2007). Their membrane topology is similar to voltage-dependent K⁺ channels (K_v) with six transmembrane domains (S1–S6). TRP channels are tetrameric, with S5 and S6 domains lining the pore. However, compared with other classical voltage- and ligand-gated ion channels, the fundamental single-channel properties of TRPs remain largely unexplored.

TRPM8, a member of the melastatin TRP subfamily, functions primarily as a neuronal cold receptor and has been characterized as the principal detector of environmental cold in the range of 15 to 30°C based on both biophysical and behavioral studies with TRPM8 knockout mice (McKemy et al., 2002; Peier et al., 2002; Bautista et al., 2007). However, TRPM8 shows polymodal activation, a general feature of most TRP channels, being activated by voltage (Brauchi et al., 2004; Voets et al., 2004, 2007), chemicals that produce the perception of cooling (e.g., menthol and icilin; McKemy et al., 2002; Peier et al., 2002; Chuang et al., 2004; Bödding et al., 2007), lipids, such as phosphatidylinositol 4,5-biphosphate (PIP₂) and lysophospholipids (Liu and Qin, 2005; Rohács et al., 2005; Vanden Abeele et al., 2006; Andersson et al., 2007), and by Ca²⁺ store depletion/iPLA₂ activation (Vanden Abeele et al., 2006). Cold- and chemically induced activation of TRPM8 generally shifts its voltage dependence (usually defined by the potential of half-maximal activation, V_1/2) toward more negative potentials (Brauchi et al., 2004; Voets et al., 2004; Vanden Abeele et al., 2006; Mälkiä et al., 2007; Matta and Ahern, 2007). Although the steepness of TRPM8 voltage dependence, which is equivalent to ∼0.6–0.9 electronic gating charges (Brauchi et al., 2004; Voets et al., 2004, 2007; Latorre et al., 2007), is 10-fold lower than that of classical voltage-gated channels such as K_v channels and threefold lower than big K channels (Cui et al., 1997; Rothberg and Magleby, 2000), voltage gating is likely to be of central mechanistic importance to TRPM8 channel function (Nilius et al., 2005).

There is evidence that voltage-dependent gating is an intrinsic TRPM8 property (Voets et al., 2004, 2007). Voets et al. (2007) reported that neutralization of positively charged residues in S4 and in the S4–S5 linker of human TRPM8 reduced the apparent gating charge, suggesting that these domains are part of the voltage sensor. Moreover, sequence alignment of TRPM8 with K_v1.2 revealed the highest degree of homology (31% identity and 52% similarity) in a region corresponding to S4 and the S4–S5 linker (Voets et al., 2007). Collectively, these observations suggest the presence of machinery within the protein that works as a voltage sensor to activate the channel on membrane depolarization. Progress has also been made toward understanding TRPM8 gating. Several studies (Brauchi et al., 2004; Voets et al., 2004, 2007) have examined the multistate process of TRPM8 activation, focusing on the interaction between temperature, voltage, and ligand binding. These studies addressed polymodal gating in terms of channel protein thermodynamics but not the single-channel gating process itself.

The complexity of multimodal activation of TRP channels suggests it may be advantageous to approach the problem by considering a simplified framework before fully integrating the results with different modulators into a global picture of channel behavior. To this end, we studied the voltage-dependent gating of the TRPM8 channel at the single-channel level at two different temperatures to gain insight into the underlying mechanism. Our analysis of TRPM8 suggests that the channel enters a minimum of seven different conformations during gating, associated with at least two open and five closed states. Correlation analysis indicated two or more independent transition pathways between open and closed states, similar to what has been observed for other TRP channels such as TRPV1 and TRPC4 (Liu et al., 2003; Zholos et al., 2004; Tsvilovskyy et al., 2009; Studer and McNaughton, 2010). These findings reveal similarities with the gating mechanism of the distantly related TRPC4 channel in that both of these channels present several open and closed conformations with independent pathways between them (Zholos et al., 2004). Furthermore, we identified the most likely transition pathways among the states for the examined models and estimated rate constants for these transitions with their voltage dependence. Importantly, we show that both cold and voltage activate TRPM8 by acting mainly through changes in the same two rate constants, suggesting possible overlap in the mechanisms of activation of TRPM8 by voltage and cold.

MATERIALS AND METHODS

Cell culture

HEK293 cells were cultured, and TRPM8 expression was induced by tetracycline as described previously (Vanden Abeele et al., 2006). In brief, cells were maintained in Dulbecco’s modified Eagle’s medium (Invitrogen) supplemented with 10% FBS (Invitrogen) and 1% kanamycin. Because this approach is based on tetracycline repressor–expressing HEK293 cells, the expression of the channel was induced with 1 µg/ml tetracycline 12–24 h before use.

Electrophysiology and solutions

Membrane currents were recorded in the whole-cell and cell-attached configurations using an amplifier (Axopatch 200B; MDS Analytical Technologies). Borosilicate glass pipettes were pulled and fire polished to resistances of ∼3–5 MΩ for the whole-cell and 15–20 MΩ for the cell-attached configurations. After formation of membrane seals (>5 GΩ of resistance), single-channel currents were filtered at 2 kHz (eight-pole low-pass Bessel) and sampled at 10 kHz with subsequent cubic spline interpolation to decrease the effective sampling interval to 10 µs. The bath solution for both whole cell and single channel initially contained 150 mM NaCl, 1 mM MgCl₂, 5 mM glucose, and 10 mM HEPES, pH 7.3 (adjusted with NaOH). Before recording cell-attached currents, the bath solution was replaced with a modified standard extracellular solution that contained an equimolar substitution of KCl for NaCl to bring the resting potential close to 0 mV. In the cell-attached configuration, the pipettes were filled with the same solution used initially for the bath, whereas in the whole-cell configuration they were filled with a solution composed of 150 mM NaCl, 3 mM MgCl₂, 5 mM EGTA, and 10 mM HEPES, pH 7.3 (adjusted with NaOH). Whole-cell currents were normalized by the cell capacitance, which was on average 12.20 ± 0.75 pF (n = 19). All membrane potentials are referenced to the inside of the cell. The holding potential was −60 mV for whole-cell measurements.

In whole-cell recordings, series resistance was compensated by ∼70%, and temperature was controlled as described previously (Vanden Abeele et al., 2006). Steady-state I-V relationships were constructed using negatively sloping voltage ramps to map the I-V relationship after an initial depolarizing step to 200 mV to activate the channel (Fig. S1). I-V relationships obtained using voltage ramp and voltage step protocols were in agreement (e.g., at 120 mV the ratio of the currents was 0.98 ± 0.02, n = 3; Fig. S1 C).

In single-channel recordings, the temperature of the bath solution was maintained either at 20°C (room temperature) or 30°C with the use of a heating filament (this was made of nichrome wire insulated with Teflon and heated using a battery placed inside the Faraday cage) that was inserted in the Petri dish. Temperature was adjusted with a resolution of 0.1°C using a digital thermometer (RS 206-3722; RS Components Ltd.) with the thermocouple head placed in the field of view close to the cell.

Data analysis

Three different groups of programs were used for the analysis of both whole-cell and single-channel data: (1) pCLAMP 9.0 (MDS Analytical Technologies), (2) QuB (Qin et al., 1996, 1997), and (3) custom software written in K.L. Magleby’s laboratory. MATLAB (The MathWorks) and Origin 8.0 (OriginLab Corporation) were also used for some of the data fitting and plotting. The analysis and simulation of single-channel recordings were performed as detailed in the following sections. In general, the different analysis methods led to the same conclusions when developing kinetic gating mechanisms, but the estimated rate constants could differ somewhat, possibly as a result of differences in methods for estimating interval durations, corrections for missed events, and sequential versus 2-D fitting of intervals. The use of different analysis methods provided an independent check on the major conclusions concerning gating mechanism.

Number of channels, conductance, idealization, and stability analysis

Only recordings showing activity of one channel were used for single-channel analysis. Appropriate calculations showed that the probability of observing apparent single-channel records if more than one channel were present was <10⁻⁵ (Colquhoun and Hawkes, 1995). Stability plots were used to test for possible run down or desensitization in channel activity (McManus and Magleby, 1988), and when instability was present, such data were not analyzed. Any baseline drift was manually corrected. Single-channel conductance at the various voltages was measured by visually setting cursors at the baseline and open channel current level for computer measurement of those openings of sufficient duration such that filtering effects on amplitude should be minimal (Colquhoun and Sigworth, 1995). The traces were idealized using two different methods: 50% threshold-crossing criteria (Colquhoun and Sigworth, 1995) and segmental K means (Qin, 2004). Open probability (P_o) reported by Clampfit was used in P_o-voltage (P_o-V) relation plots. The slope of the log(P_o-V) relationship at very negative voltages was used to estimate the effective gating charge (Schoppa et al., 1992; Sigworth, 1994).

Cationic conductance activation curves, or P_o values measured at different test potentials, were fitted by the Boltzmann equation in the following form:

$$A=\frac{A_{\max }}{\left(1+e^{\left(\raisebox{1ex}{$\left(V-V_{1/2}\right)$}\!\left/ \!\raisebox{-1ex}{$k$}\right.\right)}\right)}\mathrm{,}$$

where A is either cationic conductance (Siemens) or P_o at potential V (in volts); A_max is its maximal value; V_1/2 is the potential at which A = 0.5 A_max; and k is the slope factor (in volts).

1-D and 2-D dwell-time analysis

Dwell-time histograms were constructed with the Sigworth and Sine transform (Sigworth and Sine, 1987), which plots the square root of the number of events counted in the logarithmically binned intervals (25 bins per decade) for either open- or closed-time interval durations, and fitted with sums of exponentials using a maximum likelihood search routine. The likelihood ratio test was used to determine the significant number of exponential components required to describe the 1-D dwell-time distributions (McManus and Magleby, 1988) to obtain an estimate of the minimal number of states entered during gating (Colquhoun and Hawkes, 1995; Colquhoun and Sigworth, 1995), where twice the natural logarithm of the likelihood ratio is distributed as χ² (Horn and Lange, 1983). To impose consistent time resolution, a dead time of 160 µs (the 10–90% rise time of the frequency response of the recording system) was used in the histograms (Colquhoun and Hawkes, 1995; Colquhoun and Sigworth, 1995). 2-D dwell-time histograms and dependency difference plots were created as described previously (Magleby and Song, 1992; Rothberg et al., 1997).

Estimating rate constants and their voltage and cold dependence

The maximum likelihood analysis methods used to estimate rate constants and evaluate kinetic models have been extensively described (Blatz and Magleby, 1986; Hawkes et al., 1990, 1992; Qin et al., 1996, 1997; Rothberg and Magleby, 1998; Colquhoun et al., 2003). Different models were fitted to either single-channel sequences of idealized events or 2-D dwell-time distributions of the events to estimate the most likely rate constants for transitions between states as well as the equilibrium occupancies of the states. Two types of fitting were performed: individual fitting to datasets at only one voltage and simultaneous (global) fitting to data obtained at multiple voltages. Fittings were performed at either 20 or 30°C. Typically, the simultaneous fitting was to data obtained at voltages ranging from 40 to 140 mV, at which it was practical to record a sufficient number of events given the experimental time constraints. The individual fitting was to data at 40 mV, at which the single-channel currents would be large enough to be measured effectively, and at 100 mV because patches held at more positive voltages had limited lifetimes. Ranking of models was based on the log likelihoods (LLs), as the numbers of free parameters for the various examined models were the same. The ability of the models to describe the data was assessed by visual comparisons of experimental and predicted dwell-time distributions and current versus voltage plots. The voltage dependence of the different rate constants at one fixed temperature was determined from the simultaneous fitting of 2-D dwell-time distributions, typically obtained over voltage ranges from 40 to 140 mV. The regulatory role of temperature was assessed by comparing the rate constants obtained from individual fits (using two different software packages) at 20 and 30°C.

Voltage sensitivity, S_v, expressed as 1/(voltage [in millivolts] producing an e-fold change in a rate constant) or as the effective partial charge, q_eff, for the transition, can be interconverted using the equation

$$S_v=\frac{q_{eff}}{\frac{RT}{F}\times 1e_o}\mathrm{,}$$

where q_eff has units of e_o (elementary charge), R is the universal gas constant, T is the absolute temperature, and F is the Faraday constant. For measurements at 20°C, RT/F was 25.26 mV, increasing to 26.12 mV for recordings at 30°C.

Predicting whole-cell and single-channel currents

The parameters (i.e., rate constants at 0 mV and their voltage sensitivities at 20 and 30°C) estimated from single-channel analysis were used to simulate whole-cell currents arising from voltage ramps and steps to compare with experimental recordings. These whole-cell current simulations were performed using QuB software. The equation to calculate voltage-dependent rates is given by

$$K\left(V\right)=K_0\times e^{(V\times S_v)}\mathrm{,}$$

where K(V) is the rate constant at membrane potential V (in millivolts), K₀ is the initial rate constant at 0 mV, and S_v is the mean voltage sensitivity determined by simultaneous fitting of data obtained at different voltages from eight different channels at each temperature, with different channels for each temperature. For the 20°C data, the projected rate constants at 0 mV were those determined in the programs during the simultaneous fitting. For the 30°C data, additional datasets were available to estimate the rate constants besides those used for the simultaneous fitting. Consequently, the projected rate constants at 0 mV were given by

$$K_0=\frac{K\left(40\right)+K\left(100\right)}{e^{\left(40\times S_v\right)}+e^{\left(100\times S_v\right)}}\mathrm{,}$$

where K(40) and K(100) are the averaged values from the individually fitted rate constants at 40 (n = 9) and 100 mV (n = 13), respectively.

To simulate whole-cell currents using a kinetic model, it is necessary to know the number of channels, which was derived by dividing the whole-cell current by the product of P_o and the unitary current at 120 mV (see Results). To simulate single-channel currents for the indicated kinetic models using QuB, the most likely rate constants estimated (as described in a previous section) for the given voltage and temperature were used, and noise values calculated by directly measuring selected open and closed sections from the recordings were applied to the open and closed states, respectively.

Statistics

Mean values are expressed as means ± SEM, where n equals the number of patches/cells. Statistical significance is denoted as *, P < 0.05 or **, P < 0.01.

Online supplemental material

Fig. S1 shows currents recorded from TRPM8 channels for voltage steps and voltage ramps and compares the I-V relationships measured using these two protocols. Fig. S2 illustrates different approaches to fitting voltage activation curves for TRPM8 channels with the Boltzmann equation. Tables S1 and S2 list mean values for the rate constants for scheme I at different voltages and temperatures. Online supplemental material is available at http://www.jgp.org/cgi/content/full/jgp.201010498/DC1.

RESULTS

Depolarization increases P_o by decreasing mean closed-interval duration and increasing mean open-interval duration

To investigate the kinetic gating mechanism of TRPM8, it was found to be useful, as a first step, to develop a minimal mechanism accounting for its voltage-dependent single-channel gating at a fixed temperature of 20°C. The analysis was then extended to 30°C to gain insight into temperature activation of the channel and to identify possible similarities between voltage and temperature activation.

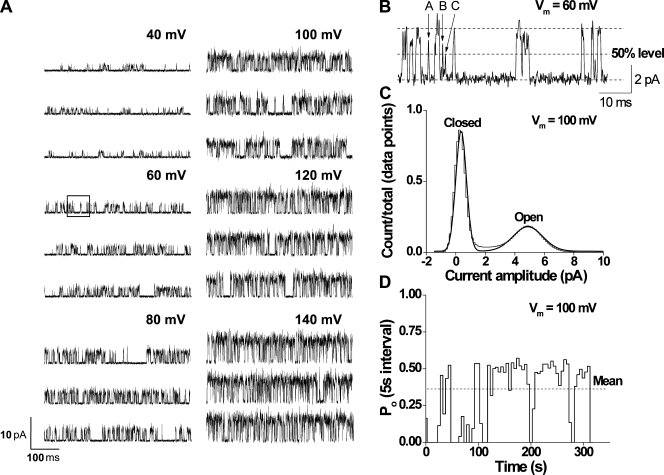
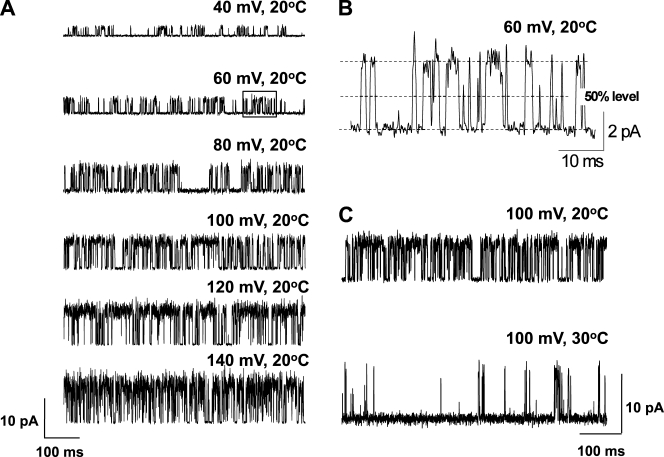
Fig. 1 A shows currents through a representative single TRPM8 channel for membrane potentials ranging from 40 to 140 mV. An increase in channel activity with depolarization is readily apparent. A short segment of recording taken from the trace at 60 mV (Fig. 1 A, boxed area) is shown in Fig. 1 B at a higher time resolution. An all-points amplitude histogram (Fig. 1 C) for the recording at 100 mV shows that two peaks can be clearly defined from the trace, indicating two main conformations of the channel, open and closed. Fig. 1 D presents a stability plot of mean P_o for successive 5-s segments of data obtained from the complete record at 100 mV. When active, the mean P_o of the channel remains relatively constant. These periods of activity are separated by longer closed intervals, resulting in a mean P_o of ∼0.33. We have previously reported such cycles of channel activity in TRPC4 as well (Zholos et al., 2004). These longer closings resulted in the apparently burst-type activity (e.g., Fig. 1 A), which is not analyzed here for the reason that such long closings occurred very infrequently (i.e., an additional long closed component was noted in several channels, but its relative contribution to the total number of events was negligible).

Figure 1.

Depolarization increases the single-channel activity of TRPM8 channels at 20°C. (A) Representative currents recorded at voltages ranging from 40 to 140 mV. Upward steps indicate channel opening. (B) Segment with extended resolution from the trace at 60 mV in A (shown in the recording in the boxed area). The letters on top of the trace indicate different brief events (A, 240 µs; B, 170 µs; C, 50 µs). (C) All-points amplitude histogram from the trace at 100 mV fitted with two Gaussian curves with means at 4.8 pA (open) and 0.2 pA (closed). (D) Stability plot showing P_o values measured over 5-s consecutive intervals for data at 100 mV (mean P_o = ∼0.33). In some records for some of the channels, there were a few very long closed intervals, even at depolarized potentials, which are not apparent because of the time base. These are seen as gaps in channel activity. Figs. 1, 3, 5, 8, 9, 11, and 13 (at 20°C) illustrate data from the same channel.

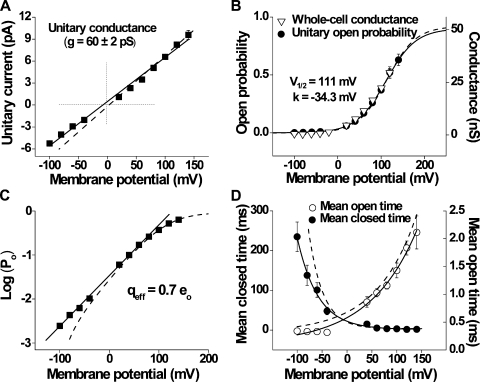
The voltage dependence of the unitary current amplitude is readily apparent from Fig. 1 A. A plot of unitary current amplitude versus voltage is approximated by a straight line (Fig. 2 A), giving a conductance of 60 ± 2 pS (n = 11 cells). However, because this channel rarely opens at negative potentials, and when it does the openings are so brief that they are usually not fully resolved, it is likely that the amplitude of the currents at negative potentials is underestimated. The dashed line in Fig. 2 A excludes these, giving a slightly higher and probably more accurate estimate of conductance based solely on the currents at positive potentials (70 ± 3 pS, n = 11 cells; compare with McKemy et al., 2002). Although the current versus voltage data are approximated by straight lines, suggesting that conductance is relatively independent of voltage, from the single-channel records in Fig. 1 B it appears that there may be somewhat different levels of open channel conductance. It will be shown in a latter section when single-channel currents are simulated with a fixed open channel conductance that apparent variations in the open channel conductance would be expected from filtering, reducing the amplitudes of brief duration intervals. Conductance was found to increase with increasing temperature (95 ± 3 pS at 30°C, n = 15 cells; not depicted).

Figure 2.

Description of the voltage-dependent properties of TRPM8 single channels and whole-cell currents at 20°C. (A) Unitary I-V plot corresponding to channel conductance of 60 ± 2 pS (solid line; n = 11 cells). An alternative measurement was also calculated (dashed line) from the values at positive membrane potentials (70 ± 3 pS; n = 11 cells). (B) P_o-V dependence (circles; n = 22 cells) was approximated by the Boltzmann relation with 111 mV for V_1/2 and –34.3 mV for the slope. The triangles plot averaged whole-cell conductance at the same test potentials (ramp protocol from −100 to 120 mV; n = 10 cells). (C) P_o plotted on a logarithmic scale against membrane potential to calculate the effective gating charge, giving an approximate value of 0.7 e_o at room temperature. (D) Mean open- and closed-interval durations change with membrane potential. Mean open times (open circles) increased from 0.34 ± 0.01 to 2.11 ± 0.30 ms (n = 9 cells; paired t test, P < 0.01), and mean closed times (closed circles) decreased from 235 ± 37 to 1.77 ± 0.49 ms (n = 9 cells; paired t test, P < 0.01) between −100 and 140 mV, respectively. Both curves were fitted with single exponentials (open-time constant = 96 mV per e-fold change; closed-time constant = 40 mV per e-fold change). Error bars (SEM) were not plotted when they were smaller than the symbols. Dashed lines in B–D are model predictions (see Results).

The increase in channel activity with depolarization (Fig. 1 A) corresponds to an increase in P_o (Fig. 2 B, circles). The P_o-V dependence is sigmoidal, with P_o increasing from 0.0025 ± 0.0011 at −100 mV to 0.63 ± 0.05 at 140 mV. These data are well described by a Boltzmann curve, with the V_1/2 of 111 mV and a slope of −34.3 mV (n = 22 cells). With appropriate scaling, the mean whole-cell conductance values superimpose the single-channel P_o estimates (n = 10 cells; Fig. 2 B, triangles). Given the linear unitary I-V relationship (Fig. 2 A), this superposition indicates that depolarization-induced increases in whole-cell currents (see Fig. 10 A) can be fully accounted for by the increased single-channel P_o. The apparent gating charge was estimated by limiting slope from the P_o-V data to obtain a value of 0.7 e_o (Fig. 2 C), which is within the range estimated in other studies (Brauchi et al., 2004; Voets et al., 2004, 2007; Latorre et al., 2007).

The relationships between voltage and mean open- and closed-interval durations were approximated by single exponential curves (Fig. 2 D). Mean open times (Fig. 2 D, open circles) increased approximately sixfold, whereas mean closed times (Fig. 2 D, closed circles) decreased ∼132-fold between −100 and 140 mV. There was an e-fold increase in the mean open times for a 96-mV increase in voltage and an e-fold decrease in the mean closed times for a 40-mV increase. This indicates that the increase in P_o with voltage arises from both a decrease in mean closed times and an increase in mean open times, with the decrease in mean closed times making the dominant contribution. Thus, the increased frequency of opening with depolarization (Fig. 1 A) arises because the closed-interval durations decrease more rapidly than the open-interval durations increase.

TRPM8 gates in a minimum of five closed and two open states

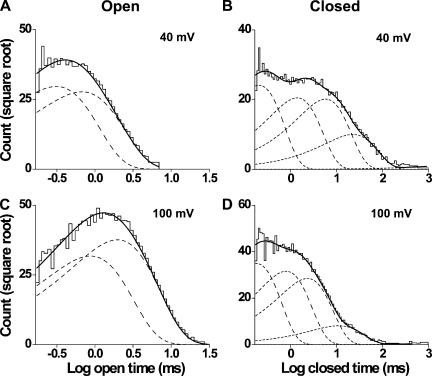
To examine TRPM8 gating kinetics, large numbers of open and closed intervals (∼55,000–380,000) were collected from each of eight single channels at 20°C over a range of membrane potentials (20–140 mV), binned to create dwell-time histograms, and fitted with sums of exponentials. Dwell-time distributions are presented in Fig. 3 for data at 40 and 100 mV from a representative channel. The open dwell times were well described by the sums of two exponential components, whereas the closed dwell times required five exponentials. The likelihood ratio test typically indicated two to three significant open and five to six significant closed components, suggesting that the channel enters a minimum of two to three open and five to six closed states during gating. The same findings were made at 30°C, as will be shown in a later section. Because the third open and sixth closed components were not consistently seen, and when present were typically of small area arising from a limited number of intervals, we focused the detailed testing of gating mechanisms on models with two open and five closed states.

Figure 3.

Open and closed dwell-time histograms at 20°C are well described by two open and five closed exponential components, respectively. (A–D) Open-time (A and C) and closed-time (B and D) histograms at 40 (top) and 100 mV (bottom; 25 bins per decade). The distributions are well described (continuous lines) by the sums of two open exponential components and five closed exponential components (dashed lines). Open-time constants (and normalized areas) are 0.31 ms (0.53) and 0.67 ms (0.47) at 40 mV and 0.87 ms (0.42) and 2 ms (0.58) at 100 mV. Closed-time constants (and normalized areas) are 0.21 ms (0.39), 1.4 ms (0.28), 5.8 ms (0.27), 23 ms (0.066), and 2,256 ms (0.00064) at 40 mV and 0.18 ms (0.39), 0.80 ms (0.32), 2.3 ms (0.26), 11 ms (0.021), and 6,314 ms (0.00019) at 100 mV.

Depolarization shifts the dwell-time distributions

As expected from the single-channel records in Fig. 1 and data in Fig. 2 D, changing the voltage from 40 to 100 mV at a fixed temperature of 20°C shifted the open dwell-time distribution toward longer openings and the closed dwell-time distribution toward shorter closings (Fig. 3). These shifts arose because depolarization shifted both of the underlying open exponential components to longer durations and shifted three of the five closed components to shorter durations (Table I). Depolarization also decreased the relative area of the longest closed component and increased the area of the briefest closed component. The net result was depolarization-induced increases in mean open time and decreases in mean closed time (Fig. 2 D).

TABLE I.

Effects of voltage on exponential components at 20°C

Exp.	40 mV		100 mV
	τa	Areab	τ	Area
	ms		ms
EC1	0.25 ± 0.02	0.35 ± 0.02	0.23 ± 0.01	0.44 ± 0.02**
EC2	1.91 ± 0.26	0.36 ± 0.02	1.13 ± 0.13*	0.37 ± 0.02
EC3	10.8 ± 2.47	0.24 ± 0.02	4.41 ± 1.05**	0.16 ± 0.02
EC4	57.9 ± 17.0	0.055 ± 0.014	19.2 ± 4.12**	0.025 ± 0.006
EC5	4,227 ± 2,067	0.0041 ± 0.0029	2,428 ± 896	0.00035 ± 0.00008*
EO1	0.49 ± 0.06	0.58 ± 0.03	0.87 ± 0.08**	0.56 ± 0.04
EO2	1.25 ± 0.21	0.42 ± 0.03	2.27 ± 0.27**	0.44 ± 0.04

All values are means ± SEM for two open and five closed exponential components (EO1–EO2 and EC1–EC5, respectively) fitted by the maximum likelihood method to dwell-time histograms from eight single-channel patches at 40 and 100 mV and 20°C. The mean values have been compared using the Wilcoxon matched pairs test (*, P < 0.05; **, P < 0.01). These averaged values should not be used to calculate P_o and mean open- and mean closed-time values. Rather, the separate values should be calculated for each channel and then averaged.

^aMean dwell times for each exponential component.

^bRelative areas for each exponential component indicating its contribution to the total number of closed or open events.

Correlation between the durations of adjacent open and closed intervals

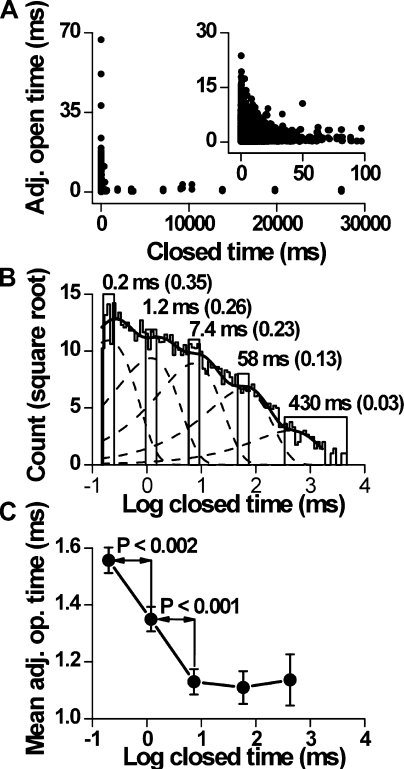
To obtain information about the connections between open and closed states at 20°C, open-interval durations were plotted against adjacent closed-interval durations. An example for a representative recording at 40 mV is shown in Fig. 4 A, in which a strong inverse relationship between the durations of adjacent open and closed intervals can be seen, similar to TRPC4 (Zholos et al., 2004), TRPV1 (Liu et al., 2003), and to that seen for other ion channels (McManus et al., 1985; Gil et al., 2001). This plot indicates that, as a rule, briefer open intervals occur adjacent to longer closed intervals, and longer open intervals occur adjacent to briefer closed intervals.

Figure 4.

Inverse correlation between the durations of adjacent open and closed intervals at 20°C. (A) Scatter plot of all adjacent open- and closed-interval durations on two different closed-time bases. Data were collected at 40 mV. The inset was taken from the main plot at lower time bases. (B) Closed dwell-time histogram described (solid line) by the sum of five underlying components (dashed lines). The bars indicate the ranges of closed intervals used to select adjacent open intervals for statistical comparison of adjacent interval durations. The closed ranges were selected to bracket the mean duration of intervals in each of the five closed components. The last range was made larger because there was reduced risk of contamination from other components. The mean durations and fractional areas for each of the closed components are indicated. The number of adjacent interval pairs for each range was, from left to right, 1,342, 1,002, 826, 364, and 226. (C) Linear-log plot of mean open times adjacent to closed intervals from each range indicated in B as well as the significance of the difference. Error bars represent SEM.

These correlations were quantified by measuring mean open time for open intervals adjacent to closed intervals in five time ranges corresponding to the mean durations of the five closed exponential components (Fig. 4 B). The mean durations of the open intervals adjacent to the first two classes of briefer closed intervals were significantly longer than those adjacent to the three classes of longer closed intervals (Fig. 4 C). Such correlations between adjacent open- and closed-interval durations require at least two independent pathways between open and closed states, i.e., two gateway states (Colquhoun and Hawkes, 1995), placing important restrictions on possible mechanisms.

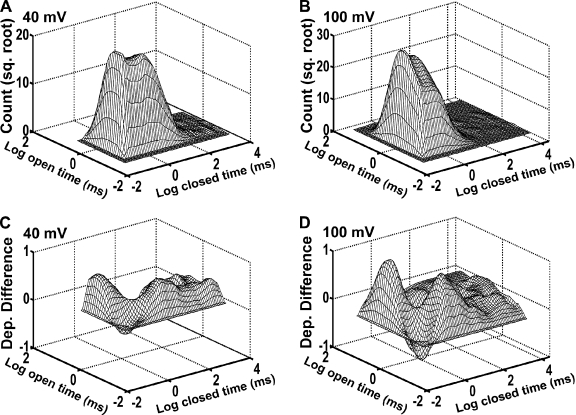
Dependency difference plots provide an additional means of examining the correlation between adjacent open- and closed-interval durations and are a powerful tool for distinguishing between possible kinetic gating mechanisms (Magleby and Song, 1992; Rothberg et al., 1997; Rothberg and Magleby, 1998, 1999). Fig. 5 (A and B) presents representative 2-D dwell-time histograms that plot the square root of the number of adjacent interval pairs against the logarithm of the durations of adjacent open and closed intervals in each pair (Rothberg and Magleby, 1998). Similar to the results in Fig. 3, increasing the voltage from 40 to 100 mV shifted closed intervals to shorter times and open intervals to longer times (Fig. 5, A and B). The dependency difference plots derived from these 2-D dwell-time distributions (Fig. 5, C and D) indicate which adjacent interval pairs are in deficit or excess over what would be expected if there were no correlation between adjacent open- and closed-interval durations (z-axis value of 0). At both 40 and 100 mV, there was an excess of long open intervals adjacent to brief closed intervals, an excess of brief open intervals adjacent to intermediate or longer closed intervals, and a deficit of brief open intervals adjacent to brief closed intervals (Fig. 5, C and D). Thus, these results suggest that depolarization changes the relative durations and numbers of the open- and closed-interval pairs without inducing major changes in the underlying gating mechanism.

Figure 5.

Kinetic structure of TRPM8 channels at 20°C as indicated by 2-D dwell-time histograms and dependency difference plots. (A and B) 2-D dwell-time histograms plotting the square root of the number of interval pairs against the logarithm of the durations of adjacent open- and closed-interval pairs at 40 mV (A) and 100 mV (B). (C and D) Dependency difference plots at 40 mV (C) and 100 mV (D; see Materials and methods). Peaks represent an excess of open intervals adjacent to closed intervals for the indicated durations of adjacent intervals when compared with a theoretical 2-D distribution that was calculated assuming the open and closed intervals distribute randomly. The valleys represent a deficit of interval pairs with the designated open and closed durations compared with a random distribution.

Ranking and testing kinetic gating mechanisms

Although fitting dwell-time histograms with sums of exponentials points to a minimal kinetic model with two open and five closed states, such analysis does not indicate the way in which the states are configured. Consequently, to gain insight into the configuration, we examined the ability of the 12 different models in Fig. 6 to describe the single-channel data. This was initially done for each model by simultaneously fitting data obtained at 20°C over a range of voltages from 20 to 140 mV to determine the most likely rate constants for the transition pathways and the likelihood that the experimental data were generated by the model. Of the 12 examined gating mechanisms (Fig. 6), schemes I, VII, and VIII consistently gave the highest (best) LL values, as indicated in Table II. To examine whether these three schemes were kinetically distinguishable, 100,000 intervals were simulated for scheme I at each of several voltages, and then these data were simultaneously fitted with scheme VII and also with scheme VIII. The LL values and the 2-D distributions and correlations between adjacent intervals predicted by schemes I and VII were essentially identical, suggesting that the schemes cannot be readily distinguished. Scheme VIII showed some small differences in terms of LL values and the areas and time constants of the components of distributions, but these were not apparent visually, indicating that the kinetics predicted by scheme VIII were almost identical to the kinetics predicted by schemes I and VII.

Figure 6.

Schemes with two open and five closed states included in the analysis.

TABLE II.

LLs for individual channels for the indicated schemes at 20°C

Scheme	Channel 1	Channel 2	Channel 3	Channel 4	Channel 5	Channel 6	Channel 7	Channel 8
I	−1,238,927	−2,147,865	−1,076,276	−2,009,329	−330,572	−551,453	−734,700	−1,346,604
II	−1,239,445	−2,148,029	−1,076,333	−2,009,488	−330,776	−551,458	−734,905	−1,346,796
III	−1,238,771	−2,148,334	−1,076,364	−2,009,821	−330,995	−551,750	−734,618	−1,346,710
IV	−1,239,780	−2,148,760	−1,076,608	−2,009,888	−330,907	−551,715	−734,993	−1,347,064
V	−1,239,538	−2,148,868	−1,076,915	−2,010,377	−330,987	−551,931	−735,148	−1,347,338
VI	−1,239,772	−2,148,738	−1,076,579	−2,009,841	−330,899	−551,714	−734,988	−1,347,080
VII	−1,238,923	−2,147,855	−1,076,201	−2,009,329	−330,572	−551,397	−734,699	−1,346,604
VIII	−1,238,966	−2,147,860	−1,076,292	−2,009,333	−330,590	−551,426	−734,709	−1,346,831
IX	−1,239,552	−2,148,334	−1,076,451	−2,009,820	−330,894	−551,659	−734,905	−1,347,093
X	−1,239,829	−2,148,342	−1,076,315	−2,010,150	−330,952	−551,515	−734,944	−1,346,806
XI	−1,238,917	−2,148,360	−1,076,302	−2,010,150	−330,766	−551,245	−734,952	−1,346,813
XII	−1,240,280	−2,148,832	−1,076,687	−2,009,375	−331,082	−552,131	−735,194	−1,346,977

Nevertheless, the LL values for these three schemes were typically close but not always identical for a given channel (Table II). Such differences may arise because the gating mechanism is more complex than for any of the examined schemes, as some channels indicated gating in more than two open and five closed states (see previous sections), and the corrections for missed events may be somewhat different for the different models, giving slightly different descriptions of the (imperfectly resolved) experimental data. Nevertheless, the analysis provides a means to rank the various schemes.

Because the 12 examined schemes in Fig. 6 had the same number of free parameters, they were ranked by comparing the LL values for each of the eight channels analyzed, as shown in Table III for each individual channel. Also included in Table III under the All channels column is the overall ranking of the schemes based on the mean rankings for all channels. Because schemes I and VII are kinetically equivalent for perfect data, they were combined in the rankings. As Table III shows, the kinetically equivalent schemes I and VII were the highest ranked schemes, followed by scheme VIII. Scheme II was ranked third.

TABLE III.

Ranking of schemes for all channels and individual channels at 20°C

Scheme	All channelsa	Channel 1	Channel 2	Channel 3	Channel 4	Channel 5	Channel 6	Channel 7	Channel 8
I, VIIb	1	3	2	1	1	1	3	2	1
VIII	2	4	1	2	2	2	2	3	6
II	3	5	3	5	4	4	4	4	3
XI	4	2	6	3	9	3	1	6	5
III	5	1	4	6	6	10	9	1	2
IX	6	7	4	7	5	5	6	4	10
X	7	10	5	4	9	8	5	5	4
VI	8	8	7	8	7	6	7	7	9
IV	9	9	8	9	8	7	8	8	8
XII	10	11	9	10	3	11	11	10	7
V	11	6	10	11	10	9	10	9	11

The rankings in this table are based on the LL values in Table II.

^aAll channels give the rankings based on the mean of the rankings for all the channels.

^bSchemes I and VII are essentially equivalent.

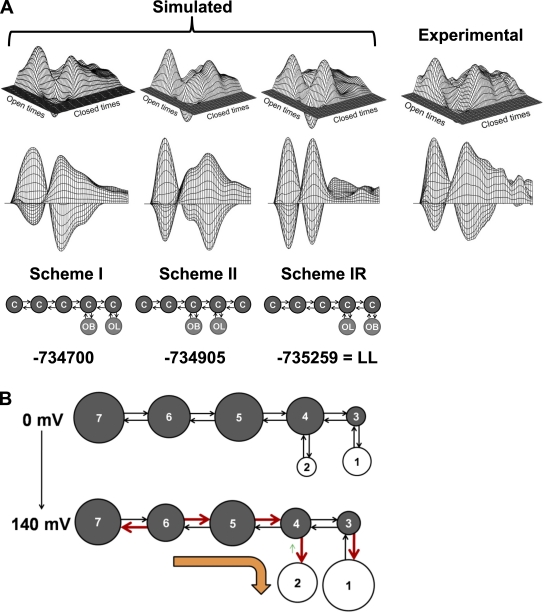
To examine whether the most highly ranked schemes could account for the correlation information in the single-channel data, we compared the predicted 2-D dependency difference plots for these schemes to the dependency difference plot for the experimental data. Also included in the comparison is scheme IR, which represents an alternative model to scheme I, obtained by reversing the positions of the brief and long open states in scheme I. An example of such a comparison for schemes I, II, and IR is presented in Fig. 7 A for channel 7 (a representative channel), which plots the experimental dependency difference plot obtained from single-channel data at 40 mV (top right) and the side view of the dependency difference plot looking directly at the closed-time axis (bottom right) and also the predicted dependency difference plots for scheme I (first column), scheme II (second column), and scheme IR (third column). (The dependency difference predictions for schemes VII and VIII appeared visually the same as for scheme I.)

Figure 7.

Scheme I describes the single-channel data under different experimental conditions. (A) Distinguishing between gating mechanisms with dependency difference plots. (top) Dependency difference plots for schemes I, II, and IR obtained by simulating and analyzing one million intervals (left three) and for representative experimental data at 40 mV and 20°C (right). (middle) Dependency difference plots obtained by rotating the top plot toward the closed times and projecting the image on a vertical plane parallel to the closed-time axis. (bottom) Schemes to be compared. In scheme IR, the position of the long opens and brief opens has been interchanged with respect to scheme I. The LL values are indicated below the plots for that scheme. Scheme I, with the best LL, gives the best approximation of the experimental data. OB and OL indicate briefer and longer open states, respectively. Compare with Fig. 5 for axis labeling. Note that log open times increase from right to left, and log closed times increase from left to right. (B) Schematic representation of the change in the rate constants of scheme I with increasing voltage and at a fixed temperature of 20°C. The areas of the states are proportional to the equilibrium occupancies estimated from the models. The thicker (red) arrows indicate a significant increase in the rate constant. The smaller (green) arrow indicates a significant decrease. The orange arrow indicates the dominant change observed with increasing voltage. The values for these changes are shown in Table IV. The mean parameters in Table IV were calculated from parameters obtained from eight separately analyzed channels.

The predicted dependency difference plots for this channel were obtained by analyzing one million simulated open and closed intervals for each scheme and are presented on top of each scheme for comparison with the experimental data on the right in Fig. 7 A. Scheme I, with the highest ranking (Table III) and the highest LL (−734,700) of the three schemes for channel 7, gave the best approximation of the excesses (peaks) and deficits (valleys) of adjacent intervals when compared with the experimental data. Scheme II, with a lower ranking (Table III) and a lower LL value (–734,905), gave a worse description of the dependency difference plot, with the excess of brief openings adjacent to closed intervals shifted to longer closed times than in the experimental data. Scheme IR, with a lower LL (–735,259) than either schemes I and II, gave an even worse description of the dependence difference, as it predicted far too few brief open intervals adjacent to the longer closed intervals. Thus, the representative data in Fig. 7 A show that scheme I is preferred over schemes II and IR because of its higher LL value and also because it gave the best description of the dependency difference data. Because scheme I is a top-ranked scheme and presents a more plausible model for voltage-dependent gating for a tetrameric channel (see parallels to big K channel in Horrigan and Aldrich, 1999 and Rothberg and Magleby, 2000) than schemes VII and VIII (which appear as Rube Goldberg devices with states stuck most anywhere), scheme I was the focus for further analysis.

Identifying voltage-dependent rate constants for scheme I

The voltage sensitivities of the rate constants for scheme I were identified by simultaneously fitting sets of single-channel data at 20°C obtained over a range of voltages, typically from 40 to 140 mV, with scheme I. The rate constants at 0 mV and their voltage dependencies were determined for the eight channels analyzed, and their mean values (mean ± SEM) are presented in Table IV. Included in the legend of this table is also an indication of the robustness of the parameters for fitting data from a single channel. Voltage sensitivity is presented as apparent partial charge movement associated with the transition. Six of the rate constants had voltage sensitivities significantly different from zero, indicating significant contributions to the voltage dependence of the gating. Specifically, the transitions C3→O1, C4→O2, C5→C4, C6→C5, and C6→C7 were significantly accelerated with increasing voltage, with four of the five changes driving the gating toward the open states. In addition, the rate constant from O2→C4 was significantly decreased with increasing voltage, increasing the time spent in O2.

TABLE IV.

Rate constants and partial charges for scheme I at 20°C

Transition	K0a	qeffb
	s−1	eo
O1-C3	3,130 ± 722c	−0.116 ± 0.064
C3-O1d	4,670 ± 536	0.158 ± 0.043**
O2-C4d	4,531 ± 1,034	−0.190 ± 0.052*
C4-O2d	230 ± 38	0.396 ± 0.101**
C3-C4	2,902 ± 586	−0.064 ± 0.068
C4-C3	525 ± 235	0.184 ± 0.078
C4-C5	1,257 ± 983	0.093 ± 0.073
C5-C4d	489 ± 288	0.252 ± 0.078*
C5-C6	54.9 ± 9.5	0.055 ± 0.031
C6-C5d	29.6 ± 4.7	0.335 ± 0.053**
C6-C7d	1.01 ± 0.28	0.224 ± 0.082*
C7-C6	1.49 ± 0.52	0.027 ± 0.135

All values are means ± SEM obtained from simultaneous fitting of scheme I to eight different channels (20°C) at voltages ranging from 20 to 140 mV.

^aRate constants at 0 mV.

^bEffective partial charge for the indicated rate constant.

^cEstimates of the robustness of the estimated parameters were also made for simultaneous fitting of voltage data from single channels. For channel 2, represented in Figs. 1, 3, 5, 8, 9, 11, and 13, the estimated SEM for rate constants O1-C3 through C6-C5 ranged from ∼3 to ∼10% of the value of each rate constant and for C6-C7 and C7-C6 was ∼25%. The estimated SEM for the voltage sensitivities for rates O1-C3 through C6-C5 ranged from ∼2.4 to ∼14% (mean of ∼8%); for rates C3-O1 and C7-C6, it was ∼19%, and for C6-C7 it was 30%.

^dTransitions that have significant partial charges were estimated using a Wilcoxon signed ranks test (*, P < 0.05; **, P < 0.01).

These voltage-dependent changes were generally consistent with analysis obtained by comparing the rate constants estimated from individually fitting scheme I to single-channel data at 40 and 100 mV for each of the eight channels, as shown in Table S1. Both the QuB and 2-D fitting methods gave essentially the same results in terms of the voltage dependence of the various rate constants. The 2-D method identified one additional significant voltage-sensitive rate constant (C5→C6) compared with the QuB method. This difference is a matter of statistical significance rather than substance, as the QuB method indicated a 1.9-fold insignificant increase, whereas the 2-D method indicated a 2.2-fold significant increase.

The significant voltage-dependent changes in rate constants in Table IV are schematically summarized in Fig. 7 B, in which the bold red rate constants are significantly increased with increasing voltage and the shortened green rate constant is significantly decreased (see Table IV for the mean ± SEM of the parameters obtained from the eight channels studied individually). The areas of the circles are proportional to the equilibrium occupancies for the various states (not components) calculated from the fitting (Shelley and Magleby, 2008). The orange arrow in Fig. 7 B indicates the dominant changes in the gating toward the open states when voltage is increased. As this arrow indicates (Fig. 7 B), increasing voltage drives the gating toward the open states, whereas decreasing voltage drives the gating toward the long closed states. In terms of scheme I (Fig. 7 B and Table IV), the voltage-dependent gating of TRPM8 arises because a large number of the rate constants are weakly voltage dependent.

Scheme I describes the voltage dependence of steady-state P_o

To determine whether scheme I could account for the voltage dependence of steady-state estimates of P_o at 20°C, we plotted P_o versus V calculated with scheme I using the experimentally determined rate constants and their partial charge estimates (Fig. 2 B, dashed line). The dashed line in Fig. 2 C, which was calculated with scheme I using the mean parameters in Table IV, gave a steeper dependence at negative potentials but essentially superimposed the data at positive potentials. The effective gating charge calculated by limiting slope from the predicted dashed line was 0.87 e_o compared with the experimental estimate of 0.7 e_o for the mean experimental data and the estimate of 0.89 ± 0.03 e_o obtained by limiting slope for TRPM8 channels by Voets et al. (2007).

The dashed lines in Fig. 2 D plot the mean open and mean closed times predicted with scheme I using the parameters in Table IV. The means are reasonably well described for potentials greater than −50 mV. For more negative potentials, the predicted mean closed times were greater than the observed closed times. It is unclear whether this deviation arises from using parameters in the model that were obtained from fitting data at potentials ≥20 mV and then projecting the gating to negative potentials, or whether the errors arise from problems associated with detecting and correcting for the very brief open intervals that occur at such negative potentials. In any case, it is noteworthy that scheme I can approximate the mean open and closed times over a 200-mV change in membrane potential (−50–150 mV).

Scheme I accounts for the voltage dependence of the single-channel kinetics

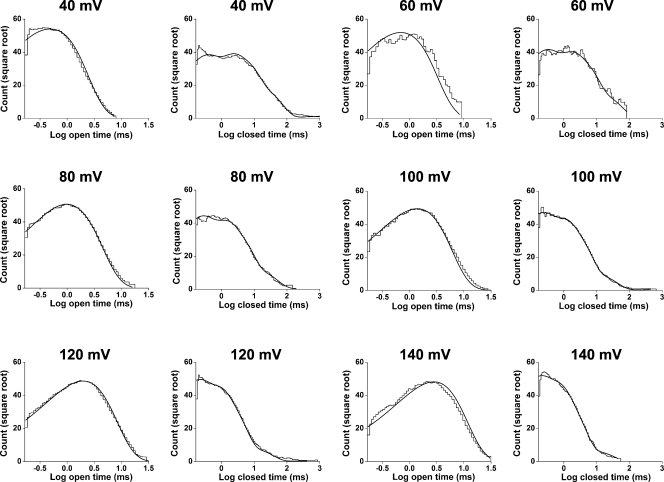
To test whether scheme I with a fixed set of parameters (rate constants and voltage sensitivities as in Table IV) could account for the single-channel data at different voltages and at a fixed temperature of 20°C, the 1-D and 2-D distributions predicted by scheme I were compared with the experimental distributions. An example for the 1-D distributions is shown in Fig. 8, in which the predicted distributions (continuous lines) gave reasonable descriptions of the experimental data over a wide range of voltages. Thus, scheme I with one set of parameters can describe the voltage dependence of the single-channel kinetics by merely changing the voltage used for the calculations.

Figure 8.

Scheme I predicts the voltage dependence of the 1-D distributions at 20°C. 2-D dwell-time distributions obtained at 40, 60, 80, 100, 120, and 140 mV were simultaneously fitted with scheme I to obtain the most likely rate constants and their voltage dependence for this scheme. Scheme I with this single set of parameters was then used to predict the 1-D open and closed dwell-time distributions for each of the indicated voltages. The predicted distributions (solid lines) gave excellent descriptions of the experimental dwell-time histograms. The plots have been normalized to a fixed number of events (70,000) to allow for easier comparison between different voltages, and a moving bin mean has been used to reduce stochastic variation in the histogram. The initial rate constants and voltage sensitivities (in units of elementary charge) were O1-C3 = 7,834 s⁻¹ (−0.334), C3-O1 = 6,140 s⁻¹ (0.105), O2-C4 = 11,054 s⁻¹ (−0.408), C4-O2 = 199 s⁻¹ (0.163), C3-C4 = 1,719 s⁻¹ (0.049), C4-C3 = 265 s⁻¹ (0.288), C4-C5 = 159 s⁻¹ (0.122), C5-C4 = 177 s⁻¹ (0.296), C5-C6 = 46.1 s⁻¹ (0.008), C6-C5 = 51.5 s⁻¹ (0.148), C6-C7 = 0.521 s⁻¹ (0.311), and C7-C6 = 0.609 s⁻¹ (−0.207).

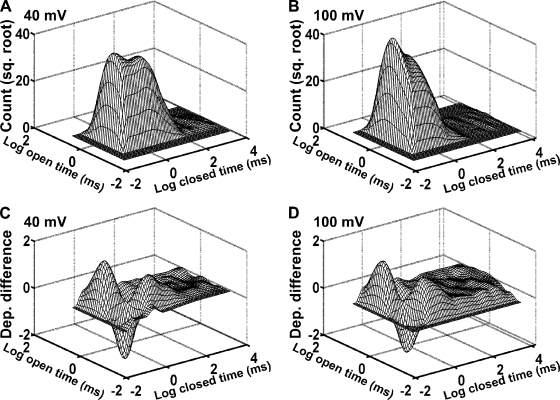
Scheme I was also able to approximate the 2-D dwell-time distributions, as can be seen by comparing the predicted 2-D distributions in Fig. 9 (A and B) with the experimental 2-D distributions in Fig. 5 (A and B). Moreover, scheme I captured the major features of the dependency difference plots (compare Fig. 9 [C and D] with Fig. 5 [C and D]). However, one difference between observed and predicted dependency difference plots is that scheme I predicts too few brief open intervals adjacent to the longest closed intervals and too many brief openings adjacent to brief closed intervals in Fig. 9 C. This difference suggests that there may be a brief open state connected to each of the intermediate (C5), longer (C6), and longest (C7) closed states, leading to a 10-state model.

Figure 9.

Scheme I approximates the 2-D dwell-time distributions and the dependency difference plots for data at 20°C. (A–D) Predicted 2-D dwell-time histograms (A and B) and dependency difference plots (C and D) for scheme I at the indicated voltages. The predicted distributions were obtained by simulating and analyzing one million open and closed intervals from scheme I at each voltage using the parameters shown in the legend of Fig. 8.

Interaction of temperature and voltage in the activation of TRPM8 whole-cell currents

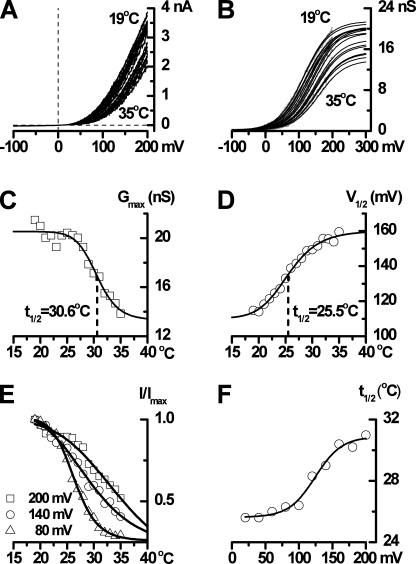
The previous sections developed a kinetic mechanism that could account for the voltage-dependent gating of TRPM8 channels at 20°C. To characterize the combined effect of voltage and cooling on TRPM8 activity, we recorded steady-state I-V relationships by depolarizing TRPM8-expressing HEK293 cells to 200 mV to activate the channel and then by applying slow, negatively sloping voltage ramps to map the I-V relationship at bath temperatures ranging from 35 to 19°C with 1°C steps (Fig. 10 A and Fig. S1). The ramp I-V relationships measured at different temperatures were further analyzed by converting them into conductance curves (G-V; Fig. 10 B, gray traces) and fitting these with the Boltzmann equation (Fig. 10 B, black lines). Cooling over this range induced both an increase in G_max by ∼50% (from 22.6 ± 10.8 to 41.4 ± 7.4 nS, n = 3–10 cells) and a leftward shift of V_1/2 from 147.2 ± 29.6 mV at 35°C to 74.4 ± 14.4 mV at 20°C (n = 3–10 cells). V_1/2 change per 10°C (between ∼30 and 20°C) was 65.8 ± 18.2 mV (n = 9 cells; Fig. 10, C and D). In contrast, the slope factor remained relatively constant. Therefore, the curves were fitted allowing G_max to change with temperature but with a shared best-fit slope, which was, on average, –34.1 ± 1.9 mV (n = 10 cells). Given that the slope factor is RT/zF, where z is the apparent gating charge, a slope of –34.1 mV corresponds to z = 0.74 e_o (at 20°C), in agreement with a q_eff of 0.7 e_o (Fig. 2 C). Fig. S2 demonstrates that free G_max and the shared best-fit slope factor give the best description of the G-V data obtained at different temperatures.

Figure 10.

Effects of voltage and temperature on TRPM8 whole-cell currents. (A) I-V relationships measured using voltage ramps (from 200 to −100 mV during 1 s) for temperatures ranging from 35 to 19°C in 1°C steps. (B) TRPM8 activation curves (gray traces) at different temperatures obtained by dividing current amplitude by driving force at each potential and fitted with the Boltzmann equation (with a best-fit shared slope factor of −38.5 mV) as shown by the superimposed smooth black lines. Cooling increases G_max and shifts activation to the left. (C) Best-fit G_max values decrease with increasing temperature in a sigmoidal manner with a t_1/2 of 30.6°C. (D) V_1/2 increases with increasing temperature in a sigmoidal manner with a t_1/2 of 25.5°C. (E) Normalized current (I/I_max) at 80, 140, and 200 mV plotted against temperature. The ratio of leak-corrected whole-cell TRPM8 currents measured at 20 and 30°C and at 120 mV was 3.90 ± 0.85, with values ranging from 1.57 to 8.76 (n = 10). (F) The temperature for half-maximal activation increases with voltage, with the temperature sensitivity appearing to saturate at lower potentials.

Alternatively, plotting normalized current at different voltages against temperature revealed that the temperature for half-maximal TRPM8 activation (t_1/2) was also voltage dependent, increasing with depolarization (Fig. 10, E and F). These experiments emphasize the notion that the effects of cold and voltage on TRPM8 appear inseparable at the whole-cell current level (Voets et al., 2004, 2007). Indeed, one interpretation is that TRPM8 is a voltage-dependent channel whose activation range and maximum P_o (which correlates to G_max) are temperature dependent (Fig. 10, B–D), but, at the same time, it is also a cold-activated channel whose temperature sensitivity is regulated by voltage (Fig. 10, E and F).

Cooling induces changes in TRPM8 gating similar to those produced by depolarization

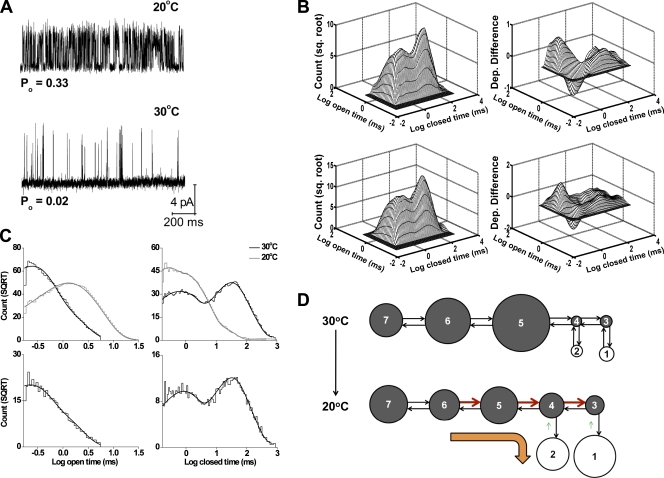
The major effects of temperature on single-channel kinetics are shown in the representative single-channel traces in Fig. 11 A and in the dwell-time distributions in Fig. 11 (B and C, top). Cooling from 30 to 20°C dramatically decreased the durations of the closed intervals and, to a lesser extent, increased the durations of the open intervals, shifting the closed dwell-time distribution to shorter intervals and the open distribution to longer intervals. These shifts increased the frequency of openings (Fig. 11 A) and also increased P_o 9.5-fold from 0.039 ± 0.012 (30°C; n = 17) to 0.37 ± 0.02 (20°C; n = 21) at 100 mV. These effects of cooling are similar to the effects of depolarization shown in Figs. 1 and 3.

Figure 11.

Experimental and predicted kinetic structure of TRPM8 channels at 30°C. (A) Representative single-channel currents recorded at 20 and 30°C (100 mV). Upward steps indicate channel opening. (B) 2-D dwell-time histogram (top left) and dependency difference plot (top right) at 30°C for the same channel analyzed for A. The predicted 2-D dwell-time distribution (bottom left) and dependency difference plot (bottom right) were obtained by simulating and analyzing 100,000 open and closed intervals using scheme I with the parameters in C. (C, top) Open and closed dwell-time histograms at 20°C (gray lines) and 30°C (black lines; 100 mV; 25 bins per decade). The plots have been normalized to a fixed number of events (70,000) to facilitate comparison, and a moving bin mean has been used to reduce stochastic variation in the histogram. (bottom) Scheme I (see below for estimated parameters) describes (continuous lines) the open (left) and closed (right) 1-D dwell-time histograms. The rate constants used to obtain these predicted 1-D and 2-D plots were O1-C3 = 2,467 s⁻¹, C3-O1 = 2,899 s⁻¹, O2-C4 = 6,069 s⁻¹, C4-O2 = 690 s⁻¹, C3-C4 = 1,443 s⁻¹, C4-C3 = 115 s⁻¹, C4-C5 = 663 s⁻¹, C5-C4 = 97 s⁻¹, C5-C6 = 4.16 s⁻¹, C6-C5 = 18.8 s⁻¹, C6-C7 = 0.33 s⁻¹, and C7-C6 = 2.91 s⁻¹. (D) Schematic representation of the change in the rate constants of scheme I with decreasing temperature. The arrows and circles can be interpreted as in Fig. 7 B. The values for these changes are shown in Table S2.

Similar to the data obtained at 20°C, 1-D dwell-time distributions at 30°C were typically described by two significant open and five significant closed exponential components. The cooling-induced changes in the areas and time constants of the exponential components that lead to the increased frequency of openings and P_o are detailed in Table V. Cooling shifted both of the open exponential components to longer durations (Table V, EO1 and EO2), doubled the area of the briefest closed component (Table V, EC1), decreased the area and time constant of the next to longest closed component (Table V, EC4), and decreased the area of the longest closed component (Table V, EC5) to negligible levels.

TABLE V.

Effects of temperature on exponential components

Exp.	30°C		20°C
	τa	Areab	τ	Area
	ms		ms
EC1	0.26 ± 0.02	0.20 ± 0.03	0.23 ± 0.01	0.44 ± 0.02**
EC2	1.11 ± 0.09	0.31 ± 0.03	1.13 ± 0.13	0.37 ± 0.02
EC3	15.6 ± 2.99	0.19 ± 0.04	4.41 ± 1.05**	0.16 ± 0.02
EC4	67.6 ± 17.5	0.25 ± 0.05	19.2 ± 4.12**	0.025 ± 0.006**
EC5	735 ± 223	0.072 ± 0.042	2,428 ± 896*	0.00035 ± 0.00008**
EO1	0.29 ± 0.03	0.77 ± 0.03	0.87 ± 0.08**	0.56 ± 0.04**
EO2	0.77 ± 0.09	0.23 ± 0.03	2.27 ± 0.27**	0.44 ± 0.04**

All values are means ± SEM for two open and five closed exponential components (EO1–EO2 and EC1–EC5, respectively) fitted by the maximum likelihood method to dwell-time histograms from 8 (20°C; as in Table I, reproduced here again to facilitate comparison) and 13 (30°C) single-channel patches at 100 mV. The mean values have been compared using the Mann-Whitney test (*, P < 0.05; **, P < 0.01). These averaged values should not be used to calculate P_o and mean open- and mean closed-time values. Rather, the separate values should be calculated for each channel and then averaged.

^aMean dwell times for each exponential component.

^bRelative areas for each exponential component indicating its contribution to the total number of closed or open events.

Fig. 11 B (top) shows 2-D dwell-time and dependency difference plots for a representative recording at 100 mV and 30°C. The dependency difference plot indicated that there was an excess of long open intervals adjacent to brief closed intervals, an excess of brief open intervals adjacent to longer closed intervals, and a deficit of brief open intervals adjacent to brief closed intervals (Fig. 11 B, top right). Consequently, the major features of the kinetic structure at 30°C are similar to those at 20°C (Fig. 5, C and D). Thus, as also observed with depolarization, cooling changes the relative durations and numbers of the open- and closed-interval pairs without inducing apparent major changes in the underlying kinetic gating mechanism. Furthermore, the observation of the same general dependencies at 100 mV and 30°C (Fig. 11 B, top right) and at 40 mV and 20°C (Fig. 5 C) suggests that membrane depolarization and cold can compensate for one another in the gating without major changes in the underlying gating mechanism.

Scheme I accounts for the voltage dependence of the single-channel kinetics in the regulatory context of temperature

To examine whether scheme I could account for the kinetic changes observed with cooling, scheme I was individually fitted to single-channel data taken from 13 different patches at 30°C and 100 mV. The rate constants for the transitions were estimated, and these values were compared with similar data obtained from eight different patches at 20°C. As shown in Table S2, both the QuB and 2-D fitting methods show that cooling significantly accelerated transitions C6→C5, C5→C4, and C4→C3, driving the gating toward the open states. In addition, two other transitions, O1→C3 and O2→C4, were significantly decreased by the cooling, increasing the time spent in the open states. Fig. 11 D summarizes these changes in a similar fashion to that shown for voltage in Fig. 7 B. Although both cold and voltage changed many of the rate constants within the model (Tables IV, S1, and S2), both activators significantly increased the rate constants between closed states C6→C5 and C5→C4 (Figs. 7 B and 11 D), shifting the distributions toward the open states (Figs. 3, 5, and 11).

To test whether scheme I could account for the single-channel data at 30°C, the 1-D and 2-D distributions predicted by scheme I were compared with the experimental distributions. An example for the 1-D distributions is shown in Fig. 11 C (bottom), where the predicted distributions (continuous lines) gave reasonable descriptions of the experimental dwell-time histograms. Scheme I was also able to approximate the 2-D dwell-time distributions obtained at 30°C, as can be seen by comparing the predicted 2-D distribution in Fig. 11 B (bottom left) with the experimental distribution in Fig. 11 B (top left). Moreover, scheme I captured the major features of the dependency difference plots (Fig. 11 B, compare top with bottom right). Thus, the general gating mechanism described by scheme I can account for the voltage dependence of the gating at both 20 and 30°C.

Scheme I approximates the response to voltage ramps and steps at different temperatures

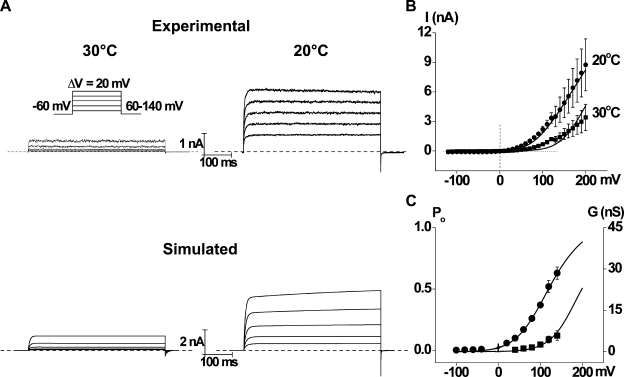
The analysis in the previous sections was based on single-channel currents obtained at constant voltages. To test whether scheme I could also account for the behavior of the whole-cell currents, experimental currents were recorded during voltage steps ranging from 60 to 140 mV (20-mV increments) at 20 and 30°C (Fig. 12 A, top). Predicted whole-cell currents for the same voltage steps were also calculated using the rate constants at 0 mV and their partial charge estimates obtained from simultaneously fitting data at different voltages and at 20°C (Table IV) and 30°C (Table VI) and are plotted in Fig. 12 A (bottom). The predicted whole-cell currents captured the general features of the experimental whole-cell currents, but there are some differences. The kinetics of activation and deactivation at 30°C were predicted to be slower than the experimental values, and there were some differences in predicted and experimental steady-state current levels. The differences in kinetics may arise in large part from statistical error, as estimates of the apparent gating charge at 30°C had much larger SEMs than estimates obtained at 20°C (compare Table IV with Table VI), and simulations showed that the kinetics were highly sensitive to changes in gating charge as small as 1.0 SEM (unpublished data). It should be noted that even whole-cell currents showed some cell-to-cell variability in their kinetics (compare Figs. 12 A [top right] with S1 A). The latter, but not the former, example shows a minor slower component of current activation, which is also present in the simulated data in Fig. 12 A (bottom right).

Figure 12.

Scheme I approximates the experimental whole-cell current traces. (A, top) Whole-cell currents measured from HEK cells expressing TRPM8 (HEK293/TRPM8) channels and evoked by voltage steps from −60 to 60 to 140 mV, with 20-mV increments, at 30°C (left) and 20°C (right). The activation could typically be approximated by a fast and slow exponential, and the deactivation could be approximated by a fast exponential. (bottom) Simulated whole-cell currents using scheme I with the initial rate constants and partial charge estimates in Table VI (left; 30°C) or in Table IV (right; 20°C). The number of channels used for the simulations was 782, derived from the mean whole-cell current of 3.35 nA at 120 mV and 20°C, unitary current of 8.25 pA (Fig. 2 A), and P_o of 0.52 (Fig. 2 B, and C in this figure). The unitary conductance was 95 pS (30°C) or 70 pS (20°C). Both activation and deactivation traces could be approximated by one or two exponentials. The predicted ratio between whole-cell currents at 20 and 30°C and at 120 mV was 5.69 (not significantly different from the value of 3.90 ± 0.85 from Fig. 10 E; P > 0.05). (B) Mean whole-cell currents at 30°C (squares) and 20°C (circles; n = 10) and I-V relationships simulated using scheme I (smooth lines) with parameters as in the simulated currents in A. I-V relationships under very long voltage steps (up to 50 s) were also simulated, giving similar steady-state values (within the experimental SEMs; not depicted). The equilibrium occupancies of the various states at the holding potential of −60 mV (calculated with QuB) were at 20°C: O1 = 0.0032, O2 = 0.0005, C3 = 0.0042, C4 = 0.0413, C5 = 0.155, C6 = 0.559, and C7 = 0.237; and at 30°C: O1 = 0.00004, O2 = 0.0001, C3 = 0.00003, C4 = 0.0037, C5 = 0.0858, C6 = 0.799, and C7 = 0.112. (C) G-V curves simulated using scheme I with parameters as in A and B are consistent with estimates of experimental P_o. After appropriate scaling (to match P_o to conductance), the simulated curves were plotted on the experimental P_o values at 20°C (circles; as in Fig. 2 B) and 30°C (squares; averaged P_o values ranged from 0.005 ± 0.001 [n = 10] at 40 mV to 0.121 ± 0.038 [n = 4] at 140 mV). P_o values were not measured at negative potentials and 30°C because the channel was seldom open. Predicted G_max changed from 46 nS at 20°C to 30 nS at 30°C (within the range measured experimentally; see Results).

TABLE VI.

Rate constants and partial charges for scheme I at 30°C

Transition	K0a	qeffb
	s−1	eo
O1-C3	2,594 ± 399	0.032 ± 0.110
C3-O1	3,519 ± 638	−0.023 ± 0.042
O2-C4	10,239 ± 1,202	−0.064 ± 0.050
C4-O2	775 ± 171	0.231 ± 0.173
C3-C4	596 ± 86	0.291 ± 0.121*
C4-C3	16.9 ± 6.1	0.903 ± 0.265*
C4-C5	866 ± 187	0.099 ± 0.156
C5-C4	74.8 ± 28.8	0.398 ± 0.159
C5-C6	70.6 ± 27.9	0.206 ± 0.235
C6-C5	12.1 ± 3.2	0.410 ± 0.218
C6-C7	0.94 ± 0.43	0.344 ± 0.218
C7-C6	5.13 ± 3.27	0.223 ± 0.213

^aRate constants at 0 mV were estimated from individually fitted rate constants at 40 and 100 mV from 9 and 13 different channels (30°C), respectively (see Materials and methods). The SEM values were estimated from the SEM of the individual experiments.

^bEffective partial charges for the indicated rate constants were obtained from simultaneous fitting of scheme I to eight different channels (30°C) at 40 and 100 mV. The significance was estimated using a Wilcoxon signed ranks test (*, P < 0.05).

Despite this variability, the mean steady-state currents were well described by scheme I at 20°C and approximated by scheme I at 30°C, as can be seen by comparing measured (Fig. 12 B, symbols) and predicted (Fig. 12 B, smooth lines) I-V relationships at 20 and 30°C. The fit at 30°C is less good than at 20°C but typically remains within the SEM of the experimental data. This probably reflects the relative paucity of single-channel data at higher temperatures and also the difficulty in measuring the smaller currents at 30°C for voltages <130 mV. There was also a reasonable correspondence between the simulated G-V curves and measured P_o-V relationships at both temperatures (Fig. 12 C). As was the case in Fig. 2 B, the G-V curves predicted from scheme I with parameters estimated at 20 and 30°C with appropriate scaling to match P_o to conductance reasonably superimpose the experimental P_o values measured at those two temperatures (Fig. 12 C). Scheme I also predicted a leftward shift of V_1/2 between 30 and 20°C of 67.8 mV, which was similar to the measured mean shift of 65.8 ± 18.2 mV. As was observed in Fig. 10, the predicted slope factor remained relatively constant at different temperatures (–30.1 at 30°C and –34.0 at 20°C, with the latter value also similar to the experimental best-fit value of –34.1 ± 1.9 mV).

Scheme I describes the single-channel currents

Fig. 13 (A and B) presents simulated single-channel currents at 20°C for scheme I over a range of voltages for comparison with the experimental single-channel currents in Fig. 1 (A and B). Except for the somewhat less stable baseline for the experimental currents, it would be difficult to distinguish simulated from experimental currents. Furthermore, even the apparent variations in open channel current in the experimental data are reproduced in the simulated data (Fig. 13 B), indicating that these variations may arise, in large part, from filtering of successive brief intervals.

Figure 13.

Scheme I accounts for the single-channel currents over a range of voltages and at two different temperatures. (A and B) Scheme I with the estimated rate constants and noise values for a representative channel at different voltages was used to simulate single-channel currents at the indicated voltages and at 20°C. A comparison of these simulated single-channel currents with the experimental single-channel currents in Fig. 1 (A and B) shows that scheme I accounts for the major features of the single-channel data at 20°C over the range of voltage. The boxed area (A) in the trace at 60 mV indicates a short segment of recording that is amplified in B. (C) Single-channel currents simulated with scheme I account for the major features of the single-channel data at 20 and 30°C (compare with Fig. 11 A).

Finally, Fig. 13 C presents simulated single-channel currents for scheme I at both 20 and 30°C and at 100 mV for comparison with the experimental single-channel currents in Figs. 1 (A and B) and 11 A. The simulated currents at the two different temperatures capture the features of the experimental currents at the same temperatures. Thus, the analysis used in this study is capable of both measuring and describing the single-channel currents from TRPM8 channels, including the fast flickering apparent in the single-channel data.

DISCUSSION

This study examines the kinetic mechanisms underlying activation of TRPM8 channels by membrane depolarization and cold and looks at the interaction between these processes (Brauchi et al., 2004; Voets et al., 2004; Vanden Abeele et al., 2006). Detailed analysis of single-channel data is used to develop a gating model that can account for the kinetics of both single-channel and macroscopic TRPM8 currents. Increased voltage and cooling increase P_o mainly by decreasing closed-interval durations (Figs. 1, 2, and 11), resulting in a dramatic increase in the frequency of channel openings (Figs. 1 and 11). Although there was also an increase in open times, there were no very long openings even at the most positive potentials and cold temperatures, in contrast with the very long closings seen at negative potentials (Fig. 2) and high temperatures (Fig. 11).

A closer look at the underlying kinetic structure of the channel revealed the basis for the increase in P_o with depolarization. Analysis of 1-D and 2-D dwell-time histograms (Figs. 3, 5, and 11 and Tables I and V) showed shifts in the underlying open exponential components toward longer openings and shifts in the closed components toward briefer closings. Dependency plots (Figs. 5 and 11) together with correlation analysis (Fig. 4) indicated that long openings were preferentially adjacent to short closings and long closings were preferentially adjacent to short openings. Similar inverse relationships have been observed for TRPC4 channels (Zholos et al., 2004) and, to some extent, for TRPV1 channels (Liu et al., 2003; Studer and McNaughton, 2010) and suggest there are at least two independent pathways between open and closed states (two gateway states; Colquhoun and Hawkes, 1995). Two independent transition pathways require a model with a minimum of two open and two closed states. However, because at least two open and five closed exponential components were required to describe the open and closed dwell-time distributions (Fig. 3 and Tables I and V), the minimum model at one temperature becomes one with two open and five closed states. The further observation of a third open and a sixth closed component (but with small areas) in some of the datasets suggests that additional open and closed states are likely. These additional states may make more significant contributions to gating in the presence of other activators. For example, we found that chemical activation of TRPM8 by lysophospholipids was associated with prominent long channel openings (Vanden Abeele et al., 2006).

We initially searched for a minimal model with two open and five closed states that was consistent with the voltage dependence of the single-channel kinetics at 20°C before addressing the effects of temperature. Scheme I (Fig. 6) could account for the voltage dependence of P_o and the mean open and closed times (Fig. 2) and also provided reasonable descriptions of the single-channel kinetics and macroscopic current kinetics over a wide range of voltages (Figs. 7–9, 11–13, and S1). In addition, we also tested a two-tiered model with five closed states on the top tier and five open states on the bottom tier, with an independent transition pathway connecting each closed state on the top tier to an open state on the bottom tier. We found that adding three additional open states did increase the LL values for all the channels studied but that there was little improvement in the visual descriptions of the data, and the additional free parameters were often poorly defined (unpublished data). Thus, the five closed and two open–state model appears to be both minimal and sufficient for the analysis presented in this paper. The topology of scheme I and the possible expanded 10-state version of scheme I with three additional open states is not uncommon among voltage-gated ion channels (Marks and Jones, 1992; Weiss and Magleby, 1992; Ríos et al., 1993; Kuo and Bean, 1994; McCormack et al., 1994; Cox et al., 1997; Horrigan and Aldrich, 1999; Jerng et al., 1999; Serrano et al., 1999; Shelley et al., 2010), suggesting that diverse voltage-gated ion channels may have some similarities in the underlying kinetic mechanisms, perhaps through some form of voltage-sensing machinery associated with each channel subunit.

Once scheme I was shown to account for the voltage dependence at 20°C, further analysis was performed on recordings at 30°C showing that the same basic kinetic mechanism was also able to describe the gating at 30°C. Comparison of the rate constants at the two temperatures then identified the rate constants (Fig. 11 D and Table S2) that are changed during physiological activation by cooling. These findings present interesting observations on the relationship between voltage and temperature activation. Most notably, there are only two significant voltage dependencies at 30°C, in the C3↔C4 step (Table VI), whereas these two transitions are not significantly voltage dependent at 20°C (Table IV). This would suggest, on the surface, that temperature can determine which rate constants are voltage dependent. Such interpretation would be consistent with the molecular information provided by Voets et al. (2007), who found that there is some overlap in the TRPM8 residues affected by both voltage and temperature. Consistent with this molecular information, the single-channel gating mechanism of TRPM8 activation by voltage and cold is remarkably similar; i.e., both activators increase P_o mainly by accelerating transitions between closed states, driving the gating toward the open states and increasing the frequency of openings (Figs. 7 B and 11 D). This suggests that both activators may use a common pathway to activate the channel. In fact, if we interpret the seven kinetic states of TRPM8 as correlates of distinct molecular conformations, it becomes plausible that residues in S4 and the S4–S5 linker identified by Voets et al. (2007) may determine common pathways of TRPM8 activation by voltage and cold.

Our whole-cell experiments (Fig. 10) indicated that there are important similarities between the effects of cold and membrane depolarization on TRPM8 activation and that reducing activation by changing one stimulus can be compensated, at least to a large degree, by an increase in the other. In terms of scheme I, in the same way that cold increases the frequency of openings, mimicking to some extent the effects of membrane depolarization, heating does the opposite, driving the gating in the direction opposite to voltage-dependent activation. Scheme I does not incorporate a specific physical (molecular) mechanism to account for temperature dependence but instead was used to obtain estimates of rate constants and voltage sensitivities at two different temperatures. The data were fitted at each temperature by optimizing both rate constants and voltage sensitivities without any constraints that might be imposed by the (unknown at this stage) underlying temperature mechanism. The net result is that the voltage sensitivities of the different rate constants appear to change. However, with a more detailed knowledge of the specific mechanism for temperature dependence, it may be possible to constrain temperature-dependent changes in voltage sensitivities to the same sets of rate constants at the different temperatures.

Alternatively, temperature may well shift the apparent voltage sensitivities of some of the rate constants. Yao et al. (2010) have recently presented data showing that changes in membrane potential can modify the temperature sensitivity of TRPV1 channels in complex ways (e.g., whole-cell currents indicate changes in temperature dependence at different voltages). Other studies have suggested that TRPM8 channels can go through significant conformational rearrangements upon cold activation, possibly as a result of changes in entropy-driven hydrophobic interactions (Brauchi et al., 2004; Zakharian et al., 2010). It is conceivable that such dramatic conformational changes might alter the interaction of S4 with other parts of the voltage-sensing domain or change the coupling between S4 and the gates. Indeed, hydrophobic residues in S4 have been shown to play an important role in the stabilization of S4 in Shaker K⁺ channels (Yang et al., 2007), and conformational rearrangements could alter this stabilization. Such changes might change the kinetic states associated with the movement of S4. Recently, a complex formed by the S4–S5 linker, PIP₂, and the TRP domain has been proposed as an allosteric modulator of TRP vanilloid channels (Latorre et al., 2009). A similar complex might modulate TRPM8 channels, as the C terminus of TRPM8 has also been shown to be involved in temperature detection (Brauchi et al., 2006). Recent studies indeed show that PIP₂ can directly gate TRPM8 through its interaction with positively charged residues in the TRP domain (Liu and Qin, 2005; Rohács et al., 2005). Thermal and voltage stimuli could be integrated at this level, as they all enhance the apparent affinity of TRPM8 channels for PIP₂ (Liu and Qin, 2005; Rohács et al., 2005). Some shared aspects of the activation pathway would explain our observation that voltage and temperature can mimic the action of the other at both the single-channel and macroscopic levels.

Voets et al. (2004) have proposed a two-state (one closed and one open) model to account for the voltage- and temperature-dependent gating of TRPM8 channels. Their two-state model was then expanded to a two-tiered 10-state model to accommodate the effects of menthol on TRPM8 gating (Voets et al., 2007). Voets et al. (2004) suggested that, even though their model could capture macroscopic features of the gating, it was likely to be too simple to be consistent with the single-channel behavior of the channel, as now has been found in our study. Brauchi et al. (2004) and Latorre et al. (2007) have proposed a more complex eight-state model of TRPM8 gating based on whole-cell currents recorded under a variety of activation conditions. Their allosteric model can explain multimodal activation of the TRPM8 channel at the whole-cell level and differs from our scheme I, whose contribution is to account for the single-channel and whole-cell currents over a wide range of voltages for each of two temperatures.

Scheme I for TRPM8 suggests that at least six of the transitions are associated with partial charge movement (have voltage sensitivity), including some opening and closing transitions as well as transitions between adjacent closed states (Fig. 7 B and Table IV). Multiple transitions with voltage dependence might be expected if each subunit has a voltage sensor and at least some voltage sensors can move in a nonconcerted manner before channel opening. The voltage dependence of actual opening and closing transitions could reflect further movement of the voltage sensors, as suggested for big K channels (Horrigan and Aldrich, 1999, 2002), or additional voltage-dependent steps. The voltage dependence of individual transitions is weak, which is consistent with only one arginine in S4 (Latorre et al., 2007; Voets et al., 2007), although the molecular basis of voltage sensitivity is not yet established for TRPM8 channels (Latorre et al., 2009).

When the direction of each voltage-sensitive transition on the apparent total gating charge is taken into account, the sum of the partial charge estimates for the various transitions (Table IV) is greater than the total effective gating charge for the channel (0.7 e_o; Fig. 2 C). This is likely to reflect the fact that analysis of the voltage dependence of P_o (Fig. 2 C) can lead to an underestimate of the effective gating charge (Schoppa et al., 1992; Sigworth, 1994). Interestingly, depolarization appeared to increase one back transition (C6→C7), which would therefore act to slow increases in P_o with depolarization, raising the paradox that one of the voltage-dependent steps may limit progress toward open states. This “backward” voltage dependence was observed for simultaneous fitting (Table IV) but not when the rate constants were determined individually at each voltage (Table S1). Furthermore, because the errors (SEM) associated with estimates of the rate constants and voltage sensitivities for the transitions between the two longest closed states (C6–C7) were ∼25% compared with ∼6–9% for the other transition pathways (probably because of the reduced number of intervals associated with the longest closed states), additional studies will be required to determine whether the backward voltage dependence is characteristic of the gating.

In conclusion, we have (a) identified a minimal gating mechanism for the TRPM8 channel that can account for the voltage dependence of both single-channel kinetics and whole-cell currents at 20 and 30°C and (b) also identified temperature-dependent rate constants responsible for cold activation. Once an expanded model that incorporates a temperature-dependent mechanism is developed, single-channel data obtained over a range of temperature and voltage could be simultaneously fitted to further explore and constrain possible mechanisms. Consequently, our findings must be viewed as only a first step in what will most likely be a long process toward revealing the combined mechanism of temperature and voltage activation at the single-channel level. We have found that the gating is highly complex and have presented models that can account for the single-channel kinetics as a function of voltage at two different temperatures. These models can serve as starting points for further investigations into mechanism and structure–function relations in thermosensitive TRPs, including activation by other stimuli.