Plasma Membrane Surface Potential: Dual Effects upon Ion Uptake and Toxicity

Abstract

Electrical properties of plasma membranes (PMs), partially controlled by the ionic composition of the exposure medium, play significant roles in the distribution of ions at the exterior surface of PMs and in the transport of ions across PMs. The effects of coexisting cations (commonly Al³⁺, Ca²⁺, Mg²⁺, H⁺, and Na⁺) on the uptake and toxicity of these and other ions (such as Cu²⁺, Zn²⁺, Ni²⁺, Cd²⁺, and H₂AsO₄⁻) to plants were studied in terms of the electrical properties of PMs. Increased concentrations of cations or decreased pH in rooting media, whether in solution culture or in soils, reduced the negativity of the electrical potential at the PM exterior surface (ψ₀^o). This reduction decreased the activities of metal cations at the PM surface and increased the activities of anions such as H₂AsO₄⁻. Furthermore, the reduced ψ₀^o negativity increased the surface-to-surface transmembrane potential difference, thus increasing the electrical driving force for cation uptake and decreasing the driving force for anion uptake across PMs. Analysis of measured uptake and toxicity of ions using electrostatic models provides evidence that uptake and toxicity are functions of the dual effects of ψ₀^o (i.e. altered PM surface ion activity and surface-to-surface transmembrane potential difference gradient). This study provides novel insights into the mechanisms of plant-ion interactions and extends current theory to evaluate ion bioavailability and toxicity, indicating its potential utility in risk assessment of metal(loid)s in natural waters and soils.

Some solutes in growth media, such as cations and organic matter, influence the bioavailability and toxicity of metals in natural waters and soils (Peijnenburg et al., 1997; Weng et al., 2004; Kopittke et al., 2010). Novel insights into the bioavailability and toxicity of metals have inspired the development of models in order to allow accurate impact assessments of metals emitted into the environment. The biotic ligand model (BLM; Di Toro et al., 2001), as an extension of the free ion activity model (FIAM), incorporates site-specific competitions among cations (commonly Ca²⁺, Mg²⁺, and H⁺) and ionic toxicants (commonly heavy metals) for binding to a biotic ligand at the cell surface. The scientific and regulatory communities have become interested in the BLM and have incorporated it into regulations. However, the BLM as the main determinant of toxicant bioavailability does not deserve uncritical acceptance, and the mechanism of the ameliorative effectiveness of cations must be considered carefully, especially in light of cation enhancement of anion toxicity (Kinraide, 2006). Previous studies (Kinraide, 2006; Wang et al., 2008) showed that global electrostatic interactions at the plasma membrane (PM) exterior surfaces, rather than site-specific mechanisms, may play the dominant role in the phytotoxicity of metals.

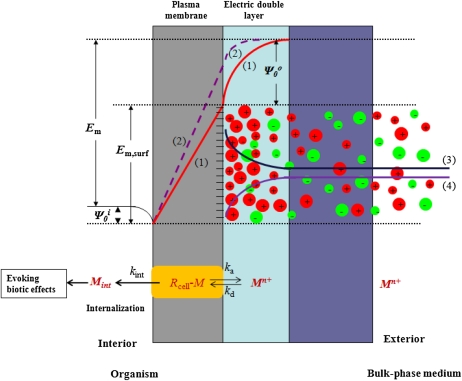
The process of metal uptake typically encompasses diffusion of the ion to the cell surface, speciation reactions, electrostatic interactions, and subsequent transport across PMs (Hille, 2001; Kinraide, 2001). The PM electrical properties play key roles in the distribution of ions at the exterior surface of PMs, in ion transport across PMs, and, hence, in ion intoxication. Three global electrical features of PMs have been recognized (Fig. 1, top; Kinraide, 2001). The first includes the negative electrical potentials at the PM exterior and interior surfaces (ψ₀^o and ψ₀ⁱ, respectively). The second is the electrical potential difference through the PM from surface to surface (E_m,surf). The last is the transmembrane electrical potential (E_m) from bulk medium to cell interior. E_m is composed of three potential differences (E_m = E_m,surf + ψ₀^o − ψ₀ⁱ) and can be measured comparatively easily by the insertion of microelectrodes into cells (Nobel, 1991). The cell wall appears to have comparatively little influence on ψ₀^o and ion concentrations at the PM surface (Gage et al., 1985; Shomer et al., 2003; Kinraide, 2004). Hence, ψ₀^o is controlled by the composition of the soil solution and little, or not at all, by soil solid matter lying external to the cell walls, except as that solid matter influences the soil solution.

Figure 1.

Top, Profile of the electrical potentials and ion distributions at the PM. Bottom, Conceptualized ion (Mⁿ⁺) transport across the PM, including dissociation/association with the active binding site (R_cell; e.g. transporter, ion channel) on the surface of the PM. Lines 1 and 2 illustrate the potential profile through the PM and electric double layer before (line 1) and after (line 2) the addition of depolarizing solutes to the bulk-phase medium. ψ₀^o is the potential difference between the bulk-phase medium and the external PM surface. E_m is the transmembrane potential difference from the bulk-phase medium to the cell interior. E_m,surf is the potential difference through the PM from surface to surface for line 1 (E_m,surf is not shown for line 2). The cell wall has been omitted for simplicity. Lines 3 (cations) and 4 (anions) represent the profile of activities from the bulk solutions to the PM exterior surface. k_a, k_d, and k_int are the association, dissociation, and internalization rate constants, respectively.

Both ψ₀^o and E_m,surf are physiologically important, because electrical potential gradients influence the distribution and transport and, hence, the biotic effects of ions. The ψ₀^o is often sufficiently negative to concentrate cations and deplete anions at the PM surface by more than 10-fold relative to the bulk-phase medium. The ionic composition of the bulk-phase medium influences ψ₀^o, and cations, commonly Al³⁺, Ca²⁺, Mg²⁺, Na⁺, and H⁺, reduce the negativity of ψ₀^o by charge screening and ion binding. Values for ψ₀^o in soil-grown plants range widely because of large variations in soil solution concentrations of cations (Wolt, 1994; Kinraide, 2003b).

E_m,surf influences ion channel gating and the driving force for ion fluxes across the PM (Hille, 2001; Kinraide, 2001). A consideration of physiological effects (such as ion uptake and intoxication) upon roots only in terms of activities in the bulk-phase medium can be misleading. The common neglect of ψ₀^o is inconsistent with its importance and may reflect the difficulty of measuring ψ₀^o. Nevertheless, several studies have considered physiological phenomena in terms of ψ₀^o (Barber, 1980; McLaughlin, 1989; Zhang et al., 2001; Kinraide, 2003a, 2006; Yermiyahu and Kinraide, 2005; Wang et al., 2008; Kinraide and Wang, 2010; Kopittke et al., 2010), and a fully parameterized Gouy-Chapman-Stern (GCS) model is now available for calculating ψ₀^o (Wang et al., 2008; Kinraide and Wang, 2010).

The aims of this study were (1) to emphasize the importance of the PM electrical properties for the transport and toxicity of ions while developing electrostatic models for uptake and toxicity, (2) to determine possible multiple effects of ψ₀^o upon ion uptake and toxicity, and (3) to apply electrostatic models, incorporating membrane surface-to-surface activities and electrical gradients, to predict the uptake and toxicity of metal ions for use in risk assessment in natural waters and soils.

THEORY

Calculation of ψ₀^o and Ion Activities at the PM Exterior Surface

The GCS model combines electrostatic theory (Gouy-Chapman theory) with ion binding (Stern model) so that ψ₀^o can be computed (Tatulian, 1999; Yermiyahu and Kinraide, 2005; Kinraide and Wang, 2010). For a clear introduction to electrostatic theory presented without the restraints upon space required here, we recommend the book chapter by Yermiyahu and Kinraide (2005), and we recommend Barber (1980) and Tatulian (1999) for clear, more in-depth theoretical treatments. This model incorporates the intrinsic surface charge density (σ₀) of a membrane, the ion composition of the bulk-phase medium, and ion binding to the membrane. A detailed analysis (Kinraide and Wang, 2010) indicates the suitability of σ₀ = –30 mC m⁻² while also noting small variability among membranes. A computer program for the GCS model may be obtained from the authors. Knowledge of ψ₀^o enables the calculation of ion activities at the PM exterior surface. The activity of ion I^Z at the PM exterior surface ({I^Z}₀^o) is computed from the activity of I ^Z in the bulk-phase medium ({I^Z}_b) according to the Nernst equation {I^Z}₀^o = {I^Z}_b exp[–ZFψ₀^o/(RT)], where Z is the charge on ion I, F is the Faraday constant, R is the gas constant, and T is temperature. F/(RT) = 25.7 when ψ₀^o is expressed in mV and T = 25°C.

Development of Electrostatic Models of Ion Uptake and Toxicity

Electrostatic Uptake Model

To evoke a biotic effect (e.g. transport, toxicity, alleviation of toxicity, enzyme activity), a metal ion must first react with physiologically active sites, R_cell (e.g. transporter, ion channel, enzyme), on the PM surface, often but not necessarily followed by uptake (Fig. 1, bottom).

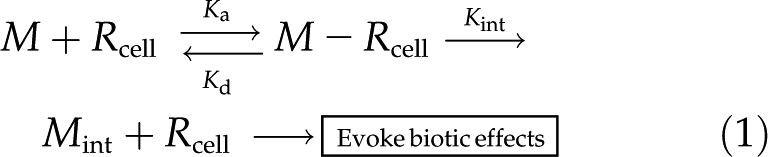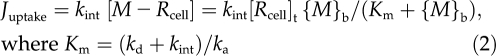where J_uptake is the ion influx, M_int represents the metal taken up with concurrent recycling of R_cell, {M}_b is the activity of metal in the bulk-phase medium, [M − R_cell] is the surface density (mol m⁻²) of metal bound to R_cell (all charges omitted for simplicity), and [R_cell]_t is the metal-binding capacity of R_cell; k_a, k_d, and k_int are the association, dissociation, and uptake rate constants. The conditional stability constant K_m-Rcell for the binding of the metal to R_cell at the external PM surface can be denoted as K_m-Rcell (= k_a/k_d). In most cases, k_int << k_d, so that K_m ≈ k_d/k_a = 1/K_m-Rcell. Equation 2 resembles the Michaelis-Menten equation that is often used to describe steady-state uptake in models such as the FIAM. However, other uptake models, expressing saturation by substrate, have been proposed (Hille, 2001; Kinraide, 2001), and other models may be equally suitable for our analyses (see Eq. 9 below). Specifically, the precise nature of the M − R_cell complex is not essential. M − R_cell may also be envisioned as restricted flow through a channel rather than an actual metal-ligand binding. The important feature of our analysis is the impact of ψ₀^o upon k_int, as developed next.

Commonly, metal ion transport across PMs is expressed in terms of k_int and its activity in the bulk-phase medium ({M}_b), rather than the activity at the PM exterior surface ({M}₀^o), but root responses to ions often correlate poorly with {M}_b and often correlate well with {M}₀^o (Zhang et al., 2001; Yermiyahu and Kinraide, 2005; Wang et al., 2008; Kinraide and Wang, 2010; Kopittke et al., 2010). Furthermore, the k_int is influenced by the electrical driving force on the ion (i.e. E_m,surf). Therefore, the objective of this study was to ascertain the dual effects of changes in ψ₀^o (changes in PM surface activity of ions and changes in E_m,surf), independent of changes in E_m, upon ion uptake and intoxication. To do so, Equation 2 was modified.

Initially, Equation 2 was modified to take into account the effect of ψ₀^o on the enrichment of cations and depletion of anions at the PM surface. This was accomplished by replacing {M}_b with {M}₀^o.

The internalization constant k_int resembles in some ways P_jZFE_m,surf/(RT) in a modified Goldman-Hodgkin-Katz flux equation (Kinraide, 2001), where P_j is a permeability coefficient. Thus, k_int is proportional to E_m,surf, which may be computed from E_m,surf = E_m − ψ₀^o + ψ₀ⁱ. E_m remained essentially constant under the conditions of our experiments, or changes were small or transient (Llamas et al., 2000; Kinraide, 2001). ψ₀ⁱ was small (≈–10 mV), and changes were small relative to changes in ψ₀^o because of high [Mg²⁺], high ionic strength, and constant pH in the cytoplasm (Marschner, 1995). Therefore, E_m,surf = A − ψ₀^o, where A is a constant equal to E_m + ψ₀ⁱ. Uptake, therefore, was driven by both the PM surface activity of ions and ψ₀^o, the latter as a surrogate for E_m,surf. Accordingly, Equation 3 was modified, yielding the electrostatic uptake model (EUM):

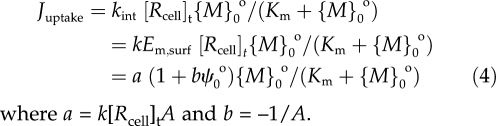where a = k[R_cell]_tA and b = –1/A.

Electrostatic Toxicity Model

When growth responds to measures of toxicant intensity, the resulting curves are often downwardly sigmoidal and can be expressed in the following equation where growth is limited by {M}_b and is expressed as relative root elongation (RRE; as percentage of nonintoxicated growth):

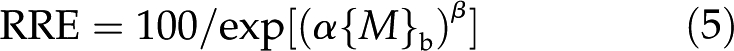where α is a strength coefficient that increases with the strength of the metal toxicity and β is a shape coefficient that confers sigmoidality when its value is greater than 1. Using {M}₀^o rather than {M}_b takes into account the effect of ψ₀^o on the enrichment of cations and depletion of anions. Thus, Equation 5 becomes

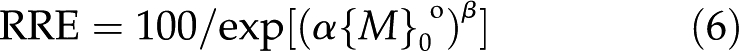This versatile equation adequately represents dose responses to most toxicants (see figure 8 in Yermiyahu and Kinraide, 2005). The electrical component of the driving force may be incorporated into Equation 6 by expanding the coefficient α to include ψ₀^o, yielding the electrostatic toxicity model (ETM):

Equations 4 and 7 now incorporate the dual effects of ψ₀^o on ion uptake and toxicity, namely, the effects upon the enrichment of cations or depletion of anions at the PM surface and upon the driving force across the PM. It is noteworthy that sometimes large differences in uptake and tolerance are observed among plant species. The differences in the α and β coefficients for Equations 4 and 7 may denote differences in uptake and sensitivity. In the case of cationic uptake and toxicity, we would expect coefficient b to have a positive value so that increasing values of ψ₀^o (i.e. decreasing negativity of ψ₀^o, resulting in increasing negativity of E_m,surf) will increase k_int, causing J_uptake to increase and RRE to decrease. In the case of anions, we would expect a negative value for b. All coefficients in Equations 2 through 7 were evaluated by regression analysis so that r² and the statistical significance of the coefficients could be evaluated. No coefficients are reported whose 95% confidence intervals encompassed 0.

RESULTS AND DISCUSSION

Effects of Coexistent Cations on Electrical Potentials and the Uptake and Toxicity of Copper

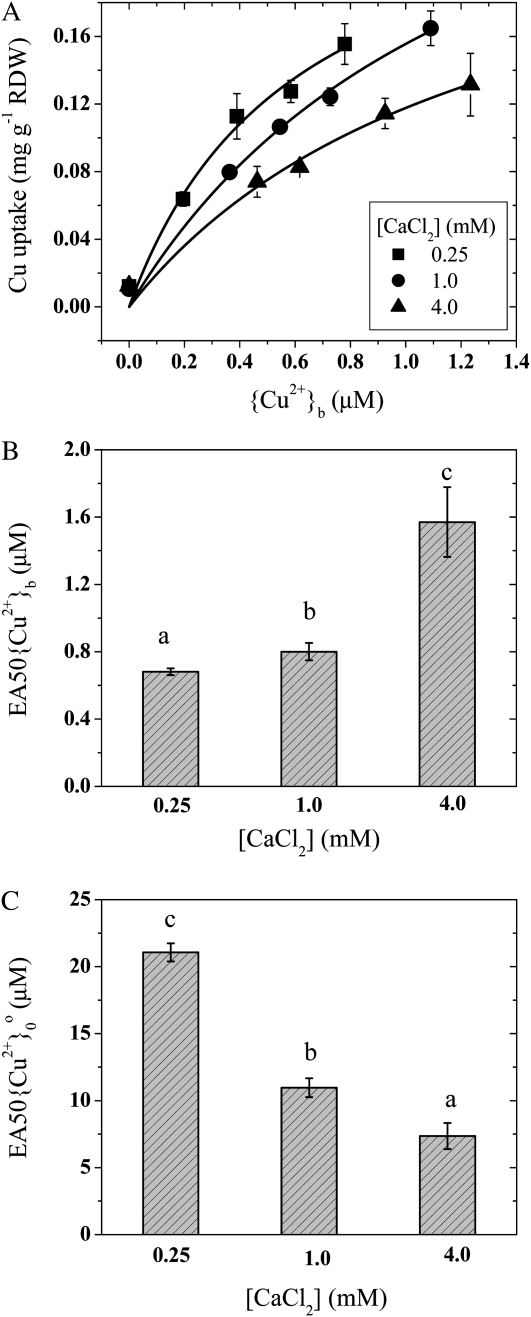
As expected, increases in Ca²⁺, Mg²⁺, or H⁺ reduced Cu²⁺ uptake and toxicity (experiments 3 and 11, Table I). Increases in Ca²⁺ concentrations from 0.25 to 4.0 mm significantly decreased the 48-h uptake of Cu²⁺ by wheat (Triticum aestivum ‘Yangmai 14’) roots (Fig. 2A). In addition, the 48-h EA50{Cu²⁺}_b (i.e. the activity of Cu²⁺ in the bulk-phase medium causing a 50% reduction in growth in 48 h) increased from 0.68 to 1.6 μm (Fig. 2B). Similar results were observed with increasing {Mg²⁺}_b and decreasing pH (data not shown). To elucidate ψ₀^o effects, we computed the 48-h EA50{Cu²⁺}₀^o (i.e. the activity of Cu²⁺ at the external surface of the PM causing a 50% reduction). These values for 48-h EA50{Cu²⁺}₀^o reflect the intrinsic sensitivity of roots to metals, but note that a decrease in EA50{Cu²⁺}₀^o reflects an increase in sensitivity. Interestingly, the intrinsic sensitivity of Cu²⁺ was increased significantly with increasing Ca²⁺, with the 48-h EA50{Cu²⁺}₀^o decreasing from 21.1 to 7.4 μm (Fig. 2C). This was consistent with our previous studies that also demonstrated that the extrinsic sensitivity to Cu²⁺ (sensitivity to {Cu²⁺}_b) decreased as ψ₀^o became less negative and that the intrinsic sensitivity to Cu²⁺ (sensitivity to {Cu²⁺}₀^o) increased (see figure 7A in Wang et al., 2008), but those effects were not explained. Reanalysis of previous studies demonstrates that decreased ψ₀^o negativity enhances the intrinsic toxicity of Cu²⁺ (Lock et al., 2007a), Co²⁺ (Lock et al., 2007b), and Ni²⁺ (Lock et al., 2007c) to barley (Hordeum vulgare).

Table I. Overview of studies used to examine ion uptake and toxicity.

For each study, the pH, total concentration of ions ([I]_t), and the calculated ψ₀^o are reported. The ψ₀^o was calculated for each medium with the standard GCS model.

Species and Source	Experiment No.	pH	[Al]t or [La]t	[CaCl2]t	[Mg]t or [Sr]t	[NaCl]t	ψ0o
			μm	mm	mm	mm	mV
Ca2+ influx into PM vesicles of wheat roots (Huang et al., 1994)	1	7.0	[AlCl3] 0–20	0.01–5.0	[MgCl2] 0–0.5 [SrCl2] 0–0.5		–87.6 to –18.9
Ca2+ influx into PM vesicles of wheat roots (Huang et al., 1996)	2	4.5	[LaCl3] 0–20	0.01–3.0			–34.7 to –5.49
Cu2+ uptake by wheat seedlings (this study)	3	5.1–6.0		0.25–3.8	[MgCl2] 0.26–4.0	1.0	–44.4 to –19.3
Zn2+ uptake by pea seedlings (Wu, 2007)	4	4.3–6.0		0.19–1.8			–57.1 to –14.9
Ca2+ uptake by wheat roots (Davenport et al., 1997)	5	6.5		0–3.1		5.0–150	–86.4 to –6.6
Na+ uptake by wheat roots (Davenport et al., 1997)	6	6.5		0.08–11		5.0–150	–61.4 to –6.6
Cd2+ uptake by pea seedlings (Wu, 2007)	7	4.0–6.0		0.04–1.6			–76.0 to –8.7
Ni2+ uptake by pea seedlings (Wu, 2007)	8	4.0–6.0		0.04–1.8			–76.0 to –8.2
Cu2+ uptake by pea seedlings (Wu, 2007)	9	4.0–6.0		0.04–1.9			–75.9 to –8.3
H2AsO4− uptake by wheat seedlings (this study)	10	4.4–6.0		0.24–4.1	[MgCl2] 0.26–3.7	0.91	–43.8 to –19.1
Cu2+ rhizotoxicity to wheat seedlings (this study)	11	5.1–6.0		0.25–3.8	[MgCl2] 0.26–4.0	1.0	–44.4 to –19.3
Cu2+ rhizotoxicity to wheat seedlings (Parker et al., 1998)	12	4.5–6.0		0.20–4.0	[MgCl2] 0–4.7		–56.6 to –12.7
Cu2+ rhizotoxicity to wheat seedlings (Kinraide, 2006)	13	4.5–5.7		0.50–8.0		0 - 10	–33.4 to –8.7
Al3+ rhizotoxicity to wheat seedlings (Tyler wheat, archived data)	14	4.3	[AlCl3] 0–20	0.40–4.0	[MgCl2] 0–3.6		–25.3 to 0.8
H2AsO4− rhizotoxicity by wheat seedlings (this study)	15	4.5–6.0		0.27–4.3	[MgCl2] 0.26–4.0	0.53–20	–44.1 to –19.1

Figure 2.

Uptake and toxicity in response to Cu²⁺ and Ca²⁺ in wheat seedlings, showing the uptake of Cu²⁺ as a function of {Cu²⁺}_b at different [CaCl₂] (A), the effect of Ca²⁺ on EA50{Cu²⁺}_b (B), and the effect of Ca²⁺ on EA50{Cu²⁺}₀ (C). Error bars indicate 95% confidence intervals. Different letters indicate significant differences among means (P < 0.01). Data are from experiments 3 and 11. RDW, Root dry weight.

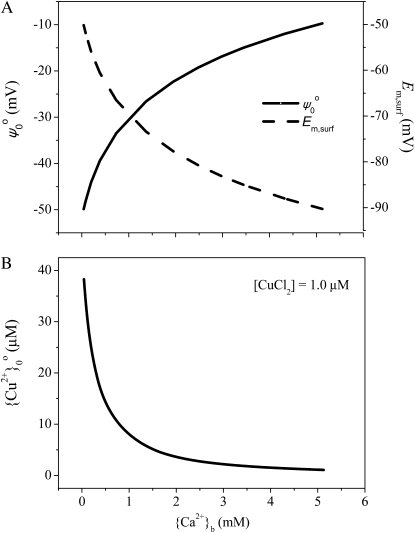
We propose that this increase in intrinsic sensitivity caused by reductions in ψ₀^o negativity results from increases in the E_m,surf negativity; this would increase the electrical driving force for cationic influxes (Fig. 3). Changes in ψ₀^o have little impact on E_m (Llamas et al., 2000; Hille, 2001; Kinraide, 2001), in contrast to effects upon E_m,surf. Consequently, changes in ψ₀^o are offset almost entirely by changes in E_m,surf (compare solid and dashed lines in Fig. 3, where E_m,surf = E_m − ψ₀^o + ψ₀ⁱ). Thus, the decreased negativity of ψ₀^o resulted in reduced attraction of Cu²⁺ to the PM surface (the {Cu²⁺}₀^o decreased from 38.3 to 1.1 μm; Fig. 3B), and hence a decreased extrinsic sensitivity, but the decreased negativity of ψ₀^o caused an increase in the negativity of E_m,surf, and hence an increased intrinsic sensitivity.

Figure 3.

Predicted electrical potential and PM surface activity of Cu²⁺ in response to Ca²⁺ activity in the bulk-phase medium. A, The ψ₀^o and E_m,surf. B, The calculated PM surface activity of Cu²⁺ at 1.0 μm CuCl₂. Data are from experiments 3 and 11.

Modeling Ion Uptake and Toxicity with Electrostatic Models (EUM and ETM)

Cu²⁺ Uptake and Toxicity Affected by Ca²⁺, Mg²⁺, or pH

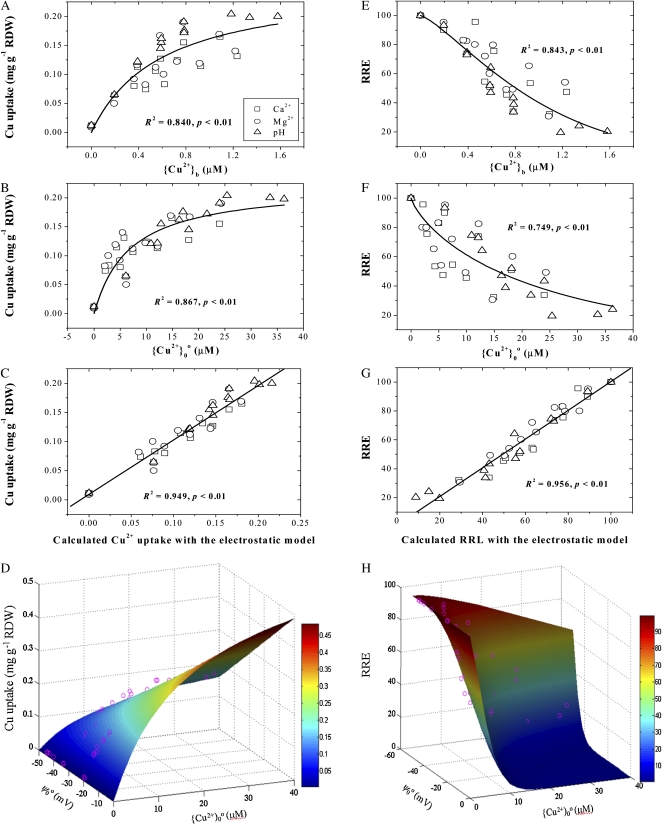
Figure 4 illustrates Cu²⁺ uptake and toxicity as functions of {Cu²⁺}_b (Fig. 4, A and E), {Cu²⁺}₀^o (Fig. 4, B and F), and calculated Cu²⁺ uptake and toxicity based on the EUM (Eq. 4) and ETM (Eq. 7; Fig. 4, C and G). The Cu²⁺ uptake corresponds to the calculated Cu²⁺ uptake (r² = 0.949; Fig. 4C) more closely than to {Cu²⁺}₀^o (r² = 0.867; Fig. 4B) or {Cu²⁺}_b (r² = 0.840; Fig. 4A). For toxicity, RRE correlates better with calculated RRE (r² = 0.956; Fig. 4G) than with {Cu²⁺}₀^o (r² = 0.794; Fig. 4E) or {Cu²⁺}_b (r² = 0.843; Fig. 4F). Also, Figure 4 illustrates the uptake (Fig. 4D) and the RRE (Fig. 4H) as functions of ψ₀^o and {Cu²⁺}₀^o. The curved surfaces are based on the electrostatic uptake and toxicity models using the parameters in Tables II and III (experiments 3 and 11).

Figure 4.

Uptake (left column) and RRE (right column) of Cu²⁺ by wheat roots as functions of {Cu²⁺}_b (first row), {Cu²⁺}₀^o (second row), and Cu²⁺ uptake or RRE calculated from electrostatic models (third row). Uptake and RRE as functions of ψ₀^o and Cu²⁺ surface activity are shown in the bottom row. In D and H, the curved surfaces denote uptake or RRE calculated from the electrostatic models, while the pink circles represent the measured values. Data are from experiments 3 and 11. RDW, Root dry weight.

Table II. Comparison of three models for ion uptake.

For the FIAM, uptake is expressed in terms of the activity in the bulk-phase rooting medium according to the equation J_int = a {M}_b/(K_m + {M}_b). For the SIAM, uptake is expressed in terms of the activity at the PM exterior surface according to the equation J_int = a {M}₀^o/(K_m + {M}₀^o). For the EUM, uptake is expressed in terms of the PM surface activity and electrical potentials (ψ₀^o) according to the equation J_int = a (1 + b ψ₀^o){M}₀^o/(K_m + {M}₀^o). {M} refers to one of the ions below; a, K_m, and b are coefficients (a resembles in some ways the J_max in the Michaelis-Menten equation); and n is the number of data points. All of the presented values for coefficients are statistically significant (95% confidence intervals do not encompass 0). All units of {M} and J_int were those used in the references. For experiments 1 and 2, J_int was expressed in nmol mg⁻¹ min⁻¹; for experiments 3, 4, and 7 to 9, J_int was expressed in mg g⁻¹ root dry weight; for experiments 5 and 6, J_int was expressed in μmol g⁻¹ root fresh weight h⁻¹. All activities are expressed in μm except for experiment 6, in which Na⁺ activities are expressed in mm.

Ion	Experiment No.	A	Km	b	n	r2
FIAM
Ca2+	1 and 2	9.72	102.40		78	0.458
Cu2+	3	0.258	10−0.22		45	0.840
Zn2+	4	0.023			54	0.821
Ca2+	5	0.011			20	0.493
Na+	6	0.113			32	0.825
Cu2+	7	0.192			54	0.685
Cd2+	8	0.154			45	0.660
Ni2+	9	0.088			54	0.626
SIAM
Ca2+	1 and 2	8.54	103.74		78	0.775
Cu2+	3	0.223	100.84		45	0.867
Zn2+	4	6.28	103.35		54	0.851
Ca2+	5	0.0027			20	0.767
Na+	6	0.0580			32	0.846
Cu2+	7	0.0059			54	0.830
Cd2+	8	0.0047			45	0.830
Ni2+	9	0.0019			54	0.834
EUM
Ca2+	1 and 2	70.9	104.54	0.0112	78	0.938
Cu2+	3	0.676	101.19	0.0136	45	0.949
Zn2+	4	56.7	104.06	0.0157	54	0.967
Ca2+	5	0.0043		0.0135	20	0.908
Na+	6	0.0776		0.0125	32	0.901
Cu2+	7	0.0186		0.0130	54	0.938
Cd2+	8	0.0104		0.0104	45	0.890
Ni2+	9	0.0076		0.0120	54	0.906

Table III. Comparison of three models for ion toxicity.

For the FIAM, toxicity is expressed in terms of the activity in the bulk-phase rooting medium according to the equation RRE = 100/exp[(α{M}_b)^β]. For the SIAM, toxicity is expressed in terms of the activity at the PM exterior surface according to the equation RRE = 100/exp[(α{M}₀^o)^β]. For the ETM, toxicity is expressed in terms of the PM surface activity and electrical potentials (ψ₀^o) according to the equation RRE = 100/exp{[α(1 + bψ₀^o){M}₀^o]^β}. {M} refers to one of the ions below; α, β, and b are coefficients: α is a strength coefficient and β is a shape coefficient. All of the presented values for coefficients are statistically significant (95% confidence intervals do not encompass 0). All activities are expressed in μm.

Ion	Experiment No.	α	β	b	n	r2
FIAM
Cu2+	11	0.933	1.29		45	0.843
Cu2+	12	1.69	0.901		51	0.745
Cu2+	13	1.72	2.32		36	0.654
Al3+	14	0.227	1.21		50	0.660
H2AsO4−	15	0.456	1.95		100	0.903
SIAM
Cu2+	11	0.040	0.781		45	0.749
Cu2+	12	0.122	0.639		51	0.878
Cu2+	13	0.312	1.88		36	0.835
Al3+	14	0.143	3.26		50	0.919
H2AsO4−	15	1.82	1.57		100	0.919
ETM
Cu2+	11	0.210	1.43	0.0187	45	0.956
Cu2+	12	0.281	0.908	0.0143	51	0.921
Cu2+	13	0.552	2.36	0.0186	36	0.889
Al3+	14	0.155	3.63	0.0164	50	0.949
H2AsO4−	15	0.628	1.94	−0.0607	100	0.937

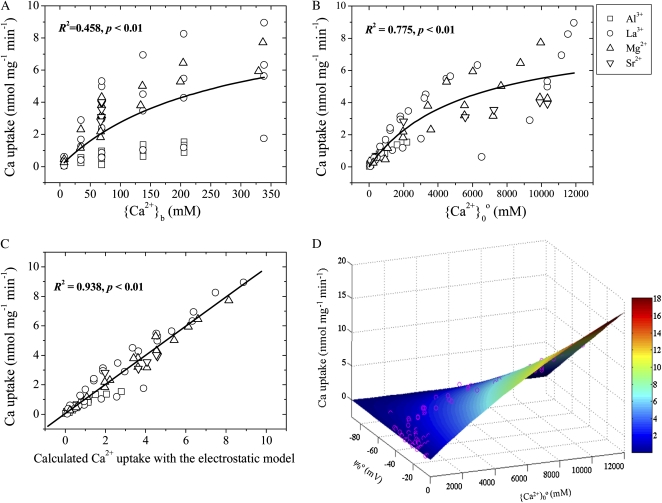
Ca²⁺ Uptake Affected by Al³⁺, La³⁺, Mg²⁺, or Sr²⁺

Huang et al. (1994, 1996) measured radiotracer Ca²⁺ influx into right-side-out PM vesicles from wheat roots (cv Scout 66) in response to variable external Ca²⁺, Al³⁺, La³⁺, Mg²⁺, Sr²⁺, and pH. E_m was controlled by the adjustment of internal and external K⁺, which, with valinomycin, clamped E_m at –100 mV. Their data demonstrate the well-known inhibitory effect of Al³⁺, La³⁺, Mg²⁺, and Sr²⁺ on short-term (5-min) Ca²⁺ uptake, which is commonly attributed to blockade or competition at a Ca²⁺ channel. However, we question whether the inhibition occurs as a consequence of channel blockade (or competition) or as a consequence of electrostatic reduction of {Ca²⁺}₀^o. An analysis of published patch-clamp studies (Kinraide, 2001) revealed that inhibition of Ca²⁺ uptake usually entails reduced unitary channel conductance rather than a reduced probability of channel openness (i.e. true blockade).

In order to investigate the possible dual effects of ψ₀^o, measured Ca²⁺ uptake was plotted against {Ca²⁺}_b and {Ca²⁺}₀^o and against calculated Ca²⁺ uptake based on the EUM (Eq. 4). Figure 5 indicates that Ca²⁺ uptake corresponds to this calculated Ca²⁺ uptake (r² = 0.938) more closely than to {Ca²⁺}₀^o (r² = 0.775) or to {Ca²⁺}_b (r² = 0.458; Table II). Figure 5D illustrates that the Ca²⁺ uptake depended on ψ₀^o and {Ca²⁺}₀^o, indicating that the effects of Al³⁺, La³⁺, Mg²⁺, and Sr²⁺ on Ca²⁺ uptake may be attributable to the dual effects of ψ₀^o rather than to a channel blockade or competition. The curved surface (Fig. 5D) is based on the EUM with the parameter values in Table II (experiments 1 and 2).

Figure 5.

Measured Ca²⁺ uptake plotted against {Ca²⁺}_b (A), {Ca²⁺}₀^o (B), or Ca²⁺ uptake calculated from the EUM (Eq. 4; C) or as a function of ψ₀^o and {Ca²⁺}₀^o (D). In D, the curved surface denotes uptake calculated with the EUM, while the pink circles represent the measured uptake. Data are from Huang et al. (1994, 1996; experiments 1 and 2), who measured Ca²⁺ influx into PM vesicles from wheat roots in a basal medium of 0.1 mm NaCl and 1.0 mm K₂SO₄ at pH 7.0 (for La³⁺, Mg²⁺, and Sr²⁺) or pH 4.5 (for Al³⁺). The E_m in all solutions was clamped at a constant –100 mV.

Na⁺ Uptake Affected by Ca²⁺ and Ca²⁺ Uptake Affected by Na⁺

Davenport et al. (1997) measured short-term (20-min) and long-term (7-d) Na⁺ unidirectional uptake into roots of two species of wheat (T. aestivum ‘Kharchia’ and Triticum turgidum ‘Modoc’) cultured in variable concentrations of NaCl and {Ca²⁺}_b. It is clear from their Figures 3, 4, and 5 that Ca²⁺ effectively inhibited Na⁺ uptake and vice versa. It was assumed that Na⁺ uptake occurred passively via Ca²⁺ channels and that the decreased Na⁺ uptake was attributable to Ca²⁺ binding to a specific site on such channels, thereby altering the gating and selectivity of the channels. However, correlation between measured and calculated uptake for both Na⁺ and Ca²⁺ was superior when using the EUM (Eq. 4; Table II, experiments 5 and 6). These results indicate that cation effects may be attributed to the dual effects of ψ₀^o rather than to specific blocking effects.

Zn²⁺, Cu²⁺, Cd²⁺, and Ni²⁺ Uptake Affected by Ca²⁺ or pH

In a study with pea (Pisum sativum ‘Lincoln’), Wu (2007) measured changes in the uptake of Zn²⁺, Cu²⁺, Ni²⁺, and Cd²⁺ in response to added Ca²⁺ and H⁺. In nearly all cases, increases in Ca²⁺ or decreases in pH reduced metal uptake. That study measured some characteristics of pea roots and considered theoretical aspects of the FIAM and the BLM. For our reanalysis, uptake data were taken from the author’s tables. For the Zn²⁺ uptake experiments, increases in Ca²⁺ concentration or decreases in pH resulted in decreases in the negativity of ψ₀^o and reductions in Zn²⁺ uptake (data not shown). The measured Zn²⁺ uptake was better correlated with the Zn²⁺ uptake calculated by the EUM (r² = 0.967) than with {Zn²⁺}₀^o (r² = 0.851) or {Zn²⁺}_b (r² = 0.821; Table II, experiment 4). Similar results were observed for Cu²⁺, Ni²⁺, or Cd²⁺ uptake (Table II, experiments 7–9).

Cu²⁺ Toxicity Affected by Ca²⁺, Mg²⁺, Na⁺, or pH

Parker et al. (1998) investigated Cu²⁺ rhizotoxicity to roots of wheat (cv Yecora Rojo) in response to variable concentrations of CuCl₂, CaCl₂, MgCl₂, and pH in a factorial array. Increases in Ca²⁺, Mg²⁺, or H⁺ alleviated Cu²⁺ stress. For our reanalysis, data were taken from their Figures 2 to 5 and Tables I and II. For each data point in the figures and tables, Cu²⁺ and Ca²⁺ concentrations, pH, and relative net elongation were recorded, and ψ₀^o and {Cu²⁺}₀^o were calculated. Measured RRE correlated more strongly with the calculated RRE based on the ETM (Eq. 7; r² = 0.921) than with {Cu²⁺}₀^o (r² = 0.878) or {Cu²⁺}_b (r² = 0.745; Table III, experiment 12). This indicates a dual effect of ψ₀^o.

Kinraide (2006) presented results from experiments assessing wheat (cv Atlas 66) seedling root elongation in solutions containing variable concentrations of CuSO₄, CaCl₂, NaCl, and pH. Increases in Ca²⁺, Na⁺, or H⁺ in the rooting medium alleviated the Cu²⁺ rhizotoxicity. This study considered the first effect of ψ₀^o upon {Cu²⁺}₀^o and the possibility of competition at a binding site at the PM surface (BLM). In our reanalysis, RRE correlated more strongly with the calculated RRE based on the ETM (Table III, experiment 13) than with {Cu²⁺}₀^o or {Cu²⁺}_b, suggesting that the ameliorative effectiveness of Ca²⁺, Na⁺, and H⁺ results from the dual effects of ψ₀^o.

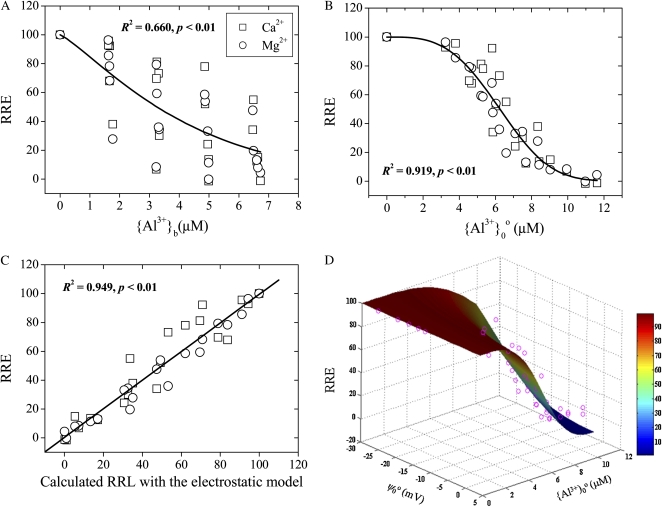
Al³⁺ Toxicity Affected by Ca²⁺, Mg²⁺, or pH

We reevaluated the Ca²⁺ and Mg²⁺ alleviation of Al³⁺ rhizotoxicity in wheat (cv Tyler) roots from data archived from, but not presented in, a study by Kinraide and Parker (1987). Two-day-old seedlings were transferred to solutions containing 0.4 mm CaCl₂ at pH 4.3 variously supplemented with AlCl₃ and MgCl₂ or additional CaCl₂. Addition of Ca²⁺ or Mg²⁺ alleviated Al³⁺ toxicity. Kinraide et al. (1992) reassessed the interactive effects of Ca²⁺ and Mg²⁺ on Al³⁺ toxicity in terms of ψ₀^o and demonstrated that the ψ₀^o plays an important role in Al³⁺-Ca²⁺ and Al³⁺-Mg²⁺ interactions by the first effect of ψ₀^o: the enhancement of cations at the PM surface. For our reanalysis, the dual effects were considered simultaneously in the ETM. Again, the correlation between measured and calculated Al³⁺ toxicity was significantly improved (Fig. 6; Table III, experiment 14), indicating that the Ca²⁺ and Mg²⁺ alleviation of Al³⁺ toxicity may be attributed to effects upon both E_m,surf and {Al³⁺}₀^o (i.e. the dual effects of ψ₀^o).

Figure 6.

Measured RRE of wheat seedlings exposed to Al³⁺ affected by Ca²⁺ and Mg²⁺. Data were taken from Kinraide et al. (1992; experiment 14). The RRE is plotted as functions of {Al³⁺}_b (A), {Al³⁺}₀^o (B), or calculated Al³⁺ toxicity based on the ETM (C) or ψ₀^o and {Al³⁺}₀^o (D).

Anion H₂AsO₄⁻ Uptake and Toxicity Affected by Ca²⁺, Mg²⁺, Na⁺, or pH

The addition of Ca²⁺ or Mg²⁺ or the reduction of pH will increase the surface activity of H₂AsO₄⁻thus the uptake and toxicity of arsenic. H₂AsO₄⁻ (arsenate) may become transformed in the roots into the even more toxic H₂AsO₃⁻ (arsenite; Pickering et al., 2000). Further transformation, translocation, and secretion from the roots may provide some relief of arsenic toxicity. Even so, one would expect ψ₀^o to have an effect upon arsenic uptake, retention, and toxicity. Our hypothesis was that the effects of ψ₀^o upon anionic arsenic toxicants would be opposite to the effects upon cationic toxicants.

Indeed, an increase in Ca²⁺ from 0.25 to 4.0 mm decreased the 48-h EA50{As(V)}_b from 2.9 to 1.7 μm, indicating an increased extrinsic sensitivity. In contrast, the corresponding EA50{As(V)}₀^o increased from 0.48 to 1.49 μm, indicating a decreased intrinsic sensitivity. In contrast to Cu²⁺, As(V) uptake was sigmoidal and thus did not comply with the Michaelis-Menten equation. This may be related to the concentrations used in our treatments and to hormesis by As(V) (Calabrese, 2008; Wang et al., 2008), which was always observed in low-arsenic treatments. A stimulation of root elongation would dilute the As(V) concentration in roots. Therefore, the uptake of As(V) was expressed using a generalized sigmoidal equation:

where J_max is the maximum influx, which occurs when {As(V)}_b is very large, and α and β resemble their counterparts in Equation 5. Regression analysis with Equation 8 for As(V) uptake yielded r² = 0.830. Subsequently, {H₂AsO₄⁻}_b was replaced with {H₂AsO₄⁻}₀^o to include the first effect of ψ₀^o upon the depletion of anions at the PM surface, and the coefficient α was expanded to α(1 + bψ₀^o) to incorporate the electrical component of the driving force (the second effect of ψ₀^o).

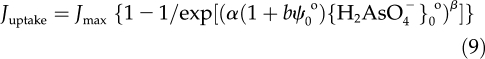In the case of anionic toxicants, b is expected to be negative, so that a decreasing negativity of ψ₀^o will decrease the value of the expanded coefficient, causing J_uptake to decrease. Regression analysis with Equation 9 indeed produced a negative value for b (–0.0649) and an increase in r² to 0.910 (Table II, experiment 10).

To assess As(V) toxicity, the measured RRE was plotted against RRE calculated on the basis of the ETM (Eq. 7) to estimate the dual effects of ψ₀^o. The correlation between RRE and the model-calculated RRE (r² = 0.937) was superior to the correlation between RRE and {H₂AsO₄⁻}₀^o (r² = 0.919) or {H₂AsO₄⁻}_b (r² = 0.903; Table III, experiment 15). As expected, the regression analysis also yielded a negative value for b in Equation 7 (b = –0.0607, close to the value of –0.0649 reported for the EUM [i.e. b in Eq. 9]).

A Dual Role for ψ₀^o Expressed in Soil Culture

A dual role for ψ₀^o appears to be expressed in soil cultures as well as in solution cultures. Ninety-four soil samples were collected from various horizons and soil series from forests in Appalachia, in the northeastern United States, The Netherlands, Sweden, and Germany (Kinraide, 2003b). Some of the soils were used in growth experiments, and growth of wheat (cv Hart), switchgrass (Panicum virgatum ‘Cave-Rock’), and subterranean clove (Trifolium subterraneum ‘Mt. Barker’) was assessed in terms of the extracted soil solutions. The plant growth in these soils was dependent on the Al³⁺ toxicity and H⁺ toxicity and on Ca²⁺ deficiency. A reanalysis of those data demonstrates the dual influence of ψ₀^o upon plant growth. When the α coefficient was expanded to α₁(1 + bψ₀^o) in the growth equations (RRE_Al = 100/exp[(α{Al³⁺}₀^o)^β], RRE_H = 100/exp[(α{H⁺}₀^o)^β], and RRE_Ca = 100{1 – 1/exp[(α{Ca²⁺}₀^o)^β]}), the r² increased by 0.315 (from 0.340 to 0.655), 0.294 (from 0.151 to0.445), and 0.072 (from 0.553 to 0.625), respectively (n = 52), and coefficients α₁ and b were significant (P < 0.05) in each case. These r² values are generally lower than those for solution culture studies, and this reflects the complexity of soils. Indeed, a better prediction was achieved when combined effects of two toxicants (Al³⁺ and H⁺) and an ameliorant (Ca²⁺) were quantified by the equation RRL = 100 × RRE_Al × RRE_H × RRE_Ca in terms of the dual effects of ψ₀^o (data not shown). Regardless, the improvements in the r² values demonstrate the importance of the dual effects of ψ₀^o upon plant growth. For a reanalysis of published soil studies demonstrating the first effect of ψ₀^o in soils, see Kinraide (2006).

Prediction of Ion Uptake and Toxicity with the FIAM, the Surface Ion Activity Model, and Electrostatic Models

All observed values from experiments 1 to 15 were plotted against the values predicted by each model (FIAM, the surface ion activity model [SIAM], the EUM, and the ETM; data not shown). The SIAM considered the effect of ψ₀^o on both surface ion activities. The SIAM predictions (r² = 0.861, n = 427 for uptake; r² = 0.802, n = 334 for toxicity) were superior to FIAM predictions (r² = 0.716 for uptake and r² = 0.721 for toxicity). The correlations for the electrostatic models (r² = 0.940 for the EUM and r² = 0.901 for the ETM), incorporating the effect of ψ₀^o on both surface ion activities and E_m,surf, were superior to the SIAM predictions. These results indicate that the electrostatic models could form the basis for the prediction of uptake and toxicity of both metal cations and metalloid anions and for the interpretation of other plant-ion interactions. In most cases, the treatment periods in this study ranged from a few minutes (some uptake studies) to a few days (toxicity studies), but studies of longer duration, especially in soils, would certainly be useful for more accurate predictions.

General Evaluation of the Electrostatic Approach to Ion Uptake and Toxicity

The BLM attempts to explain toxicity and alleviation in terms of metal ion binding to cell surface ligands as a key step leading to toxicity. It is proposed in the BLM that alleviation of toxicity by cations is caused by the competition of those ions with the toxic ions for binding to the same ligands. These assumptions may be true but are not verified in most cases. Also, the BLM fails to interpret the enhancement of the uptake and toxicity of arsenate or selenate anions by the treatments that reduce the toxicity of toxic cations (Kinraide, 2003a; Wang et al., 2008). Our study shows that electrostatic mechanisms provide a unified interpretation of both phenomena: the cation reduction of cation uptake and toxicity and the cation enhancement of anion uptake and toxicity.

The alleviation of cation toxicity by site-specific mechanisms, such as competitive binding, may occur in some cases. For example, Weng et al. (2004) and others have noted significant reductions in metal-induced toxicity with reductions in pH in the 6 to 7 range. Such pH reductions would change ψ₀^o by less than 1 mV in most media, a change far too small to account for toxicity reductions. Instead, some key ligands, contributing little to ψ₀^o, such as sites on ion channels or enzymes, may bind H⁺ strongly enough for pH shifts from 7 to 6 to be effective. Despite clear evidence for site-specific mechanisms (such as competition), such mechanisms appear to be unimportant in many cases (Kinraide, 2006; Wang et al., 2008). In those cases, including those in this study, the dual effects of ψ₀^o are sufficient to explain the ion-toxicant interactions (Kinraide, 2006; Wang et al., 2008; this study).

The GCS model, incorporating the parameter values used by us, appears to be quite robust (Yermiyahu et al., 1997; Zhang et al., 2001; Wang et al., 2008; Kinraide and Wang, 2010), and a fully parameterized GCS model is available from the authors. The model is suitable for the calculation of ψ₀^o and for the interpretation of many plant responses to changes in the composition of the aqueous exposure medium.

CONCLUSION

This study provides evidence that PM surface ion activities, as determined by ψ₀^o, are often superior to activities in the bulk-phase medium as indicators of plant-ion interactions. This study also indicates that ψ₀^o plays an additional role: it is a determinant of E_m,surf, the electrical component of the driving force for ion uptake. Our findings indicate that these dual effects of ψ₀^o play important roles in ion uptake and toxicity in both soil and solution cultures and that the electrostatic uptake and toxicity models provide a novel approach for predicting the uptake and toxicity of both metal cations and metalloid anions. The electrostatic uptake and toxicity models do not negate entirely the BLM. Site-specific competition surely explains some features of ion toxicity and alleviation. Irrespective of whether the mechanisms invoked by the BLM play a role in any given situation, electrostatic effects surely do and should be incorporated into any model, including the BLM, of ion toxicity and the ionic alleviation or enhancement of toxicity.

MATERIALS AND METHODS

Uptake and Toxicity Bioassay Experiments

Data for ion uptake and root elongation in response to the ionic environment were compiled for analysis from previous studies employing solution culture (references in Table I) and soil culture. In addition, data for the uptake and toxicity of copper and As(V) in wheat (Triticum aestivum) roots were collected from experiments conducted as part of this study [experiments 3 and 11 for copper and experiments 10 and 15 for As(V)]. The plant species used and a summary of culture conditions are presented in Table I. For detailed experimental methods (except for this study), refer to the corresponding references in Table I.

Experiments 3 and 11: Effects of Ca²⁺, Mg²⁺, and pH on Cu²⁺ Uptake and Toxicity

Three sets of uptake and toxicity bioassay experiments were performed, one each for three Ca²⁺ concentrations (0.25, 0.98, and 3.78 mm), three Mg²⁺ concentrations (0.26, 1.0, and 4.0 mm), and three pH values (5.1, 5.5, and 6.0). In each medium, six Cu²⁺ concentrations (0.25–2.0 μm) and a control were tested. Further details of the growth experiments and precautions for the preparation of the test solutions have been presented previously (Wang et al., 2008). For acute toxicity tests, 2-d-old wheat (cv Yangmai 14) seedlings with uniform root length (1–2 cm) were cultured in darkness for 48 h at 25°C in acid-washed polyethylene beakers containing 500 mL of test medium. Each treatment was performed with three or four replicates and eight seedlings per replicate. At termination, the two longest roots of each seedling were measured, and the mean value of 16 measured values per replicate was recorded. The plants were transferred to a 10 mm Ca(NO₃)₂ solution for 10 min to remove cell wall-bound copper. Roots were dried at 40°C, weighed, and digested with 5 mL of ultrapure concentrated HNO₃. Copper was determined by flame atomic absorption spectrometry (Varian 220Z).

Experiments 10 and 15: Effects of Ca²⁺, Mg²⁺, Na⁺, and pH on As(V) Uptake and Toxicity

For As(V) uptake, three sets of experiments were performed, one each for three Ca²⁺ concentrations (0.24, 1.0, and 4.1 mm), three Mg²⁺ concentrations (0.26, 0.83, and 3.7 mm), and three pH values (4.4, 5.3, and 6.0). In each medium, five H₂AsO₄⁻ concentrations (0.75–3.0 μm) and a control were tested. For As(V) toxicity experiments, four sets of experiments were performed, one each for Ca²⁺ (0.27–4.3 mm), Mg²⁺ (0.26–4.0 mm), Na⁺ (1.4–20.1 mm), and pH (4.5–6.6). In each medium, five arsenate concentrations (0.67–26.7 μm) and a control were tested. These uptake and growth experiments were similar to experiments 3 and 11. At termination, the plants were transferred to an ice-cold phosphate buffer solution for 10 min to remove cell wall-bound arsenic (Zhang et al., 2009). Roots were dried at 40°C, weighed, and digested with 5 mL of ultrapure concentrated HNO₃. Arsenic was determined by atomic fluorescence spectrometry (AF-160A; Beijing Haichuang Analytical Instrument Co.).

Data Treatment and Statistics

Ion species and activities were calculated using the visual MINTEQ (version 2.51) chemical equilibrium program (U.S. Environmental Protection Agency). The speciation calculations included atmospheric CO₂ (10^−3.5 atm). Relative root elongation was calculated by the formula RRE = 100(RL_T − RL_S)/(RL_C − RL_S), in which RL_T is the mean root length in the presence of toxicants, RL_C is the root length in the corresponding toxicant-free control, and RL_S is root length at the time of seedling transfer to the test medium. Uptake and toxicity were plotted, and curved surfaces were fitted by regression analysis using Origin Professional 6.0 and MATLAB 7.0. Significance levels are P < 0.05 for all reported regressions and coefficients.