Analysis of Microtubule Dynamic Instability Using a Plus End Growth Marker

Abstract

Regulation of microtubule dynamics is essential for many cell biological processes, and is likely to be variable between different subcellular regions. We describe a computational approach to analyze microtubule dynamics by detecting growing microtubule plus ends. Our algorithm tracks all EB1-EGFP comets visible in an image time-lapse sequence allowing the detection of spatial patterns of microtubule dynamics. We use spatiotemporal clustering of EB1-EGFP growth tracks to infer microtubule behaviors during phases of pause and shortening. The algorithm was validated by comparison to manually tracked, homogeneously labeled microtubules, and by analysis of the effects of well-characterized inhibitors of microtubule polymerization dynamics. We used our method to analyze spatial variations of intracellular microtubule dynamics in migrating epithelial cells.

Introduction

Microtubules are polymers of α/β-tubulin dimers that stochastically switch between phases of growth and shortening. These dynamics are generally reported by four parameters: the rates of growth and shortening and the frequencies of switching between these phases, referred to as catastrophes and rescues¹. Conventional analysis of intracellular microtubule dynamics involves microinjection² or expression of fluorescently labeled tubulin³ to homogenously label the microtubule network, and time-consuming, computer-assisted hand-tracking of individual microtubule ends over time^2,4. Although computational modeling has improved the efficiency and reliability of this method⁵, the analysis remains limited to microtubules near the cell periphery, where ends of labeled microtubules can be observed over sufficient periods of time. Sub-stoichiometric labeling⁶ allows microtubule observation deeper in the cell and could permit end tracking relative to the microtubule lattice, but the identification of microtubule ends and filaments in this context is an unresolved challenge; to date, only a few papers describe hand-measured data from limited numbers of microtubules^4,7.

An alternative strategy to visualize microtubule polymerization utilizes proteins that specifically recognize a structural property of growing microtubule plus ends, such as fluorescently-tagged End Binding Proteins 1 and 3 (EB1- or EB3-EGFP) ^8–10. The exponential decay of available binding sites results in the characteristic comet-like fluorescence profiles of EGFP-tagged EBs. Fast turnover¹¹ causes rapid loss of EB fluorescence from non-polymerizing microtubule ends and rapid appearance of EB comets when microtubules start growing.

Here, we describe a computational strategy to extract microtubule growth rates from EB1-EGFP time-lapse image sequences and introduce an approach to infer parameters of microtubule dynamics in pause and shortening phases without visible comets. We detect EB1 comets, track the comets to measure microtubule growth rates, and spatiotemporally cluster EB1 growth tracks into more complete trajectories, which include inferred shortening and pause phases (Supplementary Fig. 1). This method allows analysis of a large population of intracellular microtubule ends in a spatially unbiased manner. Software packages implementing these algorithms are available at lccb.hms.harvard.edu and as Supplementary Software 1.

Results

EB1-EGFP Comet Detection and Tracking

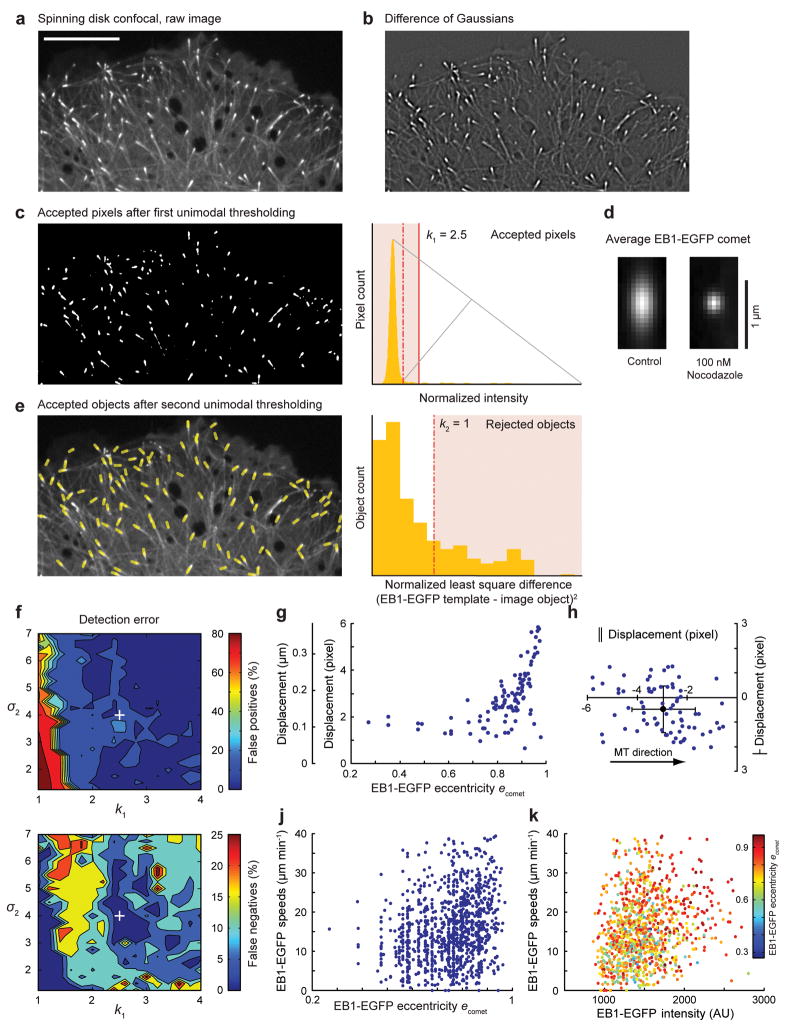
To identify EB1-EGFP comets in each frame of a time-lapse sequence (Fig. 1a), we calculated the difference of two Gaussian (DoG) transformations with standard deviations σ₁ and σ₂ adjusted to enhance the band of image frequencies associated with EB1-EGFP comets (Supplementary Note 1 and Fig. 1b). We used unimodal thresholding¹² to remove background pixels (Supplementary Note 2 and Fig. 1c) and individual objects likely corresponding to EB1 comets were then generated by connected component labeling of the thresholded DoG image (Fig. 1c). To discriminate against selected objects that are not true comets, we selected by template matching objects that conform to the average shape of EB1-EGFP comets (Supplementary Note 3 and Fig. 1d). For both thresholding steps, user-defined coefficients k₁ and k₂ were introduced to adjust the automatically detected threshold if required for specific imaging conditions. All adjustable parameters are summarized in Supplementary Table 1. Because the average EB1 comet shape is determined for each image, the detection is robust against variations throughout the time-lapse sequence, for example during acute application of microtubule polymerization inhibitors that reduce the polymerization rate (Fig. 1d). A list of EB1 comets was thus obtained for each frame (Fig. 1e), including the position of the object centroid, the magnitude of EB1-EGFP comet eccentricity and the angular direction of its main axis.

Figure 1. EB1-EGFP Comet Detection.

(a) Spinning disk confocal image of a cell expressing EB1-EGFP. (b) Difference of two Gaussian (DoG) transformation applied to image in a). (c) Accepted pixels (white) after unimodal intensity thresholding; The plot (right) shows the histogram of normalized DoG intensities; grey lines illustrate construction of the unimodal threshold; dashed red line, automatic threshold; solid red line, threshold modified for confocal images. (d) Average EB1-EGFP comets in a control and nocodazole-treated cell. (e) Positions and orientation of accepted comets (yellow lines, overlaid on raw image) based on automatic thresholding. The plot (right) shows the histogram of the normalized least squares difference between individual comet images and the average of all comets in this frame. (f) Contour plots show detection error (top, false positives; bottom, false negatives) as a function of σ₂ and k₁. The white cross indicates the detection parameters used in (a) ([σ₁, σ₂, k₁, k₂] = [1, 4, 2.5, 1]. (g) Displacement of computer-detected EB1-EGFP comet position relative to hand-detected microtubule end as a function of comet eccentricity (g) and as a function of orientation relative to the microtubule direction (h). Only comets with an eccentricity e > 0.8 (~70% of the total comet population in this image) were used in (h). Solid circle, mean displacement; error bars, s.d. (n = 95) (j, k) EB1-EGFP comet eccentricity (j) and intensity (k) are plotted versus comet speed.

To validate the detection algorithm, the positions of ~120 hand-detected EB1-EGFP comets were compared to automatically detected objects for different pairs of σ₂ and k₁ because these parameters are most sensitive to imaging conditions (Fig. 1f). Because the detection algorithm is sensitive to image intensity variations at the size scale of EB1-EGFP comets, in confocal images in which a low EB1-EGFP signal is evident along the length of microtubules, k₁ was increased to k₁ > 2 to avoid a large number of false positive detections. In widefield images, however, in which EB1-EGFP along the microtubule lattice is obfuscated by out-of-focus light, the default pixel intensity threshold of k₁ = 1 worked robustly (Supplementary Fig. 2).

The detection error was quantified by the percentage of false positives (100(1-M/D)) and the percentage of false negatives (100(1-M/G), where D is the number of computer-detected comets, G is the number of hand-selected comets, and M is the number of matches between those two sets). There was low correlation between σ₂ and false positive detections over most of the range of σ₂ values tested. Similarly, false negative detections did not follow a clear trend, but a shallow minimum was evident around σ₂ = 4 indicating that detection was most successful when σ₂ matched the expected length scale of EB1-EGFP comets (Fig 1f). The detection performance was similar in widefield images, and was largely independent of the precise shape of the comet as the algorithm was successfully applied to other plus-end tracking proteins (Supplementary Fig. 2). Detection was also largely insensitive to simulated high frequency pixel noise (Supplementary Fig. 3). A small number of undetectable EB1-EGFP comets is expected in every image due to proximity or overlap, which results in objects that do not pass the template matching of the detection algorithm. However, these events should not introduce a systematic error in the detected EB1-EGFP comet population. Moreover, temporary comet occlusion is largely compensated by subsequent growth track clustering.

The elongated shape of EB1-EGFP comets implies that the comet centroid is systematically located behind the very tip of the microtubule. For growth rate measurements this offset is irrelevant as long as it remains constant over time. To assess the magnitude of potential temporal variation in the offset we determined the difference between computationally-defined EB1-EGFP comet positions and manually detected intensity maxima, which co-localize with the microtubule tip. As expected, the difference increased with comet eccentricity (Fig. 1g). Perpendicular to the microtubule direction it was small (0.49 ± 0.94 pixel) and below the accuracy of manual detection. For highly elongated comets, the difference was 2.95 ± 1.26 pixel along the direction of the microtubule (Fig. 1h); we estimated that the standard deviation of this difference was sufficiently small to have minor impact on the analysis of microtubule growth (Supplementary Note 4). Because the elongation of the EB1-EGFP comet depends on the rate of microtubule growth¹⁰, we expected a positive correlation between comet eccentricity and speed. Indeed, we found that the fastest comets had a high eccentricity, although the distribution also included many slower comets with equally high eccentricity (Fig. 1j). In contrast, no obvious correlation existed between eccentricity and EB1-EGFP peak intensity (Fig. 1k). Overall, this indicates complex kinetics of EB1 interactions with microtubule ends or fluctuations of microtubule end structures in cells.

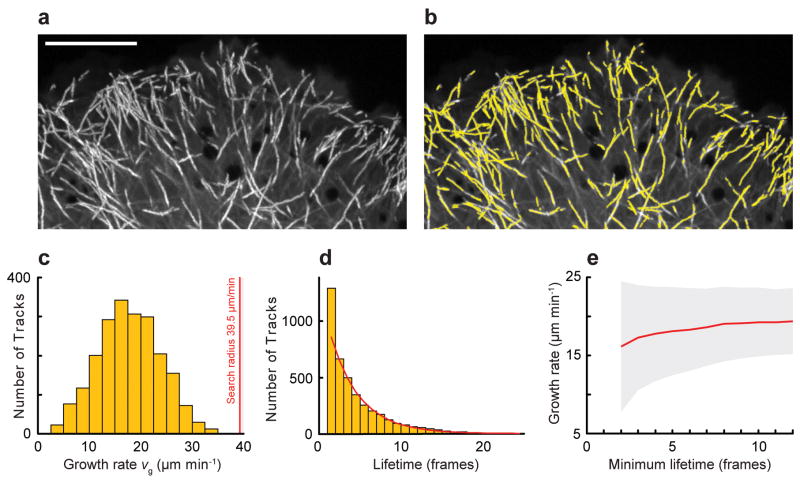
Detected EB1-EGFP comets were tracked using a Kalman filter-based multi-object tracking algorithm¹³ (Supplementary Note 5 and Fig. 2). As expected for random switching from growth to shortening, the track lifetime follows an exponential decay¹⁴ with a mean lifetime τ = 3.6 frames (Fig. 2d). Because the number of tracks with a lifetime of 2 frames was higher than expected, we suspected that a significant subpopulation of very short tracks resulted from detection or tracking errors. Analysis of the variance of the growth rate histogram as a function of minimal lifetime further indicated a very high standard deviation for short tracks (Fig. 2e). Thus, subsequent analysis only included growth tracks with a lifetime of 4 frames and greater. To evaluate the combined performance of the detection and tracking algorithms we compared computer-generated tracks with simulated differences in spatial (Supplementary Fig. 4) and temporal resolution (Supplementary Fig. 5). We found that the algorithm performed robustly at magnifications that satisfy the Nyquist sampling criterion (effective pixel size of <100 nm), and that a temporal sampling of 1–2 frames s⁻¹ was sufficient to achieve good track reconstruction of microtubule growth.

Figure 2. EB1-EGFP Object Tracking.

(a) Maximum intensity projection of EB1-EGFP time-lapse sequence (75 frames, 0.4 s frame⁻¹). Growing microtubule ends appear as bright tracks. Scale bar, 10 μm. (b) Computer-generated growth tracks (yellow) with a minimum lifetime of 4 frames. (c) Histogram of growth velocities. The red line is the maximum search radius. (d) Histogram of growth track lifetimes. Red line, least-squares fit of a single exponential decay excluding the first data point. (e) Mean growth rates as a function of minimum growth track lifetime. Grey area, standard deviation.

EB1-EGFP Growth Track Cluster Assignment

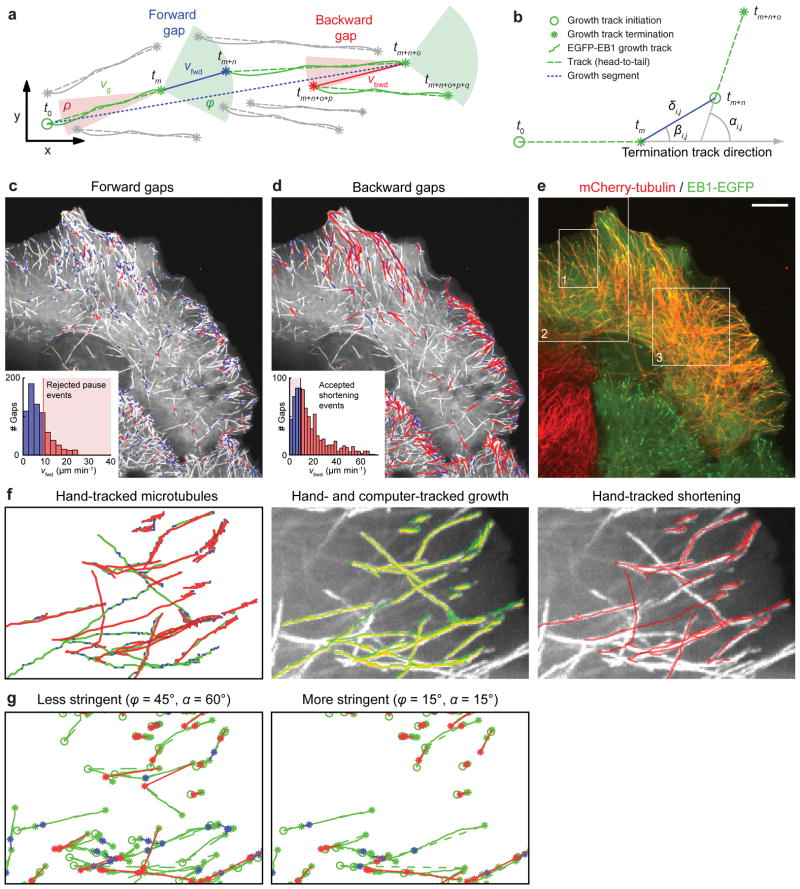
Microtubules are stiff¹⁵ and over the short time intervals used to observe microtubule polymerization dynamics they translocate little. As a result, microtubule shortening, rescues and pauses predominantly occur along the path defined earlier by the growing microtubule end. Thus, time-shifted, nearly parallel EB1-EGFP tracks with significant spatial overlap have a high probability of belonging to the same microtubule. To detect events of microtubule shortening and pausing in addition to the microtubule growth directly visible in EB1-EGFP sequences and to infer parameters of their associated dynamics, we developed a computational scheme to cluster tracks that fulfill defined geometrical and temporal constraints based on a priori assumptions about intracellular microtubule behavior (Fig. 3a).

Figure 3. EB1-EGFP Growth Track Clustering.

(a) Schematic of growth track clustering. Green and red cones, spatiotemporal search space for candidate links to subsequent growth tracks at the end of a terminating growth track. Grey tracks with an initiation point inside a cone are not selected for linking by the clustering algorithm; gray tracks with an initiation point outside any cone do not participate in the clustering. v_g, growth rate derived from EB1-EGFP tracks; v_fwd and v_bwd, inferred velocities of forward (blue) and backward (red) gaps, respectively; t_x defines the time point of initiation or termination of a growth track. (b) Variables defining the cost of a candidate link between growth tracks. (c, d) Overlay of forward gaps (c) and backward gaps (d) on a maximum intensity projection of EB1-EGFP time-lapse sequence (97 frames, 0.6 s frame⁻¹). Blue, slow gaps; red, fast gaps. Insets, histograms of forward (c) and backward (d) gap speeds and unimodal thresholds used to reject fast (c) and slow (d) gaps. (e) Image of cell expressing mCherry-tubulin and EB1-EGFP. Boxes indicate image regions used for validation. Scale bar, 10 μm. (f) Left, hand-tracking of 19 microtubules in region 1 indicated in (e). Periods of growth (green), shortening (red), and pauses (blue) are shown; middle, hand-tracked (green) and computer-tracked (yellow) growth; right, hand-tracked shortening overlaid on the EB1-EGFP maximum intensity projection of the entire sequence. (g) Track clusters obtained by two different settings for the cone openings. Color coding for lines, circles (growth track start) and asterisks (growth track and gap ends) as in (a).

Given an EB1-EGFP growth track terminating at time t, we considered all track initiations in the interval [t+1, t+T_max] in cones with a forward opening angle ϕ = ±45° and a backward opening angle ρ = ±10° as candidate links that could potentially represent a continuation of the terminated growth (forward link) or shortening (backward link), respectively. The narrow backward cone reflects the tendency of microtubules to shorten along the preceding growth trajectory⁴. For each candidate link we then calculated the maximal allowable distance for forward (C_fwd) and backward gaps (C_bwd) as:

$$C_{\text{fwd}}=V_{max}min(\mathrm{\Delta }{t}_{\text{gap}},\sqrt{T_{max}})$$ (1)

$$C_{\text{bwd}}=min(\gamma V_{max}\mathrm{\Delta }{t}_{\mathit{gap}},V_{\text{med}}{T}_{max})$$ (2)

V_max represents the 95^th percentile of the speed distribution from all participating growth tracks, and Δt_gap is the time between termination and initiation of the two candidate tracks. Equation (1) assumes that short time gaps mainly result from temporary occlusion of growing microtubule ends due to noise, overlap, or out-of-focus motion, where the comet reappears at a distance proportional to the growth rate and Δt_gap. Long time gaps more likely represent bona fide pauses. During such pauses a microtubule end undergoes a random walk of short growth and shortening events, and the comet reappears at a distance proportional to the square root of time points without detectable EB1-EGFP comet. In equation (2), γ takes into account that microtubule shortening is generally faster than growth^3,4. V_medT_max, where V_med is the median of the growth track speed distribution, safeguards against the combinatorial explosion of candidate links in dense EB1 comet fields. Furthermore, candidate links were considered only when the directional change α_i,j between the two associated tracks was less than α_max = 60° (Fig. 3b), because microtubules rarely bend more than 60° over short distances¹⁶.

From the set of candidate links that fulfilled the distance and angular criteria we then selected the largest possible subset of links with overall minimal cost using linear assignment^17,18. The cost for an individual candidate link c_i,j was defined as

$$c_{i,j}={\delta }_{i,j}(||cos({\alpha }_{i,j})||-||cos({\beta }_{i,j})||),$$ (3)

which gives preference to pairs of tracks in close proximity (δ_i,j), with a low bending angle (α_i,j), and with small transversal shifts (β_i,j). Although the methods currently used may generate some false positive links, the selection is fairly robust because all tracks compete for links simultaneously. In a typical EB1-EGFP time-lapse sequence, each growth track termination associated with ~200 candidate links that fulfilled the temporal (T_max) and angular criteria (ϕ, ρ and α_max). Applying the distance cutoffs (C_fwd and C_bwd) reduced this to an average of 3 competing track initiations. As expected, the majority of links were positioned in the cell periphery where microtubules more frequently switch between growth and shortening (Fig. 3c, d).

Forward gaps during which EB1-EGFP comets are invisible could be due to periods of pause or very slow growth during which the EB1-EGFP signal becomes too dim to be detected, or due to very fast-growing EB1-EGFP comets that are temporarily out-of-focus. We therefore calculated the forward gap speed v_fwd as the distance between the last point in the terminating track and the first point in the linked growth track divided by the gap duration (Fig. 3a, c). Typically, less than 15% of the forward gaps had a speed larger than the slowest 30% of the growth tracks. This indicated that most forward gaps represented true microtubule pausing. A small forward translocation is expected even for true pause events because of the latency of detectable EB1-EGFP comet formation at the end of a newly growing microtubule (Supplementary Note 6). Similar to forward gaps, backward gaps contain information about microtubule shortening events, and as above we calculated a backward gap speed v_bwd (Fig. 3d). Of note, the histograms of both v_fwd and v_bwd sharply decayed towards the last bin below the maximally allowable velocity. This is an indication that the distance cutoffs in Eq. (1) and (2) were set sufficiently large to capture the majority of clusters of aligned growth tracks (Fig. 3c, d).

Algorithm Validation

To evaluate the performance of growth track clustering, we recorded dual-wavelength time-lapse sequences of cells expressing both EB1-EGFP and mCherry-tubulin (Fig. 3e). Because mCherry-labeled microtubules were too dense in the cell interior to directly observe dynamic ends (Supplementary Fig. 6), we hand-tracked 19 microtubules in a peripheral cell region in which microtubule ends were clearly visible (Fig. 3f and Video 2). Detection and tracking of EB1-EGFP comets was accurate as indicated by the overlap of hand- and computer-tracked growth (Fig. 3f and Video 3).

Although clustered growth tracks and hand-tracked microtubule trajectories were similar, qualitative comparison showed that many shortening events were missed (Fig. 3g). This was expected because the clustering algorithm cannot detect shortening that is not preceded or followed by a growth track within the distance and angle criteria. However, a high percentage of false negatives is acceptable as long as the population of microtubules analyzed is sufficiently large and unbiased to provide a representative readout of overall microtubule dynamics. To quantitatively test this, we compared hand-tracked rates of growth, pause, and shortening, and pause durations to those obtained by computational analysis. Importantly, the definition of growth, pause, and shrinkage events by hand-tracking relies on user-defined judgment as to when a microtubule undergoes a change in velocity. The definition of these events by growth track clustering relies on the detection of EB1-EGFP comets as molecular markers of microtubule growth. Therefore, prior to a comparison of hand- and computer-tracking, the hand-tracked measurements had to be corrected to account for the differences in assumptions (Supplementary Note 7).

Even after these corrections, hand-tracked growth and shortening rates were significantly higher than the computer-inferred rates (Table 1). This deviation originated in the fundamentally different definitions of growth, pause, and shortening events in hand- and computer-tracking. Specifically, computer-tracked growth events contain a subset of events where the microtubule end moves very slowly without loss of the EB1-EGFP comet. In hand-tracked trajectories such events would be classified as pauses. Similarly, computer-inferred backward gaps contain very slow events that would be classified as pauses in hand-tracked trajectories, in addition to phases of true microtubule shortening. We determined a threshold for a computer-generated growth track or backward gap to be accepted as a significant growth or shortening event by analysis of the velocity distribution of forward gaps, which includes both pauses and gaps due to unobserved growth events (Supplementary Note 8). This filtering resulted in excellent agreement between computer-inferred and hand-tracked growth and shortening rates (Table 1). Thus, although comparisons between computational analysis and hand-tracking cannot be made directly, reasonable assumptions about the limitations of both methods confirmed that the growth and shortening rates we inferred are representative of microtubule polymerization dynamics. A discrepancy between computer-inferred and hand-tracked pause durations remained (Table 1), likely due to the latency of EB1-EGFP comet formation and disappearance (Supplementary Note 6). Thus, pause durations inferred by the clustering algorithm are not directly comparable to hand-tracking of homogenously labeled microtubules. Similarly, because shortening events interrupted by pauses will be combined into a single phase, the computer-inferred v_bwd is not a direct measure of the microtubule depolymerization rate. Nevertheless, we expect that molecular conditions that change microtubule polymerization dynamics will result in relative changes of these computer-inferred parameters.

Table 1. Comparison between computer-inferred and hand-tracked microtubule dynamics.

Both computer-inferred rate measurements using EB1-EGFP comet tracking and cluster analysis and hand-tracked microtubule trajectories of homogeneously labeled microtubules were adjusted to make the underlying assumptions more comparable as explained in the text. Pauses per microtubule are not initially defined in segment-by-segment hand-tracked data sets. Values are means ± standard deviation.

	Growth (μm min−1)	Shortening (μm min−1)	Pause (μm min−1)	Pause duration (sec)
Computer-inferred (raw)	16.8 ± 7.4 n = 2799	17.6 ± 14.7 n = 775	7.2 ± 5.2 n = 704	6.9
Computer-inferred (corrected)	18.7 ± 7.4 n = 2351	24.4 ± 14.3 n = 499	4.6 ± 2.4 n = 517	8.2
Hand-tracked (raw, segment-by-segment)	21.7 ± 8.4 n = 582	39.4 ± 22.6 n = 283
Hand-tracked (corrected, head-to-tail)	19.1 ± 7.4 n = 122	24.9 ± 12.8 n = 70	4.3 ± 3.4 n = 105	3.0

The clustering algorithm also generated erroneous connections between growth tracks not belonging to the same microtubule. To quantify the frequency of such events, we overlaid clustered trajectories generated with two different stringencies onto to mCherry-tubulin and EB1-EGFP channels (Videos 4–6) and verified computer-assigned growth, pause, and shortening phases, as well as catastrophes and rescues. Within the region analyzed (Fig. 3e), the software accumulated 475 microtubule growth tracks lasting at least 4 frames. At the less stringent parameter set (ϕ=45°, α=60°) 329 tracks clustered into 118 trajectories with an average lifetime of 17 seconds. For the more stringent parameters (ϕ=15°, α=15°) 226 tracks clustered into 91 trajectories with a 14 second average lifetime. Only 8% of the trajectories were identical between the two analyses, indicating the sensitivity of the clustering process in selecting viable track connections (Fig. 3g). Because of the high microtubule density, about half of the computer-assigned events could not be observed clearly. However, if we only considered events that we could visually confirm as true or false, our algorithm showed good performance (Supplementary Table 2). As expected, the high stringency parameter set was more accurate, and with both parameter sets, the software more robustly connected microtubule growth tracks interrupted by pause rather than shortening events. However, the better performance at high stringency comes at the expense of less data, which bears the risk that some of the heterogeneity of microtubule behavior is lost.

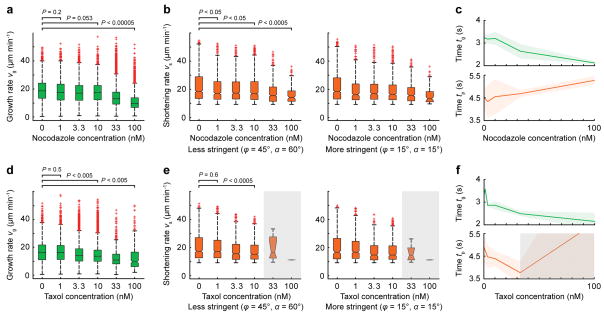
We next tested whether the computational analysis detected well-characterized responses to pharmacological microtubule dynamics inhibitors. At low concentrations, nocodazole inhibits both growth and shortening rates and increases the time microtubules spend in pause¹⁹, and we detected statistically significant effects on these parameters at concentrations as low as 10 nM (Fig. 4a–c). Similarly, low taxol concentrations reproduced published effects²⁰ (Fig. 4d–f). This demonstrates that although our computational analysis is sufficiently sensitive to detect expected differences in microtubule polymerization dynamics. In addition, the results obtained with two different clustering parameter sets were similar, indicating that false positives are sufficiently low so as to not significantly affect correctly clustered microtubule growth tracks.

Figure 4. Effects of Microtubule Inhibitors.

(a, d) Growth rates, (b, e) inferred shortening rates using two different sets of clustering parameters and (c, f) times spent in growth and pause as a function of (a–c) nocodazole, and (d–f) taxol concentration. The shaded areas in c and f indicate the standard deviation, and the grey area in the taxol experiment indicates unreliable results due to very few growing microtubules (< 5–10% of control), which resulted in low clustering efficiency. Data is pooled from n = 3 cells for both experiments; distributions comprise n > 3000 measurements for each concentration except those in the gray areas. Statistical significance of the difference between concentrations is determined by a permutation t-test (see Methods).

Effects of microtubule acetylation and spatial cues

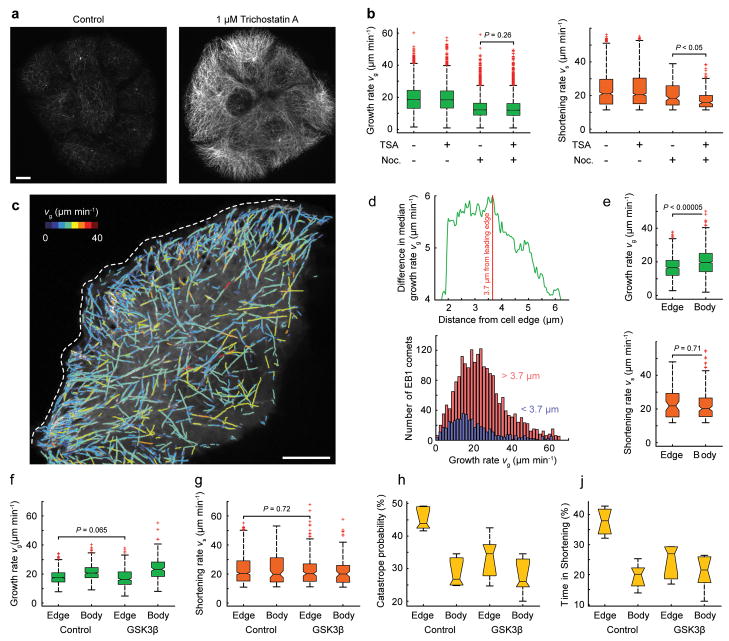
Armed with our new software tool, we examined two long-standing questions in the field: first, we tested whether tubulin acetylation²¹ alters microtubule polymerization dynamics. We treated cells with Trichostatin A (TSA), a broad specificity histone deacetylase inhibitor that inhibits the tubulin-specific deacetylase HDAC6²² (Fig. 5a). We could not detect statistically significant differences in microtubule dynamics when cells were treated with TSA alone. However, in cells simultaneously incubated with 50 nM nocodazole the inferred shortening rate in TSA-treated cells decreased significantly (Fig. 5b). This indicates that tubulin acetylation may protect microtubules from nocodazole-induced depolymerization.

Figure 5. Effects of Tubulin Acetylation and Spatiotemporal microtubule Regulation in Migrating Cells.

(a) Immunofluorescence staining of acetylated microtubules in control and Trichostatin A-treated cells. (b) Growth and shortening rates in the presence of the indicated compounds. Data pooled from n = 3 cells (each distribution comprises n > 3000 measurements) and tested by permutation t-test (see Methods). (c) Computed growth tracks overlaid on a maximum intensity projection of an EB1-EGFP time-lapse sequence at the edge of a cell monolayer (77 frames, 0.4 s frame⁻¹). Growth tracks are color-coded by growth rate as indicated; the dashed white line indicates the leading edge. (d) Difference in median growth rate of microtubule populations in the cell body (red) and cell edge (blue) as a function of distance from the edge. The plot below shows the regionally separated histograms of growth rates. (e) Growth and inferred shortening rates in the cell body and at the cell edge. (f) Growth and (g) inferred shortening rates, (h) catastrophe probability (estimated as the fraction of backward links in the total population of links), and (j) the time spent shortening, in regions of the cell edge compared to the cell body in control and GSK3β (S9A)-expressing cells. (e – g) Data pooled from n = 6 cells (distributions comprise n > 3000 measurements) and tested by permutation t-test (see Methods). Scale bars, 10 μm.

Second, we examined spatial gradients of intracellular microtubule dynamics. We and others have reported that microtubules grow more slowly at the cell edge^23,24. We thus determined the distance from the cell edge at which the difference in the median microtubule growth rate between the edge and interior microtubule populations was largest. In three cells analyzed, this distance varied between 3.7 μm and 6.4 μm (Fig 5c, d). The median growth rate in the cell body was 19.7–22.7 μm/min compared to 16.6–17.1 μm/min closer to the cell edge. The inferred shortening rate was not significantly different (Fig. 5e) but at the cell edge a larger fraction of the links between growth tracks were backward links (44–60% in comparison to 35–43% in the cell interior), consistent with the observation that peripheral microtubules more frequently switch between growth and shortening^23,25.

We recently reported that GSK3β inactivation may be required for spatial microtubule dynamics regulation in migrating epithelial cells²⁴, but we did not measure significant shifts in the spatial gradient of growth rates between control cells and cells expressing constitutively active GSK3β(S9A). Here, we first confirmed this result using our new method for identifying spatial gradients in microtubule dynamics (Fig 5f). Our clustering algorithm then revealed a large decrease in catastrophe probability at the cell edge and a decrease in the percentage of time microtubules spent in the shortening phase (Fig. 5g–i). This demonstrates that GSK3β regulates specific aspects of microtubule polymerization dynamics and is consistent with the hypothesis that GSK3β inactivation increases cell edge microtubule interactions with the cortical cytoskeleton²⁴. Importantly, the clustering algorithm was able to detect these differences even though growth and shortening rates in the cell edge of control and GSK3β(S9A)-expressing cells were not significantly different.

Discussion

We present a framework for the analysis of intracellular microtubule polymerization dynamics based on automatic tracking of a microtubule plus end marker such as EB1-EGFP, and geometric clustering of growth tracks. Because we never observed growing microtubules without associated EB1, and no condition has been reported that selectively removes EB1 from a subset of growing microtubule ends, EB1-EGFP is a faithful reporter of the entire intracellular microtubule population. Since EB1-EGFP overexpression may influence microtubule dynamics by enhancing growth rates²⁶, stabilizing microtubules against catastrophes²⁷, or by disrupting the localization of other plus end-tracking proteins²⁸, it is important that our algorithm allows comet detection at low expression levels. The algorithm may be used with other plus end markers such as EGFP-CLIP-170, allowing independent experimental validation. In addition, because a universal EB1-binding motif has been identified²⁹, artificial plus end trackers will likely be available soon that only minimally affect microtubule dynamics.

Because EB1-EGFP only labels growing microtubules, microtubule behavior has to be interpolated when microtubules stop growing. We introduced several assumptions about the average behavior of microtubules, including maximum rates, allowed angles for direction changes, and the observation that microtubules shorten along the track previously defined by the growing end, to link growth tracks probably belonging to the same microtubule. The linking was designed to prefer exclusion of uncertain events. Thus, our algorithm produces a relatively low number of false positives, but a high number of false negatives. We estimate that only 20–30% of pause and shortening events are captured.

Although we have performed an extensive validation of our clustering algorithm by visual comparison with time-lapse sequences that included homogeneously labeled microtubules, we currently have no formal way to quantify the frequency of clustering errors. This is an important caveat because different imaging conditions or different intracellular densities of growing microtubule ends may affect clustering efficiency. Thus, when using this method, thorough experimental controls must be performed to avoid the propagation of systematic errors (Supplementary Note 9). It is also important to note that measurements inferred by cluster analysis are not directly comparable to traditionally reported parameters of microtubule dynamics because the assumptions underlying both analysis methods are fundamentally different. For example, terminal shortening cannot be detected by our approach, and backward gaps may include pauses and short growth phases that do not produce a detectable EB1-EGFP comet. Nevertheless, our data show that large numbers of growing microtubule ends measured throughout the cell reveal robust and spatially differentiated variations in microtubule polymerization behavior between experimental conditions. Our approach will thus complement and enhance conventional analysis, which typically reports the dynamics of very few microtubules tracked at the cell edge.

There is no mathematical reason precluding the adaptation of our approach to the analysis of microtubule dynamics in more physiological three dimensional cell culture systems. In fact, the generalization of tracking and clustering has already been demonstrated in a study of kinetochore dynamics in mitotic spindles³⁰. Detection of highly eccentric EB1-EGFP comets in 3D will be more complex because of the unequal optical resolution in lateral and axial directions. Thus, the comet shape in 3D will depend on microtubule orientation, and the detection bandpass filter used here will have to be replaced by more sophisticated, orientation invariant methods. However, full 3D analysis will also require faster acquisition at sufficient temporal and axial resolution and further development of brighter, more photostable fluorescent probes. However, the ease of EB1-EGFP imaging makes our method attractive for high-content screening applications, in which microtubule dynamics may be relevant indicators of cell state.