A Latent Variables Examination of Processing Speed, Response Inhibition, and Working Memory during Typical Development

Abstract

The present study addressed three related aims: (1) to replicate and extend previous work regarding the non-unitary nature of processing speed, response inhibition, and working memory during development, (2) to quantify the rate at which processing speed, response inhibition, and working memory develop and the extent to which the development of these latter abilities reflect general changes in processing speed, and (3) to evaluate whether commonly used tasks of processing speed, response inhibition, and working memory are valid and reliable when used with a developmentally diverse group. To address these aims, a latent variables approach was used to analyze data from 147 participants 6 to 24 years of age. Results showed that processing speed, response inhibition, and working memory were separable abilities and that the extent of this separability was stable cross the age range of participants. All three constructs improved as a function of age; however, only the effect of age on working memory remained significant after processing speed was controlled. The psychometric properties of tasks used to assess the constructs were age invariant, thus validating their use in studies of executive development.

Executive functions are a set of inter-related abilities that promote purposeful behavior (Lezak, 1995). Although differences among investigators remain in terms of taxonomic specifications, working memory and response inhibition have empirical support as major subdivisions within the executive collective (Huizinga, Dolan, & van der Molen, 2006; Miyake, Friedman, Emerson, Witzki, Howerter, & Wager, 2000). Working memory enables us to maintain and manipulate information that is relevant to achieving a particular goal (Baddeley & Hitch, 1974), whereas response inhibition allows us to suppress actions that are highly prepotent but which have been rendered inappropriate (Nigg, 2000). These abilities play an important role during development: improvements mediate the acquisition of other skills (e.g., Bjorklund & Douglas, 1997; McClelland, Cameron, Connor, Farris, Jewkes, & Morrison, 2007; Riggs, Jahromi, Razza, Dillworth-Bart, & Muelle, 2006; St. Clair-Thompson & Gathercole, 2006), whereas deficits have been implicated in disorders such as autism (Robinson, Goddard, Dritschel, Wisley, & Howlin, 2009) and ADHD (Martinussen, Hayden, Hogg-Johnson, & Tannock, 2005; Willcutt, Doyle, Nigg, Faraone, & Pennington, 2005).

Given the importance of working memory and response inhibition in a developmental context, there has been considerable interest in understanding how these critical abilities develop (see, for example, Welsh, Friedman, & Spieker, 2006). Working memory and response inhibition have been the focus of countless studies involving children. A general finding to emerge from this body of literature is that working memory and response inhibition improve as children age; however, studies have yielded contradictory findings regarding the precise rate at which these abilities develop and are fully mature. Take, for example, two studies in which the development of response inhibition was examined. In one study, Gerstadt, Hong, and Diamond (1994) reported that response accuracy on a Stroop-like task reached asymptote levels of performance at around 7 years of age, suggesting that response inhibition develops rapidly and is mature relatively early in life. In another study, Williams, Ponesse, Schachar, Logan, and Tannock (1999) reported that response speed on the stop signal task improved in a linear fashion in children 6 to 17 years of age, suggesting that response inhibition develops at a more protracted rate and is not mature until late adolescence or early adulthood. Similar inconsistencies characterize studies in which the development of working memory has been examined (e.g., Gathercole, Pickering, Ambridge, & Wearing, 2004; Luciana, Conklin, Hooper, & Yarger, 2005; Luciana & Nelson, 1998).

Although it is not entirely clear why studies that have ostensibly examined the same underlying construct have yielded contradictory results, one potential issue may be related to widespread use of single-task designs in which a construct is examined using only one task. One assumption of single-task designs is that tasks are pure measures of underlying constructs. This assumption is faulty, however, because all tasks are necessarily multi-factorial in nature. Take, for example, the stop signal task, in which participants must withdraw a speeded response following the presentation of a signal. The stop signal task is a commonly used measure of response inhibition because it requires that participants inhibit a prepotent tendency to respond; however, it also requires that participants perceive task instructions, comprehend task demands, maintain task set, and attend to experimental stimuli. If the proportion of variance on the stop signal task which is attributable to response inhibition is considerably smaller than that which is attributable to other cognitive processes, then the function relating task performance and age will not accurately reflect how response inhibition develops (rather, it may provide a better indication of age-related changes in goal maintenance and attention, for example). Another assumption of single-task designs is that tasks are perfectly reliable. This assumption also is faulty, because some degree of error is inherent in all tasks. Returning to the example of the stop signal task, error may arise from random sources, as when participants experience momentary lapses of attention, or from sources that are more systematic in nature, as when participants learn to anticipate the stop signal from implicit cues given by the examiner. Tasks with large amounts of error will have poor reliability and may be unlikely to produce consistent results across studies, even when the same task is used.

A related issue that may account for inconsistencies in the development literature pertains to tasks that are commonly used to assess response inhibition and working memory during development. Because most tasks were initially developed for use with adults, children and adolescents are usually administered adult-based tasks that have normative data for youth or versions of these tasks that have been modified for use with younger age groups. Tasks that are commonly used to assess response inhibition include the stop signal task, stimulus-response compatibility task, and go/no go task, whereas tasks that are commonly used to assess working memory include item recognition tasks, simple and complex span tasks, and variants of the n-back task. Although these tasks have become well-established measures of response inhibition and working memory in the development literature, remarkably little is known regarding the extent to which they provide equivalent measures of the underlying constructs in participants of different ages. Thus, it is unclear whether the psychometric properties of these tasks change over the course of development.

A final point of consideration is the extent to which processing speed is treated as a possible mediator of age-related change. Processing speed refers to the efficiency with which information is processed (Kail & Salthouse, 1994). Studies have demonstrated that age-related improvements in processing speed contribute to age-related improvements in other abilities – including those that are subsumed under the rubric of executive function, such as response inhibition (e.g., Christ, White, Mandernach, & Keys, 2001) and working memory (e.g., Fry & Hale, 1996). An illustrative example is provided by Span, Ridderinkhof, and van der Molen (2004), who administered tasks of processing speed, response inhibition, and working memory to participants 8 to 79 years of age. In their study, confirmatory factor analysis was used to test a model specifying separate latent factors of processing speed and executive function (which comprised response inhibition and working memory). Group differences between children and young adults on the executive function factor were no longer significant after the processing speed factor was statistically controlled, suggesting that developmental differences in response inhibition and working memory were mediated by differences in the efficiency with which children and young adults were able to process information. Few studies have controlled for processing speed when examining age-related changes in these constructs.

The present study was undertaken to address three related aims: (1) to replicate and extend previous work regarding the non-unitary nature of processing speed, response inhibition, and working memory during development, (2) to evaluate whether commonly used tasks of processing speed, response inhibition, and working memory are valid and reliable when used with a developmentally diverse group, and (3) to quantify the rate at which processing speed, response inhibition, and working memory develop and the extent to which the development of these latter abilities reflect more general changes in processing speed. These aims were addressed using an approach known as latent variables analysis (LVA). The advantages of LVA over traditional analytic methods have been elegantly summarized by Miyake et al. (2000) and Huizinga et al. (2006). Briefly, LVA is a multivariate approach that entails the use of multiple tasks to assess constructs of interest. The commonality amongst these tasks is then statistically extracted, resulting in latent variables which exclude variance due to error and to idiosyncratic properties of individual tasks. Compared with individual tasks, latent variables are more reliable and provide purer measures of underlying constructs. Because LVA circumvents many of the limitations that are associated with single-task designs, it is well-suited for exploring questions regarding the organization and development of executive functions.

Method

Participants

One-hundred-fifty-three participants were recruited from Washington University and the St. Louis community. Participants ranged from 6 to 24 years of age and comprised four age groups: early childhood (6 to 8 years), late childhood (9 to 12 years), adolescence (13 to 17 years), and young adulthood (18 to 24 years). It was expected that very young children would not be able to participate in the study without the tasks being substantially modified (e.g., longer stimulus durations, fewer trials, etc.). As such, a lower age limit of 6 years was selected to reduce the problem of measurement invariance. An upper age limit of 24 years was selected because performance on tasks of processing speed, response inhibition, and working memory was expected to reach asymptote by this age. Despite these restrictions, we believe that our age range permitted us to examine meaningful changes in each construct of interest. No participants had a history of diagnosed attention or learning disability, major medical or psychiatric illness, neurological injury with loss of consciousness, or mental retardation. Demographic information is presented in Table 1.

Table 1.

Participant Demographics

	Age Group
	Early Childhood	Late Childhood	Adolescence	Young Adulthood	Group Difference
N	38	38	39	38
Gender (F:M)	21:17	17:21	19:20	19:19	NS
% Caucasian	79	84	77	66	NS
Mean (SD) Years of Age	7.8 (.8)	11.1 (1.1)	15.0 (1.4)	21.1 (1.7)	EC < LC < A < YA**
Mean (SD) Years of Education	1.8 (1.0)	5.1 (1.1)	9.0 (1.5)	13.7 (1.3)	EC < LC < A < YA**
Mean (SD) Vocabulary T Score	60.9 (13.2)	60.1 (8.2)	56.6 (8.4)	60.8 (7.1)	NS
Mean (SD) Matrix Reasoning T Score	58.4 (9.7)	56.7 (8.7)	52.5 (7.2)	57.5 (6.4)	A < EC, LC, YA*
Mean (SD) IQ	118.6 (15.4)	115.1 (13.2)	108.1 (11.7)	116.2 (8.4)	A < EC, LC, YA**

NS denotes an effect in which p > .05.

^**p < .001.

^*p < .05

Procedure

The study was conducted in a single session lasting 2.5 to 3 hours, including time for breaks. Informed consent and assent (for participants younger than 18) were obtained at the outset of the session. During the session, participants worked with a trained research assistant in a separate room of the lab in which distractions were minimized. Tasks were administered in the same order for all participants (Vocabulary, Go/No-Go, Word List – Part I, Recognition Span – Shape/Location, Digit Span, Recognition Span – Location/Shape, Word List – Part 2, Matrix Reasoning, 2-Back – Letter/Location, Simple Reaction Time, 2-Back – Location/Letter, Verbal Fluency, Stimulus-Response Compatibility, Wechsler Individual Achievement Test). Some of these tasks are the focus of a separate study and will not be discussed here further. Youth received $10 and young adults received 1 course credit for each hour of participation. This procedure was approved by the Research Ethics Board at Washington University in St. Louis.

Measures

Several criteria were established to guide the selection of tasks, including (1) being well-established in the development literature, (2) possessing good psychometric properties (e.g., adequate distribution of scores and lack of floor or ceiling effects across the age range), and (3) showing evidence of robust age-related change above and beyond that which is attributable to processing speed. All of the tasks that were selected for inclusion in our study met these criteria based on either pilot data from our lab or on other published works.

Wechsler Abbreviated Scale of Intelligence

The two-subtest version of the Wechsler Abbreviated Scale of Intelligence (Wechsler, 1999) was administered to estimate general intellectual functioning. Participants were required to define words (Vocabulary) and complete complex visual designs (Matrix Reasoning). For each subtest, raw scores were converted to T scores using normative data from same-aged participants. These T scores were summed to estimate overall IQ.

Simple Reaction Time Task

The simple reaction time task assessed processing speed (e.g., Kiselev, Espy, & Sheffield, 2010). On each trial, a fixation appeared at the center of the screen for 300 ms and was followed by a blank interstimulus interval of 600 to 2400 ms. After the interstimulus interval, an arrow appeared at the centre of the screen and remained visible until participants pressed the spacebar or 2000 ms elapsed. Participants were instructed to respond to the arrow as quickly and as accurately as possible and were provided with feedback after each response. Following disappearance of the arrow, there was a blank intertrial interval of 1000 ms before the next trial began. Ten practice trials and 40 experimental trials were administered. Response speed and accuracy were recorded. Mean correct RT was selected as an indicator for the LVA.

Go/No-Go Task

Go and no-go trials of the task assessed processing speed and response inhibition, respectively (e.g., Brocki & Bohlin, 2004). One of four shapes (circle, square, triangle, or diamond) was randomly designated as a non-target for each participant. On each trial, a shape appeared at the center of a screen and remained visible until participants pressed the spacebar or 2000 ms had elapsed. Participants were instructed to respond as quickly and as accurately as possible any time a target shape appeared (i.e., go trial) but to withhold their response whenever the non-target shape appeared (i.e., no-go trial). Feedback was provided after each response. Following disappearance of the shape, there was a blank intertrial interval of 1000 ms before the next trial began. Twenty practice trials and 200 experimental trials were administered. Experimental trials consisted of 150 go trials and 50 no-go trials that were presented in the same pseudorandom sequence for each participant. Response speed and accuracy were recorded. The no-go false alarm rate was computed by dividing the number of incorrect responses on a no-go trial divided by the total number of no-go trials. Mean correct go RT and the no-go false alarm rate were selected as indicators for the LVA.

Stimulus-Response Compatibility Task

The compatible and incompatible conditions of the stimulus-response compatibility task assessed processing speed and response inhibition, respectively (e.g., Christ et al., 2000). These conditions were presented in a blocked format. At the beginning of each block, instructions appeared on the computer screen and were read aloud by the examiner. In the compatible condition, participants were instructed to press ‘v’ when the left circle turned grey and ‘m’ when the right circle turned grey (i.e., response button on the same side as the stimulus). In the incompatible condition, participants were instructed to press ‘m’ when the left circle turned grey and ‘v’ when the right circle turned grey (i.e., response button on the opposite side of the stimulus). In both conditions, each trial began with the presentation of three horizontally aligned circles at the center of the screen. After 300 ms, the central circle was highlighted for 500 ms and then 300 ms later one of the peripheral circles turned grey. The circles remained on the screen until participants pressed a response key or 3000 ms elapsed. Participants were instructed to respond as quickly and as accurately as possible. After the circles disappeared, there was a blank intertrial interval of 2000 ms before the next trial began. Participants completed a practice block of 10 compatible trials followed by a practice block of 10 incompatible trials and then 96 test trials in which the two conditions were presented in alternating blocks of 16 trials each. Response speed and accuracy were recorded. Error rates were computed by dividing the number of incorrect responses by the total number of trials. Because the inclusion of mean correct RT and error rate from the same condition would cause some of our models to be underidentified¹, mean correct RTs were selected for inclusion in the LVA as they provided a broader range of values across the age range of participants.

2-Back Task

The letter and location conditions of the 2-back task assessed working memory updating (e.g., Vuontela, Steenari, Carlson, Koivisto, Fjällberg, & Aronen, 2003). On each trial, one of nine letters (A, C, F, H, J, N, P, Q, S) appeared at one of nine locations along an imaginary circle eccentric to a central fixation. The letter remained on the screen until participants pressed the spacebar or 2000 ms elapsed. In the letter condition, participants were instructed to press the spacebar any time the letter on the current trial was the same as the letter that appeared two trials previously (regardless of location). In the location condition, participants were instructed to press the spacebar any time the location on the current trial was the same as the location that appeared two trials previously (regardless of the letter). Participants were instructed to respond as quickly and as accurately as possible and were provided with feedback after every response. Following disappearance of the letter, an intertrial interval of 1000 ms was presented before the next trial began. Twenty-four practice trials and 96 experimental trials were administered in each condition. Response speed and accuracy were recorded. Error rates were computed by dividing the sum of incorrect responses on a non-target trial and failures to respond on a target trial by the number of trials that were presented. Because the inclusion of mean correct RT and error rate from the same condition would cause some of our models to be underidentified², error rates were selected for inclusion in the LVA as they varied across our age range of participants and were derived from all trial types (unlike mean correct RT, which was derived from trials on which a correct response was made).

Recognition Span Task

The shape and location conditions of the recognition span task assessed working memory storage (e.g., Lehto, Juujarvi, Kooistra, & Pulkkinen, 2003; Luciana & Nelson, 1998). On each trial, a series of shapes (ranging in number from 2 to 12) appeared at different locations in a 3×4 grid, with each shape remaining on the screen for 1500 ms and separated by a 500 ms blank interstimulus interval. After presentation of the last shape in the series, the grid appeared with all 12 shapes in all 12 locations and remained on the screen until participants indicated the order in which the shapes or locations had appeared. In the shape condition, participants were instructed to point to the shapes in correct serial order (regardless of location). In the location condition, participants were instructed to point to the locations in correct serial order (regardless of shape). An intertrial interval of 500 ms was then presented before the next trial began. In each condition, participants completed 12 discrimination trials (1 shape or location in a series), 2 practice trials (2 shapes or locations in a series), and 18 experimental trials (2 to 12 shapes or locations in a series). Experimental trials were administered using a staircase method, such that correct responses resulted in an item being added to the series (to a maximum of 12 items), whereas incorrect responses resulted in an item being subtracted from the series (to a minimum of 2 items, which also was the starting point). The maximum number of items recalled in the shape and location conditions was selected as an indicator for the LVA.

Digit Span Task

The forward and backward conditions of the Digit Span subtest from the Wechsler Intelligence Scale for Children – III (Wechsler, 1991) assessed working memory storage and updating, respectively. The task required that participants listen to a series of digits and repeat the series in correct forward or backward order. Two trials were presented at each level of difficulty. Presentation began with two digits in a series. As the level of difficulty increased, the number of digits presented in a series increased by 1 to a maximum of 9. The test was discontinued when both trials at a given level of difficulty were incorrectly recalled. One point was allocated for each correct response for a maximum of 16 points. The number of points recorded in the forward and backward conditions was selected as an indicator for the LVA.

Data Preparation

Data were missing for 1 participant (early childhood group) on the stimulus-response compatibility task due to experimenter error and for 6 participants (2 each from the early childhood and late childhood groups and 1 each from the adolescent and young adult groups) on the go/no-go task due to a programming glitch. Missing values were replaced using the method of data imputation provided by LISREL 8.80 (Jöreskog & Sörbom, 2006). Using this procedure, missing values were replaced with m > 1 data sets. The m data sets were then combined to obtain unbiased overall estimates and standard errors. Technical details of this procedure are provided by Schafer (1997).

Analyses of RT were conducted using only trials on which correct responses were made. Trials on which anticipatory, omission, or accuracy errors occurred were excluded from analyses. For all RT tasks, anticipatory errors were defined as responses executed within 200 ms of stimulus onset and omission errors were defined as failures to execute a response within 2000 to 3000 ms of stimulus onset, depending on the task. Accuracy errors were defined as incorrect key press responses. Individual RTs that exceeded 3 standard deviations of the overall mean were replaced with a value that was exactly ± 3 standard deviations from the mean of the entire sample. This method of replacement affected less than 1% of observations.

Descriptive statistics for the tasks are presented in Table 2. Reliability was assessed using Cronbach’s alpha (except for the Digit Span Task, which was assessed using the split-half method and is reported here from the manual for the WISC-III). Internal consistency was generally high, with the exception of the go/no-go task. Because the no-go false alarm rate did not change as a function of age and had low associations with other measures of response inhibition (rs with mean correct RT and error rate from the incompatible condition of the stimulus-response compatibility task were .13 and .28, respectively), this indicator was dropped from further analyses. This left a final set of 10 indicators to assess processing speed, response inhibition, working memory storage, and working memory updating in the LVA.

Table 2.

Descriptive Statistics for Tasks as a Function of Age Group

	Age Group
	Early Childhood		Late Childhood		Adolescence		Young Adulthood
Task (Reliability)	M	SD	M	SD	M	SD	M	SD	Age Association
Simple Reaction Time (.96)
RTa	467.11	112.93	375.89	69.50	347.07	67.18	281.60	40.69	−.65**
SRC Compatible Condition (.96)
RTa	636.92	188.73	489.14	198.49	386.72	75.79	325.94	53.49	−.61**
Error Rate	.04	.05	.03	.04	.01	.02	.01	.01	−.42**
SRC Incompatible Condition (.95)
RTb	796.32	234.06	575.91	239.72	447.46	106.58	364.43	61.55	−.64**
Error Rate	.12	.10	.08	.06	.05	.05	.02	.02	−.46**
Go/No-Go (.49)
Go RTa	540.77	100.65	447.78	81.80	398.91	90.00	330.21	48.48	−.67**
No-Go False Alarm Rateb	.10	.09	.09	.05	.06	.05	.09	.06	−.11
Digit Span (.85)
Forward Totalc	8.13	1.93	9.61	1.91	10.08	2.22	11.61	2.72	.47**
Backward Totald	4.42	1.73	5.76	1.75	6.33	1.97	8.03	2.64	.56**
RS Shape Condition (.92)
Maximum Spanc	3.58	1.00	4.82	1.14	5.00	0.76	5.61	0.97	.58**
RS Location Condition (.94)
Maximum Spanc	5.37	1.00	6.08	0.97	6.67	0.93	7.21	0.99	.60**
2B Letter Condition (.81)
RT	1035.54	126.37	886.44	137.62	720.10	130.08	666.92	126.03	−.71**
Error Rated	.21	.11	.12	.07	.08	.05	.05	.06	−.61**
2B Location Condition (.92)
RT	997.33	160.10	815.39	155.48	682.46	132.07	590.80	109.99	−.71**
Error Rated	.22	.13	.09	.09	.06	.07	.03	.03	−.58**

^**p < .001

^aIndicators selected to assess processing speed (Cronbach’s alpha = .87).

^bIndicators selected to assess response inhibition (Cronbach’s alpha = .07).

^cIndicators selected to assess working memory storage (Cronbach’s alpha = .69).

^dIndicators selected to assess working memory updating (Cronbach’s alpha = .47).

To satisfy the assumptions required for confirmatory factor analysis (CFA; Kline, 2005), the final set of 10 task indicators was subjected to further processing to ensure that all data were univariate, bivariate, and multivariate normal. Univariate normality was achieved by transforming indicators that had significantly skewed and/or kurtotic distributions (i.e., distributions in which either of these values was greater than twice the standard error). Bivariate normality was achieved by inspecting scatterplots of each pairwise combination of indicators and identifying participants who were outliers. Lastly, multivariate normality was achieved by computing Mahalanobis’ d² to determine the extent to which participants deviated from the population centroid. Participants with disproportionately large values of Mahalanobis’ d² also were identified. Six participants were excluded from analyses during this process, including 2 in the early childhood group, 2 in the late childhood group, 1 in the adolescent group, and 1 in the young adult group.

In the last stages of data preparation, total scores from the forward and backward conditions of the digit span task and maximum spans from the shape and location conditions of the recognition span tasks were inflected to ensure that higher values denoted worse performance across all indicators. Several of the indicators also were re-scaled to ensure that the indicator with the largest variance did not differ from the indicator with the smallest variance by more than a factor of 10. Re-scaling was done to avoid the computational pitfalls that may arise when variables have greatly different variances (Kline, 2005).

Results

Models of Processing Speed, Response Inhibition, and Working Memory

Based on prior studies of children (Brocki & Bohlin, 2004; Huizinga et al., 2006; Lehto et al., 2003) and young adults (Miyake et al., 2000), it was hypothesized that processing speed, response inhibition, working memory storage, and working memory updating would be separable abilities in individuals between 6 and 24 years of age. To test this hypothesis, four multi-group measurement models were simultaneously fit to the covariance matrices of the early childhood, late childhood, adolescent, and young adult groups (Appendix A). The models differed with respect to the number of latent factors that were specified: the one-factor model consisted of a single latent factor representing general resources (CFA 1), the two-factor model specified separate latent factors of processing speed and executive function (CFA 2), the three-factor-model specified separate latent factors of processing speed, response inhibition, and working memory (CFA 3), and the four-factor model specified separate latent factors of processing speed, response inhibition, working memory storage, and working memory updating (CFA 4). All analyses were conducted with LISREL 8.80 (Jöreskog & Sörbom, 2006) using maximum likelihood estimation. Latent factors were assigned a scale by imposing a unit loading identification constraint (i.e., the factor loading of a reference variable was set to equal 1.0). Because errors in the compatible and incompatible conditions of the stimulus-response compatibility task were expected to correlate over time (given the blocked nature of the task), the error terms of these conditions were allowed to covary in each model.

Appendix A.

Covariance Matrix of Task Indicators Used in the Latent Variables Analysis as a Function of Age Group

Group		Indicator	1	2	3	4	5	6	7	8	9	10
Early Childhood (n = 36)	1	Simple RT	.63
	2	SRC Compatible RT	1.63	14.60
	3	GNG Go RT	.35	1.65	.49
	4	SRC Incompatible RT	1.86	15.32	1.56	20.06
	5	DS Forward Total	.39	1.81	.59	1.77	3.82
	6	DS Backward Total	.48	2.62	.47	3.84	2.07	4.05
	7	RS Max Shape	.25	1.07	.17	1.31	.51	.91	.99
	8	RS Max Location	.26	1.67	.31	1.91	.94	.59	.49	.85
	9	2B Location Error Rate	.04	.19	.02	.27	.04	.10	.07	.06	.02
	10	2B Letter Error Rate	.03	.11	.01	.18	.05	.04	.06	.03	.01	.01
Late Childhood (n = 36)	1	Simple RT	.56
	2	SRC Compatible RT	1.99	19.04
	3	GNG Go RT	.37	2.51	.58
	4	SRC Incompatible RT	2.20	19.29	2.73	24.40
	5	DS Forward Total	−.23	2.32	.04	1.53	3.77
	6	DS Backward Total	.11	.95	.14	1.67	1.08	3.45
	7	RS Max Shape	.13	.82	.09	1.19	.85	.95	1.30
	8	RS Max Location	.24	1.52	.23	2.32	.07	.25	.43	.71
	9	2B Location Error Rate	.03	.11	.02	.18	−.01	.03	.06	.06	.02
	10	2B Letter Error Rate	.01	.14	.03	.21	.03	.05	.04	.03	.01	.01
Adolescence (n = 38)	1	Simple RT	.48
	2	SRC Compatible RT	1.63	12.82
	3	GNG Go RT	.24	1.40	.43
	4	SRC Incompatible RT	1.95	12.51	1.78	17.55
	5	DS Forward Total	.43	2.82	.09	2.45	4.70
	6	DS Backward Total	.37	2.87	.27	3.38	1.57	4.05
	7	RS Max Shape	.26	.95	.08	1.28	.73	.36	.58
	8	RS Max Location	.15	.73	.18	1.77	.42	.41	.10	.89
	9	2B Location Error Rate	.03	.14	.00	.22	.01	.10	.02	.06	.02
	10	2B Letter Error Rate	.03	.12	.02	.17	.07	.09	.03	.04	.01	.01
Young Adulthood (n = 37)	1	Simple RT	.36
	2	SRC Compatible RT	1.68	12.22
	3	GNG Go RT	.23	1.28	.37
	4	SRC Incompatible RT	1.68	11.51	1.41	13.16
	5	DS Forward Total	.43	2.68	.61	3.14	6.69
	6	DS Backward Total	.50	3.45	.41	3.08	2.83	5.59
	7	RS Max Shape	.25	1.67	.24	1.42	1.48	1.05	.97
	8	RS Max Location	.12	.85	.22	.83	.84	.97	.39	.99
	9	2B Location Error Rate	.02	.19	.00	.16	.10	.14	.04	.02	.02
	10	2B Letter Error Rate	.00	.01	.00	−.03	.10	.06	.02	.04	.00	.01

Fitting of the models occurred in order of increasing complexity (i.e., parameters were successively added), beginning with the model that had the fewest latent factors (CFA 1) and ending with the model that had the most latent factors (CFA 4). A variety of indices were used to evaluate model fit: the χ² statistic and Root Mean Square Error of Approximation (RMSEA) were selected to provide measures of global fit, the Comparative Fit Index (CFI) was selected to provide a measure of incremental fit, and Akaike’s Information Criterion (AIC) was selected to provide a measure of parsimonious fit. These indices were selected because they provide information about different types of model fit and have the desirable property of being relatively insensitive to small sample sizes (e.g., N < 150, Hu & Bentler, 1995). The fit of the models was directly compared using the χ² difference test, which determined whether fit improved as a function of increasing model complexity. The χ² difference test was conducted by subtracting the value of χ² for the nested model from the value of χ² for the fuller model and assessing the significance of the χ² difference using the appropriate degrees of freedom (df_full – df_nested). A model was retained when (1) indices of absolute, incremental, and parsimonious fit were adequate (i.e., a non-significant χ² , RMSEA less than .05, an upper bound of the 90% confidence interval for the RMSEA less than or equal to .08, a CFI of .95 or higher, and a low value of AIC relative to the other models tested), (2) the χ² difference test was significant, and (3) all parameters within the model were significant and in the expected direction.

As shown in Table 3, indices of absolute, incremental, and parsimonious fit were poor for the first two models but were generally acceptable for the three and four-factor models. These findings indicate that the covariance matrices implied by the models were a good fit to the covariance matrix generated by the sample, that the models had an acceptable amount of error, that the models provided a better fit relative to the null model (i.e., a model assuming no covariances amongst the indicators), and that the overall good fit of the models did not simply reflect the inclusion of more parameters. Because a direct comparison of the models revealed that the three-factor model was statistically superior to the four-factor model (as revealed by a non- significant χ² difference) and all parameters in this model were significant and in the expected direction (ps < .05), the three-factor multi-group measurement model was retained. This model is consistent with the hypothesis that processing speed, response inhibition, and working memory are separable abilities in participants spanning a broad age range.

Table 3.

Fit Indices for the Multi-group Measurement Models

CFA	Factors	χ2	df	p	RMSEA	90% CI	CFI	AIC
1	G	253.49	136	< .001	.16	.13 –.19	.86	421.49
2	PS EF	227.88	132	<.001	.14	.11 – .17	.88	403.88
3	PS INH WM	149.03	128	.10	.07	.00 – .11	.95	333.03
4	PS INH WMS WMU	139.80	116	.07	.08	.00 – .12	.95	347.80

Comparison	Description	Δχ2	Δdf	p
CFA 1 vs. 2	G fractionated into PS and EF	25.61	4	<.001
CFA 2 vs. 3	EF fractionated into INH and WM	78.85	4	<.001
CFA 3 vs. 4	WM fractionated into WMS and WMU	9.23	12	.68

Note: G = general resource, EF = executive function, PS = processing speed, INH = response inhibition, WM = working memory, WMS = working memory storage, WMU = working memory updating.

Age Invariance of Processing Speed, Response Inhibition, and Working Memory Tasks

Although the tasks selected for inclusion in our study are commonly used in developmental studies, we had no a priori hypotheses regarding the extent to which they would provide equivalent measures of the underlying constructs in individuals 6 to 24 years of age. Metric invariance was explored by assessing three variations of the three-factor multi-group measurement model. The models differed in the number of constraints that were imposed across the early childhood, late childhood, adolescent, and young adult groups. To determine whether associations amongst the latent factors were equivalent across groups, the first variation placed a constraint on factor correlations (CFA 5). To determine whether associations between indicators and latent factors also were equivalent across groups, the second variation placed constraints on factor correlations and factor loadings (CFA 6). In the third variation of the model, factor correlations, factor loadings, and error variances were all constrained to be equal across groups (CFA 7). This latter model provided the most stringent test of metric invariance and enabled us to determine whether the reliability of the indicators was similar across the age range of participants. Fitting of the models was conceptually similar to that which was previously described, except that models were fit in order of decreasing complexity (i.e., parameters were successively removed). Thus, a model was retained when (1) fit indices were adequate (as previously defined), (2) the χ² difference test was not significant, and (3) all parameters within the model were significant and in the expected direction.

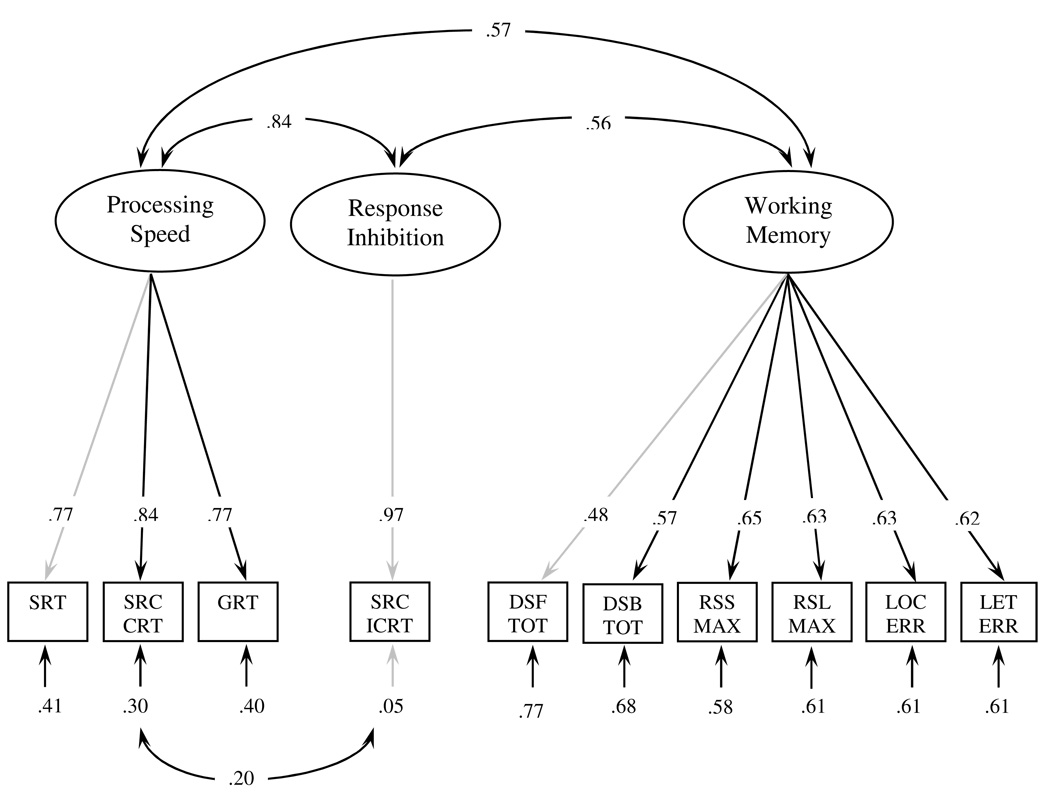
As shown in Table 4, indices of absolute, incremental, and parsimonious fit were acceptable for all three variations of the three-factor multi-group measurement model. Direct comparison of the models revealed that the imposition of constraints did not cause an appreciable degradation in model fit (as revealed by a non-significant χ² difference) and that all parameters in the fully constrained model were significant and in the expected direction (ps < .05). Based on these results, the fully constrained variation of the three-factor measurement model was retained (Figure 1). This model is consistent with the hypothesis that measures of processing speed, response inhibition, and working memory are valid and reliable in participants spanning a broad age range.

Table 4.

Fit Indices for Models of Invariance

CFA	Constraint	χ2	df	p	RMSEA	90% CI	CFI	AIC
4	None (original model)	149.03	128	.09	.07	.00 – .11	.95	333.03
5	Factor correlations	168.52	149	.13	.06	.00 – .10	.94	310.52
6	Factor correlations and factor loadings	184.17	170	.22	.05	.00 – .09	.94	284.17
7	Factor correlations, factor loadings, and error variances	212.34	197	.22	.05	.00 – .09	.94	258.34

Comparison	Description	Δχ2	Δdf	p
CFA 4 vs. 5	Effect of constraining factor correlations	19.49	21	.55
CFA 5 vs. 6	Effect of further constraining factor loadings	15.65	21	.79
CFA 6 vs. 7	Effect of further constraining error variances	27.64	27	.43

Figure 1.

Standardized solution for the three-factor multi-group measurement model with latent factors of processing speed, response inhibition, and working memory. SRT = Simple RT; SRC-CRT = Stimulus-Response Compatibility Task - Compatible RT; GRT = Go/No-Go Go RT; SRC-ICRT = Stimulus-Response Compatibility Task - Incompatible RT; DSF TOT = Digit Span Forward Total Score; DSB TOT = Digit Span Backward Total Score; RSS MAX = Recognition Span - Maximum Shape Span; RSL MAX= Recognition Span - Maximum Location Span; LOCERR = 2-Back Location Error Rat; LETERR = 2-Back Letter Error Rate.

Development of Processing Speed, Response Inhibition, and Working Memory

Given the extant developmental literature, it was hypothesized that processing speed, response inhibition, and working memory would improve in a non-linear manner in individuals between 6 and 24 years of age and that age-related improvements in the latter two constructs would be mediated by concomitant improvements in processing speed. Age-related change on the latent factor scores was examined using two sets of hierarchical regression analyses, the results of which are presented in Table 5. Age was treated as a continuous variable in both analyses.

Table 5.

Hierarchical Regression Analyses of Latent Factor Scores

Construct	Model		ΔR2	ΔF	β	t
	Step 1:	Age	.64	251.64**	−.80	15.86**
Processing Speed	Step 2:	Age	.05	20.38**	−2.16	−7.07**
		Age × Age			1.38	4.51**
	Step 1:	Age	.60	217.95**	−.78	−14.76**
	Step 2:	Age	.06	23.86**	−2.30	−7.28**
		Age × Age			1.54	4.88**
	Step 1:	Processing Speed	.89	1233.94**	.95	35.13**
Response Inhibition	Step 2:	Processing Speed	.001	1.72	.90	20.20**
		Age			−.06	−1.31
	Step 3:	Processing Speed	.003	3.53	.87	18.40**
		Age			−.43	−2.12*
		Age × Age			.35	1.88
Working Memory	Step 1:	Age	.40	95.06**	−.63	−9.75**
	Step 2:	Age	.04	9.81*	−1.89	−4.65**
		Age × Age			1.27	3.13*
	Step 1:	Processing Speed	.73	402.11**	.86	20.05**
	Step 2:	Processing Speed	.01	4.44*	.98	13.92**
		Age			.15	2.11*
	Step 3:	Processing Speed	.000	.08	.98	13.08**
		Age			.24	.74
		Age × Age			−.08	−.28

Note: Age denotes the linear effect of age. Age × Age denotes the quadratic effect of age.

^**p < .001,

^*p < .05

In the first set of analyses³, scores for a given latent factor served as the dependent variable, the linear effect of age was entered as an independent variable in the first step, and the quadratic effect of age was entered as an independent variable in the second step. In this way, it was possible to determine whether the relationship between age and latent factor scores was best characterized by a linear function (i.e., a significant effect of age to the first order) or non-linear function (i.e., significant effect of age to the second order). In instances in which the relationship between age and latent factor scores was non-linear, either the minimum or maximum of the quadratic function was computed to determine the age at which there were no further improvements in the underlying construct. Results revealed significant linear and quadratic effects of age on processing speed, response inhibition, and working memory. Each construct improved most rapidly between early to late childhood and showed minimal improvements thereafter. Inflection points occurred at 23.3 years for processing speed, 21.5 years for response inhibition, and 21.1 years for working memory.

The second set of analyses⁴ were similar to those just described, except that processing speed was entered as an independent variable in the first step whilst the linear and quadratic effects of age were entered as independent variables in the second and third steps, respectively. This enabled us evaluate the contribution of processing speed to age-related change in the other two constructs. Results revealed that processing speed accounted for a significant proportion of variance in response inhibition (89%) and working memory (73%)⁵. After controlling for processing speed, only the linear effects of age on working memory remained significant. These findings indicate that age-related improvements in response inhibition and working memory are largely mediated by concomitant improvements in processing speed, but that working memory shows an independent effect of age even after the contribution of processing speed is taken into account.

Given significant age group differences in IQ, one may question whether age-related improvements in processing speed, response inhibition, and working memory were attributable to age-related differences in overall level of intellectual function. To address this concern, we re-ran both sets of regression analyses controlling for IQ and the interaction of IQ and age. Neither effect approached significance (ps > .10) and the overall pattern of results was unchanged.

Discussion

The organization of executive abilities during development has been the focus of considerable empirical study. Previous work has demonstrated that processing speed is separable from response inhibition and working memory (Span et al., 2004), that response inhibition and working memory also are separable (Brocki & Bohlin, 2004; Huizinga et al., 2006; Lehto et al., 2003), and that the tripartite structure of working memory is in place by early to mid childhood (Gathercole et al., 2004; Kail & Hall, 2001). Our first aim was to replicate and extend this body of work by examining the non-unitary nature of processing speed, response inhibition, and working memory in the context of a single study with participants spanning a broad age range. To determine whether the theoretical distinction amongst these constructs was empirically supported, LVA was used to to assess four a priori measurement models that were simultaneously fit to early childhood, late childhood, adolescent, and young adult groups. The three-factor and four-factor measurement models provided reasonably good fits to the covariance matrices that were generated by our sample. Both models specified separate latent constructs of processing speed and response inhibition but varied in their treatment of working memory: working memory was represented as a unitary construct in the three-factor model but was fractionated into separate storage and updating components in the four-factor model. Although the four-factor model was more consistent with theories of working memory (e.g., Baddeley & Hitch, 1974) and empirical work has shown that these components are behaviorally dissociable (Kail & Hall, 2001) and mediated by different neural substrates (see Wager & Smith, 2003, for a review), the more parsimonious three-factor model was retained because it was statistically superior to the four-factor model in direct model comparisons.

The results of our study indicate that processing speed, response inhibition, and working memory are statistically separable by 6 years of age and that the extent of this separability is stable until 24 years of age. Although our results highlight invariance in the organization of executive function during much of development, a growing body of evidence suggests that executive functions emerge as a unitary ability in the preschool years (Wiebe, Espy, & Charak, 2008; Wiebe, Sheffield, Nelson, Clark, Chevalier, & Espy, in press; Willoughby, Blair, Wirth, & Greenberg, 2010) and become fractionated into dissociable yet inter-related components shortly thereafter (Brocki & Bohlin, 2004; Huizinga et al., 2006; Lehto et al., 2003). Qualitative changes in the organization of executive function are consistent with the age-differentiation hypothesis of cognition (e.g., Garrett, 1946; Li, Lindenberger, Hommel, Aschersleben, Prinz, & Baltes, 2004), which posits that cognitive abilities arise from a unitary construct that becomes increasingly differentiated as children age. Our understanding of this process as it applies to executive functions is currently quite limited; however, this will be an interesting avenue to pursue in future research.

Although the tasks of processing speed, response inhibition, and working memory that were used in our study are well-established in the development literature, remarkably little is known regarding the extent to which they possess psychometric properties that are stable across development. To determine whether these tasks provide equivalent measures in individuals of different ages, a series of constraints was added to parameters in the best-fitting multi-group measurement model described above. The most restrictive version of the model, which provided the strictest test of metric invariance, constrained factor correlations, factor loadings, and error variances across the early childhood, late childhood, adolescent, and young adult groups. Factor loadings may be interpreted as validity coefficients and error variances may be interpreted as reliability coefficients and approximations to Chronbach’s α (Jöreskog & Sörbom, 1993). Constraining these parameters did not produce an appreciable degradation in model fit, indicating that the tasks used in our study were valid and reliable in participants spanning our age range.

Having established that the psychometric properties of our tasks were age invariant, the final aim of our study was to examine the rate at which latent factors of processing speed, response inhibition, and working memory develop. We found that processing speed, response inhibition, and working memory improved most rapidly between early and late childhood and reached a plateau in early adulthood. After controlling for processing speed, only the effect of age on working memory remained significant. These results are consistent with previous work showing that processing speed, response inhibition, and working memory have a protracted course of development (e.g., Kail, 1991; Jerger, Pearson, & Spence, 1999; Luna, Garver, Urban, Lazar, & Sweeny, 2004 ; Williams et al; 1999; Wright, Waterman, Prescott, & Murdoch-Eaton, 2003) and that age-related improvements in these latter abilities are ameliorated once age-related improvements in processing speed are taken into account (e.g., Christ et al., 2001; Fry & Hale, 1996; Span et al., 2004).

Although there is a paucity of research in which the developmental interrelationships among executive abilities have been modeled, it has been suggested that age-related improvements in processing speed, response inhibition, and working memory may unfold via a developmental cascade. Consistent with this notion, there is a growing body of evidence showing that processing speed mediates gains in other cognitive abilities – including those that are subsumed under the rubric of executive function (Christ et al., 2001; Fry & Hale, 1996; Kail, 2007; Nettlebeck & Burns, 2010; Span et al., 2004). In the context of our cross-sectional study, we found that processing speed accounted for considerable variance in working memory and response inhibition across development. One possible explanation of this finding is that increases in processing speed enable children to maintain and manipulate more information during the acquisition of goals and to more quickly interpret contextual cues which determine whether or not a behavior is appropriate for goal attainment. These ideas are speculative, however, and require empirical study.

Several limitations of our study warrant mention. First, the scope of our study was limited to two critical aspects of the executive construct – namely, working memory and response inhibition. These abilities were selected for several reasons: they are common to many different theories of executive function, suggesting a degree of consensus in terms of their centrality in understanding executive processing (e.g., Lyon & Krasnegor, 2002), they are thought to play an important role in the context of typical and atypical development (e.g., Welsh, 2002), and they are well represented in the development literature (e.g., Diamond, 2006). Although cognitive flexibility has been identified as another critical component of the executive collective (Huizinga et al., 2006; Lehto et al., 2003; Miyake et al., 2000), this construct was not examined in our study.

Second, response inhibition was measured using a single indicator and thus was subject to the same limitations that are associated with single-task designs (i.e., task impurity and error). It is unclear whether this limitation would have been rectified my including more indictors, however, as other studies have shown that multiple indicators of response inhibition fail to converge upon a unitary construct (Huizinga et al., 2006; van der Sluis, de Jong, & van der Leij, 2007). This lack of convergence may suggest that tasks which are commonly used to assess response inhibition in youth actually assess other aspects of the inhibitory construct. For example, Friedman and Miyake (2004) have demonstrated that at least two components of inhibition may be dissociated: the ability to resist memory intrusions from previously relevant information (i.e., resistance to proactive interference) and the ability to ignore irrelevant information and suppress the expression of dominant, automatic, and prepotent responses (i.e., distractor-response inhibition). In future studies, it will be important to include a wider variety of measures that capture these different facets of inhibitory control.

Lastly, we limited our age range of participants to 6 and 24 years of age. A lower age limit of 6 years was selected to minimize problems associated with the selection of appropriate tasks. However, imposition of this lower age limit precluded us from assessing models of processing speed, response inhibition, and working memory in preschool-age children and examining how these constructs change earlier in development. Though beyond the scope of our paper, a review of this literature is provided by Garon, Bryson, and Smith (2008).

In spite of these limitations, the present investigation used a relatively novel statistical approach to validate measures of processing speed, response inhibition, and working memory that are commonly used in developmental studies and to address unanswered questions regarding the organization and maturation of these abilities in the period spanning childhood to young adulthood. In so doing, we have demonstrated that latent variables analysis is a versatile statistical tool that has the potential to make a significant contribution to future studies of executive development.