Using tensor product splines in modeling exposure–time–response relationships: Application to the Colorado Plateau Uranium Miners cohort

SUMMARY

An adequate depiction of exposure–time–response relationships is important in assessing public health implications of an occupational or environmental exposure. Recent advances have focused on flexible modeling of the overall shape of latency. Methods are needed to allow for varying shapes of latency under different exposure profiles. A tensor product spline model is proposed for describing exposure–response relationships for protracted time-dependent occupational exposure histories in epidemiologic studies. The methods use flexible multi-dimensional techniques to jointly model age, latency and exposure–response effects. In analyzing data from the Colorado Plateau Uranium Miners cohort, a model that allows for varying exposure-dependent latency shapes is found to be superior to models that only allowed for an overall latency curve. Specifically, the model suggests that, at low exposure levels risk increased at short latencies followed by a slow decline for longer latency periods. On the other hand, risk was higher but did not change much by latency for higher exposure levels. The proposed methodology has the advantage of allowing for latency functions that vary by exposure levels and, conversely, exposure–response relationships that are influenced by the latency structure.

INTRODUCTION

In examining the risk of chronic diseases (e.g. cancer), one should properly model not only the exposure–response relationship but also the effect of time since exposure (usually known as latency). Although this is relatively straight-forward for ‘instantaneous’ exposures, e.g. radiation exposure from the atomic bomb explosions, because time since exposure is well defined, problems occur when dealing with ‘protracted’ exposure histories that are received incrementally over many years, as in most occupational or environmental exposures. Time since exposure is no longer clearly defined for such extended exposures, and using time since first or last exposure arbitrarily singles out the first or last exposure as particularly meaningful. Moreover, most epidemiologic analyses so far have relied on parametric specifications of either time-related factors (e.g. latency) or exposure–response relationships. In many practical applications, such as the analysis of effects of radon exposure on lung cancer in the Colorado Plateau Uranium Miners, it is important to identify, and appropriately model, the ‘primary’ modifier of the exposure–response relationship (e.g. latency, age at exposure or attained age). This is necessary because estimating the effects of attained age and age at exposure directly, as arbitrary functions, would lead to fundamental problems of identifiability similar to those involved in age-period-cohort analysis.

Methods that have been proposed to deal with these issues could be broadly classified in two classes; namely, mechanistic and empirical models. The Armitage–Doll multi-stage model [1] and the Moolgavkar–Knudson two-stage model [2] specify mechanistic models for time-related factors within the framework of a presumed model of carcinogenesis. Biologically based analysis using mechanistic models have been applied to data from the Colorado Plateau Miners cohort [3, 4]. However, the exact number of stages in the multi-stage process of carcinogenesis is generally unknown, and empirical models may provide an appealing alternative (or a way of informing a subsequent mechanistic analysis) in order to avoid model misspecification. At the empirical level, existing methods either assume pre-specified parametric forms for both latency and dose–response relationships or allow one of the components (latency or dose–response) to be modeled flexibly. None has tried to allow simultaneous flexible modeling of these two dimensions.

In this paper, we focus on empirical models. For the relatively simple situation of an instantaneous (rather than protracted) exposure, the underlying hazard rate λ at age t as a result of exposure z at age u takes the form of a proportional hazards model. Specifically, we consider a log-linear relative risk (RR) model (i.e. logistic model), which has the following form:

$$\lambda (t,z,u)={\lambda }_0(t)exp\{f(z;\beta )g(t,u;\alpha )\}$$ (1)

In this framework, f (z; β) and g(t,u; α) describe the exposure–response component and the effects of temporal modifiers such as age at exposure and latency, respectively. A log-linear model that is analogous to (1) for extended exposure histories of the form z(u)_u<t, where z(u)_u<t is the exposure received at age u for any age prior to current age t, could be given as

$$\lambda (t,z(·))={\lambda }_0(t)exp\left\{{\int }_0^{t}f(z(u);\beta )g(t,u;\alpha )\text{d}u\right\}$$ (2)

The model given by (2) assumes dose multiplicativity, i.e. each increment of exposure at age u is assumed to contribute independently to the RR at any later age t with the magnitude of each contribution possibly modified by factors such as latency or age at exposure in the same way as if there were a single instantaneous increment. The assumption of dose multiplicativity implies that later exposures do not modify the effects of earlier exposures on a multiplicative scale. This assumption is clearly not satisfied in situations where long, low-intensity exposures appear to have a higher risk than short, high-intensity exposures. This phenomenon, known as the ‘inverse exposure-rate effect’, was observed in the BEIR IV committee’s analysis on the effects of radon daughters on lung cancer [5]. Various forms have been assumed for f and g, ranging from completely parametric forms to some attempts at using relatively flexible forms for one of them (e.g. [6, 7]). In addition to the assumption of dose multiplicativity, several approaches that have been proposed in the past [7] also made a number of additional assumptions in using the general form of (2), namely, (a) parametric forms of at least one of f (z(u)) and g(t,u), and (b) multiplicative effect of f (z(u)) and g(t,u).

We have chosen to use the log-linear RR model in our proposed exploratory techniques, because it was computationally more stable compared with others (such as the linear excess RR model) and could be easily implemented via standard software in many applications. In situations where other models are more appropriate, one could easily refit the model based on the results of the exploratory modeling procedure.

In this paper, we propose to relax some of the assumptions in either of the above types of models in order to develop more flexible, and hence hopefully more realistic, models. Specifically, we focus on descriptive methods for simultaneous modeling of both latency effects and exposure–response relationships. The approach uses regression splines on each component and then uses the tensor product approach (as opposed to more exact but computationally more demanding ones such as using thin-plate splines) to construct a two-dimensional approximation of the resulting surface [8], building on earlier applications of tensor product splines in biostatistical modeling [9, 10]. We apply these methods to extensively analyze latency effects, exposure–response relationships and their possible interactions in the Colorado Plateau Uranium Miners cohort. In this paper, we use working level (WL) as a unit of measure for documenting exposure to radon decay products, known as ‘daughters.’ One WL is equal to approximately 200 pc/l. Working level months (WLM) are defined as the integrated WLs over time in months.

MATERIALS AND METHODS

Background and review

To put our proposed models in proper context, we briefly summarize existing methods [7] that allow for RR estimates to vary with latency, assuming protracted exposures. Here, latency effects are thought of as a weight function of the exposure–response relationship. The simplest method assesses exposure–response relationships via exposure that is lagged by a pre-specified latent period, making it prone to model misspecification when the assumed latency is incorrect or when effects of exposure increments vary by latency. Such a scenario could arise when dealing with protracted exposures, where the increased risk associated with exposure may not only be a function of some overall measure of exposure but is also influenced by latency.

The cumulative exposure model uses total cumulative exposure as the effective exposure, essentially giving equal weight to exposures at all time points. Its assumptions contradict the well-established observation that disease risk following exposure (for example, as in the relationship between lung cancer and radon exposure, [7]) starts at background levels, rises to a peak and then may decline to null (or decay exponentially). This model could be improved upon by (i) examining the general pattern of how the RR estimates change across a contiguous series of latency intervals via completely stratified models within each latency interval or (ii) using a piecewise constant model to allow for common overall, and hence more robust, adjustment of covariates over pre-specified latency intervals [7, 11]. Both approaches suffer from the discrete nature of the latency weight function and from arbitrary choices of latency intervals. In the piecewise constant model, effect estimates depict changes in risks per unit exposure received during the corresponding latency interval. Similarly, the sum of all interval-specific estimates gives an estimate of the linear predictor in the RR model associated with an entire exposure history. But, the weights in adjacent latency intervals are likely to be correlated leading to potential instability in the latency-interval-specific relative effect estimates, especially when the intervals are small in size. In contrast, the bilinear model [7] uses a continuous latency weight function. Specifically, the model estimates (i) the time it takes before there is an effect of exposure, (ii) the time of maximal effect of exposure and (iii) how long an effect lasts. The model fits a latency weight function that is constructed by two lines that are attached at an inflection point (usually constrained to be 1) that gives the estimate of the peak in relative effects. An exponential decay weight function could be used beyond the inflection point at which the maximum effect is achieved. Biologically, this might be a better depiction of some agents (such as TCDD) that may be retained in the body and then slowly released into the body system. The rate of decline of the exponential decay curve is affected by the number of years required for the effect to be reduced by one-half, the so-called half-life of internal dose/exposure [7].

In this paper, we focus on empirical models that could be useful when the form of the exposure–time–response relationship is not fully known, as in most practical situations. Earlier models using splines [12] fit piecewise polynomials within a series of latency intervals and then join the piecewise curves in a smooth function by putting appropriate constraints on the estimation process. This model has been applied to the Colorado Plateau Uranium Miners data on radon exposure and lung cancer [13]. We employ this spline-based modeling paradigm in order to allow for estimation of risk of exposure at any given latency point and then weighing risk estimates via parameters of a flexible two-dimensional surface.

Visualizing effects of exposure and time-related variables

In order to motivate our two-dimensional model on exposure and latency, let us first consider the more flexible model for exposure rates z(u) received between birth and t, given by

$$\lambda (t,z(·))={\lambda }_0(t)exp\left\{{\int }_0^{t}f(z(u),t,u)\text{d}u\right\}$$ (3)

under the assumption of dose multiplicativity and proportionality of hazards, and suppressing all regression parameters for now. We further introduce a slightly simplified version of (3) by focusing on latency, i.e. t −u, as a temporal modifier leading to

$$\lambda (t,z(·))={\lambda }_0(t)exp\left\{{\int }_0^{t}f(z(u),t-u)\text{d}u\right\}$$ (4)

Note that models (3) and (4) contain model (2) as a special case. In fact, model (2) could be fitted via a product of two one-dimensional splines, say f (z(u)) and g(t −u) for dose and latency, respectively. Such types of models were recently proposed by Abrahamowicz and MacKenzie [14], even though they did not consider protracted exposures. With modifications along the lines proposed in this paper to allow for protracted exposures, the models of Abrahamowicz and MacKenzie [14] would form an important class of models that are relatively more flexible to those proposed in Hauptmann et al. [12]. Opting for an even more general model, we propose to fit a two-dimensional surface in z(u) and (t −u). This relaxes the assumption of multiplicativity of the effects of exposure (z(u)) and latency (t −u) in model (2). Specifically, we use tensor product splines as a natural extension of the use of uni-dimensional regression splines as in [12, 13]. Note that there is an implicit assumption that risk estimates are the same at all levels of attained age in the two-dimensional surfaces we estimate using this new proposed approach.

Even though tensor product splines are approximations of truly multi-dimensional smoothers such as the thin-plate spline, they have the advantage of being formed as tensor products of the component uni-dimensional sets of basis functions [15]. Consider a set of linearly independent (basis) functions {δ_j1: j₁= 1,…,q₁} defined on interval T ⊂ ℛ based on exposure z(u). Similarly, consider another set of linearly independent (basis) functions {ε_j2: j₂ = 1,…,q₂} defined on the interval U ⊂ ℛ based on (t −u) for modeling latency. Then, one could define a two-dimensional surface on a rectangle T ×U ⊂ ℛ² by taking a tensor product of their two spaces of basis functions as the set of all linear combinations of tensor products of linear combinations of their basis functions, i.e.

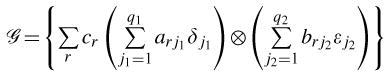(5)

which is the same as the set of all linear combinations of tensor products of the basis functions

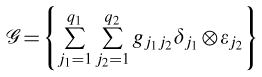(6)

Let {τ₁,… τ_m1} and {ν₁,…, ν_m2} define regularly spaced sequences such that T = [τ₁, τ_m1] and U = [ν₁, ν_m2]. For tensor product cubic splines, the cubic splines on each knot sequence are then finite-dimensional spaces of dimensions q₁ = m₁ + 2 and q₂ = m₂ + 2, respectively. We proceed by defining by splitting T ×U into rectangular panels, small rectangles of the form [τ_r, τ_r+1]× [ν_s, ν_s+1]. Over each panel, the function is the product of a cubic function in t and a cubic function in u. The functions are then fit together smoothly at the joins between the panels, by requiring that they have continuous first and second derivatives. In simple words, this modeling approach creates a design matrix for the two-dimensional surfaces by first generating the basis functions for the exposure and latency variables and then calculating all pairwise products of the basis function. Note that the RR estimates at exposure and latency combinations could be obtained by exponentiating the parameter estimates, g_j1j2, of the tensorproduct splines basis functions in (6).

In setting up the basis functions on each of the two dimensions, one could choose from several classes of smoothers (see [16] for an exhaustive list of smoothers and their relative merits). In this paper, we use B-spline basis functions that are derived in terms of divided differences and they are themselves piecewise cubics with minimal support (i.e. being non-zero) over a span of at most five distinct knots [8]. Note that B-splines, while adequately flexible for our purposes, are inherently parametric in nature once the number and position of the knots are fully specified. This makes the operation of the integral, under dose multiplicativity, manageable and allows for applicability of all statistical properties that are pertinent to fully log-linear (parametric) model forms. Similar ideas have been discussed recently [12]. We also further note that the method allows for use of other smoothing techniques such as natural splines, when erratic tail-end behaviors are of concern.

For inference, we use likelihood ratio test procedures to compare simple models such as one that fits a term for cumulative exposure with spline-based models of varying degree of complexity. The form of the likelihood depends on the type of analysis being considered, which could be based on the Poisson, proportional hazards or conditional logistic paradigms. In this paper, we mainly use the conditional logistic form. It is important to note that spline-based models with different numbers and positions of knots are not nested. The implication of this is that one cannot use likelihood ratio tests either to choose the number and position of knots or to make comparisons among various spline models. Hence, whenever we make comparisons between non-nested spline-based models, we use another criterion that is designed to enable comparisons between non-nested models, the Akaike information criterion (AIC) [17], which takes the following form:

$$\text{AIC}=-2\times \text{loglik}+2\times \text{DF}$$ (7)

where −2×loglik is the deviance. Here, the smaller the value of the AIC, the better the fit of the model to the observed data.

The issue of selecting the number and position of knots could be regarded as a model selection problem and has been discussed in several papers. For example, Friedman [18] proposes the multivariate adaptive regression spline procedure by combining stepwise forward and backward procedures to find the best number and position of knots based on a goodness-of-fit criterion, given a maximum number of knots and a minimum distance between knots. Hauptmann et al. [12] discuss two approaches to determine the positions of a given number of knots; a profile likelihood search for the best-fitting spline model, which is effective but computationally cumbersome, and a simple alternative that places knots in such a way that the study population accumulated approximately constant proportions of its cumulative exposure between any two adjacent knots [13]. In this paper, we follow this last approach and conduct a grid search for the choice of best number of knots on each dimension by considering the median and the two tertiles on each dimension to determine whether we should use 0,1 or 2 knots on each dimension.

A major effort in our research was the implementation of the new proposed modeling techniques in the EPICURE package by writing scripts for the two-dimensional tensor product spline in a way that allows for the integration over time due to protracted occupational exposures via a conditional logistic modeling paradigm. We then used the R package for plotting purposes, even though one could equally use any other software package with flexible graphical capability. The new EPICURE scripts (Hirosoft International Inc., Seattle, WA) are available from the authors.

RESULTS: ANALYSIS OF THE COLORADO PLATEAU URANIUM MINERS COHORT

The Colorado Plateau Uranium Miners cohort has been previously described in detail [7]. Briefly, the cohort consists of 3347 Caucasian males who were recruited between 1950 and 1960, with mortality data collected through 1990 [19]. This cohort was assembled to study the effects of occupational exposure to radioactive radon gas and its progeny and smoking on lung cancer mortality. The results in this paper are based on conditional logistic modeling on a nested case–control data set (see [7] for more details) that included up to 40 controls for each lung cancer death, randomly selected from those who were in the study at the age of death of the case and had attained the age of death of the case during the same 5-year calendar period. For each subject, radon dose histories were given as radon exposure (in WLM) by five-year age intervals and, in integrals such as (4), functions of dose were computed up to the attained age of the case in the case–control set, assuming constant dose rate z(u) over each interval. Linear interpolation was used when computing over a partial age group. In assembling this data set, subjects were allowed to serve as controls for more than one case. The final data set consisted of 2704 miners including 263 lung cancer deaths resulting in 10 322 records for the analysis. Note that a full Cox regression can be done by including all the controls in the risk set. Sampling 40 controls made the computations feasible.

Details on the exposure assessment have been provided in [7]. Briefly, exposure reconstruction was conducted in order to estimate the annual radon exposures in WLM, by linking measured radon levels obtained from the mines (via measurements or estimation) to miner work histories [5, 20]. Our analysis will be restricted to those miners who began working in the mines after 1950, due to scarcity of reliable data prior to this period. The purpose of this calculation was to approximate exposure up to the diagnosis of lung cancer. Hence, exposure summaries that are used in this paper are computed by accumulating exposure only up to two years prior to the reference age (i.e. lagging exposures by two years), to make sure that post diagnosis exposures are not included in the cumulative exposure. For this example, the exposure z(u) is defined as the average annual exposure rate in WLs when the subject was u years old.

Descriptive data are provided in Table I. Here, cases and controls that were pooled from the nested case–control sets, stratified by age of death of the case into <60 and ≥60 years, are compared with respect to the distribution of exposure rate by latency. The median exposure rate levels were similar between cases and controls during the 0–9 years of latency, but higher median exposure rates were observed for cases during latency periods of more than 9 years. The total cumulative radon exposure levels (in WLM) were generally higher in cases, more so in the <60 age group (data not shown). Table I indicates that the proportion exposed declines during latency of 30 or more years. Hence, we limit our tensor product modeling to <25 years of latency in order to avoid sparsity of data.

Table I.

Distribution of radon exposure rates by categories of latency in cases and controls from the nested case–control data set^*.

	Age <60 years		Age ≥60 years
	Controls	Cases	Controls	Cases
Number of records†	5360	134	4699	129
Exposure rate during previous 30 years (WL)‡
First quartile	2.7	5.7	2.6	3.8
Second quartile (median)	5.3	8.8	5.1	6.2
Third quartile	9.4	13.3	8.9	10.5
Radon exposure rates during 0–9 years of latency (WL)
No exposure (per cent)	66	57	80	77
Median among exposed	4.1	4.2	3.5	3.3
IQR§	5.7	8.5	4.5	4.0
Radon exposure rates during 10–19 years of latency (WL)
No exposure (per cent)	38	28	47	39
Median among exposed	4.2	7.6	4.5	5.6
IQR	7.0	10.9	6.7	8.2
Radon exposure rates during 20–29 years of latency (WL)
No exposure (per cent)	48	44	35	33
Median among exposed	5.8	9.3	5.4	8.4
IQR	7.5	9.7	7.1	10.6
Radon exposure rates during 30+ years of latency (WL)
No exposure (per cent)	85	78	72	70
Median among exposed	6.6	7.5	7.4	6.1
IQR	10.3	11.7	11.4	15.3

Note: A subject’s rate in a latency interval is computed as total exposure (WLM) within the latency interval divided by the time worked in a mine within the latency interval.

^*Computed up to two years prior to the case’s age at death.

^†Subjects may be controls in multiple case–control sets.

^‡Computed as the total cumulative exposure during the past 30 years divided by the time exposed.

^§Inter-quartile range= third quartile-first quartile.

Table II gives results from the various models for exposure and latency for the log-linear logistic model. These results were obtained by using tensor product B-spline functions. The log-linear model that uses cumulative exposure had a deviance value of 1878.7 with one degree of freedom. A piecewise constant model that had intervals of 0–9, 10–19, 20–29, 30+ years on latency, and 0, 0–99, 100–199, 200–299, 300+ WLM on exposure had a deviance of 1791.7 with 16 degrees of freedom. Several tensor product spline-based models were fitted based on linear, quadratic and cubic polynomial splines with no knots, a knot at the median (20 years for latency and 63 WLs for exposure) or two knots at the tertiles (at 15 and 24 years for latency and at 42, and 92 WLs for exposure). All of these spline-based two-dimensional models were found to be superior to the cumulative exposure model. As the piecewise model on both latency and exposure and the various spline-based models are not nested within each other, the AIC was used for model comparison. As reported in Table II, models that fitted tensor product two-dimensional spline surfaces that were based on a no-knot cubic spline for latency and a cubic spline for exposure with one knot placed at the median value of 63 WLs had the smallest AIC value and hence gave the best fit for the data. Figure 1 gives a pictorial presentation of the proposed model as a two-dimensional surface for the best-fitting model with no-knot cubic polynomial for latency and a cubic spline with a knot at 63 WLs for exposure. The x- and y-axes are latency (in years) and annual exposure (in WL), respectively, whereas the z-axis is the estimated RR/WL at any given combination of latency and exposure values. The two-dimensional tensor product spline model (with no-knot cubic spline latency function and linear spline with one knot at the median for exposure) gave a statistically better fit relative to a model that fitted a no-knot cubic spline weight function for latency with a global linear function for exposure (LR= 61.6; p<0.001), indicating that the functional form of the exposure–time–response relationship is more complicated than one that assumes global linearity for exposure with latency-dependent effect estimates, as in the latency spline model of [13]. We note that, however, the results from [13] are based on the excess RR model and not on the log-linear form that we have used in this paper.

Table II.

Analysis of deviance table for comparison of various specification of the two-dimensional log-linear model for exposure and latency.

Latency model (knots [years])*	Exposure model (knots [WL])*	Model DF	Deviance	LRT† statistic (DF)	p-Value	AIC
Cumulative exposure		1	1878.7	—	—	1880.7
Piecewise constant	Piecewise constant	16	1791.7	87.0 (15)	<0.001‡	1823.7
Cubic (none)	Linear (none)	4	1840.0	38.7 (3)	<0.001‡	1848.0
	Linear (63)	8	1778.4	61.6 (4)	<0.001§	1794.4
	Linear [42,92]	12	1771.9	68.1 (8)	<0.001	1795.9
	Quadratic (None)	8	1799.0	41.0 (4)	<0.001	1815.0
	Quadratic (63)	12	1774.0	66.0 (4)	<0.001	1798.0
	Quadratic [42,92]	16	1768.5	71.5 (8)	<0.001	1800.5
	Cubic (None)	12	1770.7	69.3 (8)	<0.001	1794.7
	Cubic (63)	16	1759.0	81.0 (12)	<0.001	1791.0
	Cubic [42,92]	20	1757.7	82.3 (16)	<0.001	1797.7

^*Degree of the polynomial in each dimension of the tensor product spline, along with the position of the knots (in brackets).

^†Likelihood ratio test.

^‡Compared with a cumulative exposure model.

^§This and subsequent models compared with a tensor-product spline model with cubic and linear polynomials (no knots) for latency and exposure, respectively.

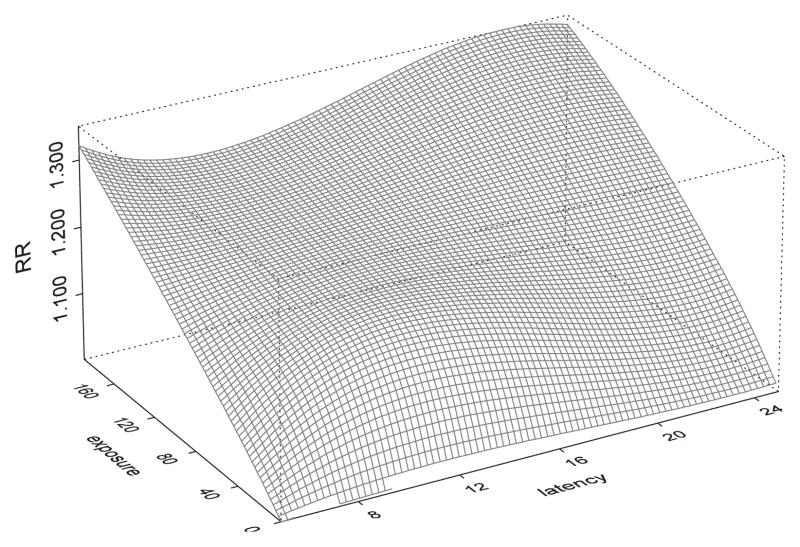
Figure 1.

Relative lung cancer risk for Colorado Plateau Uranium Miners as a function of latency (in years) and annual radon exposure levels (in WL of radon exposure). The two-dimensional tensor product spline-based model used a no-knot cubic spline (i.e. a cubic polynomial) for latency and a cubic spline with an interior knot at the median value of 63 WLs for radon exposure.

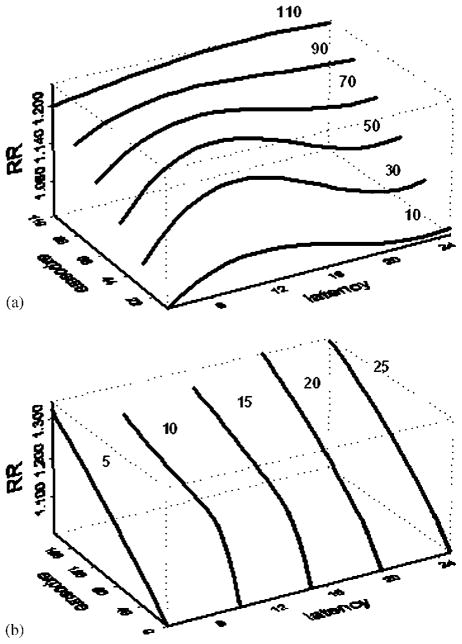
The values of the two-dimensional surface could be interpreted as changes in RR per year at average annual exposure rate z(u) and latency t −u. A better understanding of what is being depicted in Figure 1 is given by the cross-sectional presentations given in Figure 2. The first panel (panel (a)) gives the exposure–response relationships at different values of latency, showing this relationships as having varying shapes while all showing increasing risk with increasing exposures. Overall, the relationships appear to be roughly linear, even though the slight curvature for latency periods of 10 and 15 years may warrant a closer investigation since they may suggest a leveling off of the risk associated with higher exposures. Panel (b) of Figure 2 gives cross sections of the surface in Figure 2, depicting the latency curves for different exposure levels (for 10,30,50,70,90 and 110 WL categories). This panel indicates that the overall risk is higher for higher exposure levels. The shape of the latency is similar for exposure levels of up to 70 WLs, showing a risk of risk for increasing latency with a peak at about 12 years of latency and declining towards background risk afterwards. For higher exposure levels (90 and 110 WL categories), the shape of the latency curve becomes flat even though it depicts higher risk compared with those for lower exposure levels.

Figure 2.

Cross sections of the relative lung cancer risk surface (based on the surface in Figure 1) for Colorado Plateau Uranium Miners as a function of latency (in years) and annual radon exposure levels (in WL of radon exposure). Panel (a) gives exposure–response curves for various levels of latency (in years) and panel (b) depicts the latency curves for various levels of exposures (in WLs).

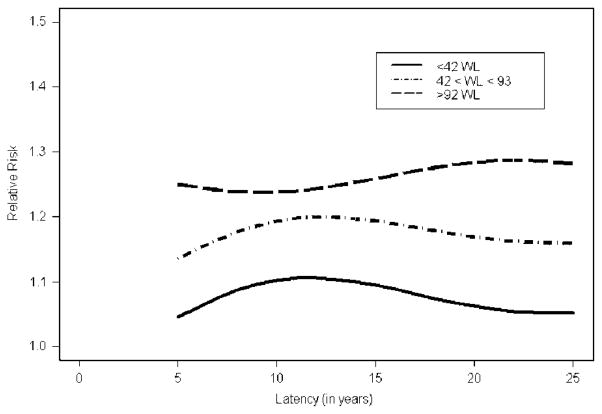
Figure 3 shows yet another, albeit simpler, presentation of the average latency curves for three exposures categories: <42, [42,92], and >92 WLs depicting the mean latency curves for the three exposure intervals, obtained by averaging over the latency curves for all exposure levels in an exposure category (e.g. by averaging the latency curves for 1,2,3,…,41 WLs for the <42 WL category). Clearly, the latency curves are different in the different exposure groups. For the exposure category [42,92] WL, the RR peaks after 10–20 years of latency and declined thereafter. In contrast, for the >92 WL exposure category, the risk estimates are relatively flat, compared with the other curves. We refrain from over-interpreting the small slight rise of risk after 15 years of latency because of sparsity of subjects with such high exposures. The heterogeneity of latency between exposure categories is completely averaged over in models that assume a common latency curve over the entire exposure range. Alternatively, one could evaluate categorical effect modification. For our data, this resulted in over-parameterized models due to sparsity of information and does not yield any useful information.

Figure 3.

Relative risk estimates as functions of latency for ‘low,’ ‘medium’ and ‘high’ categories of exposure given by <42, [42,92] and >92 WLs of radon exposure, respectively.

Various summary RR estimates could be extracted from the proposed tensor-product-based model. For example, consider a miner who is exposed at a constant rate of, say, 4 WLs starting at age 20 and ending at age 30. Then, a scientifically interesting question would be ‘what is the estimated RR at any attained age?’ At an attained age of 40, this miner would have received 48 WLM for each of the 10 years at 10–20 years latency period, leading to an RR value of 4.8. The same miner at an attained age of 50 years would have an RR estimate of 2.5. These are computed as the area under the appropriate annual exposure curve (Figure 2) over the latency period of exposure. One of the advantages of the tensor-product spline approach is that it allows the latency curve to vary by levels of radon exposure. For example, a hypothetical miner that gets exposed to 8 WLs during the ages of 20 and 30 years would have about 100 WLM exposure during each of the 10 years of exposure. According to the model depicted in Figure 1, this miner would have RR estimates of 9.6 and 5.1 at ages 40 and 50 years, respectively. Considering a more extreme example at high exposure levels, a hypothetical miner who gets exposed to 50 WL during the ages of 20 and 30 years would have about 600 WLM exposure during each of the 10 years of exposure. According to the model depicted in Figure 1, this miner would have RR estimates of 22.3 and 13.9 at ages 40 and 50 years, respectively.

Finally, we note that the so called ‘curse of dimensionality,’ the phenomenon of proliferation of parameters in light of limited information in using multi-dimensional smooth terms, is inherent in many flexible models [16] such as ours. We do not think that it is a problem in our analysis due to the richness of our data and also because our model is additive, with the exception of the two-dimensional term on exposure and latency. Moreover, the use of B-splines as building blocks of our tensor-product splines makes our model inherently parametric. In general, however, caution should be taken while using the proposed models if data are sparse and/or any additional multi-dimensional terms are considered in the model.

DISCUSSION

In this paper, we have proposed a method that uses spline-based flexible modeling approaches on both the latency and exposure–response parts of the model. The resulting model allows the analyst to look at the problem in both dimensions without restrictive assumptions on the three-way relationships between latency, exposure and disease risk. Specifically, the method allows for the latency function to vary by exposure levels and, conversely, the exposure–response relationship to be affected by the latency structure. Hopefully, this method allows the analyst to detect hitherto undetectable features of the data. At the very least, one could think of the new proposed method as an exploratory tool for determining whether more simpler models are adequate. Both the bilinear model and the spline-based univariate model are special cases of the proposed tensor-product spline-based model. Hence, one could test whether the tensor-product-based model is superior to the simpler models. In the case of the Colorado Plateau Uranium Miners data, we found that the tensor-product-based model resulted in a significantly improved fit, suggesting that the latency function was different at different exposure levels.

The proposed tensor-product spline models give a highly visual depiction of the exposure–time–response relationship and, hence, could serve as a graphical tool for choosing an appropriate, perhaps simpler, model. A point on the f (z,v) surface can be interpreted as the change in the log rate ratio given an exposure rate z experienced v years in the past. Thus, we can visually assess the effect of latency at different exposure rates or, perhaps more interestingly, look at the effect of exposure rate as a function of latency. We note that this approach is somewhat different than what is typically called ‘dose rate effects,’ which refers to the effect of receiving the same cumulative exposure at different dose rates. Because exposure could be experienced any time in the past, a ‘pure’ dose rate effect would require that the effect of exposure rate is constant in latency and proportional to dose. In particular, there would be no ‘latency effect.’ Perhaps of more interest is whether there is evidence of an exposure rate effect after controlling for latency. This may be assessed by adding a ‘dose rate’ summary term to the fitted spline model.

Because the basis functions are piecewise cubic polynomials, the model is inherently parametric. Hence, all standard testing procedures can be applied to the model once the two-dimensional basis functions are constructed, essentially giving a completely parametric model. In fact, all the other models that we described in Section 2 are special cases of the tensor-product spline-based model. This is also true for other parametric smoothers such as natural splines, which may prove to be useful in situations where stability at the ends of the data is of concern. A promising research topic is the adoption of the models proposed in [14] to allow for protracted exposure histories, and the comparison of their performance in relation to the uni-dimensional models (e.g. [12]) and our fully two-dimensional models.

The issue of how to choose the number and positions of the knots on both the latency and exposure–response of the model requires some care and skill. One should conduct an exploratory analysis to determine whether there is enough information in the data to fit these relatively rich models. Specifically, one needs to make sure that there is enough variation in the rate and duration of exposure histories [7]. In this paper, we used the AIC to choose the best-fitting and most parsimonious model. More research is needed on objective and relatively automated ways of choosing the number of knots and their locations.

In this paper, we have focused on exploratory empirical models. However, given that mechanistic models have been applied to the Colorado Plateau Miners data [3, 4], we emphasize the need for a comprehensive and systematic comparison between the performance of such models and the various empirical models summarized in this paper, including our newly proposed models. This is probably best done via a carefully designed simulation study along with parallel analysis of data sets such as those from the Colorado Plateau Miners cohort. We consider this to be another important area for future research.

A limitation of our proposed model is the lack of uncertainty estimates for our two-dimensional surfaces. Although it is possible to use well-established analytic and resampling techniques to construct confidence bands around uni-dimensional smooth curves [12, 16], methods are not readily available for analogous techniques for two-dimensional surfaces. Hence, caution should be taken against unwarranted over-interpretation of features of surfaces in regions with inadequate information. We consider the development of uncertainty estimates for the proposed two-dimensional surfaces to be an important area for future research.