Abstract
We report on recent efforts to develop predictive models for the pressure and other flow variables in the focal region of shock wave lithotripters. Baseline simulations of three representative lithotripters (electrohydraulic, electromagnetic, and piezoelectric) compare favorably with in vitro experiments (in a water bath). We proceed to model and investigate how shock focusing is altered by the presence of material interfaces associated with different types of tissue encountered along the shock path, and by the presence of cavitation bubbles that are excited by tensile pressures associated with the focused shock wave. We use human anatomical data, but simplify the description by assuming that the tissue behaves as a fluid, and by assuming cylindrical symmetry along the shock path. Scattering by material interfaces is significant, and regions of high pressure amplitudes (both compressive and tensile) are generated almost 4 cm postfocus. Bubble dynamics generate secondary shocks whose strength depends on the density of bubbles and the pulse repetition frequency (PRF). At sufficiently large densities, the bubbles also attenuate the shock. Together with experimental evidence, the simulations suggest that high PRF may be counter-productive for stone comminution. Finally, we discuss how the lithotripter simulations can be used as input to more detailed physical models that attempt to characterize the mechanisms by which collapsing cavitation models erode stones, and by which shock waves and bubbles may damage tissue.
Keywords: Shock wave lithotripters, Predictive models, Cavitation, Anatomy
Introduction
The motivation for this work is to develop numerical simulations for the physical processes occurring during shock wave lithotripsy (SWL) that may be used to predict and understand the mechanisms that lead to stone comminution and tissue injury. There are three aspects of the near-focal stresses (for a fluid, simply the pressure) generated by the lithotripter pulse that lead to different potential mechanisms for damage. For the stone, the compressive part of the wave is internally reflected within the stone to produce tension and stress concentrations that lead to crack inception and growth [1, 2]. The tensile part of the wave has the potential to nucleate cavitation bubbles whose collapse near the stone may lead to secondary shocks and stresses that erode the surface of the stone, or that generate waves and stress concentrations within it [3-6]. Cavitation bubbles are also implicated in tissue damage, potentially through dilation of vessels or through large stresses generated during collapse [7-11]. Finally, there is the differential strength of the focused wave that leads to shearing of tissue [12-14].
A prerequisite to understanding the mechanisms by which stones are pulverized and by which tissue damage may occur is to correctly predict the stresses (for a fluid, simply the pressure) occurring in the focal region of the lithotripter. These may be measured experimentally in vitro, but measurement of pressure fields in vivo is complicated. Even in vitro it is difficult to map the entire acoustic field, and it is difficult to independently control bubbles or bubble clouds that are produced by the shocks. Numerical simulations, while representing an idealized situation, nevertheless provide a full spatial and temporal representation of the pressures occurring as a result of the lithotripter pulse.
Certain aspects of the focal region acoustics may be predicted from geometrical acoustics [15], and extensions thereof that account for some effects of nonlinearity, e.g. the KZK equation [16] and geometrical shock dynamics [17]. Owing to advances in computer speed, it is now possible to directly simulate lithotripter acoustics, at least in a homogeneous fluid, using the fully nonlinear Euler equations [18, 19]. These latter simulations produce solutions of the governing conservation laws and eliminate the need to make corrections to account for nonlinearity or assumptions about the off-axis variation of the focusing beam. The cost for these gains is a requirement of large computational resources.
This paper summarizes a research effort that has been devoted to improving the fidelity of these computational models, through advances in computational techniques, and by inclusion of more complicated physical effects such as the effect of inhomogeneous sound speed and densities of different types of fluids and tissues (e.g. water, kidney, fat, muscle, etc.) encountered along the shock path, and by including models for the coupled effect of cavitation bubbles in the focal region.
In order to understand how these effects vary according to the particular lithotripter, we model one representative each from three different classes of lithotripters: the (unmodified) Dornier HM3 (electrohydraulic) [20], the piezoelectric lithotripter array (piezoelectric) [21], and the XX-Es (electromagnetic) [22]. In the next section, we provide a summary of the simulation methodology and show validation results that compare the predicted focal region pressures to previous experiments (in a water bath) for all three lithotripters.
The main results are divided into two parts. In “Models including cloud cavitation”, the model is modified to account for the growth and collapse of a cloud of cavitation bubbles in the focal region. Such bubble clouds are commonly observed in in vitro experiments [10, 23-27]. Bubbles can have multiple effects on the focal region pressures. First, if a sufficiently dense cloud of bubbles is encountered by the initial shock, the bubbles will scatter and attenuate the acoustic energy. Indeed, our simulations show that clouds of sufficient density shield the stone from the shock’s energy. Since the pulse repetition frequency (PRF) is the principle treatment parameter that would control the bubble number density and gas content, the models strongly implicate shielding as the mechanism responsible for observed decreases in comminution efficacy with higher PRF [28]. Secondly, when these bubbles are excited by the tensile part of the wave, they grow explosively and collapse violently, producing secondary shocks and concentrating energy in the focal region. Cloud collapse can produce local pressures that readily exceed those of the initial shock, and are thought to contribute to stone comminution and tissue damage [7, 8, 28-31].
Next, in “Scattering and absorption by tissue”, we modify the simulations to study the role of material interfaces, e.g. the interfaces between different tissue types or between the body cavity and its surroundings, encountered along the shock path. The effects of high-intensity sound on tissue have been studied at least as far back as 1927 [32]. Researchers then sought a more complete understanding of the acoustic properties of tissue, and in 1950, the specific gravity and sound speed of living human tissue were measured as 1.06 and 1,540 m/s, respectively [33]. In the context of SWL, the presence of soft tissue in the shock path has been shown to have a non-negligible effect on focal pressure waveforms. In vivo measurements in pigs have shown waveforms of similar appearance to the in vitro case but with suppressed amplitudes [34]. In vitro experiments have shown that when layers of soft tissue, nominally the same thickness as seen by a shock wave traveling through the body, are placed upstream of the focus, the waveform amplitudes are attenuated and additional peaks are introduced [12].
A full accounting for the effects of tissue type and structure (elasticity, nonisotropy, etc.) on the shock dynamics is beyond the scope of present computational resources and mathematical models. However, two principle mechanisms that are expected to be present in any situation are: firstly, the scattering of waves by gross anatomical features across which sound speed and density differ; and, secondly, the much stronger absorption of (high frequency) acoustic energy due to the complex molecular structure of the material, as compared to a thermoviscous fluid. We therefore model tissue as a fluid, but include variations in sound speed and density associated with a representative model of the human anatomy (however simplified), and also include a model to account for the frequency-dependent absorption which has been previously modeled for KZK models of absorption of ultrasonic waves. In fact, we show that absorption is not particularly strong for the lithotripter pulse; scattering, even with simplified geometries, however, leads to strong modifications to the focal region acoustics, and secondary peaks of maximum (compressive) and minimum (tensile) pressures that can occur up to 4 cm postfocus.
The paper concludes by summarizing the findings from the simulations, and we provide an outlook for future model enhancements, and for how the existing lithotripter simulation tool can be exploited to provide input and boundary conditions for more detailed models of stone comminution and tissue injury.
Baseline simulation models
For comparison with in vitro experiments, we first consider SWL in a water bath, for which the material is homogeneous and for which thermoviscous absorption is negligible. The material in this section is documented in greater detail in a thesis [35] and in a forthcoming publication [36]. The motion and pressure are governed by the compressible, nonlinear Euler equations, plus equations representing conservation of mass and energy, and an equation of state for water. For the latter, we use the stiffened-gas equation of state [37], which is essentially identical under the present conditions to what would be obtained with the more familiar Tait equation of state [38, 39]. We choose parameters of the equation of state to provide an atmospheric density of 1,000 kg/m3 and a (small signal) sound speed of 1,500 m/s.
The governing differential equations are discretized with a second-order finite-volume Godunov method with slope limiters. We use a Cartesian grid with Adaptive Mesh Refinement [40-42]. The lithotripter reflector geometry is treated with a level set-based Ghost Fluid Method. The specific lithotripter geometries are drawn in Fig. 1. We use three grid levels for all of our simulations. The base, or first level grid is spatially uniform with a resolution of 0.5 mm. The second level grid is a factor of two finer than the first level grid, and the third level grid is a factor of 16 finer than the first level grid. Thus, the smallest spatial scale in our simulations is 31.25 μm. The smallest temporal scale is then 18.75 ns. The grid is refined when the difference between normalized densities in adjacent cells is greater than a prescribed threshold. Grid convergence was established by noting changes of less than 1% in computed amplitudes and pulse widths when resolutions were increased by 50%.
Fig. 1.
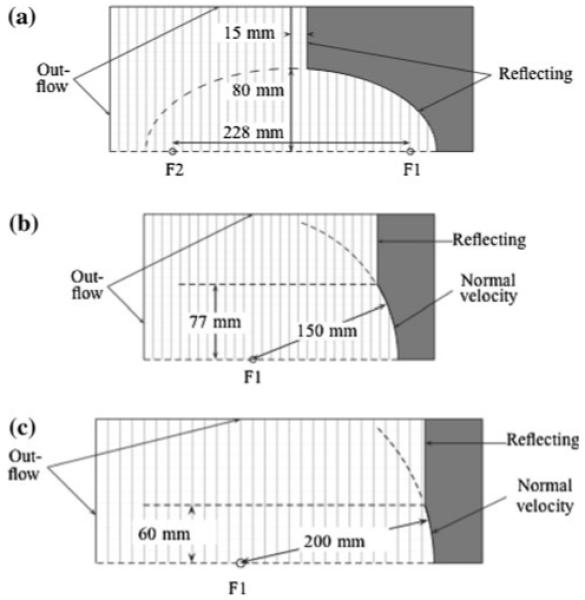
Schematic diagram of the 3 lithotripters considered in this study: a Dornier HM3, b Boston University Piezoelectric Lithotripter Array, and c XX-Es
The electrohydraulic lithotripter we model is the (original, unmodified) Dornier HM3, which is considered the “gold standard” of shock wave lithotripters and has been both used and studied extensively since SWL first became popular [20, 43]. The HM3 consists of a spark gap formed by a pair of electrodes positioned at one focus (F1) of a truncated ellipsoidal reflector [44]. The kidney stone is positioned at the second focus (F2) of the reflector. In the simulations, we model the shock source as a small region of mass and energy addition at F1, where the geometry and temporal rate of mass addition are modeled after the presence of a vaporization event at F1 produced by the spark. Using a spherical bubble model, we calibrate the source model to emulate the observed collapse time and maximum bubble radius [25] at F1 for a research HM3 model set at 18 kV. The detailed procedure and equations are discussed in [35].
The piezoelectric lithotripter we model is the piezoelectric lithotripter array (hereafter abbreviated as PLA), a research machine used by Chitnis et al. [21] to study the customization of focal acoustic fields. We must emphasize that the PLA was neither designed for nor intended to be used in a clinical application. A total of 170 elements line the inner surface of a 150-mm-radius spherical cap with an aperture diameter of 154 mm. The firing of each element is independently controlled, and by fixing the relative timing of the firing of different elements, the resulting acoustic field was customized in various ways. The kidney stone is positioned at the geometrical focus of the truncated spherical cap. To simulate the lithotripter, we first consider an axisymmetric case where each ring of piezoelectric elements is fired simultaneously. The displacement of each ring is simulated by adding a small velocity normal to the surface. We use the measured focal pressure that is obtained by firing the single, center element and work backward (assuming linear acoustics, which is valid for the low amplitudes obtained when firing a single element) in order to calibrate the wall motion for each element. An additional complication for the piezoelectric lithotripter is the small inter-element delays [O (10 ns)]. It proves necessary to model this jitter in the computational model in order to obtain good agreement with measured data, as provided below (see [35] for details).
The electromagnetic lithotripter we model is the XX-Es, a wide-focus and low-amplitude machine [22]. A spherically shaped solenoid with a 200 mm radius of curvature and a 120 mm aperture diameter is used to displace a copper diaphragm, generating a self-focusing shock wave that first travels through a water-filled rubber coupling cushion and then into the body. The kidney stone is positioned at the geometrical focus of the spherical diaphragm. From a computational perspective, the treatment of the motion of the copper diaphragm is the same as the piezoelectric elements. We need to find a normal velocity that generates the observed focal pressure waveforms. Unfortunately, we could not find measured values in the literature, so we adapt membrane displace curves measured for a different lithotripter (Lithostar Modularis by Siemens) and calibrate them to produce the best possible agreement with measured waveforms produced with a shock generator voltage of 10 kV [22].
A plot of pressure versus time at F2 is compared with corresponding experimental data for each lithotripter in Fig. 2. For each lithotripter, the wave field at an instant in time close to when the shock arrives at F2 is also shown. The salient features of each focal pressure signature are well-captured by the numerical model. The agreement is least satisfactory for the HM3; however, the numerical results are within the uncertainty associated with the natural variations associated with the spark discharge event (along with electrode wear, alignment issues, etc.) that give rise to disparate measured values. By and large, peak positive and negative pressures, and durations of the positive and negative pulses fall within the range of available experimental measurements.1
Fig. 2.
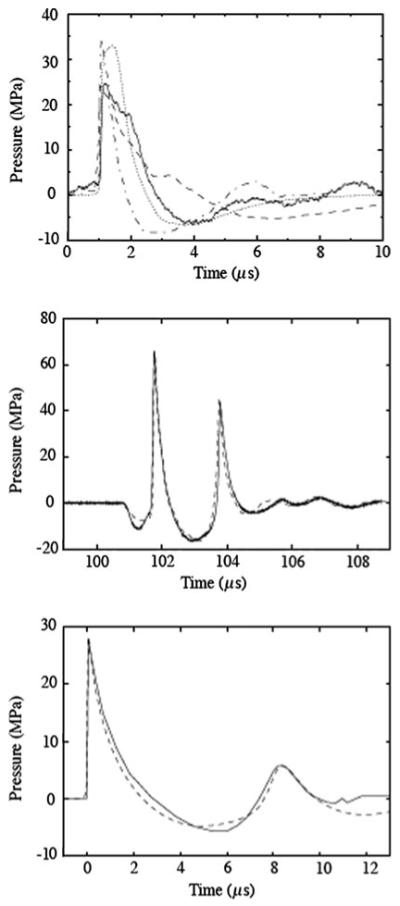
Pressure versus time at the focus of each lithotripter: Dornier HM3 (top), piezoelectric lithotripter array (middle), XX-Es (bottom). HM3: experimental measurements from (Y. Pishchalnikov, 2008, personal communication) (solid), [20] (dashed), [44] (dash dotted); numerical data (dotted). PLA: experimental measurements from (P. Chitnis, 2008, personal communication) (solid); numerical data (dashed). XX-Es: experimental measurements from [22] (solid); numerical data (dashed)
A variety of other metrics for the wave fields that are of interest for characterizing different lithotripters are reported in [35, 36].
Models including cloud cavitation
We now modify the simulation model to account for the dynamics of a cloud of bubbles in the focal region of the lithotripter. Photographic evidence [27] of bubble clouds taken with high-speed cameras suggests that collective effects (interactions amongst a large number of bubbles) are important in SWL, at least in in vitro experiments. The photographs, a typical example of which is reproduced in Fig. 3, allow us to make rough estimates for the number density of bubbles, N < 40 bubbles/cm3, the typical maximum bubble radius (after cavitation) near F2, Rmax <0.7 mm, and cloud collapse times from about 280–370 μs. These parameters give an upper bound on the void fraction of about 5%, while 2% may be a more typical value. In either case, the void fraction is far in excess of the values required to expect significant effects of collective bubble dynamics [45]. These parameters can also be used in a different way to infer that collective effects are important. A single bubble nucleus exposed to a short duration (negative) pressure excursion will grow and decay according to a Rayleigh collapse time which is a linear function of the maximum bubble radius [18]. Cloud collapse times reported above exceed the Rayleigh collapse time (computed via the Gilmore equation) by a factor of about [3]. This indicates that the bubble at F1 is continually forced in tension by the expansion of the bubble cloud as a whole, an effect that can only be captured by accounting for the collective distribution of bubbles.
Fig. 3.
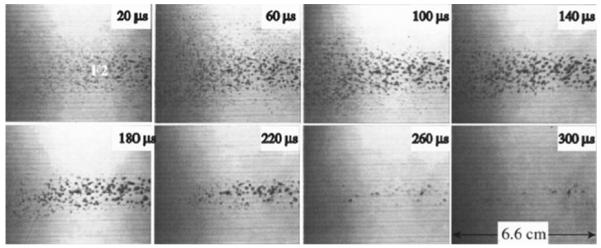
Photograph of the bubble cloud produced by a research HM3 lithotripter set at 18 kV, reproduced from [27]
Numerical model
Collective bubble effects can arise from interactions of bubbles in two distinct ways. The first effect is modeled directly and consists of indirect bubble–bubble interaction. As bubbles grow or shrink, they induce a radial motion in the liquid. This motion, in turn, leads to local changes in pressure and mixture density, and, hence, feed back on the bubble dynamics. This interaction occurs even for very low void fractions and, as we show, has a significant effect on the bubble dynamics in SWL. The second effect, which we neglect, is direct bubble–bubble interaction. This would occur when two neighboring bubbles directly feel each others’ presence; such interactions may be locally important at low void fractions, but on average they are only likely to be significant for void fractions higher than the upper bound of 5% expected in in vitro experiments of SWL.
The complete details of the numerical framework2 we use for simulating the bubbly medium have been previously published [18]. We use a two-phase flow model based on prior work [46, 47]. The transport equations for the bubbly mixture are derived by ensemble averaging over possible configurations of the bubble field. The physical analogue of this approach is averaging the results of a large number of experiments with random initial positions of variously sized bubble nuclei. The mixture equations are not closed under averaging, and a number of additional assumptions must be introduced. The set of assumptions represent a difficult balance between those that are physically motivated (and can be verified either a priori or a posteriori) and those that are required to obtain a computationally tractable model but that cannot be validated in detail with presently available experimental measurements. The most important assumption is that the mixture remains dilute, meaning there is an upper limit of the void fraction (ratio of gas/vapor volume to total volume) that can be considered, less than about 2%. Averaged mixture properties are assumed to vary slowly in space as compared to an individual bubble, which, aside from the immediate action of the shock front, is reasonable for lithotripter pulses. Finally, the bubbles are assumed to remain spherical in shape and are neither created nor destroyed (number density is conserved). This final approximation may break down during violent bubble collapse, when the presence of shape instabilities of the bubbles (or re-entrant jets) could lead to fragmentation of bubbles and changes to the bubble number density.
The averaged transport equations are closed by posing a model for the spherical dynamics of a single “potential” bubble located at a particular point in the field and driven there by the local pressure. We use the Gilmore model [48] for the bubble dynamics since it can capture large bubble growth and violent collapse. Although more complex bubble models which include heat and mass transfer effects can model more accurately the energy losses (especially during collapse), they did not impact the overall flow field in any significant way compared to the simpler Gilmore model and resulted in a significant increase in computational run times.
Bubble cloud effect and enhanced collapse energy
The simulations proceed as before, by specifying the initial pulse generated by the spark-vaporization event at F1. In the case of the bubble flow, we must also specify the initial bubble nuclei size (we assume it is uniform in space), and the number density of bubbles. Since the directly observable quantities (maximum bubble size and collapse time) are outputs of the simulations, we must calibrate the values by making simulations for a variety of initial nuclei sizes and number densities and select those that most closely match the observables [18]. For the selected parameters, the simulations effectively reproduce the observed extent and collapse time of the bubble cloud in experiments. Further validations (not presented here) include good agreement for the (non-trivial) structure of the bubble cloud produced by a dual-pulse lithotripter [18].
An example calculation demonstrating the collective effects we described above is shown in Fig. 4. The radius of a bubble located at F2 is plotted alongside the pressure at F2 for two cases: a case with zero number density of bubbles (so that a single bubble, initially of radius 20 μm, is isolated at F2 and has no back-effect on the pressure field), and a cloud cavitation case with an initial bubble radius of 20 μm and a number density of N = 20 bubbles/cm3. One can observe the much delayed collapse of the cloud compared to the single bubble. In the pressure signal, it is apparent that the bubble at F2 is exposed to a long duration but weakly negative pressure that causes it to continue to grow for a much longer time, and results in a larger bubble. Before the final collapse at F2, a series of weaker shocks are felt there as bubbles in the periphery of the cloud, whose growth times and sizes are smaller than the bubbles in the center, collapse. These compressions of the bubbles along the centerline of the focal region cause the bubbles to collapse more violently, and, in so doing, they release more energy than they would in isolation.
Fig. 4.
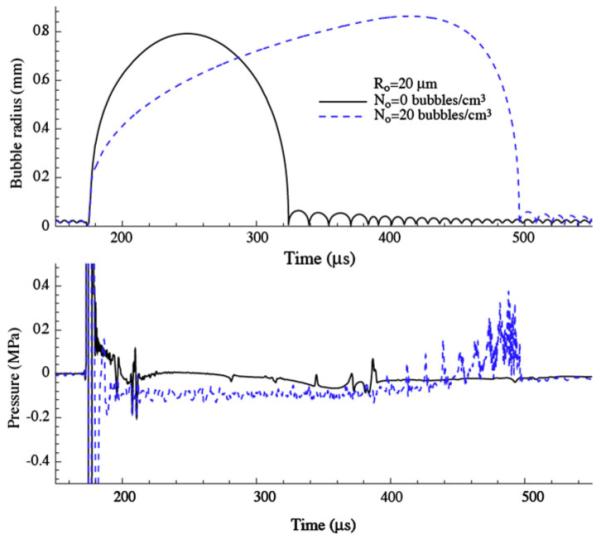
Bubble radius and pressure at F2 for HM3 simulation with and without cloud cavitation (parameters listed on the plot). Note that N = 0 bubbles/cm3 corresponds to an isolated bubble at F2 that has no feedback on the lithotripter pressure field
By considering the energy released by a bubble at the focal point of the lithotripter, the stone damage potential of given test conditions can be estimated. The dependence of the energy on bubble cloud initial parameters (nuclei radii and density) is shown in Fig. 5. The energy of each collapse was normalized by the energy released by the case where only a single small bubble is present. From the simulation results shown in Fig. 5, the energy released increases monotonically with the radius of nuclei in the absence of bubble cloud interaction (N = 0). However, for the finite number density cases, there is a clear optimum above which the interference from the bubble cloud on the wave propagation (cloud shielding) outweighs the additional energy gained from cloud collapse. The energy released for the optimum conditions increases while the nuclei size decreases with increasing number density.
Fig. 5.
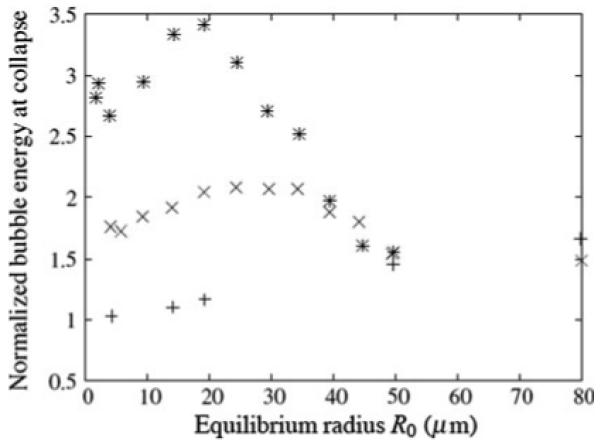
Normalized energy released at bubble collapse as a function of equilibrium radius R_0. N = 0 (plus sign), N = 10 (cross), N = 20 (asterisk) bubbles/cm3
Pulse repetition frequency
Although important, the above discussion only considers the impact of a single shock wave event in the field of the lithotripter. Since the therapeutic use of SWL requires the firing of thousands of shock waves, the rate of delivery can play a significant role. Evan et al. [28] have shown that high pulse repetition frequencies (PRF) can result in lower stone comminution efficiency (e.g. remaining fragments over a certain size as a function of the number of shocks delivered). Since the shock and bubble activity occur on the micro- and millisecond timescales, respectively, it may seem at first surprising that variations in the PRF in the range of 0.5–2 Hz would have a significant impact on comminution. Sapozhnikov et al. [9] provided evidence that slow diffusion of non-condensible gas in and out of bubbles (i.e. rectified diffusion) occurs on a timescale commensurate with PRF. Experimental observations, as presented in [9, 49], have shown that the cavitation field is far more extensive, and with higher void fractions, at higher PRF.
If the time delay between pulses is shorter than the time required for the return diffusion, bubble nuclei will grow after each cycle until an equilibrium is reached. Rectified diffusion in single bubble cavitation has been studied empirically and numerically [50], but its impact on SWL has been difficult to clearly assess. In the present work, we estimate rectified diffusion effects in our numerical simulations based on conditions at the focal point and can show a significant impact of variation of the PRF on the bubble activity for equilibrium conditions (no net change in bubble nuclei size). In particular, we can show a significant impact on the energy released by collapsing bubbles at the focal point under these conditions. We hypothesize that the observed lower comminution effectiveness at high PRF is related to this observation.
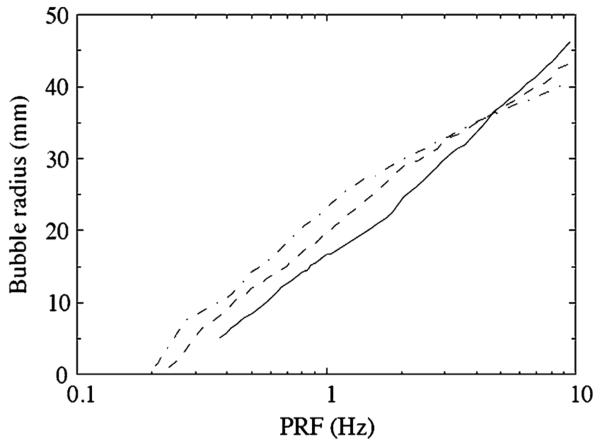
Using a more comprehensive model for bubble dynamics including gas diffusion (see [18] for details), the net rectified diffusion for a bubble located at the focal point of the lithotripter was calculated for a variety of lithotripter conditions. By assuming that the pressure field experienced by the bubble is approximately independent of the rectified diffusion, we can reuse the focal pressure from a single lithotripter pulse repeatedly to obtain estimates for the change in equilibrium radius as a function of PRF. It was found that repeated pulses (at a given value of PRF) led eventually (after hundreds of shocks) to a steady-state condition where the equilibrium radius was large enough so that the net diffusion over a cycle is zero. Figure 6 shows the final result of the calculation: a map between PRF and equilibrium radius for different values of the number density, N, of bubbles. As is expected, the bubble equilibrium radius increases with increasing PRF, and for reasonable values of PRF it also increases with N.
Fig. 6.
Impact of PRF on the steady state bubble equilibrium size for different bubble nuclei densities. N = 0 (solid), N = 10 (dashed), N = 20 (dash dotted)
Examining again Fig. 5 together with Fig. 6 shows that for a number density of N = 10 bubbles/cm3, there is an optimal PRF of 3 Hz beyond which the energy released by a bubble near the focus decreases with increasing PRF. For N = 20, the optimal value is lowered to about 1 Hz. It is important to note that these are just estimates, but the trend seems to support the idea that higher PRF can lead to less effective comminution efficiency, by encouraging sufficient cavitation activity so as to shield the stone from the incident pulse [9]. It is important to note that in the experiments [9], it was found that for higher PRF, the void fraction increased (as in our model), but the increase was attributed to an increase in bubble nuclei number density due to greater probability that fission occurs during bubble collapse when the bubbles are large. Our analysis assumes that number density is constant, but one can surmise from Fig. 6 that equilibrium radius and number density are increasing functions of PRF, and we can conclude that bubble shielding could, in either case, be correlated with decreasing comminution efficiency.
Scattering and absorption by tissue
In this section we consider how shock focusing and focal region stresses and strains might be modified by soft tissue encountered along the shock path. The two effects we consider, scattering by interfaces demarking different types of tissue and frequency-dependent absorption of mechanical energy, may be modeled by considering tissue to behave, on short timescales, as a fluid but with a spatially dependent distribution of density, sound speed, and absorptive proprieties. To provide a realistic geometry, we use digitized data from the Visible Human Project to establish initial conditions for our simulations. The VOXEL-MAN Group (VMG) at the University Medical Center Hamburg-Eppendorf has made sample data available, and one sample image is of the human midsection [51], reproduced in Fig. 7. The scattering by the anatomical features will depend, of course, on the full three-dimensional geometry and the particular shock path. While in principle our model can handle any geometry, three-dimensional computations are very computationally intensive.
Fig. 7.
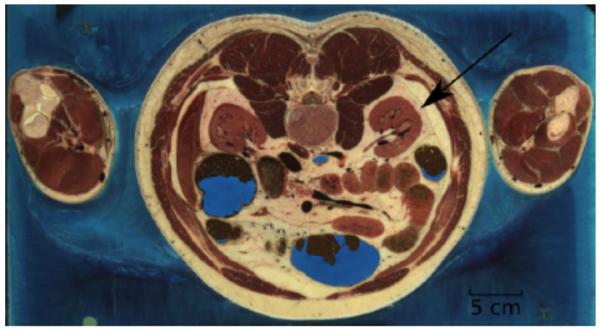
Segmented anatomical data made available by the VOXEL-MAN Group. Our chosen blast path is indicated by the arrow
Before moving on to those geometries, we consider here a much simplified version, whereby we assign a typical shock path to the left kidney that is aligned with the approximate center of the convex surface, opposite the renal artery, as shown on the sketch. We then take the local geometry in this slice and overlay it on our axisymmetric lithotripter geometry, as shown in Fig. 8. Thus we revolve the kidney structure around the axis of the shock path, a simplification which is only roughly indicative of the full three-dimensional geometry of the anatomy in the vicinity of the shock path. We recognize that the axisymmetric geometry may potentially exaggerate the strength of focusing through a lensing effect. A real anatomical environment without axisymmetric features would produce less coherent scattering. With this limitation in mind, our model still provides an important step beyond water bath simulation efforts and allows us to make statements about the ways in which focusing may be affected by the presence of a heterogeneous soft tissue environment. Future three-dimensional calculations and experimental validation will be required to more carefully assess the strength of any secondary focusing.
Fig. 8.
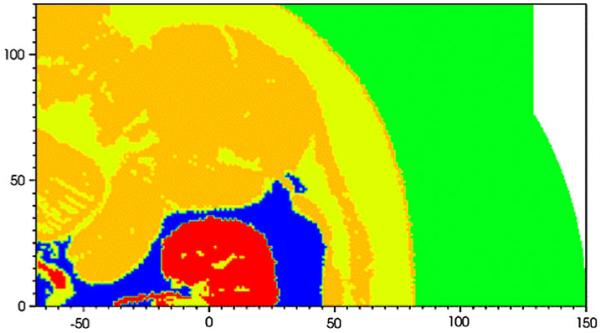
Flooded contour plot of sound speed at t = 0 for the PLA simulation. The units of distance on the abscissa and ordinate are in mm. The focus is at (0,0). Kidney (red), fat (blue), general soft tissue (dark yellow), unclassified tissue (yellow), water (green)
Using the segmented VMG data, we were able to assign values of density and sound speed to different classes of soft tissue. The density of all tissue except kidney and fat was set to 1,025 kg/m3. The kidney tissue was given a density of 1,050 kg/m3, while fat was prescribed a density of 900 kg/m3. The values are summarized in Table 1. We adjusted the thermodynamic parameters for each different class of tissue to provide a different ambient sound speed, whose values are also listed in Table 1. Some tissue was specifically marked as unclassified, and we decreased the sound speed in this region to fall between general soft tissue and fat. The tissue classified as general is mostly muscle. Figure 8 shows contour plots of sound speed for the particular case of the PLA.
Table 1.
The sound speeds in materials of different density
| Tissue type | Density (kg/m3) | Sound speed (m/s) |
|---|---|---|
| Water | 1,000 | 1,500 |
| Unclassified | 1,025 | 1,535 |
| General | 1,025 | 1,555 |
| Fat | 900 | 1,465 |
| Kidney | 1,050 | 1,575 |
We chose these values for density and sound speed after surveying the literature. Wide ranges of values have been reported for different tissue types, and we selected what we believe are reasonable values. While selecting different values would alter the results, the trends and comparisons with the water bath results should be relatively insensitive to the specific densities and sound speeds we show in Table 1.
Absorption
Among the many ways soft tissue effects the propagation of ultrasound, absorption is one of the most important. Mechanical energy is absorbed by the tissue and transformed into thermal energy, manifesting as an increase in the temperature of the tissue. One difficulty with modeling absorption is an absorption law is usually provided in the frequency domain, i.e. we are told how much waves of a particular frequency are attenuated as they travel through a given thickness of tissue. We compute solutions to the equations in our code, however, as a function of time, not frequency. Yang and Cleveland [52] overcame this problem by using a modified form of the KZK equation to simulate the propagation of nonlinear acoustic beams through a tissue-like material. The frequency-dependent absorption was approximated via the use of two relaxation processes. Details can be found in the cited reference. Following this example, we modified our own code to include the same relaxation processes. The details of the various necessary numerical manipulations can be found elsewhere [35].
Interestingly, a variety of calculations (that also included scattering effects, described below) showed that absorption did not play a significant role in modifying the focal-region pressures or strains for lithotripter pulses, which of course have a much more significant concentration of energy at lower frequencies than an associated burst of ultrasound. Calculations were made both with and without the absorption model. These revealed only a small attenuation of the pressure, on the order of 10%, which was fairly spatially uniform over the focal region. Further results for absorption are presented in [35], but we turn now to scattering which has a much larger impact on the computed focal region pressures.
Scattering
The effects of scattering of the focal waveforms are now discussed. The flow variable most commonly studied in SWL is the peak positive pressure associated with the focusing shock. Figure 9 shows flooded contours of maximum pressure (over all times) for the Dornier HM3 for the water bath case and the case where the VMG data is used. The 20 MPa contour is drawn on top of the flooded contours. For the water bath case, the contour levels are similar to those previously reported [20, 26], and the maximum pressure occurs about 13 mm postfocus. When the tissue interfaces are included, the radial extent of the region enclosed by the 20 MPa does not change significantly, but there is a broader region postfocal that is illuminated with low (<20 MPa) pressure levels, and a pronounced secondary peak is found about 35 mm postfocus, a distance that would typically fall outside the kidney.
Fig. 9.
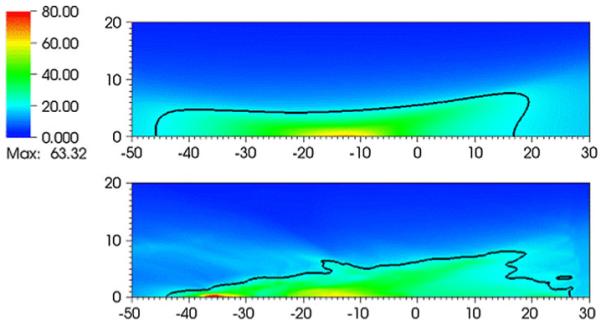
Flooded contour plots of maximum pressures (MPa) for the Dornier HM3: water bath (top) and VOXEL-MAN Group (bottom) cases. The units of distance on the abscissa and ordinate are in mm. The focus is at (0,0). The 20 MPa contour line is drawn
Figure 10 shows the maximum recorded pressure along the axis as a function of distance from the focus for all three lithotripters. The plot highlights the broad focal zone and low amplitude of XX-Es and the narrow focal zone and high amplitude of the PLA. All lithotripters show a secondary maximum between 30 and 40 mm post-focus, but the effect is most pronounced for the HM3.
Fig. 10.
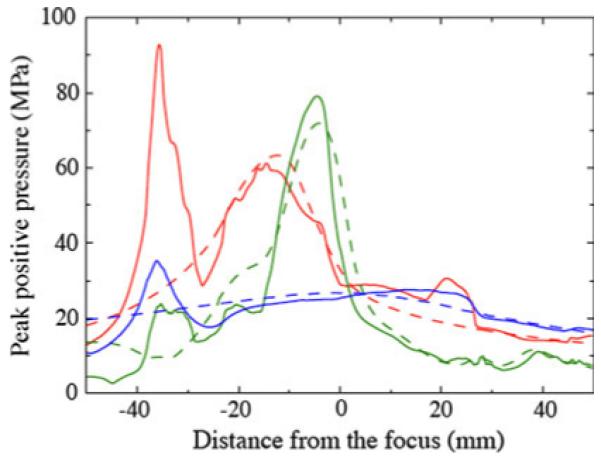
Peak positive pressure recorded along the axis as a function of distance from the focus: water bath (dashed), VMG data (solid); HM3 (red), PLA (green), XX-Es (blue)
Peak negative pressures provide insight regarding where the areas of most intense cavitation are likely to be found. Figure 11 shows the peak negative pressure as a function of distance from the focus along the axis for each lithotripter. For the HM3, the peak negative pressure for the water bath case of −7 MPa is found 10 mm prefocal, which agrees with published measurements [43]. Significant deviations are seen in the postfocal region for the VMG case, where peak negative pressures of −16 MPa are found 30 mm postfocus, a region where the water bath case shows pressures of −4 MPa. This increase by a factor of four in negative pressures could produce much more energetic cavitation activity than water bath predictions would indicate. Aside from the amplitude of the negative pressure, cavitation activity may also be significantly altered by the fast oscillations in the negative pressure. The effect is again strongest for the HM3.
Fig. 11.
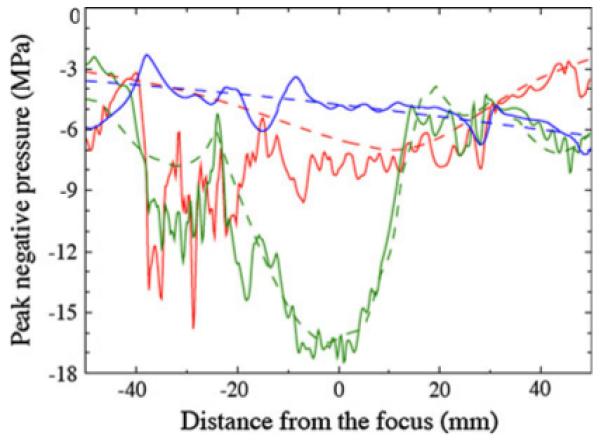
Peak negative pressure recorded along the axis as a function of distance from the focus: water bath (dashed), VMG data (solid); HM3 (red), PLA (green), XX-Es (blue)
The Dornier HM3 is most sensitive to the scattering effect found with the introduction of different tissue types, while the XX-Es is least sensitive to this effect. The motivation for creating the XX-Es was to produce a “wide-focus and low-amplitude” machine that would be more robust to perturbations in the region near the stone. Because the shock front is of nearly uniform strength and the aperture is smaller than the HM3, the shock front is perturbed less as it traverses interfaces between different tissue types. In the case of the HM3, the shock front extends comparatively farther in the radial direction, and the near-axis portion of the front is substantially stronger than the off-axis portion. Material interfaces further disrupt the focusing front that is already of nonuniform strength, and this increased sensitivity is manifested in the plots showing the variation in flow variables along the axis.
We would like to know the role the focal acoustics of each lithotripter plays in terms of the damage potential to nearby soft tissue. As discussed in “Introduction”, one commonly discussed mechanism of soft tissue damage is trauma resulting from the violent collapse of cavitating bubbles. A second proposed mechanism is shearing of tissue as a result of variability in the strength of the focusing shock front. Stronger portions of the shock front cause larger tissue displacements than weaker portions of the front. Sufficiently large changes in relative displacement between nearby points in the tissue will cause tearing.
As a surrogate for damage potential via shear, we use a maximum shear strain estimate. As our simulation runs, we integrate the computed velocities to approximate the displacement of a small soft tissue element at each moment in time. Taking the gradients of these estimated displacements produces strain values. Using linear arguments, we rotate the coordinate system and calculate the maximum shear strain at each point in the domain at each instant in time. We then record the peak value over the course of the simulation and report this as our estimate for the maximum shear strain experienced by each soft tissue element (see [35] for details).
Estimates for the strain induced by the passage of a single shock wave through tissue are less than 2% [35, 53]. Freund et al. [53] noted these values are much less than 10% threshold that is seemingly required to initiate damage in kidney parenchyma and proposed a cumulative shear hypothesis. Rather than the shear induced by a single shock, it could be the cumulative effect of many (hundred, possibly thousands of) shock waves that initiate damage in SWL. While it is beyond the scope of this work to simulate the firing of hundreds of shocks that would occur in a SWL treatment, we can identify areas where our shear strain estimates are highest and thus are most likely to be sites of damage via the cumulative shear hypothesis.
Figure 12 shows shear strain magnitudes along the axis for the different lithotripters. The values computed using the VMG data are compared with those computed in the water bath domain. Along the axis, introducing the VMG data slightly reduces estimated shear strains within 30 mm of the focus. However, from 30 to 40 mm postfocus, the estimated shear strains are much larger than would be expected from the water bath simulations, with the difference for the Dornier HM3 being a factor of three between the two cases. We have thus found a region along the axis that is worthy of further study in terms of the expected strain fields, while the water bath simulation alone would have provided no indication of such a region.
Fig. 12.
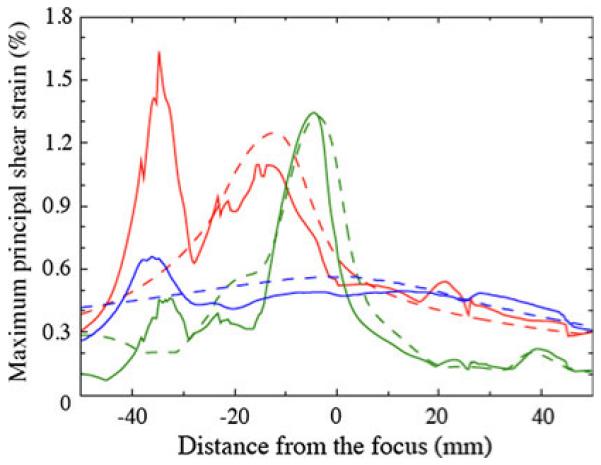
Maximum principal shear strain (%) recorded along the axis as a function of distance from the focus: water bath (dashed), VMG data (solid); Dornier HM3 (red), PLA (green), XX-Es (blue)
Figures 13 and 14 show flooded contour plots of maximum shear strain in the focal region for the Dornier HM3 and PLA, respectively. Maximum strains in the focal region are found along the axis in both cases, 35 mm postfocus for the Dornier HM3 and 5 mm postfocus for the PLA. If the stone is positioned at the geometrical focus, the largest strains are found elsewhere, which is an obvious concern in protecting against shock-induced damage to nearby tissue. For the Dornier HM3, the plane normal to the axis at F2 (where the stone is ostensibly sitting) shows strains are locally highest 4 mm off-axis, which is in agreement with previous calculations [53]. Downstream of the focus, peak strains are often found along the axis with a monotonic decay away from the axis. In any case, strains at the geometrical focus are neither largest locally, because larger strains are found 4 mm off-axis, nor globally, as peak values are found axially nearly 4 cm downstream. Artifacts in these figures are the result of the limited resolution the VMG data (where the voxel size is 1 mm).
Fig. 13.
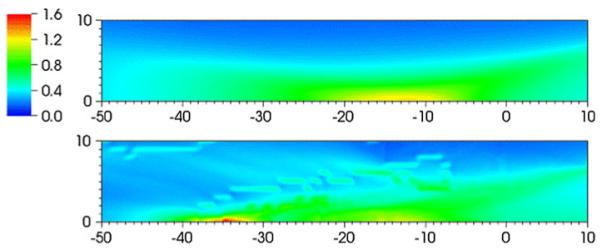
Flooded contour plot of maximum shear strain (%) in the neighborhood of the focus or the Dornier HM3. The units of distance on the abscissa and ordinate are in mm. The focus is at (0,0). Results for the water bath case (top) and using VOXEL-MAN Group data (bottom)
Fig. 14.
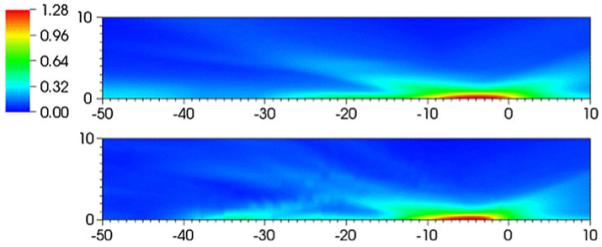
Flooded contour plot of maximum shear strain (%) in the neighborhood of the focus for the piezoelectric lithotripter array. The units of distance are in mm. The focus is at (0,0). Results for the water bath case (top) and using VOXEL-MAN Group data (bottom)
We note in passing that our strain estimates are an order of magnitude larger than those reported by Freund et al. [53]. The difference occurs because Freund et al. estimated the net strain after passage of the pulse, whereas we have reported the maximum instantaneous strain occurring during the pulse.
Conclusions
In this paper we summarized the development of a simulation tool to predict the pressure fields and other flow variables generated by representative lithotripters. We simulated the Dornier HM3 (electrohydraulic), the PLA (piezoelectric), and the XX-Es (electromagnetic) lithotripters. For the HM3, we used a simple model of the spark/vaporization event at F1 to provide the direct shock wave, whereas for the PLA and XX-Es machines, we directly model the element displacements. Baseline simulations in a water bath show reasonable agreement with measured waveforms for all cases. We also provide models for two important effects that alter the lithotripter pulses in non-trivial ways. In particular, we consider the effect of a cloud of cavitation bubbles excited by the negative pressures associated with the pulse, and the scattering and absorption of waves by tissue and by interfaces between different types of soft tissue with varying density and sound speed.
The cloud cavitation model reproduces observed features of cavitation in the Dornier HM3. In particular, the presence of multiple bubbles retards the collapse of bubbles near F2, and, at least when the void fraction is not too large, ultimately causes them to collapse more violently (and energetically). This latter effect is associated with the sequence of bubble collapse in the cloud: the peripheral bubbles collapse first and concentrate energy (compress) the interior bubbles. For higher bubble number density and/or initially larger bubbles, however, the presence of the bubbles has a significant effect on the incident shock focusing. Negative components of the reflected wave arriving first (and prefocal) incite explosive bubble growth, which in turn delays and de-focuses other components of the focused wave. The result is lower peak pressures and a shielding of the focal region. These competing effects (higher energy of collapse at low void fraction versus shielding at high void fraction) provide for an optimal level of cavitation activity that may be associated with observations of decreased stone comminution efficiency at higher PRF. At high PRF, there is insufficient time for non-condensible gas to dissolve from the bubble between each shock; as a consequence, bubbles initially grow larger with each subsequent shock (rectified diffusion) until they reach an asymptotic state after hundreds of shocks. Experiments have also shown that larger bubbles at high PRF may undergo fission during collapse which leads to an increase in number density. Thus, high PRF corresponds, either via larger bubbles or more bubbles, to higher void fractions and ultimately to shielding the stone from the incident shock.
We used real anatomical data segmented and labeled by the VOXEL-MAN Group to establish initial conditions for our simulations. Our simulations were restricted to axisymmetric geometries which produce a rough approximation to the full three-dimensional anatomical geometry in the vicinity of the shock path, but which may lead to an overestimate of the effects of inhomogeneous shock propagation due to a lensing effect. Different tissue types were distinguished by different initial densities and sound speeds. The interfaces between different material types perturb the focusing wavefronts. Peak positive and negative pressures, along with estimates of maximum shear strains, peak 30–40 mm postfocus for all three lithotripters. These results deviate strongly from what is expected from the water bath simulations. In addition to demonstrating the concern of using in vitro results to make statements about damage in vivo, we have identified a particular region that should be further explored with more accurate geometries and solid mechanic models in the hopes of better understanding the role of damage via shear in SWL.
We have examined the data from the various simulations with an eye toward understanding the impact of lithotripter design and treatment parameters on stone comminution and tissue injury. However, there remain many interesting and potentially useful ways to utilize the simulation data. We provide a few examples of how the data may be used to inform or calibrate more detailed models of specific aspects of comminution and injury. First, to understand the mechanics of stone fracture, Cleveland and Sapozhnikov computed solutions to the equations of linear elasticity to model wave propagation in kidney stones, both in simplified geometries [1] and in real stones mapped via micro computed tomography [54]. They used simplified descriptions of the incident pulse as initial and boundary conditions near the surface of the stone. The present lithotripter simulations could be coupled to such elastic wave propagation models to provide insights into the effects of lithotripter design and scattering by tissue and bubbles on stress concentrations in stones. Next, Johnsen and Colonius [55, 56] studied the detailed shock-induced collapse of a single bubble as would occur when a bubble nucleus near a stone is exposed to the initial lithotripter compression front. They found that shock-induced bubble collapse can significantly amplify the pressure felt on the surface of the stone. Collapse of cavitating bubbles generated by the tensile portion of the lithotripter pulse is also of obvious import in understanding erosion of the stone surface. The present simulations give some indications of the enhancement of collapse energy due to concerted cloud collapse, but future efforts should combine the full lithotripter simulations with more detailed bubble collapse models to directly evaluate the erosive characteristics of cavitation as a function of lithotripter design, etc. Finally, Freund et al. [53] modeled the microstructure of the renal parenchyma as a set of parallel tubes embedded in an interstitial gel and computed estimates for the degree to which repeated shocks would cumulatively shear soft tissue in the blast path. Such models depend on good estimates for the stresses and strains experienced by tissue in different regions of the kidney, which can be provided by the lithotripter models discussed here.
Acknowledgments
This work was funded by the National Institutes of Health through a Program Project Grant, Grant No. DK43881. The authors thank Mike Bailey, Robin Cleveland, Andrew Evan, Jonathon Freund, Eric Johnsen, James McAteer, Yuri Pishchalnikov, Oleg Sapozhnikov, James Williams, and the entire PPG team for their longstanding collaboration and numerous contributions to this work. We also thank Ralf Deiterding for his abundant help with using AMROC and for producing several customizations of the software particular to our simulation efforts. Finally, we thank Yuri Pishchalnikov and Parag Chitnis for the measured data that are shown in Fig. 2.
Footnotes
An additional feature of the computational waveform is the gradual rise in pressure just following the main shock front. This feature is absent from experimental measurements, though it is observed in independent simulations of the HM3 [19]. The feature was confirmed to be independent of the grid resolution, and does not therefore appear to be an artifact of the numerical method. In a more detailed study [35], we attributed this wave feature to perfect axisymmetric focusing that increases the amplitude of the shock on axis and causes it to propagate (through nonlinearity) with higher speed, thus racing ahead of components of the compression front generated from portions of the wavefront that are arriving from off axis. Indeed, as the amplitude of the shock produced at F1 is reduced, this feature disappears and the sharp shock front is followed by an immediate expansion. We speculate that slight departures from strict axisymmetry in the real device may reduce the on-axis amplitude by a sufficient amount to delay the on-axis portion of the shock from getting ahead of the reflected components.
Our computations with the cloud cavitation model used a slightly different base numerical method than was described in the previous section, and only the HM3 geometry was considered. The details of the numerical method for this section are provided in a thesis [18], but we note here that sufficient resolution was used to ensure that various output quantities of interest were independent of the grid.
References
- 1.Cleveland RO, Sapozhnikov OA. Modeling elastic wave propagation in kidney stones with application to shock wave lithotripsy. J Acoust Soc Am. 2005;118:2667–2676. doi: 10.1121/1.2032187. [DOI] [PubMed] [Google Scholar]
- 2.Sapozhnikov OA, Maxwell AD, McConaghy B, Bailey MR. A mechanistic analysis of stone fracture in lithotripsy. J Acoust Soc Am. 2007;121:1190–1202. doi: 10.1121/1.2404894. [DOI] [PubMed] [Google Scholar]
- 3.Crum LA. Cavitation microjets as a contributory mechanism for renal calculi disintegration in ESWL. J Urol. 1988;140:1587–1590. doi: 10.1016/s0022-5347(17)42132-x. [DOI] [PubMed] [Google Scholar]
- 4.Sass W, Brünlich M, Dreyer H-P, Matura E, Forberth W, Priesmeyer H-G, Seifert J. The mechanisms of stone disintegration by shock waves. Ultrasound Med Biol. 1991;17:239–243. doi: 10.1016/0301-5629(91)90045-x. [DOI] [PubMed] [Google Scholar]
- 5.Zhu S, Cocks FH, Preminger GM, Zhong P. The role of stress waves and cavitation in stone comminution in shock wave lithotripsy. Ultrasound Med Biol. 2002;28:661–671. doi: 10.1016/s0301-5629(02)00506-9. [DOI] [PubMed] [Google Scholar]
- 6.Pishchalnikov YA, Sapozhnikov OA, Bailey MR, Williams JC, Jr, Cleveland RO, Colonius T, Crum LA, Evan AP, McAteer JA. Cavitation bubble cluster activity in the breakage of kidney stones by lithotripter shockwaves. J Endourol. 2003;17:435–446. doi: 10.1089/089277903769013568. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Lifshitz DA, Williams JC, Jr, Sturtevant B, Connors BA, Evan AP, McAteer JA. Quantitation of shock wave cavitation damage in vitro. Ultrasound Med Biol. 1997;23:461–471. doi: 10.1016/s0301-5629(96)00223-2. [DOI] [PubMed] [Google Scholar]
- 8.Evan P, Willis LR, McAteer JA, Bailey MR, Connors BA, Shao Y, Lingeman JE, Williams JC, Jr, Fineberg NS, Crum LA. Kidney damage and renal functional changes are minimized by waveform control that suppresses cavitation in shock wave lithotripsy. J Urol. 2002;168:1556–1562. doi: 10.1016/S0022-5347(05)64520-X. [DOI] [PubMed] [Google Scholar]
- 9.Sapozhnikov OA, Khokhlova VA, Bailey MR, Williams JC, Jr, McAteer JA, Cleveland RO, Crum LA. Effect of over-pressure and pulse repetition frequency on cavitation in shock wave lithotripsy. J Acoust Soc Am. 2002;112:1183–1195. doi: 10.1121/1.1500754. [DOI] [PubMed] [Google Scholar]
- 10.Bailey MR, Crum LA, Evan AP, McAteer JA, Williams JC, Jr, Sapozhnikov OA, Cleveland RO, Colonius T. Cavitation in shock wave lithotripsy, volume Cav03-OS-2-1-006 of fifth international symposium on cavitation; Osaka, Japan. CAV2003.2003. pp. 1–12. [Google Scholar]
- 11.Bailey MR, Pishchalnikov YA, Sapozhnikov OA, Cleveland RO, McAteer JA, Miller NA, Pishchalnikov IV, Connors BA, Crum LA, Evan AP. Cavitation detection during shock-wave lithotripsy. Ultrasound Med Biol. 2005;31:1245–1256. doi: 10.1016/j.ultrasmedbio.2005.02.017. [DOI] [PubMed] [Google Scholar]
- 12.Howard D, Sturtevant B. In vitro study of the mechanical effects of shock-wave lithotripsy. Ultrasound Med Biol. 1997;23:1107–1122. doi: 10.1016/s0301-5629(97)00081-1. [DOI] [PubMed] [Google Scholar]
- 13.Lokhandwalla M, Sturtevant B. Mechanical haemolysis in shock wave lithotripsy (SWL): I. Analysis of cell deformation due to SWL flow-fields. Phys Med Biol. 2001;46:413–437. doi: 10.1088/0031-9155/46/2/310. [DOI] [PubMed] [Google Scholar]
- 14.Lokhandwalla M, McAteer JA, Williams JC, Jr, Sturtevant B. Mechanical haemolysis in shock wave lithotripsy (SWL): II. In vitro cell lysis due to shear. Phys Med Biol. 2001;46:1245–1264. doi: 10.1088/0031-9155/46/4/323. [DOI] [PubMed] [Google Scholar]
- 15.Hamilton MF. Transient axial solution for the reflection of a spherical wave from a concave ellipsoidal mirror. J Acoust Soc Am. 1993;93:1256–1266. [Google Scholar]
- 16.Averkiou MA, Cleveland RO. Modeling of an electrohydraulic lithotripter with the KZK equation. J Acoust Soc Am. 1999;106:102–112. doi: 10.1121/1.427039. [DOI] [PubMed] [Google Scholar]
- 17.Cates J, Sturtevant B. Shock wave focusing using geometrical shock dynamics. Phys Fluids. 1997;9:3058–3068. [Google Scholar]
- 18.Tanguay M. PhD thesis. California Institute of Technology; 2004. Computation of bubbly cavitating flow in shock wave lithotripsy. [Google Scholar]
- 19.Iloreta JI, Zhou Y, Sankin GN, Zhong P, Szeri AJ. Assessment of shock wave lithotripters via cavitation potential. Phys Fluids. 2007;19:086103. doi: 10.1063/1.2760279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Coleman, Saunders J, Preston R, Bacon D. Pressure waveforms generated by a Dornier extracorporeal shock-wave lithotripter. Ultrasound Med Biol. 1987;13:651–657. doi: 10.1016/0301-5629(87)90063-9. [DOI] [PubMed] [Google Scholar]
- 21.Chitnis PV, Barbone PE, Cleveland RO. Customization of the acoustic field produced by a piezoelectric array through inter-element delays. J Acoust Soc Am. 2008;123:4174–4185. doi: 10.1121/1.2912448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Eisenmenger W, Du X, Tang C, Zhao S, Wang Y, Rong F, Dai D, Guan M, Qi A. The first clinical results of ‘wide-focus and low-pressure’ ESWL. Ultrasound Med Biol. 2002;28:769–774. doi: 10.1016/s0301-5629(02)00507-0. [DOI] [PubMed] [Google Scholar]
- 23.Coleman J, Saunders JE, Crum LA, Dyson M. Acoustic cavitation generated by an extracorporeal shockwave lithotripter. Ultrasound Med Biol. 1987;13:69–76. doi: 10.1016/0301-5629(87)90076-7. [DOI] [PubMed] [Google Scholar]
- 24.Coleman, Choi M, Saunders J, Leighton T. Acoustic emission and sonoluminescence due to cavitation at the beam focus of an electrohydraulic shock wave lithotripter. Ultrasound Med Biol. 1992;18:267–281. doi: 10.1016/0301-5629(92)90096-s. [DOI] [PubMed] [Google Scholar]
- 25.Zhong P, Cioanta I, Cocks FH, Preminger GM. Inertial cavitation and associated acoustic emission produced during electrohydraulic shock wave lithotripsy. J Acoust Soc Am. 1997;101:2940–2950. doi: 10.1121/1.418522. [DOI] [PubMed] [Google Scholar]
- 26.Bailey MR, Blackstock DT, Cleveland RO, Crum LA. Comparison of electrohydraulic lithotripters with rigid and pressure-release ellipsoidal reflectors. I acoustic fields. J Acoust Soc Am. 1998;104:2517–2524. doi: 10.1121/1.423758. [DOI] [PubMed] [Google Scholar]
- 27.Sokolov DL, Bailey MR, Crum LA. Use of a dual-pulse lithotripter to generate a localized and intensified cavitation field. J Acoust Soc Am. 2001;110:1685–1695. doi: 10.1121/1.1394221. [DOI] [PubMed] [Google Scholar]
- 28.Paterson RF, Lifshitz DA, Lingeman JE, Evan AP, Connors BA, Fineberg NS, Williams JC, Jr, McAteer JA. Stone fragmentation during shock wave lithotripsy is improved by slowing the shock wave rate: studies with a new animal model. J Urol. 2002;168:2211–2215. doi: 10.1016/S0022-5347(05)64357-1. [DOI] [PubMed] [Google Scholar]
- 29.Evan P, Willis LR, Lingeman JE, McAteer JA. Renal trauma and the risk of long-term complications in shock wave lithotripsy. Nephron. 1998;78:1–8. doi: 10.1159/000044874. [DOI] [PubMed] [Google Scholar]
- 30.Coleman AJ, Saunders JE. A review of the physical properties and biological effects of the high amplitude acoustic field used in extracorporeal lithotripsy. Ultrasonics. 1993;31:75–89. doi: 10.1016/0041-624x(93)90037-z. [DOI] [PubMed] [Google Scholar]
- 31.Blomgren PM, Connors BA, Lingeman JE, Willis LR, Evan AP. Quantitation of shock wave lithotripsy-induced lesion in small and large pig kidneys. Anat Rec. 1997;249:341–348. doi: 10.1002/(SICI)1097-0185(199711)249:3<341::AID-AR4>3.0.CO;2-X. [DOI] [PubMed] [Google Scholar]
- 32.Wood RW, Loomis A. The physical and biological effects of high frequency sound-waves of great intensity. Philos Mag. 1927;4:417–436. [Google Scholar]
- 33.Ludwig GD. The velocity of sound through tissues and the acoustic impedance of tissues. J Acoust Soc Am. 1950;22:862–866. [Google Scholar]
- 34.Cleveland RO, Lifshitz DA, Connors BA, Evan AP, Willis LR, Crum LA. In vivo pressure measurements of lithotripsy shock waves in pigs. Ultrasound Med Biol. 1998;24:293–306. doi: 10.1016/s0301-5629(97)00270-6. [DOI] [PubMed] [Google Scholar]
- 35.Krimmel J. PhD thesis. California Institute of Technology; 2010. Numerical simulation of wave focusing and scattering in shock wave lithotripsy. [Google Scholar]
- 36.Krimmel J, Colonius T. Numerical simulation of shock focusing in shock wave lithotripsy. 2010 in preparation. [Google Scholar]
- 37.Harlow F, Amsden AA. Fluid dynamics. Los Alamos Scientific Laboratory; 1971. Technical Report LA-4700. [Google Scholar]
- 38.Cole RH. Underwater explosions. Princeton University Press; Princeton, NJ: 1948. chap 2. [Google Scholar]
- 39.Thompson PA. Compressible-fluid dynamics. McGraw-Hill; New York: 1972. chap 2. [Google Scholar]
- 40.Deiterding R. PhD thesis. Brandenburgische Technische Universtät, Cottbus; 2003. Parallel adaptive simulation of multi-dimensional detonation structures. [Google Scholar]
- 41.Deiterding R. Construction and application of an AMR algorithm for distributed memory computers. In: Plewa T, Linde T, Weirs VG, editors. Adaptive mesh refinement—theory and applications; Proceedings of the Chicago workshop on adaptive mesh refinement methods; Springer, Berlin. 2005.pp. 361–372. [Google Scholar]
- 42.Deiterding R, Radovitzky R, Mauch SP, Noels L, Cummings JC, Meiron DI. A virtual test facility for the efficient simulation of solid material response under strong shock and detonation wave loading. Eng Comput. 2006;22:325–347. [Google Scholar]
- 43.Sokolov DL, Bailey MR, Crum LA, Blomgren PM, Connors BA, Evan AP. Prefocal alignment improves stone comminution in shockwave lithotripsy. J Endourol. 2002;16:709–715. doi: 10.1089/08927790260472845. [DOI] [PubMed] [Google Scholar]
- 44.Cleveland RO, Bailey MR, Fineberg N, Hartenbaum B, Lokhandwalla M, McAteer JA, Sturtevant B. Design and characterization of a research electrohydraulic lithotripter patterned after the Dornier HM3. Rev Sci Instrum. 2000;71:2514–2525. [Google Scholar]
- 45.Brennen CE. Fission of collapsing cavitation bubbles. J Fluid Mech. 2002;472:153–166. [Google Scholar]
- 46.Zhang D, Prosperetti A. Ensemble phase-averaged equations for bubbly flows. Phys Fluids. 1994;6:2956–2970. [Google Scholar]
- 47.Biesheuvel A, van Wijngaarden L. Two-phase flow equations for a dilute dispersion of gas bubbles in liquid. J Fluid Mech. 1984;148:301–318. [Google Scholar]
- 48.Gilmore FR. The growth or collapse of a spherical bubble in a viscous compressible liquid. California Institute of Technology; 1952. Technical Report 26-4. [Google Scholar]
- 49.Pishchalnikov YA, McAteer JA, Williams JC., Jr Effect of firing rate on the performance of shock wave lithotripters. BJU Int. 2008;102:1681–1686. doi: 10.1111/j.1464-410X.2008.07896.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Matula TJ, Hilmo PR, Storey BD, Szeri AJ. Radial response of individual bubbles subjected to shock wave lithotripsy pulses in vitro. Phys Fluids. 2002;14:913–921. [Google Scholar]
- 51.VOXEL-MAN Group Segmented inner organs of the visible Human male. 2010 http://www.voxel-man.de/data/
- 52.Yang X, Cleveland RO. Time domain simulation of nonlinear acoustic beams generated by rectangular pistons with application to harmonic imaging. J Acoust Soc Am. 2005;117:113–123. doi: 10.1121/1.1828671. [DOI] [PubMed] [Google Scholar]
- 53.Freund JB, Colonius T, Evan AP. A cumulative shear mechanism for tissue damage initiation in shock-wave lithotripsy. Ultrasound Med Biol. 2007;33:1495–1503. doi: 10.1016/j.ultrasmedbio.2007.03.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Cleveland R, Luo H, Willaims J. Stress waves in human kidney stones: shear dominates spall in shock wave lithotripsy. J Urol. 2007;177:415. [Google Scholar]
- 55.Johnsen E, Colonius T. Implementation of WENO schemes in compressible multicomponent flow problems. J Comput Phys. 2006;219:715–732. [Google Scholar]
- 56.Johnsen E, Colonius T. Shock-induced collapse of a gas bubble in shockwave lithotripsy. J Acoust Soc Am. 2008;124:2011–2020. doi: 10.1121/1.2973229. [DOI] [PMC free article] [PubMed] [Google Scholar]