Effect of different modes of viral spread on the dynamics of multiply infected cells in human immunodeficiency virus infection

Abstract

Infection of individual cells with more than one HIV particle is an important feature of HIV replication, which may contribute to HIV pathogenesis via the occurrence of recombination, viral complementation and other outcomes that influence HIV replication and evolutionary dynamics. A previous mathematical model of co-infection has shown that the number of cells infected with i viruses correlates with the ith power of the singly infected cell population, and this has partly been observed in experiments. This model, however, assumed that virus spread from cell to cell occurs only via free virus particles, and that viruses and cells mix perfectly. Here, we introduce a cellular automaton model that takes into account different modes of virus spread among cells, including cell to cell transmission via the virological synapse, and spatially constrained virus spread. In these scenarios, it is found that the number of multiply infected cells correlates linearly with the number of singly infected cells, meaning that co-infection plays a greater role at lower virus loads. The model further indicates that current experimental systems that are used to study co-infection dynamics fail to reflect the true dynamics of multiply infected cells under these specific assumptions, and that new experimental techniques need to be designed to distinguish between the different assumptions.

1. Introduction

The dynamics of HIV infection during various stages of the disease have been analysed in detail over the years, both from an experimental point of view, and with the help of mathematical models. Most of this work is based upon the assumption that cells are infected only with single virus particles and omits from consideration the possibility that multiple HIV particles frequently co-infect the same cell. Strong evidence, however, has accumulated that co-infection occurs frequently in vivo and that it can contribute significantly to the dynamics and evolution of the virus in vivo. This evidence is reviewed in detail in §2. Co-infection has a variety of important consequences for the disease process, including the occurrence of viral recombination, phenotypic complementation between viruses within the same cell, and in general altered competition and evolutionary dynamics of the virus [1–8].

Apart from exploring these complex interactions, however, it is also important to gain an understanding of the basic dynamics of multiple infection. Previous studies have provided important first steps in this regard. Using viruses bearing different fluorescent protein reporter genes, the dynamics of dually infected cells has been documented during exponential growth phases in vitro and in vivo in human thymic tissue within SCID-hu Thy/Liv mice [1,6,9]. It was found that the number of dually infected cells correlated with the square of the overall number of infected cells. Theoretical studies analysed those dynamics using a mathematical model [10,11]. This model was based on ordinary differential equations and reproduced the experimental observation in specific parameter regions, and generalized this result by predicting that the number of cells infected with i viruses correlates with the ith power of the overall number of infected cells (more precisely, it correlates with the ith power of singly infected cells, which is the dominant infected cell population).

Here, we build on this theoretical study and extend it to include further biological complexities. As with most mathematical models that study the dynamics of HIV infection, the previous models [10,11] assumed that all virus transmission occurred via free virus and that cells and viruses mix perfectly. Both assumptions, however, might be violated to a certain degree in HIV-1 infection. There is experimental evidence that viral spread via cell to cell transmission, brought about by the formation of the virological synapse [12–14] is many fold more efficient than infection via cell-free virus [15] and could play an important role in HIV dynamics. In addition, it is clear that HIV-1 replication occurs primarily in the lymphoid tissues, which are spatially structured and where cells and viruses are not likely to mix perfectly [16,17]. Hence, we construct a new cellular automaton modelling framework that examines basic dynamics of co-infection, taking into account different modes of virus spread through the target cell population.

In the limit where the cellular automaton assumes viral spread via free virions and ignores spatial aspects, the results from the previous differential equation modelling are reproduced. If, however, the model allows for viral spread via cell to cell transmission or for spatially restricted virus spread, then the model properties become different. In these cases, the multiply infected cell populations tend to correlate linearly with the singly infected cell population. Hence, co-infection plays a more significant role in the dynamics already at lower virus loads. In addition, the model suggests that experiments based on reporter viruses labelled with different colours do not reflect the true dynamics in the context of cell to cell transmission of the virus, or spatially restricted viral spread. While the true correlation between multiply infected and singly infected cells is linear in these scenarios, the experiments are predicted to yield results that are not distinguishable from the scenario where virus transmission occurs via free virions and where perfect mixing of cells and viruses occurs. The reason for this discrepancy is that a disproportionately large number of cells will be infected with multiple copies of the same type of reporter virus and these cells are counted as singly infected rather than multiply infected in those experiments. Hence, new experimental techniques will have to be devised to distinguish between the different scenarios and to examine the dynamics of multiple infection in more detail.

2. The biology of hiv co-infection

Until fairly recently, the concept of co-infection has not played a prominent role in HIV research. This probably stems at least in part from the early observation that infection leads to the down-modulation of the CD4 receptor (reviewed in [18,19]), and the more recent observation that HIV also downmodulates the CCR5 and CXCR4 viral coreceptors [20] from the cell surface, reducing the susceptibility of cells to reinfection over time. In fact, three separate HIV proteins—Nef, Vpu and Env—mediate CD4 down-modulation [21,22], emphasizing its biological significance. Furthermore, it was also observed quite early in the epidemic that infection frequency of cells in blood is low, of the order of 1 in 1000 to 1 in 100 000, leading to the incorrect assumption that the probability of two infection events in the same cell must be exponentially lower.

Over time it has become clear that this picture is not correct and that co-infection with two or more viruses, i.e. multiple infection of cells, is a frequent phenomenon that plays an important role in the natural history of HIV. First and perhaps foremost, HIV-1 replication occurs predominantly in the lymphoid tissues, where the concentration of target cells is higher than in the blood, and cell to cell contact facilitates transmission of multiple virions between cells. Even when few infected cells can be identified in mucosal tissues, they are observed to be infected with multiple viruses [16], and in situ staining in splenocytes of HIV-1 patients observed an average of three to four integrated proviruses per cell and sequencing of HIV-1 nucleic acids in these cells confirms multiple infection with divergent viruses and recombination between them [23]. During acute infection of macaques with a pathogenic strain of SIV, an average of 1.5 viruses per cell was observed, indicating co-infection of a large fraction of cells [24]. The recent description of cell to cell transmission of HIV via virological synapse formation [12–14] dramatically illustrates how multiple infection of cells can be locally generated.

Although CD4 loss from the cell surface is a consequence of HIV-1 infection, it is not clear that its primary function is to prevent reinfection (superinfection) of cells prior to virion production. Instead, removal of CD4 from the cell surface has been shown by several groups to increase the infectivity of the newly produced virions [25,26], allowing more Env protein to associate with virions and increasing viral pathogenesis [27]. Further, there is an 18–24 h delay between infection of a cell and production of viral proteins that modulates CD4 expression, during which the cell remains susceptible to reinfection (reviewed in [18,28]). Thus, inhibition of superinfection is only operative during the productive phase of infection. Since the lifespan of a productively infected T cell in vivo is only about 0.5–1 day, once virus production is underway in the cell, superinfection at this late stage would most likely be unhelpful to the virus.

Experimental systems to study the dynamics of multiple infection have frequently used recombinant viruses bearing different reporter genes, allowing quantification of cells infected with one or both viruses [1,6,9]. These studies, carried out in tissue culture or in vivo within human thymic tissue in SCID mice (SCID-hu Thy/Liv mice) have made it abundantly clear that multiple infection is a natural consequence of HIV-1 replication. Over many rounds of replication in tissue culture or in the SCID-hu Thy/Liv system, multiple infection proceeds without apparent inhibition, despite the ability of HIV-1 to inhibit reinfection, resulting in frequent recombination [1]. The inference is that the pace of HIV-1 replication exceeds the inhibition effect, and that fostering multiple infection, rather than inhibiting it, may be to the benefit of the virus.

Recombination is the best studied outcome of multiple infection. It can have important implications for the evolution of HIV in vivo. Recombination can potentially speed up the rate of evolution by bringing together different advantageous alleles into a single genome. On the negative side (from the virus' standpoint), recombination can also break up existing advantageous allelic combinations or it can lead to the inactivation of viable viruses if they are co-infected and recombine with defective viruses. The effect of recombination on the evolutionary dynamics in vivo is complex, and can depend on several population genetic phenomena, such as the degree of epistasis. This has been studied in a variety of theoretical papers [8,29–33].

There are other important consequences of co-infection for virus dynamics. Viruses defective in vital functions can be phenotypically complemented during co-infection, resulting in chimeric virions bearing mixtures of genes and proteins from more than one parental strain [6,7], and recombination can repair the defect at the genetic level [6,7]. Viruses with essentially zero fitness can replicate as a result of complementation during co-infection [6].

3. The model

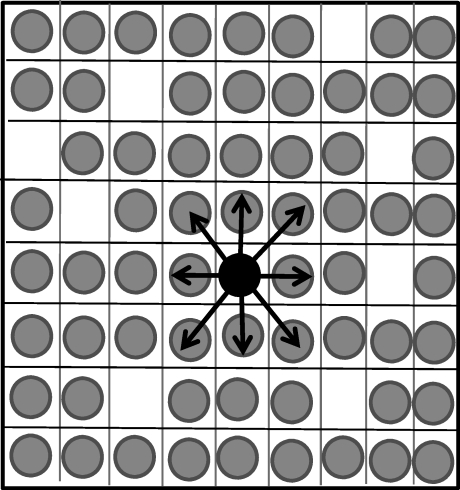
We employ a stochastic simulation in the form of a cellular automaton (figure 1). In the most basic setting, the rules of the simulation are as follows. Assume a two-dimensional square grid that consists of n × n spots. Each spot can either be empty, occupied by an uninfected cell, or occupied by an infected cell. The infected cell can harbour i viruses, where i = 1 … n. At each time step, the grid is randomly sampled n² times. Depending on the status of the chosen spots, the following events can happen. If a spot is empty, production of an uninfected cell can occur with a probability L. If a spot contains an uninfected cell, death occurs with a probability d, and the spot becomes empty. If the spot contains an infected cell, two events can occur. The cell can die with a probability a, resulting in an empty spot. With a probability B, the infected cell can transmit a virus particle to a susceptible cell. Both uninfected and infected cells are susceptible to new infection. If an uninfected cell becomes infected, it contains one virus. If a cell bearing i viruses becomes infected, it contains i + 1 viruses. Note, however, that not each infection event is necessarily successful. The destination spot in which the offspring virus is put is chosen randomly from some set of neighbouring spots (the size of this set can vary and could contain all spots, see below). The virus is only passed on to another cell if that destination spot contains a susceptible cell. Otherwise, no infection event occurs.

Figure 1.

Schematic explanation of the cellular automaton model. We assume the existence of a grid that contains n × n spots. These spots can either contain uninfected cells (grey), infected cells (black) or be empty. In the case of spatially restricted virus growth, an infected cell can pass its virus only to its nearest neighbouring target cells, as shown. If we assume perfect mixing, then an infected cell can pass its virus to any cell in the system with equal probability (not shown), and the two-dimensional spatial arrangement becomes irrelevant. See text for details.

This is the basic setting in which to explore the effect of co-infection on the dynamics of HIV infection. Further assumptions that underlie the infection events are as follows. In the simplest setting, we assume mass action or perfect mixing in the context of infection. That is, an infected producer cell can pass its virus to any other susceptible cell with equal probability. (In this case, the spatial arrangement of the n × n spots is irrelevant). At the other end of the spectrum, an infected cell can pass on the virus only to its nearest neighbours. In the two-dimensional setting, a cell has eight nearest neighbours (figure 1). In between these extremes, it can be assumed that the probability to infect a cell is a function of the distance between the producer cell and the target cell (details described below).

Related to spatial restrictions in virus spread, data indicate that besides transmission of free virus, cell to cell transmission might be an important means of virus spread, brought about by the formation of the virological synapse [12–14]. We will incorporate this by assuming that two individual cells can pair up with each other for a defined period of time, enabling the virus to pass from one cell to the other. Details are presented in the relevant section.

We start by exploring the model in the form described so far. Subsequently, we add further biological complexities and examine their effects. In particular, we include virus-induced receptor down-modulation, where permissiveness to reinfection decays over time, as well as heterogeneity in susceptibility to infection among cells.

The model has been analysed by extensive numerical simulations. Because the simulations are stochastic in nature, the averages over many runs are considered for each parameter set, and the variation is expressed in terms of the standard deviation. Details of particular runs are given in the figure legends. To make sure that results are robust, the parameter space was sampled by randomly drawing the log₁₀ of individual parameter values from a uniform distribution between −6 and 0. In the basic setting, there are four parameters: (i) the probability to produce a new target cell, L; (ii) the probability for an uninfected cell to die, d; (iii) the probability for an infected cell to pass on its offspring virus to another cell, B; and (iv) the probability for an infected cell to die, a. The probabilities were varied, with the obvious restriction that the probabilities for events occurring with infected cells, a + B < 1. In the more complex model versions that include further probabilities (e.g. for cell to cell transmission of the virus), those parameters were sampled according to the same principles. Parameter combinations in which the virus failed to establish a persistent infection were ignored. Ten thousand simulations were run this way for each model version across a computer cluster.

Two different grid sizes were used: 800 × 800 and 1000 × 1000. The simulations were generally started with a grid that was filled with uninfected cells. A certain number N₀ of initially infected cells were distributed randomly across this grid. The value of N₀ was randomly varied between one infected cell and 20 per cent of the grid being filled with infected cells. It will be discussed how the results depend on the initial conditions.

Note that so far we have not been able obtain crucial parameter estimates for this model, since this requires further experimental work. Hence, in the figures, parameter values were chosen for the purpose of illustration. The sampling of the parameter space, however, indicates that the described results are mostly robust and do not depend on the particular parameter combinations. Results that were only observed in specific parameter ranges or in the context of specific initial conditions are clearly identified as such. The results for the different scenarios will be described in turn.

4. Results and discussion

4.1. Perfect mixing of viruses and cells

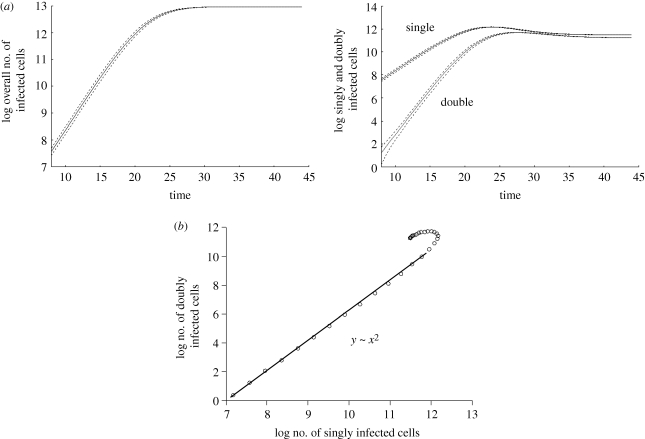
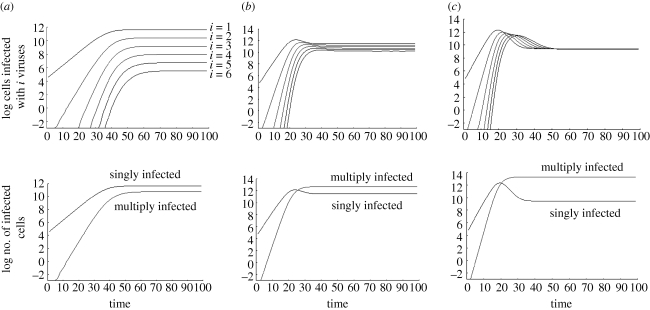
Here, we ignore any spatial restrictions on virus spread and assume that viruses and cells mix perfectly. This scenario should be closest to the previous modelling approaches discussed above, which are based on ordinary differential equations [11]. We observe that the virus population grows exponentially on average, and subsequently converges towards a stable equilibrium (figure 2). This may or may not involve damped oscillations, depending on the parameter values. We find that during the growth phase and at equilibrium, the abundance of the individual infected cell populations correlates with the number of viruses present in cells (figure 3). That is, cells infected with one virus are most abundant, followed by cells infected with two, three viruses, etc. If the replication rate of the virus is relatively fast, then this dominance hierarchy can be temporarily altered during the virus decline phase following peak virus load, when the number of uninfected target cells becomes limiting relative to the amount of virus present (figure 3).

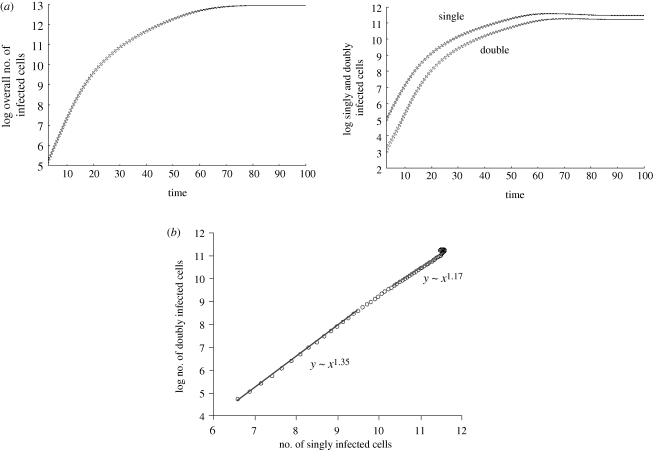
Figure 2.

Computer simulation results assuming perfect mixing of cells. Average population sizes are plotted, and the dotted line represents the standard deviations. (a) Basic growth pattern. The overall virus population on average grows exponentially and subsequently converges to an equilibrium. The graph demonstrating the growth curves for singly and doubly infected cells shows a similar pattern. The population of doubly infected cells grows faster than the population of singly infected cells. (b) During growth, the number of doubly infected cells correlates with the square of the number of singly infected cells. The graph shows the growth phase during which both populations grow exponentially on average. Linear regression during the exponential growth phase was used to obtain the correlations. At very low numbers, the growth pattern is more stochastic and this is not shown. Parameters were chosen as follows: grid size, 800 × 800; L = 0.5; d = 0.001; B = 0.5; a = 0.1.

Figure 3.

Equilibrium properties. The time course for cells infected with 1, 2, 3, … , 6 viruses is plotted, depending on the overall rate of viral spread (determined by the balance of the viral replication rate and the death rate of infected cells). (a) For slow viral spread rates, the difference in the abundance of the individual infected cell subpopulations is relatively large, and the singly infected cell population is more abundant than the sum of all multiply infected cells. (b) Increasing the viral spread rate brings the abundance of the individual infected cell subpopulations closer, and now the overall number of multiply infected cells is higher than the number of singly infected cells. (c) For faster viral spread rates, the abundances of the individual infected cell subpopulations become even closer to each other. In the limit for infinitely fast viral spread, the infected cell subpopulations will converge to becoming identical. As in the previous parameter region, the overall number of multiply infected cells is higher than the number of singly infected cells. Standard deviations were not plotted in order to make the graphs easier to read. Parameters were chosen as follows: grid size, 800 × 800; L = 0.5; d = 0.001; B = 0.5. For (a) a = 0.3, (b) a = 0.1, (c) a = 0.01.

During exponential growth, the model confirms the observation derived from the previous differential equation model [11] regarding the correlation between multiply and singly infected cells. That is, the number of doubly infected cells correlates with the square of the number of singly infected cells (figure 2). In general, the number of cells infected with i viruses correlates with the ith power of the number of singly infected cells. That is, as virus load rises, the number of co-infected cells rises relative to the number of singly infected cells.

At equilibrium, the abundance of the different infected cell subpopulations depends largely on the overall rate of virus spread (figure 3a–c). This is determined by the viral replication kinetics (rate of virus production and rate of infection), as well as by the death rate of infected cells. The faster the rate of virus replication and the lower the death rate of infected cells, the faster the virus spreads through the population of host cells. For relatively slow rates of viral spread, the difference in abundance of the infected cell subpopulations is relatively large (figure 3a). The faster the rate of virus spread, the less is the difference in the abundance of the infected cell subpopulations (figure 3b,c). In the limit, for fast virus spread rates, the abundances of the infected cell subpopulations converge to becoming identical (not shown). We can also look at the overall number of multiply infected cells (infected with two, three, four viruses, etc.) relative to the number of singly infected cells (figure 3). During the growth phase, the overall number of multiply infected cells rises relative to the number of singly infected cells. At equilibrium, the relative abundances depend on the rate of virus spread. For slow virus spread, the singly infected cells are more abundant than the overall population of multiply infected cells. For faster viral spread, the population of multiply infected cells becomes more abundant than the population of singly infected cells (figure 3b,c).

We also analysed the model that considers viruses labelled with two different colours [1], tracking the number of cells infected with dual-colour viruses rather than tracking the ‘true’ number of co-infected cells (which include cells infected with two viruses of the same colour). As with the previously published differential equation model [11], the results when tracking cells infected with both colours are qualitatively identical to those obtained when tracking all infected cells containing two viruses (not plotted here). These results hold true if cells and viruses mix perfectly. In the following sections, we will examine the model behaviour if this assumption is violated.

4.2. Spatially constrained virus spread

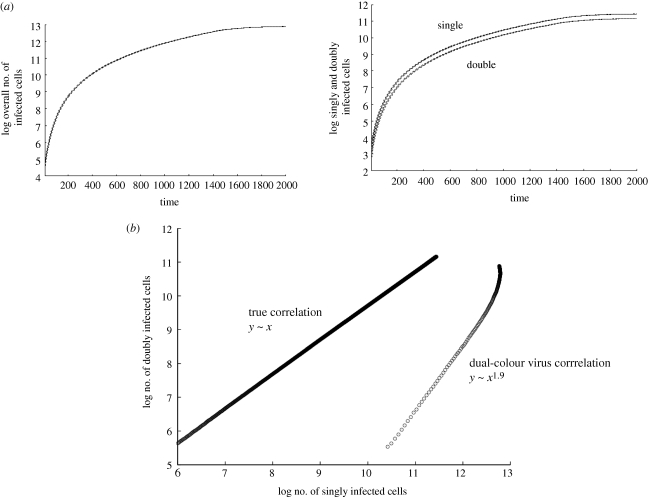
Here, we consider the scenario where virus spread is spatially restricted, in particular we assume that an infected cell can pass its offspring virus only to its direct neighbours (eight cells in our set-up). As has been observed in previous modelling of HIV spread in the context of spatial limitations [34], the virus population grows slower than exponential (figure 4a). In our model, we call this pattern ‘surface growth’, characterized by the square root of the virus population growing linearly with time. The reason is that the infected cells are clustered together in a mass, and only the infected cells at the surface of this mass contribute to virus spread. Following this growth phase, the average populations eventually converge towards an equilibrium (figure 4a). While this is an extreme scenario and such a growth pattern has not been observed in experimental systems tested thus far, it is instructional to analyse it. This will provide a basis for understanding the dynamics under intermediate degrees of spatial restrictions of virus growth.

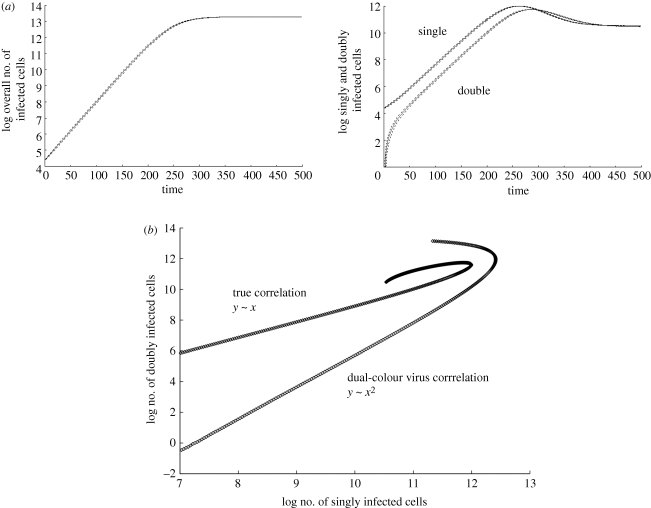
Figure 4.

Computer simulation results assuming highest spatial restriction with regard to infection. Average population sizes are plotted, and the dotted line represents the standard deviations. (a) Basic growth pattern. The infected cells grow slower than exponential because of the spatial restriction. Only cells on the surface of an infected cell cluster can pass on the virus to new target cells. With this growth law, the square root of the number of infected cells grows linearly in time (not shown here). The same pattern applies to the subpopulations of infected cells. The number of doubly infected cells grows with the same rate as the number of singly infected cells. (b) The number of doubly infected cells correlates directly with the number of singly infected cells during the growth phase. This graph also plots the correlation between cells infected with single-colour virus and cells infected with dual-colour virus, derived from a simulation of dual-colour virus experiments [1]. In contrast to the ‘true’ picture, the number of cells infected with single-colour virus correlates almost with the square of the number of cells infected with dual-colour virus. Linear regression during the exponential growth phase was used to obtain the correlations. See text for further details. Parameters were chosen as follows: grid size, 800 × 800; L = 0.5; d = 0.001; B = 0.5; a = 0.1.

During the growth phase in this scenario, we observe a different correlation between the number of co-infected cells and the number of singly infected cells. Now, the number of cells infected with i viruses correlates directly with the number of singly infected cells (figure 4b). This means that the relative importance of co-infection does not increase as the virus population grows to higher levels. The relative importance of co-infection remains constant throughout the growth phase from low to high virus loads. During the growth phase, and at equilibrium, the average abundance of the infected cell subpopulation scales with the number of viruses present in the cell, i.e. singly infected cells are most abundant, followed by cells containing two, three, four viruses, etc. The faster the overall spread, the closer the abundance of the individual subpopulations of infected cells. Again, the overall number of multiply infected cells is less abundant than the singly infected cells population for slow rates of viral spread, and becomes more abundant than the singly infected cell population at higher viral spread rates (plots not shown).

Next, we examine the scenario where viruses bearing different reporter genes, representing different strains of equal fitness, are followed over time (figure 4b). In cells that are infected with multiple copies of each reporter virus, i.e. more than one green fluorescent protein (GFP) virus and more than one yellow fluorescent protein (YFP) virus [1], we assume that the probability to transmit the virus of a given colour is proportional to the frequency of this virus in the cell. Interestingly, under these assumptions, the simulations yield different results. If the simulation is started with the initial infected cells (infected with one type of virus each) scattered randomly through the target cell grid, then we find that the number of dual-colour cells (e.g. GFP/YFP double-positive) does not correlate directly with the number of single-colour cells (e.g. GFP+YFP− and GFP−YFP+) during the growth phase of the virus. Instead, the number of dual-colour cells tends to correlate almost with the square of the number of singly infected cells (figure 4b). Hence, the dual-colour experiment does not accurately reflect the true dynamics of co-infection in this scenario. The reason is that cells that are multiply infected with viruses of identical colour (and which are missed in dual-colour experiments) account for a disproportionately large fraction of co-infected cells, as a result of the spatial restrictions assumed here. If a cell can only infect its nearest neighbours, then it is likely to pass on a virus labelled with the same colour multiple times to the same cell, hence the discrepancy. The reason for the correlation being close to square and not exactly square is as follows. While spatial restriction renders repeated transmission of an identically labelled virus to the same cell likely, this is not the only possibility as an infected cell does have potentially eight nearest neighbours to which the virus can be passed on. However, it is unlikely that experimental data are accurate enough to pick up such a subtle difference. Therefore, experiments with dual-colour viruses are predicted to give rise to a squared correlation between the number of doubly infected cells and the number of singly infected cells, while the true correlation is linear under the assumptions of this iteration of the model.

Note that in the simulation of the dual-colour virus experiment, the predicted correlation can depend on the spatial distribution of the initial number of infected cells. The above results hold for large ranges of initial distributions, where cells are randomly scattered across the grid. Different results are obtained if initial conditions are such that during growth, the cells infected with viruses of two colours are clustered together and surrounded by a larger cluster of cells that is infected with single-colour viruses. In this case the population of cells infected by single-colour viruses will grow faster than the population of cells infected with viruses of both colours. This is because the cluster of cells containing single-colour viruses is larger and more cells are at the periphery of the cluster where they can give rise to new cells of the same type.

So far we have considered strong spatial restriction where an infected cell could only pass on its offspring virus directly to the neighbouring target cells. However, there is a continuum between this assumption and perfect mixing of the cells. We explore this continuum by assuming that in principle, an infected cell can pass on the offspring virus to any other cell on the grid, but that the probability of infection declines with the distance between the source cell and the target cell. The distance over which the virus can travel to infect a target cell is determined by the expression 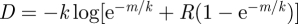. This provides a random number between 0 and m, where m is the maximum distance (i.e. number of spots in the grid) that the virus can in principle travel to infect a cell. R is a uniformly distributed random number, and the parameter k determines how steep the distribution of the resulting random number D is. If k → ∞, then the distribution of D tends to uniform and the virus can reach any position in the grid with equal chance. This corresponds to the perfect mixing extreme. On the other hand, if k → 0, then the distribution of D is very steep and the probability for the virus to reach a target cell declines very fast with distance. This end of the spectrum corresponds to extreme spatially restricted virus spread. Intermediate values of k allow for a continuum between these extremes.

In this case, the results are ‘intermediate’ between those of the perfect mixing and the extreme spatial restriction scenarios. The virus growth pattern is intermediate, consisting of two phases: an exponential phase, followed by a slower ‘surface growth’ phase (figure 5a). Initially, growth is exponential because there are many cells that can be infected with relatively large probabilities. During later stages of growth, however, a mass of infected cells has formed and only cells on the surface of this mass can pass on the virus to uninfected cells, leading to slower virus growth. The more the cells mix, the longer is the exponential growth phase. During the exponential growth phase, the number of cells infected with i viruses scales anywhere from linearly to the ith power of the number of singly infected cells (figure 5b), depending on the exact degree of mixing. As virus growth slows down, this correlation tends further towards linear (figure 5b). Simulating the experiments with dual-colour viruses, the results regarding the dynamics of multiply infected cells again deviate from the true picture, and results become more accurate as the degree of cell mixing is increased (plots not shown).

Figure 5.

Computer simulation results assuming an intermediate degree of spatial restriction with regard to infection. Average population sizes are plotted, and the dotted line represents the standard deviations. (a) The basic growth pattern is intermediate between the one found for perfect mixing and extreme spatial restriction. At the beginning, growth is exponential. Subsequently, growth slows down such that the square root of the number of infected cells grows linearly in time. Finally, the average populations converge to equilibrium. The higher the degree of mixing, the more pronounced the exponential growth phase. (b) The correlation between the number of doubly infected cells and the number of singly infected cells lies between linear and square, depending on the exact degree of mixing. As growth slows down, the correlation tends further towards linear. Linear regression during the beginning and the end of the exponential growth phase was used to obtain the correlations. Parameters were chosen as follows: grid size, 800 × 800; L = 0.5; d = 0.001; B = 0.5; a = 0.1.

4.3. Cell to cell transmission of the virus

Here, we assume that for virus transmission to occur, two cells have to become linked via the virological synapse [12–14]. We assume that at each time interval, free cells (infected and uninfected) have a probability p to form a synapse with a randomly chosen partner cell. Infected cells that are connected to another cell can pass on their offspring virus to the partner cell with a probability B. In addition, at each time interval, there is a probability q that linked cells break apart. In this case, average virus growth is exponential, followed by convergence to an equilibrium (figure 6a). As before, the abundance of the infected cell subpopulations scales with the number of viruses in the cells. The faster the viral replication rate, the closer the abundance of the infected cell subpopulations are to each other. During the growth phase, the number of cells infected with i viruses scales linearly with the number of singly infected cells (figure 6b). However, in simulations of the dual-colour virus experiments, the number of cells infected with two colours scales with the square of the number of cells infected with a single colour (figure 6b). Hence, again, the dual-colour virus experiments do not accurately reflect the dynamics of multiply infected cells. The reason is that because of synapse formation, the repeated transmission of a virus with identical colour to the same cell plays a very important role, and these multiple infection events with similar viruses are not picked up by experiments using dual-colour viruses.

Figure 6.

Computer simulation results assuming virus spread via cell to cell transmission through the formation of the virological synapse. Average population sizes are plotted, and the dotted line represents the standard deviations. (a) The basic growth pattern shows an exponential increase in the number of infected cells, followed by convergence to equilibrium. During this phase, the population of singly and doubly infected cells grows at the same rate. (b) Consequently, the correlation between the number of singly infected and doubly infected cells is linear during the growth phase. However, in simulations of the dual-colour virus experiments, the number of double-colour cells correlates with the square of the number of single-colour cells. Linear regression during the exponential growth phase was used to obtain the correlations. Parameters were chosen as follows: grid size, 800 × 800; L = 0.5; d = 0.001; B = 0.2; a = 0.01; p = 0.2; q = 0.4.

4.4. Additional complexities

Here, we introduce further biological complexities into the model and examine their effects on the dynamics of multiply infected cells. So far, we have assumed that co-infection remains possible throughout the lifespan of the infected cells. It is known that receptor down-modulation does occur, inhibiting superinfection [18,19]. However, this process requires about 1 day following infection with the first virus during which time a cell remains reinfectible [18,28]. Given that the lifespan of infected cells is less than 2 days on average in vivo [35–37], the above simulations without explicit inclusion of superinfection inhibition appear to be a reasonable approximation. Nevertheless, we explicitly introduce superinfection inhibition and examine the resulting dynamics. The computer simulation keeps track of the time steps since initial infection. This can be done in the context of two different assumptions, both of which yield the same general result. It can be assumed that after a defined number of time steps, t_thr, further infection immediately becomes impossible, because the receptor levels on the cell have declined significantly. Alternatively, it can be assumed that the probability of infection continuously declines with time since the original infection.

These effects have already been examined by previous theoretical studies [10,11,31], and many of the results reported in the context of our current model coincide with those. Nevertheless, it is important to include these results for completeness.

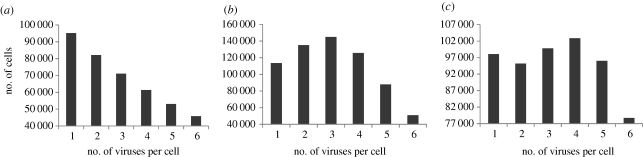
For now, we assume that cells and viruses mix perfectly. The results during the growth phase of the virus population remain unaffected. When the average populations converge to equilibrium, however, the dominance hierarchy of the individual infected cell populations (one, two, three viruses, etc. per cell) can be affected by receptor down-modulation, depending on the model parameters (figure 7). As mentioned in previous sections, in the absence of receptor down-modulation, the singly infected cells are the dominant population followed by cells infected with one, two, three viruses, etc. (figure 7a). In the presence of receptor down-modulation, however, cells infected with more than one virus can be the dominant population (figure 7b). In this figure, cells infected with three viruses are dominant, while cells infected with fewer or more viruses are less abundant. The reason is as follows. The receptors remain long enough for a certain amount of co-infection to occur. However, loss of the receptor reduces further co-infection. Hence, cells infected with an intermediate amount of virus (e.g. n viruses) are less likely to be infected and are less likely to be lost to give rise to cells infected with n + 1 viruses. Hence, the population of cells infected with n viruses gains in abundance relative to other cells. The exact shape of the distribution, and which cell population is most abundant, of course depends on model parameters. The simulation can also give rise to distributions with more than one peak. In figure 7c, there is a ‘local peak’ for cells infected with a single virus, and there is a second peak for cells infected with four viruses.

Figure 7.

Distribution of the number of viruses among cells at equilibrium. These simulations are based on the model that assumes perfect mixing of cells and viruses. The distribution is plotted once the populations have on average converged to a steady state. Data are based on 100 individual runs of the simulation. (a) Simulation assuming absence of receptor down-modulation. The dominance of the infected cell subpopulations ranks with the number of viruses per cell. (b) Simulation taking into account receptor down-modulation and a consequent reduction in permissiveness to further infection of infected cells. In this case, the dominance hierarchy is altered and cells infected with three viruses are most abundant. (c). Another simulation assuming the occurrence of receptor down-modulation. In this simulation, receptor down-modulation takes slightly longer than in (b). Now, two peaks are observed, one for cells infected with a single virus, and one for cells infected with four viruses. Parameters were chosen as follows: grid size, 1000 × 1000; L = 0.5; d = 0.001; B = 0.5; a = 0.05. (a) No receptor down-modulation; (b) t_thr = 10; (c) t_thr = 15. The grid size was chosen to be larger in this set of simulations than in other figures to allow rarer cell populations to be presented more accurately.

In general, the rate of receptor down-modulation (and the consequent reduction in permissiveness to infection) determines the dominance hierarchy of the infected cell populations as follows. If receptor down-modulation occurs relatively fast, then the singly infected cells are most abundant, simply because in this scenario, permissiveness of infection is reduced so fast that the chances are low for co-infection to occur. If receptor down-modulation takes a relatively long time, then the results converge to those observed in the simulations that do not take receptor down-modulation into account. In this case, it essentially takes longer than the lifespan of an infected cell for the infection permissiveness to decline. The altered dominance hierarchies are found for intermediate rates of receptor down-modulation, where receptors remain long enough for significant co-infection to take place, but receptor loss occurs within the lifespan of infected cells.

It is interesting to consider these patterns in the context of experimental data. During virus growth, data indicate that starting from a low initial number of viruses, the singly infected cells are the most abundant population, and that the abundance of cells ranks with the number of viruses they are infected with [1]. This is in agreement with our model. During the growth phase, this is the predicted dominance hierarchy under all conditions. It is only at equilibrium that the model predicts altered dominance hierarchies as described above. In a paper by Jung et al. [23], fluorescence in situ hybridization was used to estimate the number of proviruses harboured by individual splenocytes from two HIV-infected patients. They found an average of three to four proviruses per cell and found two peaks in the distribution: one for singly infected cells, and one for cells infected with three viruses. This is reminiscent of our model simulation results presented in figure 7c. While the nature of and the reason for this distribution needs to be investigated in more detail, we can hypothesize that the occurrence of receptor down-modulation in infected cells could be the driving factor that produces such distributions. It seems likely that in patients who were sampled, the virus population was in an approximate steady state. Following the acute phase of the infection, virus load typically settles around a steady state that shifts slowly over time. Our model suggests that in such a steady state, receptor down-modulation can lead to distributions of viruses among cells that are observed in the experimental data. At this stage, however, we have no experimental evidence to support this hypothesis, and other explanations could account for such a distribution. In particular, cells infected with more than one virus can become the dominant population if the number of uninfected target cells are limiting. In the simulations, this is typically seen when virus load reaches its peak. Because of limited target cell availability, the virus population declines before converging to equilibrium, and temporarily altered dominance hierarchies can occur during this phase of the dynamics. For this scenario to be observed, the replication rate of the virus needs to be relatively high, as demonstrated in figure 3c. However, this seems reasonable based on observed replication kinetics [1]. Because this scenario only occurs in a limited phase of replication, it may not explain the virus distribution patterns found in vivo.

We achieve similar results when we incorporate receptor down-modulation into the models that assume spatially restricted virus spread or virus spread via cell to cell transmission. In these cases, the dominance hierarchy can not only be reversed when the average population sizes converge to equilibrium, but also during the virus growth phase. This is because the multiply infected cell populations grow with the same rate as the singly infected cell population in these cases.

Another complication that we introduced into our model was the assumption that not all cells are equally susceptible to infection, but that there is heterogeneity among the cells in the probability with which they can become infected. Upon production, each cell was assigned this probability with a random number generator and the simulation was run as before. No changes in the results described so far have been found.

5. Conclusion

The analysis presented in this paper has shown that the dynamics of co-infected cells can depend crucially on the mode of virus spread. Further, it has shown that the use of dual-colour viruses has inherent limitations in their interpretation when virus spread is spatially restricted or if significant amounts of virus infection occurs via cell to cell transmission. Labelling viruses with more than two colours would not improve the ability to analyse multiple infection with identical viruses. Analysis of viral nucleic acids within single infected cells will be required to directly parse these issues. The model presented here can exactly track the true number of multiply infected cells in silico and thus provide a useful tool to understand the nature of co-infection dynamics under various modes of virus spread. While virus growth experiments in small culture dishes with cell monolayers are likely to approximate perfect mixing rules (and can thus be analysed correctly with coloured viruses; [1]), the rules of HIV spread in vivo, especially in lymphoid tissue, should be examined more closely. Once these rules have been established in more detail, they can be incorporated into the model to obtain predictions about the co-infection dynamics under the experimentally observed assumptions.

In a study of the relationship between infection frequency, co-infection and recombination [1], the use of reporter viruses will, however, show the correct relationship between infection and recombination between divergent viruses, represented by the different reporter viruses. The number of dual-colour cells accurately represents the cells infected with divergent viruses (divergent by this criterion), thus the conclusion that diversification by recombination proceeds by the square of the infection frequency is a valid conclusion of this work.