Noncontact estimation of intercellular breaking force using a femtosecond laser impulse quantified by atomic force microscopy

Abstract

When a femtosecond laser pulse (fsLP) is focused through an objective lens into a culture medium, an impulsive force (fsLP-IF) is generated that propagates from the laser focal point (O_f) in a micron-sized space. This force can detach individual adherent cells without causing considerable cell damage. In this study, an fsLP-IF was reflected in the vibratory movement of an atomic force microscopy (AFM) cantilever. Based on the magnitude of the vibration and the geometrical relationship between O_f and the cantilever, the fsLP-IF generated at O_f was calculated as a unit of impulse [N-s]. This impulsive force broke adhesion molecule-mediated intercellular interactions in a manner that depended on the adhesion strength that was estimated by the cell aggregation assay. The force also broke the interactions between streptavidin-coated microspheres and a biotin-coated substrate with a measurement error of approximately 7%. These results suggest that fsLP-IF can be used to break intermolecular and intercellular interactions and estimate the adhesion strength. The fsLP-IF was used to break intercellular contacts in two biologically relevant cultures: a coculture of leukocytes seeded over on an endothelial cell monolayer, and a polarized monolayer culture of epithelial cells. The impulses needed to break leukocyte–endothelial and interepithelial interactions, which were calculated based on the geometrical relationship between O_f and the adhesive interface, were on the order of 10^-13 and 10^-12 N-s, respectively. When the total impulse at O_f is well-defined, fsLP-IF can be used to estimate the force required to break intercellular adhesions in a noncontact manner under biologically relevant conditions.

In multicellular organisms, cell–cell and cell–matrix adhesions are essential for tissue homeostasis and are mediated by a variety of adhesion molecules such as integrins, cadherins, and immunoglobulin superfamily members (1–3). To date, several methods have been developed to quantify cell adhesion strength in vitro. The cell aggregation assay is a simple method that determines the ability of specific adhesion molecules to bind cells in suspension (4). Single-cell force spectroscopy (SCFS) can measure cell–cell adhesion at the level of individual molecules by immobilizing cells and loading a tensional force on the intercellular interface (5).

Although the above methods are widely used, they are limited in that the measurement conditions are quite artificial. Here, we propose that a femtosecond laser pulse (fsLP) can be used to break intercellular adhesions in biologically relevant cultures in a noncontact manner. When an infrared fsLP is focused through an objective lens in the vicinity of a target cell, a stress wave is formed at the laser focal point (O_f), along with a shockwave and a cavitation bubble (6). The short packet of the stress wave acts as an impulsive force on the cells.

The stress wave is initiated by the multiphoton absorption of water. The efficiency of this absorption depends on the peak pulse intensity, defined as the ratio of the pulse energy to the pulse duration. Accordingly, the pulse energy threshold for stress wave generation is much lower for the femtosecond laser compared to other lasers. When the pulse energy is set slightly higher than the threshold, the laser can generate a strong impulsive force that is localized only in the vicinity (a few tens of micrometer in diameter) of the O_f. It is very difficult to generate this type of local impulsive force with other methods (e.g., with gunpowder, electric sparks, or optical breakdown (7) via nanosecond or picosecond lasers).

Previously, we developed a single-cell manipulation technique using a femtosecond laser that generates a compact impulsive force. By targeting the femtosecond laser in the vicinity of a target cell, this technique dissociates the adherent cell of interest from the culture scaffold (8–11). This irradiation does not appear to damage cellular functions such as cell growth or cell differentiation (10, 11). Although this technique was thought to be applicable to manipulate cells and estimate cell adhesion strength, there are currently no methods to quantify the impulsive force localized in a micron-sized region.

In the present study, we devised a unique system to measure local impulsive forces using atomic force microscopy (AFM). In this system, the impulsive force (fsLP-IF) generated by a femtosecond laser at O_f was estimated based on the bending movement of an AFM cantilever and expressed as a unit of impulse [N-s]. After defining the F₀, the fsLP was focused in cell cultures that mimic in vivo settings, and the fsLP-IF needed to break the intercellular adhesions in a noncontact manner was estimated.

Results

Estimation of the Femtosecond Laser-Induced Impulsive Force.

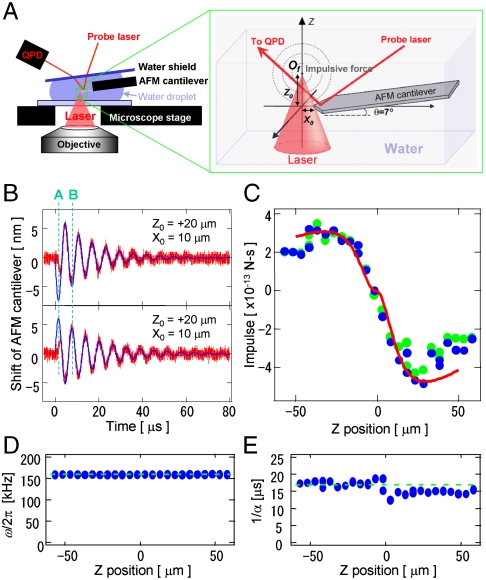
Fig. 1A shows the experimental setup of the impulse measurement. A single fsLP (800 nm, 120 fs) was focused into the water near the top of the AFM cantilever (Fig. S1A). A probe laser was introduced to monitor the cantilever shift, and the reflected light was observed using a quadrant photo detector (QPD). The difference between the top and bottom side voltages of the QPD was converted to the position shift with a linear coefficient of 15 mV/nm.

Fig. 1.

Measurement of the femtosecond laser impulse by AFM. (A) Experimental setup of the AFM-assisted impulse measurement system. (B) Transient oscillations of an AFM cantilever induced by an fsLP when O_f is higher (top side) or lower (bottom side) than the AFM cantilever tip. The red and blue lines indicate the observation data and fitting results using Eq. 1, respectively. (C–E) The Z-position dependence of the impulse of F (C), oscillation frequency of ω/2π (D), and damping time of 1/α (E) that were estimated from the oscillations of the AFM cantilever. The blue dots are the result of least-square fitting of Eq. 1 when F, ω, and α were treated as variable parameters. The green dots in Care the fitting results when ω and α were treated as constants, indicated as green broken lines in D and E. The red line in C is the Z-position dependence of the total impulse calculated by Eq. 2.

Representative results of the transient oscillation of the cantilever with a spring constant of 44 N/m are shown as red lines in Fig. 1B. When the laser with a pulse energy of 170 nJ/pulse was focused through a 10× objective lens (N.A. 0.125), the cantilever transiently vibrated with an amplitude on the order of a few tens of nanometers. The amplitude was dampened over a few tens of microseconds because of the viscosity of water. The direction of the initial shift “A” was inverted on the border of the Z₀ origin, indicating that the impulsive force pushed the cantilever.

When the fundamental vibration of the cantilever is initiated by an impulsive force of the delta function, the transient oscillation is expressed as

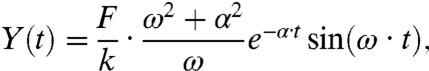[1]

where F is the impulse loaded on the AFM cantilever (i.e., the integral of the force with respect to time [N-s]) and k is the spring constant of the cantilever (12). The angular velocity ω and damping constant α strongly depend on the viscous drag of water.

When the data in Fig. 1B were fit by Eq. 1, the oscillation after the second shift “B” was well-reproduced. The motion before the “B” shift can be interpreted as follows: (i) the impulsive force cannot be approximated as the delta function—i.e., the impulsive force loading time is not extremely shorter than the vibration cycle (6 μs); and (ii) the bending modes of the cantilever, except for the fundamental mode with frequency ω, were simultaneously excited and interfered. As an approximation, the influence of these phenomena in the calculation was minimized by extrapolating the former vibration prior to the “B” shift by the latter oscillation. The transient oscillation was measured as a function of the O_f in the optical axis (Z direction). Least-square fitting with Eq. 1 was performed, where F, ω, and α were considered variable parameters and k was a constant. Fig. 1 C–E shows the Z-position dependence of F, ω, and α, respectively, when the distance between O_f and the top of the cantilever was set to (X₀, Y₀) = (10,0) μm. The reproducibility of the fitting was identical to that of the fitting shown in Fig. 1B (Fig. S2A).

In all of the analyzed data, the oscillation frequency ω and damping time α were virtually constant, whereas F varied widely with changes in the Z position. The value of F was nearly the same when it was treated as the only variable (green dots in Fig. 1C). The oscillation frequency ω agreed well with the harmonic frequency of the fundamental bending mode of the AFM cantilever in water. These results suggest that the approximation using Eq. 1 is reliable. Therefore, in the rest of our analyses, ω and α were treated as constants in Eq. 1.

Next, the total impulse F₀ generated at O_f was estimated from the geometrical relationship between O_f and the cantilever (Fig. S1 B and C). When F₀ generated at point (0, 0, Z₀) propagates spherically as a short wave packet, the impulse at the small fraction Δs on the AFM cantilever is given by

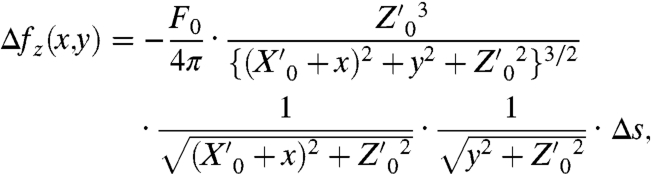[2]

where 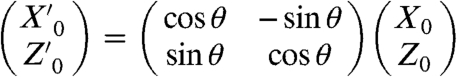according to Eqs. S1–S6. The angle of the cantilever θ is 7 °. The total impulse loaded on the cantilever (F) was calculated from the area integration of Δf_z on the cantilever. When F₀ was 16 × 10^-12 N-s, the experimental result was well-reproduced (red line in Fig. 1C). The asymmetry between the location of O_f above and below the cantilever location is due to the attachment angle θ of the cantilever. We obtained F₀ using the above procedure to estimate the intercellular breaking force (Fig. S2 B–E).

Estimation of Intercellular Adhesion Strength.

In the cell aggregation assay, stromal cells that exogenously express a particular adhesion molecule(s) are rotated in a single-cell suspension. The ability of the adhesion molecule(s) to mediate cell–cell adhesion is expressed as the percentage of cells that are aggregated by the rotation process.

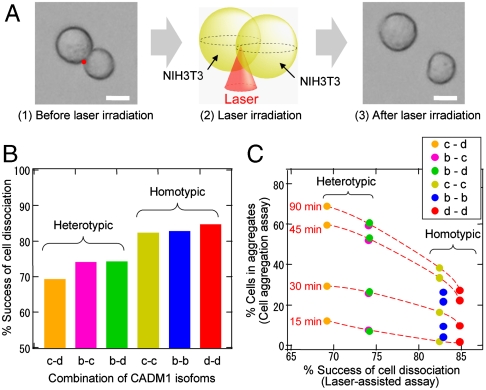
In the current study, the fsLP-IF was used to dissociate the intercellular adhesions in cell aggregates that formed in the aggregation assay. We previously used this assay to examine the adhesive properties of cell adhesion molecule-1 (CADM1, alternatively named Necl-2), a member of the immunoglobulin superfamily, using NIH3T3 fibroblasts that exogenously express CADM1 isoform c (Fig. S3) (13, 14). These cells were aggregated using a standard procedure. The resultant homotypic cell aggregates were embedded in a viscous bactoagar matrix. The O_f of the fsLP was set at the edge of the interface of two-cell aggregates (Fig. 2A). When a single pulse of 230 nJ was focused through a 10× objective lens, some, but not all, of the two-cell aggregates were dissociated. There was no considerable cell damage, suggesting that direct laser ablation is negligible in the cell dissociation. We tested 30 two-cell aggregates in 1 h and calculated the frequency by which these two-cell aggregates were dissociated.

Fig. 2.

Femtosecond laser-induced dissociation of the two-cell aggregates that formed in the cell aggregation assay. (A) Microphotographs of a two-cell aggregate that was obtained by rotating single-cell suspensions of NIH3T3 fibroblasts (1), and its dissociation induced by femtosecond laser irradiation (3). Laser focal points are indicated as red dots on the left microphotograph (1) and schematically presented in the middle graphic (2). Bar = 10 μm. (B) Percentage of cell dissociation by femtosecond laser irradiation. One (homotypic) or two (heterotypic) types of CADM1 isoforms expressed in NIH3T3 fibroblasts that formed two-cell aggregates are shown on the horizontal axis. (C) There was an inversely proportional relationship between the percentage of cell dissociation by the fsLP-IF (horizontal axis) and the percentage of aggregated cells (vertical axis). Homotypic and heterotypic aggregation assays were performed, and the percentages of cells in aggregates were plotted at four timepoints (15, 30, 45, and 90 min) and connected with a red broken line.

Similar experiments were performed on homotypic two-cell aggregates using NIH3T3 cells expressing two other CADM1 isoforms, b and d (Fig. S3), and on heterotypic two-cell aggregates by mixing two types of NIH3T3 cells expressing different CADM1 isoforms at a ratio of 1∶1. In the latter assay, one of the two cell types was fluorescently prelabeled, and the heterotypic combination was determined by fluorescence imaging. As shown in Fig. 2B, the frequency of cell dissociation was higher in homotypic aggregates than heterotypic aggregates.

NIH3T3 cells were subjected to homotypic and heterotypic cell aggregation assays. In every combination, heterotypic aggregates contained more cells than homotypic aggregates at all of the examined timepoints (Fig. 2C). As roughly shown by the broken lines in the figure, the percentage of cells that were incorporated into aggregates was inversely proportional to the frequency of the two-cell aggregate dissociation that was induced by laser irradiation, except for the homotypic aggregation of isoform b. Thus, the ability of the fsLP-IF to break intercellular adhesions appeared to depend on the intercellular adhesion strength, which in this case was dominated by the CADM1 isoforms. Thus, the intercellular adhesion strength can be estimated from the minimal impulsive force needed to dissociate cells.

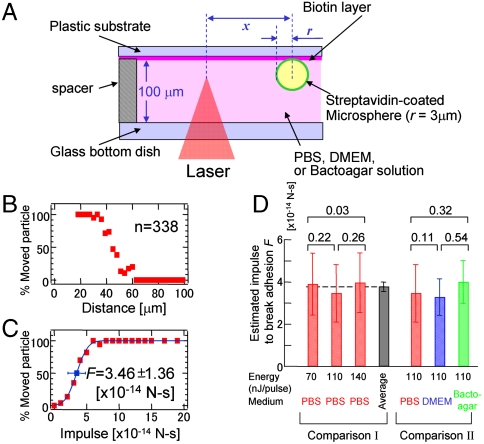
Next, we calculated the uncertainty of the estimated impulsive force. As a model, streptavidin-coated microspheres (6 μm in diameter) were bound to a biotin-coated substrate in PBS (Fig. 3A). By focusing the fsLP (110 nJ/pulse) through a 10× objective lens, an fsLP-IF was loaded at the ventral side of the microspheres (Fig. S4). The percentage of microspheres that moved (P_move) was calculated as a function of the distance between O_f and the microspheres. The percentages were calculated using 338 microspheres that were at various distances from O_f (Fig. 3B). P_move drastically decreased from 100 to 0 as O_f increased from 30 to 60 μm.

Fig. 3.

Femtosecond laser-induced movement of streptavidin-coated microspheres that adhered to a biotin-coated substrate. (A) Schematic presentation of the method used to load the fsLP-IF onto a streptavidin-coated microsphere adhering to biotin-coated substrate. (B and C) Histograms of the percentage of particles that moved by the fsLP-IF as a function of the distance between the laser focal point and the sphere center (B) and of the impulse estimated by Eq. 3 (C). A femtosecond laser with a pulse energy of 110 nJ/pulse was focused into the PBS medium. The blue line in C is the least-square fitting of Eq. 4. The blue box and error bar on the line indicate F and δF in the function, respectively, corresponding to the estimated median impulse and its standard deviation to break the interaction. (D) Comparison I: F (solid bar) and δF (error bar) estimated in PBS medium by 70-, 110-, and 140-nJ pulses and their average. Comparison II: F and δF estimated in PBS, DMEM, and a 0.2% bactoagar solution by a 110-nJ pulse. Numbers at the top of the bar graph indicate the Z score calculated as Z = |F₁-F₂|/[(δF₁)²-(δF₂)²]^1/2. When Z is < 1.96, there is no significant difference between the median impulses F₁ and F₂ (P < 0.05).

From Eqs. S8–S14, the impulse f loaded on a microsphere is given by

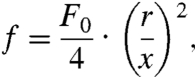[3]

where r is the sphere radius and x is the distance between O_f and the sphere center (Fig. 3A). According to the AFM result under the implemented laser conditions, the impulse at F₀ was 30 × 10^-12 N-s. Impulses loaded on 338 spheres were calculated independently, and P_move was calculated as a function of the impulse f (Fig. 3C). Assuming that the adhesion strength between the sphere and substrate is in a Gaussian distribution, P_move can be expressed as a cumulative distribution function:

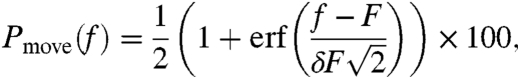[4]

where F and δF correspond to the median impulse needed to move a microsphere and its standard deviation, respectively. The experimental result was well-reproduced by the least-square fitting of Eq. 4 (blue line in Fig. 3C). F was estimated to be 3.46 × 10^-14 N-s according to the present measurement.

Similar experiments were performed in PBS using pulse energies of 70 and 140 nJ/pulse (Fig. S5 A–C). The mean and standard deviation of the three F estimates was 3.78 ± 0.28 × 10^-14 N-s (Comparison I in Fig. 3D), indicating that the present system has a measurement error of approximately 7%. The median impulse F was also estimated in PBS, DMEM, and a bactoagar solution using a pulse energy of 110 nJ/pulse (Comparison II in Fig. 3D and Fig. S5 D–F). There were no significant differences in the estimated F values between any pairs of different conditions in either Comparison I or II in Fig. 3D, although the largest estimates were approximately 113% and 120% of the smallest estimates in Comparisons I and II, respectively (Fig. 3D).

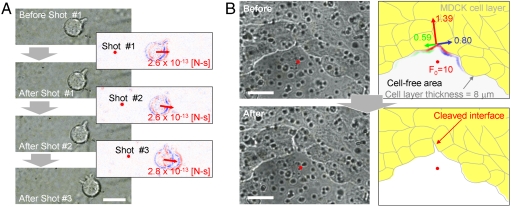
The impulsive force needed to break intercellular adhesions was also measured in two different biologically relevant cultures. The physical aspects of the interaction between circulating leukocytes and blood vessel walls were previously examined using SCFS and cocultures of leukocytes (HL-60 cells) on human umbilical vein endothelial cell (HUVEC) monolayers (15, 16). We prepared a similar coculture on a cover slip and set the cover slip HUVEC-side down on a glass-bottomed dish with thin rubber spacers (Fig. S6A). When a single fsLP of 35 nJ/pulse was focused through a 40× objective lens (N.A. 0.9) at the ventral side of an adherent HL-60 cell, the HL-60 cell moved approximately 1–3 μm toward the opposite side of O_f (Fig. 4A). The movement looked like slipping, not rolling, on the HUVECs. The second and third laser shots caused a similar slipping movement.

Fig. 4.

Femtosecond laser-induced intercellular dissociation of HL-60 leukocytes attached to HUVECs (A) and the MDCK cell–cell interface (B). (A) Left, microphotographs of an adherent HL-60 leukocyte before and immediately after irradiation with three serial laser pulses. Right, differential images between the left-top and left-bottom microphotographs. Blue and red contrasts indicate the degree to which the brightness is increased and decreased, respectively. Bar = 10 μm. The laser focal point and impulse loading on the leukocyte are indicated as red dots and red arrows, respectively. The value of the impulse was estimated by Eq. 3. (B) Microphotographs (left) and their graphics (right) of an MDCK cell monolayer before (top side) and after (bottom side) the laser irradiation. Multiple black dots in the left photographs are the pores of the permeable filter on which the MDCK cells were cultured. The laser was focused on the cell-free area at the positions indicated with red dots in the photographs and graphics. In the top graphic, the magnitudes of the impulse loaded onto the margin of the MDCK cell monolayer are described as a contour of the margin with RGB colors. The impulse is divided into three directions: parallel to the direction from the laser focal point to the cleaved interface among MDCK cells (red arrow), and the directions that are perpendicular to the right (blue arrow) and left (green arrow) of the red arrow. The depth of the color gradation indicates the magnitude of the impulse. The total magnitudes are indicated by the arrow length and are displayed beside each arrow. The unit of these impulses and F₀ is × 10^-12 [N-s]. Bar = 10 μm.

From Eq. 3 and the F₀ estimated by AFM (Fig. S2C), the impulse f that was required to induce slipping was estimated to range from 2.6 to 2.8 × 10^-13 N-s (Fig. 4A). Similar estimates were obtained from 50 randomly selected HL-60 cells, suggesting that, at most, three cellular protrusions that extended from HL-60 cells and attached to HUVECs (“tethers”) were ruptured with every slipping movement (see SI Text).

We next attempted to estimate the fsLP-IF needed to break the intercellular adhesion between epithelial cells. Madin–Darby canine kidney (MDCK) epithelial cells were seeded into a culture insert with a porous filter bottom to make an epithelium-like polarized monolayer in 3 days. The filter with the MDCK cell monolayer was then set on a glass-bottomed dish as in the leukocyte-endothelial experiment described above (Fig. S6B). A representative result is shown in Fig. 4B.

When a single fsLP of 20 nJ/pulse was focused through a 40× objective lens at 4 μm below the filter in a cell-free area, the cell interface was cleaved in the vicinity of O_f. From the estimated 10 × 10^-12 N-s impulse F₀ (Fig. S2D), impulses loaded along the front surface of the cell layer were calculated in two orthogonal axes (Fig. S7A): one to push (Eq. S21) and one to divide the cleaved cell-cell interface (Eq. S22). The impulses are displayed as color gradations on the contour of the edge of the cell layer in the top graphic of Fig. 4B. The former and latter impulses integrated at the front line of the cleaved cell–cell interface were 1.39 and (0.59 + 0.80) × 10^-12 N-s, respectively. Similar experiments were performed to dissociate six cell–cell interfaces surrounding different cell-free areas, yielding former and latter impulses of 1.85 ± 0.36 and 2.08 ± 0.61 × 10^-12 N-s, respectively (Table S1). According to these estimations, MDCK cells appeared to adhere to each other with an impulse on the order of 10^-12 N-s.

Discussion

When the fsLP is focused in water, the fsLP-IF loaded on objects is assumed to be composed of two components—i.e., a laser-induced shockwave and a watery jet flow along with cavitation bubble generation and collapse. The laser-induced shockwave should impact the AFM cantilever within less than a few tens of nanoseconds after the laser is focused. By contrast, 5 μs or more are needed for the watery jet flow to fully impact the cantilever (10). Under the latter time scale, we detected the full response of the cantilever. Even when a soft cantilever (0.2 N/m) with a fast response was used instead of the presented cantilever, the movement was dominated by the response with a time scale of μs. These results suggest that the watery jet flow is the main component of the impulsive force loaded on the cantilever. Because the first motion of the cantilever was in the opposite direction of O_f, the forward flow caused by cavitation bubble generation is likely to be a major force that moves the cells in our assays.

Several methods in which a tensional force is loaded on cells are widely used to measure intracellular adhesion strength. In SCFS (5), a cell immobilized on an AFM cantilever is attached to substrate-cultured cells (adhesion phase). A tensional force is loaded on the interface between the cells by retracting the cantilever. During this de-adhesion phase, the rupture forces of single intermolecular bonds are estimated from discrete step-wise changes in the tensional force, which is loaded at a constant rate [N/s]. However, it can be difficult to estimate the overall strength of intercellular adhesion using SCFS. In the de-adhesion phase, SCFS detects not only the summation of the rupture forces of individual intermolecular bonds but also cellular tension due to cellular deformation. Importantly, both the intermolecular rupture force and the cellular tension are functions of the force-loading rate (17).

The laser-assisted measurement conditions used here ideally correspond to the SCFS de-adhesion phase in which the force-loading rate is extremely high. Under this condition, cellular deformation should be negligible. In fact, the MDCK cell layer cleaved like brittle material (Fig. 4B). Therefore, the intercellular breaking force is equivalent to the total rupture forces of individual intermolecular bonds. Given the force-loading time and rate, the number of intermolecular bonds that comprise the overall intercellular adhesion can theoretically be determined. Instead of the force-loading time and rate, we estimated the actual time needed for the intercellular separation based on high-speed imaging data. Together with the assumption that the impulse (momentum) due to the watery jet flow is conserved when it is transferred to cells, we roughly calculated the total rupture force in N. Our estimates were comparable to those that were previously determined by SCFS (see SI Text).

The accuracy of our measurement system was estimated using streptavidin-coated microspheres and biotin-coated substrates (Fig. 3). The difference between the largest and smallest estimates in Fig. 3D was larger in Comparison II (change in medium; ∼20%) than in Comparison I (change in pulse energy; ∼13%). When the medium in which the fsLP is focused is changed from PBS to DMEM or a bactoagar solution, the (i) generation of the impulsive force, (ii) propagation of the impulsive force, and (iii) motion of the microsphere after force loading are inevitably altered. Process i is mainly dominated by multiphoton absorption and by the cyclic absorption of the electronically excited state of a water molecule. It is minimally affected by minor compounds that have dissolved in the water. Processes ii and iii are defined by the jet flow properties of the medium.

According to our past observations with high-speed imaging, the media viscosity minimally affects cavitation bubble generation, although the collapse rate drastically increased with increasing viscosity. Because cell movement was induced by cavitation bubble generation, alterations in processes i to iii are likely to negligibly affect the adhesive strength estimation in the present assays. However, alterations in the other processes cannot be excluded. The microsphere-substrate adhesion strength may vary with PBS, DMEM, and the bactoagar solution, because DMEM and the bactoagar solution contain more compounds than PBS. These additional compounds may promote or interfere with streptavidin-biotin binding. Although the present measurement system was not sufficiently precise to investigate this possibility, it can be used to estimate the intercellular breaking forces without considering the physical aspects of the fsLP-IF in various cell culture media.

In conclusion, the primary benefit of fsLP-IF as a tool for cell–cell dissociation is that a strong force can be transiently loaded onto a cell without mechanical contact. Indeed, we could dissociate two-cell aggregates of CADM1-expressing NIH3T3 fibroblasts and cleave MDCK epithelial cell–cell interfaces without mechanical holding, despite the relatively large adhesion strengths of both systems [∼10^-11N-s (Fig. S8C) and 10^-12 N-s, respectively]. Because the fsLP-IF can dissociate cell–cell adhesion without mechanically manipulating the cells, fsLP-IF, unlike SCFS, can be used for high-throughput analysis under biologically relevant, live-cell conditions. Although optical tweezers are also a promising tool to manipulate single cells, they cannot be used to break the intercellular interactions shown in Figs. 2–4 because of their weak, pN-order loading force (18). Our fsLP-IF measurement system is a powerful tool to dissociate and evaluate the strength of intercellular adhesions. This system will yield more accurate estimations of the strengths of physiological and pathological adhesions among various cell pairs. We are currently using this system to examine how neuro-immune crosstalk is modulated by the kinetic strength of neurite-immune cell adhesion.

Materials and Methods

Experimental Setup of the AFM-Assisted Impulse Measurement System.

The experimental setup is shown in Fig. S1A. A fundamental pulse (wavelength: 800 nm, pulse duration: 120 fs) from a regeneratively amplified femtosecond Ti:sapphire laser system (Hurricane, Spectra Physics) was introduced into an inverted microscope (IX71, Olympus). Two types of objective lenses were used, a 10× objective lens (Plan N; 0.25 aperture, Olympus) and a 40× objective lens (Uapo /340; 0.9 aperture, Olympus). Although the beam diameter satisfies the back aperture diameter of the 40× objective lens, that of the 10× objective lens is two times larger than the beam diameter. Thus, the practical numerical aperture of the 10× objective lens is 0.125.

The laser focal point O_f was adjusted in the image plane by tuning the collimator lenses before the microscope and was checked based on the ablation patterns of a carbon-doped polymer film. The Z position of O_f was controlled by mechanically shifting the microscope stage from the image plane. The accuracy of the Z position resulting from the mechanical precision of the microscope stage was less than 5 μm.

A tipless silicon AFM cantilever (thickness: 4 μm, width: 30 μm, length: 119 μm, force constant: 44 N/m, resonance frequency in air: 320 kHz) (TL-NCH, NanoWorld) with a glass water shield plate was attached to the head of the AFM (Nano-R2, Pacific Nanotechnology). The AFM head and a glass substrate were mounted on the microscope stage. The water shield plate and glass substrate were modified to be hydrophilic. The space between them was filled with water, into which the femtosecond laser was focused.

The difference between the top and bottom side voltages of the QPD was directly monitored with an oscilloscope (DP4104, Tektronix). The time offset of the position shift was locked by a photodiode. The difference in voltage was converted to the position shift with a linear coefficient of 15 mV/nm, which was estimated by pushing the cantilever on the glass substrate using a piezoelectric motor.

Cell Aggregation Assay and Femtosecond Laser Irradiation of Two-Cell Aggregates.

NIH3T3 mouse fibroblastic cells were transfected with pCX4-bsr plasmids expressing the CADM1 isoforms and were selected using blasticidin S resistance as described previously (3). Stably transformed subclones were isolated. Exogenous expression of the CADM1 isoforms was confirmed by Western blot analyses using an antibody against the CADM1 C terminus (Fig. S3) as previously described (19).

Homotypic and heterotypic cell aggregation assays using these subcloned cells were performed as previously described (13). Briefly, for the homotypic assays, 1 × 10⁶ NIH3T3 subcloned cells were singly suspended in 0.5 ml HBSS containing 2% FBS. For the heterotypic assays, two subclones (0.5 × 10⁶ cells each) were suspended in 0.5 ml HBSS containing 2% FBS at a ratio of 1∶1, after one of the two subclones was labeled with the DiI fluorescent dye (Molecular Probe). The cell suspensions were transferred to siliconized 1.5-ml microcentrifuge tubes and rotated at 20 rpm. At the indicated time points, aliquots (20 μl) were sampled from the tubes to evaluate the degree of aggregation.

For the laser irradiation of the aggregates, a 1% bactoagar solution in HBSS was incubated at 43 °C prior to the assay. Twenty minutes after initiating the tube rotation, an aliquot (100 μl) of the cell suspension was mixed with 150 μl of HBSS containing 2% FBS and 50 μl of the prewarmed 1% bactoagar solution. The aliquot was plated on a glass-bottomed 35-mm culture dish and incubated for several minutes at room temperature so it was embedded in a viscous matrix of bactoagar (final concentration, 0.2%). The culture dishes were placed on the automated stage of an inverted microscope equipped with epifluorescence and a femtosecond laser. Random fields of view were examined for two-cell aggregates. Immediately before laser irradiation, heterotypic two-cell aggregates were identified based on the fluorescent labeling of either of the two cell types.

Femtosecond Laser Irradiation of Biotin-Adhered Streptavidin-Coated Microspheres.

The streptavidin-coated microsphere suspension (1.37% Solids-Latex, d = 6 ± 0.245 μm) (Polyscience) was diluted 1,000-fold with PBS. The bottom of a biotin-coated clear strip plate (Reacti-Bind™, Thermo) was cut from the tube and used as a biotin-coated substrate. The diluted microsphere suspension (100 μl) was placed on the substrate and incubated for 1 day at 37 °C with 90% humidity. During this process, all of the streptavidin-coated microspheres adhered to the biotin substrate. When Dulbecco’s Modified Eagle Medium (DMEM) or 0.2% bactoagar was used, the PBS buffer displaced these mediums after the incubation. The sample substrate was placed adhesion-side down on a glass-bottomed cell culture dish (35 mmϕ, MatTek Co.) as shown in Fig. 3A. The space between the substrate and the culture dish was maintained using 100 μm spacers and filled with medium.

A single shot femtosecond laser was focused through the 10× objective lens into the medium at approximately 3 μm from the substrate in the Z direction. After laser irradiation, the microspheres near the laser focal point were categorized based on whether they moved from their initial position (Fig. S4C). This experiment was performed 60 times. Approximately 300 microspheres were categorized and sorted as a function of the distance between O_f and the sphere center. From these results, a histogram with a 3-μm interval was constructed (Fig. 3B and Fig. S5 A–F, left). The percentage of particles that moved was calculated as A/(A + B) × 100, where A and B correspond to the number of microspheres that did (A) or did not (B) move. The distance was converted to the impulse loaded on the mesosphere (i.e., with Eq. 3). The histograms shown in Fig. 3C and Fig. S5 A–F, right) were constructed as a function of impulse with an interval of 10^-14 N-s.

Femtosecond Laser Irradiation of the Leukocyte–Endothelial Coculture.

HL-60 human promyelocytic leukemia cells were purchased from American Tissue Culture Collection. HL-60 cells were cultured in RPMI containing 10% FBS and differentiated into neutrophil-like cells by adding 10 nM phorbol myristate acetate (PMA) for 3 to 5 days. Human umbilical vein endothelial cells (HUVECs; Lonza) were cultured in EGM-2 medium (Lonza) and plated on human fibronectin-coated (Sigma) cover slips that were placed in a 24-well tissue culture plate. Confluent HUVECs were stimulated with tumor necrosis factor (TNF)-α (100 ng/ml) for 12 h at 37 °C immediately before initiating the coculture. After washing the HUVECs twice with PBS, 2 × 10⁴ PMA-treated HL-60 cells in 0.7 ml RPMI medium containing 10% FBS were added to each well. For laser irradiation, the cover slip was gently removed from the culture plate and placed HUVEC-side down on a glass-bottomed dish (Iwaki) with silicon spacers (Fig. S6A). The space between the cover slip and the bottom of the dish was filled with a thin layer of culture medium.

To dissociate leukocyte–endothelial adhesions (Fig. 4A), laser shots of a constant pulse energy were repeatedly administered. The first shot was focused 50 μm from the target leukocytes, the second was focused 3 μm closer to the target, and the remaining shots were repeated in the same manner until the target leukocyte slipped on the HUVECs. The process was video-recorded, and the distance from O_f to the target leukocyte cell was measured for each slipping movement of the target leukocyte.

Femtosecond Laser Irradiation of MDCK Epithelial Cell Monolayers.

Madin–Darby canine kidney (MDCK) cells were purchased from American Tissue Culture Collection and cultured in RPMI with 10% FBS. An MDCK cell monolayer with an acellular area was established using 12-well culture inserts that were bottomed with permeable filters containing 0.4-μm pores and coated with type I collagen (Biocoat culture insert, BD Biosciences). A 3-mm silicon cube was placed in the center of the permeable filter, and MDCK cells were seeded at a density of 5 × 10⁴ cells/12-well culture insert that was placed inside a well filled with RPMI. The cells were grown to confluence around the silicon cube for 3 days, and then the silicon cube was manually but gently removed to leave a sharp-margined acellular area.

For the laser irradiation, the filter was removed from the insert with a scalpel and placed MDCK cell-side down on a glass-bottomed dish (Iwaki), which was filled with a thin layer of culture medium (Fig. S6B). In some experiments, the filters were fixed with formalin, embedded in paraffin, cut into sections, and stained with hematoxylin and eosin to confirm that an epithelium-like monolayer had successfully formed (Fig. S6C).

Calculation of the Femtosecond Laser Impulse.

The specifics of the calculation procedures are presented in SI Text.