Local balancing influences global structure in social networks

Although social networks can often be viewed as graphs in their most basic form, many networks of interest include explicit sentiments (positive or negative views) of the nodes (constituent entities, also known as vertices) toward each other. This is particularly the case in geopolitics, settings where networks of firms compete in the creation of standards, and situations where polarization is frequent, such as in national elections, etc. The classical theory of structural balance developed by Heider (1) suggests how nodes may modify their relationships locally to maintain a type of balance within triads of nodes; this theory has been enriched in terms of explicit temporal dynamics by Kulakowski et al. (2). The work of Marvel et al. (3) in PNAS shows a rigorous analysis of these dynamics and brings out interesting properties and applications thereof.

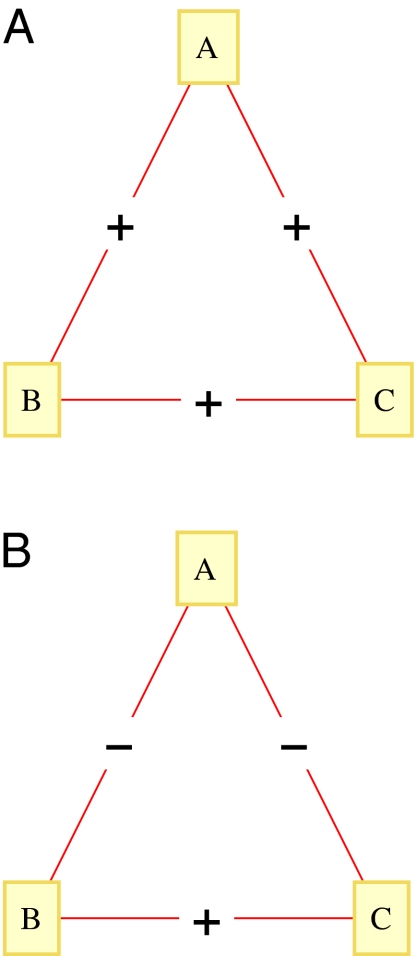
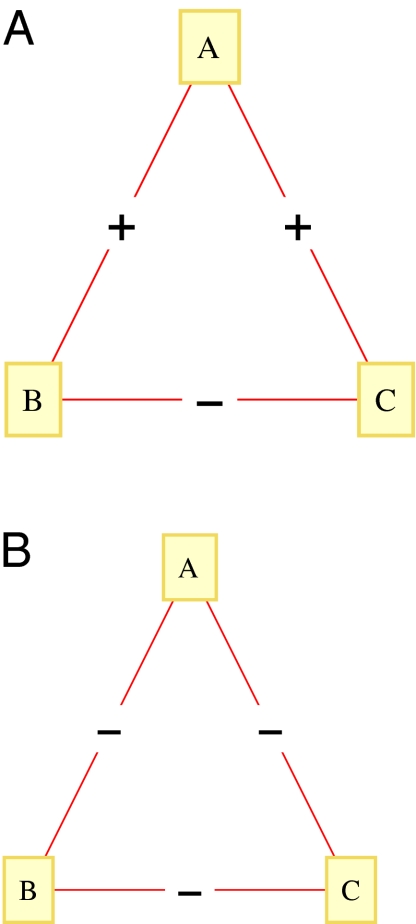
Let us first recall the notion of structural balance (1). Suppose we have three entities, A, B, and C; each pair of distinct entities has a link labeled + that denotes a positive sentiment or − that indicates a negative sentiment (all pair-wise relationships will be symmetric in our discussion: the sentiment that u displays to v is precisely the sentiment that v holds to u). Clearly, a triangle with all three links positive can be considered stable or balanced; invoking the idea that an enemy of my enemy is my friend, Heider (1) also postulates the triangle with exactly one positive link to be balanced. These two possibilities are shown in Fig. 1. Additional postulates by Heider (1) that an enemy of my friend is my enemy and that a friend of my enemy is my enemy suggest that the two possibilities depicted in Fig. 2 are unstable or unbalanced. The postulates by Heider (1), thus, suggest that the two types of triangles in Fig. 2 will try to locally repair themselves to be one of the two balanced types. For instance, given the first (unstable) configuration of Fig. 2, A may try to convince B and C to become friendly with each other; the failure of such an attempt may make A unfriendly to either B or C. Either way, this local repair leads to a balanced triangle. Similarly, the weakest enmity (say, the one between B and C) in the second configuration of Fig. 2 may lead to a strategic friendship (between B and C) to gang up against the third entity (A).

Fig. 1.

(A) A balanced triad. (B) A balanced triad.

Fig. 2.

(A) An unbalanced triad. (B) An unbalanced triad.

We will assume for much of this discussion, as does ref. 3, that we have an n node complete network: one in which there is a link between each pair of participants. In this case, the work of Cartwright and Harary (4) proves a necessary and sufficient condition for all triangles to be balanced: that the nodes can be partitioned into two sets, S₁ and S₂, (with one of the two allowed to be empty) such that there is complete positive sentiment within each of these two sets and complete negative sentiment between the two sets. In other words, full balance holds in a complete network if and only if there is perfect polarization, represented by the subsets S₁ and S₂. However, this structural characterization does not have the temporal dimension, which was explicit in the discussion above on local repairs that lead to structural balance. Let us next introduce an interesting temporal dynamics suggested by Kulakowski et al. (2), which is the main object of study by Marvel et al. (3).

The model of ref. 2 is as follows. We let the ties be numerical values of any sign (rather than just + or −), with the obvious meaning that ties of higher absolute value refer to more strongly held positive or negative opinions. Given the initial values of the ties at time t = 0 and a numbering of the nodes as 1, 2, … , n, let x_i,j(t) denote the tie value between i and j at time t. As an example with n = 3, we may have x_1,2(0) = 0.7, x_1,3(0) = 8, and x_2,3(0) = −3.5. The first and second are weak and strong positive links, respectively, whereas the third can be viewed as a medium negative link. Note that this triangle is not structurally balanced. Assuming continuously varying time, the basic temporal dynamics of ref. 2 are that for all nodes i and j (Eq. 1),

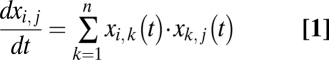Let us interpret this for the main case where i and j are distinct (the case where i = j is harder to interpret and less important for our discussion; see ref. 3 for a suggested interpretation). Note that each index k for which x_i,k(t) and x_k,j(t) are of the same sign increases the derivative in Eq. 1 and hence, encourages i and j to strengthen their tie, something that is suggested by the balanced configurations of Fig. 1. Recall that a triangle of + and − values containing nodes i, j, and k where the tie between i and k is of the same type like that between j and k, is balanced if and only if the tie between i and j is a +. Similarly, each index k for which x_i,k(t) and x_k,j(t) are of opposite signs encourages i and j to weaken their tie, as suggested by Fig. 2. Because the ties have arbitrary numerical values, it is natural to scale these encouragements by the product x_i,k(t) × x_k,j(t). Thus, Eq. 1 is well-motivated by structural balance theory.

Letting X(t) denote the n × n matrix of ties at time t, the above setting is that we are given the initial condition X(0) along with the differential equation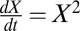, with X² = X × X denoting the usual matrix product. A basic question then is whether this dynamics typically leads to a state where all triangles are balanced. It is easy to verify that, once such a state is reached, the system will forever remain in it, although the actual tie values may change. Such a convergence would then suggest that this dynamics is well-motivated by structural balance and worthy of further study. It was found through simulations in ref. 2 that such a convergence does indeed hold for essentially any value of the initial matrix X(0).

The main analytical results of ref. 3 are verifications and strengthenings of the above empirical evidence. It is first shown in ref. 3 that, with any reasonable distribution for the initial matrix X(0), the system indeed converges to balance. That is, we are led to perfect polarization into sets S₁ and S₂, as proved by ref. 4. In fact, as is common in the theory of spectral partitioning, such a partitioning can be read off as the positive and negative components of an appropriate eigenvector (5). More specifically, suppose we write the eigendecomposition of X(0) as X(0) = QD(0)Q⁻¹, where D(0) is the diagonal matrix whose entries λ₁ ≥ λ₂ ≥ … ≥ λ_n are the eigenvalues of X(0) and Q is the orthogonal matrix whose columns are the eigenvectors of X(0) that correspond respectively to λ₁, λ₂, … , λ_n. Then, it is shown in ref. 3 that, under essentially any reasonable distribution for X(0), all entries

Full balance holds in a complete network if and only if there is perfect polarization.

in the first column ω₁ of Q will be nonzero with high probability and that the eventual polarization can be read off as S₁ being the set of positive components of ω₁ and S₂ being the set of negative components.

An additional useful result of ref. 3 concerns the case of large n. Suppose the entries of X(0) are sampled independently from distributions that, for simplicity, are bounded, centrally symmetric about zero, and have the same (mean and variance) pairs—one pair for all of the diagonal entries and one pair for all of the off-diagonal entries. Then, the common mean μ of the off-diagonal entries is shown to play a critical role in the large-n limit: if μ > 0, essentially all nodes go into one cluster S₁ with high probability, whereas if μ ≤ 0, the sizes of S₁ and S₂ become asymptotically equal with high probability. Although the case of completely connected social networks is less realistic for large n, these asymptotic results are shown to hold empirically, even for moderate n values that are less than 100. The dynamics of Eq. 1 are also shown to accurately predict the eventual polarizations in certain moderately sized networks, including one on international relations.

Thus, ref. 3 provides substantial analytical motivation for studying a basic temporal dynamics of those social networks in which the signs of ties are important; its approach underscores the usefulness of spectral methods in the analysis of large networks. This work (3) also suggests many interesting directions for further development. First, can an analogous theory be developed for more realistic models of (social) networks as opposed to the completely connected ones studied here? The second direction concerns rescalings of Eq. 1 motivated by the fact that Eq. 1 typically leads to the entries of x_i,j(t) growing unboundedly with time. Can convergence be proven for natural rescaling that keeps the x_i,j(t) bounded? One such rescaling is suggested in ref. 2, whereas another, motivated by the renormalization approach of Kleinberg (6), is to consider the matrix X(t) divided by its Frobenius norm. Also, can the convergence time in such rescalings be related to the eigenvalue gap of X(0) (5)? Third, dynamics that consider the second configuration of Fig. 2 to be balanced allow convergence to multiple clusters S₁, S₂, S₃, … (7). Can we develop and analyze temporal dynamics that correspond to this natural relaxation of structural balance? A further direction, motivated by the possible goal of networks converging to a desired final outcome (such as almost all pairs of nodes being connected by positive links), is, given limited resources that can help us intervene and alter the ties of a few links, how should these be used judiciously with a given dynamics to nudge the network toward the desired outcome?