Abstract
Rapid advances in sequencing technologies set the stage for the large-scale medical sequencing efforts to be performed in the near future, with the goal of assessing the importance of rare variants in complex diseases. The discovery of new disease susceptibility genes requires powerful statistical methods for rare variant analysis. The low frequency and the expected large number of such variants pose great difficulties for the analysis of these data. We propose here a robust and powerful testing strategy to study the role rare variants may play in affecting susceptibility to complex traits. The strategy is based on assessing whether rare variants in a genetic region collectively occur at significantly higher frequencies in cases compared with controls (or vice versa). A main feature of the proposed methodology is that, although it is an overall test assessing a possibly large number of rare variants simultaneously, the disease variants can be both protective and risk variants, with moderate decreases in statistical power when both types of variants are present. Using simulations, we show that this approach can be powerful under complex and general disease models, as well as in larger genetic regions where the proportion of disease susceptibility variants may be small. Comparisons with previously published tests on simulated data show that the proposed approach can have better power than the existing methods. An application to a recently published study on Type-1 Diabetes finds rare variants in gene IFIH1 to be protective against Type-1 Diabetes.
Author Summary
Risk to common diseases, such as diabetes, heart disease, etc., is influenced by a complex interaction among genetic and environmental factors. Most of the disease-association studies conducted so far have focused on common variants, widely available on genotyping platforms. However, recent advances in sequencing technologies pave the way for large-scale medical sequencing studies with the goal of elucidating the role rare variants may play in affecting susceptibility to complex traits. The large number of rare variants and their low frequencies pose great challenges for the analysis of these data. We present here a novel testing strategy, based on a weighted-sum statistic, that is less sensitive than existing methods to the presence of both risk and protective variants in the genetic region under investigation. We show applications to simulated data and to a real dataset on Type-1 Diabetes.
Introduction
Common diseases such as diabetes, heart disease, schizophrenia, etc., are likely caused by a complex interplay among many genes and environmental factors. At any single disease locus allelic heterogeneity is expected, i.e., there may be multiple, different susceptibility mutations at the locus conferring risk in different individuals [1].
Common and rare variants could both be important contributors to disease risk. Thus far, in a first attempt to find disease susceptibility loci, most research has focused on the discovery of common susceptibility variants. This effort has been helped by the widespread availability of genome-wide arrays providing almost complete genomic coverage for common variants. The genome-wide association studies performed so far have led to the discovery of many common variants reproducibly associated with various complex traits, showing that common variants can indeed affect risk to common diseases [2], [3]. However, the estimated effect sizes for these variants are small (most odds ratios are below 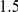 ), with only a small fraction of trait heritability explained by these variants [4]. For example, at least
), with only a small fraction of trait heritability explained by these variants [4]. For example, at least 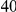 loci have been identified for height, but these loci together explain only
loci have been identified for height, but these loci together explain only 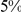 of the
of the 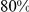 estimated heritability for this trait [5]. One possible explanation for this missing heritability is that, in addition to common variants, rare variants are also important.
estimated heritability for this trait [5]. One possible explanation for this missing heritability is that, in addition to common variants, rare variants are also important.
Evidence to support a potential role for rare variants in complex traits comes from both empirical and theoretical studies. There is an increasing number of recent studies on obesity, autism, schizophrenia, epilepsy, hypertension, HDL cholesterol, some cancers, Type-1 diabetes etc. [6]–[15] that implicate rare variants (both single position variants and structural variants) in these traits. From a theoretical point of view, population genetics theory predicts that most disease loci do not have susceptibility alleles at intermediate frequencies [16], [17].
With rapid advances in next-generation sequencing technologies it is becoming increasingly feasible to efficiently sequence large number of individuals genome-wide, allowing for the first time a systematic assessment of the role rare variants may play in influencing risk to complex diseases [18]–[21]. The analysis of the resulting rare genetic variation poses many statistical challenges. Due to the low frequencies of rare disease variants (as low as 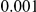 , and maybe lower) and the large number of rare variants in the genome, studies with realistic sample sizes will have low power to detect such loci one at a time, the way we have done in order to find common susceptibility variants [5], [22]. It is then necessary to perform an overall test for all rare variants in a gene or, more generally a candidate region, under the expectation that cases with disease are different with respect to rare variants compared with control individuals. Several methods along these lines have already been proposed. One of the first statistical methods proposed for the analysis of rare variants [23] is based on testing whether the proportion of carriers of rare variants is significantly different between cases and controls. A subsequent paper by Madsen and Browning [24] introduced the concept of weighting variants according to their estimated frequencies in controls, so that less frequent variants are given higher weight compared with more common variants. Price et al. [25] extended the weighted-sum approach in [24] to weight variants according to externally-defined weights, such as the probability of a variant to be functional. One potential drawback for these methods is that they are very sensitive to the presence of protective and risk variants.
, and maybe lower) and the large number of rare variants in the genome, studies with realistic sample sizes will have low power to detect such loci one at a time, the way we have done in order to find common susceptibility variants [5], [22]. It is then necessary to perform an overall test for all rare variants in a gene or, more generally a candidate region, under the expectation that cases with disease are different with respect to rare variants compared with control individuals. Several methods along these lines have already been proposed. One of the first statistical methods proposed for the analysis of rare variants [23] is based on testing whether the proportion of carriers of rare variants is significantly different between cases and controls. A subsequent paper by Madsen and Browning [24] introduced the concept of weighting variants according to their estimated frequencies in controls, so that less frequent variants are given higher weight compared with more common variants. Price et al. [25] extended the weighted-sum approach in [24] to weight variants according to externally-defined weights, such as the probability of a variant to be functional. One potential drawback for these methods is that they are very sensitive to the presence of protective and risk variants.
We introduce here a new testing strategy, which we call replication-based strategy, and which is based on a weighted-sum statistic, but that has the advantage of being less sensitive to the presence of both risk and protective variants in a genetic region of interest. We illustrate the proposed approach on simulated data, and a real sequence dataset on Type-1 diabetes.
Methods
We assume for ease of exposition, and without loss of generality, that an equal number of cases and controls have been sequenced in a genetic region of interest. In what follows, for the sake of fixation, we will be concerned with the situation where rare variants in the region increase susceptibility to disease. We discuss first a one-sided testing strategy to test for the presence of variants conferring risk to disease.
We partition the variants observed in cases and controls into distinct groups, according to the observed frequencies of the minor allele in cases and controls. More precisely, group 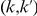 contains all variants that have exactly
contains all variants that have exactly 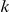 copies of the minor allele in controls, and exactly
copies of the minor allele in controls, and exactly 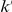 copies of the minor allele in cases. Let
copies of the minor allele in cases. Let 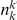 be the size of group
be the size of group 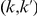 . Note that the set of
. Note that the set of 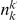 represents a summary of the original data, that in some sense contains all the information the data can tell us about the presence of disease variants in the region under investigation. For the purpose of testing for the presence of risk variants, we choose to focus only on variants that are likely to be risk variants, i.e., those variants with
represents a summary of the original data, that in some sense contains all the information the data can tell us about the presence of disease variants in the region under investigation. For the purpose of testing for the presence of risk variants, we choose to focus only on variants that are likely to be risk variants, i.e., those variants with 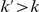 . A summary of the data is shown in Table 1.
. A summary of the data is shown in Table 1.
Table 1. Data summary.
| k/k′ | 1 | 2 | 3 | 4 | 5 |  |
| 0 | 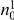 |
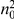 |
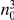 |
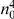 |
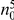 |
 |
| 1 | 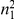 |
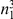 |
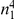 |
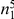 |
 |
|
| 2 | 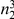 |
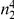 |
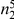 |
 |
||
| 3 | 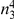 |
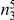 |
 |
|||
| 4 | 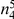 |
 |
||||
 |
Variants are classified according to the number of times they appear in controls (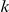 ) and cases (
) and cases (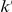 ). Only variants with higher observed count in cases compared with controls (i.e., more likely to be risk variants) are considered.
). Only variants with higher observed count in cases compared with controls (i.e., more likely to be risk variants) are considered.
We define the following weighted-sum statistic, where each variant in group 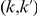 is assigned a weight
is assigned a weight 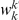 , and hence:
, and hence:
| (1) |
where 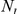 is an upper threshold on the number of occurrences of a variant in controls.
is an upper threshold on the number of occurrences of a variant in controls.
The choice of a good weighting scheme is very important for the performance of the approach. There are several possible ways to define the weights, including several already in the literature. Madsen and Browning [24] use data-dependent weights, with
where 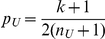 is the estimated frequency based on controls only, and
is the estimated frequency based on controls only, and 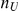 is the number of controls. Price et al. [25] discuss the possibility of incorporating external weights, based on predictions about variants being functional.
is the number of controls. Price et al. [25] discuss the possibility of incorporating external weights, based on predictions about variants being functional.
For our approach we define a set of data-dependent weights, as follows. For a variant that occurs 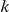 times in controls and
times in controls and 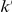 times in cases with
times in cases with 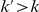 , a natural weight is the negative log of the probability of a variant occurring at most
, a natural weight is the negative log of the probability of a variant occurring at most 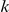 times in controls and at least
times in controls and at least 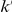 times in cases, under the null hypothesis of the variant not being associated with the disease:
times in cases, under the null hypothesis of the variant not being associated with the disease:
The statistic 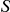 above can then be written as:
above can then be written as:
Since the number of mutations at a rare variant position follows approximately a Poisson distribution, the probability 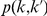 of observing at a variant position at most
of observing at a variant position at most 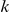 mutations in controls, and at least
mutations in controls, and at least 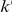 mutations in cases is calculated as
mutations in cases is calculated as
where 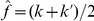 is the estimated variant frequency based on the observed number of occurrences in both cases and controls, and ppois is the Poisson distribution function. Note that the higher the observed frequency in cases compared with controls (i.e., the higher
is the estimated variant frequency based on the observed number of occurrences in both cases and controls, and ppois is the Poisson distribution function. Note that the higher the observed frequency in cases compared with controls (i.e., the higher  ), the higher the weight will be, and hence
), the higher the weight will be, and hence 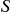 tends to be larger when more variants are seen at higher frequencies in cases versus controls. We employ a standard permutation procedure to evaluate the significance of
tends to be larger when more variants are seen at higher frequencies in cases versus controls. We employ a standard permutation procedure to evaluate the significance of 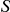 by randomly permuting the case/control label, and repeating the procedure described above for each permuted dataset, thus quantifying the extent to which the observed value of
by randomly permuting the case/control label, and repeating the procedure described above for each permuted dataset, thus quantifying the extent to which the observed value of 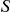 is significantly higher compared to the null expectation.
is significantly higher compared to the null expectation.
The strategy described above is inherently one-sided, because we focus on variants that have higher observed frequency in cases compared with controls, i.e., more likely to be risk variants. This test can be used symmetrically to test for the presence of protective variants. Without any prior knowledge on the direction of the association, two one-sided statistics need to be computed. If 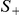 and
and 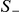 are the two one-sided statistics as defined in eq. (1), then a max-statistic can be used that calculates the maximum of the two, i.e.,
are the two one-sided statistics as defined in eq. (1), then a max-statistic can be used that calculates the maximum of the two, i.e., 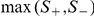 , and the statistical significance can be assessed by permutation.
, and the statistical significance can be assessed by permutation.
Incorporation of External Biological Information
If external information is available on the plausibility of a rare variant to be related to disease, it is of interest to be able to incorporate such information into our testing strategy. Such information has proved essential in the mapping of the disease genes for two monogenic disorders [26], and may well prove important for mapping disease genes in more complex diseases. It is straightforward to extend the proposed approach to take into account such information. If we denote by 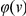 the probability that a variant
the probability that a variant  is functional, then we can rewrite the statistic
is functional, then we can rewrite the statistic 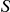 above as:
above as:
where 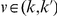 signifies that variant
signifies that variant  occurs
occurs 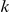 times in controls, and
times in controls, and 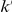 times in cases. In particular, if
times in cases. In particular, if 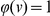 for all variants
for all variants  then we recover the statistic S above, where functional information was not used. If on the other hand a variant is not functional, then
then we recover the statistic S above, where functional information was not used. If on the other hand a variant is not functional, then 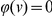 , and this variant is ignored.
, and this variant is ignored.
Results
Simulated Data
Simulation model
We evaluated both the Type-1 error and the power for the proposed approach using data simulated under various genetic and disease models, and compared the results to those obtained using several existing approaches. Li and Leal [23] proposed one of the very first statistical methods for association testing with rare variants, based on collapsing rare variants in a genetic region together. In this approach, each individual is called a carrier if the individual contains at least one rare variant in the region. Then the strategy is to assess whether the proportion of carriers in affected individuals is significantly different from the proportion of carriers in unaffected individuals. A subsequent approach proposed by Madsen and Browning [24] is based on a weighted-sum statistic. A feature of this approach, especially relevant in large samples, is that variants are weighted according to their estimated frequencies from unaffected individuals, such that less frequent variants are assigned higher weights compared to more frequent variants.
The first set of simulations is based on a neutral Wright-Fisher model. Using the software package Genome [27] we generated 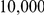 haplotypes according to a coalescent model, resulting in a total of
haplotypes according to a coalescent model, resulting in a total of 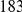 single nucleotide variants (SNVs) in the region (see Text S1 for more details). For the second set of simulations, we assume that the rare variants in the region are under weak purifying selection (as discussed in [16]), and use Wright's distribution [28] to sample the frequency at each variant:
single nucleotide variants (SNVs) in the region (see Text S1 for more details). For the second set of simulations, we assume that the rare variants in the region are under weak purifying selection (as discussed in [16]), and use Wright's distribution [28] to sample the frequency at each variant:
where 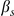 and
and 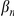 are scaled mutation rates, and
are scaled mutation rates, and  is the selection rate;
is the selection rate;  is a normalizing constant. As in [16] and [24], we take
is a normalizing constant. As in [16] and [24], we take 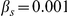 ,
, 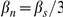 , and
, and  . The main difference between the two simulation models is that the variant frequency spectra are different, with proportionally more rare variants under the second model compared with the first model (e.g.,
. The main difference between the two simulation models is that the variant frequency spectra are different, with proportionally more rare variants under the second model compared with the first model (e.g.,  out of the total of
out of the total of 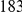 variants have frequency below
variants have frequency below 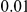 under the second model, while only
under the second model, while only 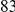 have this low frequency under the first model).
have this low frequency under the first model).
With respect to the disease model, we assume varying number of disease susceptibility variants (DSVs) between 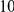 and
and 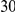 , chosen at random from the generated polymorphisms that had low frequency (less than
, chosen at random from the generated polymorphisms that had low frequency (less than 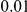 ). We assume two possible values for the total population attributable risk (PAR):
). We assume two possible values for the total population attributable risk (PAR): 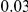 and
and 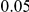 . The total PAR is distributed among all the disease variants. In one scenario, all disease variants have the same PAR, equal to the total PAR divided by the number of disease susceptibility variants. Perhaps a more realistic scenario is to assume unequal PAR for the different DSVs, and to this end we assume that individual variants' PARs are uniformly sampled from
. The total PAR is distributed among all the disease variants. In one scenario, all disease variants have the same PAR, equal to the total PAR divided by the number of disease susceptibility variants. Perhaps a more realistic scenario is to assume unequal PAR for the different DSVs, and to this end we assume that individual variants' PARs are uniformly sampled from 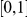 , and then renormalized to make them sum to the same total PAR of
, and then renormalized to make them sum to the same total PAR of 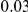 or
or 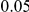 . In addition to the uniform distribution, we have also used an exponential model for the distribution of the individual PARs. In Supplemental Figure S-1 in Text S5 we show an example of the possible relationship between the odds ratio and the frequency at a disease variant, assuming
. In addition to the uniform distribution, we have also used an exponential model for the distribution of the individual PARs. In Supplemental Figure S-1 in Text S5 we show an example of the possible relationship between the odds ratio and the frequency at a disease variant, assuming 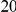 disease variants with frequencies between
disease variants with frequencies between 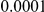 and
and 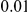 , and a total PAR of
, and a total PAR of 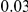 or
or 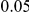 .
.
Type-1 error
We evaluated the Type-1 error for both the proposed and the existing approaches using the two simulation models discussed above (neutral and weakly-purifying selection). We assume two possible sample sizes, 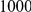 and
and 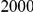 , with equal number of cases and controls. As shown in Table 2, the Type-1 error is well controlled at the nominal levels
, with equal number of cases and controls. As shown in Table 2, the Type-1 error is well controlled at the nominal levels 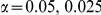 and
and 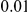 for all three methods.
for all three methods.
Table 2. Type-1 Error for the three approaches: collapsing (C), weighted-sum (WS ), and replication-based (R).
), and replication-based (R).
| Sim. Model | Sample Size |  |
C | WS
|
R |
 |
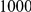 |
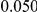 |
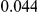 |
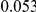 |
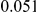 |
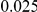 |
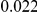 |
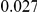 |
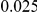 |
||
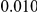 |
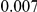 |
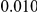 |
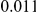 |
||
 |
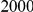 |
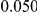 |
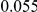 |
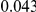 |
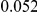 |
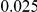 |
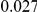 |
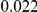 |
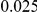 |
||
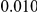 |
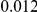 |
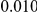 |
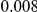 |
||
 |
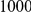 |
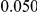 |
 |
 |
 |
 |
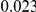 |
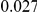 |
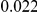 |
||
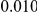 |
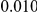 |
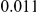 |
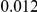 |
||
 |
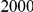 |
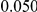 |
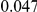 |
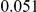 |
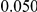 |
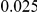 |
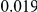 |
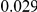 |
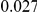 |
||
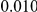 |
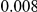 |
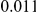 |
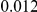 |
Results for two genetic simulation models are shown: variants under a neutral evolution model (1), and variants under a weakly-purifying selection model (2). The sample size is the total number of individuals sequenced, with equal numbers of cases and controls. Nominal  levels:
levels: 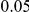 ,
, 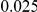 , and
, and 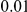 .
.
Power
We evaluated the power for all three methods assuming two models for generating the genetic data, and several complex disease models. For the genetic data, as explained above, two scenarios are illustrated: a first one where the variant frequencies are generated using a neutral coalescent model, and a second one where the variants are under weakly-purifying selection. For the underlying disease models, a varied number of disease susceptibility variants are assumed, that contribute equally, or unequally to the total PAR. For the latter scenario, the individual variant PAR are sampled from a uniform distribution (results for an exponential sampling distribution are shown in Supplemental Table S-1 in Text S3). To make the comparison fair among the different methods considered the same threshold of 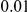 was used on the frequency of the variants included in the three testing methods.
was used on the frequency of the variants included in the three testing methods.
Power estimates for a series of simulation experiments are shown in Table 3. Note that the results are based on two-sided testing for all three methods and 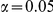 . For the same total PAR, the power decreases with increasing number of disease variants, due to the correspondingly smaller contribution of each disease variant. Also, the power increases for all methods when the weakly-purifying selection simulation model is used as opposed to the neutral model, due to the lower number of rare variants that are actually observed under the former model compared with the latter model. However, given the same sampling distribution for the frequency of the variants, the power did not vary much between the different ways the individual PARs were sampled. The key factor is the total PAR for the region. Overall the proposed approach is consistently and substantially more powerful than both the collapsing and the weighted-sum approaches across the multiple scenarios that we have considered, and under both models to generate the variant frequencies.
. For the same total PAR, the power decreases with increasing number of disease variants, due to the correspondingly smaller contribution of each disease variant. Also, the power increases for all methods when the weakly-purifying selection simulation model is used as opposed to the neutral model, due to the lower number of rare variants that are actually observed under the former model compared with the latter model. However, given the same sampling distribution for the frequency of the variants, the power did not vary much between the different ways the individual PARs were sampled. The key factor is the total PAR for the region. Overall the proposed approach is consistently and substantially more powerful than both the collapsing and the weighted-sum approaches across the multiple scenarios that we have considered, and under both models to generate the variant frequencies.
Table 3. Power Estimates (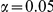 ) for the three approaches: collapsing (C) versus weighted-sum (WS
) for the three approaches: collapsing (C) versus weighted-sum (WS ) versus replication-based (R).
) versus replication-based (R).
| PAR = 0.03 | PAR = 0.05 | ||||||||
| Sim. Model | Sample Size | Disease Model | #DSVs | C | WS
|
R | C | WS
|
R |
 |
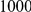 |
Eq PAR | 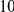 |
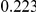 |
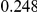 |
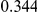 |
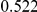 |
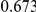 |
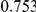 |
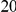 |
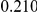 |
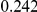 |
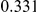 |
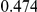 |
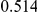 |
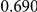 |
|||
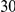 |
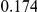 |
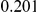 |
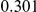 |
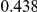 |
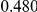 |
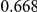 |
|||
 |
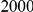 |
Eq PAR | 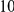 |
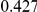 |
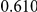 |
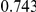 |
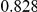 |
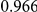 |
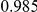 |
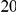 |
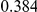 |
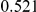 |
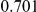 |
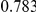 |
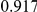 |
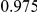 |
|||
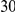 |
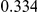 |
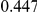 |
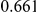 |
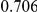 |
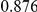 |
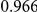 |
|||
 |
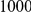 |
Uneq PAR | 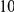 |
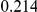 |
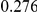 |
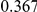 |
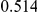 |
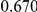 |
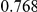 |
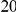 |
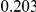 |
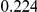 |
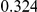 |
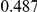 |
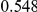 |
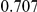 |
|||
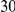 |
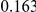 |
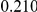 |
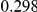 |
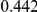 |
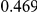 |
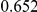 |
|||
 |
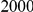 |
Uneq PAR | 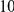 |
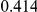 |
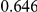 |
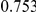 |
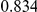 |
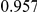 |
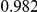 |
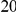 |
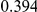 |
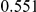 |
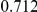 |
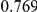 |
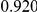 |
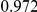 |
|||
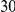 |
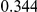 |
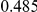 |
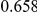 |
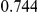 |
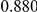 |
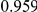 |
|||
 |
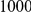 |
Eq PAR | 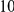 |
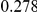 |
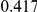 |
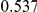 |
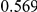 |
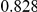 |
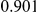 |
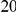 |
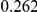 |
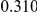 |
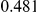 |
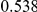 |
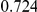 |
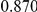 |
|||
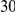 |
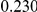 |
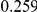 |
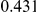 |
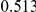 |
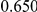 |
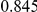 |
|||
 |
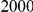 |
Eq PAR | 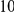 |
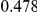 |
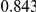 |
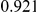 |
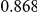 |
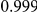 |
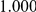 |
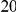 |
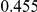 |
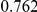 |
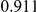 |
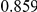 |
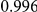 |
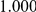 |
|||
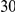 |
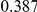 |
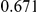 |
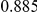 |
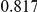 |
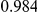 |
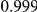 |
|||
 |
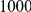 |
Uneq PAR | 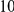 |
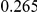 |
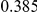 |
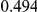 |
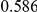 |
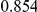 |
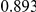 |
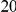 |
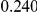 |
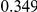 |
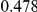 |
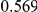 |
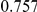 |
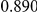 |
|||
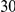 |
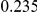 |
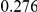 |
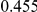 |
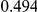 |
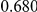 |
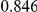 |
|||
 |
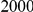 |
Uneq PAR | 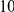 |
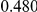 |
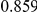 |
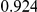 |
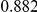 |
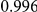 |
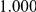 |
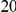 |
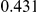 |
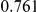 |
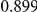 |
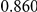 |
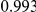 |
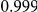 |
|||
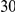 |
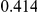 |
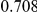 |
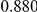 |
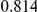 |
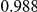 |
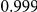 |
|||
Two genetic simulation models are assumed: neutral variants (1), and mildly deleterious variants (2). Varying number of DSVs are assumed, that can contribute equally or unequally to the total PAR. The sample size is the total number of individuals sequenced, with equal numbers of cases and controls. All tests are two-sided, i.e., testing for the presence of risk or protective variants in the region of interest.
Sensitivity to presence of both risk and protective variants
So far we have assumed scenarios where only variants that increase risk are present in a genetic region. However, sometimes it may be the case that both risk and protective variants are present in a genetic region of interest, for example when multiple genes in a set or pathway are tested together. This can also be true when individuals from the two extremes of a phenotype distribution are chosen to be studied. In such situations, the two existing methods discussed can suffer substantial loss of power, depending on the relative contributions of the two classes of variants. We show here that the proposed approach is less sensitive to such mixture, the principal reason being the inclusion of only those variants that may confer risk, and exclusion of the variants that are unlikely to be risk variants when we test for the presence of risk variants, and similarly when we test for the presence of protective variants.
In Table 4 we show power estimates when we test for the presence of risk or protective variants, given the existence of both risk and protective variants in the region. We assume that there are 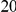 risk variants in the region, and the number of protective variants is between
risk variants in the region, and the number of protective variants is between 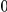 and
and 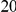 . As in the previous simulations, the total PAR for the
. As in the previous simulations, the total PAR for the 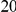 risk variants can take two values,
risk variants can take two values, 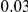 and
and 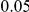 , while each protective variant has the same per-variant PAR, equal to the total PAR divided by
, while each protective variant has the same per-variant PAR, equal to the total PAR divided by 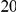 . Therefore, when the number of protective variants is
. Therefore, when the number of protective variants is 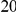 the overall contribution to disease is the same for risk and protective variants. This is of course the worst case scenario, and the Collapsing and Weighted-Sum approaches suffer from substantial loss of power in such cases. Even the proposed approach is not insensitive to such scenarios; however the loss in power is considerably less than that for the other two methods.
the overall contribution to disease is the same for risk and protective variants. This is of course the worst case scenario, and the Collapsing and Weighted-Sum approaches suffer from substantial loss of power in such cases. Even the proposed approach is not insensitive to such scenarios; however the loss in power is considerably less than that for the other two methods.
Table 4. Power Estimates (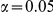 ) for two-sided tests, testing for the presence of risk or protective variants, when there is a mixture of risk and protective variants in the region of interest.
) for two-sided tests, testing for the presence of risk or protective variants, when there is a mixture of risk and protective variants in the region of interest.
| PAR = 0.03 | PAR = 0.05 | |||||||
| Sim. Model | #Risk | #Protective | C | WS
|
R | C | WS
|
R |
 |
 |
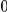 |
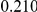 |
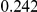 |
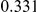 |
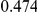 |
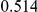 |
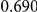 |
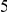 |
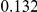 |
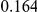 |
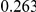 |
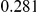 |
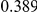 |
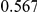 |
||
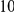 |
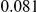 |
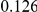 |
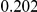 |
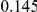 |
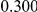 |
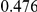 |
||
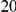 |
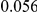 |
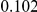 |
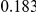 |
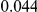 |
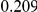 |
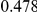 |
||
 |
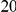 |
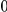 |
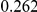 |
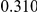 |
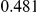 |
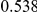 |
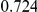 |
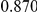 |
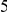 |
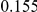 |
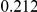 |
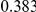 |
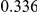 |
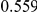 |
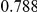 |
||
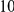 |
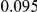 |
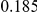 |
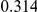 |
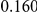 |
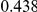 |
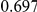 |
||
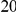 |
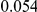 |
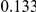 |
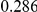 |
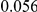 |
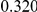 |
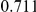 |
||
In addition to 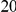 risk variants in the region, there are between
risk variants in the region, there are between 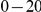 protective variants as well. Simulation model corresponds to one of the two scenarios: neutral variants (1), and mildly deleterious variants (2). The total sample size is
protective variants as well. Simulation model corresponds to one of the two scenarios: neutral variants (1), and mildly deleterious variants (2). The total sample size is 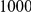 cases and controls. Collapsing (C) vs. weighted-Sum (WS
cases and controls. Collapsing (C) vs. weighted-Sum (WS ) vs. replication-based (R).
) vs. replication-based (R).
Type-1 Diabetes Dataset
We also applied our approach to a dataset on Type 1 Diabetes (T1D), published by Nejentsev et al. [15]. In their paper, the authors resequenced exons and splice sites of ten candidate genes in 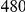 cases and
cases and 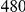 controls (more details on the dataset are in Text S2). In their study, rare variants were tested individually, and two SNVs in gene IFIH1 and two other SNVs in gene CLEC16A were found to be protective against T1D.
controls (more details on the dataset are in Text S2). In their study, rare variants were tested individually, and two SNVs in gene IFIH1 and two other SNVs in gene CLEC16A were found to be protective against T1D.
Here we reanalyze the dataset using the proposed approach, and two of the existing approaches. For each gene and each method, we perform two-sided tests, testing for the presence of risk or protective variants. Results are in Table 5. As in [15] we found one gene, IFIH1, to be significant with all three methods (P-value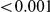 for all three methods). For this gene, controls were enriched for rare mutations compared with cases. Some evidence of enrichment in protective variants was also observed in another gene, CLEC16A, although the P-values do not remain significant after multiple testing correction.
for all three methods). For this gene, controls were enriched for rare mutations compared with cases. Some evidence of enrichment in protective variants was also observed in another gene, CLEC16A, although the P-values do not remain significant after multiple testing correction.
Table 5. Type-1 diabetes results.
| Gene | #SNVs | C | WS
|
R |
| IFIH1 | 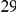 |
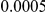 |
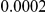 |
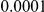 |
| CLEC16A | 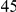 |
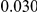 |
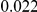 |
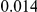 |
Two-sided P-values for the top two genes. An upper frequency threshold of 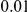 was used for the variants considered for testing.
was used for the variants considered for testing.
Discussion
We have proposed here a new testing strategy to examine associations between rare variants and complex traits. The approach is based on a weighted-sum statistic that makes efficient use of the information the data provides on the presence of disease variants in the region being investigated. The proposed test is based on computing two one-sided statistics, designed to quantify enrichment in risk variants, and protective variants, respectively. This aspect allows the proposed approach to have substantially better power than existing approaches in the presence of both risk and protective variants in a region. Even when only one kind of variants is present, we have shown via simulations that the proposed approach has consistently better power than existing approaches. An application to a previously published dataset on Type-1 Diabetes [15] confirmed the original finding, namely that rare variants in IFIH1 confer protection towards disease.
The weights underlying our weighted-sum statistic depend only on the data at hand. However, external information on the likelihood of a variant to be functional could prove very useful, and could be combined with the information present in the data to improve power to identify disease susceptibility variants. Such information has been successfully used to identify the genes for several monogenic disorders [26]. Price et al. [25] discuss a weighted-sum approach with externally-derived weights, and show that such information can be very useful using several empirical datasets. We have also described a natural way to take into account such external functional predictions within the proposed framework.
Since empirical data are only now becoming available, it is not known how often both risk and protective variants are present in a particular disease gene. When both types of variants are present, it seems appealing to be able to combine the two types of signals. It is possible to extend the proposed approach to take advantage of both kinds of disease variants, and we discuss such an extension in Text S4. We noticed in our simulation experiments that such a hybrid approach can have much improved power when both types of variants are present, but this comes at the price of reduced power when only one type of variants is present. Therefore, depending on the underlying disease model, both approaches could provide useful information.
The proposed approach is applicable to a case-control design and therefore is susceptible to spurious findings due to population stratification. Population stratification has been shown to be an important issue in the context of common variants. For rare variants, differences in rare variant frequencies between populations are likely to be even more pronounced. Development of new methods, and extension of existing methods are necessary to adequately address the issue. Alternatively, family-based designs offer the advantage of being robust to false positive findings due to population stratification.
Replication of association signals in independent datasets is an essential aspect of any disease association study, and has become standard practice for common variants. Rare variants, due to their low frequencies and potential modest effects, are normally tested together with other rare variants in the same unit, e.g., gene. Therefore a reasonable first replication strategy is at the level of the gene. Follow-up of individual variants in the gene can be performed to investigate whether any of the rare variants in the gene can be found to be significantly associated with disease.
Finding rare disease susceptibility variants is a challenging problem, especially due to their low frequencies and the probable moderate effects on disease. So far the methods proposed in the literature have focused on case-control designs. However, for rare variants, family-based designs may prove very useful. Not only are they robust against population stratification, but they may also offer increased power due to the increased likelihood of affected relatives to share the same rare disease variants. Continued development of novel statistical methods for identifying rare disease susceptibility variants is needed for population-based designs, and especially for family-based designs.
Software implementing these methods is available at: http://www.mailman.columbia.edu/our-faculty/profile?uni=ii2135.
Supporting Information
Simulation model 1.
(0.04 MB PDF)
Type-1 diabetes dataset.
(0.04 MB PDF)
Power estimates when individual variants' PAR are sampled from an exponential distribution.
(0.05 MB PDF)
Capitalizing on the presence of both risk and protective variants.
(0.11 MB PDF)
Relationship between odds ratios and frequencies for the simulated scenarios.
(0.56 MB PDF)
Footnotes
The authors have declared that no competing interests exist.
This work was supported by NIH grants 1R03HG005908, R01MH087590, and R01MH081862. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Lander E, Kruglyak L. Genetic dissection of complex traits: guidelines for interpreting and reporting linkage results. Nat Genet. 1995;11:241–247. doi: 10.1038/ng1195-241. [DOI] [PubMed] [Google Scholar]
- 2.McCarthy MI, Abecasis GR, Cardon LR, Goldstein DB, Little J, et al. Genome-wide association studies for complex traits: consensus, uncertainty and challenges. Nat Rev Genet. 2008;9:356–369. doi: 10.1038/nrg2344. [DOI] [PubMed] [Google Scholar]
- 3.Hindorff LA, Junkins HA, Mehta JP, Manolio TA. A catalog of published genome-wide association studies. Available at http://www.genome.gov/26525384.
- 4.Maher B. Personal genomes: The case of the missing heritability. Nature. 2008;456:18–21. doi: 10.1038/456018a. [DOI] [PubMed] [Google Scholar]
- 5.Manolio TA, Collins FS, Cox NJ, Goldstein DB, Hindorff LA, et al. Finding the Missing Heritability of Complex Diseases. Nature. 2009;461:747–753. doi: 10.1038/nature08494. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fearnhead NS, Wilding JL, Winney B, Tonks S, Bartlett S, et al. Multiple rare variants in different genes account for multifactorial inherited susceptibility to colorectal adenomas. Proc Natl Acad Sci USA. 2004;101:15992–15997. doi: 10.1073/pnas.0407187101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Cohen JC, Kiss RS, Pertsemlidis A, Marcel YL, McPherson R, et al. Multiple rare alleles contribute to low plasma levels of HDL cholesterol. Science. 2004;305:869–872. doi: 10.1126/science.1099870. [DOI] [PubMed] [Google Scholar]
- 8.Fearnhead NS, Winney B, Bodmer WF. Rare variant hypothesis for multifactorial inheritance: susceptibility to colorectal adenomas as a model. Cell Cycle. 2005;4:521–525. doi: 10.4161/cc.4.4.1591. [DOI] [PubMed] [Google Scholar]
- 9.Cohen JC, Pertsemlidis A, Fahmi S, Esmail S, Vega GL, et al. Multiple rare variants in NPC1L1 associated with reduced sterol absorption and plasma low-density lipoprotein levels. Proc Natl Acad Sci USA. 2006;103:1810–1815. doi: 10.1073/pnas.0508483103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ji W, Foo JN, O'Roak BJ, Zhao H, Larson MG, et al. Rare independent mutations in renal salt handling genes contribute to blood pressure variation. Nat Genet. 2008;40:592–599. doi: 10.1038/ng.118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Stefansson H, Rujescu D, Cichon S, PietilŠinen OP, Ingason A, et al. Large recurrent microdeletions associated with schizophrenia. Nature. 2008;455:232–236. doi: 10.1038/nature07229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Walsh T, McClellan JM, McCarthy SE, Addington AM, Pierce SB, et al. Rare structural variants disrupt multiple genes in neurodevelopmental pathways in schizophrenia. Science. 2008;320:539–543. doi: 10.1126/science.1155174. [DOI] [PubMed] [Google Scholar]
- 13.Weiss LA, Shen Y, Korn JM, Arking DE, Miller DT, et al. Association between microdeletion and microduplication at 16p11.2 and autism. N Engl J Med. 2008;358:667–675. doi: 10.1056/NEJMoa075974. [DOI] [PubMed] [Google Scholar]
- 14.Helbig I, Mefford HC, Sharp AJ, Guipponi M, Fichera M, et al. 15q13.3 microdeletions increase risk of idiopathic generalized epilepsy. Nat Genet. 2009;41:160–162. doi: 10.1038/ng.292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Nejentsev S, Walker N, Riches D, Egholm M, Todd JA. Rare variants of IFIH1, a gene implicated in antiviral responses, protect against type 1 diabetes. Science. 2009;324:387–389. doi: 10.1126/science.1167728. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Pritchard JK. Are rare variants responsible for susceptibility to common diseases? Am J Hum Genet. 2001;69:124–137. doi: 10.1086/321272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Pritchard JK, Cox NJ. The allelic architecture of human disease genes: common diseaseÐcommon variant… or not? Hum Mol Genet. 2002;11:2417–2423. doi: 10.1093/hmg/11.20.2417. [DOI] [PubMed] [Google Scholar]
- 18.Mardis ER. The impact of next-generation sequencing technology on genetics. Trends Genet. 2008;24:133–141. doi: 10.1016/j.tig.2007.12.007. [DOI] [PubMed] [Google Scholar]
- 19.Shendure J, Ji H. Next-generation DNA sequencing. Nat Biotechnol. 2008;26:1135–1145. doi: 10.1038/nbt1486. [DOI] [PubMed] [Google Scholar]
- 20.Tucker T, Marra M, Friedman JM. Massively parallel sequencing: the next big thing in genetic medicine. Am J Hum Genet. 2009;85:142–154. doi: 10.1016/j.ajhg.2009.06.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Metzker ML. Sequencing technologies - the next generation. Nat Rev Genet. 2010;11:31–46. doi: 10.1038/nrg2626. [DOI] [PubMed] [Google Scholar]
- 22.Morris AP, Zeggini E. An evaluation of statistical approaches to rare variant analysis in genetic association studies. Genet Epidemiol. 2009;34:188–193. doi: 10.1002/gepi.20450. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Li B, Leal SM. Methods for detecting associations with rare variants for common diseases: application to analysis of sequence data. Am J Hum Genet. 2008;83:311–321. doi: 10.1016/j.ajhg.2008.06.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Madsen BE, Browning SR. A groupwise association test for rare mutations using a weighted sum statistic. PLoS Genet. 2009;5:e1000384. doi: 10.1371/journal.pgen.1000384. doi: 10.1371/journal.pgen.1000384. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Price AL, Kryukov GV, de Bakker PI, Purcell SM, Staples J, Wei LJ, Sunyaev SR. Pooled association tests for rare variants in exon-resequencing studies. Am J Hum Genet. 2010;86:832–838. doi: 10.1016/j.ajhg.2010.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ng SB, Buckingham KJ, Lee C, Bigham AW, Tabor HK, et al. Exome sequencing identifies the cause of a mendelian disorder. Nat Genet. 2009;42:30–35. doi: 10.1038/ng.499. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Liang L, Zoellner S, Abecasis GR. GENOME: a rapid coalescent-based whole genome simulator. Bioinformatics. 2007;23:1565–1567. doi: 10.1093/bioinformatics/btm138. [DOI] [PubMed] [Google Scholar]
- 28.Wright S. Adaptation and selection. Genetics, Paleontology, and Evolution. Princeton Univ Press. 1949:365–389. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Simulation model 1.
(0.04 MB PDF)
Type-1 diabetes dataset.
(0.04 MB PDF)
Power estimates when individual variants' PAR are sampled from an exponential distribution.
(0.05 MB PDF)
Capitalizing on the presence of both risk and protective variants.
(0.11 MB PDF)
Relationship between odds ratios and frequencies for the simulated scenarios.
(0.56 MB PDF)


