An anthropomorphic phantom for quantitative evaluation of breast MRI

Abstract

Purpose: In this study, the authors aim to develop a physical, tissue-mimicking phantom for quantitative evaluation of breast MRI protocols. The objective of this phantom is to address the need for improved standardization in breast MRI and provide a platform for evaluating the influence of image protocol parameters on lesion detection and discrimination. Quantitative comparisons between patient and phantom image properties are presented.

Methods: The phantom is constructed using a mixture of lard and egg whites, resulting in a random structure with separate adipose- and glandular-mimicking components. T₁ and T₂ relaxation times of the lard and egg components of the phantom were estimated at 1.5 T from inversion recovery and spin-echo scans, respectively, using maximum-likelihood methods. The image structure was examined quantitatively by calculating and comparing spatial covariance matrices of phantom and patient images. A static, enhancing lesion was introduced by creating a hollow mold with stereolithography and filling it with a gadolinium-doped water solution.

Results: Measured phantom relaxation values fall within 2 standard errors of human values from the literature and are reasonably stable over 9 months of testing. Comparison of the covariance matrices of phantom and patient data demonstrates that the phantom and patient data have similar image structure. Their covariance matrices are the same to within error bars in the anterior-posterior direction and to within about two error bars in the right-left direction. The signal from the phantom’s adipose-mimicking material can be suppressed using active fat-suppression protocols. A static, enhancing lesion can also be included with the ability to change morphology and contrast agent concentration.

Conclusions: The authors have constructed a phantom and demonstrated its ability to mimic human breast images in terms of key physical properties that are relevant to breast MRI. This phantom provides a platform for the optimization and standardization of breast MRI imaging protocols for lesion detection and characterization.

INTRODUCTION

Dynamic contrast-enhanced (DCE) MRI with Gd-DTPA has been shown to be useful in screening women at high risk of breast cancer as well as in evaluating the extent of disease.^{1, 2} In 2007, the American Cancer Society released guidelines recommending screening MRI as an adjunct to x-ray mammography for women with a 20%–25% lifetime risk of developing breast cancer³ and DCE-MRI has been used increasingly in the clinic.^{4, 5} Despite recent advances, many issues remain to be fully addressed in DCE-MRI. Although DCE-MRI demonstrates high sensitivity, it has a well-documented low and variable specificity (26%–97%).^{6, 7, 8} In addition, there has been debate over a possible link between increased MR use in breast cancer imaging and an increase in the number of more extensive surgeries and mastectomies being performed at some institutions.^{9, 10, 11, 12, 13, 14, 15, 16, 17, 18}

In response to these issues, recent standardization efforts in the breast MR community have resulted in a breast MR lexicon^{19, 20} and a set of standardized quantities and symbols for kinetic analysis of Gd-DTPA tracer washout.²¹ Review papers have discussed the variety of protocols used and given general recommendations regarding which protocol to use for a given clinical scenario.^{22, 23} However, standards for specific breast MRI acquisition protocols are still needed. In particular, quantitative assessment of MR protocols and their efficacy for different clinical situations has not yet been adequately addressed.

To perform quantitative comparisons of imaging protocols in terms of lesion detection and characterization, a phantom that mimics anatomical tissue structure in addition to contrast properties is required. Breast anatomy is composed of interlacing fat- and water-containing tissues that produce imaging artifacts (e.g., chemical shift artifact) and can hinder lesion detectability. The importance of realistic phantom structure in the evaluation of imaging systems for the purpose of abnormality detection was demonstrated in a study by He et al.,²⁴ in which both phantom and patient data were used to perform reader studies evaluating compensation methods for myocardial SPECT image reconstruction algorithms. They found that phantoms with more complicated, realistic image structures resulted in performance measures for defect detection that more closely matched results derived from patient data than studies with more simplistic phantoms. The optimal reconstruction parameters derived from the more realistic phantoms were significantly different from those derived from more simplistic phantoms.

In the context of breast imaging, the importance of realistic phantoms was demonstrated in a study investigating the utility of different imaging modalities to evaluate silicone breast implants.²⁵ The authors reported how only a more realistic and complex phantom revealed important differences between the evaluated imaging modalities.

A small number of breast MR phantoms have already been described in literature.^{26, 27} Mazzara et al.²⁶ and Liney et al.²⁷ both described phantoms where a homogeneous layer of adipose-mimicking material (Crisco or lard) surrounds an interior homogeneous region of glandular-mimicking material (polysaccharide material TX-151 or a “commercial jelly product”) in a cylindrical container. In the phantom of Mazzara et al.,²⁶ a version with an implant was also created. A lesion was included in the phantom of Liney et al.²⁷ as a capsule filled with Gd-DTPA-doped water. In both cases, the T₁ and T₂ relaxation times of the materials were measured and found to be in good agreement with breast tissue values. In addition, the American College of Radiology (ACR) phantom for accreditation (http://www.acr.org/accreditation/mri.aspx) is available for the quantitative evaluation of image quality parameters such as resolution, signal to noise ratio, and the presence of artifacts.

While existing phantoms do address some needs of the imaging community, there are currently no phantoms available that reproduce the appearance of and variability in the anatomical structure seen in human images. Similarly, no phantoms are available with well-characterized lesions and variable tissue structure. Such a phantom would allow researchers to investigate how imaging technique parameters interact with anatomically relevant structure to affect the clinician’s end goal, which, in the case of breast cancer imaging, is lesion detection and characterization. Therefore, for the quantitative comparison of diagnostic efficacy and for protocol selection, the appearance and variability of structures in the phantom and its similarity with patient data become critical aspects of the phantom.

In this study, we describe a physical, tissue-mimicking phantom for the quantitative assessment of breast MRI protocols in terms of lesion detection and characterization in the presence of complex, human-like, anatomical structures. Important requirements for such a phantom include T₁ and T₂ relaxation parameters similar to those in adipose and glandular human breast tissues, a random phantom structure that mimics anatomical structures in patients, the ability to actively suppress the signal from the adipose-simulating component in the phantom, and a realistic enhancing lesion. In this study, we present a phantom that addresses all of the above properties.

MATERIALS AND METHODS

Phantom construction

The phantom was constructed using refined lard to simulate adipose tissue and coagulated, fresh egg whites to simulate fibroglandular tissue. The lard (Goya Foods, Secaucus, NJ or Marquez Brothers International, Inc., San Jose,CA) and fresh eggs (Davidson’s Safest Choice Pasteurized Shell Eggs, National Pasteurized Eggs, Inc., Lansing, IL) were both purchased from local supermarkets.

Lard was chosen to simulate adipose tissue since it has a similar composition, is very stable, and is readily available. Human white adipose tissue consists mostly of lipids in the form of triglycerides.²⁸ Myristic, palmitic, palmitoleic, stearic, oleic, and linoleic fatty acids make up more than 90% of the triglyceride component.²⁸ Lard is composed entirely of lipids, 97.9% of which are in the form of triglycerides,²⁹ where the same six fatty acids make up over 90% of the total lipid content.³⁰ The shelf-life for lard is indicated by the manufacturer to be at least a year and a half with no refrigeration necessary.

Egg whites were chosen to simulate glandular tissue since they have a similar composition, unique functional properties that aid in structure formation, and are also readily available. In addition to adipose tissue, the human female breast is also made up of ducts, lobules, and the associated fibrous stromal compartment^{31, 32} that make up the so-called “glandular” portion of the breast. Both ducts and lobules consist of epithelial and myoepithelial cells surrounded by a basement membrane that is made up of primarily laminin and type IV collagen proteins.^{33, 34} The main extracellular matrix component of the interstitial stromal compartment is type I collagen protein.^{34, 35} Therefore, a large part of the glandular tissue is made up of proteins.

In addition, we know that a significant fraction of glandular breast tissue is made up of water. One study showed that normal patient glandular breast tissue has a water content of 41%–76% by weight.³⁶ Therefore, a glandular-mimicking phantom material should be high in both water and protein content. The inclusion of cells would be not only expensive but also unrealistically unstable. Egg whites provide a good first order match to human glandular tissue makeup. Egg whites are made up of mostly water (87.6%) and proteins (10.9%).³⁰ The major proteins are ovalbumin, ovotransferrin, ovomucoid, ovoglobulin G2, ovoglobulin G3, and lysozyme, which make up about 91.9% of the total protein content of egg whites.³⁷ While the types of protein in egg whites and human breast tissue differ, the elemental composition of different proteins is almost indistinguishable.³⁸ In addition, all proteins are made up of amino acids, which all bind H in similar ways. Therefore, we expect that the MRI signal of the proteins in egg whites would be similar to those in human breast tissue. In addition to being readily available, egg whites also have several functional properties that make them ideal for forming structures with no intervening septum. They coagulate irreversibly after heating³⁹ and do not dissolve into the surrounding material. While the shelf-life of egg whites is markedly less than that of refined lard, we will heat the egg whites, store them in an air-tight container, and mix them with a preservative to improve the shelf-life as much as possible. The true shelf-life of both phantom components will be measured as described in Sec. 2B.

A custom, air-tight plastic jar was developed to contain the phantom materials and simulate the shape of the human breast. The jar shape was defined by a half-sphere combined with a cylindrical portion, where the total internal volume was fixed to a typical breast volume of 425 ml.⁴⁰ The lid attaches to the jar body via a ring of 24 screws through a gasketed connection and has two fill ports that are sealed with Teflon tape-coated screw plugs. The half-sphere jar shape was chosen to approximate the shape of the majority of breast patients based on visual inspection of clinical breast MRI images and ease of fabrication. Although this approximation roughly simulates the shape of many patients, there is certainly a large variation in patient breast shape including conical shapes and shapes distorted due to the contact of the breast with the coil. Such differences can have important implications on effective breast shimming.⁴¹ It would be possible to modify the jar shape of the phantom to mimic some of these other shapes or even to use segmented patient images to produce irregular jar shapes, but this would not affect the T₁ and T₂ of the phantom material and is outside of the scope of the current study.

To fill the phantom jar, a preservative (0.2% w∕v Dowicil 75, The Dow Chemical Co., Midland, MI) was added to raw egg whites prior to pouring into melted lard and heating for 30 s while stirring at a constant rotational velocity. The lard was heated until it reached either 100 or 110 °C and stirred at a constant velocity of either 125 or 350 rpm. These different lard temperatures and stirring velocities were used to create a set of phantoms with different tissue structures in an attempt to mimic the type of variation seen in patient data. Air bubbles were removed by placing the phantom in a vacuum for 20 min. The mixture was then cooled at room temperature in the sealed jar and rotated once during cooling to help redistribute the egg whites in the lard. This rotation helps create a layer of lard around the edges of the jar. The phantoms were constructed with a density of approximately 24% glandular-mimicking material by volume. This breast density is similar to densities measured on patient populations using MRI. A study that estimated breast density using MRI in a high-risk cohort of 35 patients found breast densities ranging from 2% to 71.4% with a mean of 28%.⁴² In the future, the density of the phantom could be varied to match the full range of densities seen in patient data by simply increasing or decreasing the amount of egg whites.

T₁ and T₂ relaxation parameter measurements

For estimation of T₁ and T₂ values, inversion recovery (IR) and spin-echo (SE) sequences were used, respectively. All scans were performed in a Siemens Magnetom 1.5 T clinical scanner using an extremity coil. The scan parameters were TR=25 s, resolution=2.5 mm×2.5 mm×2.5 mm, five slices separated by 7.5 mm each, TI=[22, 35, 45, 75, 100, 150, 200, 250, 400, 500, 600, 900, 1000, 1500, 2500, 4500] ms for the IR sequence, and TE=[15, 20, 25, 30, 35, 40, 50, 70, 75, 95, 100, 120, 150, 200, 300] ms for the SE sequence.

The T₁ and T₂ relaxation times of the lard and egg compartments were estimated from reconstructed magnitude images using maximum-likelihood estimation (MLE) with a Rician data model. The maximization of the likelihood was implemented using a limited-memory Broyden–Fletcher–Goldfarb–Shanno method with bounds⁴³ in the R programming language. The Gaussian noise variance, σ², was estimated using the MLE equation for estimation from a background region in a magnitude data set.⁴⁴ For our data, two rectangular bands of 11×47 pixels on either side of the imaged sample, located at the edge of the image, were designated as background voxels and used in the above calculation. The large dimension of the background regions covered the full image field of view and the small dimension was chosen to select enough pixels to reasonably sample the noise probability distribution while staying as far away from the object as possible.

For lard, relaxation values were estimated using a lard-filled tube, assuming monoexponential signal behavior. The formulas for MLE of monoexponential T₁ and T₂ relaxation times have been presented in literature.^{45, 46} We used the T₂ equations as previously presented and expanded the monoexponential T₁ signal equation to include an additional parameter to correct for imperfect inversion pulses since this is known to significantly affect T₁ measurements even on 1.5 T systems.^{47, 48} All coefficients for fits to lard data were forced to be positive. The mean and standard deviation of the estimated relaxation values for all voxels within a hand-selected circular region of interest (ROI) were taken as the estimated relaxation value and its error. The number of voxels included in the ROI was typically 145, which represents the number of voxels included in the user-selected circular ROI across each of the five imaged slices. The circular ROIs were selected to include as much of the object as possible, while avoiding pixels on the edge of the object that had partial volume mixing with the surrounding air.

The relaxation values of the egg component were calculated on the phantom itself since the relaxation values of egg are known to vary with the preparation technique.⁴⁹ A double-exponential signal equation was used to fit the data with the T₁ and T₂ values of lard fixed to those estimated above; the amounts of egg and lard, the inversion pulse correction, and the T₁ and T₂ values of egg were free parameters for each voxel. All free parameters were forced to be positive during the fitting except for the T₁ value of egg, which was restricted to values between 500 and 5000 ms. The reported relaxation values and their errors were calculated as the mean and standard deviation weighted by the egg fraction for all voxels, within a hand-selected, circular ROI, with an egg fraction of at least 50% and a proton density of at least 50% of the maximum value in the sample (on average, about 480). The circular ROIs were selected to include as much of the object as possible, while avoiding pixels on the edge of the object that had partial volume mixing with the surrounding air.

The above process was repeated for three different phantoms manufactured using different construction parameters (lard heating temperatures and constant rotational velocities) to ensure that variations in the production method did not cause variations in the relaxation values outside of the human range.

The estimated phantom relaxation values were compared to the published human data. All published studies found where both T₁ and T₂ values were calculated separately for both adipose and glandular breast tissues on a 1.5 T magnet were included in our analysis.^{50, 51, 52, 53} Error bars were taken directly from the respective values reported in the publications.

The stability of the relaxation values over time was measured by repeating the above process approximately every other week over a period of 9 months. During this time, the phantom was stored at room temperature.

Comparison of image structure

The phantom’s structure was quantitatively compared to the patient data using covariance matrices. The covariance matrix measures how each pixel in the image co-varies, on average, with every other pixel, given a population of such images (from either phantoms or patients).⁵⁴ The full covariance matrix of a vector (or image) g with M elements (equal to N² for an image or ROI with N×N pixels) will be an M×M matrix with elements given by

$$K_{ij}=⟨\left(g_i-{\overline{g}}_i\right){\left(g_j-{\overline{g}}_j\right)}^{*}⟩,$$

where the overbar indicates an average and the ^* indicates complex conjugation. If g_i and g_j are statistically independent and i≠j, then K_ij=0. If i=j, then K_jj is equal to the variance of g_j. Since g is a random vector, we must average over many instances of g in order to get a good estimate of K.

Since we have a limited number of images available relative to the number of elements that must be computed for a full covariance matrix, we have averaged the covariance matrix over all positions within an image ROI, therefore, assuming wide-sense stationarity within that ROI (Ref. ⁵⁴) and reducing the variance of the estimate of K at the expense of position-dependent information. We will refer to this matrix as the stationary covariance matrix. It represents the average direction-dependent correlation strength over all positions in the ROI and is an estimate of the texture in the images to second order. The stationary covariance matrix has a size of 2N−1×2N−1 and is given by

$$K_{pq}^{\text{stationary}}={⟨K_{i\left(i+p+qN\right)}⟩}_{i∊\left[\left(m+nN\right)∊S\right]},$$

where p and q are “offset” indices (both ∊[−(N−1),…,(N−1)]) in the x and y directions, respectively. The physical meaning of p and q is that they are relative offset values. So, $K_{pq}^{\text{stationary}}$ is the element of K^stationary that holds the average covariance over all pixel pairs in the ROI that are separated by p pixels in the x direction and q pixels in the y direction. Another way to state this is that the covariance element $K_{pq}^{\text{stationary}}$ describes the correlation between any pixel in the ROI and its neighbor p pixels to the right and q pixels up. The element $K_{00}^{\text{stationary}}$ is at the center of the matrix. The two-dimensional indices m and n both run from 0 to N−1 over the two-dimensional ROI in the x and y directions, respectively. The one-dimensional index i is simply a one-dimensional version of the indices m and n that runs over every pixel in the ROI (∊[0,…,N²−1]) and is equal tom+nN. The average over the elements of the full covariance matrix only includes elements for which a (p,q) offset ROI pixel exists, denoted by the set S. Therefore, the number of samples that contribute to the calculation of the element $K_{pq}^{\text{stationary}}$ of the stationary covariance matrix varies with the exact p,q indices and is given by (N−|p|)(N−|q|). We can see from this equation that stationary covariance elements describing correlations with more distant pixels pairs (large p and q values) have fewer samples. Also note that both the full and the stationary covariance matrices are symmetric, so K_ij=K_ji and $K_{ij}^{\text{stationary}}=K_{ji}^{\text{stationary}}$.

For each phantom or patient data set, the largest square ROI was selected by-hand which still contained only breast tissue. The ROI size varied with the breast size for patient data (between 35×35 and 150×150 voxels), but stayed constant for phantom data (70×70 voxels). This ROI was applied to a set of slices (between 26 and 92 slices∕patient depending on the breast size and 61 slices∕phantom) of the left breast where enough breast tissue was present to fill the chosen ROI.

Multiple slices were included in the stationary covariance matrix calculation by concatenating all ROIs from all slices into a single g vector. This provided a single, in-plane, stationary covariance matrix for each patient or phantom, which we will refer to as a patient- or phantom-specific stationary covariance matrix. This matrix was also normalized by the average voxel variance (the central pixel of the stationary covariance matrix) to highlight the relative correlation fall-off with spatial position.

An overall stationary covariance matrix for the entire patient or phantom population was then calculated by first converting all patient-specific stationary covariance matrices to the same spatial scale (0.625 mm∕voxel) using a cubic convolution interpolation with an interpolation parameter of −0.5 (Ref. ⁵⁵) if necessary. The difference between the original and the interpolated covariance matrices was inspected to ensure differences were negligible. Finally, all of the resultant matrices were averaged. Error bars on the overall stationary covariance matrix were estimated by calculating the standard deviation of the patient-specific stationary covariance matrices values at each offset position.

To understand whether the difference among patient-specific stationary covariance matrices was due to instrumentation error or anatomical variations, simulated ROIs were created with only Rician noise. In all cases, the noise variance was set to 1 since the final covariance is normalized by its maximum value, which is equivalent to the average pixel variance. Simulated ROIs were chosen to have a conservative size of 35×35 voxels, which is equal to the smallest ROI used for the covariance calculations on the patient data. Sets of between 5 and 95 simulated ROIs were created to bracket the range of the number of slices selected in the patient data. The root mean squared (RMS) variation in the simulated, Rician-noise only, patient-specific stationary covariance estimate was then calculated for five different offsets (4–20 mm) by averaging over all offsets whose absolute values $\left(\sqrt{p^2+q^2}\right)$ were within 4 mm of the specified offset. The RMS variation was calculated as a function of the number of ROIs used in the covariance estimation (corresponding to the number of patient slices). This process was repeated on 11 independent realizations to improve the RMS estimates and compare to the variation in the patient-specific stationary covariance matrices.

Coded patient data were taken from the National Cancer Institute’s (NCI) Clinical Genetics Branch’s Breast Imaging Study data archive. The use of the data was authorized under appropriate IRB approval from both the NCI and the FDA. In the study, a total of 194 high-risk patients was imaged using various MR imaging protocols and scanner types. Patients were enrolled between June 2002 and February 2007 and included in the study if they were between 25 and 56 yr of age and considered at high genetic risk of developing breast cancer. See Ref. 56 for additional study details.

Seventy-seven patients with MRI data collected on a 1.5 T Philips machine with a seven-channel, dedicated breast coil and with the same pre-contrast imaging sequence were selected for additional analysis. Thirteen were excluded because of the presence of an implant or diagnosis of breast cancer before or during the course of the NCI breast imaging study. Sixty-four patients remained for the final analysis. Precontrast, T₁-weighted, gradient-echo, fat-suppressed images were available for each patient with an in-plane resolution ranging from 0.586 to 0.664 mm and a slice thickness ranging from 1.9 to 2.3 mm. Twenty phantoms were fabricated and imaged using the same scanner type, breast coil, and imaging sequence for comparison with the patient data.

Enhancing lesion

An enhancing, mass-like lesion was designed to be included in the phantom. We have designed and manufactured two simulated lesions using stereolithography to simulate round and lobular morphologies. The simulated lesions consist of hollow plastic molds with 0.6 mm thick walls and can be filled with a gadolinium-doped water solution. Neither of the plastic molds have any internal structure. The lesion with the round morphology is a 1 cm internal diameter sphere with an internal volume of 523.6 mm³. The lobular lesion is a 1 cm internal diameter sphere with three additional lobulations and has an internal volume of 563.2 mm³. The stereolithography printer resolution was 0.0508×0.0508×0.1016 mm³ for these parts. An inner diameter of 1 cm was chosen for the lesions in this study, but this size could be easily varied in future implementations.

These lesions are suspended in the phantom via small tubes that are attached to the lid of the phantom jar and are added into the phantom itself when the jar is sealed and allowed to cool. Once the phantom is completely cooled and the lard and egg whites have solidified, the lesion is filled with 4.5 mM GdCl₃ (anhydrous gadolinium chloride, 99.99%, Sigma-Aldrich, St. Louis, MO) in de-ionized water. This concentration of gadolinium was chosen to be similar to that of patients at the peak of a typical gadolinium contrast agent washout curve. Note that the concentration of gadolinium in the lesion is a fixed value in the current study. In future studies, we plan to extend this lesion model to include temporally dynamic behavior.

We obtained chemically selective fat-suppressed, 3D gradient-echo MRI images of phantoms with each of the two lesion types using a Siemens Magnetom 1.5 T clinical scanner with an extremity coil. The scan parameters were resolution=0.75 mm×0.75 mm×0.75 mm, matrix size=192×192×72, TR=3.86 ms, TE=1.36 ms, and flip angle=10°.

RESULTS

Figure 1 shows example patient and phantom images acquired with clinical systems. T₁- and T₂-weighted images of the phantom were acquired using standard clinical breast protocols from two different institutions with two different clinical scanners (1.5 T Philips and 1.5 T General Electric both with dedicated breast coils). Our phantom provides a breast shape and internal tissue structure that are much improved over currently available phantoms.

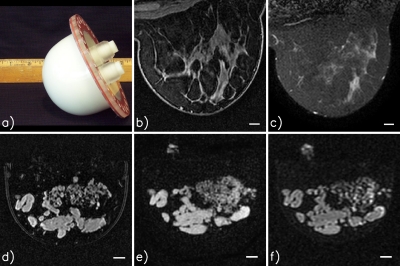
Figure 1.

Example patient and phantom images. All MRI images were acquired with a dedicated breast coil using either a 1.5 T Philips or a 1.5 T General Electric (GE) scanner: (a) Photograph of a phantom; (b) patient, T₁-weighted, fat-suppressed, Philips scanner; (c) patient, T₂ SPAIR (spectral adiabatic inversion recovery), fat-suppressed, Philips scanner; (d) phantom, T₁-weighted, fat-suppressed, Philips scanner; (e) phantom, T₁-weighted, fat-suppressed, GE scanner; and (f) phantom, T₂-weighted, fat-suppressed, GE scanner. All scale bars are 10 mm. The bright signal near the top of images (e) and (f) is from glandular-mimicking phantom material in the fill ports of the phantom jar.

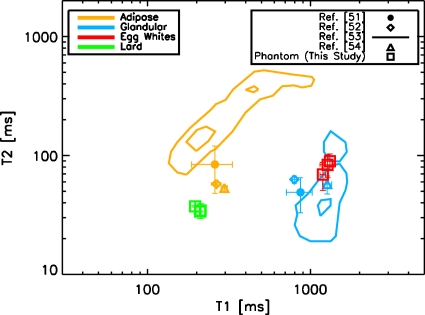
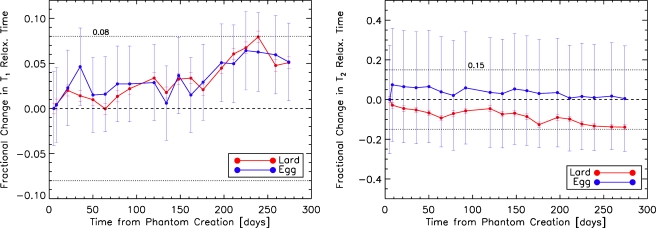
Figure 2 shows the comparison of phantom T₁ and T₂ relaxation parameters with the corresponding published human values. Values for three different phantoms with different construction parameters are shown. Phantom relaxation values fall within two times the standard error of the human data. The match between the human and the phantom data is particularly good for T₁ values, which are more relevant when evaluating DCE-MRI since the images are T₁-weighted. The results of the stability analysis are shown in Fig. 3. Over a 9 month period, the T₁ and T₂ values are stable to within 8% and 15%, respectively, for both lard and egg whites. The data indicate that the phantom materials may be stable over an even longer time period since the values have not yet strongly deviated from their values at production time. We will continue to monitor the stability until the values change significantly. In Mazarra et al.,²⁶ when their phantom was stored at room temperature for 6 months, they stated that no noticeable degradation was seen and the T₁ and T₂ values had less than 10% random variations. For the phantom presented in Ref. 27, data evaluating the shelf-life were not presented and the shelf-life was stated as being “several months” when refrigerated. Therefore, our phantom performs at least as well as currently available breast phantoms in terms of stability.

Figure 2.

Comparison of phantom T₁ and T₂ values with human data from the literature. Error bars are one standard error. The lines plotted for the study of Graham et al. (Ref. ⁵²) indicate contours that include the calculated 12.5% and 87.5% probability of their measured tissues. The T₁ and T₂ values of the phantom materials fall within 2 standard errors of the human data for both the adipose- and the fibroglandular-mimicking compartments. Data points for the phantom materials were measured on three different phantoms constructed using different lard temperatures and stirring velocities. The phantom T₁ values are a better match to human data than the T₂ values and are the primary determinants of image contrast for DCE-MRI studies.

Figure 3.

Fractional change in T₁ (left) and T₂ (right) relaxation times of lard and egg whites as a function of time since phantom production date. All data points have been normalized by the relaxation value on the phantom production date. T₁ and T₂ relaxation values of both lard and egg are stable to within 8% and 15%, respectively, over a period of 9 months. Errors bars are the standard deviation over all voxels included in the computation for a single data set.

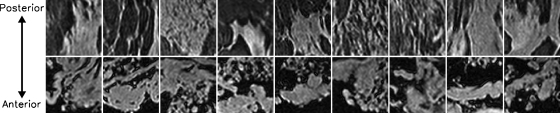
Figure 4 shows example phantom and patient ROIs. A visual comparison between these ROIs indicates that the phantom has a random structure that resembles the complicated patient data image structure. We observe that the patient data appear to have a directional preference in the anterior-posterior direction, whereas the phantom is more isotropic. Furthermore, the fat suppression in the phantom images appears to be slightly improved as compared to that of patient data. This may be due to the fact that there is no torso attached to the phantoms, resulting in improved shimming of the phantom, or that the spectral shape of the fat signature in the phantom may be less complicated than that of patients. There may also be more homogeneity of the material types within a voxel in the phantom than in the patient data, resulting in the appearance of better fat suppression.

Figure 4.

Example ROIs (cropped to 3.5 cm×3.5 cm) selected from the patient (top row) and phantom (bottom row) fat-suppressed, T₁-weighted data. Note the resemblance in heterogeneity of the interlacing adipose and glandular tissues between phantom and patient images. Structures in the patient data appear to be more anisotropic than those in the phantom data and tend to elongate along the anterior-posterior direction. The phantom data also appear to have slightly better fat-suppression than the patient data.

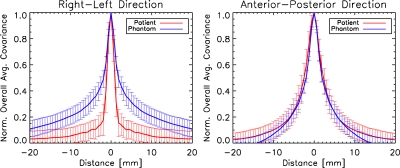
Figures 56 compare patient and phantom covariance matrices. Figure 5 shows images of the patient and phantom overall stationary covariance matrices, while Fig. 6 shows horizontal and vertical cuts through those matrices. Our data suggest that the covariance length of the patient and phantom images is similar along the anterior-posterior direction. In the right-left direction, they differ by about 2 standard error bars, with the phantom images having a larger correlation length than the patient data. In general, the phantom data are more isotropic than that of the patient, which tends to have structures that elongate along the anterior-posterior direction. Interestingly, the error bars of the patient and phantom data are similar, which indicates a similar range of variability among the two populations.

Figure 5.

Overall stationary covariance matrices for the patient and phantom data sets. The matrices are scaled to have the same intensity at their peak. The phantom and patient overall stationary covariance matrices have a similar covariance length in the anterior-posterior direction. However, the phantom has a larger covariance length than the patient in the right-left direction.

Figure 6.

Cuts through the patient and phantom overall stationary covariance matrices (shown in Fig. 6) in the right-left and anterior-posterior directions. The patient and phantom overall stationary covariance matrices are the same to within their error bars along the anterior-posterior direction, but differ in the right-left direction. Error bars are the standard deviation of the individual patient- (n=64) and phantom-specific (n=20) stationary covariance matrices at each distance.

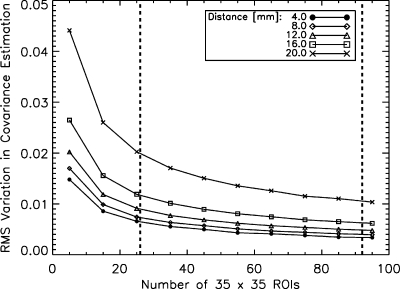
Figure 7 shows the results of simulations run to estimate the amount of instrumentation error included in the error bars in Fig. 6. RMS variations in the stationary covariance matrix estimations are plotted as a function of the number of ROIs used in the estimate. The ROIs were simulated images created with only Rician noise. The results for five different offset distances are shown. For 26–92 ROIs, the magnitude of the RMS instrumentation error in the stationary covariance ranges from 0.003 to 0.020, depending on the offset distance and the number of ROIs. The corresponding error bars in Fig. 6 range from 0.053 to 0.096 for the same set of offset distances. The fact that the RMS instrumentation errors are less than the size of the error bars in Fig. 6 indicates that these error bars represent mostly anatomical variation.

Figure 7.

RMS variation in the stationary covariance estimate due to Rician instrumentation noise only as a function of the number of 35×35 voxel ROIs used in the estimation. Five different offset distances are shown. Compared to the size of the error bars in Fig. 6, which describe both anatomical and instrumentation errors, the instrumentation errors shown here are much less than the size of the error bars in the actual data in Fig. 6. This indicates that the error bars in Fig. 6 represent mostly anatomical variation.

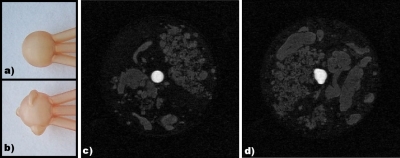
Images of the lesions before inclusion in the phantom as well as fat-suppressed, T₁-weighted, gradient-echo MRI images of two phantoms with the two different simulated lesion types are shown in Fig. 8. We are able to produce complex lesion morphologies and to fill those with a gadolinium-doped water solution whose concentration can be varied by the user to investigate different contrast agent doses. With the addition of the enhancing lesion, the phantom can be used to study the effect of image protocol parameters on lesion detection and characterization.

Figure 8.

(a) Photograph of round-shaped, mass-like simulating lesion (sphere internal diameter=10 mm). The three tubes toward the right connect the lesion with the phantom jar lid and allow for filling of the lesion with contrast agent as well as future dynamic contrast agent experiments. (b) Photograph of lobular-shaped, masslike simulating lesion (3 lobulations plus 10 mm internal diameter sphere diameter). (c) Fat-suppressed, T₁-weighted, gradient-echo image (0.75 mm isotropic resolution, coronal slice) of a complete phantom with the round-shaped simulating lesion inserted and filled with gadolinium-doped water. (d) The same as (c) with the lobular-shaped simulating lesion.

DISCUSSION

We have described a breast MR phantom, developed for quantitative evaluation of breast MRI techniques, which mimics breast tissue properties including T₁ and T₂ relaxation values, fat suppression, image structure, and lesion morphology and peak enhancement. We have also presented a method for quantitatively comparing the image structure of phantom data with that of patient data. This method permits formulating approaches to further improve the phantom design and production methods.

Our phantom design can be used to quantitatively compare T₁-weighting methods and fat-suppression techniques of different imaging protocols, coils, contrast agent dose, and scanners at 1.5 T in terms of lesion detection. The phantom could be validated and used to compare performance at other field strengths as well. Since the lesion volumes are known, the effect of imaging protocol parameters on the ability to estimate lesion volume can also be investigated. Another important application of the phantom is performing direct lesion detectability comparisons across different institutions since the exact same phantom set can be imaged at a variety of locations. Such comparisons may help illuminate the cause of variations in clinical performance among institutions by determining the contribution of scanner and software variability.

An extension of the phantom design allowing for the investigation of dynamic parameters is underway. This will be achieved by modifying the current static lesion design to include validated contrast agent washout kinetics. Once the dynamic lesion is included, the phantom can be applied to the optimization of additional breast MRI parameters such as spatial vs temporal resolution trade-offs. We expect that the phantom will also be useful for quantitative evaluation of x-ray imaging since the phantom materials were selected to be similar to human breast tissue components. We are therefore currently working toward characterizing the x-ray properties of the phantom.⁶⁰ Such a dual-modality phantom would be useful not only for quantitative evaluation of separate modalities but also direct comparisons between x-ray and MRI modalities to help understand which modality is optimal for a given imaging situation. A manuscript is also currently in preparation that discusses a dynamic lesion.

One of the limitations of the phantom design is an improved fat suppression compared to patient data. In addition, tissue structures in the right-left direction are, on average, larger in the current phantom design than those in patient data. Further work is necessary to determine the cause of the difference in fat suppression between patient and phantom images. If the cause of this is improved field homogeneity in the phantom, this could be addressed by purposely misadjusting the shim settings of the MR scanner or by adding distributed quantities of an MR-invisible material with a different susceptibility constant to the outside of the phantom. Another probable explanation for the difference is that human adipose tissue contains more than only lipids. It also contains vascular cells and is held in a matrix of collagen fibers. The total lipid content of human adipose tissue is 60%–85%, but adipose tissue also contains 5%–30% water and 2%–3% protein.²⁸ In contrast, the adipose-mimicking material used in our phantom is 100% lipid. A future version of the phantom may address this discrepancy by mixing additional proteins or other organic elements found in vascular cells into the adipose-mimicking material; however, the most appropriate materials to be used and their shelf-life must be carefully considered. Variations in fat suppression due to breast shape could be addressed by modifying the phantom jar to reproduce different breast shapes, such as conical shapes and those distorted by contact with the coil.

In terms of tissue structures, the phantom does have more isotropic tissue structures than those in patient data; however, the overall size of these structures is similar to that of patient data and presents a significant improvement over what is currently available. The fact that the overall size of structures in the phantom is similar to patient data implies that optimizations performed with the phantom should be appropriate when evaluating detectability as a function of lesion size. Since the phantom has a more isotropic structure than patient data, we expect isotropic lesions to be more difficult to detect in the phantom than in patient data. Similarly, anisotropic lesions will be easier to detect in the phantom than in patient data. The fact that these differences are quantitatively evaluated in the phantom means that optimization trends derived from the phantom can be intelligently interpreted in terms of their translation to clinical imaging.

Although the phantom covariance is more isotropic than the patient data, the phantom data do exhibit some amount of anisotropy which is perpendicular in direction to the anisotropy in the patient data. This suggests that it may be possible to adjust the phantom production to improve the phantom tissue structure. Some possibilities include modifying the stirring parameters while the egg is coagulating in the heated lard, rotating the entire phantom while cooling to room temperature, or perhaps pushing the raw egg whites through a grid while they enter the heated lard in order to create long, filamentary structures. This approach might also provide fiber-like structures with some ability to control the corresponding distribution of sizes.

CONCLUSION

The breast MRI community currently lacks a realistic, anthropomorphic phantom that can be used to quantitatively evaluate the effect of MRI protocol parameters on lesion detectability. In this study, we propose a phantom that addresses this need. Other quantitative MRI phantoms, such as the ACR accreditation phantom and the DCE-MRI phantom under development by the Quantitative Imaging Biomarkers Alliance at the Radiological Society of North America (http://qibawiki.rsna.org), are important tools in MRI technique optimization because they allow for precise measurement of parameters such as slice thickness, resolution, and relaxation time estimation. However, these phantoms are intended for optimization of specific image quality parameters and have no anthropomorphic shape or structure. Therefore, they are unable to probe exactly how MRI technique parameters influence lesion detectability. Anthropomorphic phantoms have been implemented in other imaging modalities and have been used to demonstrate that simple, non-anthropomorphic phantoms produce misleading results when used to optimize imaging systems.^{24, 57, 58, 59} The phantom described in this work will provide a much-needed platform for better understanding the interaction of breast MRI acquisition parameters with lesion detection and estimation.

Clinical applications of breast MRI have been rapidly evolving and have demonstrated potential to improve the detection and characterization of breast lesions, particularly for high-risk patients with dense breast tissue, when compared to the current standard-of-care methods. However, the advantages of breast MRI have been overshadowed by issues of performance variability and false positive findings. Our phantom design helps address these issues by allowing quantitative comparisons across breast MRI systems and protocols and by directly relating image acquisition parameters to lesion detection and estimation. Such comparisons will contribute to the standardization of breast MRI and address some of the concerns associated with its widespread clinical use.