Rheometric properties of canine vocal fold tissues: Variation with anatomic location

Abstract

Objective

To evaluate the in vitro rheometric properties of the canine vocal fold lamina propria and muscle at phonatory frequencies, and their changes with anatomic location.

Methods

Six canine larynges were harvested immediately postmortem. Viscoelastic shear properties of anterior, middle, and posterior portions of the vocal fold cover (lamina propria) as well as those of the medial thyroarytenoid (TA) muscle (vocalis muscle) were quantified by a linear, controlled-strain simple-shear rheometer. Measurements of elastic shear modulus (G’) and dynamic viscosity (η’) of the specimens were conducted with small-amplitude sinusoidal shear deformation over a frequency range of 1 Hz to 250 Hz.

Results

All specimens showed similar frequency dependence of the viscoelastic functions, with G’ gradually increasing with frequency and η’ decreasing with frequency monotonically. G’ and η’ of the canine vocalis muscle were significantly higher than those of the canine vocal fold cover, and η’ of the canine vocal fold cover was significantly higher than that of the human vocal fold cover. There were no significant differences in G’ and in η’ between different portions of the canine vocal fold cover.

Conclusion

These preliminary data based on the canine model suggested that the vocalis muscle, while in a relaxed state in vitro, is significantly stiffer and more viscous than the vocal fold cover during vibration at phonatory frequencies. For large-amplitude vocal fold vibration involving the medial portion of the TA muscle, such distinct differences in viscoelastic properties of different layers of the vocal fold should be taken into account in multi-layered biomechanical models of phonation.

Introduction

Due to the frequent practical difficulty in obtaining immediately post-mortem human larynges for basic laryngeal research, animal models of the larynx have often been used for experimentation and studies of laryngeal physiology, phonatory function, and the biomechanics of phonation [1, 2]. Among the different animal models, the canine larynx has been a popular model for phonatory research, because of the gross morphologic and anatomic similarities between the canine and the human larynges. The canine model has been historically used widely for a variety of experiments despite some important structural differences, such as the lack of a well-defined vocal ligament in the lamina propria when compared to the human larynx [1–3]. With this anatomic difference, the canine vocal fold lamina propria or mucosa can be referred to as the vocal fold cover.

Excised canine larynges have been used for quantifying biomechanical properties of the vocal folds [4, 5]. Rheometric properties, or viscoelastic shear properties are among the most critical types of tissue biomechanical properties for the vocal folds, because the mucosal wave that propagates on the surface of the vocal fold lamina propria during phonation is a shear wave [6]. The rheometric properties of the canine vocal fold cover have been examined previously, in order to evaluate the effect of freezing and postmortem tissue changes on such properties [7]. Knowledge of the viscoelastic shear properties of different anatomic locations of the vocal fold is important for the understanding of phonatory mechanics, so that properties of different vocal fold tissue layers and different parts of the vocal fold lamina propria can be better defined in computational biomechanical models of phonation for more accurate predictions of vocal fold vibratory behavior, such as eigenmodes and fundamental frequency [8, 9]. In particular, very little is known about the rheometric properties of the medial thyroarytenoid (TA) muscle or vocalis muscle. While the vocalis muscle is normally not directly involved in self-sustained oscillation of the vocal fold, it may become part of the vibratory tissue during large-amplitude vibration for high-intensity (loud) phonation [10]. The viscoelastic shear properties of the TA muscle may also affect phonation when surgical materials for vocal fold augmentation are implanted or injected laterally into the muscle layer, displacing some of the TA muscle medially into the lamina propria in the paralyzed vocal fold [11, 12].

Previous measurements on the viscoelastic shear properties of vocal fold tissues and phonosurgical biomaterials were often made at frequencies lower than the typical phonatory frequency range [7, 13–15], which is around 100–200 Hz for male and around 200–300 Hz for female in speech. Such rheometric measurements should be conducted at higher frequencies in the phonatory range, such that the viscoelastic data become directly applicable to phonation. Recent studies have reported breakthroughs in the frequency range of measurements achieved [12, 16, 17]. In particular, a linear, controlled-strain, simple-shear rheometer system capable of empirical measurements of viscoelastic shear properties at frequencies of up to 250 Hz was reported by Chan and Rodriguez [16]. With this rheometer, the present study attempted to quantify the rheometric properties of canine vocal fold tissues at frequencies of phonation, in order to examine the dependence of such properties on anatomic location, and to compare with previous data reported for the normal human vocal fold cover [16]. The focus was to compare the viscoelastic shear properties of anterior, middle, and posterior portions of the vocal fold cover with those of the medial TA (vocalis) muscle.

Materials and Methods

Canine vocal fold tissue specimens

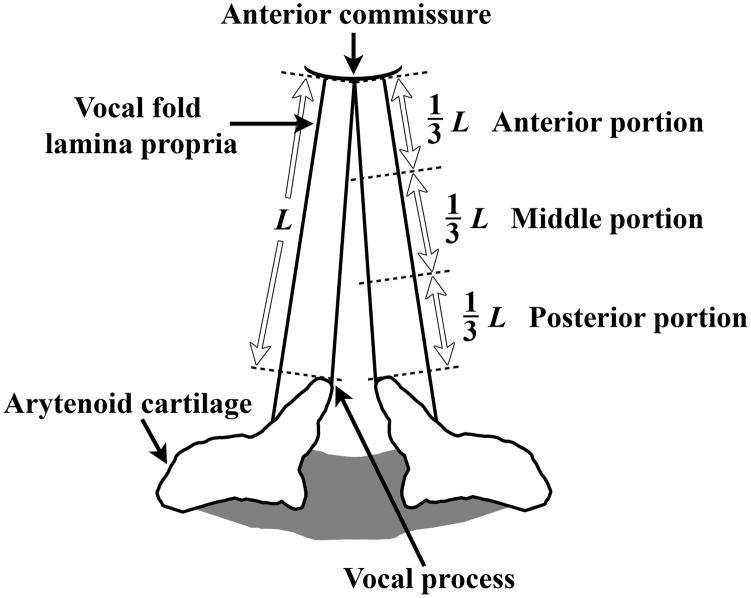
Six excised larynges were harvested from 2-year-old male dogs (average weight 59.1 lbs) immediately postmortem following experiments requiring animal sacrifice for other research purposes (pulmonary experiments). The experimental and euthanization protocols were approved by the Institutional Animal Care and Use Committee of UT Southwestern Medical Center, and was in accordance with the U.S. Public Health Service Policy on Humane Care and Use of Laboratory Animals, the NIH Guide for the Care and Use of Laboratory Animals (NIH Publication #85-23 Rev. 1985), and the Animal Welfare Act (7 U.S.C. et seq.). The larynges were stored in phosphate buffered saline (PBS) solution and immediately transferred to our laboratory, where rheometric experiments were conducted. Phonomicrosurgical instruments were used for dissecting each larynx, with the vocal fold cover (lamina propria) divided into three equal portions, i.e., anterior, middle, and posterior portions, together with the medial TA muscle (vocalis muscle) (Figure 1). Each specimen was subjected to rheometric measurements separately. All anatomic locations were tested for the vocal folds of five larynges, whereas for one larynx only the TA muscle and the middle portion of the vocal fold cover were tested.

Figure 1.

Schematic of the canine vocal fold cover (mucosa or lamina propria), illustrating three distinct anatomic locations for rheometric measurements: anterior portion, middle portion, and posterior portion ( L = length of the membranous vocal fold).

Rheometric instrumentation and experiments

A controlled-strain, linear, simple-shear rheometer system (ELF 3200, Bose Corporation, ElectroForce Systems Group, Eden Prairie, MN) was used for viscoelastic characterization of tissue specimens. As illustrated in Figure 2, a specimen was subjected to a translational simple shear between two parallel, rectangular acrylic tissue plates. With displacement feedback control, the upper plate was attached to the shaft of a linear motor through an actuator, applying a translational displacement (x) to the specimen at prescribed magnitude and frequency. A linear variable differential transformer (LVDT) was used as the displacement transducer for estimation of shear strain of the specimen. The resulting shear force (F) at the lower plate was detected by a piezoelectric force transducer. All mechanical testing was performed in a transparent acrylic environmental chamber, where water at the base of the chamber was heated to maintain the ambient air temperature at around 37°C, with a high relative humidity.

Figure 2.

The principle of linear simple-shear rheometry for quantifying the viscoelastic shear properties of tissue specimens at phonatory frequencies (after Chan and Rodriguez [16]).

The distance between the tissue plates, or gap size (d) of the rheometer was set to be around 0.3 to 0.5 mm, such that there was complete contact between each specimen and the tissue plates with an area of contact smaller than the overlapping area of the tissue plates. A digital camera was mounted directly above the chamber and photos of the specimen mounted between the tissue plates were taken, in order for determination of the area of contact (A) between the specimen and the upper plate through analysis of scaled images of the specimen. A frequency sweep was performed, which involved oscillatory shear deformation of the specimen in small amplitude (at 1.0–2.0 % strain), over a frequency range of 1–250 Hz.

The rheometer was controlled by the Wintest software (Bose Corporation), with data collected for the displacement signal output of the LVDT and the force signal output of the piezoelectric force transducer, digitized at 8196 samples per second. The digitized signals were processed by the Wintest software after the experiments to calculate the amplitudes of the two signals, and the phase shift between them. With these data, the elastic shear modulus (G’) and dynamic viscosity (η’) of the specimen were calculated as functions of frequency, according to the theory of linear viscoelasticity [13, 16].

Results

Viscoelastic shear properties of the canine vocal fold tissue specimens examined, and their variations with anatomic location are displayed in Figures 3 and 4. Figure 3 shows the elastic shear modulus (G’) of three distinct portions of the canine vocal fold cover, in comparison with that of the canine vocalis muscle and with data previously reported for the normal human vocal fold cover [16]. Data are shown across the frequency range of 1–250 Hz on a log-log scale, as a standard display for rheometric measures [13, 16]. The data points represent mean values, with the error bars indicating the standard deviations (only upper error bars are shown to facilitate graphical clarity). Figure 4 shows the dynamic viscosity (η’) of different portions of the canine vocal fold cover and the canine vocalis muscle, again in comparison with the human vocal fold cover [16].

Figure 3.

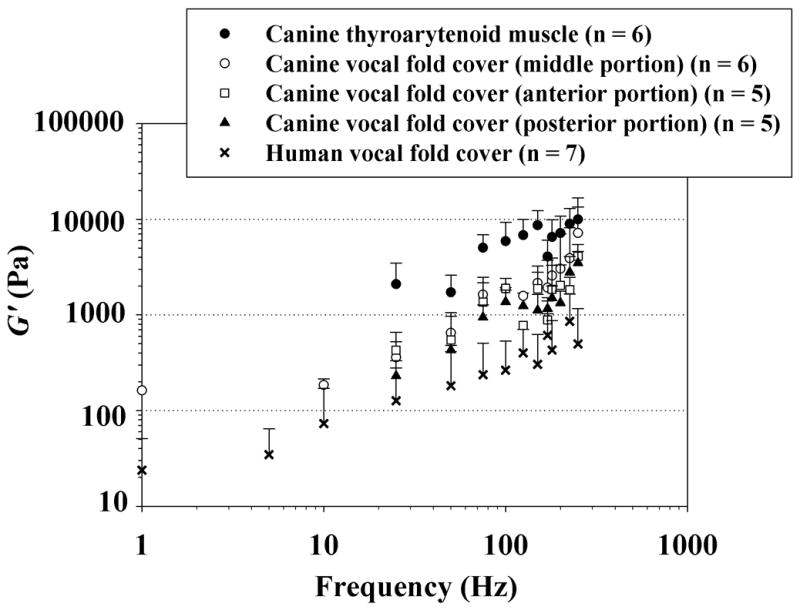
Elastic shear modulus (G’) of the canine vocal fold cover (n = 5 for the anterior and posterior portions; n = 6 for the middle portion), canine vocalis muscle (medial thyroarytenoid muscle) (n = 6), and the human vocal fold cover based on Chan and Rodriguez [16] (n = 7).

Figure 4.

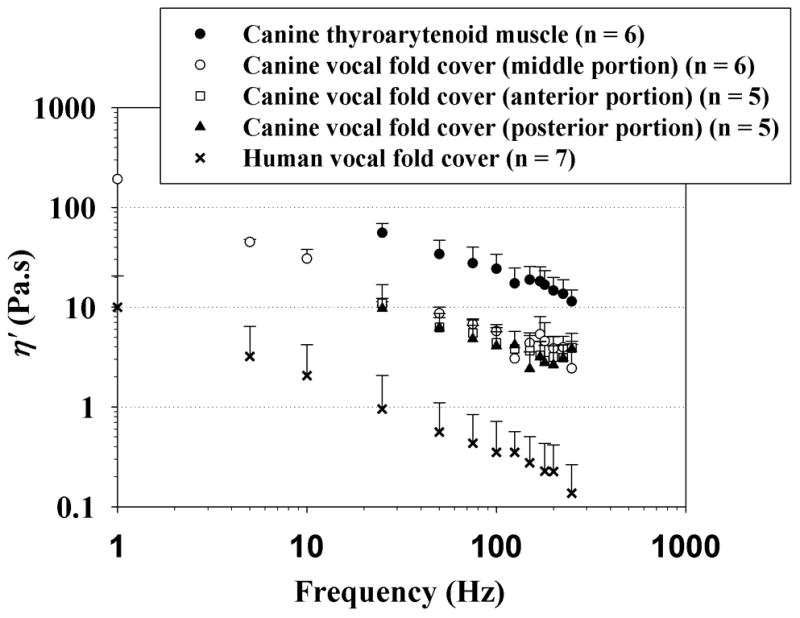
Dynamic viscosity (η’) of the canine vocal fold cover (n = 5 for the anterior and posterior portions; n = 6 for the middle portion), canine vocalis muscle (medial thyroarytenoid muscle) (n = 6), and the human vocal fold cover based on Chan and Rodriguez [16] (n = 7).

It can be seen that a similar frequency dependence of the viscoelastic functions (i.e., similar slope for the curves) was observed for all specimens, with G’ gradually increasing with frequency and η’ decreasing with frequency monotonically. To capture the dependence of G’ and η’ on frequency quantitatively, a power law relationship could be used to parametrize the data, as described in Chan and Rodriguez [16]:

$$G’=a{f}^b\text{or}logG’=loga+\mathit{b}logf$$ (1)

$$\eta ’=a{f}^b\text{or}log\eta ’=loga+\mathit{b}logf$$ (2)

where a and b are coefficients for the parametrization, and f is frequency in Hz. Linear least-squares regression analysis was performed to curve-fit the data to Equations (1) and (2), with the coefficient a indicating the magnitude (level) of the curve and the coefficient b indicating the slope of the curve on the log-log scale. Table 1 shows the results of the curve-fitting, including the coefficients a and b, and the coefficient of determination R ² as a statistical indication of the goodness of fit. Both G’ and η’ were well described by the power law for all specimens, with at least moderately high values of R ².

Table 1.

Results of least-squares regressions for the parametric description of elastic shear modulus (G’) and dynamic viscosity (η’) of the canine vocal fold cover (n = 16); three portions of the canine cover: anterior (n = 5), middle (n = 6), and posterior (n = 5); canine vocalis muscle (n = 6); and the human vocal fold cover [16] (n = 7) according to Equations (1) and (2). R ² is coefficient of determination indicating the goodness of fit.

G’ = a f b	a (Pa.s)	b	R2
Canine vocal fold cover (n = 16)	39.431	0.871	0.797
Canine middle cover (n = 6)	33.366	0.964	0.795
Canine anterior cover (n = 5)	55.997	0.785	0.815
Canine posterior cover (n = 5)	30.144	0.846	0.781
Canine vocalis muscle (n = 6)	233.533	0.766	0.801
Human vocal fold cover (n = 7)	19.736	0.540	0.743

η’ = a f b	a (Pa.s 2)	b	R2
Canine vocal fold cover (n = 16)	76.651	−0.593	0.749
Canine middle cover (n = 6)	99.636	−0.615	0.738
Canine anterior cover (n = 5)	69.670	−0.601	0.834
Canine posterior cover (n = 5)	60.646	−0.562	0.867
Canine vocalis muscle (n = 6)	253.311	−0.535	0.915
Human vocal fold cover (n = 7)	9.718	−0.691	0.927

To determine whether differences in the coefficients a and b among the different anatomic locations were statistically significant or not, one-way analysis of variance (ANOVA) was conducted, with the level of significance (alpha) at 0.05. Results of ANOVA revealed statistically significant differences in the coefficient a among the canine vocal fold cover, canine vocalis muscle, and the human vocal fold cover for both G’ and η’ (p < 0.001), whereas there were no significant differences in the coefficient b among the canine vocal fold cover, canine vocalis muscle, and the human vocal fold cover for both G’ and η’ (p > 0.05) (Table 2). To examine whether they were significantly different from one another in the coefficient a, post-hoc Tukey tests were performed for pairwise comparisons for G’ and η’. For G’, significant differences were found between the canine vocalis muscle and the canine vocal fold cover, and between the canine vocalis muscle and the human vocal fold cover. For η’, Tukey tests showed significant differences between the canine vocalis muscle and both canine and human vocal fold cover, and between the canine and the human vocal fold cover. Since a was a representation of the magnitude whereas b indicated the slope of the best-fit curve, these findings confirmed that there was a similar frequency dependence of G’ and η’ among the canine vocal fold cover, canine vocalis muscle, and the human vocal fold cover, but there were significant differences in the magnitude of G’ and η’ among them. In particular, the magnitudes of G’ and η’ for canine vocalis muscle were significantly higher than those for both the canine and the human vocal fold cover, whereas the canine vocal fold cover showed significantly higher η’ than the human vocal fold cover.

Table 2.

Results of one-way ANOVA for the parametric curve-fitting coefficients a and b, and post-hoc Tukey tests for pairwise comparisons of the coefficient a for elastic shear modulus (G’) and dynamic viscosity (η’) among the canine vocal fold cover (n = 16), canine vocalis muscle (n = 6), and the human vocal fold cover [16] (n = 7).

Viscoelastic function	Parametric coefficient	F (2, 26)	p value
G’	a	9.200	< 0.001
	b	0.719	0.497
η’	a	41.876	< 0.001
	b	3.093	0.063

Pairwise comparisons for G’ (coefficient a)	p value	Pairwise comparisons for η’ (coefficient a)	p value
Canine muscle vs. human cover	0.002	Canine muscle vs. human cover	< 0.001
Canine muscle vs. canine cover	0.002	Canine muscle vs. canine cover	< 0.001
Canine cover vs. human cover	0.845	Canine cover vs. human cover	0.010

Next, one-way ANOVA was performed to examine the differences in the coefficients a and b among the three portions of the canine vocal fold cover (anterior, middle, and posterior), as compared to the human vocal fold cover (Table 3). Results showed significant differences in the coefficient a for η’ (p < 0.001), whereas no significant differences were found in a for G’, nor in b for both G’ and η’ (p > 0.05). Post-hoc Tukey tests were performed to compare the three portions of the canine vocal fold cover with one another and with the human vocal fold cover in terms of the coefficient a for η’ (Table 3). Significant differences in the magnitude of η’ were found between the human vocal fold cover and all portions of the canine vocal fold cover, but not among the different portions of the canine vocal fold cover.

Table 3.

Results of one-way ANOVA for the parametric curve-fitting coefficients a and b for elastic shear modulus (G’) and dynamic viscosity (η’), and post-hoc Tukey tests for pairwise comparisons of the coefficient a for η’ among three portions of the canine vocal fold cover: anterior (n = 5), middle (n = 6), and posterior (n = 5); and the human vocal fold cover [16] (n = 7).

Viscoelastic function	Parametric coefficient	F (3, 18)	p value
G’	a	1.129	0.363
	b	0.549	0.627
η’	a	16.853	< 0.001
	b	1.083	0.381

Pairwise comparisons for η’ (coefficient a)	p value
Human vs. canine cover (middle)	< 0.001
Human vs. canine cover (posterior)	0.005
Human vs. canine cover (anterior)	0.001
Canine cover (middle vs. anterior)	0.197
Canine cover (middle vs. posterior)	0.063
Canine cover (anterior vs. posterior)	0.922

Discussion

The current rheometric data indicated that canine vocal fold tissues, regardless of the anatomic location, showed similar patterns of frequency dependence of the viscoelastic functions, with the elastic shear modulus G’ gradually increasing with frequency and the dynamic viscosity η’ decreasing with frequency monotonically (Figs. 3 and 4). These observations were consistent with those of previous studies on vocal fold viscoelasticity [7, 13, 15, 16], and supported the validity of the power law relationship used for parametric description of the data (Equations 1 and 2). G’ quantifies the elastic energy storage in viscoelastic tissues and is an indication of the tissue stiffness under linear oscillatory shear, whereas η’ quantifies the viscous energy loss in tissues and represents the tissue resistance to linear oscillatory shear [16]. Data on G’ and η’ indicated that the canine vocalis muscle was significantly stiffer and more viscous than the canine vocal fold cover as well as the human vocal fold cover, whereas the canine vocal fold cover was significantly more viscous than the human vocal fold cover (Table 2). Specifically, all three different portions (anterior, middle, and posterior portions) of the canine vocal fold cover were significantly more viscous than the human vocal fold cover, but no significant differences in shear stiffness and viscosity were found among the different portions of the canine vocal fold cover (Table 3). The overall trends of the present data are comparable to previously reported data on viscoelastic shear properties of the canine vocal fold cover at lower frequencies [15]. In particular, the magnitudes of G’ and η’ at 50 Hz were in the same orders of magnitude as those in previous measurements [15].

Kurita et al. reported that the layered structure of the canine vocal fold lamina propria is different from that of human. The canine has essentially a two-layer structure, i.e., cover and body (or vocalis muscle), without a vocal ligament [3]. This is related to the differences in distributions of matrix proteins such as collagen and elastin among the human and canine vocal fold lamina propria. For instance, unlike the human vocal fold, which has a higher elastin concentration in the deeper layers of the lamina propria, the canine vocal fold has a thin band of elastin fibers concentrated just deep to the basement membrane zone in the superficial layer or cover [18]. The canine also has a thicker vocal fold cover due to the absence of the vocal ligament, and vocal fold vibration is likely affected by this difference in geometry as well as the observed differences in viscoelastic shear properties between canine and human. The histological differences in the layered structure of the vocal fold lamina propria among canine and human were consistent with our observation of the canine vocal fold cover being stiffer than the human vocal fold cover, especially at phonatory frequencies (Fig. 3), although the differences in the curve-fitting coefficient a for G’ did not reach statistical significance.

Hyaluronic acid (HA) is a major component of the vocal fold lamina propria and significantly contributes to the regulation of tissue viscosity [19, 20]. An increasing concentration of HA would lead to tissue viscosity increasing in nearly an exponential way until a plateau is reached [21]. Hahn et al. found that the mean HA level in the canine vocal fold was 3–4 times higher than that of human [22], consistent with our observation that the canine vocal fold cover was significantly more viscous than the human vocal fold cover (Fig. 4).

By quantifying the viscoelastic shear properties of different anatomic locations of the vocal fold, it becomes possible for one to precisely define their variations along the length and the depth of the vocal fold, i.e., to define such properties for different parts and layers of the vocal fold in computational models of phonation, specifically in multilayered biomechanical models. This would facilitate the model output to be more physiologically realistic, e.g., in terms of the predictions of vocal fold vibratory behavior, such as the eigenmodes and fundamental frequency of vibration [8, 9]. In particular, the current data indicated that in a relaxed state the vocalis muscle is significantly stiffer and more viscous than the vocal fold cover during vibration at phonatory frequencies, implying that the threshold for large-amplitude vocal fold vibration involving the vocalis muscle is high, i.e., the vocalis muscle would not be easily set into vibration together with the vocal fold cover. Nonetheless, a limitation of the current study is that the TA muscle specimens were examined in vitro, i.e., without any natural muscle tone or tension. In physiologic situations in vivo, the viscoelastic properties (both tensile properties and shear properties) of the vocalis muscle likely change upon muscle activation and changes in length and tension during vocal fold posturing. Further studies on the viscoelastic properties of the vocalis muscle at different levels of muscle activation would be required to provide data on this issue.

Conclusion

The results of this rheometric study indicated that the canine vocalis muscle, while in a relaxed state in vitro, was significantly stiffer and more viscous than the canine vocal fold cover, as well as the human vocal fold cover. The anterior, middle, and posterior portions of the canine vocal fold cover were all significantly more viscous than the human vocal fold cover, but no significant differences in tissue stiffness and viscosity were observed among the different portions of the canine vocal fold cover. As phonation threshold pressure is directly related to the tissue viscosity of the vocal fold [6], these results suggested that it may be more difficult to set the canine vocal folds into vibration when compared to human, particularly for large-amplitude vocal fold vibration involving the vocalis muscle. Distinct differences in viscoelastic shear properties of different anatomic locations of the vocal fold should be taken into account in defining multilayered biomechanical models of phonation.