Imputation methods for doubly censored HIV data

Abstract

In medical research, it is common to have doubly censored survival data: origin time and event time are both subject to censoring. In this paper, we review simple and probability-based methods that are used to impute interval censored origin time and compare the performance of these methods through extensive simulations in the one-sample problem, two-sample problem and Cox regression model problem. The use of a bootstrap procedure for inference is demonstrated.

1. Introduction

Most statistical methods developed for the analysis of event time data assume that the origin time is known, but allow the event to be censored. Data that are censored both at the origin and at the event time are referred to as doubly censored data. HIV studies have provided many examples for doubly censored data. In this paper, we are interested in the distribution of time from HIV infection to death. The exact time of HIV infection is usually interval censored and death is subject to right censoring. This is the doubly censored situation considered here. However, that the term ‘doubly censored data’ is also used for situations where both the origin and the event time are interval-censored, for example, in De Gruttola and Lagakos [1] and Sun [2].

Doubly censored data can, in principle, be analysed using a maximum likelihood approach, but this approach can be challenging, both numerically and theoretically, particularly when covariates are involved. Maximum likelihood has been applied to the regression analysis of doubly censored data in Kim et al. [3], with both origin and event time being interval censored, using the discrete proportional hazards model. For the continuous proportional hazards model, Sun et al. [4] propose an estimating equation procedure to estimate the regression parameters and show that the estimator is asymptotically unbiased and normally distributed. The procedure is difficult to implement and can be intractable when the sample size is large. In addition, the method is challenging to implement when the covariates are interval censored, as is the case in our motivating example of Xiang et al. [5]. In contrast, if the origin time (HIV infection time) can be imputed reasonably, the missing value of the covariate for this study (age at the time of HIV infection) will be imputed simultaneously, then the analysis of doubly censored data with imputation is a straightforward analysis of the right-censored data.

Imputation is a general method for missing-data problems. One simple approach is to impute infection time using the right limit of the interval in which the infection time is censored. This typically corresponds to the date of diagnosis or to the date of study entry, and is expedient when no negative diagnostic test precedes the first positive test, as in Xiang et al. [5] and Tillmann et al. [6]. Another common approach is to impute infection time using the midpoint of the interval [7–9]. Law and Brookmeyer [10], however, have shown that, under certain distributional assumptions consistent with the data from the studies of HIV disease, Kaplan–Meier estimates of survival based on this method are considerably biased when censoring intervals are longer than two years. Yet another method of imputation is by the left limit of the interval. In many HIV studies, however, including our motivating example, the left limit may correspond to either date of birth or a date before the HIV epidemic emerged, and in this case the left-point imputation is likely to be unreasonable. For this reason, the left-limit imputation is not included in the following sections.

Other imputation methods impute the infection time of a subject based on Ĝ, an estimate of the marginal distribution G of HIV infection time. For example, Gauvreau et al. [11] adopt the self-consistency algorithm of Turnbull [12] to estimate G, and then impute the expected infection time based on Ĝ conditional on the subject’s interval. Goggins et al. [13] suggest a Monte Carlo EM algorithm to estimate G, and then repeatedly impute infection times based on random draws from Ĝ conditional on the subjects’ intervals. The estimated distribution of HIV infection time, Ĝ, is treated as if known when imputing infection times.

Pan [14] uses the approximate Bayesian bootstrap scheme [15,16] to take B bootstrap samples D^b from the original data D, b = 1, …, B, then obtain Ĝ_b using the self-consistency algorithm, and then repeatedly impute B infection times based on random draws from Ĝ_b, b = 1, …, B. Finally, the results are combined using Rubin’s multiple imputation (MI) formula [17]. Geskus [18] compares the midpoint imputation, the conditional mean imputation, and MI methods for the bias and mean-squared error (MSE) of the estimator of Kaplan–Meier curves. In his simulation study, under some distributional assumptions for one-sample data, the conditional mean imputation stands out as the preferred method.

In Section 2, both simple imputations and probability-based imputations are outlined, and the MI inference procedure and bootstrap inference procedure are introduced. In Sections 3 and 4, simulations are described and the numerical performance of the different imputation methods is compared. Section 5 presents conclusions and further discussion.

2. Imputation methods

For simplicity, let HIV infection be the origin event and death the endpoint event. Let X_i and Y_i denote HIV infection time and death time for subject i, i = 1, …, n. Assume X_i is interval censored X_i ∈ [L_i, R_i]. We assume Y_i is possibly right censored as in Sun et al. [4], Goggins et al. [13], and Pan [14]. Imputation methods can be classified into simple imputation methods and probability-based imputation methods.

2.1. Simple imputation methods

Right-point imputation refers to imputing the infection time by the right limit R_i of the interval and is denoted by RIGHT; midpoint imputation refers to imputing the infection time by the midpoint of the interval [L_i, R_i] as (L_i + R_i)/2 and is denoted by MID. When HIV infection and death both occur between two successive screening tests, that is L_i < X_i < Y_i < R_i, the MID uses midpoint of the interval [L_i, Y_i] as the infection time.

2.2. Probability-based imputation methods

Probability-based imputation requires estimating the distribution G for HIV infection time X_i based on observed intervals. The non-parametric maximum likelihood estimator (NPMLE) of G with interval censored data is fully developed in the statistical literatures. Groeneboom and Wellner [19] characterize the NPMLE and propose an iterative convex minorant algorithm for computing the estimate. Turnbull [12] proposes a self-consistency algorithm which can be realized as an application of the EM algorithm introduced by Dempster et al. [20]. The details of these algorithms can be found in Sun [21]. Turnbull’s self-consistency algorithm is used throughout this paper due to its simplicity of implementation.

Assume that the infection time X is a discrete random variable with a set of possible values x = {x₁, x₂, …, x_m} associated with a set of probabilities g = (g₁, g₂, …, g_m), respectively, where x₁ < x₂ < … < x_m. Suppose for subject i, there are r_i possible values of infection time y_i = (y_i1, …, y) ∈ [L_i, R_i] associated with probabilities p_i = (p_i1, …, p_iri), i = 1, …, n. Note that both y_i and p_i are subsets of x and g, respectively. Let h_i = (h_i1, …, h_iri), the conditional probability for subject i taking the value is y_ik is $h_{ik}=p_{ik}/{\sum }_{q=1}^{r_i}{p}_{iq}$, k = 1, …, r_i, conditioning on the interval [L_i, R_i] and g.

Conditional mean imputation has been previously used [11,18] but conditional median and conditional mode appear to be new methods for imputation.

2.2.1. Conditional mean imputation (MEAN)

For subject i, the expected time of infection is $E(X_i\mid X_i\in [L_i,R_i],\mathbf{g})={\mathbf{y}}_{\mathbf{i}}{\mathbf{h}}_{\mathbf{i}}^{\prime }$. Therefore, infection time X_i can be imputed by ${\mathbf{y}}_{\mathbf{i}}{\mathbf{h}}_{\mathbf{i}}^{\prime }$.

2.2.2. Conditional median imputation (MEDIAN)

Infection time X_i is imputed by the median of y_i weighted by the probability vector h_i. In case the median is not unique, X̂_i is taken as the average of medians.

2.2.3. Conditional mode imputation (MODE)

Infection time X_i is imputed by the mode of y_i: the value corresponding to the maximum probability among h_i. That is X̂_i = y_ik, where k =max_1≤k≤ri {ĥ_ik}. In case the mode is not unique, X̂_i is taken as the average of modes.

2.2.4. Multiple imputation

MI is a commonly used method. For m = 1, …, M, randomly sample $y_{ik}^m$ from y_i with replacement using the conditional probability vector h_i as weight. Let D denote the original data set with interval-censored origin event, D̂^m denote the data set that replaces the interval censored origin event by the mth imputation. Then D̂^m is analysed using the regular right censored data method. Let θ̂_m be the estimate of the parameter of interest obtained from the mth imputed data set D̂^m, m = 1, …, M. The MI estimate of θ is ${\overline{\theta }}_M=(1/M){\sum }_{m=1}^M{\widehat{\theta }}_m$.

2.2.5. Random imputation (RAND)

Randomly sample one value of y_ik from the vector y_i using the conditional probability vector h_i as weight. Then the infection time X_i is imputed by y_ik. This is a special case of MI, where M = 1.

2.3. Bootstrap inference procedure

The imputation methods in the previous section provide ways to estimate population parameters of interest for doubly censored data. To derive standard errors, Rubin’s variance estimation formula [17] has been used in MI inference [14,22,23]. The formula adds an expression for between-imputation variance to an expression for average within-imputation variance, to incorporate imputation uncertainty. An alternative bootstrap inference procedure for doubly censored data is introduced here.

Suppose B bootstrap samples D^b, b = 1, …, B, are generated from the doubly censored data D. An estimate θ̂ of parameter θ is computed based on the imputed data D̂ by imputing infection times using a method described in Sections 2.1 and 2.2. A 100(1 − α)% empirical bootstrap confidence internal (EBCI) of θ for the chosen imputation procedure is given by [θ̂^l, θ̂^u], where θ̂^l and θ̂^u are the empirical 100(α/2) and 100(1 − α/2) percentiles of the bootstrap distribution of θ̂ [24].

Since estimation with right-censored data consumes very little in computing time, the bootstrap procedure for doubly censored data described above will not be computationally intensive, making it potentially attractive in practice.

2.4. Motivating example

Xiang et al. [5] examined the effect of co-infection with GBV-C virus on the survival of HIV-infected patients. The data set is doubly censored in that the origin time (HIV infection) is interval censored and the endpoint event (death) is right censored. The date of subjects’ first known positive HIV test is used as the right limit of the interval: the right limit ranges from 1988 to 1999. 1 January 1978 (or date of birth for subjects born after 1 January 1978) is treated as the left limit of the interval, because it is reasonable to assume that no HIV infections occurred prior to 1 January 1978 in this population [25]. The data set has 362 subjects with mean interval width of 11.4 years.

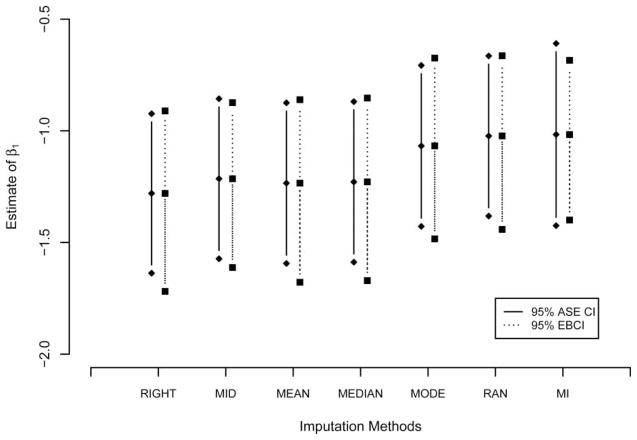
We applied all seven imputation methods described in Section 2. Results are summarized in Figure 1. The estimate of β₁, log(hazard ratio) of GBV-C co-infection, varies from − 1.0 to − 1.3 based on different imputation methods. For all but MI the 95% asymptotic standard error (ASE) CI of β₁ is the confidence interval based on the ASE of β₁ from the Cox model, treating imputed date as if it were known. The 95% ASE CI underestimates the variability of β₁ by ignoring the imputation uncertainty and the 95% EBCI is wider than the 95% ASE CI for every imputation method except for MI. In MI, an ASE is computed based on Rubin’s variance formula [17] to attempt to account for imputation uncertainty and only in this case is the 95% ASE CI wider than the 95% CI.

Figure 1.

Estimate of Cox regression coefficient for the Xiang study by seven imputation methods.

To assess the performance of point estimates based on these seven imputation methods and the validity of using bootstrap inference for doubly censored data, simulation studies are implemented. Section 3 describes the design of the simulations, and Section 4 presents the results.

3. Simulation design

Simulation studies are designed: (1) to evaluate the Kaplan–Meier estimator in the one-sample problem, (2) to evaluate the size and power of the logrank test in the two-sample problem and also a new bootstrap-based test which is introduced in Section 4.2, and (3) to evaluate the regression coefficient estimate from the Cox proportional hazards model [26] adjusting for an interval-censored covariate (to be consistent with the motivating example), based on seven imputation methods. We also assess the validity of the bootstrap inference procedure through simulation studies.

Distributions for the infection time X and the subsequent survival time T are the key parts of simulation studies for doubly censored data. Law and Brookmeyer [10] assume a log-logistic distribution for HIV infection time X with restriction X ∈ [1978, 1986] (subjects involved in their study were exposed to HIV from early 1978 to mid-1985) and a Weibull distribution W (2.51, 11.66) for survival time T, to evaluate the effect of midpoint imputation on the Kaplan–Meier estimator and logrank test. In a study to assess the effect of a binary covariate using the Cox model, Goggins et al. [13] adopt a log-normal distribution LN(3.8, 0.3) for X, and simulate survival time T₁ for one group from W (2.5, 70.1) and survival time T₂ for another group from W (2.5, 60) so that the logarithm of hazard ratio β₁ is 0.389. This mimics the haemophilia data described by Kim et al. [2]. To investigate RIGHT, MID, and MEAN imputation methods for Kaplan–Meier estimator, Geskus [18] specifies a shifted log-logistic distribution for the infection time X, X ∈ [1980, 1997] and W (2, 11) for survival time T. Pan [14] uses a similar simulation design to that in Goggins et al. [13].

3.1. Distribution for X and interval censoring

The variable X is simulated from a log-normal distribution as in Goggins et al. [13] and Pan [14], and is truncated with an upper limit of 65 and with parameters chosen so that the simulated data are similar to the real data in Xiang et al. [5]. Specifically, X is distributed as log-normal LN(3.55, 0.24) and truncated to [0, 65]. To mimic screening studies, we simulate a subject’s first visit as a random number from a uniform distribution U (0, 5). After the first visit, each subject is scheduled to have annual follow-ups. Whether or not a subject completes each annual follow-up is modelled as an independent Bernoulli variable. The probability of making an annual visit P can be tuned to result in intervals with specified average censoring width of w years for X. A subject’s HIV infection time X_i is accordingly censored between two consecutive visits, X_i ∈ [L_i, R_i], i = 1, …, n. These intervals are then used to obtain an NPMLE Ĝ of G using Turnbull’s self-consistency algorithm. For convenience, we refer to the simulation setting described here as the G_A setting.

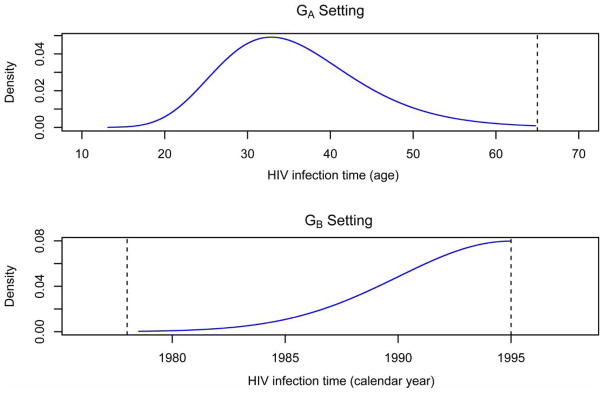
Suppose HIV-positive subjects entered the HIV study before the year 1995. Given HIV infections before 1978 are extremely rare [25] it is reasonable to assume the HIV infection time X is between 1978 and 1995. The HIV infection time X is simulated from a truncated normal distribution N(1995, 5) with upper limit 1995. Assume that for half of the subjects, we are able to establish intervals for HIV infection time based on their annual seronegative tests. For these subjects, censoring intervals are generated using the algorithm described in the above paragraph. The NPMLE Ĝ for the distribution of X is estimated using only these subjects. For the other half of the subjects, it is known that they were HIV-positive only at the time of entry. If an individual was born before 1978, we use 1978 as the left limit, otherwise we use his/her birth year as this person’s left limit. For convenience, we refer the simulation setting described here as the G_B setting. Table 1 summarizes both G_A and G_B settings, and Figure 2 portrays the distribution of X in these two settings.

Table 1.

Two simulation settings: G_A and G_B.

Specifications	GA setting	GB setting
Sample size	n	n
Dist. of X	LN(3.55, 0.24)	N(1995, 5)
Range of X	X ∈ [0, 65]	X ∈ [1978, 1995]
NPMLE Ĝ	based on n intervals	based on n/2 intervals
Dist. of T
One-sample	W (2, 10)	W (2, 10)
Two-sample	(1) W (2, 10) vs. W (2, 12.84)	W (2, 10) vs. W (2, 12.84)
	(2) LN(2.2, 04) vs. LN(2.4, 0.4)	LN(2.2, 04) vs. LN(2.4, 0.4)
Cox model	W (2, 10 · exp(−zβ/2))	W (2, 10 · exp(−zβ/2))
Right censoring for T	10%	10%

Figure 2.

True distribution for HIV infection time X in two simulation settings.

3.2. Distribution for T and right censoring

For the one-sample problem, the survival time T is simulated from a Weibull distribution W (2, 10). For the two-sample problem, a binary covariate is used to indicate group membership. T is simulated from two different distributions for two groups with equal sample size n/2. Distributions considered for the two groups include Weibull W (2, 10) vs. W (2, 12.84), and log-normal LN(2.2, 0.4) vs. LN(2.4, 0.4). To compare the size of a test resulting from different imputation methods, T is simulated from the same distribution for the two groups with equal sample size n/2, either W (2, 10) or LN(2.2,0.4).

For the Cox regression problem, survival time T is simulated from the distribution W (γ, λ) where λ = λ₀ · exp(−zβ/γ), resulting in a proportional hazards model with log (H R) = β. To mimic the study by Xiang et al., we let z = (z₁, z₂) denote the GBV-C co-infection (yes/no) and age at HIV infection, respectively, with corresponding coefficients β = (β₁, β₂) = (−0.5, 0.1). We set γ = 2 and λ₀ = 10.

In all scenarios, a censoring random variable C is simulated from W (γ, a · λ), where a is a positive coefficient. As in Goggins et al. [13], Sun et al. [4] and Pan [14], the survival time T is subject to right censoring. The coefficient a can be tuned so that Pr(T ≤ C) = 0.9, that is T is subject to 10% random right-censoring.

For each problem, 1000 independent doubly censored data sets are repeatedly simulated. For each simulated data set, 1000 bootstrap data sets are generated to obtain the 95% EBCI for the parameter of interest. Specifically, in the one-sample problem, the pointwise 95% EBCI for the survival function is calculated; in the Cox regression model, the 95% EBCI for β₁ is constructed. To facilitate comparison, the results based on the data with exact HIV infection time X and the right-censored survival time T are also included (these data are refered to as exact data). With MI for the missing data problems, Rubin [17, p. 114] shows that in most situations there is little advantage in producing and analysing more than a few imputed data sets, and claims that only 3–10 imputations may be needed. For the doubly censored data, Pan [23] suggests that M = 5 or M = 10 would suffice. We use M = 10 for the MI method. The RAND method corresponds to M = 1.

4. Simulation results

4.1. One-sample problem

The survival probability S(t) at 2.5, 5, 7.5, and 10 years after HIV infection is estimated by the Kaplan–Meier estimator, using different imputation methods to impute the infection time X. The probability of making an annual visit is chosen to be P = 0.3, which results in an average interval width about 5.3 years. Seven imputation methods are compared with respect to bias, mean squared error (MSE) and coverage probability of 95% EBCI.

Table 2 summarizes results for the Kaplan–Meier estimator of survival function for n = 200 in the G_A and G_B settings, with the results for the G_B setting displayed in parentheses. The true values for the S(t) at (2.5, 5, 7.5, 10) years after HIV infection are (0.94, 0.78, 0.57, 0.37), respectively. In the G_A setting, all imputation methods give similar bias and MSE except RIGHT for which the bias and MSE is much larger. All imputation methods except the methods RIGHT and MI give acceptable coverage probability of 95% EBCI. Methods MID and MEAN have the smallest biases, followed by MEDIAN. MEAN has smaller bias than MID in the early years, but MID has smaller bias at, and after 7.5 years. MID, MEAN, and MEDIAN have comparable MSEs to that of the exact data. In the G_B setting, the probability-based imputation methods perform better than the simple imputation methods for the Kaplan–Meier estimator in terms of bias, MSE, and coverage probability of 95% EBCI. Indeed, both RIGHT and MID work badly for the G_B setting.

Table 2.

Comparison of imputation methods for the Kaplan–Meier estimator with heavy interval censoring.

Imputation	Years after HIV infection
	2.5	5	7.5	10
	S(t) = 0.9394	0.7788	0.5698	0.3679
	Bias ×102
EXACT	0.00 (0.05)	−0.05 (0.05)	0.01 (−0.02)	−0.16 (−0.07)
RIGHT	18.85 (13.92)	21.31 (16.85)	18.97 (15.63)	14.23 (11.98)
MID	−0.22 (−3.30)	0.26 (−11.55)	−0.65 (−21.11)	−1.59 (−25.46)
MEAN	−0.15 (−2.17)	0.02 (−4.71)	−1.12 (−7.29)	−1.99 (−7.61)
MEDIAN	0.43 (−0.95)	0.09 (−2.63)	−1.26 (−4.62)	−2.28 (−5.08)
MODE	2.29 (2.75)	0.89 (1.37)	−1.35 (−1.24)	−2.95 (−3.13)
RAND	2.42 (0.43)	1.16 (−2.73)	−1.02 (−6.18)	−2.91 (−7.91)
MI	2.44 (0.54)	1.12 (−2.77)	−1.15 (−6.27)	−2.87 (−8.01)
	MSE ×102
EXACT	0.03 (0.03)	0.09 (0.09)	0.14 (0.13)	0.13 (0.12)
RIGHT	3.65 (2.02)	4.68 (2.97)	3.73 (2.57)	2.12 (1.54)
MID	0.03 (0.12)	0.08 (1.38)	0.14 (4.52)	0.16 (6.58)
MEAN	0.03 (0.07)	0.09 (0.30)	0.15 (0.67)	0.18 (0.72)
MEDIAN	0.03 (0.04)	0.09 (0.17)	0.15 (0.36)	0.19 (0.41)
MODE	0.10 (0.15)	0.12 (0.27)	0.19 (0.46)	0.25 (0.62)
RAND	0.10 (0.03)	0.10 (0.16)	0.15 (0.51)	0.22 (0.77)
MI	0.08 (0.02)	0.08 (0.14)	0.12 (0.50)	0.19 (0.75)
	Coverage probability of 95% EBCI
RIGHT	0.0 (0.0)	0.0 (0.1)	0.1 (0.9)	1.2 (5.1)
MID	91.7 (22.8)	94.7 (0.1)	92.3 (0.0)	90.7 (0.0)
MEAN	97.8 (70.2)	96.3 (62.3)	93.6 (47.8)	90.2 (45.4)
MEDIAN	99.2 (94.6)	97.6 (86.2)	94.0 (76.1)	90.6 (72.0)
MODE	96.3 (99.7)	99.0 (99.8)	98.0 (99.2)	93.3 (98.5)
RAND	89.7 (98.9)	97.3 (85.2)	95.3 (56.5)	88.3 (38.6)
MI	74.3 (93.8)	94.6 (81.8)	92.2 (51.4)	84.4 (33.1)

Note: Numbers not in parenthesis are based on G_A setting; numbers in parenthesis are based on G_B setting. Sample size n = 200, 1000 simulated data sets, and 1000 bootstraps per simulated dataset.

4.2. Two-sample problem

Let F₁ and F₂ be the distribution functions for groups 1 and 2, respectively. For the right-censored data, under the null hypothesis H₀: F₁ = F₂, the logrank test statistic S is asymptotically a standard normal N(0, 1) random variable. There are two tests for which the power and size can be estimated. One is for the regular logrank test by ignoring the fact that the origin time is imputed. The second is a new test that incorporates the double censoring, where the asymptotic distribution of the logrank statistic S is not known. The latter test is based on the bootstrap empirical distribution of the logrank statistic. For convenience, we call the latter the empirical logrank (ELR) test. The power for the ELR test is defined as the probability that the 100(1 − α)% EBCI of S exclude 0, based on the data simulated under an alternative hypothesis H₁: F₁ ≠ F₂. The size for the ELR test is defined as the probability that the 100(1 − α)% EBCI of S exclude 0, based on the data simulated under the null hypothesis H₀.

The results for power and size comparison in the G_A and G_B settings are shown in Table 3. In the G_A setting, the probability of making an annual visit P is set as 0.3 for both groups resulting in a mean interval width w = 5 years for each group. For each imputation method, the power of the ELR test and of the regular logrank test is similar. The power based on MODE and RAND tends to be smaller than that from the other imputation methods. Overall, the loss in power using MEAN imputation is negligible compared to the EXACT approach where the original time is known. The size of the logrank test is close to the 5% nominal level. The size of the ELR test is also close to the 5% nominal level, except that the size based on MODE or RAND tends to be lower than nominal. Overall, the size of both tests based on MEDIAN is closer to the 5% nominal level than that of other imputation methods.

Table 3.

Comparison of imputation methods for power and size of two-sample tests with heavy interval censoring.

Distribution of T			Imputation methods
	Test	EXACT	RIGHT	MID	MEAN	MEDIAN	MODE	RAND	MI
	Power
W (2, 10) vs. W (2, 12.84)	Logrank	0.895	0.872	0.871	0.868	0.865	0.851	0.845	0.877
	ELR	–	0.871	0.866	0.871	0.860	0.844	0.862	0.874
	Logrank	(0.911)	(0.892)	(0.809)	(0.893)	(0.899)	(0.845)	(0.836)	(0.894)
	ELR	(−)	(0.892)	(0.814)	(0.892)	(0.894)	(0.858)	(0.856)	(0.892)
LN (2.2, 0.4) vs. LN(2.4, 0.4)	Logrank	0.882	0.800	0.828	0.833	0.823	0.776	0.778	0.821
	ELR	–	0.804	0.828	0.825	0.807	0.754	0.783	0.820
	Logrank	(0.889)	(0.844)	(0.727)	(0.851)	(0.862)	(0.784)	(0.760)	(0.836)
	ELR	(−)	(0.849)	(0.722)	(0.850)	(0.847)	(0.791)	(0.784)	(0.847)
	Size
W (2, 10) vs. W (2, 10)	Logrank	0.048	0.043	0.054	0.054	0.054	0.061	0.050	0.055
	ELR	–	0.048	0.052	0.056	0.047	0.041	0.043	0.053
	Logrank	(0.054)	(0.052)	(0.037)	(0.052)	(0.053)	(0.057)	(0.058)	(0.053)
	ELR	(−)	(0.050)	(0.036)	(0.054)	(0.052)	(0.041)	(0.035)	(0.056)
LN (2.2, 0.4) vs. LN(2.2, 0.4)	Logrank	0.043	0.056	0.055	0.056	0.051	0.054	0.057	0.052
	ELR	–	0.063	0.060	0.059	0.048	0.039	0.039	0.057
	Logrank	(0.042)	(0.047)	(0.026)	(0.040)	(0.038)	(0.047)	(0.036)	(0.042)
	ELR	(−)	(0.050)	(0.023)	(0.036)	(0.031)	(0.029)	(0.023)	(0.037)

Note: Numbers not in parenthesis are based on G_A setting; numbers in parenthesis are based on G_B setting. Sample size n = 200, 1000 simulated data sets, and 1000 bootstraps per simulated dataset.

In the G_B setting, the probability of making an annual visit P is again 0.3 but for half of subjects, the other half having the left limit of the interval being 1978. The power of the ELR test is similar to that of the logrank test. Overall, the power based on the MEDIAN and MEAN is greater than the one based on other imputation methods. The MID, MODE, and RAND methods perform worst in terms of power. The size of the logrank test based on the MID method is lower than nominal. The size of the ELR test based on MID, MODE, and RAND methods is also low.

In the case where the mean interval width w is 2.1 years (P = 0.65) for both groups in the G_A setting (see Table 4 of the technical report by Zhang et al. [27]), the power of each imputation method is closer to the test with exact data comparing to the scenario where mean interval width is about 5 years. This is reasonable since more information is lost in the case of heavy interval censoring for origin event. The sizes of the ELR test and the regular logrank test are comparable and close to the 5% nominal level.

4.3. Cox regression problem

For doubly censored data with interval-censored HIV infection time X, once X is imputed using the imputation methods described in Section 2, we can make inference based on the methods for the right-censored data. If we regard the date of birth as time 0, then the HIV infection time X can be treated as age at HIV infection. For subject i, let X_i, z_2i, and T_i denote the HIV infection time, age at HIV infection, and time from HIV infection to death, respectively, for i = 1, … n. Let X̂_i denote the imputed HIV infection time for subject i regardless of the imputation methods. Since the HIV infection time X is interval-censored, so is age at HIV infection z₂. Once X is imputed as X̂, z₂ is estimated by ẑ₂ = X̂. The survival time of interested T_i is then estimated by ${\widehat{T}}_i=T_i^{\ast }+R_i-{\widehat{X}}_i$, where $T_i^{\ast }$ is the time from study entry to event. The performance of β̂₁, the estimator of Cox regression coefficient β₁ after adjusting for z₂, is of interest.

The results for the G_A and G_B settings with β = (−0.5, 0.1) and heavy interval censoring (mean interval width w = 5.3 years) for HIV infection time are summarized in Table 4. In the G_A setting, the estimator of β₁ is a little biased (towards 0) for all seven imputation methods with the bias percentage ranging from 1.2–4.3%. The method MID has the smallest bias, followed by the RIGHT, MEAN, MODE, and MEDIAN. The estimator based on RAND and MI has relatively larger bias. These results are based on the same 1000 simulated data sets for each of the seven imputation methods. Treating each simulated data as a block, a two-way ANOVA can be carried out to test for differences among biases of the seven imputation methods. Overall, biases of seven imputation methods differ significantly (F_6,6×999 = 37.69, p < 0.001). The bias using the MID method is significantly smaller than the bias based on any other imputation method (p < 0.001). The mean ASE of β̂₁ based on the MI is slightly larger than those based on other imputation methods, since it incorporates the between-imputation variability using Rubin’s variance formula [17]. There are some differences (F_6,6×999 = 2.61, p = 0.016) among the MSEs of the seven imputation methods but the differences are small. Table 4 gives coverage probability, power, and size for testing β₁ = 0 based on two different estimation procedures. The first is based on the asymptotic standard error using the normality assumption of β̂₁. The second is based on the 2.5 and 97.5% empirical bootstrap quantiles. All seven imputation methods work reasonably well. For the method MI, the coverage probability of 95% ASE CI is slightly bigger than 0.95; the ASE power is the smallest one; and the ASE size is below the 5% nominal level.

Table 4.

Comparison of imputation methods for β = (−0.5, 0.1) under the Cox model with heavy interval censoring.

	EXACT	Imputation methods
		RIGHT	MID	MEAN	MEDIAN	MODE	RAND	MI
Mean of β̂1	−0.5036 (−0.5021)	−0.4832 (−0.4897)	−0.4938 (−0.4764)	−0.4829 (−0.4919)	−0.4813 (−0.4920)	−0.4823 (−0.4838)	−0.4792 (−0.4845)	−0.4786 (−0.4849)
SD(β̂1)	0.1569 (0.1606)	0.1578 (0.1589)	0.1600 (0.1614)	0.1569 (0.1596)	0.1561 (0.1597)	0.1590 (0.1610)	0.1585 (0.1619)	0.1554 (0.1568)
Mean ASE(β̂1)	0.1554 (0.1553)	0.1552 (0.1552)	0.1553 (0.1553)	0.1551 (0.1553)	0.1551 (0.1553)	0.1552 (0.1553)	0.1551 (0.1553)	0.1585 (0.1605)
MSE	0.0246 (0.0258)	0.0252 (0.0253)	0.0256 (0.0266)	0.0249 (0.0255)	0.0247 (0.0256)	0.0256 (0.0262)	0.0255 (0.0264)	0.0246 (0.0248)
Coverage of 95% CI (ASE)	0.949	0.943	0.946	0.952	0.953	0.940	0.948	0.957
Coverage of 95% EBCI	–	0.938	0.944	0.948	0.949	0.955	0.953	0.942
Coverage of 95% CI (ASE)	(0.942)	(0.947)	(0.944)	(0.945)	(0.945)	(0.949)	(0.935)	(0.956)
Coverage of 95% EBCI	(−)	(0.947)	(0.943)	(0.945)	(0.947)	(0.949)	(0.949)	(0.940)
Power (ASE)	0.904	0.881	0.882	0.876	0.878	0.882	0.864	0.861
Power (EBCI)	–	0.890	0.887	0.884	0.880	0.875	0.877	0.885
Power (ASE)	(0.912)	(0.903)	(0.870)	(0.901)	(0.903)	(0.890)	(0.887)	(0.883)
Power (EBCI)	(−)	(0.912)	(0.872)	(0.908)	(0.906)	(0.898)	(0.899)	(0.909)
Size (ASE)	0.044	0.048	0.052	0.052	0.052	0.056	0.048	0.040
Size (EBCI)	–	0.059	0.060	0.057	0.055	0.052	0.054	0.059
Size (ASE)	(0.060)	(0.062)	(0.053)	(0.064)	(0.064)	(0.055)	(0.061)	(0.042)
Size (EBCI)	(−)	(0.065)	(0.053)	(0.062)	(0.066)	(0.051)	(0.055)	(0.060)

Note: Numbers not in parenthesis are from G_A setting; numbers in parenthesis are from G_B setting. Sample size n = 200, 1000 simulated data sets, and 1000 bootstraps per simulated dataset.

In the G_B setting, the estimator of β₁ also shows some bias towards 0 for all seven imputation methods. The estimate β̂₁ based on any imputation method is small with the bias percentage ranging from 1.6–4.7%. The method MID has the largest bias; the methods MEAN and MEDIAN have the smallest biases. Overall, there are significant differences between the seven imputation methods in biases (F_6,6×999 = 41.95, p < 0.001). The bias using the MID method is significantly larger than the bias based on any other imputation method (p < 0.001). Again, the mean ASE of β̂₁ based on MI is slightly bigger than the one based on other imputation methods. There are significant differences (F_6,6×999 = 4.92, p < 0.001) among the MSEs based on the seven imputation methods. All imputation methods work reasonably well for the coverage probability of 95% CI, power, and size. For the method MI, the coverage probability of 95%ASE CI is slightly bigger than 0.95; the ASE power is the smallest one except MID; and the ASE size is below the 5% nominal level.

In the scenario G_A with light interval censoring for HIV infection time (w = 2.1 years, see Table 6 of the technical report by Zhang et al. [27]), the bias of β̂₁ shrinks for every imputation method, resulting in bias percentage ranging from 1–2%. In the scenario G_B with light interval censoring for HIV infection time (w = 2.1 years, see Table 7 the technical report), the bias of β̂₁ also shrinks for every imputation method, resulting in bias percentage ranging from 0.5–4.3%.

5. Discussion

In the one-sample scenario, the method RIGHT does not perform well in terms of estimating the Kaplan–Meier curve. The method MID works very well in the G_A setting, but fails in the G_B setting, when half of the left limits of the interval correspond to the date 1978. Caution is therefore suggested in using simple imputation methods to impute the actual HIV infection time. The probability-based imputation methods perform well for estimating the Kaplan–Meier curve in both simulation settings. Methods MEDIAN and MODE stand out as preferred ones in estimating the Kaplan–Meier curve.

In the two-sample scenario, the regular logrank test and ELR test perform similarly in terms of power and size regardless of imputation methods. Methods MEAN and MEDIAN are recommended for their robust performance in both simulation settings.

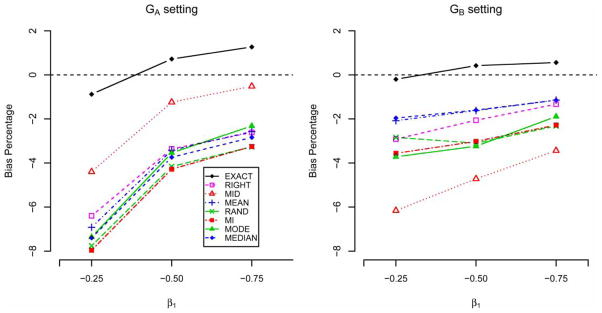
In the Cox model scenario, all seven imputation methods yield acceptable bias in estimating Cox regression coefficient. We also studied the performance of seven imputation methods for different values of the Cox regression coefficient. As shown in Figure 3, all imputation methods tend to yield a downward bias, and the bias’ percentage appears to decrease as the magnitude of the Cox regression coefficient increases. The method MID works well in the G_A setting, but fails in the G_B setting. Though the method RIGHT works well in both simulation settings, it fails in a scenario when both groups have different interval censoring widths (data not shown). Overall, probability-based imputation methods, especially MEAN and MEDIAN, appear to perform robustly against different simulation settings.

Figure 3.

Bias percentage for the estimator of β₁ based on seven imputation methods for data with n = 200 and w = 5.3 years.

To account for the imputation uncertainty, Pan [14] adopts the method MI and makes inference by using the variance formula proposed by Rubin [17] under a Bayesian inference framework. The validity of using Rubin’s formula in a frequentist framework has been discussed by Zhang [28] and Nielsen [29]. Our simulation results show that validity of this procedure may be questionable in the scenarios examined in this paper. For the Cox regression problem in the simulation studies, the comparison between mean ASE(β̂₁) and SD(β̂₁) implies that using Rubin’s formula may overcorrect the standard error of β̂₁ and this is also evident in Figure 2. Zhang [28] presents rules for making MI inferences with missing data. Those rules are not directly applicable for doubly censored data.

In all the problems considered, as the interval width decreases, the performance of each imputation method improves. In the simulation studies note also that, ignoring the uncertainty in the imputed date of origin event, the usual inference based on the ASE performs surprisingly well. The bootstrap inference procedure is recommended, however, since the computational demand with imputation methods is not excessive. Zhang et al. [30] propose a Bayesian approach to analyse doubly censored data by making a parametric assumption for the interval-censored origin and treating it as an unknown quantity. This approach could be used as an alternative to the bootstrap inference procedure.