Peak Capacity Optimization in Comprehensive Two Dimensional Liquid Chromatography: A Practical Approach

Abstract

In this work we develop a practical approach to optimization in comprehensive two dimensional liquid chromatography (LC×LC) which incorporates the important under-sampling correction and is based on the previously developed gradient implementation of the Poppe approach to optimizing peak capacity. The Poppe method allows the determination of the column length, flow rate as well as initial and final eluent compositions that maximize the peak capacity at a given gradient time. It was assumed that gradient elution is applied in both dimensions and that various practical constraints are imposed on both the initial and final mobile phase composition in the first dimension separation. It was convenient to consider four different classes of solute sets differing in their retention properties. The major finding of this study is that the under-sampling effect is very important and causes some unexpected results including the important counter-intuitive observation that under certain conditions the optimum effective LC×LC peak capacity is obtained when the first dimension is deliberately run under sub-optimal conditions.

1. Introduction

Comprehensive two dimensional liquid chromatography (LC×LC) is, due to its advantages in achieving high resolving power, becoming more and more attractive especially to those who deal with complex samples [1–4]. This mainly results from the “multiplicative advantage” which is a consequence of the so-called product rule when LC×LC is done under ideal conditions [5]. LC×LC has gained enormous success in the field of proteomics, even though analysis times are typically several hours for each sample [6–8]. Because of its high efficiency, fast gradient reverse phase chromatography (RPC) has been incorporated into LC×LC and has shown promising applications in the analysis of various samples with complex matrices such as maize extracts and urine [9,10]. Recent developments in LC×LC include a careful comparison of the separating power of LC×LC and one dimensional liquid chromatography (1DLC) as a function of the overall analysis time [11], theoretical [12–14] and experimental studies of the optimal second dimension analysis time [15], and other important issues including the use of parallel second dimension columns [16,17] and the use of sophisticated second dimension gradients [18–20] as well as protocols for the optimization of LC×LC [21].

Peak capacity is the most important metric for measuring the separating power of a LC×LC system. As mentioned above, under ideal conditions the total peak capacity of LC×LC should be the product of the peak capacities of the first dimension (¹n_c) and the second dimension (²n_c). However, to achieve “ideal” conditions, a number of criteria must be strictly satisfied. First, the first dimension and second dimension separation must be totally uncorrelated for the sample of interest [5,22]. Second, peaks from the samples under investigation must cover the whole 2D separation space [23]. Third, the sampling of the first dimension effluent for the second dimension separation must be fast enough to avoid resolution loss due to “under-sampling” effects [24]. Murphy et al. suggested that 3–4 fractions should be sampled for each first dimension peak; Davis et al. developed an equation (given below) to quantitatively estimate the under-sampling effect as a function of first dimension average peak width and second dimension cycle time [25,26]. Li et al. and later Potts et al. in more detail examined the consequences of the second dimension re-equilibration time and other factors related to under-sampling and the effective peak capacity [12,13]; Horie et al. suggested that the best first dimension modulation period (sampling time) would be 2.2–4 times the standard deviation of the first dimension peak [27]. Considering the fact that in general the above three criteria are never fully complied with real LC×LC systems, Stoll et al. proposed that the effective 2D peak capacity (n′_c,2D) should be calculated as per Eq. 1 [11]:

$$n_{c,2D}^{\prime }={}^{1}n_c\times {}^{2}n_c\times f_{\mathrm{cov}erage}\times \frac{1}{\langle \beta \rangle }$$ (1)

Here, f_coverage is the coverage factor corresponding to the peak distribution on the 2D separation space; and <β> is the Davis-Stoll-Carr (D-S-C) under-sampling correction factor (see Glossary).

The importance of the peak capacity lies in the fact that the total number of observed peaks in a complex mixture as well as the number of observed single component peaks increase monotonically with an increase in peak capacity [28–31]. Thus, the general objective of optimization is usually to maximize the peak capacity in a fixed analysis time or to achieve a desired peak capacity in the shortest time. Various optimization approaches have been developed to investigate the optimal separation conditions for both 1DLC and LC×LC. Plumb et al. studied the influence of small porous particles and temperature on chromatographic performance, and they concluded that high column temperature enables a peak capacity of about 1000 in 1D gradient elution [32]. Wang et al. developed an approach to optimizing peak capacity in 1D gradient chromatography, based on the Poppe method [33] for isocratic chromatography, which enables the choice of appropriate columns, particle size, column length, and eluent velocity [34]. Interestingly, Wang et al. showed that conventional high performance liquid chromatography (HPLC) instrumentation is able to give comparable peak capacities to those obtained in ultrahigh pressure liquid chromatography (UHPLC), but at much lower pressures by using a long set of columns packed with large particles in long gradient runs at elevated temperatures [35]. Furthermore, because of the strong and complex interactions between all variables (e.g. flow rate and mobile phase composition) during optimization, Wang et al. recommended that one should first select the desired particle size, gradient time, and the highest achievable temperature, then optimize the flow rate and finally the mobile phase composition [36].

Optimization of LC×LC is a relatively new yet important research topic. Obviously, in view of the f_coverage factor in Eq. 1 increasing orthogonality will raise the effective peak capacity in a practical LC×LC system [37]; Jandera et al. explored this approach by choice of the proper columns and the careful optimization of the mobile phase and gradient for each dimension [18–20]. Schoenmakers et al. proposed a protocol to establish the optimal conditions including column length and diameter, particle size, flow rate, and second dimension loop size [21]. They studied a LC×SEC (size exclusion chromatography) system. To compensate for the under-sampling effect, they took the maximal retention time in the second dimension (²t_R) to be equal to the standard deviation of the corresponding peak in the first dimension (¹σ_t). Such a sampling rate is actually much too fast, approximately twice that recommended by Murphy et al. and three to four times faster than suggested by Horie et al. and will lead to sub-optimal peak capacities. Horvath et al. discussed optimization strategies for both offline and online LC×LC [14,38]. The major difference between online and offline LC×LC is that in online LC×LC the first dimension and the second dimension are directly coupled and separations are simultaneously carried out in both dimensions. In offline work aliquots of the first dimension are collected, stored, and analyzed later thus the two dimensions are fully decoupled. Putting aside issues related to the coverage factor they suggested that, the effective peak capacity of online LC×LC would likely not exceed 10,000 even if the LC×LC system were run under extraordinary conditions.

In this work, we aim to develop a practical approach to optimization in LC×LC based on both the previously developed gradient implementation of the Poppe method of optimizing peak capacity in gradient LC and which also quantitatively accounts for the important under-sampling correction. We postulated four distinct cases based on the retention properties of different classes of solutes, and for each case we compared optimization results obtained by two different methods.

2. Theory and Computational Methods

Eq. 1 shows how to calculate the effective 2D peak capacity of a LC×LC system. In this section, we introduce details of the calculations and the corresponding theory.

2.1 First dimension peak capacity (¹n_c)

We assume that gradient elution is used in both dimensions, the practical reasons for this choice in LC×LC have been made clear in previous work [1,11]. The simplest working equation for the first dimension peak capacity is [39]:

$${}^{1}n_c=\frac{{}^{1}t_g}{{}^1\varpi }=\frac{{}^{1}t_g}{4\cdot {}^1\stackrel{‒}{\sigma }}$$ (2)

where ¹t_g is the first dimension gradient time and ¹ϖ is the first dimension average peak width. The peak capacity clearly varies with the desired resolution. When unit resolution is required then ¹ϖ is taken as 4 ${}^1\stackrel{‒}{\sigma }$ leading to the right-hand form in Eq. 2. Another important assumption in this study is that all peaks have similar peak widths, which was confirmed to be true in the following calculations. Snyder later defined the “sample peak capacity” as [39]:

$${}^{1}n_c=1+\frac{{}^{1}t_{R,\mathit{last}}-{}^{1}t_{R,\mathit{first}}}{{}^1\varpi }$$ (3)

Here ¹t_R,first and ¹t_R,last are the retention times of the first and last peak, respectively. For the current calculations based on practical cases, we neglected the number 1 on the right hand side of Eq. 3, which causes little impact in our final conclusions. Wang et al. thoroughly discussed these two different ways to calculate 1D gradient peak capacity and showed that Eq. 3 is of more practical value in LC optimization [36]. Thus in the current study, all calculations and optimizations of the first dimension peak capacity were based on Eq. 3 unless otherwise noted.

Various groups [40,41] have considered the dependence of peak capacity on the properties of the gradient system including the obvious factors of gradient time, plate count, initial and final mobile phase composition and flow rate. These derivations start with Eq. 2 and thus essentially assume that the first peak can be arranged to elute at the column dead time (t_o), and the last to elute t_g later, i.e. at t₀+t_g. One then imposes an equation relating the peak variance to the column dead time, the elution factor at the column exit (k_e), the isocratic retention factor in the initial eluent of the gradient (k_o), and isocratic plate count (N). A somewhat controversial gradient compression factor (G) may or may not be included [40,41]. Under conditions of zero system dwell time and assuming that linear solvent strength theory (LSST) of gradient elution is valid [42] it is easily shown that [43]:

$$k_e=\frac{k_o}{{\mathit{bk}}_o+1}$$ (4)

where b is the so-called gradient slope defined as:

$$b=S\Delta \varphi \frac{t_o}{t_g}$$ (5)

Here S and Δϕ represent the solute's sensitivity to a change in eluent composition and the difference in the final and initial volume fractions (φ) of strong solvent in the eluent, respectively.

For a column of fixed length Neue [41] appears to be the first to arrive at the approximate solution given below but more refined forms have since appeared [43,44] although these too make a number of approximations:

$$n_c\approx \frac{S\Delta \varphi \sqrt{N}{t}_g}{G(S\Delta \varphi t_o+t_g)}\approx \frac{{\alpha }_1{t}_g}{{\alpha }_2+t_g}$$ (6)

This equation is readily derived once it is assumed that bk_o >> 1. It is this final assumption that causes considerable trouble in that in order to use Eq. 2 we must assume that the first peak (see Eq. 3) is unretained, i.e. k_o is very small. Thus unless we can assume that the gradient slope (b) is large we are imposing two contradictory approximations to derive Eq. 6. For low molecular weight solutes such as we are concerned within this paper b is almost always less than unity.

2.2 Retention times and peak width

We used the LSST of gradient elution [42] to predict retention times and the corresponding peak widths at a given temperature. This method was shown in detail in a previous paper [36]. Briefly retention times were predicted as follows:

$$t_R=t_o+t_D+\frac{t_o}{b}\ln [b(k_o-\frac{t_D}{t_o})+1]$$ (7)

and peak widths were calculated using:

$${\omega }_{1∕2}=\frac{2.35G{t}_o(1+k_e)}{\sqrt{N}}$$ (8)

Here t_R is the peak retention time; t_D is the system dwell time; ω_1/2 is the half-height peak width.

2.3 Second dimension peak capacity (²n_c)

The Guiochon group [14] has used equations of the form of Eq. 6 in their work on optimization of online LC×LC. In prior experimental work on very fast gradient elution [12] we attempted to fit measured peak capacities to Eq. 6 but found that Eq. 9 (with α₁′ = 44.01, α₂′ = 0.04 s⁻¹ for our specific system) gave a slightly better fit.

$${}^{2}n_c={\alpha }_1^{\prime }(1-\exp (-{\alpha }_2^{\prime }\times {}^{2}t_g))$$ (9)

Here ²t_g is the second dimension gradient time. The data used were experimentally measured with a homologous series of alkylphenones on the second dimension column under the practical conditions used in this lab [12,13,36]. These practical conditions include fixed column length, high flow rate, and most importantly that the final eluent composition (²ϕ_fin) was adjusted as t_g was varied to assure that the last peak eluted near the end of gradient. The approximate nature of Eq. 9, the need to adjust ²ϕ_final and most likely the complete neglect of all extra-column broadening are the likely causes of why Eq. 6 fails. Eq. 9 simply fits experimental data better than does Eq. 6.

In principle, the second dimension peak capacity can be further improved by also varying column length and flow rate. It makes a significant difference to do this in the first dimension of the LC×LC system but doing so is not as important in optimizing the second dimension because the column must be kept as short as possible to limit the second dimension cycle time. In addition, a recent study of maize extracts showed that the second dimension peak capacity could also be fit in the same mathematical form as that in Eq. 9 with slightly different coefficients [15]. Since the chemical species used in this study were similar to those used previously [12,13,15], we will continue to use Eq. 9 in the following calculations. We are certain that the differences between Eq. 6 and 9 are trivial and a change in equation form would not alter the conclusions of this paper.

2.4 Under-sampling effect

As mentioned above, the under-sampling effect has been studied by Murphy et al. [24], and later by Davis et al. [25,26], Tanaka et al. [27], Horvath et al. [14], and Potts et al. [13]. In this study, we, as did the Guiochon group, base our results on the D-S-C equation for the quantitative estimation of the under-sampling effect:

$$\langle \beta \rangle =\sqrt{1+3.35{\left(\frac{{}^{2}t_c}{{}^1\varpi }\right)}^2}$$ (10)

where ²t_c is the second dimension cycle time. It is equal to the first dimension sampling time, and in our experiment settings also equal to the second dimension gradient time (²t_g) plus the second dimension re-equilibration time (²t_eq which was held constant at 3 seconds throughout the study):

$${}^{2}t_c={}^{2}t_g+{}^{2}t_{\mathit{eq}}$$ (11)

2.5 Effective 2D peak capacity (n′_c,2D)

Although of vital importance, the effect of f_coverage is not discussed in this paper and we assumed that it is a constant (equal to 1 in this study) in all the calculations. If different fixed values of f_coverage were used, they would not affect the conclusions of this study except for the comparison of the peak capacities of 1DLC and LC×LC; however, using experimental f_coverage values Stoll et al. showed that the effective peak capacity of practical LC×LC will exceed that of optimized 1DLC in about 10 minutes [11], which is in good agreement with the results in this study. By substituting Eq. 3, 9, 10, and 11 into Eq. 1, the effective 2D peak capacity can be calculated as follows:

$$n_{c,2D}^{\prime }=\frac{{}^{1}t_{R,\mathit{last}}-{}^{1}t_{R,\mathit{first}}}{{}^1\varpi }\times \frac{1}{\sqrt{1+3.35{\left(\frac{{}^{2}t_g+3}{{}^1\varpi }\right)}^2}}\times 44.05\times (1-\exp (-0.04\times {}^{2}t_g))$$ (12)

A little reorganization of the right side of Eq. 12 leads to a clearer expression which is beneficial in analyzing the effects of different variables on the effective 2D peak capacity (discussed later):

$$n_{c,2D}^{\prime }=\frac{{}^{1}t_{R,\mathit{last}}-{}^{1}t_{R,\mathit{first}}}{\sqrt{{\left({}^1\varpi \right)}^2+3.35{({}^{2}t_g+3)}^2}}\times 44.05\times (1-\exp (-0.04\times {}^{2}t_g))$$ (13)

2.6 Optimizer and optimization protocol

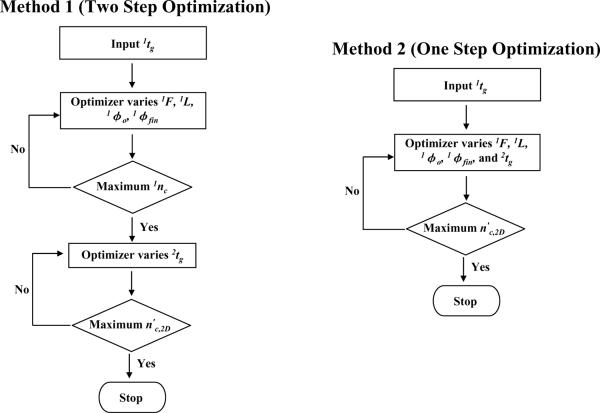
One of the most important aspects of this paper is the protocol used to optimize gradient elution. We followed the approach previously described [21,34] and used by us [36]. Basically this is a variant of the procedure devised by Poppe for the optimization of isocratic elution LC [33]. However, instead of optimizing the plate count at a given column dead time the sample peak capacity (see Eq. 3) of Snyder [39] is maximized at the desired gradient time. The optimizer used is the Solver function of Microsoft Excel (2003). We must input various system (temperature, maximum pressure, and viscosity), column (particle size, column diameter, reduced van Deemter coefficients) and solute parameters (diffusion coefficients, solvent sensitivity (S) and retention factors in pure water (k_w)). The first dimension peak capacity (Eq. 3) is then optimized by varying column length, flow rate, ¹φ_o, and ¹φ_fin. The effective 2D peak capacity optimization (Eq. 12) additionally requires that ²t_g be optimized. All parameters are subject to various physical constraints (see section 2.7). Figure 1 outlines two distinct optimization protocols: method 1 (two step optimization) and method 2 (one step optimization):

1. In method 1 (two step optimization) the first step is to maximize ¹n_c with regard to the variables without concerning one's self with the under-sampling correction. After selecting a gradient time the maximum value of ¹n_c is obtained by varying ¹F, ¹L, ¹φ_o, and ¹φ_fin. In the second step one then optimizes the second dimension by varying ²t_g taking into consideration both the under-sampling process and the effect of ²t_g on ²n_c.

2. In method 2 (one step optimization) one from the outset works in 5 dimensional space and optimizes the final effective LC×LC peak capacity in what amounts to one step. The effective 2D peak capacity (n′_c,2D) in this method is the global maximum obtained by simultaneously varying five variables (¹F, ¹L, ¹φ_o, ¹φ_fin, and ²t_g).

Figure 1.

Flow diagrams for method 1 (two step optimization) and method 2 (one step optimization) optimization. In method 1, the same conditions are used in the LC×LC system and then the effective LC×LC peak capacity of this system is further maximized by varying ²t_g. In method 2, the optimized first dimension conditions may not be the same as those found in method 1. See the Theory and Computational Methods section for additional details. ¹n_c is computed from Eq. (3) and n′_c,2D is from Eq. (12) or (13).

2.7 Assumptions and constraints

We summarize here the chief assumptions and constraints in the optimization calculations keeping in mind that the purpose of the calculations is to simulate realistic experiment results, so some practical assumptions must be imposed, e.g., the calculation of the second dimension peak capacity and under-sampling factor.

• (1)Gradient elution is used in both dimensions.
• (2)All peaks have similar peak widths.
• (3)f_coverage is unity in all the calculations regardless of the gradient times.
• (4)The first dimension column length must be larger than 3 cm.
• (5)The temperature is held constant.
• (6)The first dimension particle size and column diameter are fixed.
• (7)The system maximum pressure is 400 bar.
• (8)The first dimension flow rate must be less than 5 mL/min.
• (9)Extra column peak broadening and extra column pressure drops are neglected.
• (10)The first dimension initial eluent is fixed as pure water, and the first dimension final mobile phase is between 20% and 80% ACN. This practical constraint was imposed because of the need to match the mobile phase strength in the two dimensions to suppress peak broadening by focusing the sample on the second dimension column.

2.8 System, column, and solute parameters

Besides the assumptions and constraints imposed in the calculations, another issue that should be emphasized is that various properties (mainly S and k_w) of different solutes were measured, but we classified all solute sets into four categories according to their LC retention characteristics as shown in Table 1 (see detailed discussion in the following section). As mentioned in section 2.6, we need to input system, column, and solute parameters into the spreadsheet for the Poppe optimization calculations. Table 2 summarizes these parameters which were obtained from previous experimental results; refer to [11,12,36] for detailed values and experimental conditions. As shown in Table 2, the maximum pressure was assumed to be 400 bar and the fixed temperature was set at 40 °C. The maximum mobile phase viscosity (η_max) was 0.69 cP when the concentration of ACN in the eluent was 19%. The maximum diffusion coefficient of all the solutes was 1.42×10⁻⁵ cm²/s, estimated using the Wilke–Chang equation [45]. To allow for a fair comparison in this study, we used the same A, B, C terms, obtained from a Zorbax SB-C18 column, in the van Deemter equation for the four mixtures in all cases.

Table 1.

Definition of the Various Sample Mixtures^a

Case	Mixture Sampleb	Mixture Type	1tR, first	1tR, last	1 φ 0c	1 φ find
1.e	A and B	Ideally retained	=1to	=1to+1tg	=0	3≤1φmaxi
2.f	C	Weakly retained	>~1to	=1to+1tg	=0	≤ 1 φ max i
3.g	D	Well retained	>1to	=1to+1tg	=0	≤ 1 φ max i
4.h		Too strongly retained	≥ 1to	>1to+1tg	=0	≤ 1 φ max i

^aThese are the conditions for optimizing the first dimension.

^bThese are the mixture designators used in the text and calculation. Both mixtures A and B have a solute which elutes at ¹t_o even when ¹φ_o=0. The second solute in mixture A elutes at a time slightly larger than ¹t_o whereas the second solute in mixture B elutes substantially later than ¹t_o. Mixture C is the same as A but the un-retained component is missing and D is the same as B but again the un-retained component is missing.

^cIt is assumed that the initial eluent composition is pure water. This is just a convenience for this work; any value could be substituted.

^dIt is assumed that there will be an upper limit of ¹φ_fin so as to avoid problems related to focusing the solutes in the second dimension. Any value would do.

^eIn case 1 it is assumed that the solute set has a species which elutes at ¹t_o even when ¹φ_o=0 as well as a species that elutes at ¹t_o+¹t_g even if ¹φ_fin<0.8.

^fIn case 2 we assume the presence of a very weakly retained solute which elutes close to or slightly later than ¹t_o.

^gIn case 3 we assume that the least retained solute elutes at a time greater than ¹t_o given ¹φ_o=0.0.

^hIn case 4 we assume that the solute set contains a solute which is so strongly retained that it elutes later than ¹t_o+¹t_g at ¹φ_fin above the allowed limit.

ⁱ¹φ_max, the maximum first dimension eluent composition, is 0.8 in this study.

Table 2.

Summary of Solute Parameters^a

Mixture	Solute Parameter
	Dmb		Se		1n(kw)h
	Ave.c	Max.d	Ave.f	Max.g	Ave.i	Max.j
A	0.98	1.22	6.79	13.15	2.37	4.59
B	1.15	1.42	6.35	8.93	5.38	8.82
C	0.98	1.22	6.79	13.15	2.37	4.59
D	1.17	1.42	6.35	8.93	5.38	8.82

^aSystem parameters and column parameters are from previous studies11, 12, 36. The temperature is 40 °C; the maximum pressure is 400 bar; the maximum eluent viscosity is 0.69 cP; the column particle size is 3.5μm; the column internal diameter is 2.1 mm; the reduced van Deemter coefficients are 1.04 (A), 15.98 (B), and 0.033 (C).

^bDiffusion coefficient (× 10⁻⁵cm²/s) of the solutes.

^cAverage diffusion coefficient of the solutes.

^dMaximum diffusion coefficient of the solutes.

^eS of the solutes.

^fAverage S of the solutes. It should be noted that for mixture A and B the solute eluting at t_o was not included.

^gMaximum S of the solutes. It should be noted that for mixture A and B the solute eluting at t_o was not included.

^hAverage 1n(k_w) of the solutes.

ⁱAverage ln(k_w) of the solutes. It should be noted that for mixture A and B the solute eluting at t_o was not included.

^jMaximum ln(k_w) of the solutes. It should be noted that for mixture A and B the solute eluting at t_o was not included.

3. Results and Discussion

During preliminary attempts to develop a very general approach to the problem of optimizing dual gradient LC×LC we realized that a better approach was to simplify the general problem. This led us to postulate four distinct smaller problems (see Table 1) based on the retention properties of different classes of solutes. Here we show the results for these four situations.

3.1 The Poppe approach to 1DLC optimization (the first step in method 1)

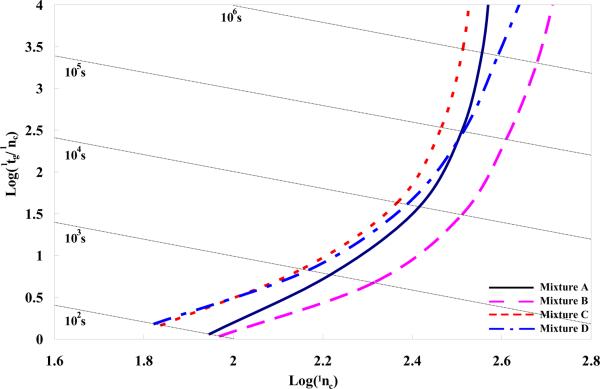
Table 1 defines the four classes of solute mixtures according to their retention properties on the first dimension column; Figure 2 shows the gradient Poppe plots of the optimized first dimension gradient peak capacity (the first step in method 1) for the four mixtures (see Table 1) on the packed bed column. It is worthwhile noting that the curves in Figure 2 represent the maximum 1DLC peak capacity at different gradient times from each individual mixture under the experimental conditions and constraints illustrated in the Theory and Computation Methods section. This gradient Poppe plot clearly resembles the Poppe plots for isocratic elution [34]. As pointed out previously [34], moving toward the right along the curves requires a longer column, a lower flow rate, and a lower ¹φ_fin. The asymptotes for all mixtures at high peak capacity tend to be vertical indicating that there is a maximum achievable peak capacity. Higher peak capacity can always be obtained in gradient 1DLC elution in a longer run, although the gain per unit time becomes very small. The optimized 1DLC peak capacities of mixture A and B have a smaller difference in high speed region than that in the high peak capacity region; the same trend was observed for mixture C and D. Mixture A and B have higher peak capacities than mixture C and D, respectively, due to the fact that they have a solute which always elutes at t_o. These four curves differ only due to differences in the solute sets particularly due to differences in S and lnk_w. However, the averages and ranges in diffusion coefficients are impacted by the solute set (see Table 2) and consequently there is a minor effect on average peak width. The major difference is due to the retention time window. Insepction of Table 3 to 5 will show that the optimized column length, flow rate, and ¹φ_fin all vary with solute set.

Figure 2.

1DLC gradient peak capacity gradient Poppe plots for the four mixtures (see Table 1) on the column. Conditions (see Table 2 for details): P_max, 400 bar; T, 40 °C; η_max, 0.69 cP; maximum D_m, 1.42×10⁻⁵ cm²/s. Coefficients of the reduced van Deemter equation (A, 1.04; B, 15.98; C, 0.033) were measured on a 50mm × 2.1mm 3.5 μ m Zorbax SB-C18 column using heptanophenone in 40% acetonitrile (v/v) at 40 °C (k = 20). Mixture A dark blue line (dash-dot); Mixture B pink line (long dashed); Mixture C orange line (short dashed); Mixture D blue line (dot).. See Table 1 for definition of solute mixtures.

Table 3.

Case 1: Results for Optimization of Mixtures A and B

1tga	1Lb	1Fb	1 φ ob	1 φ finb	1ncc	Δ(1t)d	Δ(1t)/1tge	1 ϖ f	2tgg	β h	1n'ci	2ncj	n'c,2Df
Method 1 and Method 2 optimization of mixture A1
5	19.7	0.59	0.00	0.46	123	5.0	1.00	0.041	11.54	10.9	11.2	16	183
12	25.0	0.47	0.00	0.40	154	12.0	1.00	0.078	12.06	6.0	25.8	17	434
24	29.0	0.40	0.00	0.33	181	24.0	1.00	0.133	13.18	3.8	47.0	18	848
49	33.4	0.35	0.00	0.25	210	49.0	1.00	0.234	15.69	2.6	79.6	21	1634
Method 1 and Method 2 optimization of mixture B1
5	9.3	1.26	0.00	0.80	142	5.0	1.00	0.035	11.48	12.6	11.3	16	183
12	14.3	0.82	0.00	0.80	189	12.0	1.00	0.064	11.82	7.2	26.3	17	436
24	20.3	0.58	0.00	0.80	228	24.0	1.00	0.105	12.57	4.6	49.4	17	859
49	29.0	0.40	0.00	0.80	268	49.0	1.00	0.184	14.40	3.1	87.3	19	1684

^aInput first dimension gradient time (min).

^bOptimum first dimension column length (cm), flow rate (mL/min), initial and final eluent compositions.

^cResulting first dimension peak capacity computed by optimizing peak capacity from Eq. 3 (method 1 optimization) or Eq. 12 (method 2 optimization).

^dDifference in the retention times (min) of the first and last peak (Δ(¹t) =¹t_R,last−¹t_R,first) under the gradient conditions as per footnote ^b.

^eRatio of quantity footnoted as per ^d. to the gradient time.

^fThe first dimension average peak width (min) under the optimized conditions.

^gThe optimized second dimension gradient time (s; see ^h).

^hThe under-sampling factor based on Eq. 10, ¹ϖ and ²t_g (see ^f and ^g).

ⁱThe effective first dimension peak capacity (=¹n_c/β, see ^c and ^h).

^jThe optimized second dimension peak capacity computed from Eq. 9 with ²t_g as per quantity footnoted as ^g.

^fOptimized effective LC×LC peak capacity computed from Eq. 12.

¹Both mixture A and mixture B have a solute which elutes at ¹t_o even when ¹φ_o=0. Except that solute, mixture A has a very weakly retained solute which elutes close to or slightly later than ¹t_o; mixture B has the least retained solute which elutes at a time greater than ¹t_o given ¹φ_o=0.0.

3.2 Case 1: ideally retained solute set

Case 1 is the simplest; in this instance there is a solute which elutes virtually at the column dead time as well as a strongly retained solute which, below acceptable maximum final eluent composition, elutes at or very near the gradient time plus the dead time. We further assume that all peaks have similar peak widths so that the peak capacity can realistically be computed from the peak width averaged over all peaks as in Eq. 3. Due to the properties of the least and most retained solutes the time window will be equal to the first dimension gradient time (see Table 1). Consequently Eq. 13 makes it obvious that the first dimension experimental conditions can only influence the effective 2D peak capacity through the average peak width, and that the conditions of the second dimension influence the effective peak capacity through the second dimension gradient time (²t_g). Clearly inspection of Eq. 13 shows that at any ²t_g value, the maximum effective peak capacity must occur at the values of ¹F, ¹L, ¹φ_o, and ¹φ_fin which minimize 1ϖ. Meanwhile, it is important to notice that while in principle the separation window (¹t_R,last−¹t_R,first) is a variable in case 1 the solute set is deliberately idealized such that the experimental conditions (¹F, ¹L, ¹φ_o, and ¹φ_fin) allow the separation window to be equal to ¹t_g. That is, the experimental variables in the gradient Poppe optimization are such that the first and last peaks are able to exactly obey the desired time constraints.

This situation differs fundamentally from that in which the peak capacity is optimized according to the definition provided by Eq. 2. If Eq. 2 and not Eq. 3 were used for computing the maximal peak capacity the optimization would follow a trajectory in which the experimental variables (¹F, ¹L, ¹φ_o, and ¹φ_fin) disregard the first and last retention times since they do not appear in Eq. 2 and thus these variables must act to merely minimize the average peak width. As shown in previous experimental work this formally leads to very high peak capacities but it does not give very good separations as the “optimized” conditions force the solutes to elute rather quickly so as to minimize the average peak widths [36].

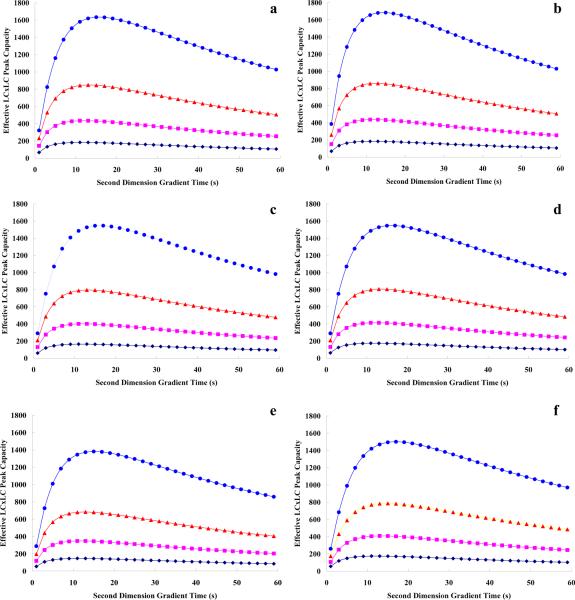
Table 3 compares the conditions which optimize the LC×LC system by method 1 and method 2 for four different first dimension gradient times using mixtures A and B both of which contain a very weakly retained species that always elutes at the dead time. Overall the solutes in mixture A are more weakly retained than those in B; mixture A required ¹φ_fin less than 0.5 to elute the last peak while mixture B required ¹φ_fin of 0.8 which is the upper limit imposed in these calculations. As predicted above, we found that the conditions which optimized the first dimension also optimized the full two dimensional separation. This was true for both mixture types for all four gradient times. This means that if one optimizes only the first dimension the same conditions can be used for the full LC×LC system. Clearly this would greatly simplify LC×LC method development for solutes falling in this class. In Table 3, we see that the peaks occupy the full time window since ¹t_R,last−¹t_R,first is exactly ¹t_g. To optimize a LC×LC system in case 1, the first dimension should be adjusted to provide the minimal ¹ϖ while making sure that the sample elutes so that the whole retention time window is occupied; this will maximize the peak capacity of the first dimension. Once the first dimension conditions that maximize the first dimension peak capacity have been found then the effective 2D peak capacity (n′_c,2D) is only dependent on the second dimension gradient time. Figure 3a and 3b demonstrates the relationship between n′_c,2D and ²t_g at four different values of ¹t_g in case 1. There exists an optimal ²t_g in both Figure 3a and 3b which produces the maximum n′_c,2D at any pre-selected ¹t_g for either of these two mixtures. For each mixture, this optimal ²t_g increased (~11 s to ~16 s) with ¹t_g which agrees well with our recent experimental results [15].

Figure 3.

Effective LC×LC peak capacity vs. second dimension gradient time. a). Mixture A in case 1 by either method 1 or method 2 optimization; b). Mixture B in case 1 by either method 1 or method 2 optimization; c). Mixture C in case 2 by method 1 optimization; d). Mixture C in case 2 by method 2 optimization; e). Mixture D in case 3 by method 1 optimization; f). Mixture D in case 3 by method 2 optimization. Dark blue diamonds: ¹t_g=5 min; pink squares: ¹t_g=12 min; orange triangles: ¹t_g=24 min; blue circles: ¹t_g=49 min. See the definitions of cases and mixtures in Table 1.

Furthermore, we noticed (see Table 3) that at each ¹t_g although the first dimension peak capacities are rather different for these two mixtures in contradistinction the optimized effective LC×LC peak capacities are very similar. For example, at 12 min (¹t_g), ¹n_c from mixture A is 154 and ¹n_c from the second mixture is 189 with a difference of about 23%, while n′_c,2D from these mixtures are 434 and 436, respectively, for all practical purposes a negligible difference. This surprising result is caused by the under-sampling effect; the higher is ¹n_c, the smaller is ¹ϖ which induces a more severe under-sampling problem. The compromise results in similar values of effective first dimension peak capacity (¹n′_c) which are 25.8 and 26.3, respectively. Based on the observation that in both cases the optimal ²t_g are similar, it is evident that the effective 2D peak capacities from these two mixtures will be similar. This is a consequence of what was predicted and discussed at length by Li et al. and Potts et al. that when the peak capacity of the first dimension exceeds a certain value the effective 2D peak capacity becomes independent of the first dimension peak capacity [12,13].

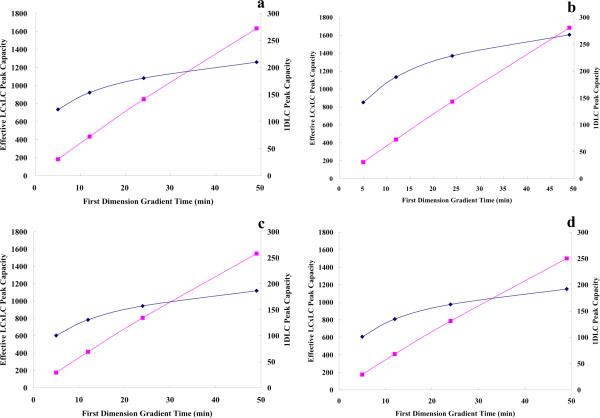
Another important result in Table 3 is that the effective peak capacity of LC×LC will exceed that of 1DLC from about 5 min onwards; this theoretically based conclusion is in good agreement with Stoll's experimentally based conclusion albeit based on a single mixture (a maize seed extract) and thus generalizes his statement that the effective peak capacity of LC×LC will exceed that of one dimensional LC in only about 5 to 10 minutes [11]. However, it should be noted that the fractional spatial coverage was taken as unity in this theoretical comparison. Figure 4a and 4b compares ¹n_c based on the optimized first dimension in method 1 and n′_c,2D for the optimized LC×LC system in method 2 as a function of the first dimension gradient time in case 1. LC×LC rapidly overtakes 1DLC and the peak capacity advantage grows as ¹t_g increases. The peak capacity of the first dimension has a strong negative curvature vs. the first dimension gradient time (see Figure 4a and 4b), while n′_c,2D is only slightly curved but ultimately becomes quite linear with ¹t_g when under-sampling is not severe [13]. The chief reason for the strong negative curvature in these plots of ¹n_c is that in 1DLC ¹ϖ also increases almost linearly with ¹t_g. However, in LC×LC the increase in ¹ϖ alleviates the loss in resolution due to under-sampling which brings about the continuing increase of the effective 2D peak capacity with ¹t_g. Clearly, the under-sampling effect plays a profound role in LC×LC; it needs careful and quantitative consideration especially when attempts are made to optimize LC×LC.

Figure 4.

Peak capacity from the optimized first dimension and the effective LC×LC peak capacity from the optimized LC×LC system (method 2 optimization) vs first dimension gradient time. a). mixture A in case 1; b). mixture B in case 1; c). mixture C in case 2; d). mixture D in case 3. Dark blue diamonds: the peak capacity from the optimized first dimension; pink squares: the effective LC×LC peak capacity from the optimized LC×LC system. See the definitions of cases and mixtures in Table 1.

3.3 Case 2: weakly retained solute set

In case 2, mixture C, which is the same as mixture A but the un-retained solute deleted (see Table 1), was used. As shown in Table 1, mixture C has a solute that elutes somewhat later than ¹t_o as well as a solute that appears at ¹t_o+¹t_g. Compared to case 1, the value of ¹t_R,last−¹t_R,first actually changes although it is still close to ¹t_g and covers most of the time window (>90%, see Table 4). Solutes in mixture C are weakly retained as compared to mixture D (see Table 1), e.g., a ¹φ_fin of only 0.36 is needed to elute the last peak in the method 1 optimization (¹t_g=5 min). In the method 2, ¹φ_fin was even smaller and hit the constraint that ¹φ_fin had to exceed ¹φ_o by at least 0.2 to assure that one is doing a gradient and not an isocratic separation.

Table 4.

Case 2: Results for Optimization of Mixture C^a

1tg	1L	1F	1 φ o	1 φ fin	1nc	Δ(1t)	Δ(1t)/1tg	1 ϖ	2tg	β	1n'c	2nc	n'c,2D
Method 1 optimization of mixture C1
5	14.4	0.81	0.00	0.36	101	4.5	0.90	0.045	11.58	10.0	10.1	16	164
12	19.1	0.61	0.00	0.31	131	11.1	0.93	0.085	12.18	5.5	23.6	17	401
24	23.5	0.50	0.00	0.26	157	22.6	0.94	0.144	13.44	3.6	43.4	18	796
49	29.1	0.40	0.00	0.20	187	46.9	0.96	0.252	16.16	2.5	73.8	21	1547
Method 2 optimization of mixture C1
5	9.2	1.27	0.00	0.20	94	4.8	0.96	0.051	11.65	8.8	10.7	16	175
12	14.3	0.82	0.00	0.20	127	11.5	0.96	0.091	12.28	5.2	24.2	17	414
24	20.2	0.58	0.00	0.20	156	23.0	0.96	0.148	13.52	3.6	43.8	18	806
49	28.9	0.40	0.00	0.20	187	47.0	0.96	0.252	16.16	2.5	73.8	21	1548

^aThe meanings of symbols in Table 4 are the same as those in Table 3.

¹Mixture C has the least retained solute which elutes close to or slightly later than ¹t_o given ¹φ_o=0.0.

Since in case 2 ¹t_R,last−¹t_R,first is still close to ¹t_g, the results should be rather similar to those in case 1. Table 4 shows the optimized conditions in method 1 and method 2 optimization at different ¹t_g values. In this case, optimal conditions in the two different optimization approaches were reasonably similar although subtle differences were indeed observed. Figure 3c and 3d show the effective 2D peak capacities in the two approaches as a function of ²t_g at different values of ¹t_g in case 2. The same general trends were observed as in case 1 (Figure 3a and 3b) that is there is an optimum ²t_g which increases with ¹t_g. Figure 4c compares the maximal ¹n_c from method 1 optimization and the maximal n′_c,2D from method 2 optimization in case 2. LC×LC has better resolving power than does 1DLC starting from 5 min, and this advantage becomes greater as ¹t_g increases; this results mainly from a decrease in the magnitude of the under-sampling correction.

3.4 Case 3: strongly retained solute set

Mixture D of case 3 is the same as mixture B in case 1 but the totally un-retained solute is excluded. The last peak from mixture D still elutes at ¹t_o+¹t_g; however, the first peak elutes at a time considerably longer than ¹t_o (see Table 1). In comparison to mixture C of case 2 the solutes in mixture D are relatively strongly retained as a high ¹φ_fin is required to elute them (see Table 5).

Table 5.

Case 3: Results for Optimization of Mixture D^a

1tg	1L	1F	1 φ o	1 φ fin	1nc	Δ(1t)	Δ(1t)/1tg	1 ϖ	2tg	β	1n'c	2nc	n'c,2D
Method 1 optimization of mixture D1
5	9.3	1.26	0.00	0.80	101	4.0	0.80	0.040	11.52	11.3	9.0	16	146
12	14.3	0.82	0.00	0.80	135	9.6	0.80	0.071	11.94	6.5	20.8	17	348
24	20.3	0.58	0.00	0.80	163	19.2	0.80	0.118	12.84	4.2	38.5	18	682
49	25.2	0.46	0.00	0.76	192	40.9	0.83	0.213	15.16	2.8	68.9	20	1381
Method 2 optimization of mixture D1
5	3.0	3.89	0.00	0.50	53	4.9	0.98	0.091	12.29	5.2	10.2	17	175
12	4.8	2.43	0.00	0.51	81	11.6	0.97	0.144	13.44	3.6	22.3	18	408
24	7.9	1.49	0.00	0.55	118	23.0	0.96	0.195	14.70	2.9	40.1	20	786
49	12.7	0.92	0.00	0.58	163	46.5	0.95	0.286	17.02	2.4	69.0	22	1500

^aThe meanings of symbols in Table 5 are the same as those in Table 3.

¹Mixture D has the least retained solute which elutes at a time greater than ¹t_o given ¹φ_o=0.0.

The most striking result in Table 5 is that the optimum conditions for method 1 and method 2 are quite different. Furthermore the first dimension must be run at sub-optimal conditions to obtain the maximum n′_c,2D. For example, at ¹t_g equal to 5 min, the value of ¹n_c that produces the highest value of n′_c,2D differs by almost two fold (101 to 53) between the two types of optimization. This counter-intuitive observation can only be rationalized by considering the under-sampling effect. The solutes in mixture D covered only 80% of the time window in method 1 optimization (¹t_g=5 min), and this coverage changed to 98% thereby increasing ¹t_R,last−¹t_R,first by the appropriate adjustment of ¹φ_fin, ¹F, and ¹L in method 2. However, ¹ϖ increased about 2.3 fold which made ¹n_c almost two times smaller in method 2 (see Eq. 3). Fortunately, β decreases with ¹ϖ (see Eq. 10), and interestingly the compromise between all of the above mentioned factors results in an increased value of ¹n′_c. The best ²t_g in method 2 is larger than in method 1, further contributing to the increased n′_c,2D. This increase ranged from 19.9% to 8.6% as ¹t_g increased from 5 min to 49 min probably because longer gradients are less sensitive to the under-sampling effect. Thus, the under-sampling correction makes it possible under certain circumstances that one can sacrifice some first dimension peak capacity and thereby obtain a higher effective LC×LC peak capacity which is the real goal of the optimization process.

Case 3 also shares some common features with cases 1 and 2. In Figure 3e and 3f, the optimal ²t_g varied from 11 s to 18 s and increased with ¹t_g. Figure 4d once again shows the nearly linear increase of n′_c,2D with ¹t_g while ¹n_c increased much slowly (explained in case 2).

3.5 Case 4: too strongly retained solute set

It is possible that some mixtures might contain extremely well retained solutes such that some components elute after ¹t_o+¹t_g even at the maximum allowable value of ϕ_fin. We did not study this case as in such instances it would be best to choose a less retentive stationary phase, e.g., by using the same type of stationary phase on a lower surface area material or to use a stronger type of mobile phase e.g. THF or acetone. Recent work in this lab shows that LC×LC allows many more types of eluents to be used in the first dimension in RP×RP including eluents which absorb very strongly in the ultra-violet or have relatively high viscosities [46].

4. Conclusions

In this study, we examined LC×LC optimization with a variety of low molecular weight solutes which had widely different retention properties. We discussed the optimized LC×LC conditions in four cases and compared results using two different optimization methods. Two different methods of optimization were considered. Mathematically method 1 (the two-step optimization) is more robust than method 2 (the one-step optimization), since each step in method 1 has fewer parameters to optimize and thus will be less prone to find false optima. However, this study shows that under certain conditions method 2 can generate a higher peak capacity than method 1; this has important significance in LC×LC optimization. The main conclusions are as follows:

1. The under-sampling of the first dimension must be quantitatively accounted for when seeking the instrumental conditions (column length, flow rate, eluent composition) that establish the optimum effective LC×LC peak capacity.

2. The optimum conditions depend strongly on the retention characteristics of the solute mixture. Four cases were considered ranging from weakly retained solutes to very strongly retained solutes.

3. In case 3 where the solutes range from the weakly retained to those which are strongly retained and thus require a rather strong final eluent composition to elute them, we found that counter-intuitively the first dimension should be run under conditions wherein a less than optimum first dimension peak capacity is used. This results from a compromise between the width of the separation space (t_R,last−t_R,first), the peak width and the impact of under-sampling on the first dimension.

4. For the weakly retained solutes (case 2) a rather different, more intuitive, result was obtained. The LC×LC system is optimized in method 2 under approximately the same conditions as those from method 1. This means that to achieve the maximum effective LC×LC peak capacity we should first approximately optimize the first dimension and then the second dimension taking the under-sampling effect into account.

5. In case 1, a hypothetical situation in which the first solute always elutes at the dead time and the last solute elutes at this time plus the gradient time, the LC×LC system is optimized in method 2 under exactly the same conditions as those from method 1.