A simple method for measuring signs of¹H^Nchemical shift differences between ground and excited protein states

Abstract

NMR relaxation dispersion spectroscopy is a powerful method for studying protein conformational dynamics whereby visible, ground and invisible, excited conformers interconvert on the millisecond time-scale. In addition to providing kinetics and thermodynamics parameters of the exchange process, the CPMG dispersion experiment also allows extraction of the absolute values of the chemical shift differences between interconverting states, $\mid \Delta \tilde{\omega }\mid$, opening the way for structure determination of excited state conformers. Central to the goal of structural analysis is the availability of the chemical shifts of the excited state that can only be obtained once the signs of $\Delta \tilde{\omega }$ are known. Herein we describe a very simple method for determining the signs of ¹H^N $\Delta \tilde{\omega }$ values based on a comparison of peak positions in the directly detected dimensions of a pair of ¹H^N-¹⁵N correlation maps recorded at different static magnetic fields. The utility of the approach is demonstrated for three proteins that undergo millisecond time-scale conformational rearrangements. Although the method provides fewer signs than previously published techniques it does have a number of strengths: (i) Data sets needed for analysis are typically available from other experiments, such as those required for measuring signs of ¹⁵N $\Delta \tilde{\omega }$ values, thus requiring no additional experimental time, (ii) acquisition times in the critical detection dimension can be as long as necessary and (iii) the signs obtained can be used to cross-validate those from other approaches.

Protein dynamics can play a critical role in many biological processes including ligand binding, catalysis, folding and molecular recognition (Korzhnev et al. 2004; Karplus and Kuriyan 2005; Boehr et al. 2006; Popovych et al. 2006; Frederick et al. 2007; Henzler-Wildman and Kern 2007; Sugase et al. 2007). Often such dynamics involve the interconversion between highly populated ground (G) states and one or more low-populated, transiently formed conformers (excited states, E) that can be important for function. Such excited states frequently escape detection by standard biophysical techniques because of their low populations and short lifetimes. However, with the development of protein-based NMR relaxation dispersion spectroscopy in the past decade, which builds upon the classic Carr-Purcell-Meiboom-Gill (CPMG) experiment (Carr and Purcell 1954; Meiboom and Gill 1958), it has become possible to study millisecond (ms) exchange processes in protein systems in detail, so long as they involve excited states that are populated to at least 0.5% (Palmer et al. 2001).

A particularly powerful feature of the CPMG experiment is that it provides structural information on ‘invisible’ excited conformer(s) because dispersion profiles are sensitive to the absolute value of the chemical shift differences between interconverting states, $\mid \Delta \tilde{\omega }\mid$. Further insight into the structure of the excited state can be obtained by measuring residual dipolar couplings (RDCs) (Igumenova et al. 2007; Vallurupalli et al. 2007) and residual chemical shift anisotropies (RCSAs) (Vallurupalli et al. 2008) using spin-state selective CPMG experiments recorded on samples under conditions of weak alignment. The development of both improved isotope labeling strategies and novel pulse schemes has led to the measurement of accurate CPMG dispersion profiles for backbone ¹H^N (Ishima and Torchia 2003), ¹⁵N (Loria et al. 1999; Tollinger et al. 2001), ¹³C^α (Hansen et al. 2008), ¹H^α (Lundstrom et al. 2009a) and ¹³C^O (Ishima et al. 2004; Lundstrom et al. 2008) nuclei, side-chain ¹³C^β (Lundstrom et al. 2009b) and methyl ¹³C (Skrynnikov et al. 2001; Lundstrom et al. 2007) spins, providing a large number of $\mid \Delta \tilde{\omega }\mid$ values to be used as structural probes.

Although $\mid \Delta \tilde{\omega }\mid$ values can be used as probes of structure they are far more useful once the sign of $\Delta \tilde{\omega }$ is obtained since then the chemical shift of the excited state is available, ${\tilde{\omega }}_E={\tilde{\omega }}_G+\Delta {\tilde{\omega }}_{EG}$ where $\Delta {\tilde{\omega }}_{EG}={\tilde{\omega }}_E-{\tilde{\omega }}_G$. In the case of ¹⁵N, ¹³CO and ¹³C^α nuclei, signs of $\Delta \tilde{\omega }$ are most routinely obtained by comparison of peak positions in HSQC/HMQC experiments recorded at multiple static magnetic fields (Skrynnikov et al. 2002), although signs can also be extracted by measurements of off-resonance R_1ρ relaxation rates using weak spin-lock fields (Trott and Palmer 2002; Korzhnev et al. 2003; Massi et al. 2004; Korzhnev et al. 2005b; Auer et al. 2009a; Auer et al. 2009b). Signs for amide proton shift differences can be obtained from the analysis of ¹H^N-¹⁵N zero- and double-quantum CPMG relaxation dispersion data provided that signs of ¹⁵N $\Delta \tilde{\omega }$ values are known (Orekhov et al. 2004; Korzhnev et al. 2005a), or alternatively by the selective R_1ρ method (Auer et al. 2009a) also used for the ¹H^α spin (Auer et al. 2009b).

In principle, signs of ¹H $\Delta \tilde{\omega }$ values are also available from a comparison of peak positions along the direct (F₂) dimension in X-¹H HSQC or HMQC spectra recorded at several magnetic fields. Such an approach is attractive for a number of reasons. (i) X-¹H correlation maps are nearly always available, even at the outset of a project and most certainly when signs are measured using other approaches that frequently involve analysis of peak positions in the indirectly detected dimensions (F₁) of HSQC and HMQC data sets (Skrynnikov et al. 2002). Peaks in F₂ in such spectra are expected to be at identical positions so that the availability of HSQC and HMQC maps offers the opportunity for cross-validation (see below). (ii) Spectra of high resolution can be recorded along F₂ with negligible increase in measurement time. (iii) In cases where resolution is critical, three-dimensional spectra can be recorded, with peak positions in the important direct detection dimension obtained with a high degree of confidence. Herein we explore the efficacy of extracting signs of ¹H^N chemical shift differences by quantifying peak positions in F₂ in two-dimensional correlation spectra recorded at 500 and 800 MHz. The extracted signs obtained in this manner (see below) from a number of different exchanging systems are subsequently compared with those obtained using other methods, and the agreement is excellent. Although the approach is found, in general, to be less sensitive than previously published methods (see below), the information is available ‘for free’ and the signs obtained can be used for cross-validation.

Consider a two-site exchange process interconverting states G and $E,G\underset{k_E}{\overset{k_G}{\rightleftharpoons }}E$, with populations of states G and E given by p_G and p_E, respectively. The exchange-induced shift of the position of a peak derived from the visible, ground state can be obtained from solution of the Bloch-McConnell equations (McConnell 1958) describing the evolution of magnetization due to chemical exchange (see eq. S1 of Supporting Information). When the populations of the states are highly skewed, k_E << k_G, and the intrinsic transverse relaxation rates are the same in each state, it has been shown (Anet and Basus 1978; Skrynnikov et al. 2002) that this shift (in rad.s^-1) can be approximated by

$${\delta }_X=k_G\frac{{\xi }_X}{1+{\xi }_X^2}$$ [1]

where ${\xi }_X=\Delta {\omega }_X∕k_E$, $\Delta {\omega }_X={\omega }_{X,E}-{\omega }_{X,G}$ and ${\omega }_{X,i}$ is the Larmor frequency (in rad.s^-1) of a spin X∈{¹⁵N, ¹³C, ¹H^N...} in state i in the absence of exchange. In the case where the coherence of interest corresponds to single quantum transverse magnetization, as considered here, eq 1 can easily be rewritten to explicitly show the dependence on the static magnetic field as follows

$${\tilde{\delta }}_X=\frac{{\delta }_X}{{\gamma }_X{B}_0}=k_G\frac{{\tilde{\xi }}_X}{1+{\left({\gamma }_X{B}_0{\tilde{\xi }}_X\right)}^2}$$ [2]

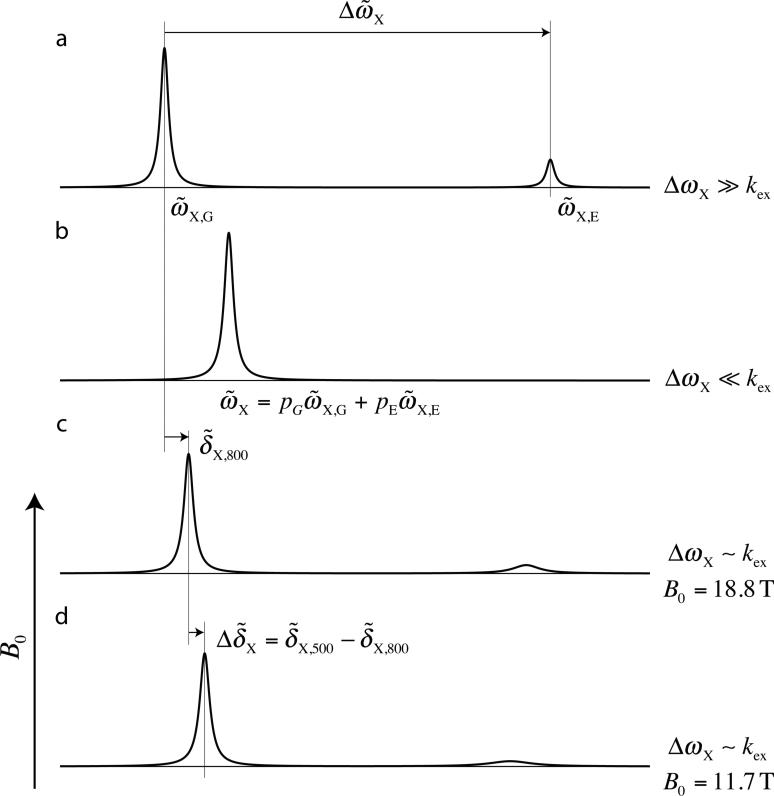
where ${\tilde{\xi }}_X={\xi }_X∕\left({\gamma }_X{\mathit{B}}_0\right)$, γ_X is the gyromagnetic ratio of the nucleus of interest and B₀ is the static magnetic field. It is clear that the absolute value of ${\tilde{\delta }}_X$ decreases with increasing magnetic field strength and, thus, the difference in peak positions measured at a pair of static magnetic fields (B_0,1 < B_0,2), $\Delta {\tilde{\delta }}_X={\tilde{\delta }}_{X,B_{0,1}}-{\tilde{\delta }}_{X,B_{0,2}}$, will have the same sign as $\Delta {\tilde{\omega }}_X$. This is the central result of Skrynnikov et al. (Skrynnikov et al. 2002), however it is worth reiterating it here as it also forms the basis of the approach used presently. Eq 2 can be understood intuitively by considering a simple picture of two-site exchange as a function of k_ex = k_E + k_G, focusing on a single spin, Figure 1. In the limit of very slow exchange (Fig. 1a), $\Delta {\omega }_X\gg k_{ex}$, the exchange contribution to the positions of peaks derived from states G and E is negligible so that ${\tilde{\delta }}_X\approx 0,\Delta {\tilde{\delta }}_X\approx 0$. In the fast exchange limit (i.e. $\Delta {\omega }_X\ll k_{ex}$, Fig. 1b) it can be shown that ${\tilde{\delta }}_X\approx p_E\Delta {\tilde{\omega }}_X$, independent of B₀, so that $\Delta {\tilde{\delta }}_X\approx 0$ as well. In contrast, in the intermediate exchange regime increasing B₀ leads to a decrease in the ratio $k_{ex}∕\Delta \omega$ and the system effectively moves towards the slow exchange regime so that ${\tilde{\delta }}_X$ decreases; hence $\Delta {\tilde{\delta }}_X$ is non-zero.

Figure 1.

Schematic illustrating the relation between ${\tilde{\delta }}_H$ and B₀ for a single spin exchanging between two sites with distinct chemical shifts. (a) In the limit $\Delta {\omega }_{\text{X}}\gg k_{\text{ex}}$ the system is in slow exchange and separate peaks are observed at positions that are essentially independent of exchange (${\tilde{\omega }}_{\text{X,G}}$ and ${\tilde{\omega }}_{\text{X,E}}$). (b) In the limit where $\Delta {\omega }_{\mathrm{X}}\ll k_{\text{ex}}$, a single peak is observed at the population weighted average of ${\tilde{\omega }}_{X,E}$ and ${\tilde{\omega }}_{X,G}$. (c,d) As B₀ increases $k_{ex}∕\Delta \omega$ decreases so that the exchanging system moves towards the slow exchange regime and hence ${\tilde{\delta }}_X$ decreases.

As a first test of the method we used a sample of [U-²H,¹⁵N] enriched Pfl6 Cro I58D (Roessler et al. 2008). This protein is a member of the Cro family of bacteriophage transcription factors with a mixed α+β fold similar to the λ Cro repressor, and the mutation at position 58 ensures a monomer structure in solution (LeFevre and Cordes 2003). Previous ¹⁵N and ¹H^N CPMG relaxation dispersion experiments established that the protein exchanges between two states with k_ex and p_E, of (1128±9) s^-1 and (5.52±0.03) %, respectively (5°C). Large residue specific ¹⁵N and ¹H^N chemical shift differences between exchanging states were also noted, ranging up to 7.1 ppm and 1.4 ppm for $\mid \Delta {\tilde{\omega }}_N\mid$ and $\mid \Delta {\tilde{\omega }}_H\mid$, respectively. It is worth noting that use of a per-deuterated sample eliminates ¹H^N J-couplings to adjacent proton nuclei that would otherwise limit the accuracy of measured amide proton peak positions in F₂. In studies of protein excited states in our laboratory highly deuterated samples are always available as the ‘isolation’ of ¹H^N spins from other proton sites offers distinct advantages in recording and analyzing ¹H^N CPMG profiles (Ishima and Torchia 2003).

Prior to analyzing amide proton exchange-induced shifts, $\Delta {\tilde{\delta }}_H^{\text{exp}}={\tilde{\delta }}_{H,500}^{\text{exp}}-{\tilde{\delta }}_{H,800}^{\text{exp}}$, from HSQC or HMQC data sets recorded at 500 and 800 MHz (in our case) it is necessary to accurately account for small differences in experimental conditions that can arise between measurements on different spectrometers – for example, slight differences in the sample temperature (< 0.5°C on our systems) or spectrum referencing. To this end we have minimized the function

$${\chi }^2=\sum _r{\left(\left(\mid \Delta {\tilde{\delta }}_{H,r}^{calc}\mid -\mid \Delta {\tilde{\delta }}_{H,r}^{\text{exp}}+offset\mid \right)∕{\tilde{\sigma }}_{H,r}\right)}^2$$ [3]

where $\Delta {\tilde{\delta }}_{H,r}^{\text{exp}}$ is the difference in the positions of peak ‘r’ in a pair of spectra recorded at 500 and 800 MHz and $\Delta {\tilde{\delta }}_{H,r}^{calc}$ is the corresponding value calculated on the basis of k_ex, p_E and residue-specific $\Delta {\tilde{\omega }}_H$ values that are obtained from fits of relaxation dispersion profiles. Values of $\Delta {\tilde{\delta }}_{H,r}^{calc}$ are obtained by numerical solution of the Bloch-McConnell equations (eq. S1 of Supporting Information). In eq 3 ${\tilde{\sigma }}_{H,r}=\sqrt{{\left({\tilde{\sigma }}_{H,r}^{calc}\right)}^2+{\left({\tilde{\sigma }}_{H,r}^{\text{exp}}\right)}^2}$ is the combined error in the calculated and experimental $\Delta \tilde{\delta }$values. Values of ${\tilde{\sigma }}_{H,r}^{\text{exp}}$ were calculated from the errors in peak positions in spectra, estimated as the standard deviation in peak locations in repeat measurements; similar standard deviations were obtained from spectra at both 500 and 800 MHz, with a median value of ${\tilde{\sigma }}_{H,r}^{\text{exp}}\approx 0.2$. Values for ${\tilde{\sigma }}_{H,r}^{\text{exp}}$ were assigned either 0.2 ppb or the measured value, whichever was largest. The corresponding ${\tilde{\sigma }}_{H,r}^{calc}$ values (median value of 0.03 ppb) were obtained from a bootstrap analysis (Press et al. 2007) described in Supporting Information. A minimum in χ² (eq 3) was found with offset = 2.85 ppb. Note that the fitting procedure to determine the best value of offset makes no assumptions about the signs of $\Delta {\tilde{\delta }}_{H,r}^{calc}$ (since the absolute value is used in eq 3) and therefore does not require a priori knowledge of the signs of $\Delta {\tilde{\omega }}_H$.

Once spectra were referenced properly values of $\Delta {\tilde{\delta }}_H^{\text{exp}}$ were obtained for all residues satisfying the following criteria:

1. $\mid \Delta {\tilde{\omega }}_H\mid$ values generated from fits of ¹H^N relaxation dispersion profiles must be greater than twice the estimated error in the shift difference, obtained from a standard bootstrap analysis (see Supporting Information). Signs were not obtained for residues for which this was not the case, since ${\tilde{\omega }}_G\approx {\tilde{\omega }}_E$. Chemical shifts of the excited state in this case are set to ${\tilde{\omega }}_G$.

2. Measured shifts, $\Delta {\tilde{\delta }}_H^{\text{exp}}$, must be at least twice as large as their estimated error, ${\tilde{\sigma }}_H^{\text{exp}}$.

3. Back-calculated shifts, $\Delta {\tilde{\delta }}_H^{calc}$, must be twice as large as ${\tilde{\sigma }}_H=\sqrt{{\left({\tilde{\sigma }}_H^{calc}\right)}^2+{\left({\tilde{\sigma }}_H^{\text{exp}}\right)}^2}$. (4) $\Delta {\tilde{\delta }}_H^{\text{exp}}$ values obtained from HMQC and HSQC data sets must predict the same sign. This criterion was always fulfilled in the data examined here.

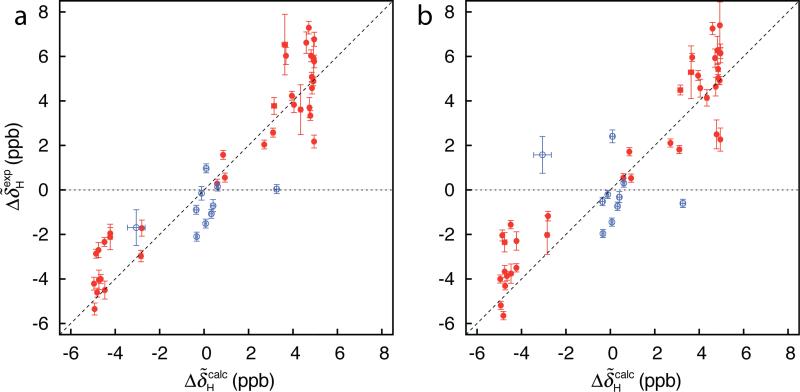
Figure 2 shows the correlation between experimental $\left(\Delta {\tilde{\delta }}_H^{\text{exp}}\right)$ and back-calculated $\left(\Delta {\tilde{\delta }}_H^{calc}\right)$ exchange-induced ¹H^N chemical shifts obtained for the Pfl6 I58D domain based on an analysis of either HSQC (a) or HMQC (b) data sets. In the case of the back-calculated shifts we have used signs that are available from ¹H^N-¹⁵N zero- and double quantum (ZQ/DQ) CPMG relaxation dispersion profiles (47 residues). Values of $\Delta {\tilde{\omega }}_H$ could be obtained for a total of 37 residues using the methodology (and selection criteria) described here, with the smallest signed $\Delta {\tilde{\omega }}_H$ value equal to 0.11 ppm. Shown in Figure 2 in red are $(\Delta {\tilde{\delta }}_H^{calc},\Delta {\tilde{\delta }}_H^{\text{exp}})$ values that satisfy criteria 1-4 above and thus sign information from $\Delta {\tilde{\delta }}_H^{\text{exp}}$ would be ‘accepted’ as correct. In blue are $(\Delta {\tilde{\delta }}_H^{calc},\Delta {\tilde{\delta }}_H^{\text{exp}})$ values that are not considered trustworthy (one or more of criteria 1-4 is not fulfilled). Importantly, the ¹H^N $\Delta {\tilde{\omega }}_H$ signs based on either analysis of ZQ/DQ experiments or on $\Delta {\tilde{\delta }}_H^{\text{exp}}$ values are in complete agreement when criteria 1-4 are satisfied (red circles).

Figure 2.

Correlation between $\Delta {\tilde{\delta }}_H^{\exp }$ and $\Delta {\tilde{\delta }}_H^{calc}$ for the Pfl6 I58D domain based on analysis of HSQC (a) or HMQC (b) data sets recorded at 500 and 800 MHz (5 °C). In red are $(\Delta {\tilde{\delta }}_H^{calc},\Delta {\tilde{\delta }}_H^{\exp })$ values satisfying criteria 1-4 in the text so that the sign from $\Delta {\tilde{\delta }}_H^{\exp }$ would be ‘accepted’ as correct, while in blue are data points that cannot be considered as trustworthy based on the same criteria; signs from $\Delta {\tilde{\delta }}_H^{\exp }$ would not be used in this case.

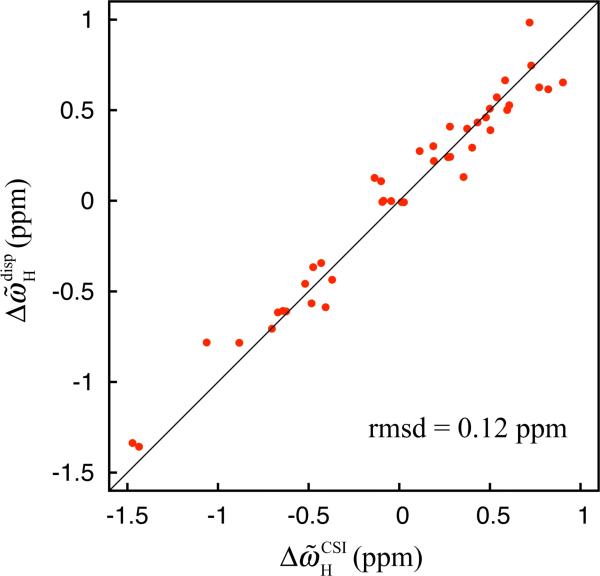
The combination of $\mid \Delta {\tilde{\omega }}_H\mid$, as measured from relaxation dispersion, and the $\Delta {\tilde{\delta }}_H^{\text{exp}}$ values reported here allows the determination of $\Delta {\tilde{\omega }}_H$ for many of the residues in the Pfl6 I58D domain that can then be used to provide insight into the nature of the excited state. Here we have predicted chemical shift differences assuming that the excited state is unfolded using residue-specific random-coil ¹H^N chemical shift values computed for each residue (Wishart et al. 1995). Figure 3 shows the comparison between such calculated values and those measured experimentally; the striking agreement (rmsd = 0.12 ppm) between the two sets of values strongly suggests that the low-populated state is fully disordered and provides further validation that the determined signs are correct.

Figure 3.

Correlation plot between ¹H^N chemical shift differences between the ground and excited states of the Pfl6 I58D domain as measured by relaxation dispersion experiments, $\Delta {\tilde{\omega }}_H^{disp}$, and predicted shift differences assuming that the excited state is unfolded, $\Delta {\tilde{\omega }}_H^{CSI}$, calculated as described by Wishart and coworkers (Wishart et al. 1995). Signs of $\Delta {\tilde{\omega }}_H^{disp}$ were determined using the experimentally measured exchange induced shifts, as described in the text.

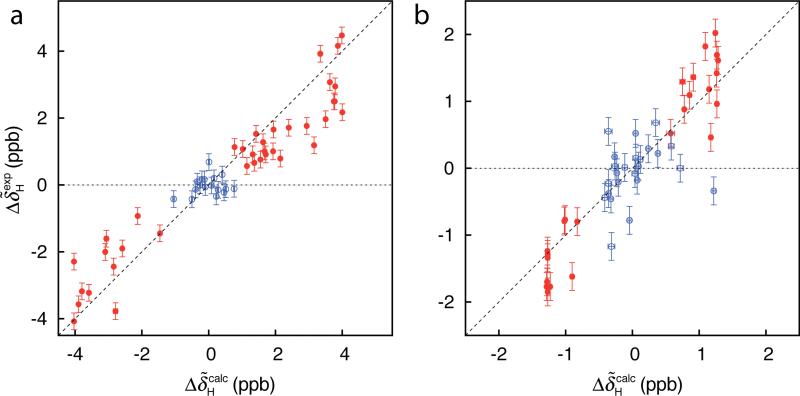
In order to test the generality of the described method for measuring signs of $\Delta {\tilde{\omega }}_H$ we have considered two other exchanging protein systems that are a more challenging ‘test’ of the approach than the Pfl6 domain discussed to this point because the excited state in each case is less populated. Specifically, in both systems a folded protein exchanges with an on-pathway folding intermediate under the conditions in each study. We have considered an FF module from the protein HYPA/FBP11 with exchange parameters k_ex = (1817±14) s^-1, p_E = (2.84±0.02)%, 30°C (Korzhnev et al. 2007) and an A39V/N53P/V55L variant SH3 domain from the Fyn tyrosine kinase (Neudecker et al. 2006), k_ex = (836±4) s^-1, p_E = (1.979±0.006)%, 20°C. Figure 4a shows the correlation between $\Delta {\tilde{\delta }}_H^{\text{exp}}$ and $\Delta {\tilde{\delta }}_H^{calc}$ for the FF domain. As described above calculation of $\Delta {\tilde{\delta }}_H^{calc}$ is based on k_ex, p_E and residue-specific $\Delta {\tilde{\omega }}_H$ values that are obtained from fits of ¹H^N relaxation dispersion data. Signs of $\Delta {\tilde{\omega }}_H$ and hence of $\Delta {\tilde{\delta }}_H^{calc}$ (eq 2) have been determined from ¹H^N-¹⁵N ZQ/DQ CPMG experiments (Orekhov et al. 2004; Korzhnev et al. 2005a). Figure 4b shows the agreement between $\Delta {\tilde{\delta }}_H^{\text{exp}}$ and $\Delta {\tilde{\delta }}_H^{calc}$ for the A39V/N53P/V55L Fyn SH3 domain. In this case signs of $\Delta {\tilde{\delta }}_H^{calc}$ were obtained from off-resonance R_1ρ experiments following the method developed by Auer et al. (Auer et al. 2009a). In total, signed $\Delta {\tilde{\omega }}_H$ values were available for 38 (FF domain) and 24 (Fyn SH3 domain) residues – with the smallest signed $\Delta {\tilde{\omega }}_H$ value equal to 0.21 and 0.14 ppm, respectively – based on measurement of $\Delta {\tilde{\delta }}_H^{\text{exp}}$. In contrast, 55 and 48 signs were obtained for the FF and SH3 domains by ZQ/DQ CPMG and R_1ρ experiments, respectively. As with the Pfl6 domain, all of the signs obtained using the methodology described herein were the same as those measured previously using other approaches.

Figure 4.

Correlation between $\Delta {\tilde{\delta }}_H^{\text{exp}}$ and $\Delta {\tilde{\delta }}_H^{calc}$ values for the (a) FF (30 °C) and (b) A39V/N53P/V55L Fyn SH3 (20 °C) domains based on analysis of HSQC data sets recorded at 500 and 800 MHz. Other details are as in the legend to Figure 2.

While the experimental results presented in this study establish the robustness of the methodology it is also apparent that there are limitations. Indeed, for every exchanging system considered here a significantly larger number of signed ¹H^N $\Delta {\tilde{\omega }}_H$ values could be obtained from either ZQ/DQ CPMG relaxation dispersion or off-resonance R_1ρ experiments. For the A39V/N53P/V55L Fyn SH3 domain, in particular, only half the number of signs that were available from R_1ρ measurements could be obtained from $\Delta {\tilde{\delta }}_H^{\text{exp}}$. This follows directly from the fact that $\mid \Delta {\tilde{\delta }}_H^{\text{exp}}\mid <2$ ppb for this system; such small changes in peak positions are difficult to measure and require careful adjustment of experimental conditions and spectrum referencing (see above). On the other hand R_1ρ experiments can be rather time consuming (1-2 days) compared to the time investment for recording a pair of HSQC data sets at two fields that would be recorded in any event for measurement of signs of ¹⁵N chemical shift differences (Skrynnikov et al. 2002). In addition, R_1ρ experiments are typically recorded in 1D mode so that peak overlap can be limiting (Korzhnev et al. 2003; Korzhnev et al. 2005b; Auer et al. 2009a). In any event, it most certainly is the case that the different classes of experiment can be complementary because they depend somewhat differently on exchange parameters (Auer et al. 2009a). Finally, we note that in principle comparison of peak positions in pairs of spectra recorded on different spectrometers can be influenced by other factors besides issues related to referencing and temperature. For systems with non-zero magnetic susceptibility anisotropies there will be field-induced differences in chemical shifts caused by fractional alignment (Tjandra et al. 1997). In practice these effects are expected to be very small. Indeed the agreement between $\Delta {\tilde{\delta }}_H^{\text{exp}}$ and $\Delta {\tilde{\delta }}_H^{calc}$ values for the three proteins considered here and, in general, the excellent agreement between signs of ¹⁵N and ¹³C^α chemical shift differences measured using a variety of different approaches (Auer et al. 2009a) including one involving a comparison of peak positions in spectra recorded at different static magnetic fields, suggests that shifts due to alignment can be neglected.

In summary, it has been shown that comparison of peak positions in the F₂ dimension of ¹H^N-¹⁵N correlation maps recorded at two or more different static magnetic fields provides a very straightforward approach for obtaining the signs of ¹H^N $\Delta \tilde{\omega }$ values. The strategy described here extends beyond amide protons and is equally applicable for ¹H^α protons as well, using U-¹³C, >50% ²H labeled proteins that are employed for measurement of ¹H^α relaxation dispersion profiles (Lundstrom et al. 2009a). Although this method does not replace other more established techniques that are more ‘sensitive’ to the sign of $\Delta \tilde{\omega }$ it is nevertheless attractive because signs are obtained from correlation maps that can be recorded rapidly and that would normally be available during the course of a relaxation dispersion NMR study.