ASB Clinical Biomechanics Award Paper 2010: Virtual Pre-Operative Reconstruction Planning for Comminuted Articular Fractures

Abstract

Background

Highly comminuted intra-articular fractures are complex and difficult injuries to treat. Once emergent care is rendered, the definitive treatment objective is to restore the original anatomy while minimizing surgically induced trauma. Operations that use limited or percutaneous approaches help preserve tissue vitality, but reduced visibility makes reconstruction more difficult. A pre-operative plan of how comminuted fragments would best be re-positioned to restore anatomy helps in executing a successful reduction.

Methods

In this study, methods for virtually reconstructing a tibial plafond fracture were developed and applied to clinical cases. Building upon previous benchtop work, novel image analysis techniques and puzzle solving algorithms were developed for clinical application. Specialty image analysis tools were used to segment the fracture fragment geometries from CT data. The original anatomy was then restored by matching fragment native (periosteal and subchondral) bone surfaces to an intact template, generated from the uninjured contralateral limb.

Findings

Virtual reconstructions obtained for ten tibial plafond fracture cases had average alignment errors of 0.39 (0.5 standard deviation) mm. In addition to precise reduction planning, 3D puzzle solutions can help identify articular deformities and bone loss.

Interpretation

The results from this study indicate that 3D puzzle solving provides a powerful new tool for planning the surgical reconstruction of comminuted articular fractures.

INTRODUCTION

Comminuted intra-articular fractures are severe injuries, with high rates of complication both short- and long-term. High-energy traumatic events that produce comminuted articular fractures such as motor vehicle crashes, falls from height, and ballistic injuries severely disrupt both osseous and soft tissues. In order for the limb to heal and function properly, it is essential that the original anatomy be restored with minimal surgical insult (Dirschl et al., 2004, Watson et al., 2000). However, reconstructing the comminuted bone fractures is challenging. The process of reducing complex fragment displacements is substantially complicated by compromised soft tissues, leaving the injured extremity at risk for infection and wound breakdown after intra-articular fracture surgery.

While diaphyseal fractures need only general alignment and stability to form abundant callus which bridges fracture gaps (Schmidt et al., 2003), intra-articular fractures require precise fragment reduction to restore the original anatomy as closely as possible (Ruedi and Allgower, 1979). Accurate articular fracture reduction is a key determinant to avoid deleterious cartilage contact stress elevations (Anderson et al., 2010, Heim, 1995). Traditionally, large surgical approaches have been used to expose the intra-articular fracture fragments and to allow for direct visualization of the displacements and the reduction. However, the secondary surgical insult from a wide approach may lead to severe complications. To avoid such risks, an alternative is to use a limited approach, where fragments are manipulated percutaneously under fluoroscopic visualization (Figure 1). Unfortunately, the diminished visibility and accessibility can lead to a less than perfect reduction – a factor likely leading to the development of post-traumatic osteoarthritis (Brown et al., 1988, Li et al., 2008). When limited approaches are utilized the surgeon must have a very clear pre-operative understanding of the size, location and displacement of the fracture fragments, which is obtained through careful assessment of imaging studies. CT imaging provides the most valuable information regarding fracture patterns and displacements (Jones et al., 2003). However, even with CT it is oftentimes difficult to identify how multiple bone fragments should be put back together in three dimensions. A detailed pre-operative reconstruction plan, including a simulation of the actual fracture reduction would make surgical management far less complex.

Figure 1.

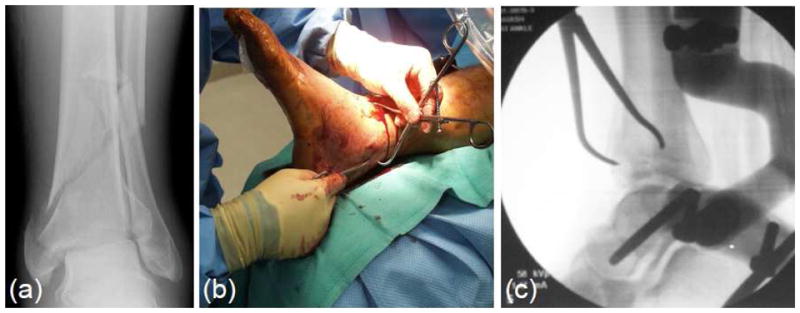
Intra-articular fractures such as the tibial plafond (a) are difficult injuries to treat. Percutaneous fracture reduction (b) under fluoroscopic guidance (c) minimizes secondary surgical insult and promotes healing.

Novel methods for 3D “puzzle solving” reconstruction of intra-articular fractures have recently been developed, with benchtop application to a surrogate model (Thomas et al., 2010). Matching native fragment bone surfaces to an intact template proved to be an effective and computationally tractable methodology. Although these methods were successful in the surrogate model, in vivo fractures are much more challenging. Whereas surrogate geometries could be obtained from high-resolution laser scans, in vivo fragment geometries are necessarily acquired from lower resolution CT data. In addition, the structure of peri-articular bone makes it less homogeneous and more susceptible to plastic deformations (i.e., crush). These factors invariably lead to alignment errors, since fragment surfaces may not precisely match the template.

The objective of the present study was to develop new puzzle solving methods that would accommodate in vivo complexities and provide accurate reconstructions of highly comminuted articular fractures. Because of the high degree of bilateral symmetry in the normal population’s lower extremities (<2%), the intact contralateral tibia was used as a template for reconstruction (Plochocki, 2004, Auerbach and Ruff, 2006). Substantial technical advancements have been achieved in order to address these added complexities. In order to evaluate these methods, we tested the hypothesis that the normal anatomy of human tibial plafond fractures can be restored by aligning fragment periosteal and subchondral surfaces to the mirrored image of the non-affected contralateral tibia. The specific aims were to develop new bone segmentation techniques that would yield accurate fragment/bone geometries from clinical CT data, and to align fragment-contralateral native surfaces in a series of tibial plafond fracture cases using advanced 3D puzzle solving algorithms.

METHODS

Clinical Management

Ten tibial plafond fractures were retrospectively studied using novel 3D puzzle solving methods (Figure 2). The fractures ranged in severity from moderate to severe, with AO/OTA classifications ranging from B1 to C3. Acute clinical management had involved the application of an external fixator to stabilize the fracture and to restore limb length. Prior to any further treatment, CT scans had been acquired of the fractured limb, and of the uninjured contralateral limb with resolutions of 0.25–0.6mm pixel spacing, and 0.3–1.0 mm slice thickness. Definitive surgical fracture reconstruction was delayed from one to two weeks until swelling had subsided, at which time the soft tissues were more tolerant to surgery. Surgical fracture reduction had been performed using a limited approach, under fluoroscopic guidance. Bone fragments had then been stabilized with screw fixation, and a post-operative CT scan had been obtained to assess reduction quality.

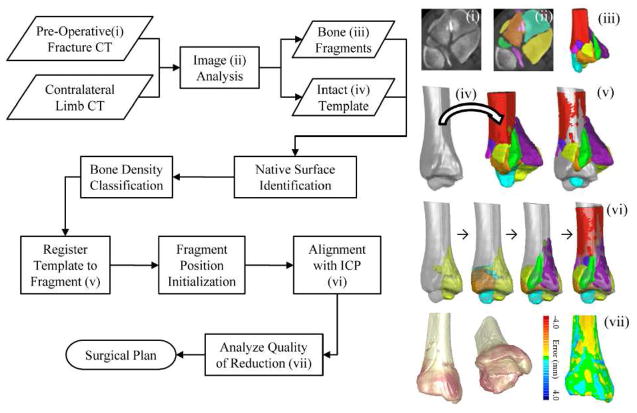
Figure 2.

A flowchart of the puzzle solving process. Intact template and fragment geometries are generated by analyzing pre-operative CT data. Native surfaces (periosteal and subchondral) are then segmented and classified from geometric and bone density information. The fracture is then reduced by first registering the template to the fracture’s base fragment, then grossly positioning fragments in a series of initialization steps, and finally precisely aligning fragment-template surfaces with an iterative closest point (ICP) algorithm. The performance of these methods in obtaining virtual reconstructions in a series of tibial plafond fracture cases was assessed.

CT Segmentation

The first step in virtual fracture reconstruction was to obtain accurate geometric models of the bony anatomy from CT scan data. The segmentation of discrete bone fragments from clinical CT data is challenging for numerous reasons. Most notably, limitations in CT spatial resolution make discernment of the bone boundaries difficult, particularly for abutting cancellous fracture edges. In addition to substantial geometric variability, many fragments include both cortical and cancellous bone, tissues with very different radiographic appearance (Figure 3a). While the intensity of cortical bone is much greater than the surrounding tissues, the intensities of cancellous and some soft tissues often overlap, making them difficult to distinguish. A largely automated image segmentation methodology was developed to extract bone and bone fragment geometries from pre- and post-surgical reduction CT scans. The image segmentation algorithm used a 3D watershed transform (Meyer, 1994), implemented in the MATLAB image processing toolbox (MathWorks, Inc; Natick, MA, USA). With a watershed analysis, image data can be conceptualized as a topographical map, where basins are separated by ridgelines. A common limitation to watershed analyses is over-segmentation, i.e. separating of an object into too many parts. In musculoskeletal CT scans, variable bone density causes small local variations in the image data. These regional differences are erroneously treated as separate basins and ultimately as discrete objects. A novel approach was used to pre-process the image data and minimize these effects. Generally, image data were manipulated by imposing regional minima in regions contained in each fragment’s boundary, topographically analogous to carving a single basin within each fragment’s region. This approach ensured that individual objects (i.e. fragments) would not be connected. A watershed algorithm was then applied to first flood those regions/seeds, and expand their boundaries up to the edges of other fragments or other non-osseous tissues. The novelty of this implementation was in the method for defining the appropriate seeds in order to yield accurate fragment models.

Figure 3.

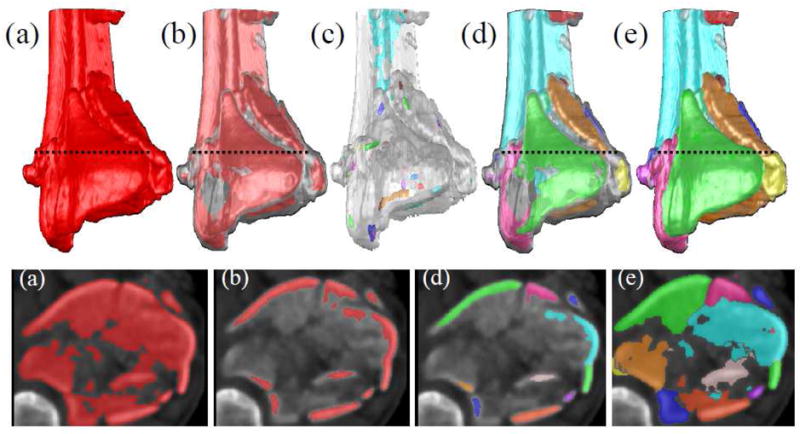
Novel image analysis techniques were developed for generating discrete fragment models that could be spatially manipulated and reduced. This process is illustrated for a comminuted tibial plafond fracture in 3D (top row) and 2D (bottom row). After the whole tibia is extracted (a) from the image volume, cancellous bone is removed with erosion, leaving only the diaphysis, metaphyseal cortex and subchondral plate (b). Seeds were placed within each cortical fragment with an extended minimum transform (c). A watershed transform propagated the seeds up to the edges of the cortical fragments (d). Those cortical fragments were subsequently used as seeds for a second watershed transform that further propagated fragment boundaries up to cancellous edges (e).

A first pass of this segmentation algorithm was used to remove the fibula and talus from the image dataset. Separate seeds were placed in the tibia, talus and fibula using simple intensity thresholding. The threshold level was set as the minimum intensity that would reliably separate the tibial and talar subchondral surfaces (typically >500HU). After imposing minima upon the seeds, the watershed algorithm was applied and the entire distal tibia was extracted (Figure 3a). Next, the fractured tibia was further segmented so that each fragment would be a single object. Since there was little variation in intensity in the regions between some fragments, simply thresholding the image was not an effective approach. To solve this problem, it was necessary to identify an isolated region within each fragment that could seed subsequent watershed operations.

It was observed that the vast majority of bone fragments included one solid piece of non-cancellous (subchondral or cortical) bone. Since these relatively dense pieces of bone were not connected, they were suitable locations for seeding the watershed algorithm. Using an intensity threshold (typically >500 HU), regions corresponding to cancellous bone were removed with erosion, leaving a mask of cortical bone (Figure 3b). Although some cortical fragments were still connected in the resultant mask, abutting cortical boundaries were separated by faint gradients. If a larger threshold was initially chosen such that all cortical fragments were separated, significant portions of cortical tissue would invariably be lost. Therefore, in order to generate a discrete seed within each cortical fragment; an extended maxima operator was applied (Figure 3c). This operator identifies groups of voxels that have intensities that are greater than their immediate surroundings by a specified threshold. For these data, an extended maxima threshold of 80HU was effective. The watershed transform then propagated the seeds to fill the remaining cortical bone volume, thereby creating discrete cortical fragments (Figure 3d). Cortical fragments that were visually judged to be over-segmented were fused together into a single object. Finally, these cortical objects were used as seeds for another watershed operation that recovered the fragments’ cancellous volume (Figure 3e). From the segmented image volume, surface meshes of the bone fragments and the contralateral tibia were created, with uniform triangle sizes of 0.1 mm². Lastly, moderate smoothing was performed on the fragment surfaces with a gaussian convolution kernel (σ = 0.6, 3x3x3 voxel neighborhood).

Fragment Mesh Segmentation and Classification

Since fragment and intact native surfaces only needed to be matched as part of the puzzle solving approach, de novo fracture edges were not included in the alignment process. Identification of the fracture surfaces was accomplished with a region-growing algorithm that propagated discrete surface patches up to boundaries of high curvature (Thomas et al., 2010). Fracture surfaces tended to have significant surface variations, causing the algorithm to segment them into many smaller surface patches. By contrast, the native surface (periosteal and subchondral bone) was smooth, resulting in a single contiguous set of patches. Therefore the set of patches with the largest surface area was reliably identified as native.

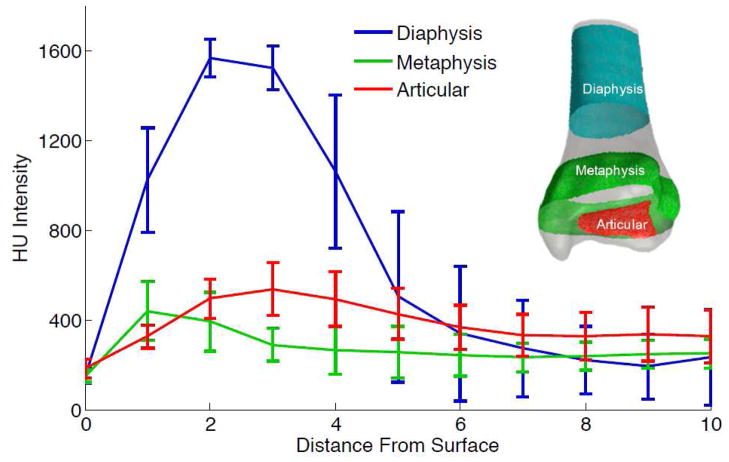
Having knowledge about the fragment’s anatomic structure allows one to develop more intelligent reconstruction algorithms. For example, an algorithm that prioritizes joint congruity would need to have the articular surface identified. Knowing that a surface patch corresponds to the diaphysis, metaphysis or subchondral plate (articular) provides useful information for coarsely aligning fragments and for improving overall algorithmic performance. The distal tibia’s variable tissue composition and variable radiographic appearance was exploited to develop such methods. Different regions of a bone have a density that uniquely varies from the outer surface to the interior. This characteristic was used to computationally classify anatomy, by modelling how CT intensities change over a distance along an inward-directed surface normal (Figure 4).

Figure 4.

Different regional bony structures of the distal tibia display different CT intensity profiles. Series-averaged profiles along the intact contralateral’s diaphysis, metaphysis and articular (subchondral) regions are shown. Statistical models for each class were derived from the collected profiles. Fracture fragment surfaces were classified by fitting their profiles to the statistical models.

The classification process started with a training phase where the user selected patches on the intact tibia’s mesh that corresponded to the diaphysis, metaphysis and the articular surface’s subchondral plate. Density profiles were collected at each facet on the triangular mesh, by measuring the HU intensity at 1mm increments beneath the surface. Gaussian mixture models were then generated from the set of profiles for each anatomic type. Next, density profiles for fragment native surfaces were collected and the probability for belonging to each model was calculated. Areas of the surface mesh that best matched the diaphyseal and metaphyseal models were labelled as periosteal, while the others were labelled as articular. Since each native surface patch is either periosteal or articular, patches were classified according to the label with maximum occurrence.

Iterative closest point (ICP) algorithms have been shown to effectively align bone fragments in previous work (Thomas et al., 2010), but classical ICP performance depends greatly upon fragments’ initial displaced positions. The computational speed and probability for an accurate solution was shown in that work to be inversely proportional to the magnitude of fragment displacement (Thomas et al., 2010). Leveraging the results from classification, and from a priori knowledge about typical fracture morphology, a series of algorithms were developed that positioned each fragment closer to their anatomic target, in order to improve alignment speed and stability.

Initializing fragment positions started with registering the diaphysis of the intact template to the fractured tibia’s most proximal segment (Figure 2iv). Next, gross axial alignment was restored by shifting the center of mass of the constellation of fragments toward the template’s primary longitudinal axis. Fragments were then rotated such that their average articular surface normal aligned to the template’s average articular surface normal. Then, limb length was “restored” by translating fragments along the longitudinal axis until fragment and template articular surfaces were at the same level. Then, fragments were rotated about their center of masses, and translated radially in order to maximize the overlap between fragment and template periosteal surfaces.

Lastly, ICP was implemented to make precise final alignment adjustments. In the order from largest to smallest native surface, ICP was used to implement rigid affine rotations and translations of each fragment, such that the cumulative distance between fragment-template surfaces was minimized (Figure 2vi) . The accuracy and speed of alignment was improved by iteratively reducing the ICP search space as each new template/fragment match was achieved.

Puzzle solution accuracies were quantified by calculating distances between the intact template and the reduced tibia’s native surface (Figure 2vii). Since the articular surface is the most clinically important to precisely reduce, it was isolated from the periosteal surface and compared to the intact anatomy. To illustrate the clinical utility of 3D puzzle solving, virtual reconstructions were also compared to the physical reconstructions achieved surgically, based upon segmentations of post-operative CT scan data.

RESULTS

There was a range in comminution severity among the ten tibial plafond fracture cases that were segmented and reconstructed (Figure 5). The number of fragments ranged from 4 to 11, of which between 2 and 6 were articular fragments. Whereas prior segmentation methods had required 8–10 hours per case (Thomas et al., 2010), this new watershed-based method enabled the processing of each case in less than 20 minutes, with minimal user intervention. To support the accuracy of the segmentation method, a trained user manually segmented each case’s largest articular fragment with an interactive Cintiq® display tablet (Wacom Co, Toyonodai, Kazoshi, Saitama, Japan). Comparison between manual and automated segmentations showed an average signed distance difference of only 0.20 (0.22 standard deviation) mm. This difference was less than the size of a single voxel, supporting the accuracy of the watershed segmentation technique.

Figure 5.

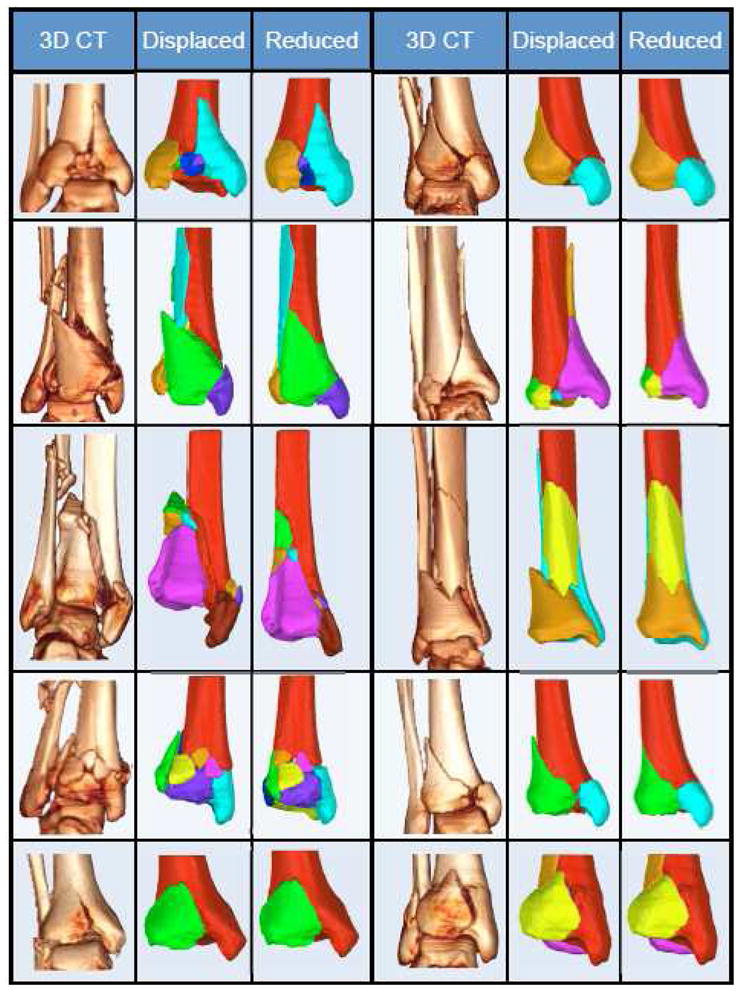
Ten clinical tibial plafond fractures are puzzle solved. Volume renderings (3DCT) and segmented fragment geometries (Displaced) illustrate this series’ range in severity and variable fracture characteristics. Puzzle solutions (Reduced) provide ideal fragment positioning data for restoring original anatomy.

Native surfaces were reliably classified as periosteal or articular by matching density profiles to Gaussian mixture models. In order to assess the intensity profile algorithm’s accuracy, its results were compared to visual classifications made by an experienced user. The intensity profile algorithm correctly classified 76% of the articular surfaces, and 77% of the periosteal surfaces. When mesh faces were grouped into patches by the region-growing operation and classified according to maximum occurrence of periosteal or articular labels, both periosteal and articular patches were correctly identified in all cases.

The automatic fragment initialization algorithm placed the fragments close to their anatomic target. Subsequently, the ICP algorithm was able to finalize each fragment’s alignment in less than one minute. Larger fragments having relatively high surface variation, such as the articular fragments, were quickly aligned. Smaller fragments with relatively flat native surfaces took more time to align. With less surface variation, the ICP test space was less constrained, and therefore greater translations and rotations had to be evaluated by the algorithm. Computational surface alignment yielded precise geometric reconstructions for the ten clinical cases, with average distance differences of 0.39 mm (standard deviation 0.50 mm) relative to their intact templates (Figure 5). The articular surfaces were generally congruent. However, five cases displayed some crush from the impact event. These cases had an average articular alignment error of 0.63 (0.17 standard deviation) mm, while cases without crush averaged 0.4 (0.11 standard deviation) mm. In addition to articular distortion, several cases displayed clear evidence of cancellous crush with gaps between fracture surfaces. In the most severe instance, the distance between one fragment’s superior surface and another’s inferior surface was 10 mm (Figure 5, Panel 6c). The majority of bone fragments were not plastically deformed; but rather fit well to both the intact template, and to adjacent other fragments.

DISCUSSION

New image analysis and reconstruction algorithms are here reported to advance 3D puzzle solving for use in clinical fracture cases. Various groups have developed virtual environments wherein fracture reduction is pre-operatively planned by manually manipulating 3D models (Citak et al., 2007). Those computational tools have been shown to improve reductions and reduce surgical time. Although such methods may be applicable to 3 or 4-segment fractures, it is impractical to manually reconstruct more highly comminuted fractures, in research and especially clinical settings. In order to minimize alignment error and manpower costs, the degree of user interaction guidance has to be minimal. The algorithms developed in this study were used to reconstruct comminuted articular fractures almost completely automatically, once fragment geometries had been segmented.

Clinical evidence suggests that anatomic fracture reduction is very important, especially at the joint surface. Articular incongruities can alter the joint mechanics and thereby predispose to joint degeneration. The degree of residual displacement that a joint can tolerate varies from site to site (Marsh et al., 2002), but some joints such as the hip have been to shown to poorly tolerate even as little as 1 mm of residual displacement after acetabular fractures (Matta, 1996). Even without preferential weighting for articular surface alignment, the puzzle solution achieved sub-millimeter accuracies for non-deformed articular fragments.

Surgery is greatly simplified when there is a priori knowledge of how to spatially manipulate fragments such that original anatomy is restored. Currently, surgeons reduce fractures by assessing fragment inter-digitations visually and by touch, typically by trial and error. Unfortunately, each “error” prolongs the procedure and adds to the surgical trauma to the fragments and the surrounding soft tissues. 3D puzzle solutions can potentially diminish this trial and error. Obviously, surgically implementing the puzzle solution requires great surgical skill. Even for the most experienced surgeons, reducing fragments to within sub-millimeter accuracies under fluoroscopic guidance is very difficult. To reduce technical demands, ongoing work seeks to develop puzzle solving into an intra-operative tool. Once real-time fragment positioning data are linked to computational models, 3D geometries can be viewed dynamically, and updated reduction instructions can be generated as deviations from the original pre-operative plan arise.

While executing the perfect reduction may be physically impossible in some cases, puzzle solving can still be used to improve reduction outcomes, by identifying difficult to appreciate bone defects. A frequent consideration in that regard arises from crushed/deformed fragments. Comparison of the puzzle solution to what was actually achieved surgically illustrates this point (Figure 6). The surgically reduced tibia in Case 1 ended up shortened by more than 2.5 cm, an outcome with likely adverse biomechanical effects. By providing precise limb length information, the puzzle solution could have enabled the surgeon to better restore the original anatomy. In Case 2, the puzzle solution showed an obvious articular defect. While perfectly repairing that defect would have been difficult if not impossible due to fragment plastic deformation, the defect was not detected intra-operatively. Had this unavoidable post reduction defect been appreciated in advance, biological intervention or engineered tissues might have been used to mitigate the associated incongruity. For Case 3, a metaphyseal void in the puzzle solution highlights a loss of bone. Had a puzzle solution been available, this structural deficiency could likely have been recognized in advance, giving the surgeon the opportunity to have either planned an alternate fragment configuration, a different fixation technique, or a bone grafting solution. Unfortunately, the physical reconstruction was less than ideal, with the joint surface angulated approximately 30° anteriorly. Lastly, Case 4’s original anatomy was well restored both computationally and surgically. These cases illustrate that useful information can be gained from puzzle solutions where fragments did, and did not align perfectly. Whereas fewer complications would be expected in cases with perfect computational reductions, those where defects can be identified preoperatively deserve attention.

Figure 6.

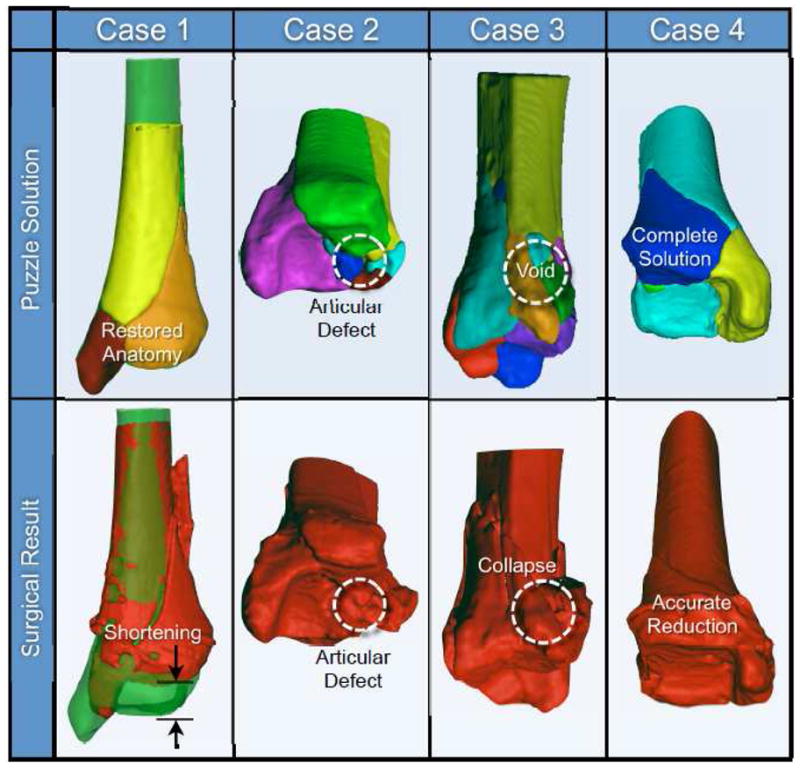
Four puzzle solutions are compared to what was achieved surgically. Inspection of the virtual solution provides prognostic information.

Besides severely comminuted fractures, puzzle-solving methods also hold attraction for more moderate fractures where the decision between operative and non-operative management is borderline. Key features that influence decision-making are oftentimes vague or difficult to assess from standard radiographic information (Martin et al., 2000). Although the surgeon may have a general idea of how fragments fit together, a puzzle solution provides precise displacement, angulation, and depression data important for making well-informed decisions. For instance, one may not be able to appreciate the magnitude of depression in a tibial plateau fracture simply from traditional imaging, whereas puzzle solving could precisely quantify it.

To further illustrate clinical practicality, a severe articular fracture case was puzzle solved prospectively. A 19 year old male presented with an open distal tibia fracture, sustained after jumping from a moving train. In addition to substantial articular fragmentation, the diaphysis was severely comminuted. For initial treatment, the fracture was spanned with an external fixator and antibiotic beads were implanted, followed by a CT scan. A complete puzzle solution was obtained within four hours and was provided to the surgeon one week prior to definitive surgery. Execution of the entire puzzle solving process in such a brief time period affords ample time for its integration into surgical planning. This case also demonstrates another application of puzzle solving. Since bone is oftentimes missing or has to be removed due to contamination or devitalisation, puzzle solving allows for custom implants for segmental defects to be designed, using rapid prototyping methodology.

Of course there are limitations to the current methods. In the present embodiment, the puzzle solutions are “end stage,” with no account taken as to how to physically achieve that configuration. The surgical approach and the status of the local neurovascular structures and other surrounding soft tissues will greatly affect how the fragments can move in space. Future embodiments of the algorithm ideally should incorporate such anatomic considerations in calculating feasible optimal trajectory paths and sequences. In addition, current methods rely on the contralateral bone as a template for reconstruction. Although rare, bilateral fractures therefore are not amenable to analysis with this methodology. Generic population-based templates could potentially be used in such cases (Thomas et al., 2008). Despite these limitations, the results from this study suggest that 3D puzzle solving is a powerful new tool for enhancing the surgical reconstruction of complex, comminuted peri-articular fractures.