Magnetic Resonance Elastography as a Method for the Assessment of Effective Myocardial Stiffness throughout the Cardiac Cycle

Abstract

Magnetic resonance elastography (MRE) is a noninvasive technique in which images of externally generated waves propagating in tissue are used to measure stiffness. The first aim is to determine, from a range of driver configurations the optimal driver for the purpose of generating waves within the heart in vivo. The second aim is to quantify the shear stiffness of normal myocardium throughout the cardiac cycle using MRE and to compare MRE stiffness to left ventricular (LV) chamber pressure in an in vivo pig model. MRE was performed in 6-pigs with 6-different driver setups including no motion, 3-noninvasive drivers and 2-invasive drivers. MRE wave displacement amplitudes were calculated for each driver. During the same MRI examination, LV pressure and MRI-measured LV volume were obtained, and MRE myocardial stiffness was calculated for 20 phases of the cardiac cycle. No discernible waves were imaged when no external motion was applied, and a single pneumatic drum driver produced higher amplitude waves than the other noninvasive drivers (P <0.05). Pressure-volume loops overlaid onto stiffness-volume loops showed good visual agreement. Pressure and MRE-measured effective stiffness showed good correlation (R² = 0.84). MRE shows potential as a noninvasive method for estimating effective myocardial stiffness throughout the cardiac cycle.

Introduction

Myocardial stiffness relates myocardial deformation (strain) to loading (stress) and is thought to affect the heart’s function. To date, the primary method of evaluating myocardial stiffness in vivo has been by inferring it from pressure-volume (P-V) relationships (1,2). For example, it has been shown that patients with diastolic heart failure exhibit increased chamber stiffness (dP/dV) (3), as do patients with myocardial ischemia and patients with myocardial infarction (4). However, P-V methods are invasive, require technical precision, assess the left ventricular (LV) chamber rather than the true intrinsic properties of the myocardium, and only provide a global measure of stiffness. Therefore, there is a need for a technique capable of noninvasively assessing true intrinsic mechanical properties of the myocardium such as shear modulus (i.e. shear stiffness or stiffness) (µ).

Magnetic resonance elastography (MRE) is a novel imaging technique that can be used to measure shear stiffness (5–9). In MRE cyclic motion is applied to a tissue and a phase-contrast MR image is acquired in which motion-encoding gradients (MEG) are synchronized with the external motion. This produces MRI images of the waves propagating in the tissue. The wave displacements obtained from these images can be mathematically converted to stiffness maps.

To date, MRE has been shown to resolve the shear stiffness of static tissues (10,11). However, there are challenges to applying this technique to dynamic organs such as the heart. These include performing faster data acquisition so as to capture the different phases of cardiac cycle and introducing external shear waves into the heart while avoiding bulk motion artifacts. A previous study (12,13) has shown the feasibility of using a cine MRE acquisition strategy in a simulated, dynamic LV spherical phantom when the acquisition is appropriately synchronized with the motion of the phantom. That study demonstrated a linear correlation between effective stiffness and pressure with the stiffness estimates being validated against an established P-V relationship.

There are two aims of this study. The first aim is to determine, from a range of driver configurations, the optimal driver for the purpose of generating waves within the heart in vivo. The second aim is to quantify the shear stiffness of normal myocardium throughout the cardiac cycle using MRE and to compare MRE stiffness to LV chamber pressure in an in vivo pig model.

Methods

Six pigs underwent cardiac MRE. In each pig six driver configurations were studied to determine the most optimal method of delivering waves to the myocardium. Shear stiffness measurements obtained from MRE wave images using the optimized driver were compared to LV pressure and MRI-measured LV volume obtained during the same MRI examination.

Evaluating MRE Drivers

Experimental Setup

In vivo cardiac MRE was performed on six pigs (mean weight: 43.2 kg; female) in compliance with our institutional animal care and use committee. The animals were anesthetized by intramuscular injections of a cocktail containing telazol (5mg/kg), xylazine (2mg/kg) and glycopyrrolate (0.06mg/kg) and were maintained using an isoflurane inhalation anesthesia (1–3%) and mechanical ventilation.

Mechanical Wave Generation

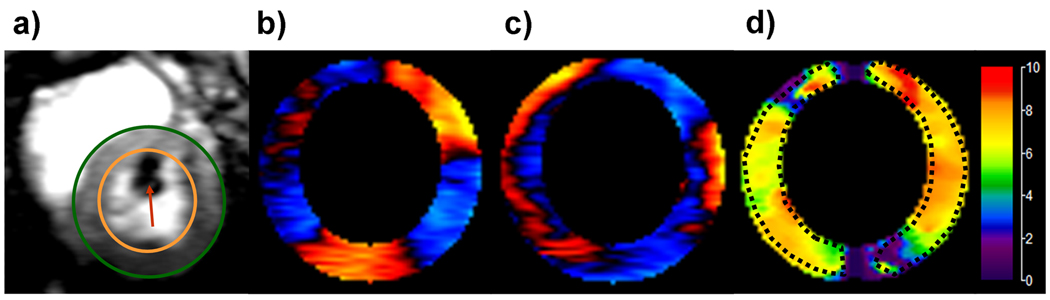
To study wave generation, mechanical waves were introduced into the heart using 6 different driver configurations (Figure 1). In the first case, no driver was used and therefore provided a control method. In the second case (Fig. 1(a) 1 Driver), one large noninvasive pneumatic drum of 13.7 cm diameter was placed on the chest wall. All the pneumatic drums in our experiments were made up of acrylic and the diaphragm i.e. drum head was made up of poly carbonate with 0.02 inches in thickness. In the third case (Fig. 1(b) 2 Drivers), two small noninvasive pneumatic drums of 8cm diameter each were placed adjacent to each other on the chest wall and were driven in phase. In fourth case (also Fig. 1(b) 2 Drivers), two small noninvasive pneumatic drums were placed adjacent to each other on the chest wall and were driven out of phase. In the fifth case (Fig. 1(c) Suture), the chest wall was opened and a thread was sutured directly to the anterior wall of the left ventricle (LV) while the other end of the thread was attached to a pneumatic driver. In the sixth case (Fig. 1(d) Direct Contact), with the chest open, a small pneumatic drum was inserted into the chest cavity and placed directly on the heart. In first four cases, the pneumatic drums were placed on the chest wall with straps and no coupling gel was used. The amplitude vibrations experienced by all the drum heads were in the range of 100–200 µm by providing equal amounts of power in all cases.

Figure 1.

Examples of the 4 experimental setups studied indicating the location of the pneumatic drivers: a) 1-driver system, b) 2-driver system, c) suture system, and d) direct-contact system. In all of the figures, the dotted white arrow shows the location of the drivers and the bold white arrow shows the pig tail pressure sensor catheter inserted into the left ventricle through the femoral artery. All the figures also show inset cartoons demonstrating all different driver setups.

Image Acquisition

All imaging was performed on a 1.5-Tesla MRI scanner (Signa Excite, GE Health Care, Milwaukee, WI). The animals were positioned in the supine position and placed feet first into the scanner. A cine gradient-echo retrospective gated MRE sequence (13) was used to measure the external motion in the myocardium in 2-chamber long-axis and a single short-axis slice. The short-axis slice was immediately basal to the papillary muscles. Mechanical waves were introduced into the heart by the 6 different methods as described above. In the first case, no driver was used and no mechanical waves were applied. This was necessary in order to determine the contribution from bulk intrinsic, physiologic motion of the heart in the MRE data. In all other experiments, the driving methods described above were implemented to deliver the motion to the heart. A phased array receive only coil was used for all acquisitions. When the chest was open the anterior and posterior coil elements were repositioned so as to be on either side of the chest. Imaging parameters included TR= 25 ms; TE= 11.7ms; FOV= 27 cm; flip angle = 30°; slice thickness = 5 mm; acquisition matrix = 256×64; receiver bandwidth = ±16 kHz; excitation frequency = 80 Hz (12.5 ms) was applied continuously with multiple cycles of motion matching the TR; heart rate =63–100 bpm; views per segment (VPS) = 4; 4 MRE phase offsets; and one 6.25-ms duration (160 Hz) MEGs applied separately in the physical x, y, and z directions to measure all components of external motion in the tissue. MRE data were collected separately at end-diastole and end-systole using an adjustable cardiac trigger delay time. MRE data was also collected in a cine acquisition (13) with 20 phases of cardiac cycle for use in the comparison of MRE stiffness to LV pressure (described below). During acquisition, the breath holds in the animals were achieved using an external ventilator. The scan time was dependent on the heart rate. For example, at a heart rate of 63 bpm, the time required for collecting each MRE phase offset was 11 seconds for one encoding direction. Therefore, the time taken to collect the 4 MRE phase offsets for one encoding direction was about 44 seconds. Using an external ventilator, these 4 MRE phase offsets were collected in a single breath hold (i.e. 44 seconds) in all the animals. Therefore, there was no image registration problem from one MRE phase offset to the other.

Image Analysis

MRE Driver Analysis

The acquired long-axis and short-axis images of all the components of external motion were masked at the epicardial and endocardial boundaries to obtain only the LV myocardium. The time-domain wave images were then processed to obtain the amplitude of the first harmonic of displacement. The mean value of the amplitude in both slices for each sensitization direction was calculated for each pig. The mean of all 3 amplitudes for all six pigs was then calculated and compared between the different driver setups.

Comparison of MRE Stiffness to Pressure

Experimental Setup

Prior to MR imaging each of the six pigs had a pressure catheter placed in the LV cavity. In addition to the experimental setup described above (Evaluating MRE Drivers), a percutaneous femoral arterial puncture was made and an 8-French introducer set was placed in the femoral artery. Under fluoroscopy, a 7-French pigtail catheter containing a MRI compatible fiber-optic pressure sensor (DL-PM-250, FOP-MIV, FISO Technologies, Inc., Quebec, Canada) (3 pigs) or a fluid-filled catheter (3 pigs) was advanced through the introducer sheath, through the aorta, and into the LV cavity to record the pressures during the cardiac cycle. Pigs were then transferred to the MRI scanner. In the scanner, catheter location in the LV was confirmed by directly visualizing the catheter on scout images and by visually evaluating the pressure waveform. LV pressure waveforms were sampled at rates of 250 Hz (fiber-optic pressure sensor) and 1 kHz (fluid-filled catheter) and were recorded using a personal computer (Core-2 Duo processor, Lenovo, Morrisville, NC).

Mechanical Wave Generation

External motion was delivered to the myocardium using the noninvasive driver (one large pneumatic drum driver) shown in Figure 1a. This driving mechanism was chosen based on the results (shown later) obtained from the different driver setups, which showed that the single noninvasive pneumatic drum produced higher amplitude waves than the other noninvasive driver setups.

Image Acquisition

The details of image acquisition and imaging parameters are the same as those described in the above section (Evaluating MRE Drivers). As stated above, for the comparison of MRE stiffness to pressure, an MRE acquisition was used which acquired 20 cardiac phases in a single acquisition instead of one in which a separate acquisition was used for end-systole and end-diastole.

Pressure Readings

The pressures in the LV chamber were recorded continuously using pressure sensors during image acquisition. Due to technical limitations, pressure measurements in 3 animals were acquired using the fiber-optic pressure sensor, and in the remaining 3 using the fluid-filled catheter.

Acquisition for LV volumes

The ventricular volumes in each pig were determined from 2D multislice, short-axis, balanced steady-state free precession images acquired covering the entire ventricle. The imaging parameters included TE= 1.8 ms, TR= 4 ms, FOV= 27 cm, flip angle= 55°, slice thickness= 8 mm, slice spacing= 0 mm, receiver bandwidth= ±125 KHz, acquisition matrix= 256×224, VPS= 10, and cardiac phases= 20.

Image Analysis

MRE Stiffness Analysis

Because many studies have approximated the heart to be spherical (4,14) and obtained clinically useful information, we similarly modeled the heart as a sphere in our analysis. The acquired short-axis images of the in-plane components of external motion in the myocardium were masked at the epicardial and endocardial boundaries to obtain only the LV myocardium as shown in Figure 2a. The masked wave images were then converted from Cartesian to radial and circumferential components of displacement as shown in Figure 2 (b, c). These components of motion were analyzed using a thin spherical shell analysis (12,13,15,16) to obtain mean shear modulus (i.e., shear stiffness) measurements for each cardiac phase for each animal shown in Figure 2(d). The artifacts at the top and bottom of the elastograms arise because of numerical instabilities due to the cotangent function in the wave equation (shown below) going to zero in these regions.

Figure 2.

a) A short-axis magnitude image during diastole with contours delineating the left ventricular (LV) myocardium and an arrow in the blood pool indicating the pressure sensor. (b,c) Magnetic resonance elastography wave images of the LV myocardium showing one offset of the radial and circumferential components of displacement, respectively. (d) The corresponding stiffness map obtained from the spherical shell analysis at a pressure of 8.61 mmHg with a mean stiffness in the region of interest of 6.4 ± 1.1 kPa.

The governing flexural motion in a spherical shell is shown in Eq.1(12,13,15,16), where a = shell mean radius, u = circumferential component of displacement, w = radial component of displacement, c_p = flexural plate speed (c_p² = E/(1-ν²)ρ), E = Young’s modulus, ρ = density (assumed to be 1000 kg/m³), ν= Poisson’s ratio, β = h²/12a², h = thickness of the shell, θ= angular position around the shell, double dots above a variable indicate differentiation with respect to time, and p_a = applied load. This applied load was assumed to be zero, since it is currently impossible to measure in vivo. It is a combination of many different factors, including changes in intrathoracic pressure, loading conditions on the right ventricle, left ventricular afterload and preload as well as intrinsic contractility, as well as the actual loading of the driver, which is affected by the chest wall, ribcage, lungs etc. Therefore, the right hand term in Eq.1 becomes zero. If the circumferential and radial displacements are known, Eq. 1 can be solved for c_p, which includes E in its definition. The shear modulus (i.e. shear stiffness or stiffness) of the material can then be calculated according to the relationship µ = E/ 2(1+ν). Unlike most MRE applications, in this case the shear stiffness found (at least currently) is the not the intrinsic mechanical stiffness but an effective stiffness which is influenced by the unknown pressure and applied load.

$${\mathrm{\beta }}^2\frac{{\partial }^3\mathrm{u}}{\partial {\mathrm{\theta }}^3}+2{\mathrm{\beta }}^2\text{cot}\mathrm{\theta }\frac{{\partial }^2\mathrm{u}}{\partial {\mathrm{\theta }}^2}-[1+\mathrm{\nu })(1+{\mathrm{\beta }}^2)+{\mathrm{\beta }}^2{\text{cot}}^2\mathrm{\theta }]\frac{\partial \mathrm{u}}{\partial \mathrm{\theta }}+\text{cot}\mathrm{\theta }[2-\mathrm{\nu }+{\text{cot}}^2\mathrm{\theta }){\mathrm{\beta }}^2-(1+\mathrm{\nu })]\mathrm{u}-{\mathrm{\beta }}^2\frac{{\partial }^4\mathrm{w}}{\partial {\mathrm{\theta }}^4}-2{\mathrm{\beta }}^2\text{cot}\mathrm{\theta }\frac{{\partial }^3\mathrm{w}}{\partial {\mathrm{\theta }}^3}+{\mathrm{\beta }}^2(1+\mathrm{\nu }+{\text{cot}}^2\mathrm{\theta })\frac{{\partial }^2\mathrm{w}}{\partial {\mathrm{\theta }}^2}-{\mathrm{\beta }}^2\text{cot}\mathrm{\theta }(2-\mathrm{\nu }+{\text{cot}}^2\mathrm{\theta })\frac{\partial \mathrm{w}}{\partial \mathrm{\theta }}-2(1+\mathrm{\nu })\mathrm{w}-\frac{{\mathrm{a}}^2ẅ}{{\mathrm{c}}_{\mathrm{p}}^2}=-{\mathrm{p}}_{\mathrm{a}}\frac{(1-{\mathrm{\nu }}^2){\mathrm{a}}^2}{\text{Eh}}$$ (1)

The spherical shell analysis assumes an isotropic material with no torsional motion (i.e. through plane component of motion) and an internal radius to be greater than the thickness of the shell. The ventricular wall is assumed to be incompressible (4,17–21) indicating the Poisson’s ratio to be 0.5(22). The analysis accounts for the geometric variation in radius and thickness across the cardiac cycle because of the existing pressure gradient in the LV chamber. The radius and thickness of the myocardium at each cardiac phase are obtained from MRE magnitude images and are incorporated into the variable β.

Volume Measurements

Volume measurements were calculated based on tracings of the MRI images made by 2 experienced observers by consensus, one (DWL) with more than 2 years of experience working full-time as a post-processing technologist whose primary responsibility is tracing volumes for a cardiac MRI clinical and research core laboratory, and the other (PAA) with 6 years experience as an attending physician dedicated to cardiac imaging. Images were analyzed off-line on an Advantage Windows 4.2 Workstation (GE Medical Systems, Milwaukee, Wisconsin) using commercially available software (Mass Analysis 6.0; MEDIS Medical Imaging Systems, Leiden, The Netherlands). Observers manually traced the LV endocardial and epicardial borders in all 20 cardiac phases. Papillary muscles and trabeculations were excluded from the LV chamber and were included in the myocardium. LV volumes were calculated by measuring the area of the LV cavity on each slice, multiplying by the slice thickness and summing all slices to obtain the LV volume.

Matching Pressure, Stiffness and Volume Measurements

MRE encoded displacements at different phases of the cardiac cycle were converted to stiffness maps as described above. The pressure measurements were simultaneously recorded during each MRE experiment. To match the pressures to the stiffness maps, the temporal resolution of each phase of the cardiac cycle was calculated based on the heart rate and number of cardiac phases reconstructed within the R-R interval. For example for a heart rate of 60 bpm (i.e. R-R interval = 1000 ms), if the number of cardiac phases reconstructed were 20, then the temporal resolution of each phase is 50 ms. MRE encoded displacements that are obtained immediately after the cardiac trigger correspond to end-systolic phase and the stiffness measurement obtained from those displacements corresponds to end-systolic stiffness. This end-systolic stiffness measurement was matched to the peak recorded pressure, which was assumed to be end-systolic pressure. The subsequent stiffness measurements were matched to the recorded pressures from its peak based on the calculated time for each phase of the cardiac cycle to obtain pressure versus stiffness plots for each pig. Similarly, the obtained volume measurements for each cardiac phase were matched to the corresponding pressures based on the calculated time (described above) to obtain P-V loops in each pig. The obtained stiffness measurements were also matched to volume measurements to obtain stiffness-volume (S-V) loops in each pig.

Statistical Analysis

Different driver setups were compared to each other. The analysis was conducted by using commercially available software JMP 7 (SAS Institute Inc., Cary, NC). To determine the significant differences between different driving mechanisms, the mean amplitudes from all pigs in all 3 directions were compared using an all pairs Tukey–Kramer HSD test. Mean values were considered to be significantly different for α< 0.05.

P-V and S-V loops in each pig were overlaid onto each other and visually inspected without formal statistical comparison.

Previous studies (12,13,23) have demonstrated a linear relationship between cavity pressure and shear stiffness for a thin-shelled spherical phantom and also a linear change in chamber stiffness with changes in LV pressure in a canine animal model. The same relationship was expected to be true for the current study. Therefore, a least-squares linear regression was performed to fit the stiffness values obtained in the myocardium to the LV cavity pressures.

Results

Evaluating MRE Drivers

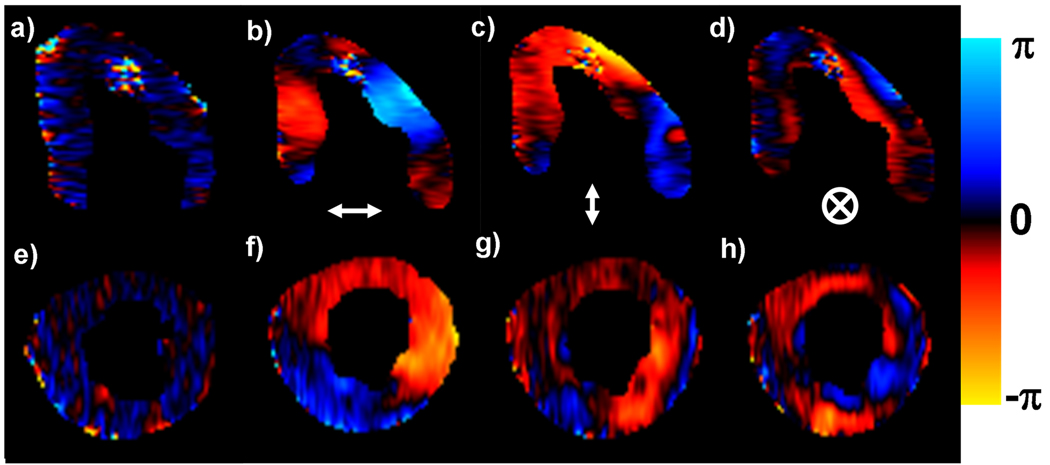
When no external motion was applied, no discernible waves were imaged, as shown in Figure 3(a, e). Figure 3(b–d, f–h) shows examples of waves induced in the heart using the 2-driver system when driven out of phase for long- and short-axis slices for all three sensitization directions at end-diastole. Therefore, the detected waves are the result of our externally applied motion and not the intrinsic physiologic motion of the heart. This is also confirmed in Figure 4, which shows that the mean amplitudes obtained from the no driver case are almost negligible and significantly different than the other driver setups.

Figure 3.

No discernible waves were imaged when no external motion was applied in a long-and short-axis end-diastolic phase of left ventricle (a,e). Wave images showing the horizontal, vertical, and through-plane components of displacement for one offset for a long-axis slice (b–d) and a short-axis slice (f–h) during end-diastole using the 2-drivers setup driving out of phase.

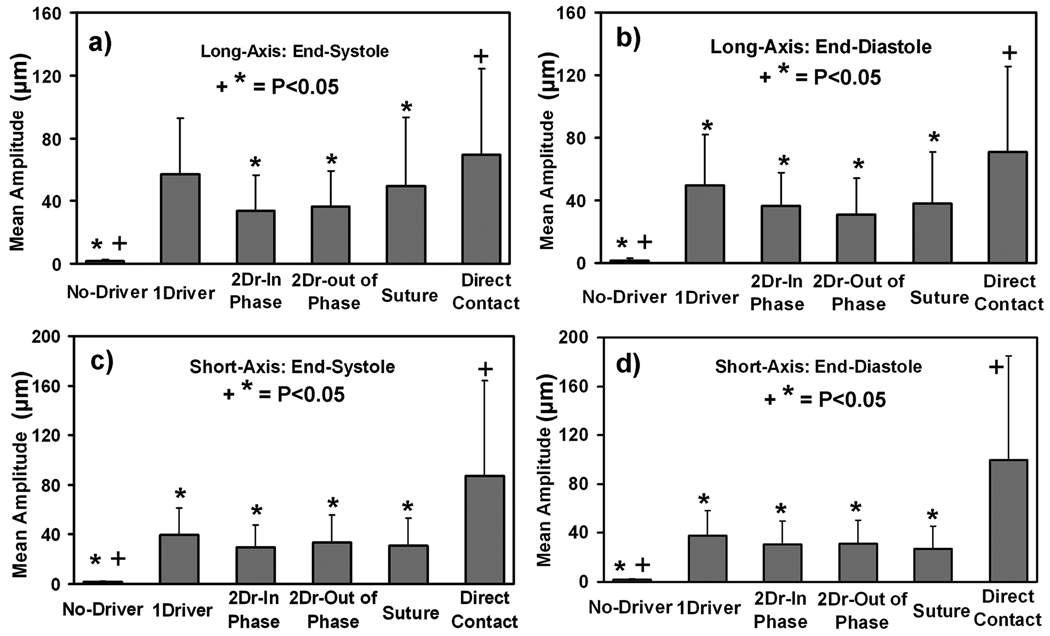
Figure 4.

(a–d) Plots of the mean displacement amplitudes from the five driver setups for the long- and short-axis slices (a,b and c,d, respectively) of the heart at end-systole and end-diastole (a,c and b,d, respectively). Error bars show ±1 standard deviation. “*” indicates the significant differences (P<0.05) between the direct contact setup and other driver setups and “+” indicates the significant differences (P<0.05) between the suture setup and other driver setups.

Significant differences were observed between different driving setups. Figure 4 shows the mean amplitude from all 6 hearts for each driver configuration in the long- and short-axis slices at end-systole and end-diastole. It can be observed from Figure 4 that the driver inserted into the chest cavity in direct contact with the heart gave significantly larger mean amplitude (P<0.05) than the other driving mechanisms for the long-axis end-diastolic phase and in both cardiac phases of short-axis, as indicated by “*”. No significant difference (P>0.05) in mean amplitudes was observed between the driver inserted into the chest cavity in direct contact with the heart and the one large noninvasive pneumatic drum driver setup in the long-axis end-systolic case. Furthermore, when the mean amplitudes from noninvasive driver setups were compared to the other invasive driver setup (i.e. suture), no significant differences (P>0.05) were observed in either the long- or short-axis cardiac phases.

Among the noninvasive driving mechanisms studied, the one large noninvasive pneumatic drum driver setup had greater or equal mean amplitudes than the other noninvasive drivers in both phases of the cardiac cycle for both long- and short-axis slices. The one large noninvasive pneumatic drum driver setup was thus considered the best for delivering waves into the myocardium.

Comparison of MRE Stiffness to Pressure

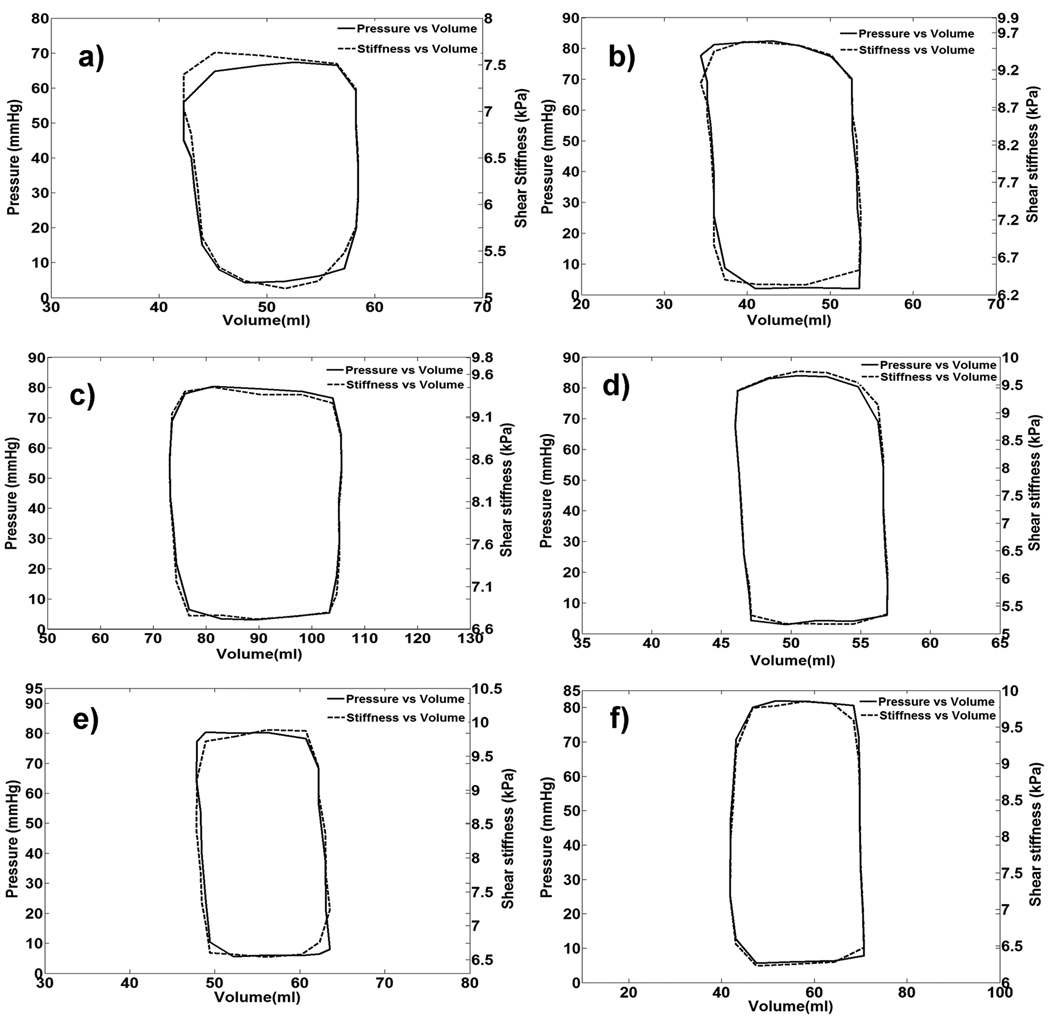
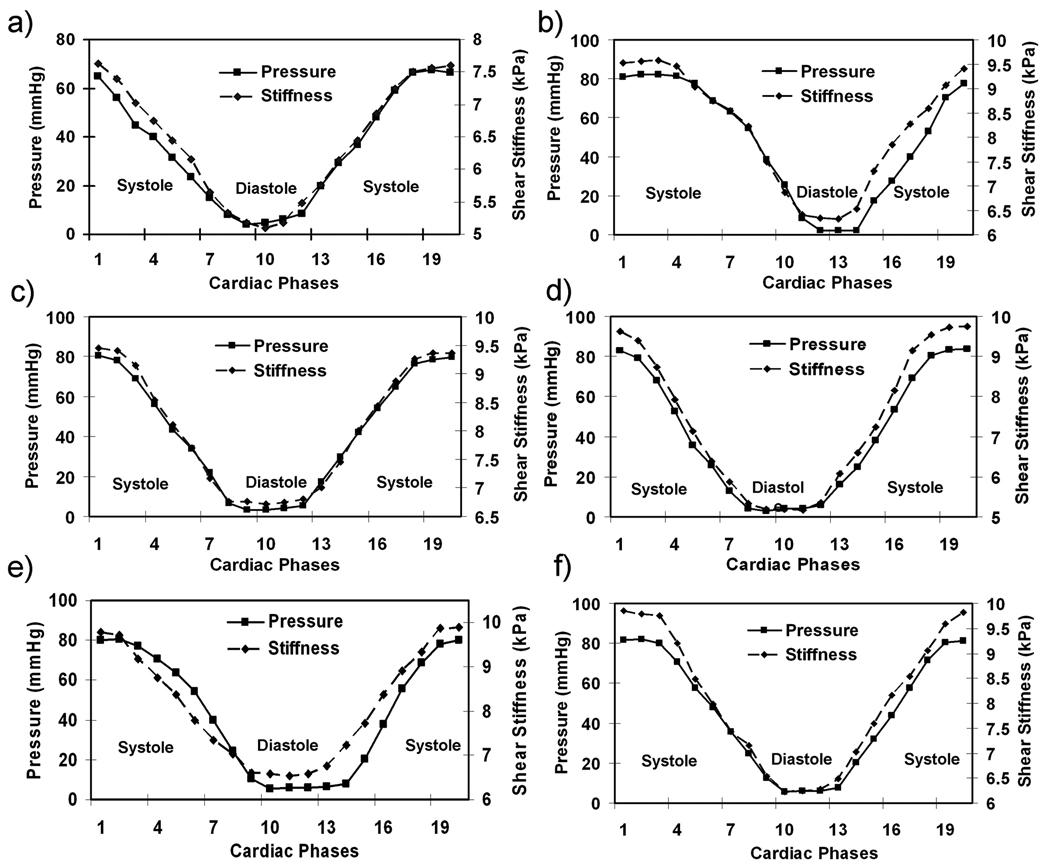
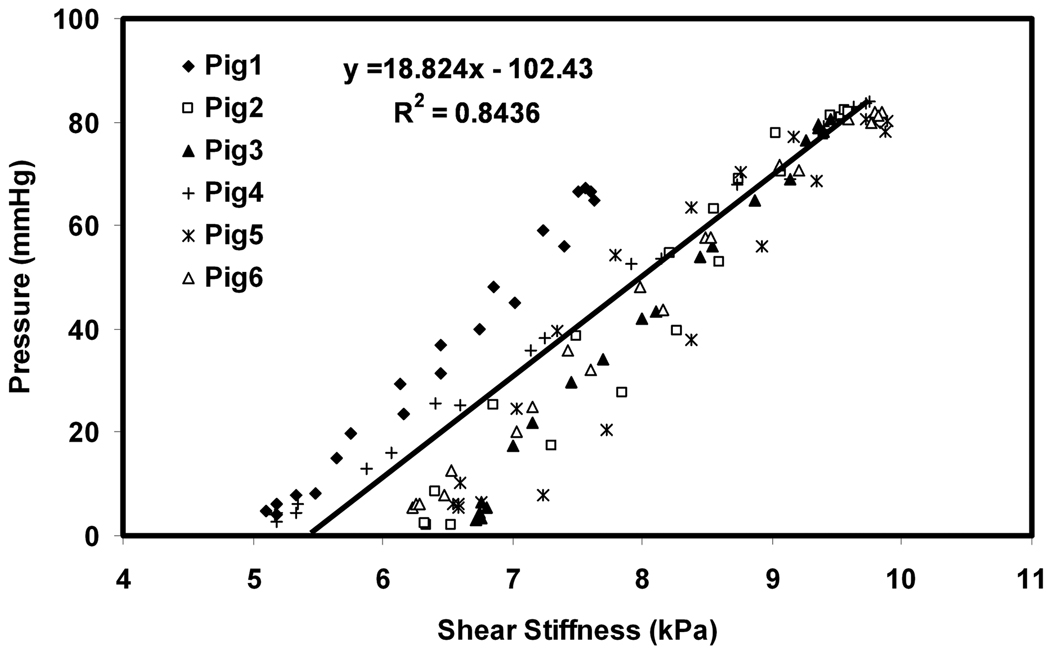
The MRE-derived stiffness of the myocardium varied throughout the cardiac cycle, and good visual agreement was observed between P-V loops and S-V loops (Figure 5). Good correlation was observed between pressure and stiffness in all the animals. Figure 6 shows the plots of shear stiffness and pressure variation during the cardiac cycle. It can be seen in each case that the myocardium is stiffer in systole (mean stiffness 9.34 ±1.9 kPa) than it is in diastole (6.03 ±1.8 kPa). Figure 7 shows the linear correlation (R² = 0.84) between stiffness and pressure obtained from all 6 animals throughout the cardiac cycle. Notice that there is significant inter-animal scatter in figure 7, as well as significant DC shifts (this can also be observed in the slightly different scales in figures 5 and 6). Some of these inter-animal variations may be due to true physiological differences, but more likely they are due to issues in the post image processing (explained later as limitations of our study). A higher linear correlation of R² ranging from 0.9 to 0.99 was observed within single animals between pressure and stiffness. The pressure in all pigs ranged from 2 to 85 mmHg and the shear stiffness ranged from 5.1 to 9.89 kPa during the cardiac cycle.

Figure 5.

(a–f) Plots of pressure versus volume and stiffness versus volume in all the animals.

Figure 6.

(a–f) Plots of stiffness and pressure changes during the cardiac cycle in all the animals. The myocardium is stiffer in systole than in diastole.

Figure 7.

A plot of stiffness versus pressure data pooled from all of the animals from all phases of the cardiac cycle. A correlation of R² = 0.84 was obtained between stiffness and pressure.

Discussion

The result of this study shows that wave generation from a single noninvasive pneumatic drum driver produces displacement amplitudes larger than other noninvasive driver systems and no discernible waves imaged when external motion was not applied. Excellent visual agreement between the S-V and P-V loops was observed. The study also shows that MRE-based estimates of shear stiffness vary cyclically throughout the cardiac cycle. Good correlation was observed between stiffness and pressure, consistent with theory (12,13,23).

The noninvasive one large pneumatic drum driver setup produced higher amplitude motion than our other noninvasive driver setups and even higher than the invasive suture setup. The amplitude differences between the drivers are due to variations in the contact area of the drivers with the body (24). In the one large pneumatic drum driver setup, the driver has a large contact surface area, compared to the 2-driver setup in which each driver has a small surface area. In the suture case, the setup has strong contact with the heart but little contact area when compared to the one large pneumatic drum driver. These results indicate that external motion can be readily induced in the heart noninvasively using a one large pneumatic driver system setup. This one large pneumatic driver system setup has shown promising results in delivering waves into abdominal organs such as liver and spleen (6,25,26).

No significant differences in mean amplitudes from all pigs were observed between end-diastole and end-systole. The MRE images were acquired in separate acquisitions during end-systole and end-diastole and after each acquisition the scanner table was brought back to the home position to adjust the ECG trigger. Therefore, the coupling of the driver to the animal’s chest wall and the position of the driver may not be the same during end-systole and end-diastole thereby causing variations in the amplitudes generated.

No discernible waves were imaged when no external motion was applied to the heart, indicating that the MRE acquisition is relatively insensitive to bulk displacements from cardiac induced motion. This is because the cardiac gated MRE acquisition encodes displacements with a temporal resolution of the applied MEGs (~6.25 ms) which is short enough that the heart, by comparison, can be considered to be static. Moreover, MRE is spectrally tuned to detect the frequency of the external motion induced from the driver that is synchronized with MEGs (7), and the MRE image processing of the wave data will further filter out the motion at frequencies other than the externally applied motion. A previous cardiac MRE study by Sack et al (27) confirmed that intrinsic motion of the heart was slow compared to MRE motion encoding gradients.

A high correlation was observed between effective stiffness and pressure. Previous in vivo human and animal studies using catheter-based measures of pressure and volume (1,2,14) have used pressure as a surrogate of stiffness and also incorporated pressure and volume into their mathematical models to indirectly calculate the stiffness. However, MRE directly calculates an effective stiffness of the object under investigation which includes both the chamber properties which vary with pressure and also intrinsic properties of the myocardium itself (including effects of active muscle contraction and relaxation). A previous study has shown that MRE is capable of measuring the stiffness of a dynamic phantom model of the LV whose properties were also validated against an established P-V relationship (12). Furthermore, an in vivo cardiac MRE study (28) performed in volunteers also indicated a linear relation between pressure and stiffness, where the stiffness measurements were calculated based on the amplitude of the waves evaluated during the cardiac cycle. These results suggest that MRE can be used to make LV based measurements of the effective shear stiffness of the myocardium rather than using the invasive procedures required for P-V analysis.

Recently, MRE studies (27,29,30) were performed in volunteers (without any simultaneous pressure measurements) in which the amplitude of wave motion within a region of interest in the heart due to an external vibration source was measured and was used to indicate changes in tissue stiffness over the cardiac cycle. Other cardiac MRE studies (31,32) have also been performed in volunteers (also without pressure measurements) in which only the vibrational wavelength at regions of interest were measured and were used to report the global stiffness of the myocardium. The present technique, however, in principle has the capability to spatially resolve the effective shear stiffness of the myocardium.

There are several limitations to the spherical shell analysis used to measure stiffness of the myocardium. It does not consider the through-plane component of motion or the effects of anisotropy, both of which are encountered when imaging in vivo cardiac tissue. Therefore, this might produce biases in the effective stiffness estimates when trying to identify normal and diseased myocardial tissues. The spherical shell analysis is a 2D analysis, but in the in vivo heart, wave propagation is more complicated because of its structure, and therefore requires a 3D analysis to obtain an accurate effective stiffness of the myocardium. Such an analysis would require a 3D MRE volume acquisition, which would require prohibitively long scan times with our current technique.

Furthermore, the spherical shell analysis requires the estimation of several high-order derivatives for the assessment of the shear modulus, and as such is sensitive to noise. Estimating these high-order derivatives can also cause errors at the edges of the tissue. The region of interests (ROI) used in this study were drawn to avoid these residual artifacts at the edges. Improper estimation of radius and thickness for use in Eq.1. will also alter the stiffness estimates. Finally, in the spherical shell analysis the load term Pa was set to zero, as there is no way currently known to us of accurately measuring Pa in vivo, therefore the stiffness measurements obtained were not absolute. Despite these limitations, we have demonstrated evidence of a linear correlation between pressure and stiffness and good agreement between S-V loops and P-V loops of the LV in vivo.

Future work for this technique involves refining the method and exploring in vivo applications of MRE in diagnosing different cardiac disease states. Accelerating the MRE acquisition using parallel imaging methods to acquire the data within a breath hold (i.e., less than about 20 seconds) would significantly reduce overall acquisition times, improve patient compliance in human studies, and reduce image registration errors.

In conclusion, we have demonstrated that cyclic variation of effective shear stiffness as measured by MRE exists during the cardiac cycle with the myocardium being stiffer in systole than it is in diastole. Excellent visual agreement was observed between S-V and P-V loops and it was also shown that the shear stiffness correlated linearly with pressure. The results motivate further research to study relationships between S-V loops and P-V loops in different disease models.