Three-Dimensional Quantitative Micromorphology of Pre- and Post-Implanted Engineered Heart Valve Tissues

Abstract

There is a significant gap in our knowledge of engineered heart valve tissue (EHVT) development regarding detailed three-dimensional (3D) tissue formation and remodeling from the point of in vitro culturing to full in vivo function. As a step toward understanding the complexities of EHVT formation and remodeling, a novel serial confocal microscopy technique was employed to obtain 3D micro-structural information of pre-implant (PRI) and post-implant for 12 weeks (POI) EHVT fabricated from PGA: PLLA scaffolds and seeded with ovine bone-marrow-derived mesenchymal stem cells. Custom scaffold fiber tracking software was developed to quantify scaffold fiber architectural features such as length, tortuosity, and minimum scaffold fiber–fiber separation distance and scaffold fiber orientation was quantified utilizing a 3D fabric tensor. In addition, collagen and cellular density of ovine pulmonary valve leaflet tissue were also analyzed for baseline comparisons. Results indicated that in the unseeded state, scaffold fibers formed a continuous, oriented network. In the PRI state, the scaffold showed some fragmentation with a scaffold volume fraction of 7.79%. In the POI specimen, the scaffold became highly fragmented, forming a randomly distributed short fibrous network (volume fraction of 2.03%) within a contiguous, dense collagenous matrix. Both PGA and PLLA scaffold fibers were observed in the PRI and POI specimens. Collagen density remained similar in both PRI and POI specimens (74.2 and 71.5%, respectively), though the distributions in the transmural direction appeared slightly more homogenous in the POI specimen. Finally, to guide future 2D histological studies for large-scale studies (since acquisition of high-resolution volumetric data is not practical for all specimens), we investigated changes in relevant collagen and scaffold metrics (collagen density and scaffold fiber orientation) with varying section spacing. It was found that a sectioning spacing up to 25 μm (for scaffold morphology) and 50 μm (for collagen density) in both PRI and POI tissues did not result in loss of information fidelity, and that sectioning in the circumferential or radial direction provides the greatest preservation of information. This is the first known work to investigate EHVT microstructure over a large volume with high resolution and to investigate time evolving in vivo EHVT morphology. The important scaffold fiber structural changes observed provide morphological information crucial for guiding future structurally based constitutive modeling efforts focused on better understanding EHVT tissue formation and remodeling.

INTRODUCTION

Current clinical options for cardiac valve replacement include mechanical and bioprosthetic devices, but these both have substantial limitations such as increased risk of thromboembolic events or decreased structural integrity, respectively.⁴ Moreover, somatic growth is not possible in either design, necessitating multiple operations to match growth in pediatric patients. An alternative paradigm for pediatric heart valve replacements utilizes engineered tissues to form a functional valve apparatus.¹⁴ In this approach, autologous cells are isolated and grown on specialized porous biodegradable scaffolds in vitro to provide sufficient mechanical and biological integrity to function upon implantation. The coordinated mechanical interplay between the degrading scaffold material, host cellular infiltration, and remodeling of the extracellular matrix (ECM) is essential to the success of this engineered tissue approach.

Engineered heart valve tissues (EHVT) created from poly-glycolic acid/poly-L-lactic acid (PGA:PLLA) co-polymer scaffolds seeded with ovine bone-marrow-derived mesenchymal stem cells (BMSCs) have been shown to function in vivo up to 20 weeks post-implantation in an ovine model with histology showing native valve tissue characteristics.^{10,12,13,16,25,26,28} Although promising, little is known about the tissue remodeling process and the detailed characteristics of the ECM constituents formed. In addition, while several investigators have focused on quantifying ECM deposition, there remains a paucity of rigorous evaluations of the physical quality of the ECM produced. ^3,20,21

To evaluate the mechanical quality of ECM formed within EHVT, biomechanical models distinguishing the ECM mechanical response from the scaffold mechanical response within the composite material are essential. To this end, we developed a general model for both pre-seeded scaffold material^7,8 and ECM-embedded scaffold⁸; both successfully predicted mechanical properties of pre-seeded scaffolds and ECM-scaffold composites. These models were limited, however, by a lack of scaffold changes (fragmentation, orientation, etc.) that need to be addressed to accurately predict ECM mechanical response from the composite response.

Rigorous three-dimensional (3D) structural analyses and quantification of constituents of interest are important to this approach. Existing methods of 3D structural analyses are difficult to use or introduce large error into the results. For example, in traditional 3D imaging techniques using light microscopy, thin histological sections are cut from paraffin or ice-embedded samples, stained, and imaged using a light microscope. Successive samples often lack registration, introducing error in the reconstruction process.²⁴ In addition, cutting and mounting of thin sections can introduce folding, bending, and tearing in the tissue which can skew results. In confocal modalities, finer out-of-plane resolutions can be obtained though at the expense of in-plane resolution. The lack of cutting and mounting sections maintains serial registration between image planes, but the sample density can limit how deep into the tissue imaging can occur, in some cases 10 μm or less.²⁴

In this study a novel means to both acquire and analyze high-resolution 3D structural data in EHVT to guide future model development was developed. As a result of the limitations of traditional 3D imaging techniques, an extended-volume scanning laser confocal microscope was utilized at the Auckland Bioengineering Institute at the University of Auckland, New Zealand.^9,24 Non-seeded PGA:PLLA scaffold, preimplant EHVT (PRI), and post-implant EHVT (POI) were investigated to elucidate structural changes during both the in vitro and in vivo phase. In addition, native ovine pulmonary valve (PV) was also evaluated as a means to test this approach for native tissues.

METHODS

EHVT Fabrication

For both PRI and POI specimens, cell isolation, culturing, and seeding, along with scaffold preparation and implantation, were performed as part of another study and has been described in detail.¹⁰ Briefly, BMSCs were isolated from female Dorset sheep, cultured and expanded, and seeded at 0.5–1.7 × 10⁷ cells/cm² onto sheets of non-woven 50:50 PGA:PLLA scaffold fabricated into valved conduits. Seeded constructs (PRI) were statically cultured for 4 weeks. For the POI tissues, these valve and conduit assemblies were implanted into the pulmonary artery of Dorsett sheep and then explanted at various time points. For this particular study, a specimen explanted after 12 weeks was used.

Extended-Volume Scanning Laser Confocal Microscope

To acquire volumetric data, a conventional scanning laser confocal microscope was used to obtain high-resolution 2D plane images with small steps through the z-direction (to obtain high-resolution cubic voxels of 1 μm³ or less). A precision two-bladed diamond-tipped ultramill was employed to cut scanned volumes from the specimen and create optically smooth surfaces as previously described.^23,24 Removing scanned volumes and scanning subsequent volumes permitted the acquisition of large volumetric data (over hundreds or thousands of microns) while maintaining a high resolution (micron or smaller) which resulted in high-resolution 3D images of large volumes.

Specimen Preparation

In the PRI and POI tissues, each leaflet was cut into three equal-sized radial strips, stored in paraformaldehyde, and shipped to the University of Auckland. In addition, a native ovine PV leaflet (“native”), excised during implant, was stored and shipped in paraformaldehyde. Full thickness sections approximately 6 mm by 3 mm were cut from the central region of each full specimen. In total, a native PV, a 4-week in vitro PRI tissue, a 12-week in vivo POI tissue, and a non-seeded PGA-PLLA co-polymer non-woven scaffold (“non-seeded scaffold”) were imaged using the EV-SLCM system. In addition, 2D image scans were performed on non-seeded 100% PGA and pre-seeded 100% PLLA to guide image analysis procedures.

Prior to scanning, a number of processing techniques were required to properly prepare the samples, as detailed in previous study.^23,24 Briefly, all specimens (except the non-seeded scaffold) were stored in 10% paraformaldehyde. Specimens were washed in PBS solution, stained with 0.15% picrosirius red for 2 days, and rinsed with Bouin’s solution. After graded alcohol dehydration, specimens were embedded in resin for the native, PRI, and POI in Procure 812 resin (ProSciTech, Queensland, Australia) and dyed Spurrs resin (ProSciTech, Queensland, Australia) for the non-seeded scaffold. Following a 24-h bake at 60 °C, specimen blocks were mounted on aluminum plates using epoxy for imaging.

Specimen Imaging

Each specimen was imaged using previously published techniques, explained in detail in previous studies.^23,24 Briefly, a 500 by 500 μm field of view was imaged at 1 μm/pixel resolution in a particular image plane with 4× line scan averaging to reduce noise. Multiple adjacent images were captured (with 50% overlap) to provide a full image plane of approximately 1.0–1.5 mm². Both the overlap and line scan aided in reducing in-plane noise to less than 1 μm (personal communication with Mr. Dane Gerneke). A series of 1 μm deep 2D image planes were captured over a specific total depth; after imaging, 80% of the imaged volume was removed using the ultramill. Specimens were imaged again at 1 μm/pixel in-plane resolution with 1 μm 2D image plane steps, and this process was repeated until the total desired specimen depth was reached. A high-resolution translation stage (0.3 μm error per 600 mm total translation per direction) maintained serial registration during milling. To assess inter- and intra-specimen variability, three to four image planes spaced 100 μm apart were acquired at various locations on the same specimen (midpoint and end on PRI, tip, midpoint, and attachment point on POI) and on different specimens (two PRI, three POI) to qualitatively assess inter- and intra-specimen variability. After imaging, 2D images were processed prior to analysis to remove noise and background illumination irregularities, assembled into 2D planes using a cross-correlation technique, and stacked into continuous 3D volumes of x–y plane images as discussed in previous studies.^23,24 The entire process resulted in errors of approximately 1 μm in all three directions (personal communication, Mr. Dane Gerneke) in full-resolution data sets.

Scaffold Analysis

To quantify scaffold information, consecutive 2D image planes were imported into a custom MatLab program. Scaffold constituents were segmented based on intensity thresholding and dilation/contraction operations. Preliminary scans showed that pre-seeded scaffold (PGA and PLLA) appeared as dark regions. In the PRI and POI specimens, PGA appeared as dark geometrical regions while the PLLA appeared as bright geometrical sections, enabling unique labeling using built-in MatLab commands. Using a previously developed algorithm,¹⁷ labeled scaffold fiber cross-sections were associated with the same scaffold fiber cross-sections in successive image planes. The scaffold fibers were represented as a series of points in 3D by calculating the cross-sections’ centroids. 3D curve tracing was then applied to the centroid points to label the scaffold fiber trajectories; the labels were then mapped back to the 3D data sets. With this method, individual scaffold fibers were tracked despite scaffold fiber overlaps.

Centroid data for each scaffold fiber through each slice enabled the calculation of the number of scaffold fibers, the scaffold fiber end-to-end distance D, defined as

$$D=R\sqrt{{(X_n-X_1)}^2+{(Y_n-Y_1)}^2+{(Z_n-Z_1)}^2,}$$ (1)

where R is a scaling factor (determined by image resolution and the resampling factor, n the total number of two dimensional sections, (X, Y, Z) the Cartesian coordinates of the scaffold fiber’s centroid. From this information the true scaffold fiber length L was computed using

$$L=R\left[\sum _{n=1}^M\sqrt{{(X_n-X_{n-1})}^2+{(Y_n-Y_{n-1})}^2+{(Z_n-Z_{n-1})}^2}\right].$$ (2)

Using scaffold fiber end-to-end distance and true scaffold fiber length, the scaffold fiber tortuosity was defined as

$$\tau =\frac{L}{D}.$$ (3)

In addition, scaffold volume fraction, scaffold fiber diameter, and minimum scaffold fiber–fiber distances were computed.

As a means to quantify changes in the scaffold fiber orientation as a function of EHVT time point, an orientation tensor was computed for each sample ^1,5,15,18 using the methods described in Appendix A. Briefly, a best fit vector p was determined for each scaffold fiber in a given sample through a summation performed for the scaffold fiber vectors over all directions, normalized by scaffold fiber length L and a weighing function F(θ_n) included to account for milling bias. Eigenvalues and the associated eigenvectors were computed for the orientation tensor, which represented overall scaffold fiber ensemble principal directions and provided a sense of the general orientation of the scaffold fibers. Additionally, a spherical histogram (based on binning over equal solid angles of the hemisphere) was created with the principal directions to further illustrate the orientation distribution of the scaffold fibers.¹⁹

Since utilizing the EV-SLCM system to acquire full 3D data sets has been found to be impractical for large specimen database,²⁴ it was prudent to determine the minimum number of 2D histological sections required to provide salient structural information in EHVT. This was performed using both metrics for the scaffold fibers and for the collagen. To evaluate the effects of sectioning frequency on scaffold fibers, the eigensolutions for a given data set were computed as a function of increased resampling rates in the milling direction. In this way, changes from the true full-resolution orientation tensor eigensolutions could reveal the impact of reduced sectioning resolution and will help guide histological sectioning frequencies. Since the scaffold analysis files began with a 3 μm sectioning spacing, additional spacings of 5 μm, 10 μm, 25 μm, and 50 μm were used. As a means to evaluate changes in computed orientation, an anisotropy index was used defined as

$${\alpha }_{ij}=1-\frac{{\lambda }_j}{{\lambda }_i}i>j,$$ (4)

where α are the eigenvalues of the fabric tensor.²² In this index, values approaching unity indicated a strong anisotropic orientation, while values approaching zero indicated a strong isotropic orientation. By comparing this index between eigenvalues as a function of sectioning frequency, it was possible to investigate potential errors from increased sectioning spacing on perceived scaffold fiber orientation.

Collagen and Cell Quantification

For collagen and cell quantification, specimen image stacks were segmented using thresholding, region-growth gradient operators, and drawing tools in order to selectively mask/highlight constituents of interest. This permitted the computation of constituent area fractions in a section-by-section manner which could be summed to provide volumetric constituent densities. Collagen, bound to picrosirius red stain, appeared as high-intensity pixels, while cell nuclei appeared as morphometrically distinct objects with higher-intensity pixels (due to the absorption and fluorescence of paraformaldehyde). The background resin had a distinguishably lower intensity, while constituents not bound to the picrosirius red stain had the lowest intensity. Occasionally, high densities of collagen produced high-intensity pixel regions, but they were morphometrically different from nuclei.

Full-specimen masks and collagen-specific masks were created and to compute collagen frequency of a given pixel region (this ensured collagen could not be erroneously segmented outside of the tissue boundary). To produce collagen distributions along a single direction, binary pixel intensities (0 for non-collagen, 1 for collagen) were summed along two directions to produce a plane-based area fraction; this was measured along each section of the third direction to show planar distributions (i.e., XY plane along Z-direction). A similar technique was employed to provide insight into cell density based on the segmentation of nuclei. Since the imaging technique could only distinguish nuclei and not entire cell volumes, however, it was only able to provide a qualitative sense of cellular distribution within the specimen, and not an accurate quantitative density measurement. As a means to count cells though the volume, the same scaffold fiber tracking technique was employed based on cell nuclei. Since the z resolution was greater than the size of the nuclei, each nucleus appeared in multiple image planes. As such, a more accurate cell count was obtained by using the same algorithm used to track scaffold fibers.

As in the scaffold fiber analysis, the effects of varied 2D sectioning frequency on measured collagen densities were investigated. In all three collagen-containing datasets (native PV, PRI, and POI), the full data set (1 μm spacing) was used as a reference, while spacings of 2 μm, 10 μm, 25 μm, and 50 μm were investigated in all three directions. Stacks of segmented images (either masked or outlined) were assembled into a single TIFF file using ImageJ (NIH, Bethesda, MD, USA). Single files were imported into VOXX (Indiana University Medical Center, Indianapolis, IN, USA), a freeware voxel-based volume rendering program. All computed values were represented as mean ± standard deviation. For the scaffold area fraction analysis, a one way ANOVA test was performed with a Dunn’s test used for pairwise comparisons (due to the failure of equal variance, a non-parametric Kruskal–Wallis ANOVA test on ranks was used to compare groups). Statistical significance was assumed when p < 0.05.

RESULTS

Native PV Collagen and Cell Analyses

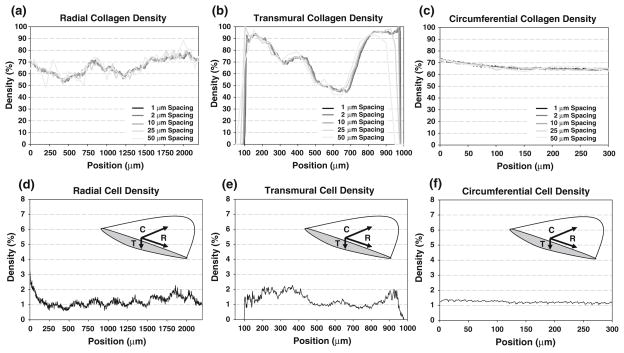
A 3D reconstruction of collagen within the native leaflet (Fig. 1a) and collagen density profiles along each of the three directions (radial, circumferential, and transmural) (Fig. 2a) were created from the image sets. Qualitatively, collagen varied transmurally showing variations from 70 to 90% (ventricularis) down to nearly 40% and back up to 95% (fibrosa); radial variation was 55–80% along the length of the leaflet, with a nearly steady collagen density of 70% along the circumferential direction. Two-dimensional histology (hematoxylin and eosin stain, 4× magnification) of the native PV showed similar qualitative trends (Fig. 1c). A reconstruction (Fig. 1b) displays the cell nuclear material from the full volume with relative density along all three directions (Fig. 2b). Slight variations seen in the transmural direction were evident, while a fairly constant (near 2%) density was seen in the circumferential direction. Additionally, a sub-volume was analyzed using the centroid tracking technique, finding 2363 unique objects throughout a 0.0101 mm³ sub-volume, and yielding a cell density of 2.33 × 10⁵ cells/mm³.

FIGURE 1.

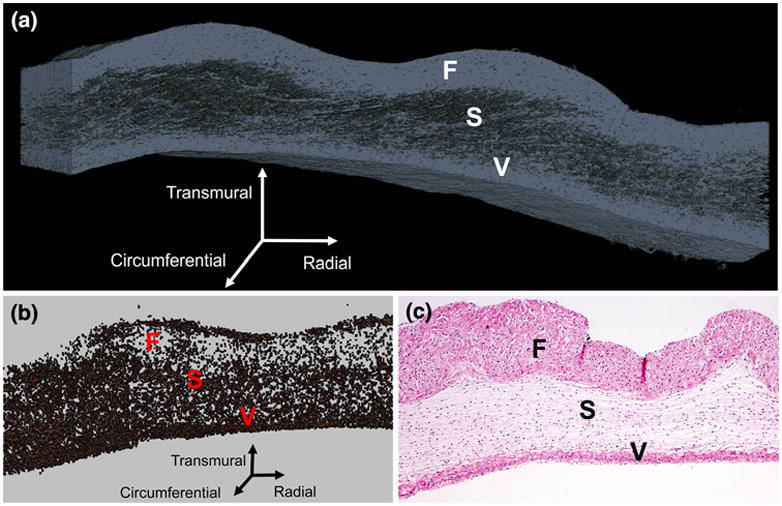
Three-dimensional reconstruction of collagen (a) and cellular material (b) in the native PV (a); traditional two-dimensional Hematoxylin and eosin histology image of the native PV with 4× magnification (c). In all images, the fibrosa (F), spongiosa (S), and ventricularis (V) layers are labeled.

FIGURE 2.

Collagen density distributions along the radial (a), transmural (b), and circumferential (c) directions in native PV with varied sectioning spacing (from 1 to 50 μm), and qualitative cell density distributions (based on cell nuclei measurements) along the radial (d), transmural (e), and circumferential (f) directions in the native PV. Inset image depicts distribution axes along central meridian of leaflet. Note the position-dependent variations in the radial and transmural directions while a relatively uniform distribution in the circumferential direction. In the collagen distributions, limited qualitative change exists can be observed with increased sectioning frequency, especially in the circumferential direction.

Pre-seeded Scaffold Analysis

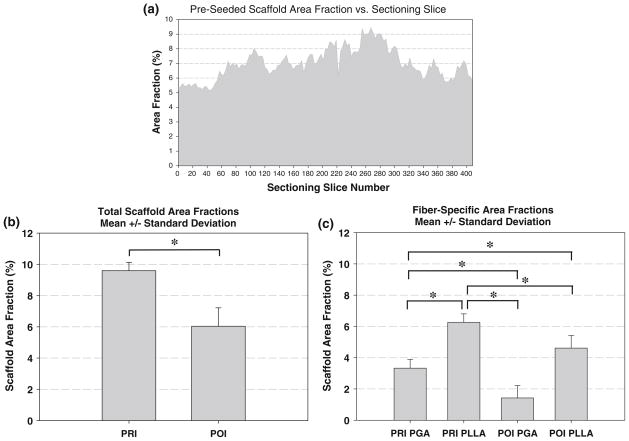
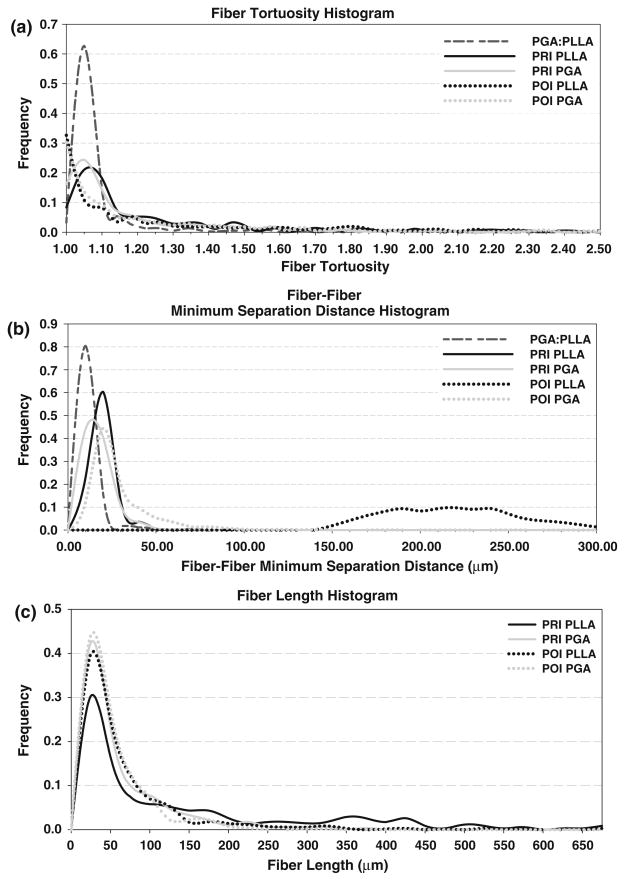
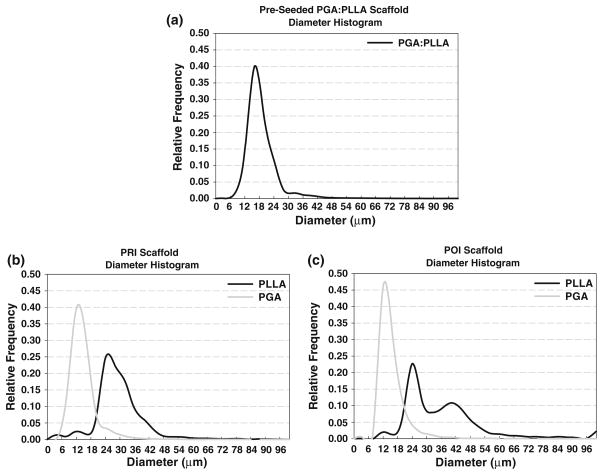
In PGA:PLLA scaffold prior to seeding with cells, a total volume of 731 μm × 989 μm × 410 μm (0.296 mm³) was sampled at a 1 μm/pixel resolution; 450 scaffold fibers were tracked. A two-dimensional imaged section of the pre-seeded scaffold along with typical imaged sections of the PRI and POI is presented alongside histology, with individual scaffold fiber type listed (Fig. 3). The scaffold fiber diameter histogram peaks within the co-polymer aligned closely with separate PGA and PLLA scaffolds (not shown) with PGA having a mean scaffold fiber diameter of 14–18 μm and PLLA having a mean scaffold fiber diameter of 22–24 μm in the individual scaffold. Similar peaks of 14–18 μm (PGA) and 20–24 μm (PLLA) in the co-polymer illustrate the ability of the imaging/analysis technique to distinguish different scaffold fiber types based on morphology. Scaffold fiber area fraction over the imaged area as a function of 2D section was computed and (Fig. 4) showed some variability throughout the volume, with a range from 5.17 to 9.43% and with a mean ± standard deviation area fraction of 7.02 ± 1.02%. A histogram of scaffold fiber tortuosity (Fig. 5) revealed a substantial frequency peak at 1.05, with nearly all scaffold fibers having a tortuosity less than 1.20. Minimum scaffold fiber separation (Fig. 5) showed a distinct peak at 10 μm with nearly all scaffold fibers within a 0–20 μm separation of one another. A length histogram was not produced for this data set because the analyzed volume compared to the fiber length was not large enough to prevent a relatively homogenous length distribution resulting from an artificial weighting (toward lower lengths) of length from the cross-preferred and out-of-plane fibers. Further, the 3D reconstructions illustrated the highly contiguous nature of the fibers.

FIGURE 3.

EV-SLCM imaging of pre-seeded scaffold (a) and PRI (b); hematoxylin and eosin staining of PRI time point specimen showing distinct PLLA and PGA scaffold fibers (c), and EV-SLCM imaging of POI (d). Note the tissue contraction around the PLLA in Fig. 3c, while the PGA shows intimate contact with the surrounding tissue. A similar histological image of a POI time point specimen was used to obtain corrected PLLA diameters for area fraction calculations.

FIGURE 4.

Pre-seeded scaffold area fraction as a function of 2D milling slice (a), total (PGA and PLLA combined) mean ± standard deviation scaffold area fraction for PRI and POI groups (b), and scaffold fiber type-specific mean ± standard deviation scaffold area fractions for PRI (PGA, PLLA) and POI (PGA, PLLA) (c) groups. Note that the asterisks indicate statistically significant differences between groups (p <0.05).

FIGURE 5.

Scaffold fiber histograms for pre-seeded PGA:PLLA, PRI, and POI specimens of tortuosity (a), scaffold fiber–fiber minimum separation distance (b), and length (c). It was possible to distinguish PLLA from PGA in the PRI and POI specimens. Note the broadening of the histogram peaks from pre-seeded to PRI to POI as well as the shift toward the 1.00 bins in tortuosity. With regard to scaffold fiber–fiber separation distance, the scaffold fibers increased distance at later time points (PRI and POI), with POI PLLA showing the largest (and broadest) separation distance peak. In the length histogram, both scaffold fiber populations show higher peaks toward the lower end of the size scale as well as less broad distributions in the POI compared to the PRI.

A reconstruction of the tracked scaffold fibers and a spherical histogram were created (Fig. 6) showing a strong preferred orientation (red arrow) in the spherical histogram and a noticeable secondary orientation (yellow arrow) orthogonal to the preferred orientation. Qualitatively, this was seen in the scaffold fiber reconstruction. Eigenvalues and associated eigenvectors for the pre-seeded fabric tensor (Table 1) corroborated the strong-preferred and cross-preferred directions within the scaffold.

FIGURE 6.

3D reconstructions of (a) pre-seeded PGA:PLLA, PRI (c) PGA and (d) PLLA, and POI (f) PGA and (g) PLLA; spherical histograms of scaffold fiber orientations in the (b) pre-seeded PGA:PLLA, (e) PRI, and (h) POI. (a). Fragmentation, especially in the PGA, is evident in the reconstructions. In addition, the spherical histogram shows increased isotropy compared to the pre-seeded scaffold histogram.

TABLE 1.

Eigenvalues and the respective eigenvectors for the pre-seeded PGA:PLLA scaffold as a function of increased sectioning spacing.

Virgin Spacing		Eigenvectors			Eigenvalues	α13	α12	α23
		X	Y	Z
3 μm	e1	−0.1574	−0.0048	0.9875	0.5310	0.6998	0.4170	0.4851
	e2	0.9875	−0.0094	0.1573	0.3096
	e3	−0.0085	−0.9999	−0.0062	0.1594
5 μm	e1	−0.1548	−0.0669	0.9857	0.5204	0.7307	0.3477	0.5872
	e2	0.9879	−0.0185	0.1539	0.3394
	e3	−0.0080	−0.9976	−0.0690	0.1401
10 μm	e1	−0.4274	−0.0450	0.9030	0.4688	0.6493	0.2176	0.5518
	e2	0.9035	0.0137	0.4283	0.3668
	e3	0.0316	−0.9989	−0.0348	0.1644
25 μm	e1	−0.9274	−0.0177	0.3737	0.4665	0.6617	0.1945	0.5799
	e2	−0.3673	−0.1475	−0.9183	0.3757
	e3	−0.0714	0.9889	−0.1303	0.1578
50 μm	e1	−0.1172	−0.1967	−0.9734	0.4546	0.7052	0.0953	0.6741
	e2	0.9929	−0.0031	−0.1189	0.4113
	e3	0.0204	−0.9805	0.1957	0.1340

As the sectioning spacing increases, the anisotropy present in the full-resolution data set is lost. With this, a sectioning spacing up to 10 μm can be tolerated without disrupting the measured scaffold orientation.

Pre-implant and Post-implant Scaffold Analyses

In the PRI and POI specimens, volumes of 731 μm × 989 μm × 339 μm (0.245 mm³) and 731 μm × 989 μm × 304 μm (0.220 mm³), respectively, were acquired and analyzed in individual specimens. Qualitatively, specimens showed minimum variation with respect to constituents of interest at different locations with the same specimen and among different specimens. In the full volumes, a total of 1853 PGA scaffold fibers and 464 PLLA scaffold fibers were identified and tracked in the PRI, and a total of 1673 PGA scaffold fibers and 2257 PLLA scaffold fibers were identified and tracked in the POI. Length histograms (Fig. 5) for both scaffold fiber populations showed a trend toward smaller fibers (both PGA and PLLA) from PRI to POI specimens: PGA and PLLA fibers initially (PRI) demonstrated broad distributions (0–200 μm) and moved to tighter distributions (0–150 μm) in the PRI specimen. Tortuosity showed similar trends between the two groups (Fig. 5). PGA and PLLA peaks were both shifted (towards 1.00) and of greater magnitude (increased frequency) in the POI tissue compared to the PRI tissue, suggesting overall straighter fibers in the POI. Minimum scaffold fiber separation histograms were generated for both PRI and POI tissues (Fig. 6), providing a sense of collagen infiltration between scaffold fibers. In the histogram, it can be seen that PLLA had a peak at 20 μm while PGA had a frequency peak at 10 μm for the PRI tissue; both distributions were broader than the pre-seeded scaffold fiber histogram peak. In the POI tissue, PGA had a peak at 20 μm, and PLLA had an exceptionally broad distribution peak between 190 μm and 240 μm.

To verify unique identification of both scaffold fiber populations and to quantify potential bulk erosion, scaffold fiber diameter was investigated. Histograms (Fig. 7) demonstrated a distinct peak at 12–14 μm for PGA and a broader peak at 28–32 μm for PLLA in the PRI tissue, suggesting unique identification of both scaffold fiber types. In the POI specimen, a distinct peak was seen at 12 μm for PGA and double peaks were seen at 24 μm and 40 μm for the PLLA. Since, as described above, preliminary histology revealed tissue shrinkage around PLLA scaffold fibers, it was necessary to estimate scaffold fiber diameter at both PRI and POI time points to more accurately reflect tissue shrinkage in the scaffold area fraction; the broader diameter histogram peaks and double peak in the POI confirmed shrinkage. It was found that PLLA had a mean ± standard deviation scaffold fiber diameter of 28.4 μm ± 3.40 μm at the PRI time point (16 scaffold fibers) and a mean ± standard deviation scaffold fiber diameter of 30.3 μm ± 3.84 μm at the POI time point (15 scaffold fibers). With this information, the discrepancies in the diameter histogram for PLLA could be corrected, yielding mean ± standard deviation area fractions of 3.33 ± 0.56% (PGA), 6.26 ± 0.54% (PLLA), and 9.59 ± 0.54% (PGA:PLLA) in the PRI and mean area fractions of 1.42 ± 0.79% (PGA), 4.61 ± 0.79% (PLLA), and 6.03 ± 1.18% (PGA: PLLA) in the POI. In all cases, mean area fractions were significantly different from one another.

FIGURE 7.

Scaffold fiber diameter histograms for pre-seeded PGA:PLLA scaffold (a), PRI (b), and POI (c) specimens. At both PRI and POI time points, PGA diameters remain fairly constant while PLLA diameter peaks broaden. This is most likely the result of tissue contraction around PLLA and resultant erroneous segmentation; this is especially evident with the double peak in the POI specimen.

In the reconstructions of both the PGA and PLLA scaffold fibers in the PRI (Fig. 6), partial fragmentation was seen in the PGA scaffold fibers but was slightly masked in the PLLA scaffold fiber reconstruction due to tissue shrinkage around the scaffold fibers. In both scaffold fiber populations, however, the spherical histogram revealed preferred (red arrow) and cross-preferred (yellow arrow) scaffold fiber orientations, though the lower population densities surrounding the directional arrows suggest less distinct orientations than in the pre-seeded specimen. The eigenvalues and respective eigenvectors for both scaffold fiber populations showed similar results (Table 2). Decreased anisotropy was seen in the POI spherical histogram (Fig. 6) as the distribution of scaffold fiber orientations became more random. Eigenvalues and respective eigenvectors for both scaffold fiber populations in the POI specimen reinforced the observations (Table 3). In addition, significant fragmentation was seen in the reconstructions.

TABLE 2.

Eigenvalues and the respective eigenvectors for PRI specimen scaffold as a function of increased sectioning spacing.

PRI Spacing		Eigenvectors			Eigenvalues	α13	α12	α23
		X	Y	Z
3 μm	e1	0.2378	0.1048	0.9656	0.4439	0.5160	0.2310	0.3706
	e2	−0.9711	0.0028	0.2389	0.3413
	e3	−0.0224	0.9945	−0.1025	0.2148
5 μm	e1	0.4123	0.1144	0.9038	0.4339	0.4855	0.2096	0.3490
	e2	0.9094	0.0074	−0.4158	0.3429
	e3	0.0543	−0.9934	0.1010	0.2232
10 μm	e1	0.6604	0.0864	0.7459	0.4352	0.4833	0.2192	0.3382
	e2	0.7462	0.0362	−0.6648	0.3399
	e3	0.0845	−0.9956	0.0406	0.2249
25 μm	e1	0.6047	0.0981	0.7904	0.4628	0.5762	0.2632	0.4249
	e2	0.7942	0.0006	−0.6076	0.3410
	e3	0.0601	−0.9952	0.0776	0.1961
50 μm	e1	0.4212	0.1161	0.8995	0.5820	0.7920	0.4899	0.5922
	e2	0.9069	−0.0679	−0.4159	0.2969
	e3	−0.0128	−0.9909	0.1339	0.1211

As the sectioning spacing increases, the slight anisotropy present in the full-resolution data set showed an increase, showing the greatest difference at 50 μm. Therefore, a sectioning spacing of 25 μm is recommended to preserve the scaffold orientation.

TABLE 3.

Eigenvalues and the respective eigenvectors for POI specimen scaffold as a function of increased sectioning spacing.

POI Spacing		Eigenvectors			Eigenvalues	α13	α12	α23
		X	Y	Z
3 μm	e1	−0.9929	0.1181	0.0111	0.3927	0.3353	0.1182	0.2462
	e2	−0.0481	−0.4871	0.8720	0.3463
	e3	0.1084	0.8653	0.4894	0.2610
5 μm	e1	−0.9898	0.1340	−0.0488	0.4638	0.5470	0.2969	0.3558
	e2	−0.1262	−0.6640	0.7370	0.3261
	e3	0.0663	0.7356	0.6741	0.2101
10 μm	e1	−0.9959	0.0791	−0.0448	0.5366	0.6599	0.4765	0.3503
	e2	0.0891	0.7492	−0.6563	0.2809
	e3	0.0183	0.6576	0.7531	0.1825
25 μm	e1	0.9629	−0.0927	−0.2536	0.5218	0.7508	0.3327	0.6265
	e2	0.1576	−0.5694	0.8068	0.3482
	e3	−0.2192	−0.8168	−0.5337	0.1300
50 μm	e1	0.6505	−0.4190	0.6335	1.0000	1.0000	1.0000	—
	e2	0.7595	0.3519	−0.5471	0.0000
	e3	0.0063	0.8370	0.5471	0.0000

As the sectioning spacing increases, the relative isotropy present in the full-resolution data set changes to a more anisotropic form until the sectioning spacing was unable to provide sufficient scaffold fiber information to perform the fabric tensor analysis. In the POI specimens, it may be sufficient to measure volume fraction since the orientation is isotropic even in the full-resolution data set.

Pre-implant and Post-implant Collagen and Cell Analysis

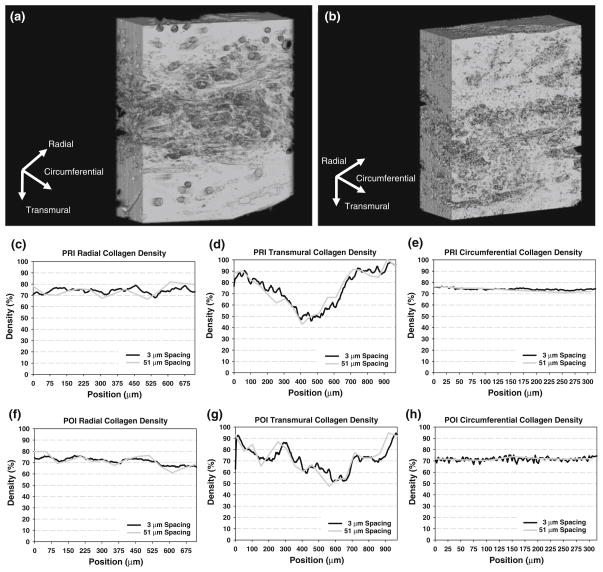
In the PRI and POI tissues (Fig. 8), collagen was segmented from the tissues, and 3D reconstructions were created. In the PRI, density profiles along each of the three directions (same as in the native PV) were generated. As in the native PV, collagen showed substantial qualitative variability with position in the transmural direction, ranging from 46.0% (central region) to 97.7% (edge regions) and much less variability in the radial (67.8–79.0%) and the circumferential (72.7–76.3%) directions. In the POI tissue, collagen density profiles in each of the three directions showed similar variability to the PRI tissue in the radial direction (65.9–76.1%) and slightly more variability in the circumferential direction (66.9–75.2%); in the transmural direction, collagen density varied from 51.2% (central regions) to 94.6% (edge regions), similar to that in the PRI tissue. Cell nuclei were not able to be segmented from the image data in the PRI and POI tissue due to the strong fluorescence of collagen and scaffold.

FIGURE 8.

3D reconstruction of collagen in PRI (a) and POI (b); PRI collagen density distributions along the radial (c), transmural (d), and circumferential (e) directions for both 3 μm and 51 μm sectioning spacings. POI collagen density distributions are shown along the radial (f), transmural (g), and circumferential (h) directions for both 3 μm and 51 μm sectioning spacings. As in the native PV, note the position-dependent variations in the radial and transmural directions while a relatively uniform distribution in the circumferential direction even in increased sectioning spacing. Most notably in the transmural direction, a more homogenous collagen distribution is seen in the POI over the PRI.

Sectioning Frequency Analysis

Though difficult to quantify specific changes, qualitatively, it was seen that the various layer-specific collagen features evident in the transmural direction of the full data set were preserved through the different sectioning frequencies; minor position-specific collagen densities were also preserved though increased sectioning frequency in the radial direction (Fig. 2). In the circumferential direction, the mean ± standard deviation of collagen was found to be 65.9 ± 2.25% (full), 65.9 ± 2.27% (2 μm spacing), 65.9 ± 2.42% (10 μm spacing), 66.1 ± 2.97% (25 μm spacing), and 66.5 ± 3.33% (50 μm spacing), indicating little change as a result of sectioning spacing differences.

As in the native PV, the PRI and POI tissues demonstrated preservation of similar features in both the radial and transmural directions (Fig. 8). For the PRI in the circumferential direction, little change was seen in collagen density, with values of 74.2 ± 0.84% (full 3 μm spacing), 74.1 ± 0.83% (6 μm spacing), 74.2 ± 0.91% (9 μm spacing), 73.9 ± 1.54% (24 μm spacing), and 73.5 ± 1.95% (51 μm spacing). In the POI circumferential direction, mean ± standard deviation was nearly constant throughout the sectioning frequency study, with values of 71.8 ± 1.95% (full 3 μm spacing), 71.9 ± 1.78% (6 μm spacing), 71.9 ± 1.88% (9 μm spacing), 71.5 ± 2.21% (24 μm spacing), and 71.8 ± 1.07% (51 μm spacing).

The effects of sectioning frequency on the fabric tensor eigenvalues were investigated (Tables 1, 2, 3). In the pre-seeded full data set, α₁₃ increased from 0.6998 to 0.7307 when sectioning spacing changed from 3 μm to 5 μm but showed a decrease to 0.7052 up to 50 μm spacing. In a different manner, α₁₂ decreased with increased sectioning spacing from 0.4170 (3 μm) to 0.0953 (50 μm); α₂₃ showed an increase with increased sectioning spacing from 0.4851 (3 μm) to 0.6741 (50 μm). In the PRI tissue, the scaffold trended differently than the pre-seeded specimen. It was observed that α₁₃ steadily increased from 0.5160 (3 μm) to 0.7920 (50 μm), α₁₂ remained near 0.2310 (3 μm) for increased sectioning spacing until it jumped to 0.4899 at 50 μm, and α₂₃ showed an initial decrease from 0.3706 (3 μm) until 25 μm, where it increased to 0.4249 and ultimately reached 0.5922 at 50 μm (Table 2). Finally, the POI tissue showed more pronounced changes with increased sectioning spacing. A substantial increase of α₁₃ from 0.3353 (3 μm) to 0.7508 (25 μm) was seen (Table 3) before the analysis algorithm was unable to compute unique eigenvectors in e₂ and e₃ at 50 μm section spacing. Both α₁₂ and α₂₃ ultimately increased from 0.1182 and 0.2462, respectively (3 μm) to 0.3327 and 0.6265, respectively, before approaching indeterminate values at 50 μm section spacing.

DISCUSSION

Overview

A novel imaging methodology and custom morphological software were utilized to obtain high-resolution 3D structural information of EHVT over a large volume. To date, this study represents the most comprehensive large-volume high-resolution structural information of EHVT and is the first known study using long-term in vivo specimens. It is the intent that this structural information serves as the basis for a new structural constitutive model of EHVT better formulated to investigate the mechanical properties of the forming and remodeling tissue phase.

Scaffold Fiber Architecture

Several important changes in PGA:PLLA non-woven scaffold were revealed in this study. Importantly, scaffold fibers remained as two morphologically identifiable populations through the PRI and POI specimens, permitting quantification of properties of both the scaffold co-polymer as a whole and individual scaffold fiber types. In the pre-seeded PGA:PLLA scaffold, a continuous scaffold fiber network was clearly evident. The highly skewed and sharply peaked tortuosity histogram indicates these scaffold fibers are fairly straight with a substantial peak at 1.05, corroborating our previously published values of 1.05–1.10.⁷ Throughout the tissue volume, scaffold area fractions ranged from 5 to 9%, with a total volume fraction of 7.02%. From the scaffold fiber–fiber separation distance histogram, scaffold fibers are at a minimum within a typical scaffold fiber diameter of each other (peak at 25 μm). Finally, both preferred and cross-preferred orientations exist as previous study confirms.⁷

This study suggests substantial scaffold fiber architectural changes as a function of longer-term implant time. Both scaffold fiber populations show a shift toward lower scaffold fiber lengths which can be explained by scaffold fiber fragmentation through both hydrolysis and, in later in vivo time points, macrophage enzymatic degradation processes.⁸ With scaffold volume fractions changing from 9.59% (PRI) to 6.03% (POI), scaffold mass is lost over the implant time. In addition, specific volume fractions of PGA and PLLA scaffold fibers in the POI indicate a similar degradation of both populations (the difference between PRI and POI scaffold fiber volume fractions was similar for both scaffold fiber types). It is interesting to note that despite differences in degradation times (PGA is faster than PLLA²⁶) both populations remain discernable at the POI time point. Potentially, scaffold fibers could be protected from increased degradation by ECM encapsulation, though further experimentation would be required to prove this hypothesis. Though previous in vitro studies have indicated that PGA degrades rapidly during culturing,^20,21 this study suggests that PGA behaves differently in the presence of PLLA or in an in vivo environment and suggests that both scaffold types should be considered in future modeling efforts of in vivo tissues.

The scaffold fibers undergo a substantial transformation from a slightly tortuous, continuous network (pre-seeded) to a straight, shorter (semi-continuous) network (PRI), ultimately transforming to an exceptionally straight, short fiber scaffold-tissue composite (POI), as indicated by the shifts in the tortuosity histograms observed with POI scaffold fibers having strong peaks near 1.00 and PRI scaffold fibers having tighter distributions at 1.00 and 1.05. Interestingly, the increase in PRI and POI scaffold fiber–fiber separation distances in PGA and PLLA compared to pre-seeded scaffold and the additional increase in scaffold fiber–fiber separation distance between PRI and POI indicates that the scaffold fibers have the potential to interact more independently of one another. Of particular note is the substantially larger minimum separation distance in the POI PLLA scaffold fibers; initially being separated by only 10 μm, PLLA takes on a broader separation distribution in the PRI time point with a peak at 20 μm and further separates by nearly an order of magnitude. PGA, however, seems to remain fairly compact, beginning at 10 μm (pre-seeded) and showing a broadened peak at 10 μm (PRI) and a further-broadened peak at 20 μm (POI) extending up to 50 μm. As shown by Engelmayr and Sacks,⁷ the interbond distance has a profound impact on the overall mechanical properties, exhibiting a nonlinear increase in effective stiffness with reduced interbond distance. This study suggests that the interbond distance remains fairly consistent for PGA from pre-seeded to PRI, with only a slight increase in the POI, while PLLA shows a slight increase from the pre-seeded state to PRI, but with a substantial increase in the POI. Therefore, the interbond distance’s effect on the effective stiffness may remain relevant for both scaffold phases in the PRI specimen but only relevant for PGA in the POI specimen.

The qualitative changes in the scaffold fiber orientation histograms from an aligned network with defined preferred and cross-preferred directions (pre-seeded) to a more isotropic distribution (PRI and POI) implies that the fragmentation, increased scaffold fiber separation, and degradation sufficiently disrupt the original scaffold network to greatly change scaffold fiber alignment. In all, it is apparent that the scaffold undergoes substantial changes from its initial state through the in vitro phase and further changes after implantation.

Collagen and Cell Content

As the major tissue structural component of EHVT, collagen in forming tissues dictates the success of the overall implant. As shown by Engelmayr,⁸ knowledge of collagen densities and distributions is foundational to appropriately modeling such tissue composites, notably when these distributions are heterogeneous and position-dependent. In the native PV, the layer-specific differences known to exist in these valves were illustrated using EV-SLCM and the developed analysis techniques.²⁷ Further, a mean collagen area fraction of 65.9% was found, corroborating well with previously published data on valve collagen content.² Cells were tracked and counted for the native PV; over the analyzed sub-volume, 2363 cells were identified, yielding a cell density of 2.33 × 10⁵ cells/mm³ and corroborating with previously published data.⁶ Distributions of cell nuclei (qualitative assessment of cell density) varied slightly in the transmural and radial directions though remained constant in the circumferential direction. This intuitively makes sense with the collagen distribution, as layer-specific collagen content could be impacted by matching layer-specific cellular distributions. Published data on layer-specific valvular interstitial cell densities qualitatively reflect our findings of transmural cellular densities, with the fibrosa and ventricularis layers showing larger (two to three times larger) cellular densities than the spongiosa layer.¹¹

In both of the PRI and POI tissues, the mean collagen density in the circumferential direction (least section-to-section variability) was larger than in the native PV (65.9%), with PRI (74.2%) slightly larger than POI (71.5%). Qualitatively, this pattern follows that which was previously observed by Hoerstrup et al.¹³ where EHVT in vitro tissue showed an increase in collagen content over native valve collagen content and a decrease after in vivo implantation for an extended period of time. One possible reason for the difference between native PV and the EHVT is the presence of non-staining constituents in the native PV such as elastin and glycosaminoglycans (GAGs). It is well known that native valvular tissue contains these constituents in addition to collagen, and though studies have shown the ability to produce such constituents in EHVT,¹³ densities may be lower than in native PV. Despite their potential presence in the EHVT, it may be at lesser amounts compared to the native PV. It is interesting to note that the POI scaffold phase decreased compared to the PRI scaffold phase, though collagen density showed a decrease between the groups. A plausible explanation could be that as the POI tissue experienced physiological forces compared to the PRI tissue, mechanical stimulation could have influenced the difference in constituent density, though further histological studies specifically investigating elastin and GAGs could help support this. Finally, we noted that variations between PRI and POI tissue collagen density distributions are evident. In the PRI tissue, collagen density varied from 46.0 to 97.7%, while the POI tissue varied from 51.2 to 94.6%. This implies that collagen may move toward a more homogenous distribution with extended in vivo physiological conditions (as opposed to short in vitro static conditions as in the PRI tissue). Previously, Engelmayr and Sacks⁸ highlighted the importance of flexural mechanical stimulation on forming more homogenous transmural collagen distributions, which are consistent with the current results.

Sectioning Frequency

Though the EV-SLCM technique provides novel high-resolution 3D structural information, its wide-spread use is not practical due to the large acquisition time for even a reasonably sized volume. Sands et al.²⁴ have previously estimated the acquisition time of a 3 mm³ volume to be nearly an entire 24-h period. It is possible, however, to use the full-resolution information to determine the minimum sectioning frequency necessary to obtain salient structural information. In this study, the effects of sectioning frequency on scaffold fiber orientation (through the fabric tensor) and on collagen distribution were investigated by varying the number of 2D image planes used in the analyses. In the scaffold fiber analysis, the anisotropy index was introduced as a means to evaluate changes in computed scaffold fiber orientation. Since each of the full-resolution data sets (pre-seeded, PRI, and POI) showed distinct specific scaffold fiber orientations (ranging from highly anisotropic to isotropic), the point at which sectioning frequency began to significantly alter scaffold fiber orientation could represent the minimum sectioning frequency for that particular tissue.

In the pre-seeded specimen, a preferred orientation existed up to 50 μm section spacing, though the distinction between directions began to disappear by 10 μm section spacing. Though at first glance this appears detrimental to future structural-based modeling efforts, the PRI tissue shows much less change as a function of sectioning spacing: in these tissues, a preferred direction exists (though not as strongly in the pre-seeded specimen) while a cross-preferred direction is not as evident, but even up to 25 μm section spacing, this structural configuration remains. At 50 μm section spacing, this appears to break down as increased anisotropy is introduced in the scaffold fiber population.

In the POI specimen, increased section spacing introduces more anisotropy to an initially fairly isotropic system. At the initial section spacing of 3 μm, all three anisotropy indices are small and similar to one another indicating an isotropic orientation. By 10 μm section spacing, the indices of two directions increases, implying a false anisotropy. A potential cause is the limited scaffold fiber length; sectioning the volume at spacings larger than the scaffold fiber length itself could prevent inaccurate computations of the fabric tensor. At 50 μm, this is evident as only one unique eigenvalue could be computed. One potential solution involves sectioning with the majority of scaffold fibers parallel to the sectioning plane, though this may decrease the number of scaffold fibers that can be captured in a single section. A better solution may involve using the full-resolution information to guide structural assumptions; since scaffold at the POI time point exist as randomly distributed, short, straight scaffold fibers, efforts to utilize the structural information can be greatly simplified. The structural information necessary for PRI time point tissues may not be relevant at this later time point, suggesting that only basic volume fraction information may be sufficient.

In the native PV, the tissue circumferential direction provided the least variation in collagen density on a section-by-section basis. By keeping the radial and transmural directions in plane with respect to the sections, the greatest amount of position-specific collagen density information could be preserved. A mean collagen area fraction of 65.9% was computed for the full data set (1 μm spacing). Increasing sectioning spacing up to 25 μm had only a 0.2% change in mean collagen area fraction; increasing sectioning spacing to 50 μm resulting in a 0.6% difference. By maintaining full-resolution sections in plane with the radial and transmural directions, the collagen distribution could be maintained with minor variations in overall collagen content up to 50 μm of sectioning spacing (in the circumferential direction).

Important for future EHVT structural analyses, the variability in the circumferential direction in both PRI and POI tissues varied little with sectioning frequency, as in the native PV. Mean collagen densities of 74.2% (PRI) and 71.8% (POI) changed to 73.9% (PRI) and 71.5% (POI) at 24 μm sectioning spacing and to 73.5% (PRI) and 71.8% (POI) at 51 μm sectioning spacing. It is evident that even at 51 μm sectioning spacing both data sets showed minimal variation in mean collagen densities compared to respective full-resolution data sets. Though the features in the other two directions (notably the transmural direction) showed distinct position-specific variability in collagen density, increasing sectioning frequency had minimal impact on the overall qualitative density distributions. Sectioning in the circumferential direction will provide sufficiently similar collagen density profiles up to 50 μm and should be used for future structural studies.

Implications for Modeling ECM Formation

In order to evaluate the mechanical quality of formed tissue, it is essential to predict the ECM phase mechanical properties from the overall composite response. Previous modeling efforts in our laboratory have resulted in a descriptive mechanical model for intact needle non-woven (NNW) scaffolds that predicted pre-seeded scaffold stiffness.⁷ When applied to tissue-scaffold composites using the rule of mixtures, however, the model was not able to account for the observed large increases in stiffness; composite stiffness values were much lower than what the model predicted. As a result, a new model was proposed based on a measured collagen distribution and a scaffold-ECM coupling factor.⁸ Though sufficient as first effort, the meso-scale composite model relies heavily on an empirically determined coupling factor. In addition, these models assume static scaffold conditions, i.e., scaffold fibers that morphologically remain the same throughout tissue accretion and subsequent remodeling. This study indicated that the scaffold undergoes substantial modification, primarily by fragmentation and orientation changes, throughout in vitro and in vivo phases. Specifically, scaffold fibers that initially formed a fairly compact and continuous network in a preferred orientation showed substantial degradation and take on a more isotropic, discontinuous, and spread architecture. Interestingly, both PLLA and PGA remained in the PRI and POI specimens. Further, in comparing the in vitro and in vivo phases, it appears that collagen becomes more homogenously distributed throughout the volume after implantation. These morphological changes must be considered in the next-generation modeling efforts to more accurately estimate the mechanical properties of forming and remodeling EHVT.

Further Applications

The imaging technique presented in this study is an extension of previous study conducted at the University of Auckland.^23,24 Of particular interest is the means to utilize the acquired high-resolution 3D information and quantitatively analyze to yield particular morphological metrics of interest. Such imaging and analysis techniques have value both latitudinally within EHVT efforts and longitudinally within general tissue morphological studies. These techniques could be applied to any collagenous tissue where relative distributions are of interest. Similarly, the techniques presented could be used to quantify scaffold structures at a variety of different states (i.e., non-seeded, in vitro culturing, etc.).

Limitations

Overall, use of the EV-SLCM system eliminated many of the errors introduced by traditional imaging techniques, and its use for engineered tissue scaffolds has not been previously published. Therefore, the lack of prior published data may bring into question the validity of the experimental results. We feel, however, that the close corroboration of morphological parameters (tortuosity, volume fraction, and diameter) determined from this study to those parameters previously published using alternative techniques strengthens our results. In addition, the use of isolated pre-seeded PGA and pre-seeded PLLA shows the ability of our techniques to distinguish both scaffold fiber populations. Histological support for correct scaffold fiber identification has been essential to this study and helps confirm our segmentation techniques for the PRI and POI specimens.

In addition, it should be noted that this study was intended to provide information on ECM formation in the bulk sense. As a result, quantifying individual collagen fibers and cells were not part of the study design. However, with the completion of this current study, important experimental details such as imaging resolution and staining protocol have been established to permit the future quantification of these metrics. Moreover, future studies into quantifying individual collagen fibers and cellular densities are been planned.

The inability of the automated segmentation techniques to consistently identify PLLA boundaries from the voids created through tissue shrinkage also introduced some error, though we feel this error relates primarily to scaffold fiber diameter and resultant area fraction computations rather than centroid measurement and resultant length, tortuosity, and orientation. We feel that the correlation of average PLLA scaffold fiber diameter measured from histology to that of the segmented PLLA scaffold fiber diameter provided an adequate means to correct tissue shrinkage-effects on segmentation. Finally, due to the time intensive nature of the technique we were only able to study a limited number of specimens. However, conventional histological images¹⁰ (e.g., Fig. 3) supported a good degree of consistency in the POI specimens, so that the current results should be representative.

Summary

This study provides novel insight into the time evolution of 3D structure of EHVT at the in vitro and in vivo phases and will help guide the development of improved constitutive models to estimate the tissue mechanical response from the tissue-scaffold composite EHVT. It is evident that both the scaffold fiber phase and the collagen phase of the tissue-scaffold composites undergo substantial structural changes from a preseeded scaffold state to a post-explant state. Specifically, the scaffold fibers changed from a slightly tortuous, fairly continuous, and oriented population (PRI) to a straight, short, randomly oriented population (POI) with PGA and PLLA scaffold fiber populations both existing in the PRI and POI specimens. The collagen density was observed to approach a slightly more homogenous transmural distribution in the POI compared to the PRI. In addition, it was shown that future 2D histological studies would benefit most from transmural sectioning with spacings no greater than 25 μm for scaffold morphology and 50 μm for collagen density in EHVT.

APPENDIX A: SCAFFOLD FIBER ORIENTATION TENSOR ANALYSIS

For the orientation tensor formulation, each vector p was normalized and converted to a spherical coordinate system based on

$$p_1=sin\theta cos\varphi ,$$ (A.1)

$$p_2=sin\theta cos\varphi ,$$ (A.2)

and

$$p_3=cos\theta ,$$ (A.3)

with θ and ϕ defined as zenith angle and azimuth angle, respectively. Since both scaffold fiber ends were not distinguishable from one another, p = −p, which limited the angles θ from $-\frac{\theta }{2}$ to $\frac{\theta }{2}$ and ϕ from $-\frac{\varphi }{2}$ to $\frac{\varphi }{2}$. A general description of the orientation state was determined by using a probability distribution function Ψ(p), done by taking the dyadic products of the vector p and integrating over the range of θ and ϕ and weighting the product by Ψ(p) where the probability of finding a scaffold fiber between θ₁ and θ₁ + dθ and ϕ₁ and ϕ₁ + dϕ was given by

$$P({\theta }_1\le \theta \le {\theta }_1+\text{d}\theta ,{\varphi }_1\le \varphi \le {\varphi }_1+\text{d}\varphi )=\mathrm{\Psi }({\theta }_1,{\varphi }_1)sin{\theta }_1\text{d}\theta \text{d}\varphi .$$ (A.4)

Restrictions placed on this function limited the integration over orientation space to unity and force the function to be an even function; however, it was not practical to compute the distribution function, and so another approach was taken. In this approach, an orientation tensor was created by forming dyadic products of the vector p and integrating it over all directions and weighting the product with the distribution function and scaffold fiber length. This created a second order tensor as

$${\mathbf{A}}_{ij}=\frac{\underset{L}{\int }\underset{p}{\int }{p}_i{p}_{j}L\mathrm{\Psi }(p,L)\text{d}p\text{d}L}{\underset{L}{\int }\underset{p}{\int }L\mathrm{\Psi }(p,L)\text{d}p\text{d}L}.$$ (A.5)

In a discrete system, the tensor components were calculated using a summation instead of integration

$${\mathbf{A}}_{ij}=\frac{\sum (p_i{p}_j)L_{n}F({\theta }_n)}{\sum L_{n}F({\theta }_n)}.$$ (A.6)

To account for the increased probability of scaffold fibers oriented normal to the sectioning plane intercepting the plane rather than scaffold fibers oriented parallel to the plane, a weighting function F(θ_n) was introduced⁵,¹⁵,¹⁸ as

$$F({\theta }_n)=\frac{1}{Lcos({\theta }_n)+dsin\mid {\theta }_n\mid }.$$ (A.7)

In this form, d was defined as the scaffold fiber diameter.

The eigensolutions (eigenvectors and associated eigenvalues) have physical significance in this analysis: the eigenvectors provide the three principal directions of the overall scaffold fiber orientation with the eigenvalues providing the relative weight each direction has in the overall scaffold fiber orientation. Hence, a purely isotropic orientation would have eigenvectors of [1,0,0], [0,1,0], and [0,0,1] and eigenvalues of λ₁ = λ₂ = λ₃ = 1/3 while a transverse isotropic orientation would have eigenvectors of [1,0,0], [0,1,0], and [0,0,1] and eigenvalues of λ₁ = λ₂ = 1/2 and λ₃ = 0.